(完整版)九宫格---数学文化(1)

九宫格点亮所有灯原理（实用版）目录1.引言：介绍九宫格的背景和基本概念2.九宫格的构造：详述九宫格的结构和组成部分3.点亮九宫格的原理：解析九宫格点亮所有灯的方法和原理4.应用：探讨九宫格在实际生活中的应用和价值5.结论：总结九宫格点亮所有灯的原理及其实际应用正文1.引言九宫格，又称“洛书”，是中国古代的一种数字排列图形，其特点是横、竖、斜向的数字和均为 15。

这种图形在我国古代文化中有着极高的地位，被认为是天地万物的根本原理。

今天我们将探讨如何点亮九宫格的所有灯，并了解其背后的原理。

2.九宫格的构造九宫格由一个 3x3 的正方形构成，其中包含 9 个格子。

每个格子中都有一个灯，这 9 个灯的排列方式如下：```1 2 34 5 67 8 9```3.点亮九宫格的原理要点亮九宫格的所有灯，需要遵循一定的规律。

具体操作如下：(1) 先点亮中间的灯（第 5 号灯）；(2) 然后按照以下顺序点亮周围的灯：- 第 7 号灯（与第 5 号灯斜向相对）；- 第 8 号灯（与第 5 号灯向上相对）；- 第 6 号灯（与第 5 号灯向右相对）；- 第 9 号灯（与第 5 号灯向下相对）；- 第 4 号灯（与第 5 号灯向左相对）；- 第 1 号灯（与第 5 号灯斜向相对）；- 第 3 号灯（与第 5 号灯向下相对）；- 第 2 号灯（与第 5 号灯向右相对）；(3) 最后，再回到第 5 号灯，整个九宫格的灯就全部点亮了。

4.应用九宫格点亮所有灯的原理在实际生活中有很多应用，比如在计算机编程、密码学、游戏设计等领域都有涉及。

此外，九宫格作为一种古老的数学工具，对于培养人们的逻辑思维和数学能力也具有很高的价值。

5.结论通过解析九宫格点亮所有灯的原理，我们可以看到古代先民们对于数学和逻辑的掌握已经达到了很高的水平。

九宫格不仅仅是一种文化符号，更是古代智慧的结晶。

九宫格数独概述九宫格数独，是一种源自18世纪末的瑞士，后在美国发展、并在日本得以发扬光大的数字谜题。

数独盘面是个九宫，每一宫又分为九个小格。

在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。

使1-9每个数字在每一行、每一列和每一宫中都只出现一次。

这种游戏全面考验做题者观察能力和推理能力，虽然玩法简单，但数字排列方式却千变万化，所以不少教育者认为数独是训练头脑的绝佳方式。

目录数独的历史数独终盘的排列组合数独的基本元素数独的基本规则基本解法举例基础摒除法唯一解法唯余解法数独的历史数独终盘的排列组合数独的基本元素数独的基本规则基本解法举例基础摒除法唯一解法唯余解法•区块摒除法•余数测试法•隐性唯一候选数法•三链数删减法•隐性三链数删减法•矩形顶点删减法•三链列删减法•关键数删减法•变形数独概述•数独的近亲•给出数字最少的有唯一解的数独数独的历史数独前身为“九宫格”，最早起源于中国。

数千年前，我们的祖先就发明了洛书，其特点较之现在的数独更为复杂，要求纵向、横向、斜向上的三个数字之和等于15，而非简单的九个数字不能重复。

儒家典籍《易经》中的“九宫图”也源于此，故称“洛书九宫图”。

而“九宫”之名也因《易经》在中华文化发展史上的重要地位而保存、沿用至今。

1783年，瑞士数学家莱昂哈德·欧拉发明了一种当时称作“拉丁方块”（Latin Squ are）的游戏，这个游戏是一个n×n的数字方阵，每一行和每一列都是由不重复的n 个数字或者字母组成的。

19世纪70年代，美国的一家数学逻辑游戏杂志《戴尔铅笔字谜和词语游戏》（D ell Puzzle Mαgαzines）开始刊登现在称为“数独”的这种游戏，当时人们称之为“数字拼图”（Number Place），在这个时候，9×9的81格数字游戏才开始成型。

填充完整后1984年4月，在日本游戏杂志《字谜通讯Nikoil》（《パズル通信ニコリ》）上出现了“数独”游戏，提出了“独立的数字”的概念，意思就是“这个数字只能出现一次”或者“这个数字必须是惟一的”，并将这个游戏命名为“数独”（sudoku）。

九宫图解法口诀（九宫格-幻方N阶最简单解法）九宫格（数字游戏）九宫格，一款数字游戏，起源于河图洛书，与洛书是中国古代流传下来的两幅神秘图案，历来被认为是河洛文化的滥觞，中华文明的源头，被誉为"宇宙魔方"。

演变过程河图上，排列成数阵的黑点和白点，蕴藏着无穷的奥秘；洛书上的图案正好对应着从1到9九个数字，并且无论是纵向、横向、斜向、三条线上的三个数字其和皆等于15，河图、洛书是现代数学中数学里的三阶幻方，中国古代叫“纵横图”。

九宫格游戏正是在纵横图的基础上发展而来的。

纵横图最初用古代数学家们的日常教学。

后来发展为人人喜欢的数学文字游戏。

在九宫格之后又衍生出便于携带的滑板类游戏——重排九宫。

3-11阶幻方简单解法•上中间1 （第一行，中间填1）•右上+1（依次向右上方填入2、3…）•倍数下移（3阶- 每到3的倍数下移+1 ，填3后下移填4）•继续右上+1（记得填几阶，几阶的陪数下移， 6之后下移填7，以此类推…）---适用所有奇阶幻方 3阶-N阶奇阶幻方当n为奇数时，我们称幻方为奇阶幻方。

3阶---横、竖、斜各方向数字之和为153阶解法5阶---横、竖、斜各方向数字之和为655阶解法7阶---横、竖、斜各方向数字之和为1757阶解法9阶---横、竖、斜各方向数字之和为3699阶解法11阶---横、竖、斜各方向数字之和为67111阶解法偶阶幻方当n为偶数时，我们称幻方为偶阶幻方。

当n可以被4整除时，我们称该偶阶幻方为双偶幻方；当n不可被4整除时，我们称该偶阶幻方为单偶幻方。

4阶幻方简单解法外对角数字互换，内对角数字互换（图绿色是不动的数字）4阶---横、竖、斜各方向数字之和为344阶4阶解法6阶---横、竖、斜各方向数字之和为1116阶6阶解6阶解法（36宫格）及以上偶阶幻方。

9宫格魔法公式摘要：1.9 宫格魔法公式的背景和起源2.9 宫格的构成和特点3.如何使用9 宫格魔法公式4.9 宫格魔法公式的应用领域5.9 宫格魔法公式的优点和局限性正文：【1.9 宫格魔法公式的背景和起源】9 宫格魔法公式，又称为洛书公式，起源于中国古代的易经文化。

它是一种通过数学运算来推演事物发展的方法，被广泛应用于风水、命理、卜卦等领域。

9 宫格魔法公式主要由9 个数字构成，分别是1、2、3、4、5、6、7、8、9，每个数字都代表了不同的事物属性。

【2.9 宫格的构成和特点】9 宫格是由9 个方格组成的一个正方形，每个方格中填写一个数字。

其中，数字1 位于正方形的中心，其他数字按照顺时针方向依次排列在周围的8 个方格中。

9 宫格的特点是每个数字与其相邻的数字之间都有一定的关系，这种关系可以用来推演事物的发展变化。

【3.如何使用9 宫格魔法公式】使用9 宫格魔法公式，首先需要根据问题确定主题，然后将9 个数字按照特定顺序填入9 个方格中。

接下来，通过观察数字之间的关系，可以得出事物发展的趋势和结果。

具体的推演方法有很多种，例如可以根据数字的五行属性、后天八卦方位等来进行分析。

【4.9 宫格魔法公式的应用领域】9 宫格魔法公式在中国传统文化中有着广泛的应用。

除了在风水、命理、卜卦等领域外，它还被应用于预测天气、分析人际关系、解决生活难题等方面。

近年来，随着人们对易经文化的重视，9 宫格魔法公式也逐渐被运用到企业管理、心理咨询等领域。

【5.9 宫格魔法公式的优点和局限性】9 宫格魔法公式的优点在于它具有一定的预测能力和指导意义，可以帮助人们更好地了解事物的发展趋势，从而采取相应的措施。

然而，9 宫格魔法公式也存在局限性，它只是一种推演方法，并不能完全决定事物的结局。

九宫格计箅方法
（原创版）
目录
1.九宫格的概述
2.九宫格的计算方法
3.九宫格的应用领域
正文
【九宫格的概述】
九宫格，又称洛书、九宫图，是一种古老的数学工具，起源于中国古代的河图洛书。

它是由九个方格组成的一个正方形，每个方格填入一个数字，这些数字按照一定的规律排列，具有独特的数学性质和应用价值。

【九宫格的计算方法】
九宫格的计算方法主要包括以下步骤：
1.确定中心数字：在九宫格的中心位置填入一个数字，通常为 5。

2.填写其他数字：根据中心数字，按照一定的规律填写其他八个方格的数字。

具体规律为：将中心数字的平方减去其他八个方位数字的平方，得到的结果即为应填入的数字。

例如，中心数字 5 的平方是 25，上方数字为 9，其平方为 81，25-81=-56，因此上方填入 -6；同理，左方填入 -1，右方填入 7，下方填入 -8，右上方填入 6，左上方填入 -9，左下方填入1，右下方填入 8。

【九宫格的应用领域】
九宫格在古代主要用于卜卦、预测等迷信活动，但在现代，九宫格作为一种独特的数学工具，其应用领域已经拓展到多个方面：
1.教育教学：九宫格作为一种有趣的数学游戏，可以帮助学生培养数
学思维和解决数学问题的能力。

2.计算机科学：九宫格的计算方法和数学性质被应用于计算机程序设计和问题求解。

3.工程技术：九宫格在工程设计、建筑规划等领域也有一定的应用。

4.文化研究：九宫格作为中国古代文化的一部分，对于研究古代数学、文化、哲学等领域具有重要的参考价值。

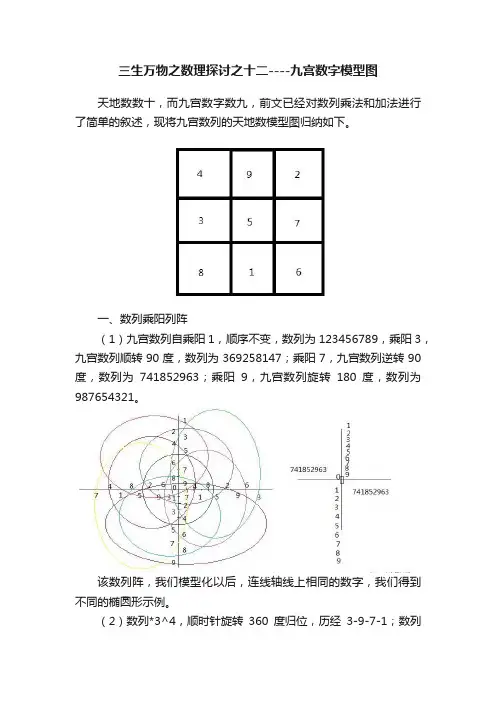
三生万物之数理探讨之十二----九宫数字模型图天地数数十，而九宫数字数九，前文已经对数列乘法和加法进行了简单的叙述，现将九宫数列的天地数模型图归纳如下。

一、数列乘阳列阵（1）九宫数列自乘阳1，顺序不变，数列为123456789，乘阳3，九宫数列顺转90度，数列为369258147；乘阳7，九宫数列逆转90度，数列为741852963；乘阳9，九宫数列旋转180度，数列为987654321。

该数列阵，我们模型化以后，连线轴线上相同的数字，我们得到不同的椭圆形示例。

（2）数列*3^4，顺时针旋转360度归位，历经3-9-7-1；数列*7^4，逆时针旋转360度归位，历经7-9-3-1。

（3）数列*9，旋转180度，数列翻转摆动，水平翻转一次，垂直翻转一次；数列*9^2，旋转360度归位。

（4）数列乘阳5，阳数归5，阴数归0，阴阳两列：13579-24680。

天数五，地数五，阳数13579，数列和25；阴数24680，数列和30；天地十数总和为55。

按照数列排列的空间方位，以步长1为计量单位归圆形，制作天地数数列模型，我们发现：阳数列以阳数5为中心，阴数列以数字0（10）为中心，天地两分，阴阳两列。

我们将阳数135合成天阳面，将240合成地阴面，我们发现，数字79和数字68立于天地之间，左右分行，天面垂象79；地面立象68，模型如图所示。

该数列16、27、38、49、50同圆，阳数135和阴数240空间展开以后成为椎体。

79和68分别形成椎型台；56和90分别形成空间椎体。

二、数列乘阴列阵依据前文数理系列所述，阴阳相参，阳数转为阴数，中宫数字5隐藏，数字和为0（10）；1397阳数分别旋转合地数，如图：。

九宫格数独概述九宫格数独，是一种源自18世纪末的瑞士，后在美国发展、并在日本得以发扬光大的数字谜题。

数独盘面是个九宫，每一宫又分为九个小格。

在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。

使1-9每个数字在每一行、每一列和每一宫中都只出现一次。

这种游戏全面考验做题者观察能力和推理能力，虽然玩法简单，但数字排列方式却千变万化，所以不少教育者认为数独是训练头脑的绝佳方式。

,数独的历史,数独终盘的排列组合,数独的基本元素,数独的基本规则,基本解法举例,基础摒除法,唯一解法,唯余解法,数独的历史数独终盘的排列组合数独的基本元素数独的基本规则基本解法举例基础摒除法唯一解法唯余解法∙区块摒除法∙余数测试法∙隐性唯一候选数法∙三链数删减法∙隐性三链数删减法∙矩形顶点删减法∙三链列删减法∙关键数删减法∙变形数独概述∙数独的近亲∙给出数字最少的有唯一解的数独,数独的历史数独前身为“九宫格”，最早起源于中国。

数千年前，我们的祖先就发明了洛书，其特点较之现在的数独更为复杂，要求纵向、横向、斜向上的三个数字之和等于15，而非简单的九个数字不能重复。

儒家典籍《易经》中的“九宫图”也源于此，故称“洛书九宫图”。

而“九宫”之名也因《易经》在中华文化发展史上的重要地位而保存、沿用至今。

,1783年，瑞士数学家莱昂哈德·欧拉发明了一种当时称作“拉丁方块”（Latin,Square）的游戏，这个游戏是一个n×n的数字方阵，每一行和每一列都是由不重复的n个数字或者字母组成的。

19世纪70年代，美国的一家数学逻辑游戏杂志《戴尔铅笔字谜和词语游戏》（Dell,Puzzle,Mαgαzines）开始刊登现在称为“数独”的这种游戏，当时人们称之为“数字拼图”（Number,Place），在这个时候，9×9的81格数字游戏才开始成型。

,填充完整后1984年4月，在日本游戏杂志《字谜通讯Nikoil》（《パズル通信ニコリ》）上出现了“数独”游戏，提出了“独立的数字”的概念，意思就是“这个数字只能出现一次”或者“这个数字必须是惟一的”，并将这个游戏命名为“数独”（sudoku）。

“九宫图”传说是远古时代洛河中的一个神龟背上的图案，故又称“龟背图”，中国古代数学史上经常研究这一神话．现有1，2，3，4，5，6，7，8，9共九个数字，请将它们分别填入九个方格中，使得每行的三个数、每列的三个数、斜对角的三个数之和都等于15；①每行的和数都相等，这个和数为15。

1 +2 + ... + 9 = 9*10/2 = 45.如论如何排，3行数字的总和一定是45。

要使得每行的和数都等于同一个数，则，这个数只能是45/3 = 15。

②使得每行，每列，2对角线的和都为15，中间的那个格子只能填5。

考虑第2行，第2列，和2对角线。

它们的总和为4*15 = 60。

在它们的总和中，中间的格子的数字共出现4次，其他位置的格子都出现了而且仅出现1次。

所以，它们的总和= 4*中间格子的数字+ 其他8个数字= 3*中间格子的数字+ 9个数字之和因此，60 = 3*中间格子的数字+ 45，15 = 3*中间格子的数字，5 = 中间格子的数字。

③数字9不能出现在4个角上的格子里。

如果数字9出现在角上的格子里了，那么为了保证对角线的3个数之和=15，它的对角的数字就只能是1了。

数字9所在的那个格子的行和列上还有4个格子要添入除了1，5，9以外的数字，并使得行和=15，列和=15。

这样，因为，9+6 = 15，所以，这4个格子中只能填入2，3，4这3个数字了。

无法实现。

因此，数字9不能出现在4个角上的格子里。

数字9只能填入第1行，或者第3行，或者第1列，或者第3列的中间的那个格子里。

④数字1和9出现在9宫格中间行或者中间列的2端的格子中。

由1），中间行或者中间列的数字之和为15，由2），中间格子的数字为5，由3），数字9只能出现在中间行或者中间列中，因此，只能由9，5，1构成1行或者1列。

⑤数字2，4和9只能在同一行或者用一列中。

假定数字9填入第1行中间的位置，数字1填入第3行中间的位置。

第1行的剩下的2个格子只能填入除9，5，1以外的6个数字。

九宫格数独概述九宫格数独，是一种源自18世纪末的瑞士，后在美国发展、并在日本得以发扬光大的数字谜题。

数独盘面是个九宫，每一宫又分为九个小格。

在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。

使1-9每个数字在每一行、每一列和每一宫中都只出现一次。

这种游戏全面考验做题者观察能力和推理能力，虽然玩法简单，但数字排列方式却千变万化，所以不少教育者认为数独是训练头脑的绝佳方式。

目录数独的历史数独终盘的排列组合数独的基本元素数独的基本规则基本解法举例基础摒除法唯一解法唯余解法数独的历史数独终盘的排列组合数独的基本元素数独的基本规则基本解法举例基础摒除法唯一解法唯余解法•区块摒除法•余数测试法•隐性唯一候选数法•三链数删减法•隐性三链数删减法•矩形顶点删减法•三链列删减法•关键数删减法•变形数独概述•数独的近亲•给出数字最少的有唯一解的数独数独的历史数独前身为“九宫格”，最早起源于中国。

数千年前，我们的祖先就发明了洛书，其特点较之现在的数独更为复杂，要求纵向、横向、斜向上的三个数字之和等于15，而非简单的九个数字不能重复。

儒家典籍《易经》中的“九宫图”也源于此，故称“洛书九宫图”。

而“九宫”之名也因《易经》在中华文化发展史上的重要地位而保存、沿用至今。

1783年，瑞士数学家莱昂哈德·欧拉发明了一种当时称作“拉丁方块”（Latin Squ are）的游戏，这个游戏是一个n×n的数字方阵，每一行和每一列都是由不重复的n 个数字或者字母组成的。

19世纪70年代，美国的一家数学逻辑游戏杂志《戴尔铅笔字谜和词语游戏》（D ell Puzzle Mαgαzines）开始刊登现在称为“数独”的这种游戏，当时人们称之为“数字拼图”（Number Place），在这个时候，9×9的81格数字游戏才开始成型。

填充完整后1984年4月，在日本游戏杂志《字谜通讯Nikoil》（《パズル通信ニコリ》）上出现了“数独”游戏，提出了“独立的数字”的概念，意思就是“这个数字只能出现一次”或者“这个数字必须是惟一的”，并将这个游戏命名为“数独”（sudoku）。

1-9 九宫格数字填写规律口诀
1-9 之间一共9 个数，加起来一共45,1+2+3+4+5+6+7+8+9=45 。

九宫格是每三个不同的数字相加是一个相同的一个数字,即45/3=15 。

列出8 种可能：159.168.249.258.267.348.357.456
统计，1 出现2 次，2 出现3 次，3 出现2 次，4 出现3 次，5 出现8 次，6 出现3 次，7 出现2 次，8 出现3 次，9 出现2 次
然后看九宫格
1、先将1 填入第1 行最中间一格；
2、沿着右斜向上方向填入下一个数字2；如果右上方的方格不在这个区域内，就将它向水平方向或竖直方向移动（水平方向向左移动到最左端的方格中，竖直方向向下移动到最下面的方格中）；
3、如果右上方的方格已经有数字，那么就将下个数字填在前一个数
字的下方；
4、如果右上方的方格向左或向右移动都不在区域内，仍然将它填在
前一个数字的下方；
5、继续以上步骤，就可以完成所有方格数字的填写。

三阶九宫简易填法-23年6月
九宫是古老的数学问题，指在3*3的方格中，填入1到9九个数字，使横竖和对角线的三个数的和相等。

九宫的解法层出不穷，简单一点的是口诀法，按口诀就可得出结果。

但这种只求结果的方法对学生的思维没有任何好处，而且按口诀的操作也不是太简单。

对于小学生，我找到一种简易的方法，既简便快速，而且对学生的思维有利。

解决问题，重要的是找到重点和关键。

对于九宫来说，横竖和对角线的三个数（四组）。

也与都与中间的方格有关，因此中间的方格是重点和关键；其次是角上的四个方格横竖和对角线（三组）有关。

也就是说，先确定了中间方格的数，再找出四角上的数，问题就迎刃而解了。

解答：
一，在1到9的九个数字中。

5处于中间，而两边的1,9；2,8；3,7和4,6显然可以和5配搭成三个数四组，每组的和相等是15.于是5满足了九宫中间方格数的条件。

于是第一步中间填5。

（图1）
二，因为三个数的和是15,15是奇数，三个数的和为奇数的可以是三奇和两偶一奇，如果角上填奇，满足对角线三奇，但两边无法满足。

所以角上只能填偶。

这样就满足了四组均是两偶一奇，所以角上的四个方格填偶。

于是。

角上对角方
三，剩下就很容易了，中边分别是9,1和7,3（15减去角上的数）（图3）
以上解答的要点是中间方格填5,四个角方格填偶数，注意2对8；4对6；1对9；3对7。

此方法简单明瞭，适合小学生，特别是能让学生理解解决问题需要找到重点和关键，再就是懂得利用奇偶性解答难题，还有就是理解了中心，配对等，如计算1到9的和，因为5处于中心且为两边的平均数，所以只需5x9=45….。

九宫格数独数独概述数独顾名思义——每个数字只能出现一次。

数独是一种源自18世纪末的瑞士，后在美国发展、并在日本得以发扬光大的数字谜题。

数独盘面是个九宫，每一宫又分为九个小格。

在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。

使1-9每个数字在每一行、每一列和每一宫中都只出现一次(如下图中已经填写完整的那样，不能重复，独立存在)。

这种游戏全面考验做题者观察能力和推理能力，虽然玩法简单，但数字排列方式却千变万化，所以不少教育者认为数独是训练头脑的绝佳方式。

数独的历史数独前身为“九宫格”，最早起源于中国。

数千年前，我们的祖先就发明了洛书，其特点较之现在的数独更为复杂，要求纵向、横向、斜向上的三个数字之和等于15，而非简单的九个数字不能重复。

儒家典籍《易经》中的“九宫图”也源于此，故称“洛书九宫图”。

而“九宫”之名也因《易经》在中华文化发展史上的重要地位而保存、沿用至今。

1783年，瑞士数学家莱昂哈德·欧拉发明了一种当时称作“拉丁方块”（Latin Square）的游戏，这个游戏是一个n×n的数字方阵，每一行和每一列都是由不重复的n个数字或者字母组成的。

19世纪70年代，美国的一家数学逻辑游戏杂志《戴尔铅笔字谜和词语游戏》（Dell Puzzle Mαgαzines）开始刊登现在称为“数独”的这种游戏，当时人们称之为“数字拼图”（Number Place），在这个时候，9×9的81格数字游戏才开始成型。

1984年4月，在日本游戏杂志《字谜通讯Nikoil》（《パズル通信ニコリ》）上出现了“数独”游戏，提出了“独立的数字”的概念，意思就是“这个数字只能出现一次”或者“这个数字必须是惟一的”，并将这个游戏命名为“数独”（sudoku）。

一位前任香港高等法院的新西兰籍法官高乐德（Wayne Gould）在1997年3月到日本东京旅游时，无意中发现了。