北邮信息论201209级期末考题

《信息论基础》参考答案一、填空题1、信源编码的主要目的是提高有效性,信道编码的主要目的是提高可靠性。

2、信源的剩余度主要来自两个方面，一是信源符号间的相关性,二是信源符号的统计不均匀性。

3、三进制信源的最小熵为0，最大熵为bit/符号。

4、无失真信源编码的平均码长最小理论极限制为信源熵（或H(S)/logr= H r （S））。

5、当R=C或（信道剩余度为0）时，信源与信道达到匹配.6、根据信道特性是否随时间变化,信道可以分为恒参信道和随参信道。

7、根据是否允许失真，信源编码可分为无失真信源编码和限失真信源编码。

8、若连续信源输出信号的平均功率为，则输出信号幅度的概率密度是高斯分布或正态分布或时，信源具有最大熵，其值为值。

9、在下面空格中选择填入数学符号“”或“"（1）当X和Y相互独立时，H（XY)=H(X）+H（X/Y）=H（Y)+H（X）。

（2)（3）假设信道输入用X表示，信道输出用Y表示.在无噪有损信道中，H(X/Y)〉 0, H（Y/X)=0,I(X；Y）<H(X)。

二、若连续信源输出的幅度被限定在【2，6】区域内，当输出信号的概率密度是均匀分布时，计算该信源的相对熵，并说明该信源的绝对熵为多少.=2bit/自由度该信源的绝对熵为无穷大.三、已知信源(1）用霍夫曼编码法编成二进制变长码;（6分)（2）计算平均码长;（4分）（3）计算编码信息率；（2分）（4）计算编码后信息传输率；（2分）（5)计算编码效率。

(2分）(1)编码结果为：（2）（3）（4）其中，（5)四、某信源输出A、B、C、D、E五种符号，每一个符号独立出现,出现概率分别为1/8、1/8、1/8、1/2、1/8。

如果符号的码元宽度为0。

5。

计算:（1）信息传输速率。

（2）将这些数据通过一个带宽为B=2000kHz的加性白高斯噪声信道传输，噪声的单边功率谱密度为。

试计算正确传输这些数据最少需要的发送功率P。

解：（1）（2）五、一个一阶马尔可夫信源，转移概率为.（1) 画出状态转移图。

信息论与编码期末考试题信息论与编码期末考试题（一）一、判断题.1.当随机变量和相互独立时，条件熵等于信熵.（）2.由于构成同一空间的基底不是唯一的，所以不同的基底或生成矩阵有可能生成同一码集.（）3.一般情况下，用变长编码得到的平均码长比定长编码大得多.（）4.只要信息传输率大于信道容量，总存在一种信道编译码，可以以所要求的任意小的误差概率实现可靠的通信.（）5.各码字的长度符合克拉夫特不等式，是唯一可译码存在的充分和必要条件.（）6.连续信和离散信的熵都具有非负性.（）7.信的消息通过信道传输后的误差或失真越大，信宿收到消息后对信存在的不确定性就越小，获得的信息量就越小.8.汉明码是一种线性分组码.（）9.率失真函数的最小值是.（）10.必然事件和不可能事件的自信息量都是.（）二、填空题 1、码的检、纠错能力取决于 .2、信编码的目的是；信道编码的目的是 .3、把信息组原封不动地搬到码字前位的码就叫做.4、香农信息论中的三大极限定理是、、 .5、设信道的输入与输出随机序列分别为和，则成立的条件..6、对于香农-费诺编码、原始香农-费诺编码和哈夫曼编码，编码方法惟一的是 .7、某二元信，其失真矩阵，则该信的= .三、计算题.1、某信发送端有2种符号,；接收端有3种符号，转移概率矩阵为.（1）计算接收端的平均不确定度；（2）计算由于噪声产生的不确定度；（3）计算信道容量以及最佳入口分布.2、一阶马尔可夫信的状态转移图如右图所示，信的符号集为.（1）求信平稳后的概率分布；（2）求此信的熵；（3）近似地认为此信为无记忆时，符号的概率分布为平稳分布.求近似信的熵并与进行比较.3、设码符号为，信空间为试构造一种三元紧致码.4、设二元线性分组码的生成矩阵为.（1）给出该码的一致校验矩阵，写出所有的陪集首和与之相对应的伴随式；（2）若接收矢量，试计算出其对应的伴随式并按照最小距离译码准则试着对其译码.（二）一、填空题 1、信编码的主要目的是，信道编码的主要目的是。

安徽大学2011—2012学年第1学期 《信息论》考试试卷（AB 合卷）院/系 年级 专业 姓名 学号一、填空题1、接收端收到y 后，获得关于发送的符号是x 的信息量是 。

2、香农信息的定义 。

3、在已知事件z Z ∈的条件下，接收到y 后获得关于事件x 的条件互信息(;|)I x y z 的表达式为 。

4、通信系统模型主要分成五个部分分别为： 。

5、研究信息传输系统的目的就是要找到信息传输过程的共同规律，以提高信息传输的可靠性、有效性、 和 ，使信息传输系统达到最优化。

6、某信源S 共有32个信源符号，其实际熵H ∞=1.4比特/符号，则该信源剩余度为 。

7、信道固定的情况下，平均互信息(;)I X Y 是输入信源概率分布()Px 的 型凸函数。

信源固定的情况下，平均互信息(;)I X Y 是信道传递概率(|)P y x 的 型凸函数。

8、当信源与信道连接时，若信息传输率达到了信道容量，则称此信源与信道达到匹配。

信道剩余度定义为 。

9、已知信源X 的熵H (X )=0.92比特/符号,则该信源的五次无记忆扩展信源X 5的信息熵5()H X = 。

10、将∞H ，6H ，0H ，4H ，1H 从大到小排列为 。

11、根据香农第一定理，对于离散无记忆信源S ，用含r 个字母的码符号集对N 长信源符号序列进行变长编码，总能找到一种无失真的唯一可译码，使每个信源符号所需平均码长满足： 。

12、多项式剩余类环[]())q F x f x 是域的充要条件为 。

13、多项式剩余类环[](1)n q F x x -的任一理想的生成元()g x 与1n x -关系为 。

14、有限域122F 的全部子域为 。

15、国际标准书号（ISBN ）由十位数字12345678910a a a a a a a a a a 组成（诸i a ∈11F ，满足：1010(mod11)ii ia=≡∑），其中前九位均为0-9，末位0-10，当末位为10时用X 表示。

《信息论基础》参考答案一、填空题1、信源编码的主要目的是提高有效性,信道编码的主要目的是提高可靠性。

2、信源的剩余度主要来自两个方面，一是信源符号间的相关性,二是信源符号的统计不均匀性。

3、三进制信源的最小熵为0，最大熵为bit/符号。

4、无失真信源编码的平均码长最小理论极限制为信源熵（或H(S)/logr= H r （S））。

5、当R=C或（信道剩余度为0）时，信源与信道达到匹配.6、根据信道特性是否随时间变化,信道可以分为恒参信道和随参信道。

7、根据是否允许失真，信源编码可分为无失真信源编码和限失真信源编码。

8、若连续信源输出信号的平均功率为，则输出信号幅度的概率密度是高斯分布或正态分布或时，信源具有最大熵，其值为值。

9、在下面空格中选择填入数学符号“”或“"（1）当X和Y相互独立时，H（XY)=H(X）+H（X/Y）=H（Y)+H（X）。

（2)（3）假设信道输入用X表示，信道输出用Y表示.在无噪有损信道中，H(X/Y)〉 0, H（Y/X)=0,I(X；Y）<H(X)。

二、若连续信源输出的幅度被限定在【2，6】区域内，当输出信号的概率密度是均匀分布时，计算该信源的相对熵，并说明该信源的绝对熵为多少.=2bit/自由度该信源的绝对熵为无穷大.三、已知信源(1）用霍夫曼编码法编成二进制变长码;（6分)（2）计算平均码长;（4分）（3）计算编码信息率；（2分）（4）计算编码后信息传输率；（2分）（5)计算编码效率。

(2分）(1)编码结果为：（2）（3）（4）其中，（5)四、某信源输出A、B、C、D、E五种符号，每一个符号独立出现,出现概率分别为1/8、1/8、1/8、1/2、1/8。

如果符号的码元宽度为0。

5。

计算:（1）信息传输速率。

（2）将这些数据通过一个带宽为B=2000kHz的加性白高斯噪声信道传输，噪声的单边功率谱密度为。

试计算正确传输这些数据最少需要的发送功率P。

解：（1）（2）五、一个一阶马尔可夫信源，转移概率为.（1) 画出状态转移图。

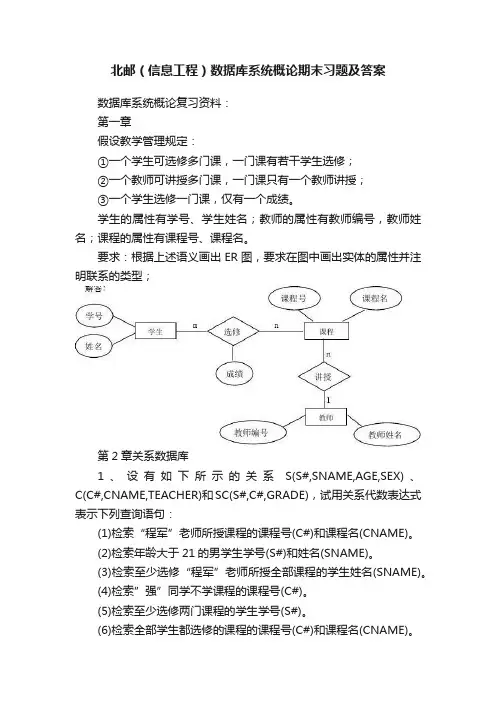
北邮（信息工程）数据库系统概论期末习题及答案数据库系统概论复习资料：第一章假设教学管理规定：①一个学生可选修多门课，一门课有若干学生选修；②一个教师可讲授多门课，一门课只有一个教师讲授；③一个学生选修一门课，仅有一个成绩。

学生的属性有学号、学生姓名；教师的属性有教师编号，教师姓名；课程的属性有课程号、课程名。

要求：根据上述语义画出ER图，要求在图中画出实体的属性并注明联系的类型；第2章关系数据库1、设有如下所示的关系S(S#,SNAME,AGE,SEX)、C(C#,CNAME,TEACHER)和SC(S#,C#,GRADE)，试用关系代数表达式表示下列查询语句：(1)检索“程军”老师所授课程的课程号(C#)和课程名(CNAME)。

(2)检索年龄大于21的男学生学号(S#)和姓名(SNAME)。

(3)检索至少选修“程军”老师所授全部课程的学生姓名(SNAME)。

(4)检索”强”同学不学课程的课程号(C#)。

(5)检索至少选修两门课程的学生学号(S#)。

(6)检索全部学生都选修的课程的课程号(C#)和课程名(CNAME)。

(7)检索选修课程包含“程军”老师所授课程之一的学生学号(S#)。

(8)检索选修课程号为k1和k5的学生学号(S#)。

(9)检索选修全部课程的学生姓名(SNAME)。

(10)检索选修课程包含学号为2的学生所修课程的学生学号(S#)。

(11)检索选修课程名为“C语言”的学生学号(S#)和姓名(SNAME)。

解：本题各个查询语句对应的关系代数表达式表示如下：(1). ∏C#,CNAME(σTEACHER=‘程军’(C))(2). ∏S#,SNAME(σAGE>21∧SEX=”男”(C)) (3). ∏SNAME{s[∏S#,C#（sc ）÷∏C#(σTEACHER=‘程军’(C))]}(4). ∏C#(C)- ∏C#(σSNAME=‘强’(S) SC) (5). ∏S#(σ[1]=[4]∧[2]≠[5] (SC × SC))(6). ∏C#,CNAME(C (∏S#,C#(sc)÷∏S#(S)))(7). ∏S#(SC∏C#(σTEACHER=‘程军’(C)))(8). ∏S#,C#（sc ）÷∏C#(σC#=’k1’∨ C#=’k5’(C)) (9). ∏SNAME{s[∏S#,C#（sc ）÷∏C#(C)]}(10). ∏S#,C#（sc ）÷∏C#(σS#=’2’(SC))(11). ∏S#,SNAME{s[∏S#(SCσCNAME=‘C 语言’(C))]}2、关系R 和S 如下图所示，试计算R ÷S 。

试题编号：重庆邮电大学2009/2010学年2学期《信息论基础》试卷（期末）（B卷）（开卷）一、填空题（共15分，每空1分）1、若一连续消息通过某放大器，该放大器输出的最大瞬时电压为b，最小瞬时电压为a。

若消息从放大器中输出，则该信源的绝对熵是；其能在每个自由度熵的最大熵是。

2、高斯白噪声信道是指。

3、若连续信源的平均功率为５ W，则最大熵为，达到最大值的条件是。

4、离散信源存在剩余度的原因是和。

5、离散无记忆信源在进行无失真变长信源编码时，编码效率最大可以达到。

6、离散无记忆信源在进行无失真变长信源编码时，码字长度是变化的。

根据信源符号的统计特性，对概率大的符号用码，对概率小的符号用码，这样平均码《信息论基础》试卷第1页《信息论基础》试卷第2页长就可以降低，从而提高编码效率。

7、八进制信源的最小熵为 ，最大熵为 。

8、一个事件发生概率为0.125，则自信息量为 。

9、在下面空格中选择填入数学符号“=，≥，≤，>”或“<”()XY H ()()Y X H Y H |+ ()()X H Y H +。

二、判断题（正确打√，错误打×）（共5分，每小题1分）1）离散无记忆等概信源的剩余度为0。

（ ） 2）离散无记忆信源N 次扩展源的熵是原信源熵的N 倍。

( ) 3）互信息可正、可负、可为零。

（ ） 4）信源的真正功率P 永远不会大于熵功率P ，即P P ≤。

（ ） 5）信道容量与信源输出符号的概率分布有关。

（ ） 三、（5分）已知信源的概率密度函数)(x p 如下图所示，求信源的相对熵。

《信息论基础》试卷第3页四、（１5分）设一个离散无记忆信源的概率空间为它们通过干扰信道，信道输出端的接收符号集为[]21,b b Y =，已知信道传输概率如下图所示。

试计算：（1）信源X 中事件1x 的自信息量；（3分） （2）信源X 的信息熵；（3分） （3）共熵)(XY H （3分） （4）噪声熵(|)H Y X ；（3分）（5）收到消息Y 后获得的关于信源X 的平均信息量。

信息论与编码期末考试题（全套）（一）一、判断题共 10 小题，满分 20 分.1. 当随机变量X 和Y 相互独立时，条件熵)|(Y X H 等于信源熵)(XH . （）2. 由于构成同一空间的基底不是唯一的，所以不同的基底或生成矩阵有可能生成同一码集.（）3.一般情况下，用变长编码得到的平均码长比定长编码大得多. （） 4. 只要信息传输率大于信道容量，总存在一种信道编译码，可以以所要求的任意小的误差概率实现可靠的通信（）5. 各码字的长度符合克拉夫特不等式，是唯一可译码存在的充分和必要条件. （） 6. 连续信源和离散信源的熵都具有非负性. （） 7. 信源的消息通过信道传输后的误差或失真越大，信宿收到消息后对信源存在的不确定性就越小，获得的信息量就越小.8. 汉明码是一种线性分组码. （） 9. 率失真函数的最小值是0. （）10.必然事件和不可能事件的自信息量都是0. （）二、填空题共 6 小题，满分 20 分.1、码的检、纠错能力取决于 .2、信源编码的目的是；信道编码的目的是 .3、把信息组原封不动地搬到码字前k 位的),(k n 码就叫做 .4、香农信息论中的三大极限定理是、、.5、设信道的输入与输出随机序列分别为X 和Y ，则),(),(Y X NI Y X I N N =成立的条件 ..6、对于香农-费诺编码、原始香农-费诺编码和哈夫曼编码，编码方法惟一的是 .7、某二元信源01()1/21/2X P X =???，其失真矩阵00a D a ??=，则该信源的max D = .三、本题共 4 小题，满分 50 分.1、某信源发送端有2种符号i x )2,1(=i ,a x p =)(1；接收端有3种符号iy )3,2,1(=j ，转移概率矩阵为1/21/201/21/41/4P ??=.（1）计算接收端的平均不确定度()H Y ；（2）计算由于噪声产生的不确定度(|)H Y X ；（3）计算信道容量以及最佳入口分布.2、一阶马尔可夫信源的状态转移图如右图所示，信源X 的符号集为}2,1,0{.（1）求信源平稳后的概率分布；（2）求此信源的熵；（3）近似地认为此信源为无记忆时，符号的概率分布为平稳分布.求近似信源的熵)(X H 并与H ∞进行比较.3、设码符号为}2,1,0{=X ，信源空间为05.005.005.005.01.01.02.04.087654321s s s s s s s s 试构造一种三元紧致码.4、设二元)4,7(线性分组码的生成矩阵为=1000101010011100101100001011G . （1）给出该码的一致校验矩阵，写出所有的陪集首和与图2-13之相对应的伴随式；（2）若接收矢量)0001011(=v ，试计算出其对应的伴随式S 并按照最小距离译码准则试着对其译码.（二）一、填空题（共15分，每空1分）1、信源编码的主要目的是，信道编码的主要目的是。

莆田学院期末考试试卷（A）卷2011 — 2012 学年第一学期课程名称：信息论与编码适用年级/专业： 09/电信（通信）试卷类别开卷（）闭卷（√）学历层次本科考试用时 120分钟《．考生注意：答案要全部抄到答题纸上，做在试卷上不给分．．．．．．．．．．．．．．．．．．．．．．．．．》．一、简答题（每小题8分，共32分）1.对于一个一般的通信系统，试给出其系统模型框图，并结合此图，解释数据处理定理。

2. 香农信息论研究了哪些内容？试讲述香农第二编码定理。

3. 什么是唯一可译码？什么是即时码（前缀码）？构造唯一可译码的充要条件？（10分）4. 什么是信源编码？什么是信道编码？为何要进行这两者编码？二、证明题（每小题6分，共6分）对于任意的事件X、Y，试证明下列不等式成立：H(X|Y)<=H(X),并说明等式成立的条件。

三、计算题（第1、5题各16分，第2题12分，第3题10分，第4题8分，共62分）1.（16分）一黑白气象传真图的消息只有黑色和白色两种，即信源X={黑,白}。

设黑色出现的概率为P(黑)=0.3，白色的出现概率P(白)=0.7。

求（1）假设图上黑白消息出现前后没有关联，求熵H(X)；（2）假设消息前后有关联，其依赖关系为P(白/白)=0.9，P(黑/白)=0.1，P(白/黑)=0.2，P(黑/黑)=0.8，求此一阶马尔可夫信源的熵H2(X)；（3）分别求上述两种信源的剩余度，比较和的大小，并说明其物理意义。

2.（12分）一信源产生概率为P(1)=0.005, P(0)=0.995的统计独立二进制数符。

这些数符组成长度为100的数符组。

我们为每一个少于3个“1”的源数符组提供一个二进制码字，所有码字的长度相等。

（1）求出为所规定的所有源符组都提供码字所需的最小码长。

（2）求信源发出一数符组，而编码器无相应码字的概率。

3.（10分）已知一个（6，3）线性分组码的全部码字为001011，110011，010110，101110，100101，111000，011101，000000。

----------------------- Page 1-----------------------北京邮电大学2006——2007 学年第一学期《信息论》期末考试试题（A 卷）标准答案姓名班级学号分数、判断题（正确打√，错误打×）（共10分，每小题1分）1）异前置码是即时码；（√）2）最大似然准则等价于最小汉明距离准则；（×）3）离散信源记忆的长度越大，信源的符号熵越小；（√）4）一维高斯信源的熵只与其均值和方差有关；（×）5）为达到并联加性高斯噪声信道容量，在信道输入总功率给定条件下应给噪声方差大的子信道分配更多的功率；（×）6）只要信息传输速率小于信道容量，总可以找到一种编码方式使得当编码序列足够长时传输差错率任意小；（√）7）离散无记忆信源的N 次扩展源的熵是原信源熵的N 倍；（√）8）仙农的AWGN 信道容量公式是在信道输入的平均功率和幅度受限条件下推导出来的；（×）s x ,x ,L,x s ,s L,s9)当马氏源的初始状态和输出给定后，那么状态 1 2, n+1 就能0 0 1 n唯一确定；（√）10)当平均失真大于其上限 D 时，率失真函数R （D）= 0 。

（√）max二、填空题（共20分，每空2分）1) 设信源的熵为0.8 比特/符号，对信源序列进行单符号编码，码序列为0、1二元序列，如果编码效率为100%，那么每信源符号平均码长为0.8 ，码序列中“0”符号出现的概率为 1/2 ，信息传输速率为 1 比特/码符号。

2) 一阶平稳马氏源的符号转移概率为p X 2 |X 1 (0 | 0) = 0.2 ，p X 2 |X 1 (1| 1) = 0.6 ，那么符号的平稳分布为p X (0) = 1/3，p X (1) = 2/3 ；信源的符号熵为 0.8879 比特/符号。

3）一维连续随机变量X 在[a，b]区间内均匀分布时，其信源熵为 log2 (b-a) 。

一、填空题（每空1分，共35分） 1、1948年，美国数学家 发表了题为“通信的数学理论”的长篇论文，从而创立了信息论。

信息论的基础理论是 ，它属于狭义信息论。

2、信号是 的载体，消息是 的载体。

3、某信源有五种符号}{,,,,a b c d e ，先验概率分别为5.0=a P ，25.0=b P ，125.0=c P ，0625.0==e d P P ，则符号“a ”的自信息量为 bit ，此信源的熵为 bit/符号。

4、某离散无记忆信源X ，其概率空间和重量空间分别为1234 0.50.250.1250.125X x x x x P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦和12340.5122X x x x x w ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦，则其信源熵和加权熵分别为 和 。

5、信源的剩余度主要来自两个方面，一是 ，二是 。

6、平均互信息量与信息熵、联合熵的关系是 。

7、信道的输出仅与信道当前输入有关，而与过去输入无关的信道称为 信道。

8、马尔可夫信源需要满足两个条件：一、 ； 二、 。

9、若某信道矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡010001000001100，则该信道的信道容量C=__________。

10、根据是否允许失真，信源编码可分为 和 。

11、信源编码的概率匹配原则是：概率大的信源符号用 ，概率小的信源符号用 。

（填短码或长码）12、在现代通信系统中，信源编码主要用于解决信息传输中的 性，信道编码主要用于解决信息传输中的 性，保密密编码主要用于解决信息传输中的安全性。

13、差错控制的基本方式大致可以分为 、 和混合纠错。

14、某线性分组码的最小汉明距dmin=4，则该码最多能检测出 个随机错，最多能纠正 个随机错。

15、码字101111101、011111101、100111001之间的最小汉明距离为 。

16、对于密码系统安全性的评价，通常分为 和 两种标准。

17、单密钥体制是指 。

信息论与编码期末复习试题含参考答案在无失真的信源中，信源输出由 H (X ) 来度量；在有失真的信源中，信源输出由 R (D ) 来度量。

要使通信系统做到传输信息有效、可靠和保密，必须首先 信源 编码，然后_____加密____编码，再______信道_____编码，最后送入信道。

带限AWGN 波形信道在平均功率受限条件下信道容量的基本公式，也就是有名的香农公式是；当归一化信道容量C/W 趋近于零时，也即信道完全丧失了通信能力，此时E b /N 0为 -1.6 dB ，我们将它称作香农限，是一切编码方式所能达到的理论极限。

保密系统的密钥量越小，密钥熵H (K )就越 小 ，其密文中含有的关于明文的信息量I (M ；C )就越 大 。

已知n ＝7的循环码，则信息位长度k 为 3 ，校验多项式h(x)= 。

设输入符号表为X ＝{0，1}，输出符号表为Y ＝{0，1}。

输入信号的概率分布为p ＝(1/2，1/2)，失真函数为d (0，0) = d (1，1) = 0，d (0，1) =2，d (1，0) = 1，则D min ＝ 0 ，R (D min )＝ 1bit/symbol ，相应的编码器转移概率矩阵[p(y/x )]＝；D max ＝ 0.5 ，R (D max )＝ 0 ，相应的编码器转移概率矩阵[p(y/x )]＝。

已知用户A 的RSA 公开密钥(e,n )=(3,55)，,则 log(1)C W SNR =+42()1g x x x x =+++31x x ++1001⎡⎤⎢⎥⎣⎦1010⎡⎤⎢⎥⎣⎦5,11p q ==()φn =40 ，他的秘密密钥(d,n )＝(27,55) 。

若用户B 向用户A 发送m =2的加密消息，则该加密后的消息为 8 。

二、判断题可以用克劳夫特不等式作为唯一可译码存在的判据。

（√ ） 线性码一定包含全零码。

（√ ）算术编码是一种无失真的分组信源编码，其基本思想是将一定精度数值作为序列的编码，是以另外一种形式实现的最佳统计匹配编码。

信息论与编码期末复习（基本上涵盖了所有考点，有了这份资料，期末绝不会挂科）1填空题1、信息论研究的主要问题是如何提高信息传输系的性和性，对应这两个性能数字通讯系统量化指标分别为和。

2、若给定离散概率空间[X,p(x)]表示的信源，则该信源中的信源消息（事件）x的自信息量可表I(x)= ；该信源平均自信息量（即信源的熵）可表示为H(X)=E[I(x)]= 。

3、在离散联合概率空间[XY,P(xy)] 上随机变量I(xy) 的数学期望H（XY）= ，若集合X与集合Y相互独立，则H（XY）= 。

4、若给定离散联合概率空间[XY,P(xy)]，则x与y之间的互信息量I(x;y)= ；平均互信息量可用熵和条件熵表示即I(X;Y)= = ，其中条件熵H(X|Y)通常称为熵，条件熵H(Y|X) 称为____________熵；若集合X与集合Y相互独立，则H(X|Y) = ，H(Y|X) = ，平均互信息量I(X;Y)= 。

5、离散信源的冗余度是R表示信源消息的可压缩____________，设信源符号集的最大熵为Ho，实际熵为Ｈ∞，则冗余度Ｒ可表示为______________；信源编码目的就是通过减少或消除信源____________来提高信息传输效率，因此信源编码亦称__________性编码，而信道编码则称__________性编码。

6、对于连续随机变量，在峰值功率受限于P m的条件下，取得最大相对熵的最佳概率密度函数是一个恒值即W opt(x)=_________,称W(x)为__________分布，这时最大相对熵H cmax=__________。

7、对于平均功率受限，均值不为零的一维连续随机变量的方差为定值时，其取得最大相熵的最佳概率密度函数为正态分布，即Wopt(x)= _________ ，最大相对熵H cmax=__________。

8、假设任一随机变量X与一正态分布随机变量具有相同的相对熵Ｈｃ，则其等效正态分布的随机变量Ｘ的熵功率为Ｐ＝；可以用信号平均功率和熵功率的相对差值_________来表示连续信源的冗余度。