数学初二上人教新资料第十一章全等三角形检测题(扶沟)

数学初二上人教新资料第十一章全等三角形检测题（扶沟）吕潭二中 八年级数学组 李铁城 赵光磊【一】填空题〔每题3分，共30分〕1.判定两个三角形全等除用定义外，还有几种方法，它们分别能够简写成_______；_______；_______；_______；_________、2、，如图，AD =AC ，BD =BC ，O 为AB 上一点，那么，图中共有 对全等三角形、3、如图，△ABC ≌△ADE ，那么，AB = ，∠E =∠ 、假设∠BAE =120°，∠BAD =40°，那么∠BAC = 、4、如图，∠ABC ＝∠DCB ，再添加条件_____ 或条件______，就能够判定△ABC ≌△DCB 、第4题图5、如图，AC ＝BD ，21∠=∠，那么△ABC ≌ ， 其判定依照是__________、6、如图，ABC ∆中，BC AD ⊥于D ，要使△ABD ≌△ACD ，假设依照“HL ”判定，还需加条件___ ＝ ___、7、如图，AC ＝BD ，D A ∠=∠，请你添一个直截了当条件， ＝ ， 使△AFC ≌△DEB 、8. 如图，在△ABC 中，∠C=90°，AD 平分∠CAB ；DE ⊥AB 于E ，假设AC=8，那么AE=________、9. 如图，线段AE ，BD 交于点C ，且AC=EC ，BC=DC ，那么AB 与DE 的关系是__________。

10. 如图：AB ⊥BC ，CD ⊥BC ，垂足分别为B ，C ，AB=BC ，E 为BC的中点，且AE ⊥BD 于F ，假设CD=4cm ，那么AB 的长度为__________。

【二】选择题〔每题3分，共18分〕AD 第5题图 第6题图 第7题图B AC BA E D 第2题图 第3题图BA DCE A 、全等三角形的对应高、对应中线、对应角的平分线相等B 、有两个角和其中一个角的平分线对应相等的两个三角形全等C 、有两条边和其中一边上的中线对应相等的两个三角形全等D 、有两条边和其中一边上的高对应相等的两个三角形全等12、一个三角形的周长为15厘米，且其中两边都等于第三边的2倍，那么那个三角形的最短边为〔〕A 、1厘米B 、2厘米C 、3厘米D 、4厘米13、在△ABC 中，∠A ＝55°，∠B 比∠C 大25°，那么∠B 的度数为〔〕A 、50°B 、75°C 、100°D 、125°14、如图，CD ⊥AB 于D ，现有四个条件：①AD=ED ②∠A=∠BED ③∠C=∠B ④AC=EB ，那么不能得出△ADC ≌△EDB 的条件是〔〕 A 、①③B 、②④C 、①④D 、②③15、如图，在中，，点，，在边上，且，，那么图中全等三角形共有〔 〕 A 、2对 B 、3对 C 、4对 D 、5对16.如图，在△ABC 中，∠ACB=9O °，AC=BC ，BE ⊥CE 于D ，DE=4cm ，AD=6cm ，那么BE 的长是 ( ) A 、2cm B 、1.5cm C 、1cm D 、3cm【三】解答题17〔10分〕.小明在练习本上画的△ABC 被墨迹污染〔如下图〕，请你关心小明用尺规作一个与原来完全重合的△。

(完整版)初二上第十一章三角形单元测试及答案(人教版)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)初二上第十一章三角形单元测试及答案(人教版)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)初二上第十一章三角形单元测试及答案(人教版)的全部内容。

（完整版）初二上第十一章三角形单元测试及答案（人教版)编辑整理：张嬗雒老师尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布到文库，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是我们任然希望（完整版）初二上第十一章三角形单元测试及答案(人教版）这篇文档能够给您的工作和学习带来便利。

同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉，前进的动力。

本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为〈（完整版）初二上第十一章三角形单元测试及答案(人教版)〉这篇文档的全部内容。

DDD DDCB ACCCC BBBBAAAAA初二上第十一章三角形单元测试及答案（人教版)（时限：100分钟 总分：100分）一、选择题：将下列各题正确答案的代号的选项填在下表中。

（每小题2分,共24分。

）1.如图，△ABC 中，∠C ＝75°,若沿图中虚线截去∠C ，则∠1＋∠2＝（ ) A 。

360° B. 180° C 。

255° D 。

145°2.若三条线段中a ＝3，b ＝5,c 为奇数, 那么由a,b,c 为边组成的三角形共有（ ）A 。

初中数学试卷鼎尚图文**整理制作第十一章 全等三角形测试题（A ）4分，共40分） 、下列说法正确的是（ ）：全等三角形是指形状相同的两个三角形 C ：全等三角形的周长和面积分别相等 C ：全等三角形是指面积相等的两个三角形 D ：所有的等边三角形都是全等三角形 2、如图：若△ABE ≌△ACF ，且AB=5，AE=2，则EC 的长为（ ）A ：2B ：3C ：5D ：2.5、如图：在△ABC 中，AB=AC ，∠BAD=∠CAD ，则下列结论：①△ABD ≌△ACD ，②∠B=∠C ，③BD=CD ，④AD ⊥BC 。

其中正确的个数有（ ）：1个 B ：2个 C ：3个 D ：4个4、如图：AB=AD ，AE 平分∠BAD ，则图中有（ ）对全等三角形。

A ：2 B ：3 C ：4 D ：5、如图：在△ABC 中，AD 平分∠BAC 交BC 于D ，AE ⊥BC 于E ，∠B=40°，∠BAC=82°，则∠DAE=（ ） ：7 B ：8° C ：9° D ：10° 、如图：在△ABC 中，AD 是∠BAC 的平分线，DE ⊥AC 于E ，DF ⊥AB 于F ，且FB=CE ，则下列结论：：①DE=DF ，②AE=AF ， ③BD=CD ，④AD ⊥BC 。

其中正确的个数有（ ） ：1个 B ：2个 C ：3个 D ：4个7、如图：EA ∥DF ，AE=DF ，要使△AEC ≌△DBF ，则只要（ ） A ：AB=CD B ：EC=BF C ：∠A=∠D D ：AB=BC8、如图：在不等边△ABC 中，PM ⊥AB ，垂足为M ，PN ⊥AC ，垂足为N ， 且PM=PN ，Q 在AC 上，PQ=QA ，下列结论：①AN=AM ，②QP ∥AM ，③△BMP ≌△QNP ，其中正确的是（ ） ：①②③ B ：①② C ：②③ D ：①9、如图：直线a ，b ，c 表示三条相互交叉环湖而建的公路，现在建立一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ）A ：1个B ：2个C ：3个D ：4个10、如图：△ABC 中，∠C=90°，AC=BC ，AD 平分∠CAB 交BC 于D ，DE ⊥AB 于E ，且AB=6㎝，则△DEB 的周长是（ ） A ：6㎝ B ：4㎝ C ：10㎝ D ：以上都不对 11、如图：AD 是△ABC 的高，E 为AC 上一点，BE 交AD 于F ，且有BF=AC ，FD=CD 。

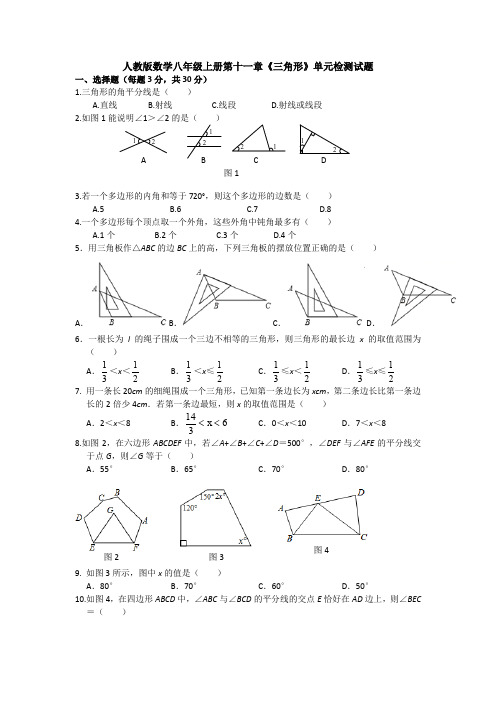
人教版数学八年级上册第十一章三角形单元检测题一、选择题(每小题3分，共30分)1．如图所示，图中三角形的个数是( )A．2个B．3个C．4个D．5个2．下列线段能构成三角形的是( )A．2、2、4 B．3、4、5 C．1、2、3 D．2、3、63．下列图形具有稳定性的是( )4．如图在△ABC中，点D是BC延长线上一点，∠B＝40°，∠ACD＝120°，则∠A等于( )A．60° B．70° C．80° D．90°5．下列命题中正确的是( )A．各角都相等的多边形为正多边形B．各边都相等的多边形为正多边形C．经过n边形的一个顶点可引(n－2)条对角线D．正方形是正多边形6．(柳州中考)如图，图中直角三角形共有( )A．1个 B．2个 C．3个 D．4个7．如图，在△ABC中有四条线段DE、BE、EG、FG，其中有一条线段是△ABC的中线，则该线段是( )A．线段DE B．线段BE C．线段EG D．线段FG8．如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A＝60°，∠B＝40°，则∠ECD等于( )A．40° B．45° C．50° D．55°9．若一个多边形的内角和小于其外角和，则这个多边形的边数是( )A．3 B．4 C．5 D．610．如图，将一张三角形纸片ABC的一角折叠，使点A落在△ABC外的A′处，折痕为DE.如果∠A＝α，∠CEA′＝β，∠BDA′＝γ，那么下列式子中正确的是( )A．γ＝2α＋β B．γ＝α＋2β C．γ＝α＋β D．γ＝180°－α－β二、填空题(每小题3分，共24分)11．如图，以AC为边的三角形有．12．如图，ED⊥AB，BC⊥AC，则△ABE中，AE边上的高是，△ABE中，AB 边上的高是，△ABC中，AC边上的高是．13．如图O是△ABC的重心，AO的延长线交BC于点E.则S△ABE＝．14．用八根木条钉成如图所示的八边形木架，要使它不变形，至少要钉上木条的根数是．15．如图所示，在△ABC中，D、E分别是AB、AC上的点，点F在BC的延长线上，DE∥BC，∠A＝46°，∠1＝52°，则∠2＝．16．在△ABC中，三个内角∠A、∠B、∠C满足∠B－∠A＝∠C－∠B，则∠B＝．17．已知某三角形的两边长分别是2和6，第三边长是奇数，则第三边长为．18．已知非直角三角形ABC中，∠A＝45°，高BD与CE所在直线交于点H，则∠BHC的度数是．三、解答题(共66分)19．(8分)如图，在△ABC中：(1)画出BC边上的高AD和中线AE；(2)若∠B＝30°，∠ACB＝130°，求∠BAD和∠CAD的度数．20．(8分)一个多边形中，每个内角都相等，并且每个外角都等于它的相邻内角的13，求这个多边形的边数及内角和．21．(8分)已知等腰三角形一腰上的中线将三角形的周长分成9cm和15cm两部分．求这个三角形的腰长和底边的长．22．(10分)如图，在△ABC中，已知AD⊥BC，∠B＝64°，∠C＝56°.(1)求∠BAD和∠DAC的度数；(2)若DE平分∠ADB，求∠AED的度数．23．(10分)若∠A与∠B的两边分别垂直，请判断这两个角的数量关系．(1)如图①，∠A与∠B的数量关系是；如图②，∠A与∠B的数量关系是；对于上面的两种情况，请用文字语言叙述：；(2)请选择图①或图②中的一种进行说明．24．(10分)如图，在△ABC中，AD平分∠BAC，P为线段AD上一个动点，PE⊥AD 交直线BC于点E.(1)若∠B＝35°，∠ACB＝85°，求∠E的度数；(2)当P点在线段AD上运动时，猜想∠E与∠B、∠ACB的数量关系(无需说明理由)．25．(12分)如图①，已知线段AB、CD相交于点O，连接AD、CB，我们把形如图①的图形称之为“8字形”．试解答下列问题：(1)在图①中，写出∠A、∠B、∠C、∠D之间的关系；(2)如图②，在(1)的结论下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于点M、N.①仔细观察，在图②中有个以线段AD为边的“8字形”；②若∠D＝40°，∠B＝36°，试求∠P的度数；③当∠D和∠B为任意角时，其他条件不变，试直接写出∠P与∠D，∠B之间的数量关系，不需说明理由．答案： 一、1-10 ACACD CBCAAA 二、11. △ABC 、△AOC 、△ACD 、△ACE 12. BC DE BC 13. S △AEC ＝12S △ABC14. 5 15. 98° 16. 60° 17. 5或7 18. 135°或45° 三、19. 解：(1)如图所示：(2)因为AD 是高，所以∠ADB ＝90°，在△ABD 中，∠BAD ＝180°－∠B －∠ADB ＝60°，因为∠ACB 是△ACD 的外角，所以∠CAD ＝∠ACB －∠ADC ＝130°－90°＝40°.解：设每个内角度数为3x ，则每个外角度数为x.设多边形边数为n ，则有nx ＝360°，3nx ＝(n －2)×180°，求得n ＝8.内角和：(8－2)×180°＝1080°.20. 解：设每个内角度数为3x ，则每个外角度数为x.设多边形边数为n ，则有nx ＝360°，3nx ＝(n －2)×180°，求得n ＝8.内角和：(8－2)×180°＝1080°. 21. 解：设腰长为xcm ，当x ＋12x ＝9时，解得x ＝6，则底边为：15－12×6＝12，此时6＋6＝12＜15，不能构成三角形；当x ＋12x ＝15时，解得x ＝10，则底边为9－12×10＝4，此时三边长分别为10cm 、10cm 、4cm ，能构成三角形，所以这个三角形腰长为10cm ，底边长为4cm.22. 解：(1)∵AD ⊥BC ，∴∠B ＋∠BAD ＝90°，∠C ＋∠CAD ＝90°.∴∠BAD ＝90°－∠B ，∠CAD ＝90°－∠C.∵∠B ＝64°，∠C ＝56°，∴∠BAD ＝90°－64°＝26°，∠CAD ＝90°－56°＝34°；(2)∵DE 平分∠ADB ，∴∠ADE ＝12∠ADB ＝12×90°＝45°.∴∠AED ＝180°－(∠BAD ＋∠ADE)＝180°－(26°＋45°)＝109°.23. 解：(1)∠A ＝∠B ；∠A ＋∠B ＝180°；如果一个角的两边与另一个角的两边分别垂直，那么这两个角的数量关系是相等或互补；(2)选择图①，∵BC ⊥AC ，BD ⊥AD ，∴∠ACB ＝∠ADB ＝90°.又∵∠AED ＝∠BEC(对顶角相等)，∴∠A ＝∠B.选择图②，∵BC ⊥AC ，BD ⊥AD ，∴∠ACB ＝∠ADB ＝90°.∵四边形的内角和等于360°，∴∠A ＋∠B ＝360°－90°－90°＝180°.(任选一种说明即可)24. 解：(1)∠E ＝25°；(2)∠E ＝12(∠ACB －∠B)．∵∠ADE ＝∠B ＋12∠BAC ，而∠E ＋∠ADE ＝90°，∴∠B＋12∠BAC ＋∠E ＝90°，∠BAC ＝180°－(∠ACB ＋∠B)，∴∠B ＋12[180°－(∠ACB ＋∠B)]＋∠E ＝90°，∴∠E ＝12(∠ACB －∠B)．25. 解：(1)∠A ＋∠D ＝∠B ＋∠C ；(2)①3；②∵∠DAB 和∠BCD 的平分线AP 和CP 相交于点P ，∴∠1＝∠2，∠3＝∠4.∵∠1＋∠D ＝∠3＋∠P ，∠2＋∠P ＝∠4＋∠B ，∴∠D －∠P ＝∠P －∠B ，即∠P ＝12(∠D ＋∠B)．∵∠D ＝40°，∠B ＝36°，∴∠P ＝12(40°＋36°)＝38°；③∠P ＝12(∠B ＋∠D)．。

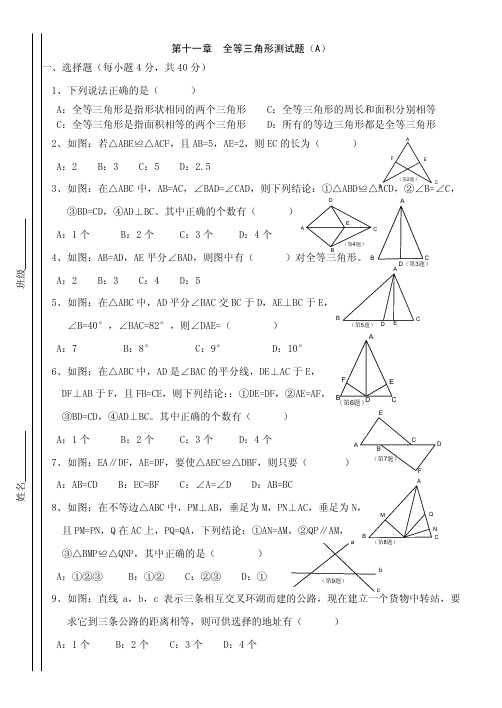
人教版数学八年级上册第十一章《三角形》单元检测试题一、选择题（每题3分，共30分） 1.三角形的角平分线是（ ）A.直线B.射线C.线段D.射线或线段 2.如图1能说明∠1＞∠2的是（ ）3.若一个多边形的内角和等于720°，则这个多边形的边数是（ ）A.5B.6C.7D.84.一个多边形每个顶点取一个外角，这些外角中钝角最多有（ ）A.1个B.2个C.3个D.4个5．用三角板作△ABC 的边BC 上的高，下列三角板的摆放位置正确的是（ ）A ．B ．C ．D ．6．一根长为l 的绳子围成一个三边不相等的三角形，则三角形的最长边x 的取值范围为（ ） A ．31＜x ＜21 B ．31＜x ≤21C ．31≤x ＜21D ．31≤x ≤217. 用一条长20cm 的细绳围成一个三角形，已知第一条边长为xcm ，第二条边长比第一条边长的2倍少4cm ．若第一条边最短，则x 的取值范围是（ ） A ．2＜x ＜8B ．6314<<x C ．0＜x ＜10 D ．7＜x ＜88.如图2，在六边形ABCDEF 中，若∠A +∠B +∠C +∠D ＝500°，∠DEF 与∠AFE 的平分线交于点G ，则∠G 等于（ ） A ．55° B ．65° C ．70° D ．80°9. 如图3所示，图中x 的值是（ ） A ．80° B ．70° C ．60° D ．50°10.如图4，在四边形ABCD 中，∠ABC 与∠BCD 的平分线的交点E 恰好在AD 边上，则∠BEC ＝（ ）121221 D C B A 图1 图2 图3 图4A ．∠A +∠D ﹣45°B ．21（∠A +∠D ）+45° C ．180°﹣（∠A +∠D ）D ．21∠A +21∠D二、填空题（每题3分，共24分）11.如图5，在△ABC 中，BD ＝CD ，∠ABE ＝∠CBE ，则线段_______是△ABC 的中线，ED 是△_______的中线；△ABC 的角平分线是_______，BF 是△_______的角平分线.12.在Rt △ABC 中，若∠C 是直角，∠A ＝30°，那么∠B ＝_______.13.图6①、②、③中，具有稳定性的是图 14.如图7，∠A +∠B +∠C +∠D +∠E ＝ 180° ．15.△ABC 的三个内角满足5∠A ＞7∠B ，5∠C ＜2∠B ，则△ABC 是 三角形（填“锐角”、“直角”或“钝角”）16定义：当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的一个内角为48°，那么这个“特征角”α的度数为 ．17.如图8，已知AO ＝10，P 是射线ON 上一动点（即P 点可在射线ON 上运动），∠AON ＝60°．（1）OP ＝ 时，△AOP 为直角三角形．（2）设OP ＝x ，则x 满足 时，△AOP 为钝角三角形．18.如图（1）），在△ABC 中，∠ABC ，∠ACB 的角平分线交于点O ，则∠BOC ＝90°+21∠A ＝21×180°+21∠A ．如图9（2），在△ABC 中，∠ABC ，∠ACB 的两条三等分角线分别对应交于O 1，O 2，则∠BO 1C ＝32×180°+31∠A ，∠BO 2C ＝31×180°+32∠A ．根据以上阅读理解，你能猜想∠BO 2018C ＝ ．D C B AEF 图5 图6图7 图8三、解答题19. 如图10，在五边形ABCDE 中满足AB ∥CD ，求图形中的x 的值．20. （1）已知三角形三个内角的度数比为1：2：3，求这个三角形三个外角的度数． （2）一个正多边形的内角和为1800°，求这个多边形的边数．21. 如图11，四边形ABCD 中，BE 、CF 分别是∠B 、∠D 的平分线．且∠A ＝∠C ＝90°，试猜想BE 与DF 有何位置关系？请说明理由．22. 已知：如图12，在△ABC 中，AB ＝3，AC ＝5． （1）直接写出BC 的取值范围是 ．（2）若点D 是BC 边上的一点，∠BAC ＝85°，∠ADC ＝140°，∠BAD ＝∠B ，求∠C ．23.如图13，在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，若∠A ＝42°． （1）求∠BOC 的度数；（2）把（1）中∠A ＝42°这个条件去掉，试探索∠BOC 和∠A 之间有怎样的数量关系．图9（1）（2）（3）图10图11 图12 图1324. 如图14，AC 平分∠DCE ，且与BE 的延长线交于点A ． （1）如果∠A ＝35°，∠B ＝30°，则∠BEC ＝ ．（直接在横线上填写度数）（2）小明经过改变∠A ，∠B 的度数进行多次探究，得出∠A 、∠B 、∠BEC 三个角之间存在固定的数量关系，请你用一个等式表示出这个关系，并进行证明． 解：（2）关系式为： 证明：25. 【探究发现】 如图15（1），在△ABC 中，点P 是内角∠ABC 和外角∠ACD 的角平分线的交点，试猜想∠P 与∠A 之间的数量关系，并证明你的猜想．【迁移拓展】 如图15（2），在△ABC 中，点P 是内角∠ABC 和外角∠ACD 的n 等分线的交点，即∠PBC ＝n 1∠ABC ，∠PCD ＝n1∠ACD ， 试猜想∠P 与∠A 之间的数量关系，并证明你的猜想． 【应用创新】已知，如图15（3），AD 、BE 相交于点C ，∠ABC 、∠CDE 、∠ACE 的角平分线交于点P ，∠A ＝35°，∠E ＝25°，则∠BPD ＝ ．参考答案：一、1.C ；2.C ；3.B ；4.C ； 5. A 提示：B ，C ，D 都不是△ABC 的边BC 上的高，故选：A ． 6. A 提示：设三角形的其他两边为：y ，z ，∵x +y +z ＝l ，y +z ＞x ∴可得x ＜21， 又因为x 为最长边大于31，∴31＜x ＜21；故选：A ． 7. B 提示：根据题意可得：第二条边长为（2x ﹣4）米，图14 图15 （1）） （2） （3）∴第三条边长为20﹣x ﹣（2x ﹣4）＝（24﹣3x ）米；由题意得⎪⎪⎪⎩⎪⎪⎪⎨⎧->-+->-+>->->4232432442324420x x x x x x x x x x x ，解得6314<<x ．故选：B ． 8. C 提示：六边形ABCDEF 的内角和是：（6﹣2）×180°＝4×180°＝720° ∵∠A +∠B +∠C +∠D ＝500°，∴∠DEF +∠AFE ＝720°﹣500°＝220°， ∵GE 平分∠DEF ，GF 平分∠AFE ， ∴∠GEF +∠GFE ＝21（∠DEF +∠AFE ）＝21×220°＝110°， ∴∠G ＝180°﹣110°＝70°．故选：C ．9. C 提示：∵图形是五边形，∴120°+150°+2x °+x °+90°＝（5﹣2）×180°， 解得：x ＝60°，故选：C ．10. D 提示：∵四边形的内角和＝360°，∴∠ABC +∠BCD ＝360°﹣（∠A +∠D ）， ∵∠ABC 与∠BCD 的平分线的交点E 恰好在AD 边上， ∴2∠EBC ＝∠ABC ，2∠ECB ＝∠BCD ，∴∠EBC +∠ECB ＝)(21BCD ABC ∠+∠=[])(36021D A ∠+∠-︒⨯， ∴∠BEC ＝180°﹣（∠EBC +∠ECB ）＝180°﹣[])(36021D A ∠+∠-︒⨯＝)(21D A ∠+∠，故选：D ．二、11.AD 、BEC 、BE 、ABD ；12.60°；13. ①②提示：∵三角形具有稳定性，∴①②具有稳定性．14. 180°提示：利用三角形的外角的性质得：∠1＝∠D +∠E ，∠2＝∠A +∠B ， 所以∠A +∠B +∠C +∠D +∠E ＝∠2+∠C +∠1＝180°，15. 钝角提示：∵5∠A ＞7∠B ，2∠B ＞5∠C ，∴5∠A +2∠B ＞7∠B +5∠C ， 即5∠A +＞5∠B +5∠C ，∴∠A ＞∠B +∠C ，不等式两边加∠A ，可得2∠A ＞∠A +∠B +∠C ，而∠A +∠B +∠C ＝180°，∴2∠A ＞180°，即∠A ＞90°， ∴这个三角形是钝角三角形．16. 48°或96°或88°提示：当“特征角”为48°时，即α＝48°；当β＝48°，则“特征角”α＝2×48°＝96°； 当第三个角为48°时，α+21α+48°＝180°，即得α＝88°， 综上所述，这个“特征角”α的度数为48°或96°或88°． 17. （1）5或20（2）0＜x ＜5或x ＞20 提示：（1）当∠APO ＝90°时，∠OAP ＝90°﹣∠AOP ＝30°， ∴OP ＝OA ＝5，当∠OAP ＝90°时，∠OPA ＝90°﹣∠AOP ＝30°， ∴OP ＝2OA ＝20，（2）当0＜x ＜5或x ＞20时，△AOP 为钝角三角形，18. +∠A 提示：如图3，根据题中所给的信息，总结可得： ∠BO 1C ＝×180°+∠A ，∠BO n ﹣1C ＝×180°+∠A ．∴当n ﹣1＝2018时，n ＝2019，即∠BO 2018C ＝+∠A ．三、解答题19. 解：∵AB ∥CD ，∠C ＝60°，∴∠B ＝180°﹣60°＝120°， ∴（5﹣2）×180°＝x +150°+125°+60°+120°，∴x ＝85°． 20. 解：（1）设此三角形三个内角的比为x ，2x ，3x ， 则x +2x +3x ＝180，6x ＝180，x ＝30， 则三个内角分别为30°、60°、90°，相应的三个外角分别为150°、120°、90°． （2）设这个多边形的边数是n ，则（n ﹣2）•180°＝1800°，解得n ＝12．故这个多边形的边数为12． 21. 解：BE ∥DF ，理由是：∵四边形内角和等于360°，∠A ＝∠C ＝90°，∴∠ABC +∠ADC ＝180°， ∵BE 、CF 分别是∠B 、∠D 的平分线，∴∠1＝21∠ABC ，∠2＝21∠ADC ， ∴∠1+∠2＝90°，∵在Rt △DCF 中，∠3+∠2＝90°，∴∠1＝∠3，∴BE ∥DF ． 22. 解：（1）2＜BC ＜8，故答案为：2＜BC ＜8（2）∵∠ADC 是△ABD 的外角∴∠ADC ＝∠B +∠BAD ＝140° ∵∠B ＝∠BAD ∴∠B ＝︒=︒⨯7014021∵∠B +∠BAC +∠C ＝180° ∴∠C ＝180°﹣∠B ﹣∠BAC 即∠C ＝180°﹣70°﹣85°＝25° 23. 解：（1）∵∠A ＝42°，∴∠ABC +∠ACB ＝180°﹣∠A ＝138°，∵BO 、CO 分别是△ABC 的角∠ABC 、∠ACB 的平分线，∴∠1＝21∠ABC ，∠2＝21∠ACB ， ∴∠1+∠2＝21（∠ABC +∠ACB ）＝＝69°，∴∠BOC ＝180°﹣（∠1+∠2）＝180°﹣69°＝111°；（2）∠BOC ＝90°+21∠A ， ∵BO 、CO 分别是△ABC 的角∠ABC 、∠ACB 的平分线，∴∠1＝21∠ABC ，∠2＝∠ACB ， ∴∠1+∠2＝21（∠ABC +∠ACB ）＝21（180°﹣∠A ），∴∠BOC ＝180°﹣（∠1+∠2）＝180-)180(21A ∠-︒＝A ∠-︒2190．24. 解：（1）∵∠A ＝35°，∠B ＝30°，∴∠ACD ＝∠A +∠B ＝65°， 又∵AC 平分∠DCE ，∴∠ACE ＝∠ACD ＝65°，∴∠BEC ＝∠A +∠ACE ＝35°+65°＝100°， （2）关系式为∠BEC ＝2∠A +∠B ． 理由：∵AC 平分∠DCE ， ∴∠ACD ＝∠ACE ，∵∠BEC ＝∠A +∠ACE ＝∠A +∠ACD ， ∵∠ACD ＝∠A +∠B ，∴∠BEC ＝∠A +∠A +∠B ＝2∠A +∠B ． 25. 解：（1）∠A ＝2∠P ，理由如下：∵BP 是△ABC 中∠ABC 的平分线，CP 是∠ACB 的外角的平分线， ∴∠PBC ＝21∠ABC ，∠PCD ＝21∠ACD ， ∵∠ACD 是△ABC 的外角，∠PCD 是△BPC 的外角，∴∠ACD ＝∠ABC +∠A ，∠PCD ＝∠PBC +∠P ，∴21∠ACD ＝21∠ABC +21∠A ， ∴21∠ABC +21∠A ＝∠PBC +∠P ， ∴∠A ＝2∠P ；（2）∠A ＝n ∠P ，理由如下：∵点P 是内角∠ABC 和外角∠ACD 的n 等分线的交点， ∴∠PBC ＝∠ABC ，∠PCD ＝∠ACE ．∵∠ACD 是△ABC 的外角，∠PCD 是△BPC 的外角， ∴∠ACD ＝∠ABC +∠A ，∠PCD ＝∠PBC +∠P ， ∴n 1∠ACD ＝n 1∠ABC +n1∠A ，∴n 1∠ABC +n1∠A ＝∠PBC +∠P ， ∴∠A ＝n ∠P ；（3）∵∠ABC 、∠CDE 、∠ACE 的角平分线交于点P ， ∴由（1）的结论知，∠BPC ＝21∠A ＝，∠CPD ＝21∠E ＝，∴∠BPD ＝∠BPC +∠DPC ＝30°，故答案为：30°．人教版八年级上册第十一章三角形单元测试(3)一、选择题(每题3分，共30分)1．如图，∠1的大小等于()A．40°B．50°C．60°D．70°(第1题)(第4题)2．下列长度的三条线段，能组成三角形的是()A．2 cm，3 cm，4 cm B．2 cm，3 cm，5 cmC．2 cm，5 cm，10 cm D．8 cm，4 cm，4 cm3．在△ABC中，能说明△ABC是直角三角形的是()A．∠A：∠B ：∠C＝1 ：2 ：2 B．∠A ：∠B ：∠C＝3 ：4 ：5 C．∠A ：∠B ：∠C＝1 ：2 ：3 D．∠A ：∠B ：∠C＝2 ：3 ：4 4．如图，在△ABC中，∠A＝80°，∠B＝40°，D，E分别是AB，AC上的点，且DE∥BC，则∠AED的度数是()A．40°B．60°C．80°D．120°5．在下列各图形中，分别画出了△ABC中BC边上的高AD，其中正确的是()6．如图，△ABC的角平分线BE，CF相交于点O，且∠FOE＝121°，则∠A的度数是()A．52°B．62°C．64°D．72°(第6题) (第7题)(第9题) (第10题)7．如图，在△ABC中，∠C＝90°，D，E是AC上两点，且AE＝DE，BD平分∠EBC.下列说法不正确．．．的是()A．BE是△ABD的中线B．BD是△BCE的角平分线C．∠1＝∠2＝∠3 D．BC是△ABE的高8．一个多边形的内角和比它的外角和的3倍少180°，这个多边形的边数是()A．8 B．7 C．6 D．59．如图，在△ABC中，∠C＝75°，若沿图中虚线截去∠C，则∠1＋∠2＝()A．360°B．180°C．255°D．145°10．如图，∠A，∠B，∠C，∠D，∠E五个角的和等于()A．90°B．180°C．360°D．540°二、填空题(每题3分，共24分)11．人站在晃动的公交车上，若分开两腿站立，还需伸出一只手抓住栏杆才能站稳，这是利用了___________________________________________________．12．正十边形每个外角的度数是________．13．已知三角形三边长分别为1，x，5，则整数x＝________.14．将一副三角尺按如图所示放置，则∠1＝________．(第14题)(第16题)(第18题)15．一个多边形从一个顶点出发可以画9条对角线，则这个多边形的内角和为________．16．如图，在△ABC中，AD是BC边上的中线，BE是△ABD中AD边上的中线，若△ABC的面积是24，则△ABE的面积是________．17．当三角形中一个内角α是另一个内角β的一半时，我们称此三角形为“半角三角形”，其中α称为“半角”．若一个“半角三角形”的“半角”为20°，则这个“半角三角形”最大内角的度数为________． 18．已知△ABC ，有下列说法：(1)如图①，若P 是∠ABC 和∠ACB 的平分线的交点，则∠P ＝90°＋12∠A ； (2)如图②，若P 是∠ABC 和外角∠ACE 的平分线的交点，则∠P ＝90°－∠A ； (3)如图③，若P 是外角∠CBF 和∠BCE 的平分线的交点，则∠P ＝90°－12∠A . 其中正确的有______个．三、解答题(23题12分，24题14分，其余每题10分，共66分)19．如图，一艘轮船在A 处看见巡逻艇C 在其北偏东62°的方向上，此时一艘客船在B 处看见巡逻艇C 在其北偏东13°的方向上．试求此时在巡逻艇上看这两艘船的视角∠ACB 的度数．(第19题)20.如图，BD ，CE 是△ABC 的两条高，它们交于O 点． (1)∠1和∠2的大小关系如何？并说明理由． (2)若∠A ＝50°，∠ABC ＝70°，求∠3和∠4的度数．(第20题)21．如图，已知AD是△ABC的角平分线，CE是△ABC的高，AD，CE相交于点P，∠BAC＝66°，∠BCE＝40°.求∠ADC和∠APC的度数．(第21题)22．如图，六边形ABCDEF的内角都相等，CF∥AB.(1)求∠FCD的度数；(2)求证AF∥CD.(第22题)23．如图，在△ABC中，∠A＝30°，一块直角三角尺XYZ放置在△ABC上，恰好三角尺XYZ的两条直角边XY，XZ分别经过点B，C.(1)∠ABC＋∠ACB＝________，∠XBC＋∠XCB＝________，∠ABX＋∠ACX＝________．(2)若改变直角三角尺XYZ的位置，但三角尺XYZ的两条直角边XY，XZ仍然分别经过点B，C，则∠ABX＋∠ACX的大小是否变化？请说明理由．(第23题)24．已知∠MON＝40°，OE平分∠MON，点A，B，C分别是射线OM，OE，ON上的动点(点A，B，C均不与点O重合)，连接AC交射线OE于点D，设∠OAC＝x°.(1)如图①，若AB∥ON，则①∠ABO的度数是________．②当∠BAD＝∠ABD时，x＝________；当∠BAD＝∠BDA时，x＝________．(2)如图②，若AB⊥OM，是否存在这样的x的值，使得△ADB中有两个相等的角？若存在，求出x的值；若不存在，说明理由．(第24题)答案一、1.D 2.A 3.C 4.B 5.B 6.B7．C8.B9.C10.B二、11.三角形具有稳定性12.36°13．514.105°15.1 800°16.617．120°18.2三、19.解：由题意可得AD∥BF，∴∠BEA＝∠DAC＝62°.∵∠BEA是△CBE的一个外角，∴∠BEA＝∠ACB＋∠CBE.∴∠ACB＝∠BEA－∠CBE＝62°－13°＝49°.答：此时在巡逻艇上看这两艘船的视角∠ACB的度数为49°.20．解：(1)∠1＝∠2.理由如下：∵BD，CE是△ABC的两条高，∴∠AEC＝∠ADB＝90°.∵∠A＋∠1＋∠ADB＝180°，∠2＋∠A＋∠AEC＝180°，∴∠1＝∠2.(2)∵∠A＝50°，∠ABC＝70°，∠A＋∠ABC＋∠ACB＝180°，∴∠ACB＝60°.∵在△AEC中，∠A＋∠AEC＋∠2＝180°，∴∠2＝40°.∴∠3＝∠ACB－∠2＝20°.∵在四边形AE O D中，∠A＋∠AE O＋∠4＋∠AD O＝360°，∠A＝50°，∠AE O＝∠AD O＝90°，∴∠4＝130°.21．解：∵CE是△ABC的高，∴∠AEC＝90°.∴∠ACE＝180°－∠BAC－∠AEC＝24°.∵AD是△ABC的角平分线，∴∠DAC＝12∠BAC＝33°.∵∠BCE＝40°，∴∠ACB＝40°＋24°＝64°.∴∠ADC＝180°－∠DAC－∠ACB＝83°.∴∠A P C＝∠ADC＋∠BCE＝83°＋40°＝123°.22．(1)解：∵六边形ABCDEF的内角都相等，内角和为(6－2)×180°＝720°，∴∠B＝∠A＝∠BCD＝720°÷6＝120°.∵CF∥AB，∴∠B＋∠BCF＝180°.∴∠BCF＝60°.∴∠FCD＝∠BCD－∠BCF＝60°.(2)证明：∵CF∥AB，∴∠A＋∠AFC＝180°.∴∠AFC＝180°－120°＝60°.∴∠AFC＝∠FCD.∴AF∥CD.23．解：(1)150°；90°；60°(2)∠ABX＋∠ACX的大小不变．理由：在△ABC中，∠A＋∠ABC＋∠ACB＝180°，∠A＝30°，∴∠ABC＋∠ACB＝180°－30°＝150°.∵∠YXZ＝90°，∴∠X BC＋∠X CB＝90°.∴∠AB X＋∠AC X＝(∠ABC－∠X BC)＋(∠ACB－∠X CB)＝(∠ABC＋∠ACB)－(∠X BC＋∠X CB)＝150°－90°＝60°.∴∠AB X＋∠AC X的大小不变．24．解：(1)①20°②120；60(2)存在．①当点D在线段O B上时，若∠BAD＝∠ABD，则x＝20；若∠BAD＝∠BDA，则x＝35；若∠ADB＝∠ABD，则x＝50.②当点D在射线BE上时，易知∠ABE＝110°，又三角形的内角和为180°，∴只有∠BAD＝∠BDA，此时x＝125.综上可知，存在这样的x的值，使得△ADB中有两个相等的角，且x＝20，35，50或125.人教版八年级上册第十一章三角形单元测试(2)一、选择题（每题3分，共30分）1．三角形的三条高所在的直线相交于一点，这个交点的位置在（）（A）三角形内（B）三角形外（C）三角形边上（D）要根据三角形的形状才能定2．下列长度的各组线段中，能组成三角形的是（）（A）1、2、3（B）1、4、2（C）2、3、4（D）6、2、33．将一副三角板按如图所示的位置摆放在直尺上，则∠1的度数为（）A．60°B．65°C．75°D．85°4．一个多边形只有27条对角线，则这个多边形的边数为（）（A）8（B）9（C）10（D）115．若正多边形的内角和是540°，则该正多边形的一个外角为（）A．45°B．60°C．72°D．90°6．已知一个多边形的内角和为540°，则这个多边形为A．三角形 B．四边形 C．五边形 D．六边形7．如图为矩形ABCD，一条直线将该矩形分割成两个多边形，若这两个多边形的内角和分别为a和b，则a+b不可能是（）A．360°B．540°C．630°D．720°8．一个三角形的两边的长分别为3和8，第三边的长为奇数，则第三边的长为（）(A) ①5或7 (B) 7 (C) 9 (D) 7或99．如果一个多边形的内角和是外角和的5倍，那么这个多边形的边数是（）A．10 B．11 C．12 D．1310．如图，AB∥CD，AD，BC相交于O，∠BAD＝35°，∠BOD＝76°,则∠C的度数是( )(A) 31° (B) 35° (C) 41° (D) 76°二、填空题（每题3分，共30分）11．如果三条线段a、b、c，可组成三角形，且a=3，b=5，c是偶数，则c的值为．第10题12．△ABC中，已知∠A=800，∠B=700，则∠C= ．13．有四条线段，长分别为3cm、5cm、7cm、9cm，如果用这些线段组成三角形，可以组成个三角形．14．如果一个三角形的三个内角的度数比为1∶2∶3，则这个三角形是三角形．15．一个直角三角形两锐角的平分线所夹的钝角为．16．在△ABC中，∠A＝50°，∠B＝30°，点D在AB边上，连接CD，若△ACD为直角三角形，则∠BCD的度数为度．17．一个多边形的每一个外角都等于360，则该多边形的内角和等于18．用7根火柴棒首尾顺次连接摆成一个三角形，能摆成不同的三角形的个数为_____．19．如图2，将一副直角三角板叠在一起，使直角顶点重合于点O ，则 ∠AOB+∠DOC= ．20．如图，在图1中，互不重叠的三角形共有4个，在图2中，互不重叠的三角形共有7个，在图3中，互不重叠的三角形共有10则在第nn 的代数式表示）.三、解答题（共60分） 21．（本题6分）如图所示，小明欲从A 地去B 地，有三条路可走：①A →B ；②A →D →B ；③A →C →B ．（1）在没有其它因素的情况下，我们可以肯定小明是走①，理由是______．（2）小明绝对不会走③，因为③路程最长，即AC +BC ＞AD +DB ，你能说明其原因吗？22．（本题6分）正在修建的中山路有一形状如图13所示的三角形空地需要绿化，拟从点A出发，将ABC △分成面积相等的四个三角形，以便种上不同的花草，请你帮助规划出图案．23．（本题7分）一个多边形的内角和比外角和多３６０度，这是几边形？ 24．（本题7分）如图，在△ABC 中，AD 是高，AE 、BF 是角平分线，它们相交于点O BAC ＝50°，∠C ＝70°.求∠DAC 和∠BOA 的度数.ＤＡＢＣＰＩＯ图1 第20题图 图3 第21题图 DE AB C图1325．（本题8分）如图，求：∠Ａ＋∠Ｂ＋∠Ｃ＋∠Ｄ＋∠Ｅ＋∠Ｆ的度数．26．（本题8分）分别测量如图所示的△ABC 和△DEF 的内角 （1）你发现了什么？（2）你有何猜想？ （3）通过什么途径说明你的猜想？27．（本题9分）如图，△ABC 中，∠C=90°，∠A=30°． （1）作图：作AB 边上的高CD ，垂足为D ； （2）求∠ACD ，∠BCD ，∠B 的度数；（3）用刻度尺测量BC 和AB ，CD 和AC ，DB 和BC ，将三组线段分别相除（即将BC •的长度除以AB 的长度，CD 的长度除以AC 的长度，DB 的长度除以BC 的长度），你发现了什么规律？28．（本题9分）一块三角形优良品种试验田，现引进四种不同的种子进行对比试验，需要将这块地分成面积相等的四块，请你设计出两种划分方案供选择，画图说明。

人教版数学八年级上册第11单元《三角形》测试答案一．选择题：本大题有10个小题，每小题3分，共30分。

在每小题给出的四题号 1 2 3 4 5 6 7 8 9 10 答案BCCAADDDAD二．填空题：本大题有6个小题，每小题4分，共24分。

11. 512. 4 13. 540° 14. 10°或60° 15. 10016. 2三．解答题：本大题有7个小题，共66分。

解答应写出文字说明、证明过程或演算步骤。

17.（本小题满分6分） 略18.（本小题满分8分）解：（1）如图，AM 、CN 为所作；···········（各2分，共4分）（2）∵AM 、BN 为△ABC 的高，∴S △ABC =21AM ·BC=21CN ·AB ， ··············（2分）∴2163===AM CN AB BC ·····················（2分） 19. （本小题满分8分） 解：∵AD 是高， ∴∠ADC ＝90°，∵AE 是角平分线，∠BAC ＝80°，∴∠CAE ＝21∠BAC ＝40°， ················（2分）∵∠EAD ＝10°，∴∠CAD ＝30°， ·····················（2分） ∴∠C ＝60°， ······················（2分） ∴∠B ＝180°﹣∠BAC ﹣∠C ＝40° ·············（2分） 20. （本小题满分10分） （1）证明：如图∵AD//BC (已知)，∴∠1=∠3 (两直线平行，内错角相等)， ···········（1.5分） ∵∠1=∠2，∴∠3=∠2 (等量代换) ·················（1.5分） ∴EF//BD (同位角相等，两直线平行) ··············（1分） （2）解：∵AD//BC(已知) ，∴∠ABC+∠A=180° (两直线平行，同旁内角互补) . ·······（1分） ∵∠A=130° (已知)，∴∠ABC=50°. ·······················（1分） ∵DB 平分∠ABC (已知) ，∴∠3=21∠ABC=25°. ····················（1分）∴∠2=∠3=25°. ······················（1分） ∵在△CFE 中，∠CFE+∠2+∠C=180°(三角形内角和定理)，∠C=70°， ∴∠CFE=85° ·······················（2分） 21. （本小题满分10分）解：证明：五边形内角和为： ( 5-2 ) ×180°=540° ······（2分） ∵5个内角都相等，∴∠A=∠B=∠AED=5540= 108° ···············（2分）∵EF 平分∠AED ，∴∠1=∠2=54° ·······················（2分） ∵四边形的内角和为360°，在四边形ABFE 中，∠3=360°- ( 108°+108°+54° ) =90° ···········（2分） ∴EF ⊥BC ························（2分） 22. （本小题满分12分）（1）90 ··························（2分） （2）在△ABC 中，∵∠ABC+∠ACB+∠A=180°， ················（1分） 即∠ABD+∠DBC+∠DCB+∠ACD+∠BAC=180°， ·······（1分） 而∠DBC+∠DCB=90°， ··················（1分） ∴∠ABD+∠ACD=90°-∠BAC ， ···············（1分） ∴∠ABD+∠BAC=90°-∠ACD=70° . ·············（1分） 又∵MN//DE ，∴∠ABD=∠BAN . ····················（1分） 而∠BAN+∠BAC+∠CAM= 180°， ··············（1分） ∴∠ABD+∠BAC+∠CAM=180° ， ···············（1分） ∴∠CAM=180°- (∠ABD+∠BAC ) =110° ···········（2分） 23. （本小题满分12分） （1）∵∠ADC 是△ABD 的外角，∴∠ADC=∠BAD+∠B=105°， ················（0.5分） ∠DAE=∠BAC−∠BAD=30°， ················（0.5分） ∴∠ADE=∠AED=75°， ···················（1分） ∴∠CDE=105°−75°=30°； ················（1分） （2）∠BAD=2∠CDE ， ···················（1分） 理由如下：设∠BAD=x ，∴∠ADC=∠BAD+∠B=45°+x ， ···············（0.5分） ∠DAE=∠BAC−∠BAD=90°−x ， ···············（0.5分）∴∠ADE=∠AED=290x+︒， ·················（1分） ∴∠CDE=45°+x−290x +︒=21x ， ················（1分）∴∠BAD=2∠CDE ； （3）设∠BAD=x ，∴∠ADC=∠BAD+∠B=∠B+x ， ···············（1分） ∠DAE=∠BAC−∠BAD=180°−2∠C−x ， ············（1分）∴∠ADE=∠AED=∠C+21x ， ·················（1分）∴∠CDE=∠B+x−(∠C+21x)=21x ， ··············（1分）∴∠BAD=2∠CDE. ·····················（1分）人教版数学八上第11单元《三角形》测试解析一．选择题1. B【考点】三角形任何两边的和大于第三边【分析】根据三角形两边的和大于第三边即可【解答】A.4+6=10，故本选项错误；B.2+3＞4，故本选项正确；C.3+4＜8，故本选项错误；D.6+7＜14，故本选项错误。

初中数学人教版八年级上册实用资料11.2 与三角形有关的角基础巩固1.（题型三角度a）如图11-2-1，将三角板的直角顶点放在直角尺的一边上，∠1=30°，∠2=50°，则∠3的度数为（）图11-2-1A.80°B.50°C.30°D.20°2.（题型一）如图11-2-2，在△ABC中，∠A=80°，∠B=40°，D，E分别是AB，AC上的点，且DE∥BC，则∠AED的度数是（）图11-2-2A.40°B.60°C.80°D.120°3.（题型一）若三角形的一个内角等于另外两个内角之差，则这个三角形是（）A.锐角三角形B.直角三角形C.钝角三角形D.不能确定4.（题型一）如图11-2-3，一根直尺EF压在三角形30°的角∠BAC上，与两边AC，AB分别交于点M，N，那么∠CME+∠BNF=（）图11-2-3A.135°B.150°C.180°D.不能确定5.（题型一）如图11-2-4，在△ABC中，∠ABD=∠DBE=∠EBC，∠ACD=∠DCE=∠ECB，若∠BEC=145°，则∠BDC=（）图11-2-4A.100°B.105°C.110°D.115°6.（题型三角度a）将一副直角三角板，按图11-2-5叠放在一起，则图中α的度数是.图11-2-57.（题型一）如图11-2-6，EF∥BC，AC平分∠BAF，∠B=80°，则∠C的度数是．图11-2-68.（知识点2）如图11-2-7，在Rt△ACB中，∠ACB=90°，CD⊥AB，则图中互余的角有对.图11-2-79.（知识点3）如图11-2-8，已知在△ABC中，∠A=40°，剪去∠A后成四边形，∠1+∠2= °.图11-2-810.（知识点2）如图11-2-9，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=40°，∠C=60°.求∠DAE的度数.图11-2-911.（题型二角度b）如图11-2-10，∠1，∠2，∠3的大小关系是.图11-2-1012.（题型一）（1）如图11-2-11（1），有一块直角三角板XYZ放置在△ABC下，恰好三角板XYZ的两条直角边XY，XZ分别经过点B，C.在△ABC中，∠A=30°，则∠ABC+∠ACB=度，∠XBC+∠XCB=度.（2）如图11-2-11（2），改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY，XZ仍然分别经过点B，C，那么∠ABX+∠ACX的大小是否发生变化？若变化，请举例说明；若不变化，请求出∠ABX+∠ACX的大小.（1）（2）图11-2-1113.（题型一、二）（1）如图11-2-12，在△ABC中，AD⊥BC于点D，AE平分∠BAC，且∠C大于∠B.求证：∠EAD=12（∠C-∠B）.（2）若把问题（1）中的“AD⊥BC于点D”改为“点F为EA上一点且FD⊥BC于点D”，画出新的图形，并说明∠EFD=12（∠C-∠B）．（3）若把问题（2）中的“F为EA上一点”改为“F为AE延长线上的一点”，则问题（2）中的结论成立吗？说明你的理由.图11-2-1214.（题型一）如图11-2-13，在Rt△ABC中，∠C=90°，点D，E分别是△ABC边AC，BC上的点，点P是一动点.令∠PDA=∠1，∠PEB=∠2，∠DPE=α.（注：四边形的内角和是360°）（1）若点P在线段AB上，如图11-2-13（1），且α=50°，则∠1+∠2= .（2）若点P在边AB上运动，如图11-2-13（2），则α，∠1，∠2之间的关系为 .（1）（2）（3）（4）图11-2-13（3）若点P运动到边AB的延长线上，图11-2-13（3），则α，∠1，∠2之间有何关系？请写出你的猜想，并说明理由.（4）若点P运动到△ABC外，如图11-2-13（4），则α，∠1，∠2之间的关系为.答案基础巩固1. D 解析：如图D11-2-1，∵BC∥DE，∴∠CBD=∠2=50°.又∵∠CB D为△ABC的外角，∴∠CBD=∠1+∠3，即∠3=∠CBD-∠1=50°-30°=20°.故选D.图D11-2-12. B 解析：∵DE∥BC，∠B=40°，∴∠A DE=∠B=40°.又∵∠A=80°，∴在△ADE中，∠AED=180°-∠A-∠A DE=180°-80°-40°=60°（三角形的内角和定理）.故选B.3. B 解析：设此三角形的三个内角分别是∠1，∠2，∠3（其中∠3最大），根据题意，得∠1=∠3-∠2，∴∠1+∠2=∠3.又∵∠1+∠2+∠3=180°，∴2∠3=180°，∴∠3=90°，∴这个三角形是直角三角形.故选B.4. B 解析：∵∠A+∠AMN+∠ANM=180°，∠A=30°，∴∠AMN+∠ANM=180°-∠A=180°-30°=150°.∵∠AMN=∠CME，∠ANM=∠BNF，∴∠CME+∠BNF=∠AMN+∠ANM=150°.故选B.5. C 解析：在△BCE中，∵∠BEC=145°，∴∠EBC+∠ECB=180°-145°=35°.∵∠DBE=∠EBC，∠DCE=∠ECB，∴∠DBC+∠DCB=2（∠EBC+∠ECB）=2×35°=70°.在△BCD中，∠BDC=180°-（∠DBC+∠DCB）=180°-70°=110°.故选C. 6. 75°解析：如图D11-2-2，∠1=90°-60°=30°，所以α=45°+∠1=45°+30°=75°.图D11-2-2 图D11-2-37. 50°解析：∵EF∥BC，∴∠BAF=180°-∠B=100°.∵AC平分∠BAF，∴∠CAB=12∠BAF=50°.∴∠C=180°-∠B-∠CAB=50°.8. 4 解析：由直角三角形的两个锐角互余，得∠ACD+∠A=90°，∠BCD+∠B=∠90°，∠A+∠B=90°.∵∠ACB=90°，∴∠BCD+∠ACD=90°.∴互余的角有4对.9. 220解析：如图D11-2-3，∠1+∠2=（∠A+∠4）+（∠A+∠3）=∠A+（∠A+∠3+∠4）=∠A+180°.∵∠A=40°，∴∠1+∠2=40°+180°=220°.10. 解：在△ABC中，∠B=40°，∠C=60°，∴∠BAC=80°.∵AE平分∠BAC，∴∠BAE=40°.又∵AD⊥BC，∠B=40°，∴∠BAD=90°-40°=50°.∴∠DAE=∠BAD-∠BAE=50°-40°=10°.能力提升11. ∠3>∠1>∠2 解析：如图D11-2-4，∵∠3=∠1+∠5，∴∠3＞∠1.∵∠1=∠2+∠4，∴∠1＞∠2.∴∠3＞∠1＞∠2.图D11-2-412. 解：（1）∵∠A=30°，∴∠ABC+∠ACB=180°-∠A=150°.∵∠X=90°，∴∠XBC+∠XCB=90°.（2）不变化．∵∠A=30°，∴∠ABC+∠ACB=150°.∵∠X=90°，∴∠XBC+∠XCB=90°.∴∠ABX+∠ACX=（∠ABC-∠XBC）+（∠ACB-∠XCB）=（∠ABC+∠ACB）-（∠XBC+∠XCB）=150°-90°=60°.13.（1）证明：在Rt△ADE中，∵∠AED+∠DAE=90°，∴∠DAE=90°-∠AED.∵∠AED=180°-∠C-∠CAE，且AE平分∠BAC，∴∠CAE=12∠BAC=12（180°-∠C-∠B）.∴∠EAD=90°-180°-∠C-1/2（180°-∠C-∠B）=12（∠C-∠B）.（2）解：如图D11-2-5（1），由三角形的内角和定理的推论，得∠FED=∠B+12∠BAC，故∠B+12∠BAC+∠EFD=90°①.在△ABC中，由三角形的内角和定理，得∠B+∠BAC+∠C=180°，即12∠C+12∠B+12∠BAC=90°②.②-①，得∠EFD=12（∠C-∠B）.（3）解：成立.理由：如图D11-2-5（2），由三角形的内角和定理的推论，得∠FED=∠AEC=∠B+12∠BAC，故∠B+12∠BAC+∠EFD=90°①.在△ABC中，由三角形的内角和定理，得∠B+∠BAC+∠C=180°，即12∠C+12∠B+12∠BAC=90°②.②-①，得∠EFD=1（∠C-∠B）.2（1）（2）图D11-2-514. 解：（1）∵∠1+∠2+∠CDP+∠CEP=360°，∠C+α+∠CDP+∠CEP=360°，∴∠1+∠2=∠C+α.∵∠C=90°，α=50°，∴∠1+∠2=140°.（2）由（1）得α+∠C=∠1+∠2，∴∠1+∠2=90°+α.（3）∠1=90°+∠2+α.理由如下：如图D11-2-6（1），∵∠2+α=∠DME，∠DME+∠C=∠1，∴∠1=∠C+∠2+α=90°+∠2+α．（4）如图D11-2-6（2），∵∠PFC=∠DFE，∴α+180°-∠1=∠C+180°-∠2，∴∠2=90°+∠1-α．（1）（2）图D11-2-6。

八年级（上）第十一章全等三角形（时间：90分钟，满分120分）章测试题一、选择题（每题3分，共30分） 1、下列说法正确的是（ ）A 、全等三角形是指形状相同的三角形B 、全等三角形是指面积相等的三角形C 、全等三角形的周长和面积分别相等D 、所有的等边三角形都是全等三角形 2、已知MB ＝ND ，∠MBA ＝∠NDC ，下列条件不能判定△ABM ≌△CDN 的是（） A 、∠M ＝∠N B 、AB ＝CD C 、AM ＝ D 、AM//3、如图，在△ABC 中∠A:∠B:∠C=3:5:10，且△MNC ≌△ABC ，则∠BCM:∠B 等于（ ）A 、1：4B 、1：5C 、2：3D 、以上都不对 4、在△ABC 和△A ／B ／C ／中，已知∠A=∠A ／，AB=A ／B ／，下列说法中错误的是（ ） A 、若增加条件AC=A ／C ／,则△ABC ≌△A ／B ／C ／（SAS ） B 、若增加条件BC=B ／C ／,则△ABC ≌△A ／B ／C ／（SAS ） C 、若增加条件∠B=∠B ／,则△ABC ≌△A ／B ／C ／（ASA ） D 、若增加条件∠C=∠C ／,则△ABC ≌△A ／B ／C ／（AAS ）5、如图,在Rt △ABC 中,∠C=90°AD 的平分∠BAC, ∠BAD=20°,则∠B 的度数为( )A. 40°B. 30°C. 60°D. 50°MABCN（第3题图）B C（第2题图）（第5题图）D（第6题图）6、如图, ∠C=90°,AD 平分∠BAC 交BC 于D,若BC=5cm,BD=3cm,则点D 到AB 的距离为( )A. 5cmB. 3cmC. 2cmD. 不能确定7、如图，从下列四个条件:①BC=B ／C ；②AC=A ／C ③∠ACB=∠A ／CB ／：④AB=A ／B ／中，任取三个为条件，余下的一个为结论，则最多可以构成正确的结论的个数是（ ）A 、1个B 、2个C 、3个D 、4个8、如图，△ABC 中，AB=AC ，三条高AD 、BE 、CF 相交于点O ，那么图中全等的三角形有（ ）A 、5对B 、6对C 、7对D 、8对 9、三角形中到三边的距离相等的点是( )A 、三条边的垂直平分线的交点B 、三条高的交点C 、三条中线的交点D 、三条角平分线的交点10、如图，E 是等边△ABC 中AC 边上的点，∠1=∠2，BE=CD ，且AD ∥BC ，则对△ADE 的形状最准确的判断是（ ）A 、等腰三角形B 、等边三角形C 、不等边三角形D 、不能确定形状 二、填空题（每题3分，共30分）11、如图，AB=AD ，∠1=∠2，添加一个适当的条件，使△ABC≌△ADE，则需要添加的条件是。