一维势垒贯穿时透射系数的计算与MATLAB分析

格式：doc
大小：15.01 KB
文档页数：4

下载文档原格式

163一维势阱和势垒问题

mn
0,
mn mn
克罗内克符号
二、势垒穿透和隧道效应
有限高的方形势垒
数学形式：
U
(
x)
0,
U 0 ,
图形形式：
x 0(P区),x a(S区) 0 x a(Q区)
U
考虑粒子的动能 E小于势垒高
U0
度 U0的情况。（ E < U0 ）
E
PQ S
o ax
U (x) 0, x 0和x a
1
(0 x a)
(x 0及x a)
2
势阱内 0 < x < a
d 2 1
dx2
2E
2
1
0
势阱外 x ≤ 0 ;x ≥a
2 0
理由:因为势壁无限高,所以粒子不能穿透势壁,故势阱外的波函数为零
定态薛定谔方程为
d 2
d x2
2E
2
0
E是粒子的总能量，E > 0，令 k
定态薛定谔方程变为
d 2
一维无限深方势阱的图形表达形式：
∞∞
U(x)
粒子只能在宽为 a 的两个无限高势壁间运动，这种势称为一维无限深方势阱。
0
ax
因为系统的势能与时间无关，因此这是一个定态问题，可以用定态薛定谔方程进行求解。
2
2
2
U
(r)
(r )
E
(r )
————定态薛定谔方程
①列出各区域的定态薛定谔方程
若在样品与针尖之间
加一微小电压Ub电子就会穿过电极间的势
垒形成隧道电流。
隧道电流对针尖与样品间的距离十分敏感。若控制隧道电流不变，则探针在垂直于样品方向上的高度变化就能反映样品表面的起伏。

量子力学3.4666势垒贯穿

（7）
以上二式说明入射粒子一部分贯穿势垒到 x a 的III区域，另一部分则被势垒反射回来。
D R 1
表明粒子数守恒
§2.8 势垒贯穿续5
（2）E<U0情形
V ( x)
1 2
2 k2 2 (E U0 )
令其中
V0
是虚数
k 2 ik 3
1 2
I
II
III
4k12 k32 D 2 (k1 k32 ) 2 sh 2 ak3 4k12 k32
（9）
此结果表明，即使 E U 0，透射系数 D 一般不等于零。隧道效应（tunnel effect）粒子能够穿透比它动能更高的势垒的现象称为隧道效应.它是粒子具有波动性的生动表现。当然，这种现象只在一定条件下才比较显著。右图给出了势垒穿透的波动图象。
代入
k1 k1 ik1a 1 C ik2 a { ( A A ') ( A A ')}e (1 )e 2 2k 2 2 k2
{ A(k1 k2 ) A '(k2 k1 )}eik2 a C (k1 k2 )eik1a
k2 k1 ik2 a ik1a C {A A ' }e e k1 k2
(k1 k2 ) 2 (k2 k1 ) 2 ) ik1a C { } Ae (k1 k2 ) 2 e ik2 a (k2 k1 ) 2 eik2 a
4k1k2 e ik1a C A 2 ik2 a 2 ik2 a (k1 k2 ) e (k2 k1 ) e
(k2 k1 ) (e e ) ik2 a ik1a C {1 } Ae e 2 ik2 a 2 ik2 a (k1 k2 ) e (k2 k1 ) e

2.8势垒贯穿

求解ቤተ መጻሕፍቲ ባይዱ性方程组
4k1k2e−ik1a C= A 2 −ik2a 2 ik2a (k1 +k2) e −(k1 −k2) e
′ A=
2 2 2i(k1 −k2 )sin k2a
(k1 −k2) e
2 ik2a
−(k1 +k2) e
2 −ik2a
A
（3）讨论
关心的问题：粒子被反射和透射的可能性有多大？
（2）解方程
ψ ″ + k 2ψ = 0 1 1 1 ″ ψ 2 + k 22ψ 2 = 0 ″ ψ 3 + k12ψ 3 = 0
x≤0 0< x<a x≥a
I II III
解得： ψ 1 = Aeik1x + A′e −ik1 x ψ 2 = Beik2 x + B′e −ik2 x ψ 3 = Ce ik1x + C ′e −ik1x
其中k3=[2µ(V0-E)/ ℏ]1/2。把前面公式中的 k2 换成 ik3，并注意 sin ik3a = i sh k3a，得：
4 k12 k 32 = 2 ( k1 + k 32 ) 2 sh 2 k 3 a + 4 k12 k 32 ( k12 + k 32 ) 2 sh 2 k 3 a = 2 ( k1 + k 32 ) 2 sh 2 k 3 a + 4k12 k 32
′ A=
2 2i(k12 −k2 )sin k2a
(k1 +k2) e
2 −ik2a
−(k1 −k2) e
2 ik2a
A
透射系数
2 J D | C |2 4 k 12 k 2 D= = = 2 2 2 2 JI | A| ( k1 − k 2 ) 2 sin 2 k 2 a + 4 k 12 k 2

一维势垒散射

。可以先看一下书上图7.7，给出了基本散射本征态的示意图。在第六章，从一个波包到本征态的转变利用的是光谱的方法。在一维势垒散射中对于每一个E都存在本征态。波包的边界条件决定了本征态的的边界条件，它们是相互对应的，
由左边入射的波包，在能量为E时的傅里叶变换得到相应的本征态相应的，本征态是完备的，可以对展开
这里，用到了7.14式，而且入射波包在态上没有投影。
现在考虑反射波包的能级光谱。它的导出与入射波包的能级光谱相似，我们也用代替，这时候取T为波包分开后足够长时间的时刻。
最后考虑透射波包的能级光谱
反射和透射系数
现在，计算反射和透射系数。将上述得到的入射光谱，反射和透射光谱代入到反射和透射系数公式，得到
但是，从图上看入射波包与出射波包存在重叠项。我们可以定义一个2 2 的相关函数矩阵。注意，这个相关矩阵是对称的 7.34是时间反演对称的表达式：从到的变换等于从到的变换。
7.2.2 S-矩阵
假定，我们只考虑在特定能量E时从
的跃迁振幅。这种振幅跃迁应该由从入射的波包与从出射的波包
的交叉项确定。因为反应物波包和生成物波包能量取值有一定的范围，当我们计算某一时刻的交叉项时,
数是有限的，这就是S-矩阵元。
通过代换和积分，得到该式与7.42比较，得到从7.45可以看出S-矩阵的矩阵元是相关函数矩阵中相应的矩阵元的傅立叶变换。
现在，得到S-矩阵
其中，
反射与透射系数 S-矩阵中的矩阵元与反射和透射系数相关，得到从左边入射的波包的反射与透射系数为
从右边入射的波包的反射和透射系数
由7.31式
，知道与相等，即从左边入射波包的透射系数与从右边的透射系数相等，
又因为透射系数反射系数和仍为1，

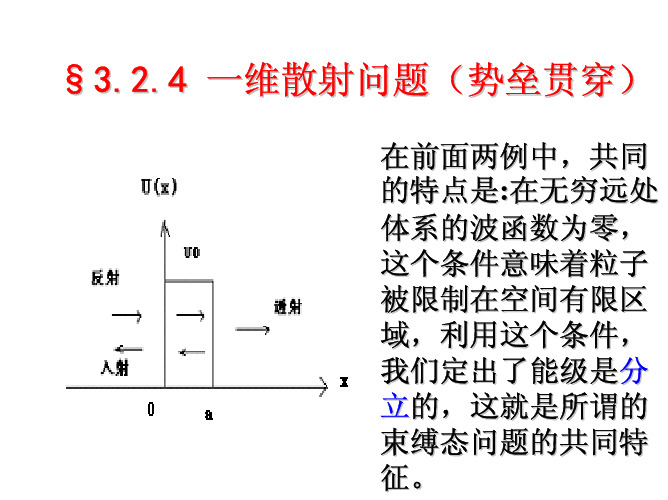
Chapter 3-2 一维定态问题(下)

(23)
k 又因 k1 和 k3同数量级， 3 a >> 1 时，
e
2 k3 a
>> 4
(24)
a + b ≥ a b , ( a > 0 , b > 0 ) li m (∵ x→ ∞ 2 k3 k1 ∴ + ≥ 2 k3 k1 k3 ⎞ 1 ⎛ k1 e 2 k3a ≥ e 2 k3a > > 4 ) + ⎜ ⎟ k1 ⎠ 4 ⎝ k3
贯穿U(x)的总D为所有小方势垒 Ddx 之乘积
D = ∏ D dx = D 0 e
dx − 2
∫
a
b
2 m (U ( x ) − E )dx
(27)
§3.3 一维谐振子
一般说来，间断型的势场并非严格意义下的物理势场。在物理上 V ( r ) 应该是 r 的连续函数。特别是在物理的实际问题中，经常需要处理连续振动体系，它们都可等价地看成无穷多个谐振子的集合。
而要级数含有限项的条件是 λ 为奇数：
λ = 2 n + 1, n = 0,1, 2...
由此可求得线性谐振子之能级为
(10)
⎛ 1⎞ E = ω ⎜ n + ⎟ , n = 0,1,2... ⎝ 2⎠
(11)
即具有零点能，能级间隔 ∆E = En+1 − En = ω ，这是量子力学的结果，它与经典谐振子及 Planck 量子论结果均不同。经典谐振子能量连续，按Planck量子论有 En = n ω ，∆E = ω ，但 E0 = 0 ，无零点能存在。
相比可略去，因而在 ξ → ∞ 时，上面的方程(6)可写为：
d ψ dξ 2
2

势垒贯穿解读课件

微电子学
微电子学是研究在微米和纳米尺度下电子行为和应用的科学。在微电子学中，势垒贯穿是一个重要的概念，用于描述电子通过势垒的传输过程。
在微电子器件中，如晶体管、二极管和集成电路，势垒贯穿决定了电子的流动和器件的性能。通过优化势垒参数，可以提高器件的开关速度和降低能耗。
量子计算
量子计算是一种基于量子力学原理的计算方式，具有经典计算无法比拟的并行性和计算速度。势垒贯穿在量子计算中扮演着关键角色。
结构设计
通过改变势垒的结构设计，如采用多级势垒、异质结等结构，实现对电子传输的更精细调控。
势垒贯穿与其他领域的交叉研究
物理与化学
势垒贯穿涉及到物理和化学等多个学科领域，交叉研究有助于深入理解势垒贯穿的机制和拓展其应用范围。
生物医学应用
势垒贯穿技术在生物医学领域如传感器、诊断和治疗等方面具有潜在的应用价值，开展交叉研究有助于推动相关领域的发展。
量子比特是量子计算的基本单元，而势垒贯穿决定了量子比特的相干性和演化过程。通过控制势垒参数，可以实现量子比特的逻辑门操作和量子算法的实现。
纳米科技
纳米科技是一门研究在纳米尺度上设计和制备材料、器件和系统的科学。在纳米科技中，势垒贯穿是一个重要的物理现象，影响纳米器件的性能和稳定性。
在纳米尺度下，材料和系统的性质与宏观尺度有很大的不同，因此需要深入研究势垒贯穿的机制和规律。通过优化势垒参数，可以提高纳米器件的效率、稳定性和可靠性。
深入了解实验中如何观测和验证量子力学中的现象。
THANKS
感谢观看
确保实验过程中使用的电压和电流在安全范围内，避免对实验人
员和设备造成伤害。
实验精度要求
在实验过程中，要确保显微镜的焦距、电压和电流的测量精度，以提高实验结果的准确性。

势垒贯穿与应用解读

势垒贯穿与应用势垒贯穿设一个质量为m 的粒子，沿x 轴正方向运动，其势能为： U(x)=0 x<0 和x>a U(x)=U 0 0≤x ≤a这种势能分布称为一维势垒。

粒子在 x < 0 区域里，若其能量小于势垒高度，经典物理来看是不能越过势垒达到 x > a 的区域。

在量子力学中，情况又如果呢？为讨论方便，我们把整个空间分成三个区域：在各个区域的波函数分别表示为ψ1 ψ2 ψ3三个区间的薛定谔方程简化为：求出解的形式是)(),0(),0(a x a x x ≥I ∏≤≤∏≤I ),()(212122x E dx x d m ϕϕ=- 0≤x ),()()(22202222x E x U dxx d m ϕϕϕ=+- ax ≤≤0),()(232322x E dxx d m ϕϕ=- a x ≥222 mEk =2021)(2 E U m k -=,0)()(12212≤=+x x k dxx d ϕϕa x x k dxx d ≤≤=-0,0)()(221222ϕϕa x x k dxx d ≥=+,0)()(32232ϕϕikxikx e A Ae -'+=ψ1x ik Be 12+=ψikx Ce =ψ3O(1)E>U 0按照经典力学观点,在E>U 0情况下，粒子应畅通无阻地全部通过势垒，而不会在势垒壁上发生反射而在微观粒子的情形，却会发生反射。

(2)E<U 0从解薛定谔方程的结果来看，在势垒内部存在波函数ψ。

即在势垒内部找出粒子的概率不为零，同时，在x>a 区域也存在波函数，所以粒子还可能穿过势垒进入x>a 区域粒子在总能量E 小于势垒高度时仍能贯穿势垒的现象称为隧道效应定义粒子穿过势垒的贯穿系数是：透射波的概率密度与入射波概率密度的比值。

势垒高度U 0越低、势垒宽a 度越小，则粒子穿过势垒的概率就越大。

隧道效应是经典力学所无法解释的由于电子的隧道效应，金属中的电子并不完全局限于表面边界之内，电子密度并不在表面边界处突变为零，而是在表面以外呈指数形式衰减，衰减长度约为1nm只要将原子线度的极细探针以及被研究物质的表面作为两个电极，当样品与针尖的距离非常接近时，它们的表面电子云就可能重叠若在样品与针尖之间加一微小电压U b 电子就会穿过电极间的势垒形成隧道电流。

一维势垒问题总结

一维势垒中的透射系数利用传递矩阵方法研究了粒子在一维势垒中运动时的粒子的透射系数,主要研究的是在一个方势垒两个方势垒中透射系数，对以上的透射系数的总结，推出了对于任意势垒中透射系数，并讨论了透射系数、反射系数与势垒宽度的关系.一维方势垒势垒模型在方势垒中，遇到的问题和值得注意的地方。

在求方势垒波函数中，首先要知道这是一个什么样问题，满足什么样的方程，方程可以写成什么样的形式，在求解方程中，波函数的形式应该怎样需要怎样的分段，分段的过程中，特别要强调的边界条件问题。

并且验证了概率流密度。

在量子力学中，粒子在势垒附近发生的现象是不一样的，能量E 大于势垒高度0u 的粒子在势垒中有一部分发生反射，而能量小于0u 的粒子也会有部分穿过势垒，这在经典力学中是不会发生的。

下面讨论的是一维散射（即在非束缚态下问题，在无穷远处波函数不趋于零）。

重点讨论的是粒子通过势垒的透射和反射，重点在于求出波函数，这就必须求解薛定谔方程，由于)(x U 是与时间无关的，此处是定态薛定谔方程。

定态薛定谔方程通式：ψψψE U m=+∇-222h 在量子力学里, 必须知道波函数ψ, 因此必须要解薛定谔方程t i U x m ∂∂=+∂∂-ψψψh h 2222一维散射问题是一个非束缚态问题(()U x 与时间无关, 而E 是正的).因此令t Ei ex t x h-=)(),(ψψ由此得到ψψψE U dx d m =+-2222h按照势能()U x 的形式, 方程(2)一般需要分成几个部分求解.将上式改写成如下形式0222=+ψψk dxd⎩⎨⎧><<<=.,0,0;0,)(0a x x a x u x U 先讨论0u E >的情形粒子满足薛定谔方程分解为三个区域：⎪⎪⎪⎩⎪⎪⎪⎨⎧>=-<<=+-<=-a x x E x dx d m a x x E x u x dx d m x x E x dx d m ),()(20),()()(20),()(233222220222211222ψψψψψψψh h h （1） ⎪⎪⎪⎩⎪⎪⎪⎨⎧>=+<<=-+<=+a x x mEx dx d a x x u E x dx d x x mEx dxd ,0)(2)(0,0)()()(0,0)(2)(323222022212122ψψψψψψh h特征方程02=++q pr r 的两个根21,r r方程 0=+'+''qy y p y 的通解两个不相等的实根21r r ≠ x r x r e C e C y 2121+= 两个相等的实根21r r = x r e x C C y 1)(21+= 一对共轭复根βαi r ±=2,1)sin cos (21x C x C e y x ββα+=注： 0=+''qy y 的通解:特征方程02=+q r ,当0<q 时，通解xq xq eC e C y ---+=21，当0>q 时，通解xq ixq ie C e C y -+=21方程（1）的解可以表示为：⎪⎪⎪⎩⎪⎪⎪⎨⎧>+=<<+=<+=-----a x de te x a x ce be x x re ae x x mEi x mE i x u E m i x u E m i x mE i x mE i ,)(0,)(0,)(223)(2)(2222100h h hh hh ψψψ （2）定态波函数321,,ψψψ再分别乘上一个含时间的因子Et i eh-，可以看到式子（2）的三式，第一项是左向右传播的平面波，第二项是由右向左传播的平面波，即入射波和反射波。

§9势垒贯穿

但是，施加一个外电场，金属中电子的所感受到的电势如图(b)所示。金属中电子面对一个势垒，能量最大的电子就能通过隧道效应穿过势垒漏出，从而导致所谓场致电子发射。
图（a）
图（b）
三，扫描隧穿显微镜（STM） STM(Scanning Tunneling Microscope) I 是观察固体表面原子情况的 A B S 超高倍显微镜。
用扫描隧穿显微镜拍摄的硅表面的象，每一个隆起处是一个硅原子。
世界上最小的文字：
1990年1月，美国加利福尼亚州圣何塞IBM阿莫登研
究中心的科学家宣称：他们利用扫描隧穿显微镜移动并重新排列氙和镍表面的单个原子以便出其公司的开
头字母：IBM。
1993年美国加州 IBM Almaden 研究中心的研究人员，用扫描隧穿显微镜(STM)操纵，将48个铁原子在铜的表面排列成一个圆圈，形成量子围栏(Quantum Corral) ，电子被束缚在其中，其波函数形成同心圆状涟漪细浪。
2 2i ( k 12 k2 ) sin k2a
C
4k1k2e A 2 ik2a 2 ik2 a ( k1 k2 ) e ( k1 k2 ) e
ik1a
A
( k1 k2 ) e
2
ik2a
( k1 k2 ) e
2
ik2 a
A
4. 透射系数和反射系数
I 透射系数：透射波几率流密度与入射波几率流密度之比称为透射系数 D = JD/JI
1。原理隧道电流 I 与样品和针尖间的距离S 关系极为敏感。
势能曲线
U U0
E
扫描探针A
S 10A
样品 B
定量关系：

一维高斯积分点坐标和权重系数计算 matlab

一维高斯积分点坐标和权重系数计算在数值分析和数值计算中，一维高斯积分是一种常用的数值积分方法。

它通过一组特定的积分点坐标和权重系数来近似计算给定函数的定积分，具有高精度和快速收敛的特点。

在实际工程和科学计算中，一维高斯积分常常被广泛应用于有限元分析、求解常微分方程和偏微分方程等领域。

掌握一维高斯积分点坐标和权重系数的计算方法及其在matlab中的实现是非常重要的。

一维高斯积分的基本思想是将定积分转化为对一组特定积分点的加权求和，从而实现对定积分的近似计算。

一维高斯积分点坐标和权重系数的选择对积分精度和收敛速度有着重要影响。

常用的一维高斯积分点坐标和权重系数的计算方法有多种，其中比较常用的是Legendre多项式求解法、Jacobi矩阵方法和递推关系法等。

这些方法在matlab 中都能够很方便地实现，下面将逐一介绍它们的原理和具体实现。

1. Legendre多项式求解法Legendre多项式是一种重要的正交多项式，在计算高斯积分点和权重系数时可以利用Legendre多项式的求解方法。

通过对Legendre多项式的根和权重的计算，可以得到一维高斯积分点坐标和权重系数的近似值。

在matlab中，可以使用`legendre`函数来计算Legendre多项式的根和权重，然后进一步得到一维高斯积分点和权重系数。

2. Jacobi矩阵方法Jacobi矩阵方法是另一种计算一维高斯积分点和权重系数的常用方法。

它通过Jacobi矩阵的特征值和特征向量来计算高斯积分点和权重系数，具有较高的计算精度和稳定性。

在matlab中，可以使用`jacobi`函数来实现Jacobi矩阵方法的计算，并进一步得到一维高斯积分点坐标和权重系数。

3. 递推关系法递推关系法是一种简单而有效的计算一维高斯积分点和权重系数的方法。

它通过递推关系来逐步计算高斯积分点和权重系数，具有较快的计算速度和较高的计算精度。

在matlab中，可以编写简单的递推算法来实现一维高斯积分点坐标和权重系数的计算。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一维势垒贯穿时透射系数的计算与MATLAB分析
Abstract：The paper firstly derives transmission coefficient for one-dimensional square barrier and one-dimensional general potential， and then uses Matlab to accurate transmission coefficients. This paper also discusses the influence of the energy of incident particles， the width and height of potential to the transmission coefficient. Then this paper discusses the influence of the width of potential to calculational error in a kind of approximate algorithm for calculating transmission coefficient in many textbooks.
Key Words：Potential barrier penetration；Transmission coefficient； Matlab
在量子力学中，对于纳米量级的薄势垒层[1]，如果向它射入能量比势垒高度低的粒子，在势垒后侧能够发现虽然很小但并不为零的粒子概率密度，这种穿透势垒的现象称为量子隧道效应[2-3]。

在理论和实践中计算出粒子贯穿势垒时的透射系数都具有重要意义。

量子力学是描述微观粒子运动的理论，其计算常复杂繁琐，但随着计算机技术的发展，使得许多繁琐计算都迎t刃而解。

以往很多作者对单方势垒
和多方势垒条件下的透射系数进行了研究，该文对一维一般势垒的透射系数进行理论推导，然后用Matlab程序对透射系数进行定量计算。

1 一维势垒贯穿概率模型的构建
1.1 一维方势垒
3 粒子贯穿一维势垒程序运行示例及讨论
3.1 粒子贯穿方势垒程序运行示例及讨论
利用2.2节中程序源代码，输入相关参数和相关势垒函数便可快速得到电子贯穿一维势垒时透射系数和反射系数。

表1为相关运行示例。

从表1中可以看到，透射系数D和反射系数R之和S为1；从A.1组中知E为0时透射系数为0，反射系数为1，即没有粒子去贯穿势垒，认为全部粒子都被反射；从B组1号和C组1～6号看到电子能量从小于势垒能量到等于势垒能量，再到大于势垒能量对一定高度和宽度的势垒进行贯穿时透射系数逐渐增大，反射系数逐渐减小；从D组1～3号到B 组1号可知用一定能量的电子去贯穿一定宽度的势垒时，随着势垒高度越大，透射系数逐渐减小，反射系数逐渐增大；从B组1～4号可知，电子入射能量一定，势垒高度一定，势垒宽度渐增，透射系数递减，反射系数递增，并且相当敏感。

由于透射系数与反射系数之和为1，当知道其一时便知
其二，接下来将用B组数据与大多数教材中的计算隧道效应透射系数的一种近似算法进行比较。

得d1=54.13%，d2=47.14%，d3=28.27%，d4=15.75%。

从d的变化可看到随着a递增，D1与B组中越接近。

B组中数据是没有经过近似处理的，属于准确值，上述的近似处理算法在势垒宽度a越小时误差越大。

3.2 粒子贯穿一般势垒程序运行示例及讨论
上面讨论了电子贯穿方势垒透射系数，接下来讨论电子贯穿一般势垒程序运行示例。

从表3中E组1号和D组1-3号可得随着一维线性势垒高度递增，透射系数递减，反射系数递增，从E.1和F组可看出，相同能量的电子贯穿相同高度势垒，势垒越厚实，透射系数越小，反射系数越大。

至此定量计算了电子贯穿一维方势垒和一维一般势垒的一些透射系数和反射系数，并定性讨论了电子入射能量与势垒宽度及高度对透射系数与反射系数的影响。

文中程序只是对电子贯穿一维势垒透射系数反射系数的计算。

如果要定量的计算别的粒子贯穿一维势垒的透射系数与反射系数，只须将程序中u换为相应粒子质量，便可快速得到结果。

4 结语
该文对粒子贯穿一维方势垒及一维一般势垒的透射系数进行理论推导，再用Matlab程序对电子贯穿一般势垒时
的透射系数进行数值计算。

从计算程序来看只需在MATLAB 软件环境下输入相关参数和势垒函数，便可快速得到粒子贯穿一维势垒时的透射系数。

该文利用所编程序，定量计算了电子贯穿一维势垒时透射系数，并定性的讨论了电子入射能量与势垒宽度及高度对透射系数的影响，而且把所得数据与周世勋所著《量子力学教程》中透射系数数据进行比较，讨论了众多教材中一种计算隧道效应透射系数的近似算法中势垒宽度对透射系数误差的影响。