地震子波波形显示及一维地震合成记录

人工合成地震记录程序设计（一）、人工合成地震记录原理：地震记录上看到的反射波波形是地震子波在地下各反射界面上发生反射时形成的。

反射波的振幅有大有小（决定于界面反射系数的绝对值）、极性有正有负（取决于反射系数的正负）、到达时间有先有后（取决于反射界面的深度）的地震反射子波叠加的结果。

如果地震子波的波形用S (t )表示，地震剖面的反射系数为双程垂直反射时间t 的函数，用R (t )表示，那么反射波地震记录形成的物理过程在数学上就可以用S (t )的R (t )的褶积表示，即某一时刻的反射波地震记录f (t )是:)()()(t R t S t f *=其离散形式为：))(()()(1t m n R t m S t n f M m ∆-⋅∆=∆∑=如果大地为多层介质，在地面记录长度内可接收的反射波地震记录为：))(()()(11t m n R t m S t n f Mm N n ∆-⋅∆=∆∑∑== 式中，n 为合成地震记录的采样序号，n =1,2,3...N ；N 为合成一道地震记录的采样点数；m =1,2,3...M ，为离散子波的采样点数；△t 为采样间隔。

这种褶积模型将地震波的实际传播过程进行了简化：1、在合成地震记录的过程中没有考虑大地的吸收作用，所有薄层的反射波都与地震子波的形式相同，只是振幅和符号不同。

2、假设地震波垂直入射到界面上，并原路径返回。

3、假设地层横向是均匀的，在深度（纵向）方向上假设密度为常数，只是速度发生变化。

4、不考虑地震波在传播过程中的透射损失。

（二）、人工合成地震记录的方法1、 反射系数序列在有速度测井资料的情况下，可以用速度曲线代替波阻抗曲线，计算反射系数序列。

在没有速度资料的情况下，可根据干扰波调查剖面分析的结果设计地质模型。

如设计的地质模型如图a 所示，图中H 为层厚度，V 为层速度，根据下式计算反射系数： 11)(--+-=N N N N N V V V V H R 式中H 为反射界面的深度，N 为反射层序号，随深度变化的反射系数序列如图b 所示。

实验一、地震子波波形显示及一维地震记录合成一、实验目的1、认识地震子波（以雷克子波为例），对子波有直观的认识。

2、利用线性褶积公式合成一维地震记录。

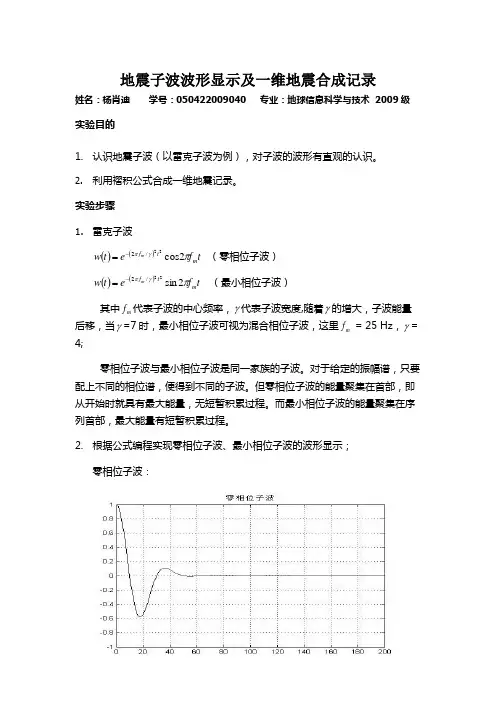
二、实验内容1、雷克子波：()()t f e t w m t f m πγπ2cos 22/2-=（零相位子波）、 ()()t f e t w m t f m πγπ2sin 22/2-=（最小相位子波）， 其中m f 代表子波的中心频率，γ代表子波频带宽度,随着γ的增大，子波能量后移，当γ=7时，最小相位子波可视为混合相位子波，这里取m f = 25 Hz ，γ= 3;2、根据公式编程实现零相位子波、最小相位子波的波形显示；3、设计反射系数)(n r (n=500)，其中0.1)100(=r ，7.0)200(-=r ，5.0)300(=r ，4.0)400(=r ，6.0)500(=r ，其它为0;4、应用褶积公式∑=-=*=Nm m n w m r n w n r n f 1)()()()()(合成一维地震记录，并图形显示；5、根据所学知识对实验结果进行分析。

三、实验要求1、独立完成程序设计工作；2、独立完成书面报告（A4纸打印）；3、提交程序源代码。

实习报告一姓名：王忠成学号：050422011042 专业年级：地信2011级当γ=3时，汇出最小相位子波和零相位子波图形，如下所示：当γ=5和γ=7时的波形图分别为：由雷克子波公式()()t f e t w m t f m πγπ2cos 22/2-=知：(2πf m /γ)2为一个指数衰减因子，当γ增大时，(2πf m /γ)2减小，故衰减变慢。

设计反射系数)(n r (n=500)，其中0.1)100(=r ，7.0)200(-=r ，5.0)300(=r ，4.0)400(=r ，6.0)500(=r ，其它为0。

应用褶积公式∑=-=*=N m m n w m r n w n r n f 1)()()()()(合成一维地震记录，对零相位子波和最小相位子波分别与r(n)褶积，汇出其图形如下：由图可知，两种波形的地震记录都有5个峰值，分别对应于5个分界面:r(100)、r(200)、r(300)、r(400)和r(500)，并且当r>0时，峰值为正，当r<0时，峰值为负。

合成地震记录制作地震,地震勘探我们知道计算合成地震记录的基本原理是,合成地震记录=子波与反射系数的褶积所以需要子波和反射系数.但是用于计算的数据一般是深度域的,要转换到时间域来必须有时深关系.所以.需要的数据:时间/深度关系数据:checkshot或者DT,用于计算反射系数的数据,一般是DT和密度(RHO B).基本步骤:1, 加载数据:如果是斜井的话,加载井斜,计算出SSTVD,设置成Prefered DS(deviation survey);如果有来自VSP或者其他可信渠道的时深关系的话加载进来,叫checkshot,就是时间,深度关系对,用于提供时深关系;加载DT,RHOB曲线;2,数据质量检查:查看checkshot数据覆盖范围,和品质;查看DT,RHOB曲线的品质,如果不好需要用well-edit或者synthetics里带的一些功能进行编辑.DT,RHOB曲线应该是做过Depth match,需要拼接的话是splice好的.3,制作合成地震记录:点击Post,依次选择时深关系,声波曲线,密度曲线(如果没有密度曲线或者品质不好也可以使用经验公式来代替),声波阻抗,反射系数,子波,合成地震记录,地震数据.软件完全是根据原理走的,如果时深关系没选,后续工作无法开展,如果没有DT,密度,就无法生成声波阻抗和反射系数...软件自带有Ricker30经验子波.如果效果不好可以自己提取子波,也可以使用时变子波.4,对比合成地震记录和井旁道实际地震记录,通过bulkshift或者拉伸压缩来调整时深关系.有时需要用c heckshot来校正DT.一般可能先使用Ricker30子波试一下,看看大致情况,如果效果不好,再尝试提取子波.这是一个反复实验的过程.合成地震记录的品质和制作的数据来源的品质有关,对比的好坏和实际地震数据的品质也有关系.总是实际情况总是复杂的.。

应用合成地震记录来标定地震层位是地震资料解释中非常重要的手段，也是将地震资料与测井资料相结合的一条纽带。

它最终使抽象的地震数据与实际的地质模型连接起来，为地震资料解释的可靠性提供了依据。

合成记录的精度将直接影响到地震地质层位标定的准确性，因此，提高合成记录的精度就成了地震层位标定的首要问题。

１合成记录的方法原理１．１合成地震记录制作的一般方法一般而言，人工合成地震记录，是利用声波和密度测井资料求取一反射系数序列，再将这一反射系数序列与某一子波反褶积得到结果。

Ｓ（ｔ）　＝　Ｒ（ｔ）　＊　Ｗ（ｔ） （１）式中 Ｓ（ｔ）　——　合成地震记录； Ｒ（ｔ）　——　反射系数序列； Ｗ（ｔ）　——　地震子波。

上式表明，合成记录的好坏与反射系数序列的求取和子波的选择有着密切的关系。

反射系数序列的准确性和精确程度又与测井资料（声波、密度）的采集、处理等过程密切相关；子波的选择，则要考虑子波的长度、相位、频率等诸多因素。

在实际工作中，所得到的结果往往不尽人意［１］，主要表现在：（１）　合成地震记录与井旁地震道附近的地震剖面层位不吻合现象较多，或者说同相轴吻合的时窗长度有限；（２）　合成地震记录与井旁地震道附近的地震剖面能量不吻合现象较多，或者说同相轴“胖瘦”程度吻合有限；（３）　合成地震记录与井旁地震道附近的地震剖面存在一定的时移。

其原因主要在于：①子波受地质条件变化的影响，难以给得恰到好处；②深—时转换存在误差；③褶积模型并不能完全准确地反应地震记录；④实际地震记录存在噪声。

１．２实用优化方法１．２．１校正测井数据首先对测井数据进行校正，对反射系数序列进行非均匀采样［２，３］。

１．２．２选择合适的子波（１）子波的类型。

常用的子波有两类，一是典型子波，如Ｒｉｃｈｅｒ、Ｔｒａｐｅｒｉｏｄ子波等；二是提取子波，提取子波一般有维纳—莱文森混相位子波提取法和自相关子波提取法两种［４，５］。

从剖面提取的实际子波制作的合成记录，虽然其合成地震记录层位精细标定应用研究＊洪余刚 陈景山 代宗仰 李凌峰（西南石油学院资源与环境学院，四川省成都市６１０５００）摘 要：通过对合成记录制作的一般方法进行分析，结合研究区实际地质、地震资料，提出合成记录的制作在层位标定中的实用优化方法，强调了子波的提取方法和子波相位引起的偏差。

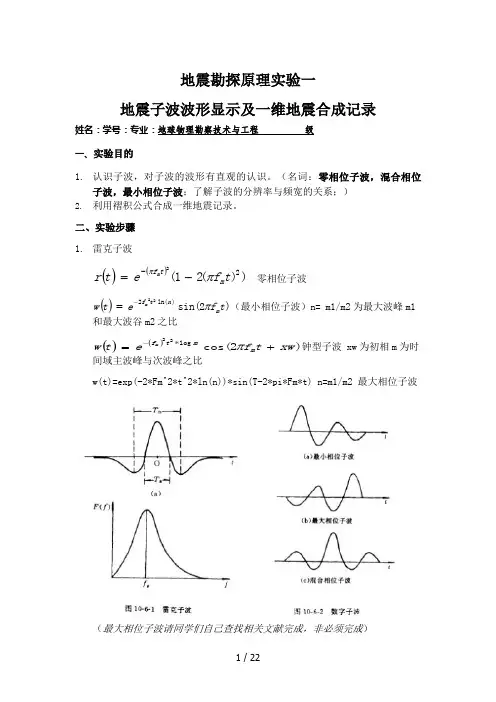
地震勘探原理实验一地震子波波形显示及一维地震合成记录姓名：学号：专业：地球物理勘察技术与工程 级 一、实验目的1. 认识子波，对子波的波形有直观的认识。

（名词：零相位子波，混合相位子波，最小相位子波；了解子波的分辨率与频宽的关系；） 2. 利用褶积公式合成一维地震记录。

二、实验步骤 1. 雷克子波()()))(21(22t f et r m t f m ππ-=- 零相位子波())2sin()ln(222t f et w m n t f m π-=（最小相位子波）n= m1/m2为最大波峰m1和最大波谷m2之比()())2cos(log *22xw t f et w m mt f m +=-π钟型子波 xw 为初相m 为时间域主波峰与次波峰之比w(t)=exp(-2*Fm^2*t^2*ln(n))*sin(T-2*pi*Fm*t) n=m1/m2 最大相位子波（最大相位子波请同学们自己查找相关文献完成，非必须完成）其中f代表子波的中心频率， t =i*dt，dt为时间采样间隔，i为时间m离散点序号; 这里可以为f = 10，25，40，100 Hz等，采样间隔dt=0.002m秒，i为0～256;2.根据公式编程实现不同频率的零相位子波的波形显示；不同中心频率的零相位子波图f = 25:mf = 100:m3.其地质模型为：设计反射系数)(n r (n=512)，n 为地层深度，其中0.1)100(=r ，为第一层介质深度；7.0)200(-=r ，为第二层介质深度；5.0)300(=r ，为第三层介质深度；4.0)400(=r ，为第四层介质深度；6.0)450(=r ，为第五层介质深度；其它为0。

地震波在介质中传播，当到达介质分界面时，发生反射和透射，反射波被检波器接受，生成地震记录。

反射系数表示地震波在两层介质分界面的能量重新分配，如r(100)=1.0，表示地震波入射到分界面时，只有一种波，反射纵波（或反射横波）。

合成地震记录业务流程一、准备工作。

咱得先把相关的数据都找齐喽。

比如说，测井数据那是相当重要的。

就像我们找宝藏得有个地图一样，测井数据就是我们合成地震记录的地图。

这里面包括声波测井曲线、密度测井曲线等。

这些数据就像是一个个小零件，缺了哪个都不行。

而且呀，我们还得确保这些数据的准确性，如果数据错了，那就好比做菜的时候盐当成了糖，做出来的东西肯定不对味。

另外呢，我们还需要有一些地质分层信息，这个就像是房子的框架结构，能让我们清楚地知道不同地层的情况，知道在哪个地层该怎么操作。

二、选择合适的子波。

子波就像是合成地震记录的画笔。

有好多不同类型的子波可以选呢。

我们得根据实际的地质情况和研究目的来挑。

如果是比较简单的地层结构，可能选个简单点的子波就够用啦。

但要是地层情况很复杂，就像一个超级复杂的迷宫一样，那我们就得找个功能强大、能适应复杂情况的子波。

这时候就得花点心思去对比不同的子波，看看哪个画出来的“画”（也就是合成的地震记录）最符合我们对这个地下情况的预期。

三、计算反射系数。

这一步就像是在做数学题，不过是很有趣的那种。

我们要根据前面准备好的测井数据，像声波和密度这些，来计算反射系数。

反射系数就像是镜子的反射率一样，它能告诉我们地震波在不同地层界面上反射的情况。

这个计算可不能马虎，要是算错了，那合成出来的地震记录就会像一个歪歪扭扭的积木塔，一点都不稳定也不准确。

我们得仔仔细细地按照公式来算，就像小心翼翼地搭积木一样，一块都不能搭错。

四、合成地震记录。

好啦，前面的工作都做好了，就到了最激动人心的合成地震记录这一步啦。

我们把选好的子波和计算好的反射系数放在一起，就像把颜料和画笔放在一起准备画画一样。

然后通过一些算法，让它们相互作用，就像魔法一样，一个地震记录就慢慢合成出来了。

这时候我们就像一个小魔法师，看着自己的作品一点点呈现出来。

不过呢，这时候还不能掉以轻心，我们还得检查这个合成出来的地震记录是不是合理。

五、验证与调整。

地震合成记录1. 引言地震合成记录是地震学领域中一项重要的技术手段，用于模拟地震波传播过程。

通过地震合成记录，我们可以了解地震波在地下介质中的传播规律，从而对地震灾害的预测和评估提供有力支持。

本文将详细介绍地震合成记录的基本原理、方法和应用，并探讨其在地震学研究和工程应用中的重要性。

2. 地震合成记录的基本原理地震合成记录是根据已知地震事件的震源信息和地下介质模型，计算出相应的地震波记录。

其基本原理是基于弹性波方程，并考虑地面条件、震源机制、地下介质参数等因素。

具体步骤如下：2.1 确定震源信息首先，需要确定地震事件的震源信息，包括震级、震源深度、震源机制等。

这些信息可以通过地震台网的监测数据、地震目录和震源机制研究等手段获取。

2.2 建立地下介质模型其次，需要建立地下介质模型，包括地震波速度、密度、各向异性等参数。

地下介质模型可通过地震勘探、钻探、地震资料分析等方法得到。

对于复杂地下介质，可以采用层状模型、体积模型等。

2.3 计算地震波传播接下来，利用弹性波方程对地震波进行数值计算。

弹性波方程是描述地震波传播的基本方程，通常采用有限差分法、边界元法、有限单元法等数值方法进行求解。

通过迭代计算，可以得到地震波在不同地点的振幅和到时。

2.4 合成地震记录最后，利用合成地震波的振幅和到时，综合考虑地面条件和观测点的位置，计算出合成地震记录。

合成地震记录通常以地震波形、功率谱、互相关函数等形式呈现。

3. 地震合成记录的方法和工具地震合成记录的方法和工具多种多样。

根据模型的复杂程度和计算效率的要求，可以选择不同的方法和工具。

下面列举一些常见的地震合成记录方法和工具：3.1 时域有限差分法时域有限差分法是地震波数值模拟的一种常用方法。

它基于地震波方程的差分形式，通过迭代求解差分方程，得到地震波的时变分布。

该方法适用于规则和不规则地震波传播模拟，并可考虑各向异性和非线性等效应。

3.2 频域边界元法频域边界元法是利用边界元法求解地震波传播问题的一种方法。

地震子波波形显示及一维地震记录合成一、实验目的1、认识地震子波（以雷克子波为例），对子波有直观的认识。

2、利用线性褶积公式合成一维地震记录。

二、实验内容1、雷克子波：零相位子波源：()()t f e t w m t f m πγπ2cos 22/2-= 程序：fm=30;r=3;t=0.002;for n=1:200w(n)=exp(-(2*pi*fm/r)^2*(t*n)^2)*cos(2*pi*fm*t*n);endfigure(1),plot(w);图像（1）：图（1）最小相位子波：()()t f e t w m t f m πγπ2sin 22/2-= 程序：fm=10;r=3;t=0.002;for n=1:200w(n)=exp(-(2*pi*fm/r)^2*(t*n)^2)*sin(2*pi*fm*t*n);endfigure(1),plot(w);图像：图（2）其中m f 代表子波的中心频率，γ代表子波宽度,随着γ的增大，子波能量后移，当γ=7时，最小相位子波可视为混合相位子波。

因而若将最小相位子波中γ=7，则可以间接地得到混合相位子波的图形为：图（3）从图（3）中可以看出，经过改变 的值后，整个雷克子波的能量发生了明显的后移；从一定程度上可以反映最小能量子波、混合能量子波、最大能量子波的图像上的区别是能量集中区域上的不同。

2、利用线性褶积公式合成一维地震记录（1）利用零相位雷克子波作为震源合成一维地震记录：程序：fm=30;r=3;t=0.002;for n=1:200w(n)=exp(-(2*pi*fm/r)^2*(t*n)^2)*cos(2*pi*fm*t*n);endfor j=1:500r(j)=0;endr(100)=1.0;r(200)=-0.7;r(300)=0.5;r(400)=0.4;r(500)=0.6; 对地层界面的反射系数进行设定for j=1:699f(j)=0;for i=1:500if(j-i>0&&j-i<200)f(j)=f(j)+r(i)*w(j-i); 褶积的主要过程endendendfigure(2),plot(f);图像：图（4）在这个一维地震记录图像上可以看出，除了100、200、300、400、500这些存在反射系数的点上发生了变化，在这些点的周围也发生了些许的变化。

子波整形提高合成地震记录质量单刚义,韩立国,张丽华,潘保芝吉林大学地球探测科学与技术学院,长春　130026 摘要:阐述合成地震记录的制作原理,利用测井数据计算出反射系数。

根据地震波传播机制,通过三维地震数据统计得到子波,由此计算出原始合成记录。

再根据过井剖面建立褶积模型,对子波进行整形,得到一个随时间变化的地震子波,最终得到与地震数据的波组特征相吻合的合成地震记录。

为精细储层描述打下了坚实的基础。

关键词:合成地震记录;褶积模型;子波整形;反射系数;深时转换;子波提取中图分类号:P 631.4 文献标识码:A收稿日期:2006207211作者简介:单刚义(19702),男,山东莱阳人,硕士研究生,主要从事地震资料的处理和解释研究工作,E 2m ail :ganyi 2shan@yahoo .com .cn .Usi ng W avelet Shap i ng to I m prove Syn thetic Se is m ogram Qua l itySHAN Gang 2yi ,HAN L i 2guo ,ZHAN G L i 2hua ,PAN B ao 2zh iColleg e of GeoE xp lora tion S cience and T echnology ,J ilin U n iversity ,Chang chun 130026,Ch inaAbstract :Syn thetic seis m ogram is the b ridge that connects seis m o logic data w ith w ell logging data ,and is also the basis of the in terp retati on of structu re and reservo ir’s seis m ic litho logy .T he accu racy of syn thetic seis m ogram directly affects the accu rate calib rati on of seis m ic geo logic ho rizon and the accu racy of reservo ir’s litho logy in terp retati on .T h rough th is p aper illu strates the p rinci p le of syn thesizingseis m ogram .T he reflecti on cofficien ts are ob tained w ith the w ell logging data .B y the p rinci p le of seis m ic w aves ,the w avelet is ex tracted from the seis m ic data of th ree di m en si on ,and the raw syn thetic seis m ogram is fin ished .T h rough bu ilding convo lu ti on m odel ,th is paper shapes w avelet ex tracted from seis m ic data ,th is w avelet varies w ith the ti m e .A t last ,the seis m ic litho logy of it is as the sam e of seis m ic data .T hu s it lays a strong foundati on fo r reservo ir fine descri p ti on .Key words :syn thetic seis m ogram ;convo lu ti on m odel ;w avelet shap ing ;reflecti on coefficien t ;dep th -ti m e conversi on ;ex tracti on of w avelet0　引　言测井和地震等资料的有机结合与综合运用是油藏描述中研究地质构造、岩性、岩相、油藏类型及预测有利含油气区等问题的基础。