动能定理全程列式习题课重点
- 格式:ppt
- 大小:1.43 MB
- 文档页数:9


动能定理综合应用特训目标特训内容目标1用动能定理解决变力做功问题(1T -5T )目标2有关动能定理的E k -x 图像问题(6T -10T )目标3用动能定理处理机车启动问题(11T -15T )目标4用动能定理处理多过程问题(16T -20T )【特训典例】一、用动能定理解决变力做功问题1如图所示的水平轨道AD 足够长,只有BC 部分是粗糙的,其长度为L =1m ,其余部分是光滑的,质量为1kg ,长度为2L 的粗细相同的匀质软绳静止在B 点的左侧(绳的右端在B 点),软绳与粗糙部分的动摩擦因数为μ=0.8,现用F =2N 的水平向右的恒力作用在软绳上,软绳始终保持伸直状态且长度不变,重力加速度为g =10m/s 2,最大静摩擦力等于滑动摩擦力,则在软绳运动的过程中,下列说法正确的是()A.软绳先做匀加速后做匀减速运动B.软绳的左端能经过B 点C.软绳的最大动能为0.5JD.软绳克服摩擦力做功4.0J【答案】C【详解】设绳子B 端向右运动位移为x ,当0≤x ≤L 时,绳子所受摩擦力F f =μx 2L mg =x2Lμmg 当L <x ≤2L 时,绳子所受摩擦力F f =μL 2Lmg =12μmg 绳子所受摩擦力随位移x 变化如图所示又F f -x 图像与坐标轴围成的面积表示物体克服摩擦力做的功W F f,当0≤x ≤L 时,W F f=12F f⋅x =x 24Lμmg ①对绳子由动能定理得Fx -W F f=12mv 2-0②当x =L 时v =0又F f max =12μmg =4N ,F =2N 得F <F f max 所以设绳子B 端向右运动位移为L 速度为零,停止运动。
A .拉力F 先比摩擦力大,后比摩擦力小,软绳先做加速运动后做减速运动。
0≤x ≤L 时,摩擦力为变力,所以加速度不恒定,A 错误;B .当x =L 时,绳子停止运动,软绳的左端不能经过B 点,B 错误;C .由①②得,当x =14×2L =0.5m 动能最大E km =Fx -x 24Lμmg =0.5J ,C 正确;D .B 端向右运动位移L 的过程中,克服摩擦力做功W F f=L 24Lμmg =14μmgL =2J ,D 错误。


第八章机械能守恒定律习题课:动能定理的应用课后篇巩固提升合格考达标练1.如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面。
设小球在斜面最低点A 的速度为v ,压缩弹簧至C 点时弹簧最短,C 点距地面高度为h ,则从A 到C 的过程中弹簧弹力做功是( )A.mgh-12mv 2 B.12mv 2-mgh C.-mgh D.-(mgℎ+12mv 2)A 到C 的过程运用动能定理可得,-mgh+W=0-12mv 2,所以W=mgh-12mv 2,故A 正确。
2.(2021湖南湘潭一中月考)如图甲所示,质量为m 的物体从高为h 的斜面顶端由静止下滑,最后停在水平面上,若该物体以v 0的初速度从顶端下滑,最后仍停在水平面上。
图乙为物体两次在水平面上运动的v -t 图像,则物体在斜面上运动过程中克服摩擦力所做的功为( )A.12m v 02-3mgh B.3mgh-12m v 02 C.16m v 02-mghD.mgh-16m v 02,由动能定理得mgh-W f=12m v12,若该物体以v0的初速度从顶端下滑,由动能定理得mgh-W f=12m v22−12m v02,由题图乙可知,物体两次滑到水平面的速度关系为v2=2v1,由以上三式解得W f=mgh-16m v02,D正确,A、B、C错误。
3.(2021山东卷)如图所示,粗糙程度处处相同的水平桌面上有一长为L的轻质细杆,一端可绕竖直光滑轴O转动,另一端与质量为m的小木块相连。
木块以水平初速度v0出发,恰好能完成一个完整的圆周运动。
在运动过程中,木块所受摩擦力的大小为()A.mv022πL B.mv024πLC.mv028πL D.mv0216πL,由动能定理得-F f·2πL=0-12m v02,所以摩擦力F f=mv24πL,选项B正确。
4.如图所示,质量为m的物体与水平转台间的动摩擦因数为μ,物体与转轴相距R,物体随转台由静止开始转动。


[目标定位] 1.进一步理解动能定理,领会应用动能定理解题的优越性.2.会利用动能定理分析变力做功、曲线运动以及多过程问题.一、应用动能定理求变力做的功1.动能定理不仅适用于求恒力做功,也适用于求变力做功,同时因为不涉及变力作用的过程分析,应用非常方便.2.利用动能定理求变力的功是最常用的方法,当物体受到一个变力和几个恒力作用时,可以用动能定理间接求变力做的功,即W 变+W 其他=ΔE k .例1 质量为m 的物体以初速度v 0沿水平面向左开始运动,起始点A 与一轻弹簧O 端相距s ,如图1所示,已知物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后,弹簧的最大压缩量为x ,则从开始碰撞到弹簧被压缩至最短,物体克服弹簧弹力所做的功为( )图1A.12m v 20-μmg (s +x ) B.12m v 20-μmgx C .μmgs D .μmg (s +x ) 答案 A解析 由动能定理得-W -μmg (s +x )=0-12m v 20,故物体克服弹簧弹力做功W =12m v 20-μmg (s +x ),A 正确.二、应用动能定理分析多过程问题1.应用动能定理解决多过程问题时,要根据问题选取合适的过程,可以分过程,也可以全过程一起研究.虽然我们列式时忽略了中间复杂过程,但不能忽略对每个过程的分析.2.在运动过程中,物体受到的某个力可能是变化的或分阶段存在的,要注意这种力做功的表达方式.例2 如图2所示,右端连有一个光滑弧形槽的水平桌面AB 长L =1.5 m ,一个质量为m =0.5 kg 的木块在F =1.5 N 的水平拉力作用下,从桌面上的A 端由静止开始向右运动,木块到达B 端时撤去拉力F ,木块与水平桌面间的动摩擦因数μ=0.2,取g =10 m/s 2.求:图2(1)木块沿弧形槽上升的最大高度(木块未离开弧形槽); (2)木块沿弧形槽滑回B 端后,在水平桌面上滑动的最大距离. 答案 (1)0.15 m (2)0.75 m解析 (1)设木块沿弧形槽上升的最大高度为h ,木块在最高点时的速度为零.从木块开始运动到弧形槽最高点,由动能定理得: FL -F f L -mgh =0其中F f =μF N =μmg =0.2×0.5×10 N =1.0 N 所以h =FL -F f Lmg=(1.5-1.0)×1.50.5×10m =0.15 m(2)设木块离开B 点后沿桌面滑动的最大距离为x .由动能定理得: mgh -F f x =0所以:x =mgh F f =0.5×10×0.151.0m =0.75 m三、动能定理在平抛、圆周运动中的应用1.与平抛运动相结合时,要注意应用运动的合成与分解的方法,如分解位移或分解速度. 2.与竖直平面内的圆周运动相结合时,应特别注意隐藏的临界条件.(1)有支撑效果的竖直平面内的圆周运动杆模型,物体能过最高点的临界条件为v min =0. (2)没有支撑效果的竖直平面内的圆周运动绳模型,物体能过最高点的临界条件为v min =rg .例3 如图3所示,ab 是水平轨道,bc 是位于竖直平面内的半圆形光滑轨道,半径R =0.225 m ,在b 点与水平面相切,滑块从水平轨道上距离b 点1.2 m 的a 点以初速度v 0=6 m /s 向右运动,经过水平轨道和半圆轨道后从最高点c 飞出,最后刚好落回轨道上的a 点,重力加速度g 取10 m/s 2,求:图3(1)滑块从c 点飞出时速度的大小; (2)水平轨道与滑块间的动摩擦因数. 答案 (1)4 m/s (2)1124解析 (1)滑块从c 点做平抛运动,设初速度为v 1,由平抛运动特点知 水平方向:x ab =v 1t ① 竖直方向:2R =12gt 2②由①②两式并代入数据得v 1=x ab2×2R g=4 m/s (2)在滑块从a 点运动到c 点的过程中由动能定理得 -mg ·2R -μmgx ab =12m v 21-12m v 2代入数据解得水平轨道与滑块间的动摩擦因数μ=1124.例4 如图4所示,质量为m 的小球用长为L 的轻质细线悬于O 点,与O 点处于同一水平线上的P 点处有一根光滑的细钉,已知OP =L2,在A点给小球一个水平向左的初速度v 0,发现小球恰能到达跟P 点在同一竖直线上的最高点B .求:图4(1)小球到达B 点时的速率;(2)若不计空气阻力,则初速度v 0为多少?(3)若初速度变为v 0′=3gL ,其他条件均不变,则小球从A 到B 的过程中克服空气阻力做了多少功? 答案 (1)gL2(2) 7gL 2 (3)114mgL 解析 (1)小球恰能到达最高点B ,则在最高点有mg =m v 2L 2,小球到达B 点时的速率v =gL2. (2)由动能定理得:-mg ⎝⎛⎭⎫L +L 2=12m v 2-12m v 20, 则v 0=7gL2(3)空气阻力是变力,设小球从A 到B 克服空气阻力做功为W f ,由动能定理得 -mg (L +L 2)-W f =12m v 2-12m v 0′2,解得W f =114mgL .1.(应用动能定理求变力做的功)如图5,一半径为R 的半圆形轨道竖直固定放置,轨道两端等高;质量为m 的质点自轨道端点P 由静止开始滑下,滑到最低点Q 时,对轨道的正压力为2mg ,重力加速度大小为g .质点自P 滑到Q 的过程中,克服摩擦力所做的功为( )图5A.14mgR B.13mgR C.12mgR D.π4mgR 答案 C解析 在Q 点,F N -mg =m v 2R ,所以v =gR ;由P 到Q 根据动能定理得mgR -W f =12m v 2,解得W f =12mgR ,故C 正确.2. (应用动能定理分析多过程问题)如图6所示,质量m =1 kg 的木块静止在高h =1.2 m 的平台上,木块与平台间的动摩擦因数μ=0.2,用水平推力F =20 N ,使木块产生位移l 1=3 m 时撤去,木块又滑行l 2=1 m 后飞出平台,求木块落地时速度的大小.(g 取10 m/s 2)图6答案 8 2 m/s解析 木块的运动分为三个阶段,先是在l 1段匀加速直线运动,然后是在l 2段匀减速直线运动,最后是平抛运动.考虑应用动能定理,设木块落地时的速度为v ,整个过程中各力做功情况分别为: 推力做功W F =F ·l 1,摩擦力做功W f =-μmg (l 1+l 2), 重力做功W G =mgh . 设木块落地速度为v 全过程应用动能定理得W F +W f +W G =12m v 2,解得v =8 2 m/s3.(动能定理在圆周运动中的应用)如图7所示,由细管道组成的竖直轨道,其圆形部分半径分别是R 和R2,质量为m 的小球通过这段轨道时,在A 点时刚好对管壁无压力,在B 点时对管内侧壁压力为mg2.求小球由A 点运动到B 点的过程中摩擦力对小球做的功.图7答案 -98mgR解析 由圆周运动的知识知,小球在A 点时:mg =m v 2AR得v A =gR设小球在B 点的速度为v B ,则由圆周运动的知识知, mg +F N B =m v 2B R 2其中F N B =12mg得v 2B =34gR 小球从A 点运动到B 点的过程中,重力做功W G =mgR . 摩擦力做功为W f ,由动能定理得: mgR +W f =12m v 2B -12m v 2A解得W f =-98mgR .4.(动能定理在平抛、圆周运动中的应用)如图8所示,竖直平面内的34圆弧形光滑管道半径略大于小球半径,管道中心线到圆心的距离为R ,A 端与圆心O 等高,AD 为水平面,B 点在O 的正下方,小球自A 点正上方由静止释放,自由下落至A 点时进入管道,从上端口飞出后落在C 点,当小球到达B 点时,管壁对小球的弹力大小是小球重力大小的9倍.求:图8(1)释放点距A 点的竖直高度; (2)落点C 与A 点的水平距离. 答案 (1)3R (2)(22-1)R解析 (1)设小球到达B 点的速度为v 1,因为到达B 点时管壁对小球的弹力大小是小球重力大小的9倍,所以有9mg -mg =m v 21R①从最高点到B 点的过程中,由动能定理得mg (h +R )=12m v 21②由①②得:h =3R ③(2)设小球到达圆弧最高点的速度为v 2,落点C 与A 点的水平距离为x 从B 到最高点的过程中,由动能定理得 -mg ·2R =12m v 22-12m v 21④ 由平抛运动的规律得R =12gt 2⑤R +x =v 2t ⑥联立④⑤⑥解得x =(22-1)R .题组一 应用动能定理求变力做的功1.如图1所示,AB 为14圆弧轨道,BC 为水平直轨道,圆弧的半径为R ,BC 的长度也是R ,一质量为m 的物体与两个轨道间的动摩擦因数都为μ,当它由轨道顶端A 从静止开始下落,恰好运动到C 处停止,那么物体在AB 段克服摩擦力所做的功为( )图1A.12μmgR B.12mgR C .-mgR D .(1-μ)mgR答案 D2.如图2所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设小球在斜面最低点A 的速度为v ,压缩弹簧至C 点时弹簧最短,C 点距地面高度为h ,则从A 到C 的过程中弹簧弹力做功是( )图2A .mgh -12m v 2B.12m v 2-mgh C .-mgh D .-⎝⎛⎭⎫mgh +12m v 2 答案 A解析 由A 到C 的过程运用动能定理可得:-mgh +W =0-12m v 2,所以W =mgh -12m v 2,故A 正确.3.(多选)质量为m 的汽车在平直公路上行驶,发动机的功率P 和汽车受到的阻力F f 均恒定不变,在时间t 内,汽车的速度由v 0增加到最大速度v m ,汽车前进的距离为s ,则此段时间内发动机所做的功W 可表示为( ) A .W =Pt B .W =F f sC .W =12m v 2m -12m v 20+F f s D .W =12m v 2m +F f s 答案 AC解析 由题意知,发动机功率不变,故t 时间内发动机做功W =Pt ,所以A 正确;车做加速运动,故牵引力大于阻力F f ,故B 错误;根据动能定理W -F f s =12m v 2m -12m v 20,所以C 正确,D 错误.4.如图3所示,小球以初速度v 0从A 点沿粗糙的轨道运动到高为h 的B 点后自动返回,其返回途中仍经过A 点,则经过A 点的速度大小为( )图3A.v 20-4ghB.4gh -v 20C.v 20-2ghD.2gh -v 20答案 B解析 从A 到B 过程中,重力和摩擦力都做负功,根据动能定理可得mgh +W f =12m v 20,从B 到A 过程中,重力做正功,摩擦力做负功(因为是沿原路返回,所以两种情况摩擦力做功大小相等)根据动能定理可得mgh-W f=12m v2,两式联立得再次经过A点的速度为4gh-v2,选B.5.如图4所示,假设在某次比赛中他从10 m高处的跳台跳下,设水的平均阻力约为其体重的3倍,在粗略估算中,把运动员当作质点处理,为了保证运动员的人身安全,池水深度至少为(不计空气阻力)()图4A.5 m B.3 m C.7 m D.1 m答案 A解析设水深h,对全程运用动能定理mg(H+h)-F f h=0,即mg(H+h)=3mgh.所以h=5 m.题组二应用动能定理分析多过程问题6.(多选)在平直公路上,汽车由静止开始做匀加速直线运动,当速度达到v max后,立即关闭发动机直至静止,v-t图象如图5所示,设汽车的牵引力为F,受到的摩擦力为F f,全程中牵引力做功为W1,克服摩擦力做功为W2,则()图5A.F∶F f=1∶3 B.W1∶W2=1∶1C.F∶F f=4∶1 D.W1∶W2=1∶3答案BC解析对汽车运动的全过程,由动能定理得:W1-W2=ΔE k=0,所以W1=W2,选项B正确,选项D错误;设牵引力、摩擦力作用下的位移分别为x1、x2,由图象知x1∶x2=1∶4.由动能定理得Fx1-F f x2=0,所以F∶F f=4∶1,选项A错误,选项C正确.7.如图6所示,斜面倾角为θ,滑块质量为m,滑块与斜面间的动摩擦因数为μ,从距挡板为s 0的位置以v 0的速度沿斜面向上滑行.设重力沿斜面的分力大于滑动摩擦力,且每次与P 碰撞前后的速度大小保持不变,挡板与斜面垂直,斜面足够长,滑块可视为质点.求滑块从开始运动到最后停止滑行的总路程s .图6答案 s 0tan θμ+v 202μg cos θ解析 滑块在斜面上运动时受到的摩擦力大小F f =μF N =μmg cos θ ① 整个过程滑块下落的总高度 h =s 0sin θ② 根据动能定理 mgh -F f s =0-12m v 20③联立以上①②③得s =s 0tan θμ+v 202μg cos θ题组三 动能定理在平抛、圆周运动中的应用8.如图7所示,一个质量为m =0.6 kg 的小球以某一初速度v 0=2 m /s 从P 点水平抛出,从粗糙圆弧ABC 的A 点沿切线方向进入(不计空气阻力,进入圆弧时无机械能损失)且恰好沿圆弧通过最高点C ,已知圆弧的圆心为O ,半径R =0.3 m ,θ=60°,g =10 m/s 2.试求:图7(1)小球到达A 点的速度v A 的大小; (2)P 点与A 点的竖直高度H ;(3)小球从圆弧A 点运动到最高点C 的过程中克服摩擦力所做的功W . 答案 (1)4 m/s (2)0.6 m (3)1.2 J 解析 (1)在A 处由速度的合成得v A =v 0cos θ代入解得v A =4 m/s(2)P 到A 小球做平抛运动,竖直分速度v y =v 0tan θ由运动学规律有v 2y =2gH由以上两式解得H =0.6 m(3)恰好过C 点满足mg =m v 2C R由A 到C 由动能定理得-mgR (1+cos θ)-W =12m v 2C -12m v 2A 代入解得W =1.2 J.9.如图8所示,AB 段为粗糙水平轨道,BC 段是固定于竖直平面内的光滑半圆形导轨,半径为R .一质量为m 的滑块静止在A 点,在水平恒力F 作用下从A 点向右运动,当运动至B 点时,撤去恒力F ,滑块沿半圆形轨道向上运动恰能通过最高点C ,已知滑块与水平轨道间的滑动摩擦力F f =mg 4,水平恒力F =mg 2,求:图8(1)滑块与水平轨道间的动摩擦因数μ;(2)滑块运动至C 点的速度大小v C ;(3)水平轨道AB 的长度L .答案 (1)0.25 (2)gR (3)10R解析 (1)滑块在水平轨道上运动时,由F f =μF N =μmg 得:μ=F f F N=0.25 (2)滑块在C 点时仅受重力.据牛顿第二定律,有:mg =m v 2C R,可得:v C =gR . (3)滑块从A 到C 的过程,运用动能定理得:(F -F f )L -2mgR =12m v 2C -0. 又F f =mg 4,F =mg 2.解得L =10R .10.如图9所示,光滑水平面AB 与一半圆形轨道在B 点相连,轨道位于竖直面内,其半径为R ,一个质量为m 的物块静止在水平面上,现向左推物块使其压紧弹簧,然后放手,物块在弹力作用下获得一速度,当它经B 点进入半圆形轨道瞬间,对轨道的压力为其重力的7倍,之后向上运动恰能完成半圆周运动到达C 点,重力加速度为g .求:图9(1)弹簧弹力对物块做的功;(2)物块从B 到C 克服阻力所做的功;(3)物块离开C 点后,再落回到水平面上时的动能.答案 (1)3mgR (2)12mgR (3)52mgR 解析 (1)由动能定理得W =12m v 2B 在B 点由牛顿第二定律得7mg -mg =m v 2B R解得W =3mgR(2)物块从B 到C 由动能定理得12m v 2C -12m v 2B =-2mgR +W ′ 物块在C 点时mg =m v 2C R解得W ′=-12mgR ,即物体从B 到C 克服阻力做功为12mgR . (3)物块从C 点平抛到水平面的过程中,由动能定理得2mgR =E k -12m v 2C ,E k =52mgR 11.如图10所示,在竖直平面内固定有两个很靠近的同心圆轨道,外圆ABCD 光滑,内圆的上半部分B ′C ′D ′粗糙,下半部分B ′A ′D ′光滑.一质量为m =0.2 kg 的小球从外轨道的最低点A 处以初速度v 0向右运动,小球的直径略小于两圆的间距,小球运动的轨道半径R =0.2 m ,取g =10 m/s 2.图10(1)若要使小球始终紧贴着外圆做完整的圆周运动,初速度v 0至少为多少?(2)若v 0=3 m/s ,经过一段时间后小球到达最高点,内轨道对小球的支持力F C =2 N ,则小球在这段时间内克服摩擦力做的功是多少?(3)若v 0=3.1 m/s ,经过足够长的时间后,小球经过最低点A 时速度v A 为多少? 答案 (1)10 m /s (2)0.1 J (3)2 m/s解析 (1)设此情形下小球到达外轨道的最高点的最小速度为v C ,则由牛顿第二定律可得mg=m v 2C R 由动能定理可知-2mgR =12m v 2C -12m v 20 代入数据解得:v 0=10 m/s.(2)设此时小球到达最高点的速度为v C ′,克服摩擦力做的功为W f ,则由牛顿第二定律可得mg -F C =m v C ′2R由动能定理可知-2mgR -W f =12m v C ′2-12m v 20 代入数据解得:W f =0.1 J(3)经过足够长的时间后,小球在下半圆轨道内做往复运动.设小球经过最低点的速度为v A ,则由动能定理可知mgR =12m v 2A 代入数据解得:v A =2 m/s.。

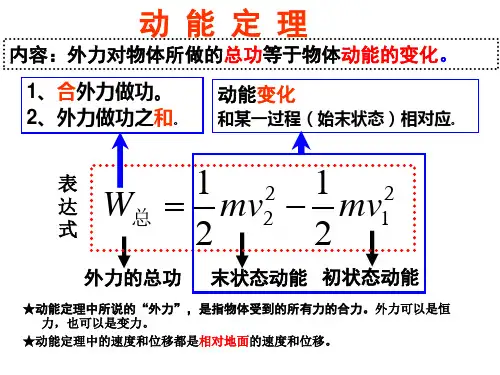



21222121mv mv W -=21222121E mv mv W k -=∆=动能和动能定理第1步:讲基础一、动能:1、定义:物体由于运动而具有的能量叫动能.2、表达式:221mv E k =3、物理意义:动能是描述物体运动状态的物理量,是标量。
4、 单位:焦耳( J ) 二、动能定理: >1、内容:合力对物体所做的总功等于物体动能的变化。
2、表达式:第2步:学技巧一、对动能定理的进一步理解 力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化,即 。
1、式中的W ,是力对物体所做的总功,可理解为各个外力所做功的代数和,也可以理解为合力所做的功。
2、式中的k E ∆,是物体动能的变化,是指做功过程的末动能减去初动能。
3、动能定理的研究对象一般是单一物体,或者是可以看成单一物体的物体系。
4、动能定理表达式是一个标量式,不能在某个方向上应用动能定理。
&二、常用应用动能定理的几种情况1、动能定理适用于恒力、变力、直线、曲线运动。
2、动能定理是标量式,不涉及方向问题。
在不涉及加速度和时间的问题时,可优先考虑动能定理。
3、对于求解多个过程的问题可全程考虑,从而避开考虑每个运动过程的具体细节。
具有过程简明、方法巧妙、运算量小等优点。
(注意动能损失:例3和例4比较)4、变力做功问题。
在某些问题中,由于力F 大小的变化或方向的改变,不能直接由αcos Fl W =来求变力F 所做的功,此时可由其做功的效果——动能的变化来求变力F 所做的功。
三、经典例题 例1、(课本例题)一架喷气式飞机,质量m=5×103 kg ,起飞过程中从静止开始滑跑的路程为s =×102m时,达到起飞速度v=60m/s ,在此过程中飞机受到的平均阻力是飞机重量的倍(k=,求飞机受到的牵引力. 分析: 研究对象:飞机研究过程:从静止→起飞(V=60m/s )适用公式:动能定理:2022121mv mv W -=合表达式:=-S f F )(221mv得到牵引力:Nkmg S mv F 42108.12⨯=+=例2、将质量m=2kg 的一块石头从离地面H=2m 高处由静止开始释放,落入泥潭并陷入泥中h=5cm 深处,不计空气阻力,求泥对石头的平均阻力。
高中物理动能定理的综合应用解题技巧讲解及练习题(含答案)一、高中物理精讲专题测试动能定理的综合应用1.一辆汽车发动机的额定功率P =200kW ,若其总质量为m =103kg ,在水平路面上行驶时,汽车以加速度a 1=5m/s 2从静止开始匀加速运动能够持续的最大时间为t 1=4s ,然后保持恒定的功率继续加速t 2=14s 达到最大速度。
设汽车行驶过程中受到的阻力恒定,取g =10m/s 2.求:(1)汽车所能达到的最大速度;(2)汽车从启动至到达最大速度的过程中运动的位移。
【答案】(1)40m/s ;(2)480m 【解析】 【分析】 【详解】(1)汽车匀加速结束时的速度11120m /s v a t ==由P=Fv 可知,匀加速结束时汽车的牵引力11F Pv ==1×104N 由牛顿第二定律得11F f ma -=解得f =5000N汽车速度最大时做匀速直线运动,处于平衡状态,由平衡条件可知, 此时汽车的牵引力F=f =5000N由P Fv =可知,汽车的最大速度:v=P PF f==40m/s (2)汽车匀加速运动的位移x 1=1140m 2v t = 对汽车,由动能定理得2112102F x Pt fs mv =--+解得s =480m2.如图所示,轨道ABC 被竖直地固定在水平桌面上,A 距水平地面高H =0.75m ,C 距水平地面高h =0.45m 。
一个质量m =0.1kg 的小物块自A 点从静止开始下滑,从C 点以水平速度飞出后落在地面上的D 点。
现测得C 、D 两点的水平距离为x =0.6m 。
不计空气阻力,取g =10m/s 2。
求(1)小物块从C 点运动到D 点经历的时间t ; (2)小物块从C 点飞出时速度的大小v C ;(3)小物块从A 点运动到C 点的过程中克服摩擦力做的功。
【答案】(1) t=0.3s (2) v C =2.0m/s (3)0.1J 【解析】 【详解】(1)小物块从C 水平飞出后做平抛运动,由212h gt = 得小物块从C 点运动到D 点经历的时间20.3ht g==s (2)小物块从C 点运动到D ,由C x v t = 得小物块从C 点飞出时速度的大小C xv t==2.0m/s (3)小物块从A 点运动到C 点的过程中,根据动能定理 得()2102f C mg Hh W mv -+=- ()212f C W mv mg Hh =--= -0.1J 此过程中克服摩擦力做的功f f W W '=-=0.1J3.如图所示,竖直平面内的轨道由直轨道AB 和圆弧轨道BC 组成,直轨道AB 和圆弧轨道BC 平滑连接,小球从斜面上A 点由静止开始滑下,滑到斜面底端后又滑上一个半径为=0.4m R 的圆轨道;(1)若接触面均光滑,小球刚好能滑到圆轨道的最高点C ,求斜面高h ;(2)若已知小球质量m =0.1kg ,斜面高h =2m ,小球运动到C 点时对轨道压力为mg ,求全过程中摩擦阻力做的功.【答案】(1)1m ;(2) -0.8J ; 【解析】 【详解】(1)小球刚好到达C 点,重力提供向心力,由牛顿第二定律得:2v mg m R=从A 到C 过程机械能守恒,由机械能守恒定律得:()2122mg h R mv -=, 解得:2.5 2.50.4m 1m h R ==⨯=;(2)在C 点,由牛顿第二定律得:2Cv mg mg m R+=,从A 到C 过程,由动能定理得:()21202f C mgh R W mv -+=-, 解得:0.8J f W =-;4.某滑沙场的示意图如图所示,某旅游者乘滑沙橇从A 点由静止开始滑下,最后停在水平沙面上的C 点.设滑沙橇和沙面间的动摩擦因数处处相同,斜面和水平面连接处可认为是圆滑的,滑沙者保持一定姿势坐在滑沙橇上不动,若测得AC 间水平距离为x ,A 点高为h ,求滑沙橇与沙面间的动摩擦因数μ.【答案】h/x 【解析】 【分析】对A 到C 的全过程运用动能定理,抓住动能的变化量为零,结合动能定理求出滑沙橇与沙面间的动摩擦因数. 【详解】设斜面的倾角为θ,对全过程运用动能定理得,因为,则有,解得.【点睛】本题考查了动能定理的基本运用,运用动能定理解题关键选择好研究的过程,分析过程中有哪些力做功,再结合动能定理进行求解,本题也可以结合动力学知识进行求解.5.如图光滑水平导轨AB 的左端有一压缩的弹簧,弹簧左端固定,右端前放一个质量为m =1kg 的物块(可视为质点),物块与弹簧不粘连,B 点与水平传送带的左端刚好平齐接触,传送带的长度BC 的长为L =6m ,沿逆时针方向以恒定速度v =2m/s 匀速转动.CD 为光滑的水平轨道,C 点与传送带的右端刚好平齐接触,DE 是竖直放置的半径为R =0.4m 的光滑半圆轨道,DE 与CD 相切于D 点.已知物块与传送带间的动摩擦因数μ=0.2,取g =10m/s 2.(1)若释放弹簧,物块离开弹簧,滑上传送带刚好能到达C 点,求弹簧储存的弹性势能p E ;(2)若释放弹簧,物块离开弹簧,滑上传送带能够通过C 点,并经过圆弧轨道DE ,从其最高点E 飞出,最终落在CD 上距D 点的距离为x =1.2m 处(CD 长大于1.2m ),求物块通过E 点时受到的压力大小;(3)满足(2)条件时,求物块通过传送带的过程中产生的热能. 【答案】(1)p 12J E =(2)N =12.5N (3)Q =16J 【解析】 【详解】(1)由动量定理知:2102mgL mv μ-=-由能量守恒定律知:2p 12E mv =解得:p 12J E =(2)由平抛运动知:竖直方向:2122y R gt ==水平方向:E x v t =在E 点,由牛顿第二定律知:2E v N mg m R+=解得:N =12.5N(3)从D 到E ,由动能定理知:2211222D E mg R mv mv -⋅=- 解得:5m /s D v =从B 到D ,由动能定理知221122D B mv mg v L m μ--= 解得:7m /s B v =对物块2B Dv v L t +=解得:t =1s ;621m 8m s L vt ∆=+=+⨯=相对由能量守恒定律知:mgL Q s μ=⋅∆相对 解得:Q =16J6.如图所示,在海滨游乐场里有一种滑沙运动.某人坐在滑板上从斜坡的高处A 点由静止开始滑下,滑到斜坡底端B 点后,沿水平的滑道再滑行一段距离到C 点停下来.如果人和滑板的总质量m =60kg ,滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ=0.5,斜坡的倾角θ=37°(sin 37°=0.6,cos 37°=0.8),斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g 取10m/s 2. 求:(1)人从斜坡上滑下的加速度为多大?(2)若由于场地的限制,水平滑道的最大距离BC 为L =20.0m ,则人在斜坡上滑下的距离AB 应不超过多少?【答案】(1)2.0 m/s 2; (2)50m 【解析】 【分析】(1)根据牛顿第二定律求出人从斜坡上下滑的加速度.(2)根据牛顿第二定律求出在水平面上运动的加速度,结合水平轨道的最大距离求出B 点的速度,结合速度位移公式求出AB 的最大长度. 【详解】(1)根据牛顿第二定律得,人从斜坡上滑下的加速度为:a 1=3737mgsin mgcos mμ︒-︒=gsin37°-μgcos37°=6-0.5×8m/s 2=2m/s 2.(2)在水平面上做匀减速运动的加速度大小为:a 2=μg =5m /s 2,根据速度位移公式得,B 点的速度为:222520/102/B v a L m s m s ⨯⨯===. 根据速度位移公式得:212005024B AB v L m m a ===. 【点睛】本题考查了牛顿第二定律和运动学公式的基本运用,知道加速度是联系力学和运动学的桥梁,本题也可以结合动能定理进行求解.7.如图甲所示,静止在水平地面上一个质量为m =4kg 的物体,其在随位移均匀减小的水平推力作用下运动,推力F 随位移x 变化的图象如图乙所示.已知物体与地面之间的动摩擦因数为μ=0.5,g =10m/s 2.求:(1)运动过程中物体的最大加速度大小为多少; (2)距出发点多远时物体的速度达到最大; (3)物体最终停在何处?【答案】(1)20m/s 2(2)3.2m (3)10m 【解析】 【详解】(1)物体加速运动,由牛顿第二定律得:F -μmg =ma当推力F =100N 时,物体所受的合力最大,加速度最大,代入数据得:2max 20m/s Fa g mμ=-=, (2)由图象得出,推力F 随位移x 变化的数值关系为:F =100 – 25x ,速度最大时,物体加速度为零,则F=μmg=20N ,即x = 3.2m(3)F 与位移x 的关系图线围成的面积表示F 所做的功,即01200J 2F W Fx ==对全过程运用动能定理,W F −μmgx m =0代入数据得:x m =10m8.如图,与水平面夹角θ=37°的斜面和半径R =1.0m 的光滑圆轨道相切于B 点,且固定于竖直平面内。