《线性系统理论》试卷及答案

R C 2《线性系统理论》试卷及答案1、（20分）如图所示RLC 网络,若e(t ）为系统输入变量r （t)，电阻R 2两端的电压为输出量y(t),选定状态变量为 x 1（t)=v 1（t ），x 2(t ）=v 2(t)，x 3（t)=i （t)要求列写出系统的状态空间描述。

2、(15分)求出下面的输入输出描述的一个状态空间描述。

y （4)+4y （3）+3y （2）+7y （1）+3y=u (3）+ 2u （1）+ 3u3、（15分）计算下列线性系统的传递函数。

[]210X 13101X y -⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦=4、(10分）分析下列系统的能控性.0111X X u a b •⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦5、（10分）分析下列系统的能观性。

[]1110a X X y Xb •⎡⎤==-⎢⎥⎣⎦6、（15分)判断下列系统的原点平衡状态x e 是否大范围渐近稳定。

12221123x x x x x x==--7、（15分）已知系统的状态方程为221012000401X X u •--⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦试确定一个状态反馈阵K,使闭环极点配置为λ1*=—2、λ2*=-3、λ3*=—4.答案：1、（20分）如图所示RLC 网络，若e （t ）为系统输入变量r （t ）,电阻R 2两端的电压为输出量y （t ），选定状态变量为 x 1(t)=v 1（t)，x 2(t ）=v 2（t ）,x 3（t)=i （t ）要求列写出系统的状态空间描述。

2、（15分）求出下面的输入输出描述的一个状态空间描述。

列出向量表示形式解出解出解出r x x x L R x x x rx LR x x x xx x C R x x x C xC x r x R x L L LL⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--=-=+=+==++1321113211311132122222112211333113000xy x xLy （4）+4y (3）+3y （2)+7y (1）+3y=u （3）+ 2u （1)+ 3u[]得出了状态空间表达式列出向量表示形式，就求导，有选取状态变量令有令⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=++=⎪⎪⎩⎪⎪⎨⎧+----=========⎩⎨⎧++==++++++++=++++++===43211025233375y ~y ~x y ~x y ~...y ~x y ~x y ~3y ~2y ~y ~3y ~7y ~3y ~4y ~u 3734p 1y ~3734p 32p y d/dtp 4214321(4)43(2)22(1)1(3)4(1)21(1)(3)(1)(2)(3)(4)2342343x x x x x x x y u x x x x x x x x y u p p p u p p p p(完整word 版)《线性系统理论》试卷及答案3、(15分）计算下列线性系统的传递函数.[]Xy u X 10103112X =⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=[][][]计算得出传递函数⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-------=-=⎥⎦⎤⎢⎣⎡-------=⎥⎦⎤⎢⎣⎡--=--==⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--==⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=----1021131)3)(2(110)()(21131)3)(2(13112)()()(1010311210103112X 1111s s s s B A Is C s G s s s s s s A Is BA Is C s G CB A Xy u X(完整word 版)《线性系统理论》试卷及答案4、（10分）分析下列系统的能控性。

线性系统参考题（三）一、线性系统的脉冲响应为()t t g t e e -=-。

该系统是一个完全能控系统，它的状态方程有三个极点，其中一个是-2。

（1）求出该系统的传递函数； （2）求出该系统的最小实现；（3）求出该系统的三阶能控标准型，这一实现与原系统的状态方程有何关系？为什么？ （4）求出该系统的三阶能观标准型，这一实现与原系统的状态方程有何关系？为什么？二、系统状态方程如下：0011[10]x x y x⎡⎤=⎢⎥-⎣⎦= （1）判断该系统的能观性。

（2）能否设计一个观测器渐近估计系统的状态（即当时间趋向无穷时，估计误差趋向零）？ （3）求出系统矩阵的特征向量；（4）若系统的厨师状态分别为0(0)1x α⎡⎤=⎢⎥⎣⎦和1(0)1x β⎡⎤=⎢⎥⎣⎦，求出相应的系统响应并说明这两个响应的特点；（5）已知系统的初始状态为1(0)1x β⎡⎤=⎢⎥⎣⎦，是否可通过测量输出完全确定系统的状态信息？三、系统的传递函数矩阵如下：2211(1)()102s s G s s ⎡⎤+⎢⎥+⎢⎥=⎢⎥⎢⎥+⎣⎦ （1）求出该系统的零点和它们相应的左右方向向量； （2）求出该系统的最小实现；（3）对于该系统是否有不为零的输入能使得输出恒等于零？若是，则写出相应的输入信号，并给出能使输出信号为零的条件；（4）在什么样的输入信号下，系统的输出不为零，但是输出的终值为零？四、考虑线性系统010*********[101]xx u y x⎡⎤⎡⎤⎢⎥⎢⎥=--+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦=其中u 是控制信号，y 是系统的输出。

（1）判断该系统的能控、能观性；（2）设计一状态反馈使得系统传递函数有一对稳定的复数根，其实部为-5，2；（3）分析在初始状态不为零时，确定系统输出性能的关键因数是什么？ （5）设计一个基于状态观测器的反馈系统；（5）画出相应的系统结构图。

参考答案一、解：（1）112()[()]11(1)(1)G s L g t s s s s ==-=-+-+（2）我们可以采用基于分式分解的约当形实现11()11G s s s =--+可直接得出状态空间描述：[]11221210101111xx u x x x y x ⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤=⎢⎥⎣⎦此实现为系统最小实现。

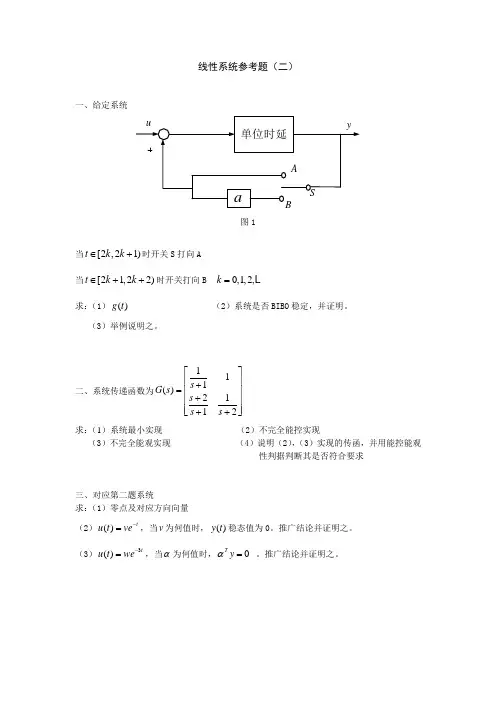
线性系统参考题（二）一、给定系统图1当[2,21)t k k ∈+时开关S 打向A当[21,22)t k k ∈++时开关打向B 0,1,2,k =求：（1）()g t （2）系统是否BIBO 稳定，并证明。

（3）举例说明之。

二、系统传递函数为111()2112s G s s s s ⎡⎤⎢⎥+=⎢⎥+⎢⎥⎢⎥++⎣⎦ 求：（1）系统最小实现 （2）不完全能控实现（3）不完全能观实现 （4）说明（2），（3）实现的传函，并用能控能观性判据判断其是否符合要求三、对应第二题系统求：（1）零点及对应方向向量（2）()tu t ve -=，当v 为何值时，()y t 稳态值为0。

推广结论并证明之。

（3）3()t u t w e -=，当α为何值时，0Ty α= 。

推广结论并证明之。

四、给定系统框图图2（1）写出状态空间表达式（2）写出状态反馈是使系统稳定（3）根据内模原理和状态反馈，设计跟踪阶跃输入信号（4）分析（3）设计结果中，w 和初状态对y 稳态和跟踪动态性能的影响。

（5）如果可以改变系统结构的话，如何改变会更好，说明理由。

五、证明xA x = ，y cx =，λ为不可观模态，A v v λ=，v 为λ特征向量，当(0)x v α=（α为非零向量）时，求证：()0m y y y '⋅⋅= 。

参考答案一、解：（1）当()()r t t δ=时，22()(1)(2)(3)(4)(5)y t t a t a t a t a t δδδδδ=-+-+-+-+-+因此，当2(1,2,)t k k == 时，22()(1)(2)(3)(4)(5)(2)ky t t a t a t a t a t a t k δδδδδδ=-+-+-+-+-++-2[]21()i ki at i δ==-∑当21(0,1,2,)t k k =+= 时，22()(1)(2)(3)(4)(5)(21)ky t t a t a t a t a t a t k δδδδδδ=-+-+-+-+-++--21[]21()i k i a t i δ+==-∑所以，[]21()()i i g t at i δ∞==-∑。

一、1、 求脉冲响应函数 系统脉冲响应为：...)4()3()2()1()(+-+-+-+-=t t t t t g f δδδδ∑∞=-=1)(i i t δ传递函数为：ss i i s s f f e ee e t g L s g --∞=---=⋅==∑1)())(()(02、 已知)sin(t r π=，求输出响应 系统响应;⎩⎨⎧=⋅≤≤-⋅-=othern nt n t t y 03.2.1212)sin()(Kπ3、 判断系统是否BIBO 稳定？若是请证明，若不是请举例论证结论不是BIBO 稳定，令系统输入为：)()(t t y ε=，则系统输出在∞→t 时，趋于无穷4、 上述系统可否用频域法求取结论 不能，系统的传递函数不是有理分式 二、已知系统：bu Ax x+=&，其中k ξξξΛ21,为k 个特征向量，k<n ，b 可用此k 个特征向量的线性组合表示。

1、 证明：此系统不完全能控证明：由题意，存在不全为零的实数组k∂∂∂K 21使得：k k b ξξξ⋅∂++⋅∂+⋅∂=K 2211因而有：)(2211k k At At e b e ξξξ⋅∂++⋅∂+⋅∂⋅=⋅Kk At k At At e e e ξξξ⋅⋅∂++⋅⋅∂+⋅⋅∂=K 2211 k t k t t k e e e ξξξλλλ⋅⋅∂++⋅⋅∂+⋅⋅∂=K 221121[]⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⋅∂⋅∂⋅∂=t k t t k k e e e λλλξξξK K212121（kλλλK 21为特征向量对应的特征根）τττd ebb eT A tTA ⎰0[][]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅∂⋅∂⋅∂⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⋅∂⋅∂⋅∂=⎰k k t k k d e e e e e e k k ξξξτξξξτλτλτλτλτλτλK KK K2121021212121因而有：n k d ebb e rank T A tTA <≤⎰)(0τττ系统不可控2、 举例说明该系统不完全能控 略3、 若该系统能控模态稳定，不能控模态不稳定，试问系统初始状态满足什么条件系统状态最终趋向于0？并说明理由。

2-17 证明：①首先证明()T T T B C A ，，是()s G 的不可简约实现（该题有问题，不是()TT TCB A，，）。

由于()s G 是对称传递函数阵，故有()()T T T C sI B B A sI C 1-1-A --=，所以()TT TBC A，，是()s G 的实现。

又因为()[]n CA CA Crank CA C A C rank n Tn TT T T =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=1-1- ，其可控； 同理可证其可观，故系统()T T T B C A ，，是可控可观的。

所以其是()s G 的不可简约实现。

②证明P 的对称性。

由题设易知，由于()T T T B C A ，，是()s G 的不可简约实现，则存在非奇异阵P ，使得TT T BCPC PB A PAP===--11，，。

由T T T T T T P P I P P P CP P B C C PB =⇒=⇒==⇒=--11 所以P 是非奇异对称阵。

③证明P 的唯一性。

由T C PB =，很容易知道1-=B C P T ，故知P 是唯一的。

综上可知，命题得证。

2-18 解：[]1 1 3- 4 2301 4 0 2- 3-0 3 2- 6-0 02 0 0 0 0 1 -=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=C B A 。

a.① ><B A |由[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==65 17 5 2 3 3 3 3 00 0 0 1 1 1 1 32B A B A AB B U 所以)53012301(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡>=<，span B A 。

② η()⇔⋂=kCAker η064 27 118- 145-16 9 34- 43-4 3 10- 13-1 1 3- 4 032=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⇔=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡x x CACA CA C故)12101301(⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=，span η ③ ><⋂B A |η即任意>⇔<⋂∈B A x |η2153012301x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=，同时有4312101301x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=故0--1 1 5 22 3 3 31 0 0 00 1 1 14321=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡x x x x ，有)1301(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡>=<⋂span B A η ④ ⊥><⋂B A |η 易知，⇔>∈<⊥B A x |[]065 17 5 2 3 3 3 3 0 0 0 0 1 1 1 1 32=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=T TxB A B A AB B x，即 065 3 0 117 3 0 15 3 0 12 3 0 1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡x 所以)0103-0010(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=><⊥，span B A 同③，可知⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=><⋂⊥0000|B A η⑤ ><⋂⊥B A |η)101-1-0123(⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⊥，span η同③可知⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡>=<⋂⊥0000|B A η⑥ ⊥⊥><⋂B A |η易知)0123(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=><⋂⊥⊥span B A η 综上可知，上述空间的维数加起来不等于4，故在上述空间的直和空间中不能取到状态空间的基底。

《线性系统理论》作业参考答案1-1 证明：由矩阵úúúúúúûùêêêêêêëé----=--121000001000010a a a a A n n nL M O M M M L L L则A 的特征多项式为nn n n n n n n n n n n n n n n n n na a a a a a a a a a a a a a a a a A I +++==+--++--=--++--=+--=--------+-----L L L M O MM ML LL L M O M M M L L L L M O MMM L L L112114322111321121)1()1(00001001)1()1(000010001000010001l l l l l l ll l l l l l l l l ll 若i l 是A 的特征值，则00001000010001)(1112121=úúúúúúûùêêêêêêëé+++=úúúúúúûùêêêêêêëéúúúúúúûùêêêêêêëé+--=-----n n i n i n i i i in n ni i i i i a a a a a a A I L M M L M O M M M L L L l l l l l l l l l u l 这表明[]Tn ii i121-l l l L 是i l 所对应的特征向量。

一、给定多项式矩阵如下：22121()12s s s s D s s s ⎡⎤⎢⎥⎢⎥⎣⎦++++=++ 1. 计算矩阵的行次数，判断系统是否行既约？2. 计算矩阵的列次数，判断系统是否列既约？3. 寻找单模矩阵，将多项式矩阵()D s 化为史密斯型。

方法1、 进行初等变换成二、设系统的传递函数矩阵为右MFD 1()()N s D s -，其中：210()21s D s s s s ⎡⎤⎢⎥⎢⎥⎣⎦-=+-+，()11N s s s ⎡⎤⎣⎦=-+ 试判断{}(),()N s D s 是否右互质；如果不是右互质，试通过初等运算找出其最大右公因子。

最大右公因子进行列变换可得()0R s ⎡⎤⎢⎥⎣⎦三、给定()G s 的一个左MFD 为：121010()1121s s G s s s s -⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦-+=+-+ 试判断这个MFD 是否是最小阶的；如果不是，求出其最小阶MFD 。

四、确定下列传递函数矩阵的一个不可简约左MFD：2110()1022s ss G s s s s s ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦+=+++五、给定系统的传递函数矩阵为223(1)(2)(1)(2)()31(1)(2)(2)s s s s s s G s s s s s s ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦+++++=+++++ 试计算出相应的评价值，并写出其史密斯--麦克米伦型。

六、给定传递函数矩阵如下：22221156()125343s s s s s G s s s s s ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦+-++=++++ 试定出其零、极点，并计算出其结构指数。

七、给定系统的传递函数矩阵如下：22211154()143712s s s s G s s s s s ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦+-++=++++ 试求出一个控制器型实现。

八、确定下列传递函数矩阵()G s 的一个不可简约的PMD22141()14332s s s s G s s s s s ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦++-=++++九、给定系统的传递函数矩阵如下：12243011()22121s s s s G s s s s s -⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦++-+=+++试设计一个状态反馈K,使得状态反馈系数的极点为：12λ*=-， 23λ*=-， 4,542j λ*=-±。

重庆邮电大学研究生考卷A学号 姓名 考试方式 班级 考试课程名称 线性系统理论 考试时间： 年 月 日一、（10分）如下图所示系统，求以u 为输入，R2上电压u2为输出的状态空间表达式。

二、（10分）某系统的状态空间表达式为：u x x x x x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡631234100010321321 ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=321]001[x x x y ，试求该系统的传递函数。

三、（15分）已知连续时间线性时不变系统状态方程如下：（1）求解状态转移矩阵)(t φ和逆矩阵)(1t -φ （2）求单位阶跃信号u (t )=1(t )作用下的状态响应四、（15分）确定使下面连续时间线性时不变系统完全能控和完全能观测的待定()()()()()()0101,0,0,11210x t x t u t t x u t t ⎛⎫⎛⎫⎛⎫=+≥== ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭Ru参数a,b 取值范围[]xb y u x x x a x x x 0010030012011321321=⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∙∙ 五、（15分）试找出李亚普洛夫能量函数，判断下列连续时间非线性时不变系统为大范围渐近稳定。

⎪⎪⎭⎫⎝⎛--+-==3221213)(x x x x x x f x 六、（15分）给定一个完全能控单输入单输出连续时间线性时不变系统：[]1 0 212 1 121 0 210 1 1x x u y x⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦=试求出非奇异变换P 把上述系统变换为能控标准型。

七、（20分）给定单输入单输出连续时间线性时不变受控的传递函数为：)8)(4(10)(++=s s s s G试确定一个状态反馈阵K 使得闭环极点配置为***1112, 4, 7λλλ=-=-=-，并写出闭环系统状态方程。

线性系统理论多年考题和答案2019级综合大题⎡400⎤⎡1⎤⎥x +⎢1⎥u x =⎢0-21⎢⎥⎢⎥⎢⎢⎣00-1⎥⎦⎣0⎥⎦y =[112]x1 能否通过状态反馈设计将系统特征值配置到平面任意位置？2 控规范分解求上述方程的不可简约形式？3 求方程的传递函数；4 验证系统是否渐近稳定、BIBO 稳定、李氏稳定；（各种稳定之间的关系和判定方法！）5 可能通过状态反馈将不可简约方程特征值配置到-2，-3？若能，确定K ，若不能，请说明理由；6 能否为系统不可简约方程设计全阶状态观测器，使其特征值为-4，-5； 7画出不可简约方程带有状态观测器的状态反馈系统结构图。

参考解答： 1.判断能控性：能控矩阵M =⎡⎣B可控，不能任意配置极点。

2按可控规范型分解AB⎡1416⎤⎢1-24⎥, rank (M ) =2. 系统不完全A 2B ⎤=⎦⎢⎥⎢⎣000⎥⎦⎡1⎢3140⎡⎤⎢1⎢⎥-1取M 的前两列，并加1与其线性无关列构成P =1-20，求得P =⎢⎢⎥⎢6⎢⎥⎢⎣001⎦⎢0⎢⎣2⎤⎡08⎢3⎥⎡1⎤⎢⎥1⎢⎥-1-1进行变换=PAP ⎢12-⎥, =PB =0, =cP =[222]⎢⎥⎢6⎥⎢⎢⎥⎣0⎥⎦001⎢⎥⎢⎥⎣⎦2⎤0⎥3⎥1-0⎥⎥6⎥01⎥⎥⎦⎧⎡08⎤⎡1⎤⎪x =⎢⎥x +⎢0⎥u12所以系统不可简约实现为⎨⎣⎦⎣⎦⎪y =[22]x ⎩3.G (s ) =c (sI -A ) -1B =4.2(s -1)(s +1) 2(s -1)=(s -4)(s +2)(s +1) (s -4)(s +2)det(sI -A ) =(s -4)(s +2)(s +1) ，系统有一极点4，位于复平面的右部，故不是渐近稳定。

G (s ) =c (sI -A ) -1B =2(s -1)，极点为4，-2，存在位于右半平面的极点，故系统不(s -4)(s +2)是BIBO 稳定。

系统发散，不是李氏稳定。

1.为什么要对连续系统进行离散化?离散化有哪些方法?它们各自的特点是什么?因为连续系统在电脑上无法实现,只能把连续系统离散化,而离散华是将连续变化的模拟量信号，转换成数字量（脉冲）信号，但是这里的离散化是非常密集的,在误差允许的范围内,可以非常的逼近原函数.这样就能用数字电子计算机（电脑）进行计算或处理。

1.前向差分法S平面左半平面得极点可能映射到Z平面单位圆外，这种方式所得到得离散滤波器可能不稳定2.后向差分法变换计算简单；S平面得左半平面映射到Z平面得单位圆内部一个小圆内因此如果D（s）稳定则变换后的D（z）也稳定；离散滤波器得过程特性及频率特性同原连续滤波器比较有一定得失真，需要较小得采样周期T。

3.双线性变换法如果D（s）稳定，则相应得D（z）也稳定；D(s)不稳定，则相应的D(z)也不稳定；所得D（z）的频率响应应在低频段与D（s）得频率响应相近，而在高频段相对于D(S)得频率响应有严重畸变。

4.脉冲响应不变法D(z)和D(s)有相同得单位脉冲响应序列；若D(z)稳定，则D（s）也稳定；D(z)存在着频率失真。

该法特别适用于频率特性为锐截止型的连续滤波器的离散化。

主要应用于连续控制器D（s）具有部分分式结构或能较容易地分解为并联结构，以及D（s）具有陡衰减特性，且为有限带宽得场合。

这时采样频率足够高，可减少频率混叠影响，从而保证D（z）得频率特性接近原连续控制器D（s）。

5.阶跃响应不变法若D（s）稳定，则相应的D（z）也稳定；D(z)和D（s）得阶跃响应序列相同；6.零极点匹配法需要先求出连续传递函数得全部零极点，计算复杂；能够保持变换前后特征频率处得增益不变；不改变系统得稳定区域，变换前后G（z）和G（s）的稳定特性不变2.多输入/多输出系统能控性和能观测性与系统传递函数矩阵的关系如何?在单输入单输出系统中，能控且能观测得充分必要条件是传递矩阵G （s ）的分母与分子之间不发生因子相消。

【关键字】理论1-1 证明：由矩阵可知A的特征多项式为若是A的特征值，则所以是属于的特征向量。

1-7 解：由于，可知当时，，所以系统不具有因果性。

又由于，所以系统是时不变的。

1-8 解：容易验证该系统满足齐次性与可加性，所以此系统是线性的。

由于而，故，所以系统是时变的。

又因为而，故，所以系统具有因果性。

1-11 解：由题设可知，随变化的图如下所示。

随变化的图如下所示。

从上述两图及所描述的系统，分析如下：当，且即时，有；当时，；当时，有；当时，有；当时，有；综上所示，该松弛系统在上述输入而激励的输出为：1-15 解：由上述齐次方程，可得两线性无关的解向量为：，所以即其基本矩阵为；状态转移矩阵为：1-17 证明：由题设我们可知故，得证。

1-19 证明：由题设可知：由上式可推出又由及习题1-17的结论可推出由以上两个结论，我们可得到 所以得证。

即 得证。

1-20 解：设其等价变换为，则可知: 由于P 是非奇异矩阵，所以。

1-24 解：易知，其中为严格真有理函数矩阵，进行下列计算： ，则所以因此，可得一个实现如下： 其模拟图如下所示。

1-25 证明：由题设知同理可知若要使得两系统零状态等价，则要满足，即满足 ，得证。

2-2 解： a,由题设可知：[]315 1 7- 1 1 1-7- 1 1 1- 1 0 1 1- 10 0 1 B A AB B 2=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=rank rank ，所以系统可控； 30 2 2 8- 14- 8-1- 3- 2-4 4 2 1 2 1 1- 10 2=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡rank CA CA C rank ，所以系统可观。

b,[]x c c c y u x x 0 1 1 0 0 1 1 0 0 0 1 0 0 1 1 321=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=•由题设可知：[]30 1 0 1 1 0 1 0 1 1 01 A B 2=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==rank B rank rankB ，所以系统可控； （1）若0321===c c c ，则系统不可观；（2）若321c c c ，，中至少有一个不等于零，则3 2 CA CA C 321132113212≠⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡c c c c c c c c c c c rank rank ，所以系统不可观； 总之，该系统不可观。