最新东北大学线性代数课件第一章_行列式
- 格式:doc
- 大小:835.00 KB
- 文档页数:23



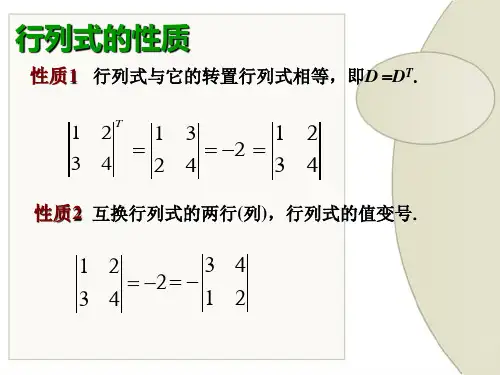
最新东北大学线性代数课件第一章_行列式东北大学线性代数课件第一章_行列式第一章行列式教学基本要求: 1. 1. 了解行列式的定义.2. 掌握行列式的性质和计算行列式的方法.3. 会计算简单的n 阶行列式.4. 了解Cramer 法则.一、行列式的定义 1. 定义nnn n nna a a a a a a a a 212222111211称为n 阶行列式,记作D (或n D 或||ij n a ),它是n 2个数(1,2,,;1,2,,)ij a i n j n ==的一个运算结果:1112121222111112121112n n n n n n nna a a a a a D a A a A a A a a a ==+++,(1.1)其中,(1,2,,;1,2,,)ij a i n j n ==为行列式位于第i 行且第j 列的元素,111(1)j j j A M +=-(1,2,,)j n =,而1j M 为划掉行列式第1行和第j 列的全部元素后余下的元素组成的1n -阶行列式,即2121222312131111j j n j j n j n n j n j nna a a a a a a a M a a a a -+-+-+=1j M 称为元素1j a 的余子式,1j A 称为元素1ja 的代数余子式.2. 基本行列式:(1)一阶行列式 a a =||. 例如,|106|106=,2121-=-.1112112212212122a a a a aa a a =-.112233122331132132a a a a a a a a a ++ 132231122133112332a a a a a a a a a ---.(4)三角形行列式①对角行列式111122nn nna a a a a =.②下三角行列式11221nn n nn a a a a a a =.③上三角行列式1111122nnn nna a a a a a =.④1(1)212111(1)nn n n n n n a a a a a --=-.⑤1(1)212111(1)nn n n n n n nn a a a a a a --=-. ⑥111(1)212111(1)nn n n n n n a a a a a a --=-.3. 行列式的性质nnn n n n a a a a a a a a a D212222111211=,nnn nn n T a a a a a aa a a D212221212111=性质1.1 D D T =. (1.2)性质1.1的意义:行列式的行所具有的性质列也具有.下面仅针对行叙述行列式的性质. 性质1.2(行列式的展开性质) 1112121222112212n n i i i i in in n n nna a a a a a a A a A a A a a a =+++, (1,2,,)i n =. (1.3)例如,行列式1214020311202302003059D A A -==+ 3214442396A A A ==+=.一个n 阶行列式有个余子式,有个代数余子式;一个元素的余子式与代数余子式或或 .应该注意到,一个元素的余子式或代数余子式与该元素的有关,与该元素的无关.性质1.3(行列式的公因子性质)11i in i in ka ka k a a =. (1.4)性质1.3还可以这样表述:用数k 乘以行列式某一行的每一个元素,等于用数k 乘以行列式.例如,24612340524052(58)116106106=?=?-=---.0.510.520.531234050.54050.5(58)29106106=?=?-=---. 推论行列式的一行元素全为零,行列式为零.性质1.4(行列式的拆分性质)11121112212111211112112121212.n i i i i in in n n nnnn i i in i i in n n nnn n nna a abc b c b c a a a a a a a a a b b b c c c a a a a a a +++=+ (1.5)性质1.4可以推广到一行有更多个数相加的情形.性质1.5 行列式两行元素对应全相等,行列式为零. 推论1 行列式两行元素对应成比例,行列式为零. 推论2 设行列式||ij n D a =,则1122i j i j in jn ij a A a A a A D δ+++=?. (1.6)这里,1,,0,.ij i j i j δ=?=?≠?ij δ为Kronecker 符号.性质1.6(行列式的不变性质)nnjn inn n j i n j i nn in jn in n n i j in i j i a a a a a a a a a a a a a ka a a a a ka a a a a ka a a a122212111111222212111111=+++. (1.7)性质1.6的意义:任何一个行列式都可化为三角形行列式,从而算出值.性质1.7(行列式的变号性质)12121212()i i inj j jnj j jni i ina a a a a a i j a a a a a a =-≠. (1.8)总结:利用性质1.6及其它性质与推论,可以更容易地将一个行列式化为“三角形”行列式.步骤如下:111211111121112122212222121212100n nn n n n n n n n nn nn nnnnna a a a a a a a a a a a a a a a a a a a a a ------'''''''→'''(n 1)(n 1)(n 1)(n 1)11121111112111(n 1)(n 1)(n 1)2221222212(n 1)100000n n n n n n n nnnnnnna a a a a a a a a a a a a a a a a -------------''''''''''''''→→→''''.例如,582900610312540610312610540312601504321-=-=-=--=-.在实际计算中,往往是“化零”与“展开”结合着进行,需要根据行列式的特点灵活地运用行列式的性质.二、行列式的计算行列式的计算过程,大多可以通过如下符号指示:交换i , j 两行(列):i j r r ?(i j c c ?);第i 行(列)提取公因子k :i r k ÷(i c k ÷);第j 行(列)的k 倍加到第i 行(列):i j r kr +(i j c kc +).例1.1 计算行列式011212120112110-----=D .解 011212120112110-----=D112121110121121210111265----?-?+---?-?=)()(46242=?+?-=.或 01120112110210101210121021102110D -----==---- 51012(1)1212(2)4211=?---=-?-=.例1.2 计算行列式0203112002003059D -=. 解 653216953021300)1(25=-=?-?=D . 或144414443939(3)(2)906D A A M M =+=-+=-?-+?=.。







东北大学线性代数课件第一章_行列式第一章 行列式教学基本要求: 1. 1. 了解行列式的定义.2. 掌握行列式的性质和计算行列式的方法.3. 会计算简单的n 阶行列式.4. 了解Cramer 法则.一、行列式的定义 1. 定义nnn n nna a a a a a a a a 212222111211称为n 阶行列式,记作D (或n D 或||ij n a ),它是n 2个数(1,2,,;1,2,,)ij a i n j n ==的一个运算结果:1112121222111112121112n n n n n n nna a a a a a D a A a A a A a a a ==+++,(1.1)其中,(1,2,,;1,2,,)ij a i n j n ==为行列式位于第i 行且第j 列的元素,111(1)j j j A M +=-(1,2,,)j n =,而1j M 为划掉行列式第1行和第j 列的全部元素后余下的元素组成的1n -阶行列式,即212121222312131111j j n j j n j n n j n j nna a a a a a a a M a a a a -+-+-+=1j M 称为元素1j a 的余子式,1j A 称为元素1ja 的代数余子式.2. 基本行列式:(1)一阶行列式 a a =||. 例如,|106|106=,2121-=-.1112112212212122a a a a aa a a =-.112233122331132132a a a a a a a a a ++ 132231122133112332a a a a a a a a a ---.(4)三角形行列式①对角行列式111122nn nna a a a a =.②下三角行列式1111221nn n nn a a a a a a =.③上三角行列式1111122nnn nna a a a a a =.④1(1)212111(1)nn n n n n n a a a a a --=-.⑤1(1)212111(1)nn n n n n n nn a a a a a a --=-.⑥111(1)212111(1)nn n n n n n a a a a a a --=-.3. 行列式的性质nnn n n n a a a a a a a a a D212222111211=,nnn nn n T a a a a a aa a a D212221212111=性质1.1 D D T =. (1.2)性质1.1的意义:行列式的行所具有的性质列也具有.下面仅针对行叙述行列式的性质. 性质1.2(行列式的展开性质)1112121222112212n n i i i i in in n n nna a a a a a a A a A a A a a a =+++, (1,2,,)i n =. (1.3)例如,行列式1214020311202302003059D A A -==+ 3214442396A A A ==+=.一个n 阶行列式有 个余子式,有 个代数余子式; 一个元素的余子式与代数余子式或 或 .应该注意到,一个元素的余子式或代数余子式与该元素的 有关,与该元素的 无关.性质1.3(行列式的公因子性质)11i in i in ka ka k a a =. (1.4)性质1.3还可以这样表述:用数k 乘以行列式某一行的每一个元素,等于用数k 乘以行列式.例如,24612340524052(58)116106106=⨯=⨯-=---.0.510.520.531234050.54050.5(58)29106106⨯⨯⨯=⨯=⨯-=---. 推论 行列式的一行元素全为零,行列式为零.性质1.4(行列式的拆分性质)11121112212111211112112121212.n i i i i in in n n nnnn i i in i i in n n nnn n nna a abc b c b c a a a a a a a a a b b b c c c a a a a a a +++=+ (1.5)性质1.4可以推广到一行有更多个数相加的情形.性质1.5 行列式两行元素对应全相等,行列式为零. 推论1 行列式两行元素对应成比例,行列式为零. 推论2 设行列式||ij n D a =,则1122i j i j in jn ij a A a A a A D δ+++=⋅. (1.6)这里,1,,0,.ij i j i j δ=⎧=⎨≠⎩ij δ为Kronecker 符号.性质1.6(行列式的不变性质)nnjn inn n j i n j i nn in jn in n n i j in i j i a a a a a a a a a a a a a ka a a a a ka a a a a ka a a a122212111111222212111111=+++. (1.7)性质1.6的意义:任何一个行列式都可化为三角形行列式,从而算出值.性质1.7(行列式的变号性质)12121212()i i inj j jnj j jni i ina a a a a a i j a a a a a a =-≠. (1.8)总结:利用性质1.6及其它性质与推论,可以更容易地将一个行列式化为“三角形”行列式.步骤如下:111211111121112122212222121212100n nn n n n n n n n nn nn nnnnna a a a a a a a a a a a a a a a a a a a a a ------'''''''→'''(n 1)(n 1)(n 1)(n 1)11121111112111(n 1)(n 1)(n 1)2221222212(n 1)100000n n n n n n n nnnnnnna a a a a a a a a a a a a a a a a -------------''''''''''''''→→→''''.例如,582900610312540610312610540312601504321-=-=-=--=-.在实际计算中,往往是“化零”与“展开”结合着进行,需要根据行列式的特点灵活地运用行列式的性质.二、行列式的计算行列式的计算过程,大多可以通过如下符号指示:交换i , j 两行(列):i j r r ↔(i j c c ↔); 第i 行(列)提取公因子k :i r k ÷(i c k ÷); 第j 行(列)的k 倍加到第i 行(列):i j r kr +(i j c kc +).例1.1 计算行列式011212120112110-----=D .解 011212120112110-----=D112121110121121210111265----⨯-⨯+---⨯-⨯=)()(46242=⨯+⨯-=.或 01120112110210101210121021102110D -----==---- 51012(1)1212(2)4211=⨯---=-⨯-=.例1.2 计算行列式0203112002003059D -=. 解 653216953021300)1(25=-=⨯-⨯=D . 或 144414443939(3)(2)906D A A M M =+=-+=-⨯-+⨯=.或 0203112002003059D -=4130203112002003650r r --=- 5112123(1)0206635365-=⨯-=-=-.例1.3 计算行列式653511311280111----=D .解 11100010821161113101410153562256D --===-------.例1.4 计算n 阶行列式121231.1232212221n n n nn D n n n n n n n n -+=---+--解 11120 3.n , n D , n , n =⎧⎪=-=⎨⎪≥⎩,,例1.5(例1.10 P 16) 计算n 阶行列式na b b b a b b b a D=.解 分析:注意到该行列式的特点是,主对角线上的元素是同一个值,主对角线之外的元素都相同,那么运用 ,有12(1)(1)(1)nn i c c na nb b b a n b a b D a n b ba =++-∑+-=+-(这时行列式 ,继续)12,,(1)00i c c i nna nb bba ba b -=+--=-(这时行列式 ,继续)1[(1)]()n a n b a b -=+--.例1.6(例1.11 P 16) 设行列式n ij a D =的阶数n 为奇数,且ji ij a a -=),,2,1,(n j i =,求D .解 分析:条件ji ij a a -=),,2,1,(n j i =表明),,2,1(0n i a ii ==,000321323132231211312n nnn nn a a a a a a a a a a a a D ------= (称为反对称行列式) (每行提取公因子-1,然后做转置运算,有)121311223213233123121*********23312300(1)00000,0n n n n nn n n nn nnna a a a a a a a a a a a a a a a a a a a a D a a a -----=---=---=----从而D =0.例1.7(例1.12 P 17) 计算n 阶行列式nn D 2112112112=. (三对角行列式)解 分析:该行列式对角线上的元素全为2,次对角线上的元素全是1,其余元素都是0.由于0元素比较多,所以利用展开性质(也说降阶法)来计算.将D n 按第1行展开,有121112M M D n ⋅-⋅=.注意到111-=n D M ,如果再将12M 按第1列展开,即有212-=n D M .于是得到一个递推公式212---=n n n D D D .现在考虑数列}{n D ,由211----=-n n n n D D D D 可知,数列}{n D 是一个等差数列,公差为12312=-=-D D ,首项21=D ,从而第n 项1+=n D n .降阶法是求三对角行列式的常用方法,但不是唯一的方法. 另解,nr r nn D 2112123012212112112112122-==3243342121032032043043111110236421211212r r r r nn--=⨯=⨯== nn n n nn 1011342030121)!1(1+-⨯-1+=n .三对角行列式的一般形式为nnn n n n a c b a c b a c b a D 111222111---=. (1.9)例1.8(例1.13 P 17) Vandermonde 行列式()1232222123111111231111n n n ji i j nn n n n na a a a D a a a a aa a a a a ≤<≤----==-∏. (1.10)记住Vandermonde 行列式的特点、结果,了解证明方法.三、行列式应用1. 求解特殊的线性方程组 考虑n 元线性方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++.,,22112222212111212111n n nn n n n n n n b x a x a x a b x a x a x a b x a x a x a (1.11) 记 111212122212n n n n nna a a a a a D a a a =,1121222212n n nn nnb a a b a a D b a a =,1111212221n n n nnna b a a b a D a b a =,,111212122212n n n na ab a a b D a a b =.定理(Cramer 法则) 若线性方程组(1.11)的系数行列式0≠D ,则该方程组有惟一解:i i x D D =(1,2,,i n =). (1.12)例1.9(例1.14 P 20) 解线性方程组⎪⎩⎪⎨⎧=---=++=-+.0 2,23 2 ,1 2321321321x x x x x x x x x 解 该方程组的系数行列式D 及D 1、D 2和D 3分别为20121312121=---=D ,31203121211-=----=D ,51013221112=---=D ,130212121213-=--=D .由于0≠D ,故方程组有唯一解:20311-==D D x ,4120522===D D x ,201333-==D D x .对于齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++,0,0,0221122221211212111n nn n n n n n n x a x a x a x a x a x a x a x a x a (1.13) 有如下结论:推论 当齐次线性方程组(1.13)的系数行列式不为零时,它只有零解.该结论也可以表述为:若齐次线性方程组有非零解, 则方程组的系数行列式必为零.2. 用行列式表示几何图形的面积和体积.3. 用行列式表示直线、平面方程和判定三点是否共线、四点是否共面.4. 用行列式解决多项式函数的插值问题.四、习题(P 26-30) 选择题:1. 112,,111010(1)01i r r n i nD --=-==--.填空题:5. 4142434441424344M M M M A A A A +++=-+-+3040222207001111==---.解答题:1. 解 414243213114204232011420A A A -++==-.2. 提示:由A 31=-2,求出x ,再计算A 12.3.(3) n 2n 222121(1)1n n n a D aD a D a a a a----=====-.(4) ()nnn112n i i i i i 111nn a d a d D a b c d .c b c b ===-∏(5) 33(1,2,4,,)(1,2,4,,)1, 1,7, 2,6(3)!, 3.i i r r i n c c i n n D n n n -=-==⎧⎪=-=⎨⎪-≥⎩(6) i i n 1112n 1n 2n 1n nc a c i i 1,2,,ni 1nx a a a a a 10x a a a 1D(x a )00x a 101+---==-----==--∏.(7) i 1i r r i n,,212n 1n1111n D 111n 111n 11+-=--=-- i 11ic c i 2,,nni 21c c ni 2,,n(n 1)(n2)nn 12i 2n(n 1)n 1211n 2n 1100n 10n 01n 0011(i 1)1n 2n 1n 000n 00n 00n1(1)(n)(1(i 1))n (n 1)n (1).2-==+=---=-----=--+----=--=--+-+=-∑∑(8) 12n 1n12n x a a 1a x a 1D a a x 10001=i i n 1i n 1ii i 1122c a c i 1,2,,nn n12n1122ar r xa i 1,2,,nn nni i 1i ini11n n i 1i ix a 0010x a 0100x a 1a a a 1x a 0010x a 0100x a 1a 01x a a (x a )(x a )(1).x a ++-=+-===--=------=-+-=--+-∑∑(11) 12n a x a a 1aa x a1D aa ax 1001++=+i n 112c ac i 1,,nn 12nni 1in1n i 1ix 0010x 0100x 1a a a 1x 0010x 0100x 1a 001(1)x a x x (1(1)).x +-====---=++=++∑∑(9)方法一 左端按最后一行展开方法二 左端按第一列展开,产生递推公式1n n n D xD a -=+. 方法三 左端产生下三角行列式.从第二列开始,依次将前一列的1x倍加到后一列上.方法四 左端从最后一列开始,依次将后一列的x 倍加到前一列,然后按第一列展开.(10) 方法一n na b ab 1a b abD 1a b ab1a b ++=++n 1n 2(a b)D abD --=+-⇒ ()()n 2n n n 1n 1n 221D aD b D aD b D aD b -----=-==-=⇒n n n 1n 1n 1n 2221D aD b D aD b D aD b -----=-=-=⇒n 1n n 1n 22n nn 1n 22n 1nD a (a b)b ab a b a ab ab ab b .------=+++++=+++++方法二n na b ab1a b abD 1a b ab1a b ++=++nnn 1nn 1n 1a abb ab1a b ab 0a b ab 11a baba b ab1a b 1a b a 01a ab bD 1a b ab1a b a ab1a b ab a bD 1a b ab1a b ---++=+++++=++++=+++n n 1a bD -=+ (1)同理,n n n 1D b aD -=+ (2)由(1)×a, (2)×b 得aD n -a n+1= bD n -b n+1,所以 D n =(b n+1-a n+1)/(b-a)=n n 1n 22n 1n a a b a b ab b ---+++++.(12) 设 1232222212311111123123111111nn n n n n n n n n n n n nn n n nnn a a a a x D a a a a x a a a a x a a a a x ----------+=,这是一个范德蒙行列式.111121111112111()()()()() nni i j i n i j nnnn i j n i j n i j n i j n n n n n n n n D x a a a a a x a a a a a x x A x A xA A =≥>≥-≥>≥≥>≥-+++++=--=--+++-+=++++∏∏∏∏123222211111231111211111 ()().n n n n n nn n n nnn n n n n nn i j n i j a a a a a a a a a a a a D x M A a a a a a -----++≥>≥==-=+++-∏的元素的余子式7. 提示:x=D x /D, D=-4 ⇒ x a b c a 11111b 11D 4111c 11-=-=-=--.8. 提示:(0,3),(2,2)→→==AB AC ,03622=-,故三角形ABC 的面积为3.五、计算实践实践指导:(1)注意到上(下)三角行列式和对角行列式的值等于其对角线上元素的乘积,所以利用行列式的性质应尽可能地把行列式化为三角形行列式;(2)利用行列式的性质尽把行列式的某一行(列)元素可能多地化为零,然后按行(列)展开,通过降阶的方式达到计算行列式的目的;(3)利用Laplace 展开式; (4)利用范德蒙行列式;(5)计算行列式的可使用的方法有定义法、性质法、降阶法、递推法、归纳法、加边升阶法及方阵行列式法等.例1 计算行列式 14 0 1 136 0 01 11 25 1. 3 13 12 113 1 1------ 解 分析:仔细观察之后发现,第2行为0的元素多且非0元素成整数比关系,因此先利用性质把这一行元素大部分化为0,然后按第2行降阶. 依照此理,接下来又选择了第1行、第3行降阶.原式2112c 2c c 3c 22 0 1 1 0 0 0 012 3 25 13 73 1 22 1 3 1 1+----=-----2522012325(1)(1)37312131+----=-⨯----211423c c c 2c c c 140011252511031033112521252(1)110311330330031233459.113-+-+--=---=---=-== 例2 计算三对角行列式1112223n n 2n 2n 1n 1n 1na b c a b c a D b c a b c a -----=.解 这类题的一般做法是产生递推公式. 按第n 行展开有1112n (n 1)n n 1n n 1n 2n 2n 1a b c a D (1)c a D a 0c b +------=-+n (n 1)(n 1)(n 1)n n 1n 1n 1n 2n n 1n 1n 1n 2a D (1)(1)b c D a D b c D .+--+---------=+--=-令n n 1n 1x y a xy b c --+=⎧⎨=⎩,则x,y 是方程2n n 1n 1z a z b c 0---+=的根,代入上式得 n n 1n 2D (x y)D xyD --=+-.()()n n 1n 1n 2n 221n 221D xD y D xD y D xD y r. (r=D xD )------=-==-=-n 2n n 1n 3n 2n 2n 1n 2n 3n 2121D xD xy x(xD xy )y r x D (x x y y )r. (r=D xD )---------=+=++==++++-对于具体的三对角行列式,一般计算会简单些.例3 计算三对角行列式n na b b a a b b a a b Da b b a a b +++=++.解 方法一 利用例2得到的递推公式.n n 1n 2D (a b)D abD --=+-n n 1n n 1n 2aD b a(aD b )b ---=+=++(这里递推公式中的x,y 显然分别为a,b )n 1n 22n1nn 1na D ab b a a b b .---==+++=+++方法二 按第一行拆分,有i i 1n nnc c n 1i 2,,nnn n 1a 0 b ba ab b a a b b a a baa b Da b ba b ba ab a a b b 0 a b 0 a baD b 0 a b aD b .---=-++++=+++++=+=+①考虑对称性,也有n n n 1D bD a -=+. ②联立①、②,解之得n 1n 1n n 1n n a b D a a b b .a b++--==+++-对称性在本题中起了重要作用. 本题还可以用数学归纳法做.例4 计算三对角行列式11223n 1nn1 a 11a a 11a a11a a 1 1a ---------.解 分析:把第2至第n+1行依次加到第1行,那么新的第1行元素将只有最后一个元素不为0,然后降阶.原式1223n 1nn0 0 111a a 11a a11a a 1 1a -----=----n 1i i 212r 21(n 1)n 1n 111a a 11a (1) 1a1a 1+=+++------∑=----1r (上三角行列式)1(n 1)n (1)(1) 1.++=--=例5 计算行列式n n 1n 111111n n 1n 122222i i n n 1n 1nn n n na ab a b a a b a b , (a b 0,i 1,,n).a a b a b ------≠=解 分析:注意到本行列式元素的特点,自然想到会要使用范德蒙行列式的结果. 易见如果第1至第n 行分别提取公因子n n 1n a ,,a ,那么可将其化为范德蒙行列式.原式()n 11111n 122n12n 22n 1nn nn b b 1a ab b 1a a a a a b b 1a a ---⎛⎫ ⎪⎝⎭⎛⎫ ⎪=⎝⎭⎛⎫ ⎪⎝⎭()nj i 12n 1j i n i j b b a a a a a ≤<≤⎛⎫=- ⎪ ⎪⎝⎭∏. 六、知识扩展1. 设123,,ααα均为3维列向量,记矩阵()123,,A ααα=,(123123,24,B αααααα=++++)12339ααα++.如果1A =,求B . (2005 一) (答案: 2)2. 已知12,αα均为2维列向量, 矩阵()()1212122,,A B αααααα=+-=,. 若6A =, 求B . (2006四) (答案: -2)3.设矩阵2112A ⎛⎫= ⎪-⎝⎭, E 为2阶单位矩阵, 矩阵B 满足2BA B E =+, 求B . (2006一) (答案: 2)提示: 方法一()()112211112211112BA B E B A E E B A E B --=+⇒-=-⎛⎫⎛⎫⇒=-== ⎪ ⎪-⎝⎭⎝⎭⇒= 方法二() 2242BA B E B A E E B A E B =+⇒-=⇒⋅-=⇒=4. 计算五阶行列式5100011001100011011aa a a D a aa a a---=------. (1996 四)5. 设有齐次方程组()()()1212121 0 22 200n n n a x x x x a x x nx nx n a x ++++=⎧⎪++++=⎪⎨⎪⎪++++=⎩, 试问a 取何值时该方程组才能有非零解? (2004 一 二) (答案: 0或(1)2n n +-)6. 已知行列式111212122212n n n n nna a a a a a D a a a =和齐次线性方程11220i i in n a x a x a x +++=, 证明:()()()12,,,11,2,,;nj j jnM M M j n j i --=≠都是该方程的解. 提示: 10,,=1,2,,()nik jk k a A i j n i j ==≠∑.。