2015年春清外冲刺班数学卷(共8套)

2015年春初二年级半期考试 数学 试题卷（适用年级：八年级 测试时间：120分钟 满分：150分） 一、精心选一选（每小题3分，共60分） 1、如果把yx y322-中的x 和y 都扩大5倍，那么分式的值（ ）A 、扩大5倍B 、不变C 、缩小5倍D 、扩大4倍2、某厂接到加工720件衣服的订单，预计每天做48件，正好按时完成，后因客户要求提前5天交货，设每天应多做x 件，则x 应满足的方程为（ ）A 、x +48720─548720= B 、x+=+48720548720C 、 572048720=-xD 、-48720x +48720=5 3、若0414=----xxx m 无解，则m 的值是（ ） A 、－2 B 、2 C 、3 D 、－34、在代数式cyx x a n m x --+++,11,33),(21,213中，分式的个数有（ ）A 、2个B 、3个C 、4个D 、5个 5、把分式方程112+-=-x x x 化为整式方程，正确的是 （ ） A 、21)1(2x x -=-+ B 、()()x x x x -=--+112 C 、()()2112x x x x -=+-+ D 、2)1(2x x x x -=+-6、若分式方程xx x x m x x 1112+=++-+产生增根，则m 的值等于（ ） A 、-1或-2 B 、-1或2 C 、1或2 D 、0或-27、若点A(2，4)在函数2-=kx y 的图象上，下列各点在此函数图象上的是（ ）。

A 、 (0，－2) B 、(23，0) C 、 (8，20) D 、（21，21） 8、若函数y=(m+1)mx +2是一次函数，则m 的值为 （ ）A 、1±=mB 、1-=mC 、1=mD 、1-≠m9、若一次函数y=(1-2m)x+3的图象经过A （1x ，1y ）和B(2x ，2y )，当1x ＜2x 时，1y ＜2y ，则m 的取值范围是（ ） A 、m ＜0 B 、m ＞0 C 、m ＜12 D 、m ＞1210、已知直线y=a cx b b+中，若ab ＞0,ac ＜0,那么这条直线不经过（ ） A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限11、若点()k k P --112，在第四象限，则ｋ的取值范围为 （ ）A 、1>kB 、21<k C 、21>k D 、121<<k 12、 一次函数n mx y +-=的图象经过第二、三、四象限，则化简22)(n n m +-所得的结果是 （ ）A 、mB 、m -C 、n m -2D 、n m 2-13、如右图，三个大小相同的正方形拼成六边形，一动点P 从点A 出发沿着A →B →C →D →E 方向匀速运动，最后到达点E ，运动过程中△PEF 的面积（S ）随时间（t ）变化的图像大致是( )14、函数()0,21≠=+=k xky k kx y 在同一坐标系中的图象大致是（ ）15、下列函数中，y 随x 的增大而减小的有（ ）①12+-=x y ② x y -=6③ 31xy +-= ④ x y )21(-=A 、1个B 、2个C 、3个D 、4个16、在□ABCD 中，AC 、BD 相交于点O ，AC ＝10,BD ＝8，则AD 的长度的取值范围是（ ） A 、AD>1 B 、1<AD<9 C 、AD<9 D 、AD>9 17、平行四边形的一条边长是10，则两条对角线的长可以是（ ） A 、10，12 B 、8，10 C 、6，8 D 、4，818、如图，若□ABCD 的面积为82cm ，点E 是AD 上一动点，则△BCE 的面积为（ ） A 、162cm B 、82cm C 、42cm D 、不能确定19、如图，在□ABCD 中，点E 在边AD 上，以BE 为折痕，将△ABE 向上翻折，点A 正好落在CD 边上的点F 处.如果△FDE 的周长为8，△FCB 的周长为22，那么FC 的长为（ ） A 、6 B 、11 C 、7 D 、820、四边形ABCD 中，对角线AC 、BD 相交于点O ，下列条件不能判定这个四边形是平行四边形的是（ ）A 、AB ∥DC ，AD ∥BC B 、AB=DC ，AD=BC C 、AO=C0，BO=DO D 、AB ∥DC ，AD=BC二、细心填一填（每空3分，共30分）21、分式xx -+212中，当____=x 时，分式没有意义；当____=x 时，分式的值为零。

江西省2015年中等学校招生考试数学冲刺试题卷说明:1.本卷共有六个大题,24个小题,全卷满分120分,考试时间120分钟.2.本卷分为试题卷和答题卷,答案要求写在答题卷上,在试题卷上作答的不给分. 一、选择题（本大题共6小题，每小题3分，共18分。

每小题只有一个是符合题意的） 1．－6的倒数是（ ） A ．61 B ．－61C ．6D ．6.0-2．下列运算正确的是（ ） A ．6a －(2a －3b )=4a －3b B ．(ab 2)3=a 3b 5C ．2x 3·3x 2=6x 5D ．(－c )4÷(－c )2=－c 23．我国许多城市的“灰霾”天气严重，影响身体健康．“灰霾”天气的最主要成因是直径小于或等于2.5微米的细颗粒物（即P M2.5），也称为可入肺颗粒物．已知2.5微米=0.0000025米，此数据用科学记数法表示为（ ）米 A ．2.5×106B ．0.25×10－5C ．2.5×10－7D ．2.5×10－64．一把锁的形状如图所示，以箭头所指的方向为主视方向，则它的俯视图可以是（ ）5．在中考体育测试中，九（2）班6位同学的立定跳远成绩（单位：m ）分别为：1.71，1.85，1.85，1.96，2.10，2.31．则这组数据的众数和极差分别是（ ） A ．1.85和0.21 B ．1.85和0.60 C ．2.11和0.46 D ．2.31和0.606．若干个正方体形状的积木摆成如图所示的塔形，平放在桌面上，上面正方体的下底四个顶点是下面相邻正方体的上底各边中点，最下面正方体棱长为1．若塔形露在外面的面积超过7，则正方体的个数至少是（ ） A ．2个B ．3个C ．4个D ．5个二、填空题（本大题共8小题、每小题3分，共24分） 7．计算：38×sin30°=_________.8．不等式组⎩⎨⎧>-≤-4231x x 的解集为_________.9．如图，矩形ABCD 中，将四边形ABFE 沿EF 折叠得到四边形HGFE ，己知∠CFG =40°，则∠DEF =_________.10．用一个半径为8，圆心角为90°的扇形围成一个圆锥的侧面，则圆锥的高为______. 11．分式方程：1-x x +x-12=2的解是___________. 12．已知点A (x 1，0)，B (x 2，0)是二次函数y =x 2+ax +a 与x 轴的两个交点，且x 1+x 2－x 1x 2=－10，则a =_________.13．在平面直角坐标系中，△ABC 的顶点坐标分别为A (1，6)，B (3，2)，C (5，2)，若△A 1B 1C 1与△ABC 的位似比为1：3，位似中心为O 1(1，0)，则点A 1的坐标为________. 14．已知在△ABC 中，∠B =90°，AB =8，BC =6，BE 为中线，△BEF 为等腰三角形（点F 在边AB 或AC 上，且不与顶点重合），则△BEF 的面积为______. 三、解答题（共4小题、每小题6分，共24分） 15．先化简x x 1-÷(x －xx 12-)，再任选一个适当的整数代入求值.16．如图，这是某个小区的道路示意图，小明家住在该小区的A 处，他每天晚饭后都要从家出发随机沿着小区内的道路散步一圈后回家(每条道路不能重复走，有的道路可以不走)。

（完整）2015年山东春季高考数学试题及详解答案编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）2015年山东春季高考数学试题及详解答案）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）2015年山东春季高考数学试题及详解答案的全部内容。

机密★启用前山东省2015年普通高校招生(春季)考试数学试题注意事项:1.本试卷分卷一（选择题）和卷二（非选择题）两部分,满分120分,考试时间120分钟。

考试结束后，请将本试卷和答题卡一并交回.2.本次考试允许使用函数型计算器,凡使用计算器的题目，最后结果精确到0。

01。

卷一（选择题，共60分）一、选择题(本大题共20个小题，每小题3分,共60分.在每小题列出的四个选项中，只有一项符合题目要求，请将符合题目要求的选项字母代号选出，填涂在答题卡上） 1。

集合{}1,2,3A =,{}1,3B =，则A B 等于（ ） A.{1,2，3} B.｛1,3｝ C 。

｛1，2｝ D 。

{2} 2。

不等式15x -<的解集是（ ）A.（6-，4） B 。

（4-,6) C.(,6)(4,)--+∞∞ D 。

(,4)(6,)--+∞∞3.函数1y x=的定义域是( ）A.{}10x x x -≠且B.{}1x x -C.{}>10x x x -≠且D.{}>1x x -4.“圆心到直线的距离等于圆的半径”是“直线与圆相切"的( )A.充分不必要条件B.必要不充分条件 C 。

充要条件 D.既不充分也不必要条件 5.在等比数列{}n a 中，241,3a a ==,则6a 的值是( ） A 。

2015年上海市春季高考数学试卷（学业水平考试）2015.01一、填空题（每小题3分，满分36分）1.设全集为{}1,2,3U =，{}1,2A =，若集合则U A =ð________.2.计算：1ii+=________（其中i 为虚数单位）. 3.函数sin 24y x π⎛⎫=+ ⎪⎝⎭的最小正周期为_______.4.计算：223lim 2n n n n→∞-=+_______.5.以()2,6为圆心，1为半径的圆的标准方程为_______.6.已知向量()1,3a = ，(),1b m =-，若a b ⊥ ，则m =_______.7.函数[]224,0,2y x x x =-+∈的值域为_______.8.若线性方程组的增广矩阵为0201a b ⎛⎫⎪⎝⎭，解为21x y =⎧⎨=⎩，则a b +=_______. 9.方程()lg 21lg 1x x ++=的解集为_______.10.在921x x ⎛⎫+ ⎪⎝⎭的二项展开式中，常数项的值为_______.11.用数字组成无重复数字的三位数，其中奇数的个数为_______（结果用数值表示）.12.已知点()1,0A ，直线:1l x =-，两个动圆均过点A 且与l 相切，其圆心分别为1C 、2C ，若动点M 满足22122C M C C C A =+，则M 的轨迹方程为_______. 二、选择题（每小题3分，满分36分）13.若0a b <<，则下列不等式恒成立的是（ ） A.11a b> B. a b -> C. 22a b > D. 33a b <14. 函数()21y x x =≥的反函数为（ ） A.()1y x x =≥ B. ()1y x x =-≤- C. ()0y x x =≥ D. ()0y x x =-≤15.不等式2301xx ->-的解集为（ ） A. 3,4⎛⎫-∞ ⎪⎝⎭ B. 2,3⎛⎫-∞ ⎪⎝⎭ C. ()2,1,3⎛⎫-∞+∞ ⎪⎝⎭D. 2,13⎛⎫⎪⎝⎭16.下列函数中，是奇函数且在()0,+∞上单调递增的为（ ） A. 2y x = B. 13y x =C. 1y x -=D. 12y x -=17.直线3450x y --=的倾斜角为（ ） A.3arctan4B. 3arctan 4π-C. 4arctan3 D. 4arctan 3π-18.底面半径为1，母线长为2的圆锥的体积为（ ） A. 2πB. 3πC.23π D.33π 19.以()3,0-和()3,0为焦点，长轴长为8的椭圆方程为（ ）A.2211625x y +=B. 221167x y +=C. 2212516x y +=D. 221716x y +=20.在复平面上，满足1i z z -=+（i 为虚数单位）的复数z 对应的点的轨迹为（ ） A.椭圆B.圆C.线段D.直线21.若无穷等差数列{}n a 的首项10a >，公差0d <，{}n a 的前n 项和为n S ，则（ ） A. n S 单调递减 B. n S 单调递增C. n S 有最大值D. n S 有最小值22.已知0a >，0b >，若4a b +=，则（ ） A.22a b +有最小值B. ab 有最小值C.11a b+有最大值 D.1a b+有最大值23. 组合数()12*22,,N m m m n n n C C C n m m n --++≥≥∈恒等于（ ）A. 2m n C +B. 12m n C ++C. 1mn C + D. 11m n C ++24.设集合{}2110P x x ax =++>，{}2220P x x ax =++>，{}210Q x x x b =++>，{}2220Q x x x b =++>其中,R a b ∈，下列说法正确的是（ ）A.对任意a ，1P 是2P 的子集；对任意的b ，1Q 不是2Q 的子集B. 对任意a ，1P 是2P 的子集；存在b ，使得1Q 是2Q 的子集C. 存在a ，使得1P 不是2P 的子集；对任意的b ，1Q 不是2Q 的子集D. 存在a ，使得1P 不是2P 的子集；存在b ，使得1Q 是2Q 的子集三、解答题（共5大题，满分48分） 25. （本题满分8分）如图，在正四棱柱中1111ABCD A B C D -，1AB =，1D B 和平面ABCD 所成的角的大小为32arctan 4，求该四棱柱的表面积.26.（本题满分8分）已知a 为实数，函数()24x ax f x x++=是奇函数，求()f x 在()0,+∞上的最小值及取到最小值时所对应的x 的值.27.（本题满分8分）某船在海平面A 处测得灯塔B 在北偏东30 方向，与A 相距6.0海里.船由A 向正北方向航行8.1海里到达C 处，这时灯塔B 与船相距多少海里（精确到0.1海里）？B 在船的什么方向（精确到1 ）？ ABCD1A 1B 1C 1D28. （本题满分12分）本题共有2个小题，第1小题满分6分，第2小题满分6分.已知点1F 、2F 依次为双曲线()2222:1,0x y C a b a b-=>的左右焦点，126F F =，()10,B b -，()20,B b（1）若5a =，以()3,4d =-为方向向量的直线l 经过1B ，求2F 到l 的距离；（2）若双曲线C 上存在点P ，使得122PB PB ⋅=-，求实数b 的取值范围.29.（本题满分12分）本题共有2个小题，第1小题满分4分，第2小题满分8分. 已知函数()()222R x f x x -=-∈ （1）解不等式()2f x <；（2）数列{}n a 满足()()*N n a f n n =∈，n S 为{}n a 的前n 项和，对任意的4n ≥，不等式12n n S ka +≥恒成立，求实数k 的取值范围.2015年上海市普通高中学业水平考试 数学卷（附加题）1.对于集合A 、B ，“A B ≠”是“A B A B ⊂≠⋂⋃”的( )(A)充分非必要条件 （B ）必要非充分条件 (C)充要条件 （D ）既非充分又非必要条件 2．对于任意实数a 、b ，2()a b kab -≥均成立，则实数k 的取值范围是（ ）(A) {}4,0- （B ）[]-4，0 (C) ](0-∞， （D ）][(40-∞-∞ ，,+)3．已知数列{}n a 满足413n n n n a a a a ++++=+（n N *∈），那么（ ）(A) {}n a 是等差数列 （B ）{}21n a -是等差数列 (C) {}2n a 是等差数列 （D ）{}3n a 是等差数列 二、填空题（本大题满分9分）本大题共有3小题，考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得3分，否则一律得0分．4．关于x 的实系数一元二次方程220x px ++=的两个虚数根为1z 、2z ，若1z 、2z 在复平面上对应的点是经过原点的椭圆的两个焦点，则该椭圆的长轴长为 ．5．已知圆心为O ，半径为1的圆上有三点A 、B 、C ，若7580OA OB OC ++=，则BC = ．6．函数()f x 与()g x 的图像拼成如图所示的“Z ”字形折线段ABOCD ，不含(0,1)A ，(1,1)B ，(0,0)O ，(1,1)C --，(0,1)D -五个点，若()f x 的图像关于原点对称的图形即为()g x 的图像，则其中一个函数的解析式可以为 ．三、解答题（满分12分）解答本题必须在答题纸相应编号的规定区域内写出必要的步骤．对于函数()f x 、()g x ，若存在函数()h x ，使得()()()f x g x h x =⋅，则称()f x 是()g x 的“()h x 关联函数”。

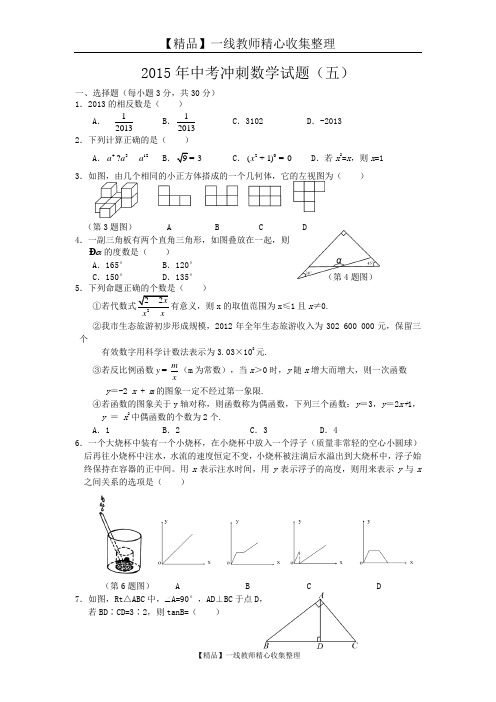
2015年中考冲刺数学试题（五）一、选择题（每小题3分，共30分） 1．2013的相反数是（ ）A ．12013-B ．12013C ．3102D ．-20132．下列计算正确的是（ ）A ．4312a a a ? B 3C ．20(1)0x +=D ．若x 2=x ，则x =13．如图，由几个相同的小正方体搭成的一个几何体，它的左视图为（ ）（第3题图） A B C D 4．一副三角板有两个直角三角形，如图叠放在一起，则αÐ的度数是（ ） A ．165° B ．120° C ．150° D ．135° （第4题图） 5．下列命题正确的个数是（ ）x 的取值范围为x ≤1且x ≠0.②我市生态旅游初步形成规模，2012年全年生态旅游收入为302 600 000元，保留三个有效数字用科学计数法表示为3.03×108元.③若反比例函数my x=（m 为常数），当x ＞0时，y 随x 增大而增大，则一次函数y ＝-2 x + m 的图象一定不经过第一象限.④若函数的图象关于y 轴对称，则函数称为偶函数，下列三个函数：y ＝3，y ＝2x+1， y ＝ x 2中偶函数的个数为2个. A ．1 B ．2 C ．3 D ．46．一个大烧杯中装有一个小烧杯，在小烧杯中放入一个浮子（质量非常轻的空心小圆球）后再往小烧杯中注水，水流的速度恒定不变，小烧杯被注满后水溢出到大烧杯中，浮子始终保持在容器的正中间。

用x 表示注水时间，用y 表示浮子的高度，则用来表示y 与x 之间关系的选项是（ ）（第6题图） A B C D 7．如图，Rt △ABC 中，∠A=90°，AD ⊥BC 于点D ， 若BD ∶CD=3∶2，则tanB=（ ）A ．32B ．23CD（第7题图） 8．已知m ，n 是关于x 的一元二次方程x 2－3x ＋a = 0的两个解，若（m －1）（n －1）=－6，则a 的值为（ ） A ．－10 B ．4 C ．－4 D ．109．小轩从如图所示的二次函数y = ax 2＋bx ＋c （a ≠0）的图象中，观察得出了下面五条信息：①ab > 0 ②a ＋b ＋c < 0③b ＋2c > 0 ④a －2b ＋4c > 0 ⑤32a b =.你认为其中正确信息的个数有（ ） A ．2个 B ．3个 C ．4个 D ．5个 （第9题图）10．如图，已知直线a//b ，且a 与b 之间的距离为4，点A 到直线a 的距离为2，点B 到直线b 的距离为3，AB=试在直线a 上找一点M ，在直线b 上找一点N ，满足 MN ⊥a 且AM+MN+NB 的长度和最短，则此时AM+NB=（ ） A ．6 B ．8 C ．10 D ．12（第10题图）二、填空题：（每小题3分，共18分） 11.若| p + 3 | = 0，则p = . 12.下列几个命题中正确的个数为 个.①“掷一枚均匀骰子，朝上点数为负”为必然事件（骰子上各面点数依次为1，2，3，4， 5，6）.②5名同学的语文成绩为90，92，92，98，103，则他们平均分为95，众数为92. ③射击运动员甲、乙分别射击10次，算得甲击中环数的方差为4，乙击中环数的方差为16，则这一过程中乙较甲更稳定.④某部门15名员工个人年创利润统计表如下，其中有一栏被污渍弄脏看不清楚数据，所以 对于“该部门员工个人年创利润的中位数为5万元”的说法无法判断对错.13.若不等式组200x b x a -⎧⎨+⎩≥≤的解集为34x ≤≤，则不等式a x + b < 0的解集为 .14.已知正比例函数y =-4x 与反比例函数ky x=的图象交于A 、B 两点，若点A 的坐标为 （x ，4），则点B 的坐标为 .15.著名画家达芬奇不仅画艺超群，同时还是一个数学家、发 明家. 他曾经设计过一种圆规如图所示，有两个互相垂直的滑槽（滑槽宽度忽略不计）， 一根没有弹性的木棒的两端A 、B 能在滑槽内自由滑动，将笔插入位于木棒中点P 处的小孔中，随着木棒的滑动就可以画出一个圆来.若AB=20cm ，则画出的圆的半径为 cm. 16.如图，△AOB 中，∠AOB=90°，AO=3，BO=6， △AOB 绕顶点O 逆时针旋转到△//A OB 处，此时线段//A B 与BO 的交点E 为BO 的中点，则线段/B E 的长 度为 .（第16题图）三、解答题（17~20每题8分，21~22每题9分，23题10分，24题12分，共72分） 17.（本题满分8分）先化简，后求值：224222aa a a a a +⎛⎫-÷ ⎪--⎝⎭，其中a = 3.18.（本题满分8分）如图正方形ABCD 的边长为4，E 、F 分别为DC 、BC 中点. （1）求证：△ADE ≌△ABF. （2）求△AEF 的面积.（第18题图）19.（本题满分8分）一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“鄂”、“州”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球. （1）若从中任取一个球，球上的汉字刚好是“鄂”的概率为多少？（2）甲从中任取一球，不放回，再从中任取一球，请用树状图的方法，求出甲取出的两个球上的汉字恰能组成“灵秀”或“鄂州”的概率P 1；（3）乙从中任取一球，记下汉字后再放回袋中，然后再从中任取一球，记乙取出的两个（第15题图）球上的汉字恰能组成“灵秀”或“鄂州”的概率为P2，指出P1，P2的大小关系（请直接写出结论，不必证明）.20.（本题满8分）甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，如图，线段OA表示货车离甲地距离y(千米)与时间x（小时）之间的函数关系；折线BCD 表示轿车离甲地距离y（千米）与x(小时)之间的函数关系.请根据图象解答下列问题：（1）轿车到达乙地后，货车距乙地多少千米？（2）求线段CD对应的函数解析式.（3）轿车到达乙地后，马上沿原路以CD段速度返回，求轿车从甲地出发后多长时间再与货车相遇（结果精确到0.01）.（第20题图）21.（本题满分9分）小明、小华在一栋电梯楼前感慨楼房真高.小明说：“这楼起码20层！”小华却不以为然：“20层？我看没有，数数就知道了！”小明说：“有本事，你不用数也能明白！”小华想了想说：“没问题！让我们来量一量吧！”小明、小华在楼体两侧各选A、B两点，测量数据如图，其中矩形CDEF表示楼体，AB=150米，CD=10米，∠A=30°，∠B= 45°，（A、C、D、B四点在同一直线上）问：（1）楼高多少米？（2）若每层楼按3米计算，你支持小明还是小华的观点呢？请说明理由.（参考数据：3≈1.73，2≈1.41，5≈2.24）（第21题图）（第22题图）22.（本题满分9分）已知：如图，AB为⊙O的直径，AB⊥AC，BC交⊙O于D，E是AC的中点，ED与AB的延长线相交于点F.（1）求证：DE为⊙O的切线.（2）求证：AB︰AC=BF︰DF.23.（本题满分10分）某商场经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具.（1）不妨设该种品牌玩具的销售单价为x 元（x > 40），请你分别用x 的代数式来表示（2）在（1）问条件下，若商场获得了10000元销售利润，求该玩具销售单价x 应定为多少元.（3）在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于540件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？24.（本题满分12分）在平面直角坐标系中，已知M 1（3，2），N 1（5，－1），线段M 1N 1平移至线段MN 处（注：M 1与M ，N 1与N 分别为对应点）. （1）若M （－2，5），请直接写出N 点坐标.（2）在（1）问的条件下，点N 在抛物线216y x x k =++上，求该抛物线对应的函数解析式.（3）在（2）问条件下，若抛物线顶点为B ，与y 轴交于点A ，点E 为线段AB 中点，点C（0，m ）是y 轴负半轴上一动点，线段EC 与线段BO 相交于F ，且OC ︰OF=2m 的值.（4）在（3）问条件下，动点P 从B 点出发，沿x 轴正方向匀速运动，点P 运动到什么位置时（即BP 长为多少），将△ABP 沿边PE 折叠，△APE 与△PBE 重叠部分的面积恰好为此时的△ABP 面积的14，求此时BP 的长度.（第24题图）2015年中考冲刺数学试题（五）参考答案及评分标准二、填空题（每小题3分，共18分）11．－3 12．1 13．x >32 14．（1，－4） 15．10 16三、解答题（17~20每题8分，21~22每题9分，23题10分，24题12分，共72分） 17．（本题满分8分） 解：24)22a a a a ---（÷2242(2)a a a a a a ⎡⎤+=-⎢⎥--⎣⎦÷22a a + 2242÷(2)a a a a a -+=- …………2分2(2)(2)2÷(2)a a a a a a +-+=-＝222÷a a a a++ …………4分＝22·2a a a a ++ …………5分 ＝a …………7分 ∴当a=3时，原式＝3 …………8分 18．（本题满分8分）（1）证明：∵四边形ABCD 为正方形 ∴AB ＝AD ，∠B＝∠D ＝90°，DC ＝CB …………2分 ∵E 、F 为DC 、BC 中点∴DE ＝12DC ，BF ＝12BC∴DE ＝BF∴△ADE ≌△ABF …………4分（2）解：由题知△ABF 、△ADE 、△CEF 均为直角三角形，且AB ＝AD ＝4，DE ＝BF ＝12×4＝2，CE ＝CF ＝12×4＝2∴S △AEF ＝S 正方形ABCD －S △ADE －S △ABF －S △CEF …………6分＝4×4－12×4×2－12×4×2－12×2×2＝6 …………8分19.（本题满分8分）解：（1）任取一球，共有4种不同结果，所以球上汉字刚好是“鄂”的概率 P=14……2分 （2）由题知树状图如下：共有12种不同取法，能满足要求的有4种，所以P 1=412=13…………7分 （3）P 1>P 2 …………8分 20.（本题满分8分）（1）根据图象信息：货车的速度V 货=3005=60（千米/时）∵轿车到达乙地的时间为4.5小时∴货车距乙地路程=300－60×4.5=30（千米）答：轿车到达乙地后，货车距乙地30千米. …………2分（2）设CD 段函数解析式为y =kx +b （k ≠0）（2.5≤x ≤4.5） ∵C （2.5，80），D （4.5，300）在其图象上∴ 2.5804.5300k b k b ⎧+=⎨+=⎩ ∴110195k b ⎧=⎨=-⎩…………4分∴CD 段函数解析式：y =110x －195（2.5≤x ≤4.5） …………5分 （3）设x 小时后两车再相遇根据图象信息：V 货车=60 V 轿车=110∴110（x －4.5）+60x =300 …………7分 ∴x ≈4.68（小时） …………8分 答：出发4.68小时后轿车再与货车相遇. 21.（本题满分9分）解：（1）设楼高为x 米，则CF=DE=x 米，由∠A=30°,∠B=45 °,∠ACF=∠BDE= 90°得AC=3x 米，BD=x 米，所以3x+x=150-10 …………3分解得x=13140+=70（3-1）（米） (5)分∴楼高70（3-1）米.(2)x=70(3-1)≈70（1.73-1）=70×0.73=51.1米＜3×20米 …………8分∴我支持小华的观点，这楼不到20层。

山东省2015年普通高校招生（春季）考试数学试题一、选择题1、集合A =｛1，2，3｝，B =｛1，3｝,则A ∩B 等于（ ） A ｛1，2，3｝ B ｛1，3｝ C ｛1，2｝ D ｛2｝2、不等式51-x <的解集是（ ）A （-6,4）B （-4,6）C （-∞,-6）∪（4，+∞）D （-∞,-4）∪（6，+∞）3、函数xx y 11++=的定义域是（ ）A {}0且1|≠-≥x x xB {}1|-≥x xC {}0且1|≠->x x xD {}1|->x x 4、“圆心到直线的距离等于圆的半径”是“直线与圆相切”的（ ） A 充分不必要条件 B 必要不充分条件 C 充要条件 D 既不充分也不必要 5、在等比数列｛a n ｝中，a 2=1, a 4=3,则a 6的值是（ ） A -5 B 5 C -9 D 96、如图所示，M 是线段OB 的中点，设向量→OA = →a ，→OB = →b ，则→AM 可以表示为A →a + 12→bB -→a + 12→b C →a -12→b D -→a - 12→b7、终边在Y 轴的正半轴的角的集合是（ ）A ⎭⎬⎫⎩⎨⎧∈+=z k k x x ,22|ππB ⎭⎬⎫⎩⎨⎧∈+=z k k x x ,2|ππC ⎭⎬⎫⎩⎨⎧∈+-=z k k x x ,22|ππD ⎭⎬⎫⎩⎨⎧∈+-=z k k x x ,2|ππO AB8、关于函数x x y 22+-=，下列叙述错误的是（ ）A 函数的最大值是1B 函数图像的对称轴是直线x=1C 函数的单调递减区间是［－１， +∞）D 函数的图像经过（２，０）9、某值日小组共有5名学生，若任意安排3名同学负责教室内的地面卫生，其余2名同学负责教室外的走廊卫生，则不同的安排方法种类是（ ）A 10B 20C 60D 10010、如图所示，直线l 的方程是（ ）A 033=--y xB 0323=--y xC 0133=--y xD 013=--y x11、对于命题p,q ，若p ∧q 是假命题，p ∨q 是真命题，则A p,q 都是真命题B p,q 都是假命题C p,q 一个是真命题一个是假命题D 无法判断12、已知函数f(x)是奇函数，当x>0时，2)(2+=x x f ,则f(-1)的值是（ ） A －３ B －１ C １ D ３13、已知点P （m,-2）在函数x y 31log =的图像上，点A 的坐标是（4，3），则|→AP |的值是（ ）A 10B 102C 26D 25 14、关于x,y 的方程122=+my x ，给出下列命题：①当m<0时，方程表示双曲线；②当m=0时，方程表示抛物线；③当0<m<1时，方程表示椭圆；④当m=1时，方程表示等轴双曲线；⑤当m>1时，方程表示椭圆；其中，真命题的个数是A 2B 3C 4D 515、5）-1（x 的二项展开式中，所有项的二项式系数之和是（ ）A 0B -1C -32D 3216、不等式组01y -x 03-y x {>+<+表示的区域（阴影部分）是（ ）yx17、甲乙丙三位同学计划利用假期外出游览，约定每人从泰山、孔府这两处景点中任选一处，则甲乙两位同学恰好选取同一处景点的概率是（ ）A 29B 23C 14D 12 18、已知向量→a =（cos 5π12，sin 5π12）, →b =（cos π12，sin π12），则→a ●→b 的值等于（） A 12 B 32 C 1 D 0 19、已知α，β表示平面，m,n 表示直线，下列命题中正确的是（ ）A 若,,n m m ⊥⊥α 则α//nB 若βαβα//,,⊂⊂n m 则n m //C 若αβα⊂m ,// 则β//mD 若βαα//,,m n m ⊂⊂ 则βα//20、已知F 1是双曲线)0,0(12222>>=-b a by a x 的左焦点，点P 在双曲线上，直线PF 1与x 轴垂直，且|PF 1|=a,则双曲线的离心率是（ ）A 2B 3C 2D 3二、填空题：21、直棱柱的底面是边长为a 的菱形，侧棱长为h ，则直棱柱的侧面积是 22、在△ABC 中，∠A=1050，∠C=450，AB=2 2，则BC=23、计划从500名学生中抽取50名进行问卷调查，拟采用系统抽样方法，为此将他们逐一编号为1-500，并对编号进行分段，若从第一个号码段中随机抽出的号码是2，则从第五个号码段中抽出的号码应是24、已知椭圆的中心在坐标原点，右焦点与圆07622=--+x y x 的圆心重合，长轴长等于圆的直径，则短轴长等于 25、集合Ｍ，Ｓ，Ｎ都是非空集合，现规定如下运算：Ｍ⊕Ｓ⊕Ｎ＝{x|x )}s N M (且),()()(⋂⋂∉⋂⋂⋂∈x M S S N N M Y Y 若集合A=b}x a |{x <<,B=d}x c |{x <<,C=f}x e |{x <<,其中a ，b ，c ，d ，e ，f 满足：①ab<0,cd<0,ef<0②a-b=c-d=e-f ；③ a+b<c+d<e+f ；则A ⊕B ⊕C= 三、解答题：26、某学校合唱团参加演出，需要把120名演员排成5排，并且从第二排起，每一排比前一排多3名，求第一排应该安排多少名演员。

2015～2016学年度八年级下学期数学期末冲刺卷二参考答案一、选择题题号 1 2 3 4 5 6 7 8 9 10 答案 C D B D D A C C C C二、填空题11﹒0或－3﹒12﹒±1﹒13﹒3﹒14﹒2﹒15﹒20﹒16﹒4.8﹒17﹒60﹒18﹒－6﹒19﹒50﹒20﹒①②④﹒三、解答题21.【解答】（1）∵x＝2+3，y＝2－3，∴x－y＝23，xy＝1，∴x2－xy+y2＝(x－y)2+xy＝(23)2+1＝12+1＝13.（2）212xx-+÷(1－12x+)＝212xx-+÷12xx++＝(1)(1)2x xx+-+×21xx++＝x－1，解方程x2－4＝0，得x＝±2，∵当x＝－2时，分母x+2＝0，没有意义，∴当x＝2时，原式＝2－1＝1.22.【解答】（1）B1（－2，4）；（2）A2（－1，－3）；（3）S菱形ABCO＝42－4×12×3－2×12＝16－6－2＝8.23.【解答】（1）该班总人数：10÷20%＝50（人），捐10元的人数为：50－6－16－10＝18（人），∵捐10元的人数是最多的，∴学生捐款的众数是10元，故答案为：10元，50；（2）补充完整图形如图，∵360°×1850＝129.6°，∴“10元”所在扇形对应的圆心角度数为129.6°；（3）x＝6518101615102050⨯+⨯+⨯+⨯＝13（元），答：该班同学平均捐款13元.24.【解答】（1）∵∠A＝∠ABC＝90°，∴AF∥BC，∴∠CBE＝∠DFE，∠BCE＝∠FDE，∵E是边CD的中点，∴CE＝DE，在△BCE和△FDE中，∵CBE DFEBCE FDE CE DE∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BCE和△FDE（AAS），∴BE＝EF，又∵CE＝DE，∴四边形BDFC为平行四边形；（2）过点D作DG⊥BC于点G，则四边形ABGD为矩形，∴BG＝AD＝10cm，∴CG＝BC－BG＝20cm，∵CB＝CD，∴CD＝30cm，在Rt△DCG中，DG＝22CD CG-＝223020-＝105，∴S四边形BDFC＝BCDG＝30×105＝3005cm2.25.【解答】（1）证明：连结BE ， ∵AD ∥BC ， ∴∠1＝∠2，∵将一张矩形纸片（矩形ABCD ）按如图方式折叠，使顶点B 和D 重合， ∴∠2＝∠3，BE ＝DE ，BF ＝DF ， ∴∠1＝∠3，∴ED ＝DF ＝DE ＝BF ， ∴四边形EBFD 是菱形；（2）解：设AE ＝x ，则DE ＝BE ＝9﹣x ， 在Rt △ABE 中，AE 2+AB 2＝BE 2， ∴x 2+32＝(9－x )2， 解得：x ＝4， ∴DE ＝9﹣4＝5，∴重叠部分三角形DEF 的面积为：12×3×5＝7.5． 26.【解答】（1）设反比例函数为y ＝kx， ∵△OAC 的面积为8，AO ＝AC ，A （﹣4，m ） ∴点C （﹣8，0），12×8×m ＝8，∴m ＝2，∴点A （﹣4，2），∵反比例函数的图象经过A （﹣4，2）、B （2，n ）两点， ∴k ＝－8，n ＝－4， ∴点B 坐标（2，－4）， ∴反比例函数解析式为y ＝－8x； （2）如图，设直线AB 的解析式为y ＝kx +b ， ∵A （－4，2），B （2，－4），∴4224k b k b -+=⎧⎨+=-⎩，解得12k b =-⎧⎨=-⎩，∴直线AB 的解析式为y ＝－x －2， 设直线AB 与x 轴交于点E ，∵对于直线y ＝－x －2，令y ＝0时，x ＝－2， ∴E （－2，0），∴OE ＝2， ∵S △OAB ＝S △OAE +S △OBE ，∴S △OAB ＝12×2×2+12×2×4＝6.27.【解答】（1）设经过x 秒，△PBQ 的面积等于8cm 2， ∵AP ＝x ，BQ ＝2x ，∴BP＝AB－AP＝6－x，∴S△PBQ＝12BP×BQ＝12(6－x)×2x＝8，整理，得x2－6x+8＝0，解得：x1＝2，x2＝4，即经过2秒或4秒，△PBQ的面积等于8cm2；（2）不会，理由如下：设经过y秒，△PBQ的面积等于10cm2，则S△PBQ＝12(6－y)×2y＝10，化简并整理，得y2－6y+10＝0，∵△＝(－6)2－4×1×10＝－4＜0，∴此方程无实数根，故△PBQ的面积不会等于10cm2.28.【解答】（1）证明：∵四边形ABCD是正方形，∴AB＝AD，∠BAD＝90°，∵AF⊥AC，∴∠EAF＝90°，∴∠BAF＝∠EAD，在△ADE和△ABF中，∵AD ABDAE BAF AE AF=⎧⎪∠=∠⎨⎪=⎩，∴△ADE≌△ABF（SAS），∴BF＝DE；（2）解：当点E运动到AC的中点时，四边形AFBE是正方形，如备用图，理由：∵点E运动到AC的中点，AB＝BC，∴BE⊥AC，BE＝AE＝12 AC，∵AF＝AE，∴BE＝AF＝AE，又∵BE⊥AC，∠F AE＝∠BEC＝90°，∴BE∥AF，又∵BE＝AF，∴四边形AFBE是平行四边形，又∵∠F AE＝90°，AF＝AE，∴四边形AFBE是正方形.。

空港实验小学2015年数学第八册半期检测卷（满分100分，时间80分钟）一、填空(每空1分，共23分)1.计算72-81÷（3×3）时，最后算（ ）。

2.三角形两边之差（ ）第三边，三角形具有（ ）性。

3.任何一个三角形都至少有（ ）个锐角，都有（ ）条高。

4.一个长方形面积是600平方米（1）如果长方形的长缩小6倍，宽扩大6倍，这时长方形面积是（ ）。

（2）如果长方形的长扩大3倍，宽扩大5倍，面积是（ ）。

5.一个三角形有两个角分别是33度和57度。

这是一个（ ）三角形。

6. 用字母表示乘法结合律是（ ）， 乘法分配律是（ ）。

7.右图中，有（ ）个三角形，有（ ）个直角三角形，有（ ）个钝角三角形， 有（ ）个等腰三角形。

8.一个等腰三角形的一条腰是5厘米，底边最长是（ ）厘米，最短是（ ）厘米，（保留整厘米数）。

9. （ ）÷12=12……10 365÷（ ）=12……5 ( ) ×24=720 10.240÷80=3，我们可以说（ ）能被（ ）整除，也可以说（ ）能整除（ ）。

二、判断，共6分 1、等边三角形既是锐角三角形，也是等腰三角形。

（ ） 2、一个因数扩大10倍，另一个因数扩大10倍，积就扩大20倍。

（ ） 3、（被除数—余数）÷商=除数 （ ） 4、等边三角形可以是直角三角形。

（ ） 5、由三条线段组成的图形叫做三角形。

（ ） 学校： 班级 ：___________________ 学生姓名：______ ____ 学号 ：_____________ -密-----------------封-----------------线-------------------内-------------------不---------------------要-----------------------答-------------------题-----------------------------------------------------------------------------------------------------------------------------------------------------------三、选择，共5分1、下面算式中第二个数能整除第一个数的是（）。

2015年全国各省地市中考数学冲刺模拟试卷一．选择题（本题8个小题，每小题有一个选项符合题意，请把符合题意选项前对应的字母填在题后的括号内。

每小题3分，共24分）1. A2. B3.D4.B5.D6.B7.A8.B1.用配方法解方程X 2-4X+2=0，下列配方正确的是 （ ）A ．(X-2)2=2B ．(X+2)2=2C ．(X-2)2=-2D ．(X-2)2=62.下列图形中，不是中心对称图形的是 （ ）3.已知直线a 、b 被直线c 所截，那么∠1的同位角是 （ ）A.∠2B. ∠3C. ∠4D.∠54.某商品原价200元，连续两次降价a ％后售价为148元，下列所列方程正确的是（ ） A ：200(1+a%)2=148 B ：200(1－a%)2=148C ：200(1－2a%)=148D ：200(1－a 2%)=1485.方程有两个实数根，则k 的取值范围是（ ） A ． k ≥1 B ． k ≤1C ． k>1D ． k<16.如图，矩形ABCD 中，AB=3，BC=4，动点P 从A 点出发，按A →B →C 的方向在AB 和BC 上移动，记PA=x ，点D 到直线PA 的距离为y ，则y 关于x 的函数图象大致是（ ）A ．B ．C ．D ．7.不等式组的解集是 （ ）A.﹣1≤x ＜2B.x ≥﹣1C.x ＜2D.﹣1＜x ≤2（A ） （B ） （C ） （D ）8.如图，△ABC 与△DEF 关于y 轴对称，已知A （﹣4，6），B （﹣6，2），E （2，1），则点D 的坐标为 （ ）A.（﹣4，6）B.（4，6）C.（﹣2，1）D.（6，2）二．填空题（本题8个小题，每小题4分，共32分）9. 8.18×108 10.1/2 11. 1或2 12.20152014 13.40 14.（1，4），（3，1） 15.∠BDE=∠BAC （答案不唯一）16. 29.财政部近日公开的情况显示，2014年中央本级“三公”经费财政款预算比去年年初预算减少8.18亿元，用科学记数法表示8.18亿元为 元．10.桶里原有质地均匀、形状大小完全一样的6个红球和4个白球，小红不慎遗失了其中2个红球，现在从桶里随机摸出一个球，则摸到白球的概率为11.如图，以O 为圆心的两个同心圆中，大圆和小圆的半径分别为3cm 和1cm ．若⊙P 与这两个圆都相切，则⊙P 的半径为 cm ．12.已知对应任意的自然数n ，抛物线y=（n 2+n ）x 2-（2n+1）x+1与x 轴相交于A ，B 两点，则|A 1B 1|+|A 2B 2|+|A 3B 3|+…+|A 2014B 2014|= ．13.如图，△ABC 的中位线DE=5cm ，把△ABC 沿DE 折叠，使点A 落在边BC 上的点F 处，若A 、F 两点间的距离是8cm ，则△ABC 的面积为 cm 3．14.过点（﹣1，7）的一条直线与x 轴，y 轴分别相交于点A ，B ，且与直线平行．则在线段AB 上，横、纵坐标都是整数的点的坐标是 ．需添加一个即可)16.若﹣2x m ﹣n y 2与3x 4y 2m+n是同类项，则m ﹣3n 的立方根是 ．三．解答题（本题有8道题，共计64分）17.计算：|-5|-( 2 -3)0+6×(13 - 12)+(-1)2． 18.某企业新增了一个化工项目，为了节约资源，保护环境，该企业决定购买A 、B 两种型号（1）该企业有几种购买方案？19.在菱形ABCD和正三角形BGF中，∠ABC=60°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，易证：PG=PC．（不必证明）（2）如图2，当点F在AB的延长线上时，线段PC、PG有怎样的数量关系，写出你的猜想，并给与证明；（3）如图3，当点F在CB的延长线上时，线段PC、PG又有怎样的数量关系，写出你的猜想（不必证明）．DE=FGPG=PCG=∠PG=PG=PG=轴上（OA<OB），且OA、OB的长分别是一元二次方程的两个根.线段AB的垂直平分线CD交AB于点C，交x轴于点D.点P是直线CD上的一个动点，点Q是直线AB上的一个动点.（1）求A、B两点的坐标；（2）求直线CD的解析式；（3）在坐标平面内是否存在点M，使以点C、P、Q、M为顶点的四边形是正方形，且该正方形的边长为12AB长.若存在，请直接写出点M的坐标；若不存在，请说明理由． x2=8∴A(6，0)，B(8，0)（3）存在，M1(2，-3)M2(10，3)M3(4，11)M4(-4，5)说明，以上各题，如果有其它正确解法，可酌情21.从全校1200名学生中随机选取一部分学生进行调查，调查情况：A、上网时间≤1小时；B、1小时＜上网时间≤4小时；C、4小时＜上网时间≤7小时；D、上网时间＞7小时．统计结果制成了如图统计图：（1）参加调查的学生有人；（2）请将条形统计图补全；（3）请估计全校上网不超过7小时的学生人数．=200×轴上（OA＜OB），且OA、OB的长分别是一元二次方程x2﹣14x+48=0的两个根．线段AB的垂直平分线CD交AB于点C，交x轴于点D，点P是直线CD上一个动点，点Q是直线AB上一个动点．（1）求A、B两点的坐标；（2）求直线CD的解析式；（3）在坐标平面内是否存在点M，使以点C、P、Q、M为顶点的四边形是正方形，且该正方形的边长为AB长？若存在，请直接写出点M的坐标；若不存在，请说明理由．答案：解：（1）解方程x2﹣14x+48=0，得x1=6，x2=8，∵OA＜OB，∴A（6，0），B（0，8）；（2）在Rt△AOB中，∵∠AOB=90°，OA=6，OB=8，∴AB==10，∵线段AB的垂直平分线CD交AB于点C，∴AC=AB=5．在△ACD与△AOB中，，∴△ACD∽△AOB，∴=，即=，解得AD=，∵A（6，0），点D在x轴上，∴D（﹣，0）．设直线CD的解析式为y=kx+b，∵C（3，4），D（﹣，0），∴，解得，∴直线CD的解析式为y=x+；（3）在坐标平面内存在点M，使以点C、P、Q、M为顶点的四边形是正方形，且该正方形的边长为AB长．∵AC=BC=AB=5，∴以点C、P、Q、M为顶点的正方形的边长为5，且点Q与点B或点A重合．分两种情况：①当点Q与点B重合时，易求BM的解析式为y=x+8，设M（x， x+8），∵B（0，8），BM=5，∴（x+8﹣8）2+x2=52，化简整理，得x2=16，解得x=±4，∴M1（4，11），M2（﹣4，5）；②当点Q与点A重合时，易求AM的解析式为y=x﹣，设M（x， x﹣），∵A（6，0），AM=5，∴（x﹣）2+（x﹣6）2=52，化简整理，得x2﹣12x+20=0，解得x1=2，x2=10，∴M3（2，﹣3），M4（10，3）；综上所述，所求点M的坐标为M1（4，11），M2（﹣4，5），M3（2，﹣3），M4（10，3）．23.（如图，直线y=﹣3x+3与x轴、y轴分别交于点A、B，抛物线y=a（x﹣2）2+k经过点A、B，并与X轴交于另一点C，其顶点为P．（1）求a，k的值；（2）抛物线的对称轴上有一点Q，使△ABQ是以AB为底边的等腰三角形，求Q点的坐标；（3）在抛物线及其对称轴上分别取点M、N，使以A，C，M，N为顶点的四边形为正方形，求此正方形的边长．24.已知在平面直角坐标系xOy中，O是坐标原点，以P（1，1）为圆心的⊙P与x轴，y轴分别相切于点M和点N，点F从点M出发，沿x轴正方向以每秒1个单位长度的速度运动，连接PF，过点PE⊥PF交y轴于点E，设点F运动的时间是t秒（t＞0）（1）若点E在y轴的负半轴上（如图所示），求证：PE=PF；（2）在点F运动过程中，设OE=a，OF=b，试用含a的代数式表示b；（3）作点F关于点M的对称点F′，经过M、E和F′三点的抛物线的对称轴交x轴于点Q，连接QE．在点F运动过程中，是否存在某一时刻，使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似？若存在，请直接写出t的值；若不存在，请说明理由．答案：证明：（1）如图，连接PM，PN，∵⊙P与x轴，y轴分别相切于点M和点N，∴PM⊥MF，PN⊥ON且PM=PN，∴∠PMF=∠PNE=90°且∠NPM=90°，∵PE⊥PF，∠NPE=∠MPF=90°﹣∠MPE，在△PMF和△PNE中，，∴△PMF≌△PNE（ASA），∴PE=PF，（2）解：①当t＞1时，点E在y轴的负半轴上，如图，由（1）得△PMF≌△PNE，∴NE=MF=t，PM=PN=1，∴b=OF=OM+MF=1+t，a=NE﹣ON=t﹣1，∴b﹣a=1+t﹣（t﹣1）=2，∴b=2+a，②0＜t≤1时，如图2，点E在y轴的正半轴或原点上，同理可证△PMF≌△PNE，∴b=OF=OM+MF=1+t，a=ON﹣NE=1﹣t，∴b+a=1+t+1﹣t=2，∴b=2﹣a，（3）如图3，（Ⅰ）当1＜t＜2时，∵F（1+t，0），F和F′关于点M对称，∴F′（1﹣t，0）∵经过M、E和F′三点的抛物线的对称轴交x轴于点Q，∴Q（1﹣t，0）∴OQ=1﹣t，由（1）得△PMF≌△PNE∴NE=MF=t，∴OE=t﹣1当△OEQ∽△MPF∴=∴=，解得，t=，当△OEQ∽△MFP时，∴=，=，解得，t=，（Ⅱ）如图4，当t＞2时，∵F（1+t，0），F和F′关于点M对称，∴F′（1﹣t，0）∵经过M、E和F′三点的抛物线的对称轴交x轴于点Q，∴Q（1﹣t，0）∴OQ=t﹣1，由（1）得△PMF≌△PNE ∴NE=MF=t，∴OE=t﹣1当△OEQ∽△MPF∴=∴=，无解，当△OEQ∽△MFP时，∴=，=，解得，t=2±，所以当t=，t=，t=2±时，使得以点Q、O、E为顶点的三角形与以点P、M、F 为顶点的三角形相似．。