初中数学破题致胜微方法(等腰直角三角形中的手拉手模型)等腰直角三角形手拉手的旋转1

初中必会几何模型（口诀突破）：手拉手模型（或旋转型）教材知识：三角形全等知识中，教材对全等三角形的图形变换概括为三种：平移型、翻折型、旋转型。

一个图形经过平移、翻折、旋转后，位置变化了，但形状、大小都没有改变，即平移、翻折、旋转前后的图形全等.归纳模型：三种变换中以旋转型为考试的热点和难点，这种变换我们往往也称为手拉手模型。

因为这种图形变换都是以等腰三角形的顶点为旋转点，进行适当旋转而成。

然后，连接对应点构造新的三角形，证明三角形全等即可解决。

划重点，上口诀：等腰图形有旋转，辨清共点旋转边。

关注三边旋转角，全等思考边角边。

模型变换：如图，△ABC是等腰三角形、△ADE是等腰三角形，AB=AC，AD=AE，∠BAC=∠DAE=a。

结论：连接BD、CE，则有△BAD≌△CAE。

模型证明：图②图③同理可证。

模型分析：（1）这个图形是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时，始终存在一对全等三角形。

（2）如果把小等腰三角形的腰长看作小手，大等腰三角形的腰长看作大手，两个等腰三角形有公共顶点，类似大手拉着小手，所以把这个模型称为手拉手模型。

（3）手拉手模型常和旋转结合，在考试中作为几何综合题目出现。

模型实例：如图，△ADC与△EDG都为等腰直角三角形，连接AG、CE，相交于点H，问：（1)AG与CE是否相等?（2)AG与CE之间的夹角为多少度?问题解答：模型实练：如图，在直线AB的同一侧作△ABD和△BCE，△ABD和△BCE都是等边三角形、连接AE、CD，二者交点为H.求证：(1)△ABE≌△DBC;(2)AE=DC；(3)∠DHA=60°；(4)△AGB≌△DFB;（5）△EGB≌△CFB（6）连接GF，GF∥AC；（7)连接HB，HB平分∠AHC.。

1 手拉手模型
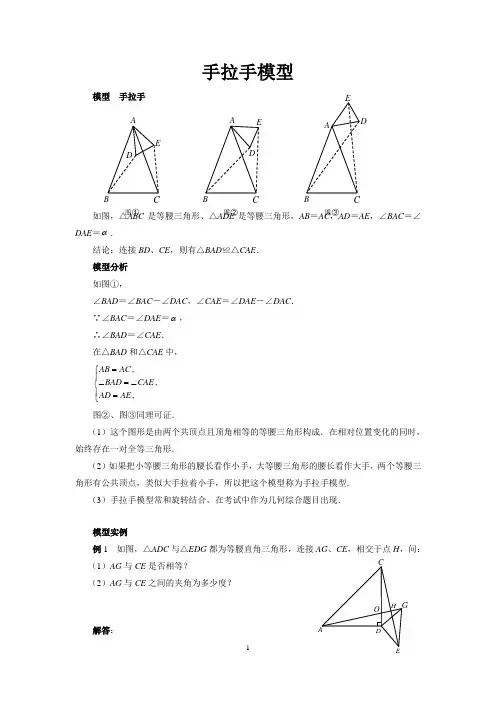
模型 手拉手
如图，△ABC 是等腰三角形、△ADE 是等腰三角形，AB ＝AC ，AD
＝AE ，∠BAC ＝∠DAE ＝α．
结论：连接BD 、CE ，则有△BAD ≌△CAE ．
模型分析
如图①，
∠BAD ＝∠BAC －∠DAC ，∠CAE ＝∠DAE －∠DAC ．
∵∠BAC ＝∠DAE ＝α，
∴∠BAD ＝∠CAE ．
在△BAD 和△CAE 中，
AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩
﹐﹐
﹐ 图②、图③同理可证．
（1）这个图形是由两个共顶点且顶角相等的等腰三角形构成．在相对位置变化的同时，始终存在一对全等三角形．
（2）如果把小等腰三角形的腰长看作小手，大等腰三角形的腰长看作大手，两个等腰三角形有公共顶点，类似大手拉着小手，所以把这个模型称为手拉手模型．
（3）手拉手模型常和旋转结合，在考试中作为几何综合题目出现．
模型实例
例1 如图，△ADC 与△EDG 都为等腰直角三角形，连接AG 、CE ，相交于点H ，问：
（1）AG 与CE 是否相等？
（2）AG 与CE 之间的夹角为多少度？
解答：
C D E A B 图① C D E A B 图② C
D E A B 图③ C D E G H A O。

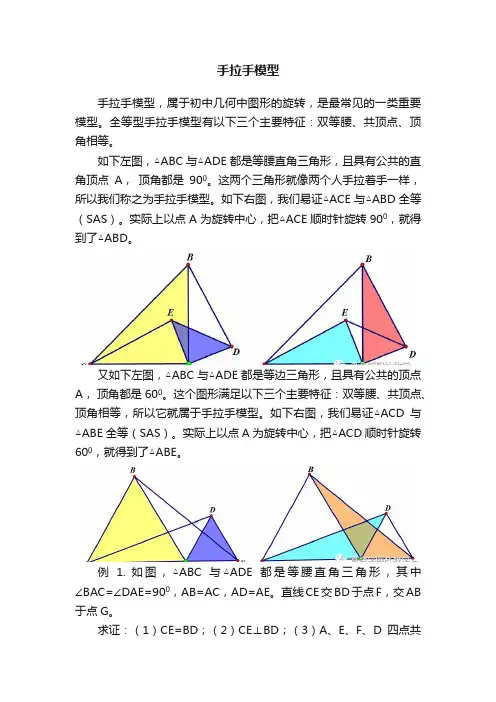
手拉手模型手拉手模型，属于初中几何中图形的旋转，是最常见的一类重要模型。

全等型手拉手模型有以下三个主要特征：双等腰、共顶点、顶角相等。

如下左图，△ABC与△ADE都是等腰直角三角形，且具有公共的直角顶点A，顶角都是900。

这两个三角形就像两个人手拉着手一样，所以我们称之为手拉手模型。

如下右图，我们易证△ACE与△ABD全等（SAS）。

实际上以点A为旋转中心，把△ACE顺时针旋转900，就得到了△ABD。

又如下左图，△ABC与△ADE都是等边三角形，且具有公共的顶点A，顶角都是600。

这个图形满足以下三个主要特征：双等腰、共顶点、顶角相等，所以它就属于手拉手模型。

如下右图，我们易证△ACD与△ABE全等（SAS）。

实际上以点A为旋转中心，把△ACD顺时针旋转600，就得到了△ABE。

例 1. 如图，△ABC与△A DE都是等腰直角三角形，其中∠BAC=∠DAE=900，AB=AC，AD=AE。

直线CE交BD于点F，交AB 于点G。

求证：（1）CE=BD；（2）CE⊥BD；（3）A、E、F、D四点共圆；（4）AF平分∠CFD。

解析：图中△ABC与△ADE都是等腰直角三角形，而且他们具有公共顶点A，顶角都是900，所以该图形就是典型的手拉手模型。

简解：(1)易证△ACE≌△ABD（SAS），所以CE=BD；（2）由△ACE≌△ABD可得：∠1=∠2。

再由八字形可得：∠GFB=∠GAC=900，所以CE⊥BD。

（3）由（2）得CE⊥BD，又∠DAE=900，所以∠DAE+∠DFE=1800。

所以A、E、F、D四点共圆。

（4）过A作AM⊥CE于M，作AN⊥BD于N。

由△ACE≌△ABD，可得他们的面积相等，又由全等得CE=BD，所以AM=AN。

所以AF 平分∠CFD。

（或者由A、E、F、D四点共圆，得到∠DFA=∠DEA=450。

所以∠EFA=∠DFA=450。

所以AF平分∠CFD。

）例2. 如下左图，点C、A、E在一条直线上，△ABC与△ADE 都是等边三角形。

模型介绍共顶点模型，亦称“手拉手模型”，是指两个顶角相等的等腰或者等边三角形的顶点重合，两个三角形的两条腰分别构成的两个三角形全等或者相似。

寻找共顶点旋转模型的步骤如下： （1）寻找公共的顶点（2）列出两组相等的边或者对应成比例的边（3）将两组相等的边分别分散到两个三角形中去，证明全等或相似即可。

两等边三角形两等腰直角三角形两任意等腰三角形*常见结论：连接BD 、AE 交于点F ，连接CF ，则有以下结论：（1）BCD ACE≅△△（2）AE BD=（3）AFB DFE∠=∠（4）FC BFE∠平分【专题说明】两个具有公共顶点的相似多边形，在绕着公共顶点旋转的过程中，产生伴随的全等或相似三角形，这样的图形称作共点旋转模型；为了更加直观，我们形象的称其为“手拉手”模型。

【知识总结】【基本模型】一、等边三角形手拉手-出全等图1图2图3图4二、等腰直角三角形手拉手-出全等两个共直角顶点的等腰直角三角形，绕点C旋转过程中（B、C、D不共线）始终有：①△BCD≌△ACE；②BD⊥AE（位置关系）且BD=AE（数量关系）；③FC平分∠BFE；图1图2图3图4手拉手模型的定义：两个顶角相等且有共顶点的等腰三角形形成的图形。

手拉手模型特点：“两等腰，共顶点”模型探究：例题精讲考点一：等边三角形中的手拉手模型【例1】．如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正三角形ABC和正三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．有下列结论：①AD＝BE；②AP＝BQ；③∠AOB＝60°；④DC＝DP；⑤△CPQ为正三角形．其中正确的结论有_____________.解：∵△ABC和△DCE是正三角形，∴AC＝BC，DC＝CE，∠BCA＝∠DCE＝60°，∴∠BCA+∠BCD＝∠DCE+∠BCD，∴∠ACD＝∠BCE，在△ACD和△BCE中∴△ACD≌△BCE（SAS），∴AD＝BE，∴①正确；∵△ACD≌△BCE，∴∠CBE＝∠CAD，∵∠ACB＝∠DCE＝60°，∴∠BCD＝60°＝∠ACB，在△ACP和△BCQ中∴△ACP≌△BCQ（ASA），∴AP＝BQ，∴②正确；PC＝QC，∴△CPQ为正三角形∴⑤正确∵△ACD≌△BCE，∴∠ADC＝∠BEC，∠DCE＝60°＝∠CAD+∠ADC，∴∠CAD+∠BEC＝60°，∴∠AOB＝∠CAD+∠BEC＝60°，∴③正确；∵△DCE是正三角形，∴DE＝DC，∵∠AOB＝60°，∠DCP＝60°，∠DPC＞∠AOB，∴∠DPC＞∠DCP，∴DP＜DC，即DP＜DE，∴④错误；所以正确的有①②③⑤变式训练【变式1-1】．如图，ABD∆，AEC∆都是等边三角形，则BOC∠的度数是()A．135︒B．125︒C．120︒D．110︒解：ABD，AEC∆∆都是等边三角形，∴=，AE ACAD AB∠=∠=︒，60∠==︒，ADB DBADAB CAE=，60∴∠=∠，DAB BAC CAE BAC∴∠+∠=∠+∠，DAC BAE∴∆≅∆，ADC ABE()DAC BAE SAS∴∠=∠，∴∠=∠+∠+∠BOC BDO DBA ABE=∠+∠BDO DBA ADC=∠+∠+∠ADB DBA∴∠的度数是120︒=︒，BOC=︒+︒1206060故选：C．【变式1-2】．如图，△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，有如下结论：①△ACE≌△DCB；②CM＝CN；③AC＝DN；④∠DAE＝∠DBC．其中正确的有（）A．②④B．①②③C．①②④D．①②③④解：∵△DAC和△EBC均是等边三角形，∴AC＝DC，BC＝CE，∠ACE＝∠BCD，∴△ACE≌△DCB，①正确由①得∠AEC＝∠CBD，∴△BCN≌△ECM，∴CM＝CN，②正确假使AC＝DN，即CD＝CN，△CDN为等边三角形，∠CDB＝60°，又∵∠ACD＝∠CDB+∠DBC＝60°，∴假设不成立，③错误；∵∠DBC+∠CDB＝60°∠DAE+∠EAC＝60°，而∠EAC＝∠CDB，∴∠DAE＝∠DBC，④正确，∴正确答案①②④故选：C．【变式1-3】．如图，△ABC和△ADE都是等边三角形，点D在BC上，DE与AC交于点F，若AB＝5，BD＝3，则＝．解：连接CE，过点F作FM⊥BC于点M，FN⊥CE于点N，∵△ABC和△ADE为等边三角形，∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝60°，∴∠BAD＝∠CAE，∴△BAD≌△CAE（SAS），∴BD＝CE＝3，∠ABD＝∠ACE＝60°，∵AB＝BC＝5，∴DC＝2，∵∠ACB＝∠ACE＝60°，FM⊥BC，FN⊥CE，∴FM＝FN，＝DC•FM，S△FCE＝CE•FN，∵S△DFC∴，∴，故答案为：．考点二：等腰直角三角形中的手拉手模型【例2】．如图，ACB ∆和ECD ∆都是等腰直角三角形，90ACB ECD ∠=∠=︒，D 为AB 边上一点，若5AD =，12BD =，则DE 的长为__________解：ACB ∆ 和ECD ∆都是等腰直角三角形，CD CE ∴=，AC BC =，90ECD ACB ∠=∠=︒，ACE BCD ∴∠=∠，在ACE ∆和BCD ∆中，CE CD ACE BCD AC BC =⎧⎪∠=∠⎨⎪=⎩，()ACE BCD SAS ∴∆≅∆，12BD AE ∴==，45CAE CBD ∠=∠=︒，90EAD ∴∠=︒，222212513DE AE AD ∴=+=+=．变式训练【变式2-1】．如图，3AB =，2AC =，连结BC ，分别以AC 、BC 为直角边作等腰Rt ACD ∆和等腰Rt BCE ∆，连结AE 、BD ，当AE 最长时，BC 的长为()A ．22B ．3C ．11D ．17解：90ACD BCE ∠=∠=︒ ，ACD ACB BCE ACB ∴∠+∠=∠+∠，即ACE DCB ∠=∠，在ACE ∆和DCB ∆中，AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩，()ACE DCB SAS ∴∆≅∆，AE BD ∴=，AC CD == ，90ACD ∠=︒，2AD ∴==，3AB = ，∴当点A 在BD 上时，BD 最大，最大值为325+=，如图，过C 作CE AD ⊥于E ，由等腰三角形“三线合一”得1DE AE ==，314BE AB AE ∴=+=+=，再由直角三角形斜边中线等于斜边一半得1DE =，BC ∴=．故选：D ．【变式2-2】．如图，在Rt ABC ∆中，AB AC =，点D 为BC 中点，点E 在AB 边上，连接DE ，过点D 作DE 的垂线，交AC 于点F ．下列结论：①AED CFD ∆≅∆；②EF AD =；③BE CF AC +=；④212AEDF S AD =四边形，其中正确的结论是（填序号）．解：AB AC = ，90BAC ∠=︒，点D 为BC 中点，12BD CD AD BC ∴===，45BAD CAD C ∠=∠=∠=︒，AD BC ⊥，BC =，DF DE ⊥ ，90EDF ADC ∴∠=∠=︒，ADE CDF ∴∠=∠，AD CD = ，BAD C ∠=∠，()AED CFD ASA ∴∆≅∆，故①正确；当E 、F 分别为AB 、AC 中点时，12EF BC AD ==，故②不一定正确；ADE CDF ∆≅∆ ，AE CF ∴=，BE AE AB += ，BE CF AC ∴+=，故③正确；ADE CDF ∆≅∆ ，ADE CDF S S ∆∆∴=，212ADF CDF ADC AEDF S S S S AD ∆∆∆∴=+==⨯四边形，故④正确；故答案为：①③④．【变式2-3】．如图，△ABC 和△CEF 均为等腰直角三角形，E 在△ABC 内，∠CAE +∠CBE ＝90°，连接BF ．（1）求证：△CAE ∽△CBF ．（2）若BE ＝1，AE ＝2，求CE 的长．（1）证明：∵△ABC和△CEF均为等腰直角三角形，∴＝＝，∴∠ACB＝∠ECF＝45°，∴∠ACE＝∠BCF，∴△CAE∽△CBF；（2）解：∵△CAE∽△CBF，∴∠CAE＝∠CBF，＝＝，又∵＝＝，AE＝2∴＝，∴BF＝，又∵∠CAE+∠CBE＝90°，∴∠CBF+∠CBE＝90°，∴∠EBF＝90°，∴EF2＝BE2+BF2＝12+（）2＝3，∴EF＝，∵CE2＝2EF2＝6，∴CE＝．考点三：任意等腰三角形中的手拉手模型【例3】．如图，在△AOB和△COD中，OA＝OB，OC＝OD，OA＜OC，∠AOB＝∠COD ＝36°．连接AC，BD交于点M，连接OM．下列结论：①∠AMB＝36°，②AC＝BD，③OM平分∠AOD，④MO平分∠AMD．其中正确的结论是_____．解：∵∠AOB＝∠COD＝36°，∴∠AOB+∠BOC＝∠COD+∠BOC，即∠AOC＝∠BOD，在△AOC和△BOD中，∴△AOC≌△BOD（SAS），∴∠OCA＝∠ODB，AC＝BD，故②正确；∵∠OAC＝∠OBD，由三角形的外角性质得：∠AMB+∠OBD＝∠OAC+∠AOB，∴∠AMB＝∠AOB＝36°，故①正确；法一：作OG⊥AM于G，OH⊥DM于H，如图所示，则∠OGA＝∠OHB＝90°，∵△AOC≌△BOD，∴OG＝OH，∴MO平分∠AMD，故④正确；法二：∵△AOC≌△BOD，∴∠OAC＝∠OBD，∴A、B、M、O四点共圆，∴∠AMO＝∠ABO＝72°，同理可得：D、C、M、O四点共圆，∴∠DMO＝∠DCO＝72°＝∠AMO，∴MO平分∠AMD，故④正确；假设MO平分∠AOD，则∠DOM＝∠AOM，在△AMO与△DMO中，，∴△AMO≌△DMO（ASA），∴AO＝OD，∵OC ＝OD ，∴OA ＝OC ，而OA ＜OC ，故③错误；变式训练【变式3-1】．如图，等腰ABC ∆中，120ACB ∠=︒，4AC =，点D 为直线AB 上一动点，以线段CD 为腰在右侧作等腰CDE ∆，且120DCE ∠=︒，连接AE ，则AE 的最小值为()A ．23B ．4C ．6D ．8解：连接BE 并延长交AC 延长线于F ，120ACB ∠=︒ ，AC BC =，30CAB CBA ∴∠=∠=︒，120DCE ACB ∠=︒=∠ ，ACD BCE ∴∠=∠，AC BC = ，CD CE =，()ACD BCE SAS ∴∆≅∆，30CBE CAD ∴∠=∠=︒，CB 为定直线，30CBE ∠=︒为定值，∴当D 在直线AB 上运动时，E 也在定直线上运动，当AE BE ⊥时，AE 最小，30CAB ABC CBE ∠=︒=∠=∠ ，90AFB ∴∠=︒，∴当E 与F 重合时，AE 最小，在Rt CBF ∆中，90CFB ∠=︒，30CBF ∠=︒，122CF CB ∴==，6AF AC CF ∴=+=，AE ∴的最小值为6AF =，故选：C ．【变式3-2】．如图，在△ABC 中，AB ＝AC ＝5，∠BAC ＝120°，以CA 为边在∠ACB 的另一侧作∠ACM ＝∠ACB ，点D 为边BC （不含端点）上的任意一点，在射线CM 上截取CE ＝BD ，连接AD ，DE ，AE ．设AC 与DE 交于点F ，则线段CF 的最大值为．解：∵∠BAC＝120°，AB＝AC，∴∠B＝∠ACB＝30°．∵∠ACM＝∠ACB，∴∠B＝∠ACM＝30°．在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）．∴AD＝AE，∠BAD＝∠CAE．∴∠CAE+∠DAC＝∠BAD+∠DAC＝∠BAC＝120°．即∠DAE＝120°．∵AD＝AE，∴∠ADE＝∠AED＝30°；∵∠ADE＝∠ACB＝30°且∠DAF＝∠CAD，∴△ADF∽△ACD．∴＝．∴AD2＝AF•AC．∴AD2＝5AF．∴AF＝．∴当AD最短时，AF最短、CF最长．∵当AD⊥BC时，AF最短、CF最长，此时AD＝AB＝．∴AF最短＝＝．∴CF最长＝AC﹣AF最短＝5﹣＝．故答案为：．【变式3-3】.【问题背景】（1）如图1，等腰ABC ∆中，AB AC =，120BAC ∠=︒，AQ BC ⊥于点Q ，则BC AB =；【知识应用】（2）如图2，ABC ∆和ADE ∆都是等腰三角形，120BAC DAE ∠=∠=︒，D 、E 、C 三点在同一条直线上，连接BD ．求证：ADB AEC ∆≅∆．（3）请写出线段AD ，BD ，CD之间的等量关系，并说明理由．（1）解：AB AC = ，120BAC ∠=︒，AQ BC ⊥，30B C ∴∠=∠=︒，BQ QC =，12AQ AB ∴=，由勾股定理得：2BQ AB ===，BC ∴=，∴BC AB ==（2）证明：BAC DAE ∠=∠ ，BAC BAE DAE BAE ∴∠-∠=∠-∠，即DAB EAC ∠=∠，在ADB ∆和AEC ∆中，AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩，()ADB AEC SAS ∴∆≅∆；（3）解：CD BD =+，理由如下：由（1）可知：DE =，ADB AEC ∆≅∆ ，EC BD ∴=，CD DE EC BD ∴=+=+．实战演练1.风筝为中国人发明，相传墨翟以木头制成木鸟，研制三年有成，是人类最早的风筝起源．如图，小飞在设计的“风筝”图案中，已知AB AD =，B D ∠=∠，BAE DAC ∠=∠，那么AC 与AE 相等．小飞直接证明ABC ADE ∆≅∆，他的证明依据是()A ．SSSB ．SASC ．ASAD ．AAS证明：BAE DAC ∠=∠ ，BAE EAC DAC EAC ∴∠+∠=∠+∠，BAC DAE ∴∠=∠，AB AD = ，B D ∠=∠，()ABC ADE ASA ∴∆≅∆，AC AE ∴=，故选：C ．2．如图，ABD ∆，AEC ∆都是等边三角形，则BOC ∠的度数是()A ．135︒B ．125︒C ．120︒D ．110︒解：ABD ∆ ，AEC ∆都是等边三角形，AD AB ∴=，AE AC =，60DAB CAE ∠=∠=︒，60ADB DBA ∠==︒，DAB BAC CAE BAC ∴∠+∠=∠+∠，DAC BAE ∴∠=∠，()DAC BAE SAS ∴∆≅∆，ADC ABE ∴∠=∠，BOC BDO DBA ABE∴∠=∠+∠+∠BDO DBA ADC =∠+∠+∠ADB DBA=∠+∠6060=︒+︒120=︒，BOC ∴∠的度数是120︒，故选：C ．3．如图，点A 是x 轴上一个定点，点B 从原点O 出发沿y 轴的正方向移动，以线段OB 为边在y 轴右侧作等边三角形，以线段AB 为边在AB 上方作等边三角形，连接CD ，随点B 的移动，下列说法错误的是()A ．BOA BDC∆≅∆B ．150ODC ∠=︒C ．直线CD 与x 轴所夹的锐角恒为60︒D ．随点B 的移动，线段CD 的值逐渐增大解：A ．OBD ∆ 和ABC ∆都是等边三角形，60ABC OBD ODB BOD ∴∠=∠=∠=∠=︒，BO BD =，BC AB =，ABC DBA OBD DBA ∴∠-∠=∠-∠，CBD ABO ∴∠=∠，()BOA BDC SAS ∴∆≅∆，故A 不符合题意；B ．BOA BDC ∆≅∆ ，90BDC BOA ∴∠=∠=︒，6090150ODC BDO BDC ∴∠=∠+∠=︒+︒=︒，故B 不符合题意；C ．延长CD 交x 轴于点E ，150ODC ∠=︒ ，18030ODE ODC ∴∠=︒-∠=︒，90BOA ∠=︒ ，60BOD ∠=︒，30DOA BOA BOD ∴∠=∠-∠=︒，60DEA DOA ODE ∴∠=∠+∠=︒，∴直线CD 与x 轴所夹的锐角恒为60︒，故C 不符合题意；D ．BOA BDC ∆≅∆ ，CD OA ∴=，点A 是x 轴上一个定点，OA ∴的值是一个定值，∴随点B 的移动，线段CD 的值不变，故D 符合题意；故选：D ．4．如图，3AB =，2AC =BC ，分别以AC 、BC 为直角边作等腰Rt ACD ∆和等腰Rt BCE ∆，连结AE 、BD ，当AE 最长时，BC 的长为()A ．22B ．3C ．11D ．17解：90ACD BCE ∠=∠=︒ ，ACD ACB BCE ACB ∴∠+∠=∠+∠，即ACE DCB ∠=∠，在ACE ∆和DCB ∆中，AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩，()ACE DCB SAS ∴∆≅∆，AE BD ∴=，2AC CD == ，90ACD ∠=︒，222AD AC CD ∴=+=，3AB = ，∴当点A 在BD 上时，BD 最大，最大值为325+=，如图，过C 作CE AD ⊥于E ，由等腰三角形“三线合一”得1DE AE ==，314BE AB AE ∴=+=+=，再由直角三角形斜边中线等于斜边一半得1DE =，2217BC CE BE ∴=+=．故选：D ．5．如图，线段OA 绕点O 旋转，线段OB 的位置保持不变，在AB 的上方作等边PAB ∆，若1OA =，3OB =，则在线段OA 旋转过程中，线段OP 的最大值是()A 10B ．4C ．5D ．5解：如图，以AO 为边，在AO 的左侧作等边AOH ∆，连接BH ，AOH ∆ ，ABP ∆是等边三角形，1AO AH OH ∴===，AB AP =，60OAH BAP ∠=∠=︒，OAP HAB ∴∠=∠，在OAP ∆和HAB ∆中，AO AH OAP HAB AP AB =⎧⎪∠=∠⎨⎪=⎩，()OAP HAB SAS ∴∆≅∆，OP BH ∴=，在OPH ∆中，BH OH OB <+，∴当点H 在BO 的延长线上时，BH 的最大值4OH OB =+=，OP ∴的最大值为4，故选：B ．6．如图，O 是等边△ABC 内一点，OA ＝3，OB ＝4，OC ＝5，将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′，则∠AOB ＝150°．解：连接OO ′，如图，∵线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′，∴BO ′＝BO ＝4，∠O ′BO ＝60°，∴△BOO ′为等边三角形，∴∠BOO ′＝60°，∵△ABC 为等边三角形，∴BA ＝BC ，∠ABC ＝60°，∴∠O ′BO ﹣∠ABO ＝∠ABC ﹣∠ABO ，即∠O ′BA ＝∠OBC ，在△O ′BA 和△OBC中，∴△O ′BA ≌△OBC （SAS ），∴O ′A ＝OC ＝5，在△AOO ′中，∵OA ′＝5，OO ′＝4，OA ＝3，∴OA 2+OO ′2＝O ′A 2，∴∠AOO ′＝90°，∴∠AOB ＝60°+90°＝150°，故答案为：150°．7．如图，△ABC与△ADE均是等腰直角三角形，点B，C，D在同一直线上，AB＝AC＝2，AD＝AE＝3，∠BAC＝∠DAE＝90°，则CD＝﹣．解：∵AB＝AC＝2，AD＝AE＝3，∠BAC＝∠DAE＝90°，∴BC＝AB＝2，DE＝AE＝3，∠BAD＝∠CAE，∠ABC＝45°＝∠ACB，在△BAD和△CAE中，，∴△BAD≌△CAE（SAS），∴EC＝BD，∠ABD＝∠ACE＝45°，∴∠ECB＝∠ECD＝90°，∴DE2＝EC2+CD2，∴18＝（2+CD）2+CD2，解得：CD＝﹣，CD＝﹣﹣（不合题意舍去），故答案为：﹣．8．如图，△ABC和△ADE均为等腰直角三角形，连接CD、BE，点F、G分别为DE、BE 的中点，连接FG．在△ADE旋转的过程中，当D、E、C三点共线时，若AB＝3，AD＝2，则线段FG的长为．解：连接BD，∠BAD＝90°﹣∠BAE，∠CAE＝90°﹣∠BAE，∴∠BAD＝∠CAE．又AD＝AE，AB＝AC，∴△ADB≌△AEC（SAS）．∴BD＝CE，∠ADB＝∠AEC＝135°，∴∠BDC＝135°﹣45°＝90°．∵△ABC和△ADE均为等腰直角三角形，AB＝3，AD＝2，∴DE＝2，BC＝3．设BD＝x，则DC＝2+x，在Rt△BDC中，利用勾股定理BD2+DC2＝BC2，所以x2+（2+x）2＝18，解得x1＝﹣﹣（舍去），x2＝﹣+．∵点F、G分别为DE、BE的中点，∴FG＝BD＝．故答案为．9．如图，△ACD和△BCE都是等腰直角三角形，∠ACD＝∠BCE＝90°，AE交CD于点F，BD分别交CE、AE于点G、H．试猜测线段AE和BD的数量和位置关系，并说明理由．解：猜测AE＝BD，AE⊥BD；理由如下：∵∠ACD＝∠BCE＝90°，∴∠ACD+∠DCE＝∠BCE+∠DCE，即∠ACE＝∠DCB，又∵△ACD和△BCE都是等腰直角三角形，∴AC＝CD，CE＝CB，在△ACE与△DCB中，∴△ACE≌△DCB（SAS），∴AE＝BD，∠CAE＝∠CDB；∵∠AFC＝∠DFH，∠FAC+∠AFC＝90°，∴∠DHF＝∠ACD＝90°，∴AE⊥BD．故线段AE和BD的数量相等，位置是垂直关系．10．如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC，AF⊥CB，垂足为F．（1）求证：△ABC≌△ADE；（2）求∠FAE的度数；（3）求证：CD＝2BF+DE．证明：（1）∵∠BAD＝∠CAE＝90°，∴∠BAC+∠CAD＝90°，∠CAD+∠DAE＝90°，∴∠BAC＝∠DAE，在△BAC和△DAE中，，∴△BAC≌△DAE（SAS）；（2）∵∠CAE＝90°，AC＝AE，∴∠E＝45°，由（1）知△BAC≌△DAE，∴∠BCA＝∠E＝45°，∵AF⊥BC，∴∠CFA＝90°，∴∠CAF＝45°，∴∠FAE＝∠FAC+∠CAE＝45°+90°＝135°；（3）延长BF到G，使得FG＝FB，∵AF⊥BG，∴∠AFG＝∠AFB＝90°，在△AFB和△AFG中，，∴△AFB≌△AFG（SAS），∴AB＝AG，∠ABF＝∠G，∵△BAC≌△DAE，∴AB＝AD，∠CBA＝∠EDA，CB＝ED，∴AG＝AD，∠ABF＝∠CDA，∴∠G＝∠CDA，∵∠GCA＝∠DCA＝45°，在△CGA和△CDA中，，∴△CGA≌△CDA（AAS），∴CG＝CD，∵CG＝CB+BF+FG＝CB+2BF＝DE+2BF，∴CD＝2BF+DE．11．已知△ABC和△ADE都是等边三角形，点D在射线BF上，连接CE．（1）如图1，BD与CE是否相等？请说明理由；（2）如图1，求∠BCE的度数；（3）如图2，当D在BC延长线上时，连接BE，△ABE、△CDE与△ADE的面积有怎样的关系？并说明理由．解：（1）BD＝CE，理由如下：∵△ABC和△ADE是都是等边三角形，∴AB＝AC，AD＝AE，∠BAC＝∠DAE，∠ABC＝∠ACB＝60°，∴∠BAD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴BD＝CE；（2）∵△ABD≌△ACE，∴∠ABD＝∠ACE＝60°，∴∠BCE＝120°；+S△CDE＝S△ADE，理由如下：（3）S△ABE∵△ABC和△ADE是都是等边三角形，∴AB＝AC，AD＝AE，∠BAC＝∠DAE，∠ABC＝∠ACB＝60°，∴∠BAD＝∠CAE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），＝S△ACE，∠ABC＝∠ACE＝60°，∴S△ABD∴∠ECD＝180°﹣∠ACB﹣∠ACE＝60°，∴∠ABC＝∠ECD，∴AB∥CE，＝S△ABC，∴S△ABE+S△CDE＝S△ADE+S△ACD，∵S△ACE+S△CDE＝S△ADE+S△ACD，∴S△ABD+S△ACD+S△CDE＝S△ADE+S△ACD，∴S△ABC+S△CDE＝S△ADE．∴S△ABE12．如图，在△ABC中，分别以AB、AC为腰向外侧作等腰Rt△ADB与等腰Rt△AEC，∠DAB＝∠EAC＝90°，连接DC、EB相交于点O．（1）求证：BE⊥DC；（2）若BE＝BC．①如图1，G、F分别是DB、EC中点，求的值．②如图2，连接OA，若OA＝2，求△DOE的面积．（1）证明：∵∠DAB＝∠EAC＝90°，∴∠EAB＝∠CAD，在△BAE和△DAC中，，∴△BAE≌△DAC（SAS），∴∠ABE＝∠ADC，∵∠BAD＝90°，∴∠DOB＝90°，即BE⊥DC；（2）解：①取DE的中点H，连接GH、FH，∵点G是BD的中点，∴GH∥BE，GH＝BE，同理，FH∥CD，FH＝CD，∵BE＝CD．BE⊥DC，∴GH＝FH，GH⊥FH，∴△HGF为等腰直角三角形，∴GF＝GH，∵GH＝BE，∴GF＝BE，∵BE＝BC，∴＝；②作AM⊥BE于M，AN⊥CD于N，在△BAE和△BAC中，，∴△BAE≌△BAC（SSS），∴∠BAE＝∠BAC＝135°，∴∠DAE＝135°﹣90°＝45°，即∠OAD+∠OAE＝45°，∵△BAE≌△DAC，∴AM＝AN，又AM⊥BE，AN⊥CD，∴OA平分∠BOC，∴∠BOA＝∠COA＝45°，∴∠DOA＝∠EOA＝135°，∴∠ODA+∠OAD＝45°，∴∠OAE＝∠ODA，∴△ODA∽△OAE，∴＝，即OD•OE＝OA2＝4，∴△DOE的面积＝×OD•OE＝2．13．如图（1），在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD，以AD 为一边在AD的右侧作等腰直角△ADF，∠ADE＝∠AED＝45°，∠DAE＝90°，AD＝AE，解答下列问题：（1）如果AB＝AC，∠BAC＝90°，∠ABC＝∠ACB＝45°．①当点D在线段BC上时（与点B不重合），如图（2），线段CE、BD之间的数量关系为CE＝BD；位置关系为CE⊥BD；（不用证明）②当点D在线段BC的延长线上时，如图（3），①中的结论是否仍然成立，请写出结论并说明理由．（2）如果AB≠AC，∠BAC≠90°，点D在线段BC上运动．试探究：当△ABC满足一个什么条件时，CE⊥BD（点C、E重合除外）？请写出条件，并借助图（4）简述CE⊥BD成立的理由．解：（1）①CE与BD位置关系是CE⊥BD，数量关系是CE＝BD．理由：如图（2），∵∠BAD＝90°﹣∠DAC，∠CAE＝90°﹣∠DAC，∴∠BAD＝∠CAE．又BA＝CA，AD＝AE，∴△ABD≌△ACE（SAS），∴∠ACE＝∠B＝45°且CE＝BD．∵∠ACB＝∠B＝45°，∴∠ECB＝45°+45°＝90°，即CE⊥BD．故答案为：CE＝BD；CE⊥BD．②当点D在BC的延长线上时，①的结论仍成立．如图（3），∵∠DAE＝90°，∠BAC＝90°，∴∠DAE＝∠BAC，∴∠DAB＝∠EAC，又AB＝AC，AD＝AE，∴△DAB≌△EAC（SAS），∴CE＝BD，且∠ACE＝∠ABD．∵∠BAC＝90°，AB＝AC，∴∠ABC＝45°，∴∠ACE＝45°，∴∠BCE＝∠ACB+∠ACE＝90°，即CE⊥BD；（2）如图（4）所示，当∠BCA＝45°时，CE⊥BD．理由：过点A作AG⊥AC交BC于点G，∴AC＝AG，∠AGC＝45°，即△ACG是等腰直角三角形，∵∠GAD+∠DAC＝90°＝∠CAE+∠DAC，∴∠GAD＝∠CAE，又∵DA＝EA，∴△GAD≌△CAE（SAS），∴∠ACE＝∠AGD＝45°，∴∠BCE＝∠ACB+∠ACE＝90°，即CE⊥BD．14．（注意：本题中的说理过程中的每一步必须注明理由，否则不得分）如图1，在△ABC 中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．（1）如果AB＝AC，∠BAC＝90°；①当点D在线段BC上时（与点B不重合），如图2，线段CF、BD所在直线的位置关系为CF⊥BD，线段CF、BD的数量关系为CF＝BD；②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立？并说明理由；（2）如图4，如果AB≠AC，∠BAC是锐角，点D在线段BC上，当∠ACB满足什么条件时，CF⊥BC（点C、F不重合），并说明理由．解：（1）①正方形ADEF中，AD＝AF，∵∠BAC＝∠DAF＝90°，∴∠BAD＝∠CAF，又∵AB＝AC，∴△DAB≌△FAC（SAS），∴CF＝BD，∠B＝∠ACF，∴∠ACB+∠ACF＝90°，即CF⊥BD．故答案为：CF⊥BD，CF＝BD；②当点D在BC的延长线上时①的结论仍成立．理由如下：由正方形ADEF得AD＝AF，∠DAF＝90°．∵∠BAC＝90°，∴∠DAF＝∠BAC，∴∠DAB＝∠FAC，又∵AB＝AC，∴△DAB≌△FAC（SAS），∴CF＝BD，∠ACF＝∠ABD．∵∠BAC＝90°，AB＝AC，∴∠ABC＝45°，∴∠ACF＝45°，∴∠BCF＝∠ACB+∠ACF＝90°．即CF⊥BD；（2）当∠ACB＝45°时，CF⊥BD．理由如下：过点A作AG⊥AC交CB的延长线于点G，则∠GAC＝90°，∵∠ACB＝45°，∠AGC＝90°﹣∠ACB，∴∠AGC＝90°﹣45°＝45°，∴∠ACB＝∠AGC＝45°，∴AC＝AG，∵∠DAG＝∠FAC（同角的余角相等），AD＝AF，∴△GAD≌△CAF（SAS），∴∠ACF＝∠AGC＝45°，∴∠BCF＝∠ACB+∠ACF＝45°+45°＝90°，即CF⊥BC．15．背景：一次小组合作探究课上，小明将两个正方形按如图所示的位置摆放（点E、A、D在同一条直线上），发现BE＝DG且BE⊥DG．小组讨论后，提出了下列三个问题，请你帮助解答：（1）将正方形AEFG绕点A按逆时针方向旋转（如图1），还能得到BE＝DG吗？若能，请给出证明；若不能，请说明理由；（2）把背景中的正方形分别改成菱形AEFG和菱形ABCD，将菱形AEFG绕点A按顺时针方向旋转（如图2），试问当∠EAG与∠BAD的大小满足怎样的关系时，背景中的结论BE＝DG仍成立？请说明理由；（3）把背景中的正方形分别改写成矩形AEFG和矩形ABCD，且，AE＝4，AB＝8，将矩形AEFG绕点A按顺时针方向旋转（如图3），连接DE，BG．小组发现：在旋转过程中，DE2+BG2的值是定值，请求出这个定值．（1）证明：∵四边形AEFG为正方形，∴AE＝AG，∠EAG＝90°，又∵四边形ABCD为正方形，∴AB＝AD，∠BAD＝90°，∴∠EAB＝∠GAD，∴△AEB≌△AGD（SAS），∴BE＝DG；（2）当∠EAG＝∠BAD时，BE＝DG，理由如下：∵∠EAG＝∠BAD，∴∠EAB＝∠GAD，又∵四边形AEFG和四边形ABCD为菱形，∴AE＝AG，AB＝AD，∴△AEB≌△AGD（SAS），∴BE＝DG；（3）解：方法一：过点E作EM⊥DA，交DA的延长线于点M，过点G作GN⊥AB交AB于点N，由题意知，AE＝4，AB＝8，∵＝，∴AG＝6，AD＝12，∵∠EMA＝∠ANG，∠MAE＝∠GAN，∴△AME∽△ANG，设EM＝2a，AM＝2b，则GN＝3a，AN＝3b，则BN＝8﹣3b，∴ED2＝（2a）2+（12+2b）2＝4a2+144+48b+4b2，GB2＝（3a）2+（8﹣3b）2＝9a2+64﹣48b+9b2，∴ED2+GB2＝13（a2+b2）+208＝13×4+208＝260．方法二：如图2，设BE与DG交于Q，BE与AG交于点P，∵，AE＝4，AB＝8∴AG＝6，AD＝12．∵四边形AEFG和四边形ABCD为矩形，∴∠EAG＝∠BAD，∴∠EAB＝∠GAD，∵，∴△EAB∽△GAD，∴∠BEA＝∠AGD，∴A，E，G，Q四点共圆，∴∠GQP＝∠PAE＝90°，∴GD⊥EB，连接EG，BD，∴ED2+GB2＝EQ2+QD2+GQ2+QB2＝EG2+BD2，∴EG2+BD2＝42+62+82+122＝260．。

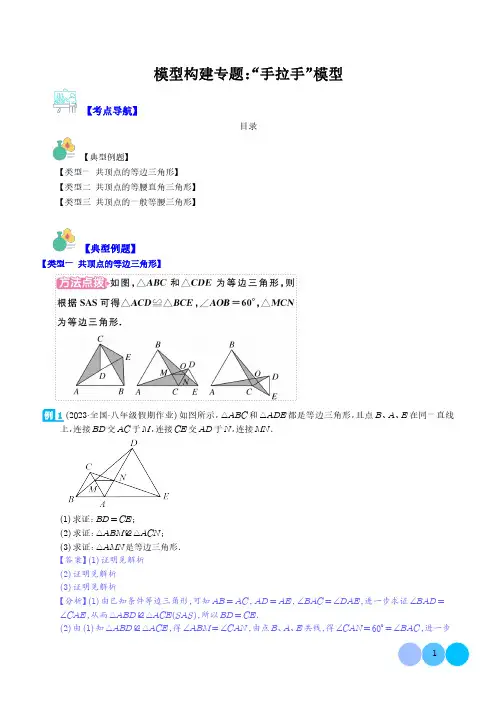
模型构建专题：“手拉手”模型【考点导航】目录【典型例题】【类型一共顶点的等边三角形】【类型二共顶点的等腰直角三角形】【类型三共顶点的一般等腰三角形】【典型例题】【类型一共顶点的等边三角形】1(2023·全国·八年级假期作业)如图所示，△ABC和△ADE都是等边三角形，且点B、A、E在同一直线上，连接BD交AC于M，连接CE交AD于N，连接MN．(1)求证：BD=CE；(2)求证：△ABM≌△ACN；(3)求证：△AMN是等边三角形．【答案】(1)证明见解析(2)证明见解析(3)证明见解析【分析】(1)由已知条件等边三角形，可知AB=AC，AD=AE，∠BAC=∠DAE，进一步求证∠BAD=∠CAE，从而△ABD≌△ACE(SAS)，所以BD=CE．(2)由(1)知△ABD≌△ACE，得∠ABM=∠CAN，由点B、A、E共线，得∠CAN=60°=∠BAC，进一步求证△ABM≌△ACN(ASA)．(3)由△ABM≌△ACN，得AM=AN，而∠CAN=60°，所以△AMN是等边三角形．【详解】(1)∵△ABC和△ADE都是等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=60°，∴∠BAD=∠CAE．在△ABD和△ACE中，AB=AC∠BAD=∠CAE AD=AE∴△ABD≌△ACE(SAS)，∴BD=CE．(2)由(1)知△ABD≌△ACE，∴∠ABM=∠ACN．∵点B、A、E在同一直线上，且∠BAC=∠DAE=60°，∴∠CAN=60°=∠BAC．在△ABM和△ACN中，∠BAM=∠CAN AB=AC∠ABM=∠ACN∴△ABM≌△ACN(ASA)．(3)由(2)知△ABM≌△ACN，∴AM=AN，∵∠CAN=60°，∴△AMN是等边三角形．【点睛】本题主要考查等边三角形的性质和判定、全等三角形判定和性质；将等边三角形的条件转化为相等线段和等角，选择合适的方法判定三角形全等是解题的关键．【变式训练】1(2023春·山西运城·八年级统考期中)如图，点C为线段AB上一点，△DAC、△ECB都是等边三角形，AE、DC交于点M，DB、EC交于点N，DB、AE交于点P，连接MN，下列说法正确的个数有个．①MN∥AB；②∠DPM=60°；③∠DAP=∠PEC；④△ACM≌△DCN；⑤若∠DBE=30°，则∠AEB=90°．【答案】①②③④⑤【分析】根据等边三角形的性质得到AC=CD，BC=CE，∠ACD=∠BCE=60°，得到∠ACE=∠BCE，∠DCE=60°，根据平行线的判定定理得到AD∥CE，根据平行线的性质得到∠DAP=∠PEC，故③正确；根据全等三角形的性质得到∠CAE=∠CDB，根据三角形的内角和得到∠DPM=∠ACM=60°，故②正确，推出△ACM≌△DCN，故④正确；根据全等三角形的性质得到CM=CN，得到△CMN是等边三角形，求得∠CMN=60°，根据平行线的判定定理得到MN∥AB，故①正确；根据三角形的内角和得到∠AEB= 90°．故⑤正确．【详解】解：∵△DAC 、△ECB 都是等边三角形，∴AC =CD ，BC =CE ，∠ACD =∠BCE =60°，∴∠ADC =∠DCE =60°，∴∠ACE =∠BCD ，∠DCE =60°，∴AD ∥CE ，∴∠DAP =∠PEC ，故③正确；在△ACE 与△BCD 中，AC =CD∠ACE =∠BCD CE =CB，∴△ACE ≌△BCD SAS ，∴∠CAE =∠CDB ，∵∠PMD =∠AMC ，∴∠DPM =∠ACM =60°，故②正确，在△ACM 与△DCN 中，∠CAM =∠CDNAC =CD ∠ACM =∠DCN =60°，∴△ACM ≌△DCN ，故④正确；∴CM =CN ，∴△CMN 是等边三角形，∴∠CMN =60°，∴∠CMN =∠ACD ，∴MN ∥AB ，故①正确；∵∠DBE =30°，∠BPE =∠APD =60°，∴∠AEB =90°．故⑤正确；故答案为：①②③④⑤．【点睛】本题考查了全等三角形的判定和性质，等边三角形的性质，平行线的判定，熟练掌握全等三角形的判定和性质是解题的关键．2(2023秋·四川凉山·八年级统考期末)如图，C 为线段AE 上一动点(不与点A ，E 重合)，在AE 同侧分别作等边△ABC 和等边△CDE ，AD 与BE 交于点O ，AD 与BC 交于点P ，BE 与CD 交于点Q ，连结PQ．求证：(1)AD =BE ；(2)△CPQ 为等边三角形；【答案】(1)见解析；(2)见解析．【分析】(1)由等边三角形的性质可知AC =BC ，CD =CE ，∠ACB =∠DCE =60°，从而可求出∠ACD =∠BCE ，即可利用“SAS ”证明△ADC ≌△BEC ，即得出AD =BE ；(2)由等边三角形的性质可知∠ACB =∠DCE =60°，AC =BC ，即可求证∠ACP =∠BCQ =60°．再根据△ADC ≌△BEC 可得出∠CAP =∠CBQ ，利用“ASA ”证明△APC ≌△BQC ，据此即可证明结论成立．【详解】(1)证明：∵△ABC 和△CDE 都是等边三角形，∴AC =BC ，CD =CE ，∠ACB =∠DCE =60°，∵∠ACD =∠ACB +∠BCD ，∠BCE =∠DCE +∠BCD ，∴∠ACD =∠BCE ，∴AC =BC∠ACD =∠BCE CD =CE，∴△ADC ≌△BEC (SAS )，∴AD =BE ；(2)证明：∵△ABC 和△CDE 是等边三角形，∴∠ACB =∠DCE =60°，AC =BC ，∴∠BCQ =180°-∠ACP -∠ECD =60°，∴∠ACP =∠BCQ =60°．∵△ADC ≌△BEC∴∠CAP =∠CBQ ．∴∠CAP =∠CBQAC =BC∠ACP =∠BCQ∴△APC ≌△BQC ASA ．∴CP =CQ ，又∵∠PCQ =60°，∴△CPQ 为等边三角形．【点睛】本题考查等边三角形的性质，全等三角形的判定和性质．熟练掌握全等三角形的判定条件是解题关键．3(2021春·广东佛山·八年级校考阶段练习)已知图1是边长分别为a 和b a >b 的两个等边三角形纸片ABC 和三角形C DE 叠放在一起(C 与C 重合)的图形．(1)将△C DE 绕点C 按顺时针方向旋转30°，连接AD ，BE ．如图2：在图2中，线段BE 与AD 之间具有怎样的大小关系？证明你的结论；(2)若将上图中的△C DE ，绕点C 按顺时针方向任意旋转一个角度α，连接AD 、BE ，如图3：在图3中，线段BE 与AD 之间具有怎样的大小关系？证明你的结论：(3)根据上面的操作过程，请你猜想当α为多少度时，线段AD 的长度最大，最大是多少？当α为多少度时，线段AD 的长度最小，最小是多少？请直接写出答案．【答案】(1)BE =AD ，证明见解析(2)BE =AD ，证明见解析(3)当α为180度时，线段AD 的长度最大，最大值为a +b ；当α为0度或360度时，线段AD 的长度最小，最小值为a -b ．【分析】(1)先由等边三角形判断出AC =BC ，CE =CD ，再由旋转判断出∠BCE =∠ACD ，进而判断出△BCE ≌△ACD ，即可得出结论；(2)同(1)的方法，即可得出结论；(3)当点D 在AC 的延长线上时，AD 最大，最大值为a +b ，当点D 在线段AC 上时，AD 最小，最小值为a -b ，即可得出结论．【详解】(1)解：BE =AD证明：∵点C 与C 1重合，△ABC 和△C 1DE ，∴△ABC 和△CDE 都是等边三角形，∴AC =BC ，CE =CD ，由旋转知，∠BCE =∠ACD =30°，在△BCE 和△ACD 中，BC =AC∠BCE =∠ACD CE =CD，∴△BCE ≌△ACD (SAS )，∴BE =AD ，(2)解：BE =AD ，证明：∵△ABC 和△CDE 都是等边三角形，∴AC =BC ，CE =CD ，由旋转知，∠BCE =∠ACD ，在△BCE 和△ACD 中，BC =AC∠BCE =∠ACD CE =CD，∴△BCE ≌△ACD (SAS )，∴BE =AD ；(3)解：当点D 在AC 的延长线上时，AD 最大，最大值为AC +CD =a +b ，如图，∴当α为180度时，线段AD 的长度最大，最大值为a +b ，当点D 在线段AC 上时，AD 最小，最小值为AC -CD =a -b ，如图，∴当α为0度或360度时，线段AD的长度最小，最小值为a-b．【点睛】此题是三角形综合题，主要考查了等边三角形的性质，全等三角形的判定和性质，判断出△BCE≌△ACD是解本题的关键．4(2023春·广东梅州·七年级校考期末)【初步感知】(1)如图1，已知ΔABC为等边三角形，点D为边BC上一动点(点D不与点B，点C重合)．以AD为边向右侧作等边ΔADE，连接CE．求证：ΔABD≌ΔACE；【类比探究】(2)如图2，若点D在边BC的延长线上，随着动点D的运动位置不同，猜想并证明：①AB与CE的位置关系为：；②线段EC、AC、CD之间的数量关系为：；【拓展应用】(3)如图3，在等边ΔABC中，AB=3，点P是边AC上一定点且AP=1，若点D为射线BC上动点，以DP 为边向右侧作等边ΔDPE，连接CE、BE．请问：PE+BE是否有最小值？若有，请直接写出其最小值；若没有，请说明理由．【答案】(1)见解析(2)平行EC=AC+CD(3)有最小值，5【分析】(1)由ΔABC和ΔADE是等边三角形，推出AB=AC，AD=AE，∠BAC=∠DAE=60°，又因为∠BAC=∠DAE，则∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE，从而利用“SAS”证明ΔABD≌ΔACE；(2)①由(1)得ΔABD≌ΔACE(SAS)，得出∠B=∠ACE=60°，CE=BD，∠BAC=∠ACE，则AB∥CE；②因为CE=BD，AC=BC，所以CE=BD=BC+CD=AC+CD；(3)在BC上取一点M，使得DM=PC，连接EM，可证ΔEPC≌ΔEDM(SAS)，EC=EM，求得∠CEM= 60°，得出ΔCEM是等边三角形，则∠ECD=60°，即点E在∠ACD角平分线上运动，在射线CD上截取CP =CP，当点E与点C重合时，BE+PE=BE+P E≥BP =5，进而解答此题．【详解】(1)证明：∵ΔABC和ΔADE是等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=60°，∵∠BAC=∠DAE，∴∠BAC-∠DAC=∠DAE-∠DAC 即∠BAD=∠CAE在ΔABD和ΔACE中，AB=AC∠BAD=∠CAE AD=AE，∴ΔABD≌ΔACE(SAS)；(2)平行，EC=AC+CD，理由如下：由(1)得ΔABD≌ΔACE(SAS)，∴∠B=∠ACE=60°，CE=BD，∴∠BAC=∠ACE，∴AB∥CE，∵CE=BD，AC=BC，∴CE=BD=BC+CD=AC+CD；(3)有最小值，理由如下：如图，在射线BC上取一点M，使得DM=PC，连接EM，∵ΔABC和ΔDPE是等边三角形，∴PE=ED，∠DEP=∠ACB=60°，∴∠ACD=180°-∠ACB=180°-60°=120°，∴∠ACD+∠DEP=120°+60°=180°，由三角形内角和为180°，可知：∠PCE+∠CEP+∠EPC=180°，∠ECD+∠CDE+∠CED=180°，∴∠PCE+∠CEP+∠EPC+∠ECD+∠CDE+∠CED=360°，又∵∠PCE+∠ECD+∠CEP+∠CED=∠ACD+∠DEP=180°，∴∠EPC+∠CDE=360°-180°=180°，∵∠EDM+∠CDE=180°，∴∠EPC=∠EDM，在ΔEPC和ΔEDM中，PE=ED∠EPC=∠EDM PC=DM，ΔEPC≌ΔEDM(SAS)，∴EC=EM，∠PEC=∠DEM，∵∠PEC+∠CED=∠DEP=60°，∴∠CEM=∠DEM+∠CED=60°，∴ΔCEM是等边三角形，∴∠ECD=60°，∠ACE=180°-∠ECD-∠ACB=180°-60°-60°=60°，即点E在∠ACD的角平分线上运动，在射线CD上截取CP =CP，连接EP ，在ΔCEP和ΔCEP 中，PC=P C∠PCE=∠P CE=60°CE=CE，ΔCEP≌ΔCEP (SAS)，∴PE=P E，由三角形三边关系可知，BE+P E≥BP ，即当点E与点C重合，BE+P E=BP 时，PE+BE有最小值BP ，∵BP =BE+CP =BC+CP=3+2=5，∴BE+PE=BE+P E≥BP =5，∴BE+PE最小值为5．【点睛】本题考查三角形综合，全等三角形的判定，正确添加辅助线、掌握相关图形的性质定理是解题的关键．【类型二共顶点的等腰直角三角形】90°．(1)【猜想】：如图1，点E在BC上，点D在AC上，线段BE与AD的数量关系是，位置关系是．(2)【探究】：把△DCE绕点C旋转到如图2的位置，连接AD，BE，(1)中的结论还成立吗？说明理由；(3)【拓展】：把△DCE绕点C在平面内自由旋转，若AC=5，CE=22，当A，E，D三点在同一直线上时，则AE的长是．【答案】(1)BE=AD，BE⊥AD(2)成立，理由见解析(3)21+2或21-2【分析】(1)利用等腰直角三角形的性质得出AC=BC，EC=DC，再作差，得出BE=AD，再用∠ACB= 90°，即可得出结论；(2)先由旋转的旋转得出∠BCE=∠ACD，进而判断出△BCE≌△ACD SAS，得出BE=AD，∠CAD=∠CBE，AC与BE交于M，AD与BE交于N，利用全等的性质和对顶角相等进而得出∠MAN+∠AMN=90°，即可得出结论；(3)分两种情况，①当点E在线段AD上时，如图3，过点C作CM⊥AD于M，求出CM=EM=12DE= 2，再用勾股定理求出AM，利用线段的加减即可得出结论；②当点D在线段AE上时，如图4，过点C作CN⊥AE于N，求出CM=EM=12DE=2，再由勾股定理求出根据勾股定理得，AN，利用线段的加减即可得出结论．【详解】(1)∵△ABC和△DCE都是等腰直角三角形，∴AC=BC，EC=DC，∴AC-DC=BC-EC，∴BE=AD，点E在BC上，点D在AC上，且∠ACB=90°，∴BE⊥AD，故：BE=AD，BE⊥AD；(2)成立；如图2，AC与BE交于M，AD与BE交于N，由题意可知：∵∠ACB=∠DCE=90°，∴∠ACB+∠ACE=∠DCE+∠CE，∴∠BCE=∠ACD，在△BCE与△ACD中：BC=AC∠BCE=∠ACD CE=CD∴△BCE≌△ACD SAS，∴BE=AD，∠CAD=∠CBE，又∵∠ACB=90°，∠BMC=∠AMN，在△ANM中，∴∠MAN+∠AMN=∠CBE+∠BMC=90°，∴∠ANM=90°，∴BE⊥AD，所以结论成立；(3)①当点E在线段AD上时，如图3，过点C作CM⊥AD于M，∵△DCE是等腰直角三角形，且CE=22，∴DE=CE2+CD2=4，∵CM⊥AD，∴CM=EM=12DE=2，在Rt△ACM中，AC=5，∴AM=AC2-CM2=52-22=21，∴AE=AM-EM=21-2；②当点D在线段AE上时，如图4，过点C作CN⊥AE于N，∵△DCE是等腰直角三角形，且CE=22，∴DE=CE2+CD2=4，∵CN⊥AD，∴CN =NE =12DE =2，在Rt △ACN 中，AC =5，∴AN =AC 2-CN 2=52-22=21，∴AE =AN +NE =21+2，综上，AE 的长为21-2或21+2，故答案为:21-2或21+2．【点睛】此题是几何变换综合题，主要考查了等腰直角三角形的性质，旋转的旋转，全等三角形的判定和性质，勾股定理，作出辅助线构造出直角三角形是解本题的关键．【变式训练】1(2023·全国·九年级专题练习)如图，在等腰直角三角形ABC 和DEC 中，∠BCA =∠DCE =90°，点E 在边AB 上，ED 与AC 交于点F ，连接AD ．(1)求证：△BCE ≌△ACD ；(2)求证：AB ⊥AD ．【答案】(1)见解析(2)见解析【分析】(1)根据∠BCA =∠DCE =90°，可得∠BCE =∠ACD ，再由等腰直角三角形的性质可得BC =AC ,CE =CD ，可证明△BCE ≌△ACD ，即可求证；(2)根据△BCE ≌△ACD ，可得∠B =∠CAD ，从而得到∠CAD +∠CAE =90°，即可求证．【详解】(1)证明：∵∠BCA =∠DCE =90°，∴∠BCE +∠ECA =∠ECA +∠ACD =90°，∴∠BCE =∠ACD ，∵△ABC 和△DEC 是等腰直角三角形，∴BC =AC ,CE =CD ，在△BCE 和△ACD 中，BC =AC∠BCE =∠ACD CE =CD，∴△BCE ≌△ACD SAS ；(2)证明：∵△BCE ≌△ACD ，∴∠B =∠CAD ，∵∠ACB =90°，∴∠B +∠CAE =90°，∴∠CAD +∠CAE =90°，即∠DAE =90°，∴AB ⊥AD ．【点睛】本题主要考查了全等三角形的判定和性质，等腰直角三角形的性质，熟练掌握全等三角形的判定和性质，等腰直角三角形的性质是解题的关键．2(2023春·八年级课时练习)(1)问题发现：如图1，△ABC与△CDE均为等腰直角三角形，∠ACB=∠DCE=90°，则线段AE、BD的数量关系为，AE、BD所在直线的位置关系为；(2)深入探究：在(1)的条件下，若点A，E，D在同一直线上，CM为△DCE中DE边上的高，请判断∠ADB 的度数及线段CM，AD，BD之间的数量关系，并说明理由．【答案】(1)AE=BD，AE⊥BD；(2)∠ADB=90°，AD=2CM+BD；理由见解析【分析】(1)延长AE交BD于点H，AH交BC于点O．只要证明△ACE≌△BCD SAS，即可解决问题；(2)由△ACE≌△BCD，结合等腰三角形的性质和直角三角形的性质，即可解决问题．【详解】解：(1)如图1中，延长AE交BD于点H，AH交BC于点O，∵△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，∴AC=BC，CD=CE，∴∠ACE+∠ECB=∠BCD+∠ECB=90°，∴∠ACE=∠BCD，∴△ACE≌△BCD(SAS)，∴AE=BD，∠CAE=∠CBD，∵∠CAE+∠AOC=90°，∠AOC=∠BOH，∴∠BOH+∠CBD=90°，∴∠AHB=90°，∴AE⏊BD．故答案为：AE=BD，AE⏊BD．(2)∠ADB=90°，AD=2CM+BD；理由如下：如图2中，∵△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，∴∠CDE=∠CED=45°，∴∠AEC=180°-∠CED=135°，由(1)可知：△ACE≌△BCD，∴AE=BD，∠BDC=∠AEC=135°，∴∠ADB=∠BDC-∠CDE=135°-45°=90°；在等腰直角三角形DCE中，CM为斜边DE上的高，∴CM=DM=ME，∴DM=2CM，∴AD=DE+AE=2CM+BD．【点睛】本题考查了全等三角形的判定和性质，等腰直角三角形的性质等知识，解题的关键是正确寻找全等三角形解决问题．3(2023·山东枣庄·统考二模)感知：如图①，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，点B在线段AD上，点C在线段AE上，我们很容易得到BD=CE，不需证明．(1)探究：如图②，将△ADE绕点A逆时针旋转α(0<α<90°)，连接BD和CE，此时BD=CE是否依然成立？若成立，写出证明过程；若不成立，说明理由．(2)应用：如图③，当△ADE绕点A逆时针旋转，使得点D落在BC的延长线上，连接CE．求：①∠ACE的度数；②若AB=AC=32，CD=3，则线段DE的长是多少？【答案】(1)BD=CE成立，证明见解析(2)①45° ②310【分析】(1)只需要利用SAS证明△ABD≌△ACE即可证明BD=CE；(2)①由等腰直角三角形的性质得到∠ABC=∠ACB=45°，再证明△ABD≌△ACE即可得到∠ABD=∠ACE=45°；②先由勾股定理得到BC=6，由全等三角形的性质得到∠ACE=∠ABD=45°，BD=CE，则∠BCE=90°，CE=9；则DE=CE2+CD2=310．【详解】(1)解：BD=CE成立，证明如下：∵△ABC和△ADE都是等腰直角三角形，∴AB=AC，AD=AE，由旋转的性质可得∠BAD=∠CAE，∴△ABD≌△ACE SAS，∴BD=CE；(2)解：①∵△ABC和△ADE都是等腰直角三角形，∴∠ABC=∠ACB=45°，∠BAC=∠DAE=90°，∴∠BAD=∠CAE，∵AB=AC，∠BAD=CAE，AD=AE，∴△ABD≌△ACE SAS，∴∠ABD=∠ACE=45°；②∵AB=AC=32，∴BC=AB2+AC2=6，∵△ACE≌△ABD，∴∠ACE=∠ABD=45°，BD=CE，∴∠BCE=∠ACB+∠ACE=90°，CE=BD=BC+CD=6+3=9；∴DE=CE2+CD2=92+32=310．【点睛】本题主要考查了全等三角形的性质与判定，勾股定理，等腰直角三角形的性质，熟知全等三角形的性质与判定条件是解题的关键．【类型三共顶点的一般等腰三角形】1(2023春·山东泰安·七年级校考开学考试)如图，△ABC与△CDE都是等腰三角形，AC=BC，CD=CE，∠ACB=∠DCE=42°，AD、BE相交于点M．(1)试说明：AD=BE；(2)求∠AMB的度数．【答案】(1)见解析(2)42°【分析】(1)由“SAS”可证△ACD≌△BCE，可得BE=AD；(2)根据全等三角形的性质可得∠CAD=∠CBE，再利用三角形内角和定理计算∠AMB．【详解】(1)解：证明：∵∠ACB=∠DCE，∴∠ACD=∠BCE，在△ACD和△BCE中，CA=CB∠ACD=∠BCE CD=CE，∴△ACD≌△BCE(SAS)，∴AD=BE；(2)∵△ACD≌△BCE，∴∠CAD=∠CBE，∵∠BAC+∠ABC=180°-42°=138°，∴∠BAM+∠ABM=∠BAC-∠CAD+∠ABC+∠CBE=∠BAC+∠ABC=138°，∴∠AMB=180°-138°=42°．【点睛】本题考查了全等三角形的判定和性质，三角形内角和，证明三角形全等是解题的关键．【变式训练】1(2023秋·辽宁抚顺·八年级统考期末)如图，已知△ABC中，AB≠AC≠BC．分别以AB、AC为腰在AB左侧、AC右侧作等腰三角形ABD．等腰三角形ACE，连接CD、BE．(1)如图1，当∠BAD=∠CAE=60°时，①△ABD、△ACE的形状是；②求证：BE=DC．(2)若∠BAD=∠CAE≠60°，①如图2，当AB=AD，AC=AE时，BE=DC是否仍然成立？请写出你的结论并说明理由；②如图3，当AB=DB，AC=EC时，BE=DC是否仍然成立？请写出你的结论并说明理由．【答案】(1)①等边三角形；②证明见解析(2)①成立，理由见解析；②不成立，理由见解析【分析】(1)①根据有一个内角是60度的等腰三角形是等边三角形即可求解；②根据等边三角形的性质可得AB=AD，AE=AC，∠DAB=∠CAE=60°，证明△BAE≌△DAC，根据全等三角形的性质即可证明；(2)①证明△BAE≌△DAC，根据全等三角形的性质即可得出结论；②根据已知可得△BAE与△DAC不全等，即可得出结论．【详解】(1)①∵△ABD是等腰三角形，△ACE是等腰三角形，∠BAD=∠CAE=60°∴△ABD、△ACE是等边三角形，故答案为：等边三角形．②证明：∵△ABD、△ACE是等边三角形，∴AB=AD，AE=AC，∠DAB=∠CAE=60°，∵∠DAC=∠DAB+∠BAC，∠BAE=∠CAE+∠BAC，∴∠DAC=∠BAE，在△BAE与△DAC中，∵AB=AD∠BAE=∠DAC AE=AC，∴△BAE≌△DAC SAS．∴BE=DC．(2)①当AB=AD，AE=AC时，成立．理由：如图，∵AB=AD，∠BAE=∠DAC，AE=AC，∴△BAE≌△DAC SAS，∴BE=DC；②当AB=DB，AC=EC时，不成立．理由：如图，∵∠BAD=∠CAE≠60°，∴AB=DB≠AD，AC=EC≠AE，∴△BAE与△DAC不全等，∴BE≠DC．【点睛】本题考查全等三角形的判定与性质，等腰三角形的性质，等边三角形的判定与性质等，熟练掌握全等三角形的判定与性质是解题的关键．2(2023秋·全国·八年级专题练习)定义：顶角相等且顶点重合的两个等腰三角形叫做“同源三角形”，我们称这两个顶角为“同源角”．如图，△ABC 和△CDE 为“同源三角形”，AC =BC ，CD =CE ，∠ACB 与∠DCE 为“同源角”．(1)如图1，△ABC 和△CDE 为“同源三角形”，试判断AD 与BE 的数量关系，并说明理由．(2)如图2，若“同源三角形”△ABC 和△CDE 上的点B ，C ，D 在同一条直线上，且∠ACE =90°，则∠EMD =°．(3)如图3，△ABC 和△CDE 为“同源三角形”，且“同源角”的度数为90°时，分别取AD ，BE 的中点Q ，P ，连接CP ，CQ ，PQ ，试说明△PCQ 是等腰直角三角形．【答案】(1)AD =BE ，详见解析(2)45(3)详见解析【分析】(1)由“同源三角形”的定义可证∠ACD =∠BCE ，然后根据SAS 证明△ACD ≌△BCE 即可；(2)由“同源三角形”的定义和∠ACE =90°可求出∠DCE =ACB =45°，由(1)可知△ACD ≌△BCE ，得∠ADC =∠BEC ，然后根据“8”子三角形即可求出∠EMD 的度数；(3)由(1)可知△ACD ≌△BCE ，可得∠CAQ =∠CBP ，BE =AD ．根据SAS 证明△ACQ ≌△BCP ，可得CQ =CP ，∠ACQ =∠BCP ，进而可证结论成立．【详解】(1)AD =BE ．理由：因为△ABC 和△CDE 是“同源三角形”，所以∠ACB =∠DCE ，所以∠ACD =∠BCE ．在△ACD 和△BCE 中，AC =BC ,∠ACD =∠BCE ,CD =CE ,所以△ACD ≌△BCE SAS ．所以AD =BE ．(2)∵△ABC 和△CDE 是“同源三角形”，∴∠ACB =∠DCE ．∵∠ACE =90°，∴∠DCE =ACB =45°．由(1)可知△ACD ≌△BCE ，∴∠ADC =∠BEC ．∵∠MOE =∠COD ，∴∠EMD =∠DCE =45°．故答案为：45；(3)由(1)可知△ACD ≌△BCE ，所以∠CAQ =∠CBP ，BE =AD ．因为AD ，BE 的中点分别为Q ，P ，所以AQ =BP ．在△ACQ 和△BCP 中，CA =CB ,∠CAQ =∠CBP ,AQ =BP ,所以△ACQ ≌△BCP SAS ，所以CQ =CP ，∠ACQ =∠BCP ．又因为∠BCP +∠PCA =90°，所以∠ACQ +∠PCA =90°．所以∠PCQ =90°，所以△PCQ 是等腰直角三角形．【点睛】本题考查了新定义，全等三角形的判定与性质，等腰直角三角形的判定，三角形内角和定理等知识，熟练掌握全等三角形的判定与性质是解答本题的关键．3(2023春·辽宁丹东·七年级统考期末)(1)如图1，两个等腰三角形△ABC 和△ADE 中，AB =AC ，AD =AE ，∠BAC =∠DAE ，连接BD ，CE ．则△ADB ≌，此时线段BD 和线段CE 的数量关系式；(2)如图2，两个等腰直角三角形△ABC 和△ADE 中，AB =AC ，AD =AE ，∠BAC =∠DAE =90°，连接BD ，CE ，两线交于点P ，请判断线段BD 和线段CE 的关系，并说明理由；(3)如图3，分别以△ABC 的两边AB ，AC 为边向△ABC 外作等边△ABD 和等边△ACE ，连接BE ，CD ，两线交于点P ．请直接写出线段BE 和线段CD 的数量关系及∠PBC +∠PCB 的度数．【答案】(1)△AEC ，BD =CE ；(2)BD =CE 且BD ⊥CE ；(3)CD =BE ，∠PBC +∠PCB =60°【分析】(1)先判断出∠DAB =∠EAC ，进而判断出△ADB ≌△AEC ，即可得出结论；(2)先判断出△DAB ≌△EAC ，得出BD =CE ，∠DBA =∠ECA ，进而判断出∠DBC +∠ECB ，即可得出结论；(3)先判断出△ACD ≌△AEB ，得出CD =BE ，∠ADC =∠ABE ，进而求出∠BPD =60°，最后用三角形外角的性质，即可得出结论．【详解】解：(1)∵∠DAE =∠BAC ，∴∠DAE +∠BAE =∠BAC +∠BAE ．即∠DAB =∠EAC ，在△ADB 和△AEC 中，AD =AE∠DAB =∠EAC AB =AC，∴△ADB ≌△AEC SAS ，∴BD =CE ，故答案为：△AEC ，BD =CE ；(2)BD =CE 且BD ⊥CE ；理由如下：∵∠DAE =∠BAC =90°，∴∠DAE +∠BAE =∠BAC +∠BAE ．即∠DAB =∠EAC ．在△DAB 和△EAC 中，AD =AE∠DAB =∠EAC AB =AC，∴△ADB ≌△AEC SAS ，∴BD =CE ，∠DBA =∠ECA ，∵∠ECA +∠ECB +∠ABC =90°，∴∠DBA +∠ECB +∠ABC =90°，即∠DBC +∠ECB =90°，∴∠BPC =180°-(∠DBC +∠ECB )=90°，∴BD ⊥CE ，综上所述：BD =CE 且BD ⊥CE ；(3)如图3所示，BE =CD ，∠PBC +∠PCB =60°，理由如下：∵△ABD 和△ACE 是等边三角形，∴AD =AB ，AC =AE ，∠ADB =∠ABD =∠BAD =∠CAE =60°，∴∠BAD +∠BAC =∠CAE +∠BAC ，∴∠CAD =∠EAB ，在△ACD 和△AEB 中，AD =AB ∠CAD =∠EAB AC =AE，∴△ACD ≌△AEB (SAS )，∴CD =BE ,∠ADC =∠ABE ，∴∠BPD =180°-∠PBD -∠BDP=180°-∠ABE -∠ABD -∠BDP=180°-∠ABD -∠ABE +∠BDP=180°-∠ABD -∠ADC +∠BDP=180°-∠ABD -∠ADB=60°，∴∠PBC +∠PCB =∠BPD =60°．【点睛】此题是三角形综合题，主要考查了等腰三角形的性质，等腰直角三角形的性质，等边三角形的性质，三角形的内角和定理，三角形外角的性质，判断出△ADB ≌△AEC 是解本题的关键．。

等腰直角三角形旋转的手拉手模型问题
“胡学数学”，陪伴每一天、成长每一天。

每周一到周六晚上9点，不见不散。

每天十分钟，越学越轻松。

—————————————————————
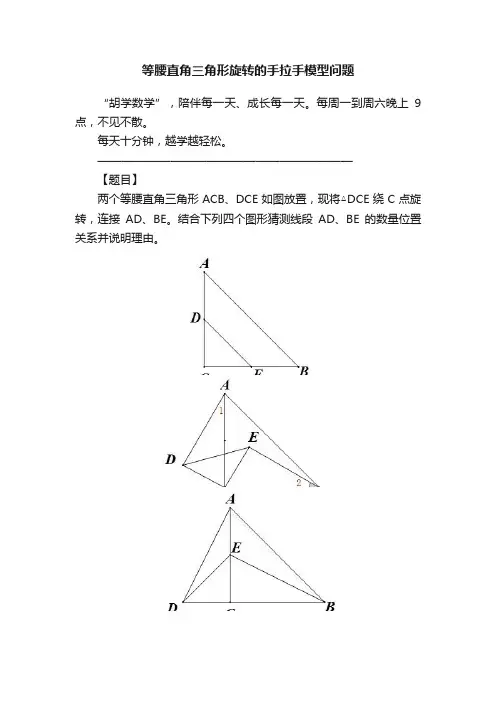
【题目】
两个等腰直角三角形ACB、DCE如图放置，现将△DCE绕C点旋转，连接AD、BE。

结合下列四个图形猜测线段AD、BE的数量位置关系并说明理由。

—————————————————————
分析：首先分类，三种情况，根据等腰得两组边相等，根据旋转得两边夹角相等，用SAS判定全等（手拉手全等模型）得AD=BE。

利用三角形全等得对应角相等结合对顶角相等，三角形中另一角也相等，（蝴蝶形证垂直）从而证出AD⊥BE。

证垂直还可以利用等腰等量代换，深层为方程思想
—————————————————————
手拉手全等模型:
蝴蝶形证垂直：
等量代换证垂直：
—————————————————————
—————————————————————
后两种同理，体会此模型中的两种方法和旋转变换中的不变性—————————————————————。

初中几何经典模型总结（手拉手模型）展开全文模型可以让同学更快的进入到几何之中，产生兴趣。

也是近来学习初中几何不可或缺的一种重要方法。

下面给大家介绍一种经典几何模型---手拉手模型，这也是历年数学中考常考的几何压轴题型之一。

手拉手模型的概念:1、手的判别：判断左右：将等腰三角形顶角顶点朝上，正对读者，读者左边为左手顶点，右边为右手顶点。

2、手拉手模型的定义：定义: 两个顶角相等且有共顶点的等腰三角形形成的图形。

（左手拉左手，右手拉右手）例如：3、手拉手模型的重要结论三个固定结论:结论1:△ABC≌△AB'C'(SAS)BC=B'C'（左手拉左手等于右手拉右手）结论2：∠BOB'=∠BAB'（用四点共圆证明）结论3: AO平分∠BOC'（用四点共圆证明）例题解析：类型一共顶点的等腰直角三角形中的手拉手例1：已知：如图△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°．求证：BD=CE．分析：要证BD=CE可转化为证明△BAE≌△CAD，由已知可证AB=AC，AE=AD，∠BAC=∠EAD=90°，因为∠BAC ∠CAE=∠EAD ∠CAE，即可证∠BAE=∠CAD，符合SAS，即得证．解答：证明：∵△ABC与△AED均为等腰直角三角形，∴AB=AC，AE=AD，∠BAC=∠EAD=90°，∴∠BAC ∠CAE=∠EAD ∠CAE，即∠BAE=∠CAD，在△BAE与△CAD中，AB=AC,∠BAE=∠CAD，AE=AD∴△BAE≌△CAD（SAS），∴BD=CE．类型二共顶点的等边三角形中的手拉手例2：图1、图2中，点B为线段AE上一点，△ABC与△BED都是等边三角形。

(1)如图1，求证：AD=CE；(2)如图2，设CE与AD交于点F，连接BF.①求证：∠CFA=60°；②求证：CF BF=AF.分析：（1）如图1，利用等边三角形性质得：BD=BE，AB=BC，∠ABC=∠DBE=60°，再证∠ABD=∠CBE，根据SAS证明△ABD≌△CBE 得出结论；（2）①如图2，利用（1）中的全等得：∠BCE=∠DAB，根据两次运用外角定理可得结论；②如图3，作辅助线，截取FG=CF，连接CG，证明△CFG是等边三角形，并证明△ACG≌△BCF，由线段的和得出结论．解答：证明：(1)如图1，∵△ABC与△BED都是等边三角形，∴BD=BE,AB=BC,∠ABC=∠DBE=60°，∴∠ABC ∠CBD=∠DBE ∠CBD，即∠ABD=∠CBE，在△ABD和△CBE中，AB=AC∠ABD=∠CBEBD=BE，∴△ABD≌△CBE(SAS)，∴AD=CE，(2)①如图2,由(1)得：△ABD≌△CBE，∴∠BCE=∠DAB，∵∠ABC=∠BCE ∠CEB=60°，∴∠ABC=∠DAB ∠CEB=60°，∵∠CFA=∠DAB ∠CEB，∴∠CFA=60°，②如图3,在AF上取一点G,使FG=CF,连接CG,∵∠AFC=60°，∴△CGF是等边三角形，∴∠GCF=60°，CG=CF，∴∠GCB ∠BCE=60°，∵∠ACB=60°，∴∠ACG ∠GCB=60°，∴∠ACG=∠BCE，∵AC=BC，∴△ACG≌△BCF，∴AG=BF，∵AF=AG GF，∴AF=BF CF.类型三共顶点正方形中的手拉手例3：如图，两个正方形ABCD与DEFG,连结CE、AG,二者相交于点H。

等腰直角三角形手拉手的旋转例：已知，在△ABC 中，∠BAC=90°，AB=AC,点D 在直线BC 上一动点（点D 不与B 、C 重合），以AD 为边作正方形ADEF ，连接CF ，如图，当点D 在线段BC 上时，求证：（1）CF=BD;（2）CF ⊥BD;分析：根据等腰直角三角形的性质求出∠ABC=∠ACB=45°，正方形的性质可得AD=AF, ∠DAF=90°,然后利用同角的余角相等求出∠BAD=∠CAF ，再利用“边角边”证明△ABD 和△ACF 全等，根据全等三角形对应边相等可得CF=BD ，全等三角形的对应角相等可得∠ACF=∠ABD ，然后求出∠BCF==90°,再根据垂直的定义证明即可.证明：（1）∵∠BAC=90°，AB=AC ，∴∠ABC=∠ACB=45°,∵四边形ADEF 是正方形，∴AD=AF,∠DAF==90°，∵∠BAD+∠CAD=∠BAC=90°，∠CAF+∠CAD=∠DAF=90°，∴∠BAD=∠CAF,在△ABD 和△ACF 中，AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△ACF ，所以CF=BD.（2）∠ACF=∠ABD,∴∠BCF=∠ACB+∠ACF=45°+45°=90°，∴CF ⊥BD;总结：（1）两个相似的共直角顶点的等腰直角三角形，旋转所形成的全等三角形相对孤立的边的关系是垂直且相等，如图，△BCD ≌△ECA ，则AE=BD.AE ⊥BD,（2）延伸：两个共顶点的全等三角形旋转90°时，对应的孤立边的位置关系是垂直且相等,如图，BC=DE.BC⊥DE.练习：1.如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD于点F,BD 分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由2.如图,已知F是正方形ABCD中BC边上一点,延长AB到E,使得BE=BF,试用旋转的性质说明:AF=CE且AF⊥CE.3.(1)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.①当点D在AC上时,如下面图1,线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;②将下面图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如下面图2,线段BD、CE 有怎样的数量关系和位置关系?请说明理由.(2)当△ABC和△ADE满足下面甲、乙丙中的哪个条件时,使线段BD、CE在(1)中的位置关系仍然成立?不必说明理由.甲:AB︰AC=AD︰AE=1,∠BAC=∠DAE≠90°;乙:AB︰AC=AD︰AE≠1,∠BAC=∠DAE=90°;丙:AB︰AC=AD︰AE≠1,∠BAC=∠DAE≠90°.1.2100027377分析：由于条件可知CD=AC，BC=CE，且可求得∠ACE=∠DCB，所以△ACE≌△DCB，即AE=BD，∠CAE=∠CDB；又因为对顶角相等即∠AFC=∠DFH，所以∠DHF=∠ACD=90°，即AE⊥BD．解：猜测AE=BD，AE⊥BD；理由如下：∵∠ACD=∠BCE=90°，∴∠ACD+∠DCE=∠BCE+∠DCE，即∠ACE=∠DCB，又∵△ACD和△BCE都是等腰直角三角形，∴AC=CD，CE=CB，在△ACE 与△DCB 中，AC DC ACE DCB EC BC =⎧⎪∠=∠⎨⎪=⎩∴△ACE ≌△DCB(SAS)，∴AE=BD ，∠CAE=∠CDB ；∵∠AFC=∠DFH ，∠FAC+∠AFC=90°，∴∠DHF=∠ACD=90°，∴AE ⊥BD ． 2.3. 分析：（1）①BD=CE ，BD ⊥CE ．根据全等三角形的判定定理SAS 推知△ABD ≌△ACE ，然后由全等三角形的对应边相等证得BD=CE 、对应角相等∠ABF=∠ECA ；然后在△ABD 和△CDF 中，由三角形内角和定理可以求得∠CFD=90°，即BD ⊥CF ；②BD=CE ，BD ⊥CE ．根据全等三角形的判定定理SAS 推知△ABD ≌△ACE ，然后由全等三角形的对应边相等证得BD=CE 、对应角相等∠ABF=∠ECA ；作辅助线（延长BD 交AC 于F ，交CE 于H ）BH 构建对顶角∠ABF=∠HCF ，再根据三角形内角和定理证得∠BHC=90°；（2）根据结论①、②的证明过程知，∠BAC=∠DFC （或∠FHC=90°）时，该结论成立了，所以本条件中的∠BAC=∠DAE≠90°不合适．解：（1）①结论：BD=CE ，BD ⊥CE ；②结论：BD=CE ，BD ⊥CE…1分理由如下：∵∠BAC=∠DAE=90°∴∠BAC-∠DAC=∠DAE-∠DAC ，即∠BAD=∠CAE∵AB=AC ，AD=AE ，∴△ABD ≌△ACE （SAS ）.∴BD=CE ，延长BD交AC于F，交CE于H．在△ABF与△HCF中，∵∠ABF=∠HCF，∠AFB=∠HFC∴∠CHF=∠BAF=90°∴BD⊥CE.（2）结论：乙．AB：AC=AD：AE，∠BAC=∠DAE=90°。

当点E在点C处时,CF=AC.当点E在点A处时,点F与点C重合.
故点F所经过的路径的长为3.
(3)取BC的中点H,当点M不与点D重合时,连接HN,
1
1
则BH= BC,∴BH= AB.
2
2
1
∵CD⊥AB,CA=CB,∴BD= AB,∴BH=BD.
2
重难·微专项6 “手拉手”模型
专项训练
∵△ABC,△BMN是等边三角形,
B的运动过程中,小亮以B为顶点作正方形BFGH,其中点F,G都在直线
AE上,如图(4).当点E到达点B时,点F,G,H与点B重合.则点H所经过的
路径长为
,点G所经过的路径长为
.
重难·微专项6 “手拉手”模型
专项训练
解:(1)∵△ABC,△BEF是等边三角形,
∴BA=BC,BE=BF,∠ABC=∠EBF=60°,
【答题关键点】
①当点P与点F重合时,可知AC垂直平分PE,结合点P
在△ABC的角平分线BD上,可知BP=PC,再结合三角函数即可求出BP
的长.
重难·微专项6 “手拉手”模型
例题
②连接AF,可证得BP∥EF,再由△BCP≌△ACE,可得△AFE为等边三
角形,进而可证得BP=EF,即可得证.
图(1)
图(2)
∴∠DCQ=∠BCE,CQ=CE.
∵∠PCB+∠QCD=∠PCQ,
∴∠PCB+∠BCE=∠PCQ=∠PCE.
重难·微专项6 “手拉手”模型
专项训练
= ,
在△QCP和△ECP中,ቐ∠ = ∠,
= ,
∴△QCP≌△ECP(SAS),
∴PQ=PE,
∴△APQ的周长=AQ+PQ+AP=AQ+PE+ AP=

E
F
B
A
2 ．如图，△ ABD 与△ BCE 都为等边三角形，连接 AE 与 CD ，延长 AE 交 CD 于点H ．
证明：（ 1 ） AE=DC ；（ 2 ）∠ AHD=60 °；（ 3 ）连接 HB ， HB 平分∠ AHC
D H C
E
A
B
3 ．将等腰 Rt △ ABC 和等腰 Rt △ ADE 按图①方式放置，∠ A=90 °， AD 边与 AB 边重合， AB=2AD=4 。将△ ADE 绕点 A 逆时针方向旋转一个角度 （ 0 ° < >180 °）， BD 的延长线交 CE 于P
初中数学常见模型
手拉手模型
模型：手拉手
如图，△ ABC 、△ ADE 是等腰三角形，AB=AC ,AD=AE ,∠ BAC= ∠ DAE=α
结论：△ BAD ≌ △ CAE
模型分析
A
E
D
B
C
图1
A E
D
E A
D
B
C
图2
B
图3
C
手拉手模型常和旋转结合，在考试中作为几何综合题目出现
模型实例
例 1.如图，△ ADC 与△ GDB 都为等腰直角三角形，连接 AG 、 CB ，相交于点 H ，
（ 5 ）△ EGB ≌ △ CFB ；（ 6 ）连接 GF ， GF ∥ AC ；（ 7 ）连接 HB ， HB 平分∠ AHC
D G
HE F
A
B
C
（ 1 ）如图②，证明： BD=CE ， BD ⊥ CE ； （ 2 ）如图③，在旋转的过程中，当 AD ⊥ BD 时，求出 CP 的长。
B
B
D
D

手拉手模型，巧妙解决数学题！
以微课堂
公益课堂，奥数国家级教练
与四位特级教师联手执教。

构造手拉手模型巧妙解题的方法思路
我们已经知道全等型手拉手模型有以下三个特征：共顶点、双等腰、顶角相等。

一个核心巧记结论：左手拉左手=右手拉右手
判断左右手：将等腰三角形顶角顶点朝上，正对读者，读者左边为左手顶点，右边为右手顶点。

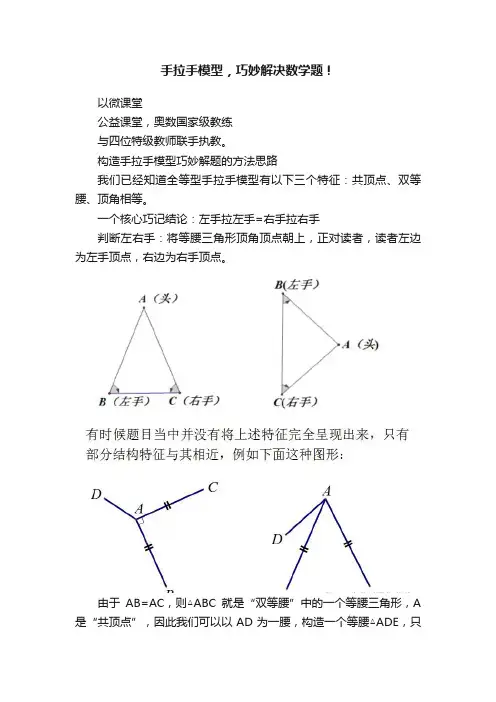
由于AB=AC，则△ABC就是“双等腰”中的一个等腰三角形，A 是“共顶点”，因此我们可以以AD为一腰，构造一个等腰△ADE，只
要∠DAE=∠BAC就符合手拉手模型了，如图：
注意：上图中在△ABC中，B是“左手”，C是“右手”，以AD
为一腰构造等腰三角形时，在AD两侧都可以构造，也就是D可以作“左手”，也可以作“右手”，具体选择那一侧要根据实际需要去选取，记住：左手拉左手=右手拉右手.
①中：△ADB≌△AEC，DB=EC；
②中：△ADC≌△AEB，DC=EB；
③中：△ADB≌△AEC，DB=EC；
④中：△ADC≌△AEB，DC=EB.
构造好手拉手模型以后，我们再根据模型的结论去解题，就轻松多了！
下面通过例题来分析讲解。

【分析】直接求CD的最大值显然不现实，所以我们要将线段CD 进行转化，可以通过构造“手拉手模型”来实现线段的转化。

△BAD
是等腰直角三角形，D是“左手”，A是“右手”，B是“共顶点”，可以以BC为一腰构造等腰直角三角形，由于D是“左手”，所以C 必须也是“左手”，因此只有如图所示一种构造方式，才能满足“左手拉左手，右手拉右手”.
《以微课堂》，由江苏省数学名师、数学奥林匹克国家一级教练
员，联手四名特级教师共同打造。

等腰直角三角形与正方形手拉手例：已知，在△ABC中，∠BAC=90°，AB=AC,点D在直线BC上一动点（点D不与B、C重合），以AD为边作正方形ADEF，连接CF，（1）如图1，当点D在线段BC上时，求证：①CF=BD;②CF⊥BD;（2）如图2，当点D在线段BC的延长线上时，其他条件不变，线段CF与BD的上述关系是否还成立？请直接写出结论即可（不必证明）；（3）如图3，当点D在线段的反向延长线上，且点A、F在直线BC的两端，其他条件不变，线段CF与BD的上述关系是否还成立？若成立，请证明你的结论；若不成立，请说明理由.分析：（1）根据等腰直角三角形的性质求出∠ABC=∠ACB=45°，正方形的性质可得AD=AF, ∠DAF=90°,然后利用同角的余角相等求出∠BAD=∠CAF，再利用“边角边”证明△ABD和△ACF全等，根据全等三角形对应边相等可得CF=BD，全等三角形的对应角相等可得∠ACF=∠ABD，然后求出∠BCF==90°,再根据垂直的定义证明即可；（2）结论仍然成立；（3）同（1）可证△ABD和△ACF全等，根据全等三角形对应边相等可得CF=BD，全等三角形对应角相等可得∠ACF=∠ABD=135°，然后求出∠BCF=90°，再根据垂直的定义证明即可.解：（1）∵∠BAC=90°，AB=AC，∴∠ABC=∠ACB=45°,∵四边形ADEF是正方形，∴AD=AF,∠DAF==90°，∵∠BAD+∠CAD=∠BAC=90°，∠CAF+∠CAD=∠DAF=90°，∴∠BAD=∠CAF,在△ABD和△ACF中，AB ACBAD CAF AD AF=⎧⎪∠=∠⎨⎪=⎩，∴△ABD≌△ACF，所以①CF=BD，∠ACF=∠ABD, ∴∠BCF=∠ACB+∠ACF=45°+45°=90°，∴②CF⊥BD;（2）当点D在线段延长线上时，线段CF与BD的上述关系仍然成立；（3）当点D在线段BC的反向延长线上，且点A、F在直线BC的两侧，线段CF与BD的上述关系仍然成立.理由：同理可证，△ABD≌△ACF，∴CF=BD，∠ACF=∠ABD=180°-45°=135°，∵∠ACB=45°，∴∠BCF=∠ACF-∠ACB=135°-45°=90°，∴CF⊥BD.总结：两个等腰直角三角形共直角顶点为手拉手模型之一，如图，其中有等腰直角三角形和正方形共直角顶点，相当于两个等腰直角三角形“手拉手”，因为正方形其中一个对角线与两边就可形成等腰直角三角形，所以有全等三角形及其性质的应用练习：在△ABC中，AB=AC，∠BAC=90︒，点D在射线BC上（与B、C两点不重合），以AD为边作正方形ADEF，使点E与点B在直线AD的异侧，射线BA与射线CF相交于点G．（1）若点D在线段BC上，如图1.①依题意补全图1；②判断BC与CG的数量关系与位置关系，并加以证明；（2）若点D在线段BC的延长线上，且G为CF中点，连接GE，AB2，则GE的长为_______，并简述求GE长的思路．图1 备用图解:(1) ①补全图形，如图1所示．图1②BC 和CG 的数量关系：BC CG =，位置关系：BC CG ⊥．证明: 如图1．∵︒=∠=90,BAC AC AB ，∴︒=∠=∠45ACB B ，︒=∠+∠9021．∵射线BA 、CF 的延长线相交于点G ，∴︒=∠=∠90BAC CAG ．∵四边形ADEF 为正方形，∴︒=∠+∠=∠9032DAF ，AF AD =．∴31∠=∠．∴△ABD ≌△ACF ．∴︒=∠=∠45ACF B ．∴45B G ∠=∠=︒，90BCG ∠=︒．∴BC CG =，BC CG ⊥． (2) 10GE =思路如下：a . 由G 为CF 中点画出图形，如图2所示．b . 与②同理，可得BD=CF ，BC CG =，BC CG ⊥；c . 由2=AB ，G 为CF 中点，可得2====CD FG CG BC ；d . 过点A 作AM BD ⊥于M ，过点E 作EN FG ⊥于N ，可证△AMD ≌△FNE ，可得1AM FN ==，NE 为FG 的垂直平分线，FE EG =；e . 在Rt △AMD 中，1AM =，3MD =，可得10AD =10GE FE AD ===。

等腰直角三角形手拉手模型的补全例：如图1，在△ABC 中，CA =CB ，∠ACB =90°，D 是△ABC 内部一点，∠ADC =135°，将线段CD 绕点C 逆时针旋转90°得到线段CE ，连接DE ．（1）① 依题意补全图形；② 请判断∠ADC 和∠CDE 之间的数量关系，并直接写出答案．（2）在（1）的条件下，连接BE ，过点C 作CM ⊥DE ，请判断线段CM ，AE 和BE 之间的数量关系，并说明理由．（3）如图2，在正方形ABCD 中，AB =2，如果PD =1，∠BPD =90°，请直接写出点A 到BP 的距离． DA B C PDC A B图1 图2分析：（1）②∠ADC +∠CDE =180°．根据旋转的性质即可解答（2）根据旋转的性质，可证明A 、D 、E 三点在同一条直线上，得到AE=AD+DE ，再根据旋转，实质得到两个等腰直角三角形手牵手相似，则可证明△ACD≌△BCE，得到AD=BE ，又CD=CE,∠DCE=90°，CM⊥DE，得到DE=2CM ，∴AE=BE+2CM.（3）作AF⊥BP 于F ，此图可看成不完整的等腰直角三角形手牵手，则相当于△ADP 绕点A 顺时针旋转90°，∴作AH⊥BP 于H ，如图，形成三角形△ABD 和△AHP 手牵手，∴△ABH≌△ADP，∴BP=BH+HP=PD+2AF，在Rt△BPD 中借助勾股定理可得31AF -=解：（1）① 依题意补全图形（如下图）；② ∠ADC+∠CDE=180°．（2）线段CM，AE和BE之间的数量关系是AE=BE+2CM，理由如下：∵ 线段CD绕点C逆时针旋转90°得到线段CE，∴ CD=CE，∠DCE=90°．∴ ∠CDE=∠CED=45°．又∵ ∠ADC=135°，∴ ∠ADC+∠CDE=180°，∴ A、D、E三点在同一条直线上.∴ AE=AD+DE.又∵ ∠ACB=90°，∴ ∠ACB－∠DCB=∠DCE－∠DCB，即∠ACD=∠BCE．又∵ AC=BC，CD=CE，∴ △ACD≌△BCE．∴ AD=BE．∵ CD=CE，∠DCE=90°，CM⊥DE．∴ DE=2CM．∴ AE=BE+2CM．（3）点A到BP的距离为312．总结：在等腰直角三角形顶角顶点的基础上，出现了一个利用腰形成的三角形时，往往借助等线段、共端点考虑用旋转的思路构造此三角形旋转90°利用等腰三角形另一腰形成三角形解决问题练习：（1）问题发现：如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．填空：①∠AEB的度数为_______；②线段AD、BE之间的数量关系为______________．（2）拓展探究如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段AM、AE、BE之间的数量关系，并说明理由．（3）解决问题在正方形ABCD中，CD=2，若点P满足PD=1，且∠BPD=90°，请直接写出点A到BP的距离．。

【中考专题】『手拉手模型』，经典结论大总结手拉手模型大家都非常熟悉了，今天我们为大家整理归类常见的手拉手模型的构造及相关结论1.左右手的判别：顶点朝上，左边顶点为左手，右边顶点为右手2.手拉手模型图两个顶点相等且共顶点的等腰三角形手拉手（左手拉左手，右手拉右手）3.手拉手经典结论①△ABD≌△ACE②BD=CE，且夹角等于∠BAC（或其补角）③AO平分∠BOE（或其外角）证明：①∵AB=AC,AD=AE且∠BAD=∠BAC+∠DAC=∠EAD+∠DAC=∠CAE∴△ABD≌△ACE（SAS）②∵△ABD≌△ACE（SAS）∴BD=CE，∠BDA =∠CEA∵∠BDA +∠DOE =∠CEA+∠DAE∴∠DOE=∠DAE=∠BAC③∵△ABD≌△ACE（SAS）∴底边BD=CE，△ABD与△ACE面积相等；∴高：A到BD距离=A到CE的距离∴AO平分∠BOE怎么样，坚持看到了这里相信你已经完全掌握了吧接下来，一道亮点颇多的题目送给你们希望大家做的开心愉快模型一△ABC为等边三角形，∠BPC=120°结论：PB+PC=PA证明方法图：证明：延长PC至D，使得CD=BP、∠ABP＋∠ACP＝180º,∠ACD＋∠ACP ＝180º,可得∠ABP＝∠ACD可得△ABP≌△ACD则△APD为等边三角形则PC+PB=PC+CD=PA模型二：△ABC为等腰直角三角形，∠BPC=90°结论：PB+PC=√2PA证明方法图：（证明过程略）模型三△ABC为顶角为120°的等腰三角形，∠BPC=60°结论：PB+PC=√3PA证明方法图：（证明过程略）模型四△ABC为等腰直角三角形，∠BPC=90°结论：PB-PC=√2PA证明方法图：（证明过程略）模型五：△ABC为等边三角形，∠BPC=150°结论：PB^2+PC^2=PA^2证明方法图：（证明过程略）模型六：△ABC为等腰直角三角形，∠BPC=135°结论：PB^2+2PC^2=PA^2证明方法图：（证明过程略）看完了这些是不是蠢蠢欲动了让我们一起创造手拉手拯救“单身狗”吧例题：（1）如图1，点P是等边三角形ABC内的一点，PA=4，PB=3，PC=5，求∠BPA．（2）如图2，点P是正方形ABCD内的一点，PA=3，PB=2√2，PC=5，求∠BPA．。

等腰直角三角形手拉手模型的补全例：如图1，在△ABC 中，CA =CB ，∠ACB =90°，D 是△ABC 内部一点，∠ADC =135°，将线段CD 绕点C 逆时针旋转90°得到线段CE ，连接DE ．（1）① 依题意补全图形；② 请判断∠ADC 和∠CDE 之间的数量关系，并直接写出答案．（2）在（1）的条件下，连接BE ，过点C 作CM ⊥DE ，请判断线段CM ，AE 和BE 之间的数量关系，并说明理由．（3）如图2，在正方形ABCD 中，ABPD =1，∠BPD =90°，请直接写出点A 到BP 的距离． DA B C PDC A B图1 图2分析：（1）②∠ADC +∠CDE =180°．根据旋转的性质即可解答（2）根据旋转的性质，可证明A 、D 、E 三点在同一条直线上，得到AE=AD+DE ，再根据旋转，实质得到两个等腰直角三角形手牵手相似，则可证明△ACD≌△BCE，得到AD=BE ，又CD=CE,∠DCE=90°，CM⊥DE，得到DE=2CM ，∴AE=BE+2CM.（3）作AF⊥BP 于F ，此图可看成不完整的等腰直角三角形手牵手，则相当于△ADP 绕点A 顺时针旋转90°，∴作AH⊥BP于H ，如图，形成三角形△ABD 和△AHP 手牵手，∴△ABH≌△ADP，∴BP=BH+HP=PD+2AF，在Rt△BPD 中借助勾股定理可得AF =解：（1）① 依题意补全图形（如下图）；② ∠ADC+∠CDE=180°．（2）线段CM，AE和BE之间的数量关系是AE=BE+2CM，理由如下：∵ 线段CD绕点C逆时针旋转90°得到线段CE，∴ CD=CE，∠DCE=90°．∴ ∠CDE=∠CED=45°．又∵ ∠ADC=135°，∴ ∠ADC+∠CDE=180°，∴ A、D、E三点在同一条直线上.∴ AE=AD+DE.又∵ ∠ACB=90°，∴ ∠ACB－∠DCB=∠DCE－∠DCB，即∠ACD=∠BCE．又∵ AC=BC，CD=CE，∴ △ACD≌△BCE．∴ AD=BE．∵ CD=CE，∠DCE=90°，CM⊥DE．∴ DE=2CM．∴ AE=BE+2CM．（3）点A到BP．总结：在等腰直角三角形顶角顶点的基础上，出现了一个利用腰形成的三角形时，往往借助等线段、共端点考虑用旋转的思路构造此三角形旋转90°利用等腰三角形另一腰形成三角形解决问题练习：（1）问题发现：如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．填空：①∠AEB的度数为_______；②线段AD、BE之间的数量关系为______________．（2）拓展探究如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段AM、AE、BE之间的数量关系，并说明理由．（3）解决问题在正方形ABCD中，，若点P满足PD=1，且∠BPD=90°，请直接写出点A到BP的距离．。

初中数学经典几何模型专题05 手拉手模型构造全等三角形【专题说明】两个具有公共顶点的相似多边形，在绕着公共顶点旋转的过程中，产生伴随的全等或相似三角形，这样的图形称作共点旋转模型；为了更加直观，我们形象的称其为“手拉手”模型。

【知识总结】【基本模型】一、等边三角形手拉手-出全等图1 图2图3 图4二、等腰直角三角形手拉手-出全等两个共直角顶点的等腰直角三角形，绕点C旋转过程中（B、C、D不共线）始终有①△BCD≌△ACE；②BD⊥AE（位置关系）且BD=AE（数量关系）；③FC平分∠BFE；图1图2图3图41、如图，点C在线段AB上，△DAC和△DBE都是等边三角形，求证：△DAB≌△DCE;DA∥EC.2、已知：△ACB和△DCE都是等腰直角三角形，∠ACB=∠DCE=90°，连结AE,BD交于点O,AE与DC交于点0，AE与DC交于点M,BD与AC交于点N.3、已知，在△ABC中，AB＝AC，点P平面内一点，将AP绕A顺时针旋转至AQ，使∠QAP＝∠BAC，连接BQ、CP，⑴若点P在△ABC内部，求证BQ＝CP；⑵若点P在△ABC外部，以上结论还成立吗？4、如图，点G是正方形ABCD对角线CA的延长线上任意一点，以线段AG为边作一个正方形AEFG，线段EB和GD相交于点H.若AB=√2，AG=1，则EB=________________.5、已知正方形ABCD和正方形AEFG有一个公共点，点G、E分别在线段AD、AB上，若将正方形AEFG 绕点A按顺时针方向旋转，连接DG,在旋转的过程中，你能否找到一条线段的长与线段DG的长度始终相等？并说明理由。

6、已知：如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC,AD=AE,点C、D、E三点在同一直线上，连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠BDC=45°；④BE2=2(AD2+AB2)其中结论正确的个数是_______【基础训练】1、已知△ABC为等边三角形，点D为直线BC上一动点（点D不与点B,点C重合）.以AD为边作等边三角形ADE,连接CE.如图1，当点D在边BC上时，求证：△ABD≌△ACE;直接判断结论BC=DC+CE是否成立（不需要证明）；如图2，当点D在边BC的延长线上时，其他条件不变，请写出BC、DC、CE之间存在的数量关系，并写出证明过程.2、如图，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点.若DE=13，BD=12，求线段AB的长.3、如图，点A、B、C在一条直线上，△ABD,△BCE均为等边三角形，连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q，连接PQ,BM.下面结论：△ABE≌△DBC;∠DMA=60°；△BPQ为等边三角形；MB平分∠AMC.其中正确的有____________4、如图1，CA=CB,CD=CE,∠ACB=∠DCE=α，AD、BE相交于点M,连接CM.求证：BE=AD;用含α的式子表示∠AMB的度数；当α=90°时，取AD、BE的中点分别为点P、Q，连接CP,CQ,PQ,如图2，判断△CPQ的形状，并加以证明.【巩固提升】1、已知△ABC和△BDE都是等腰直角三角形，∠ACB＝∠BED＝90°，AB＝2BD，连接CE．（1）如图1，若点D在AB边上，点F是CE的中点，连接BF．当AC＝4时，求BF的长；（2）如图2，将图1中的△BDE绕点B按顺时针方向旋转，使点D在△ABC的内部，连接AD，取AD 的中点M，连接EM并延长至点N，使MN＝EM，连接CN．求证：CN⊥CE．2、如图，△ABC中AB＝AC＝5，tan∠ACB＝，点D为边BC上的一动点（不与点B、C重合），将线段AD绕点A顺时针旋转得AE，使∠DAE＝∠BAC，DE与AB交于点F，连接BE．（1）求BC的长；（2）求证∠ABE＝∠ABC；（3）当FB＝FE时，求CD的长．3、如图1，在△ABC中，∠ACB＝90°，AC＝BC，D为AB上一点，连接CD，将CD绕点C顺时针旋转90°至CE，连接AE．（1）求证：△BCD≌△ACE；（2）如图2，连接ED，若CD＝2，AE＝1，求AB的长；（3）如图3，若点F为AD的中点，分别连接EB和CF，求证：CF⊥EB．4、如图，△ABC和△EDC都是等腰直角三角形，C为它们的公共直角顶点，连接AD、BE，点F为线段AD的中点，连接CF．（1）如图1，当D点在BC上时，试判断线段BE、CF的关系，并证明你的结论；（2）如图2，把△DEC绕C点顺时针旋转一个锐角，其他条件不变时，请探究BE、CF的关系并直接写出结论．5、如图1，在△ABC中，AB＝AC，∠BAC＝90°，D、E分别是AB、AC边的中点．将△ABC绕点A顺时针旋转a角（0°＜a＜180°），得到△AB′C′（如图2），连接DB'，EC'．（1）探究DB'与EC'的数量关系，并结合图2给予证明；（2）填空：①当旋转角α的度数为时，则DB'∥AE；②在旋转过程中，当点B'，D，E在一条直线上，且AD＝时，此时EC′的长为．6、如图，∠AOB＝120°，OC平分∠AOB，∠MCN＝60°，CM与射线OA相交于M点，CN与直线BO相交于N点．把∠MCN绕着点C旋转．（1）如图1，当点N在射线OB上时，求证：OC＝OM+ON；（2）如图2，当点N在射线OB的反向延长线上时，OC与OM，ON之间的数量关系是（直接写出结论，不必证明）专题05 手拉手模型构造全等三角形答案【专题说明】两个具有公共顶点的相似多边形，在绕着公共顶点旋转的过程中，产生伴随的全等或相似三角形，这样的图形称作共点旋转模型；为了更加直观，我们形象的称其为“手拉手”模型。

初中数学几何模型之——手拉手模型，跟我学-应对中考轻松自
如
一、模型一：手拉手模型----旋转型全等
（1）等边三角形
手拉手-等边旋转
【条件】：△OAB和△OCD均为等边三角形；
【结论】：①△OAC≌△OBD；②∠AEB=60°；③OE平分∠AED
（2）等腰直角三角形
手拉手-等腰直角旋转
【条件】：△OAB和△OCD均为等腰直角三角形；
【结论】：①△OAC≌△OBD；②∠AEB=90°；③OE平分∠AED
（3）顶角相等的两任意等腰三角形
手拉手-等腰旋转
【条件】：△OAB和△OCD均为等腰三角形；且∠COD=∠AOB
【结论】：①△OAC≌△OBD；②∠AEB=∠AOB；③OE平分∠AED
二、模型二：手拉手模型----旋转型相似
（1）一般情况
【条件】：CD∥AB，将△OCD旋转至右图的位置
【结论】：①右图中△OCD∽△OAB→→→△OAC∽△OBD；
②延长AC交BD于点E，必有∠BEC=∠BOA
（2）特殊情况
【条件】：CD∥AB，∠AOB=90° 将△OCD旋转至右图的位置
【结论】：①右图中△OCD∽△OAB→→→△OAC∽△OBD；
②延长AC交BD于点E，必有∠BEC=∠BOA；
③BD/AC=OD/OC=OB/OA=tan∠OCD；
④BD⊥AC；
⑤连接AD、BC，必有AD2+BC2=AB2+CD2；
⑥S△BCD=1/2AC×BD。