实验七：离散系统的Z域分析

当 z > a 时，这是无穷递缩等比级数。
1 z X ( z) = 此时， = 1 − az −1 z − a
z > a 收敛域：
0
j Im[ z ]
a
*收敛域一定在模最大的极点 所在的圆外。
Re[ z ]
信号与系统
第7章 离散时间信号与系统的z域分析
13 /82
3.左边指数序列 x(n) = −b nu (−n − 1)
的形式 ，其中x2+Ax+B是实数范围内的不可约 多项式，而且k是正整数。这时称各分式为原 分式的“部分分式”。
信号与系统
第7章 离散时间信号与系统的z域分析
19 /82
M X ( z ) 通常， 可表成有理分式形式： b z −i ∑ i B( z ) = i =0N X ( z) = A( z ) 1 + ∑ ai z −i
z −n < ∞
n1 ≤ n ≤ n2 ;
信号与系统
第7章 离散时间信号与系统的z域分析
7 /82
因此，当时，只要，则 n= z − n 1/ z n , ≥0 同样，当时，只要，则 n <= 0 z z ,
n −n
z≠0 z≠∞ z
z −n < ∞
−n
<∞
所以收敛域至少包含，也就是除 0< z <∞ “有限平面” z= (0, ∞) z 。 ∞外的开域，即所谓
9 /82
(3)左边序列
x(n), n ≤ n2 x ( n) = n > n2 0,
X ( z)
n = −∞
= x ( n) z ∑ ∑ x ( n) z
−n n = −∞
n2

数字信号处理实验报告实验名称：离散系统的Z 域分析学号：姓名： 评语： 成绩： 一、实验目的1、掌握离散序列z 变换的计算方法。

2、掌握离散系统系统函数零极点的计算方法和零极点图的绘制方法，并能根据零极点图分析系统的因果性和稳定性。

3、掌握利用MATLAB 进行z 反变换的计算方法。

二、实验原理与计算方法1、z 变换离散序列x (n )的z 变换定义为：。

∑∞-∞=-=n n z n x Z X )()(在MATLAB 中可以利用符号表达式计算一个因果序列的z 变换。

其命令格式为：syms n; f=(1/2)^n+(1/3)^n;ztrans(f)2、离散系统的系统函数及因果稳定的系统应满足的条件一个线性移不变离散系统可以用它的单位抽样响应h (n )来表示其输入与输出关系，即y (n )= x (n )* h (n )对该式两边取z 变换，得： Y (z )= X (z )· H (z )则： )()()(z X z Y z H =将H (z )定义为系统函数，它是单位抽样响应h (n )的z 变换，即∑∞-∞=-==n n z n h n h Z z H )()]([)(对于线性移不变系统，若n <0时，h (n )=0，则系统为因果系统；若，则系统稳∞<∑∞-∞=n n h |)(|定。

由于h (n )为因果序列，所以H (z )的收敛域为收敛圆外部区域，因此H (z )的收敛域为收敛圆外部区域时，系统为因果系统。

因为，若z =1时H (z )收敛，即∑∞-∞=-=n n z n h z H )()(，则系统稳定，即H(z)的收敛域包括单位圆时，系统稳定。

∞<=∑∞-∞==n z n h z H |)(||)(1因此因果稳定系统应满足的条件为：，即系统函数H (z )的所有极点全部落在1,||<∞≤<ααz z 平面的单位圆之内。

3、MATLAB 中系统函数零极点的求法及零极点图的绘制方法MATLAB 中系统函数的零点和极点可以用多项式求根函数roots ()来实现，调用该函数的命令格式为：p=roots(A)。

F ( z) z
n0 n
z z 1
即：
z u(n) z 1
z 同理： -u (-n-1) z 1
3．单位冲激序列
F ( z)
即：
n
( n) z

n
1
( n) 1
表6-1 常用离散序列的z变换对
6.2 z变换的性质
1、线性 a1x1 (n) a2 x2 (n) a1 X1 ( z) a2 X 2 ( z)
k m k x ( k ) z ] 1
m 1 m k x(n m) u(n) z X ( z ) x(k ) z k 0
3) 若f (k )是因果序列，其单边z变换为 f (k ) (k ) F ( z ) Z [ f (k－m) (k )] z m F ( z ) m 1 常用 m m k Z [ f ( k m ) ( k )] z F ( z ) z f ( k ) z k 0

n
归一化 T=1
X ( z ) x ( n) z
n 0

n
单边Z变换
二、Z变换的定义
单边Z变换
X ( z ) x ( n) z n
n 0

双边Z变换
X ( z)
n
x ( n) z

n
幂 - n中的n指出 x n 的位置
级数的系数是 x n
1O 1
n
1O 1
n
1O 1
n
x n m un , x n m un 较x n un 的长度有所增减 .
（3）性质证明：
证明：若 f (n) (n) F ( z) 则 令

实验6 离散时间系统的z 域分析（综合型实验）一、实验目的1） 掌握z 变换及其反变换的定义，并掌握MATLAB 实现方法。

2） 学习和掌握离散时间系统系统函数的定义及z 域分析方法。

3） 掌握系统零极点的定义，加深理解系统零极点分布与系统特性的关系。

二、实验原理与方法 1. z 变换序列(n)x 的z 变换定义为(z)(n)znn X x +∞-=-∞=∑ （1）Z 反变换定义为11(n)(z)z 2n rx X dz jπ-=⎰（2）MATLAB 中可采用符号数学工具箱ztrans 函数和iztrans 函数计算z 变换和z 反变换： Z=ztrans(F)求符号表达式F 的z 变换。

F=iztrans(Z)求符号表达式Z 的z 反变换 2. 离散时间系统的系统函数离散时间系统的系统函数H(z)定义为单位抽样响应h(n)的z 变换(z)(n)znn H h +∞-=-∞=∑ （3）此外连续时间系统的系统函数还可由系统输入与输出信号z 变换之比得到(z)(z)/X(z)H Y = （4）由（4）式描述的离散时间系统的系统时间函数可以表示为101101...(z)...MM NN b b z b z H a a z a z----+++=+++ （5） 3. 离散时间系统的零极点分析MATLAB 中可采用roots 来求系统函数分子多项式和分母多项式的根，从而得到系统的零极点。

此外还可采用MATLAB 中zplane 函数来求解和绘制离散系统的零极点分布图，zplane 函数的调用格式为：zplane(b,a) b 、a 为系统函数分子分母多项式的系数向量（行向量） zplane(z,p) z 、p 为零极点序列（列向量） 系统函数是描述系统的重要物理量，研究系统函数的零极点分布不仅可以了解系统单位抽样响应的变化，还可以了解系统频率特性响应以及判断系统的稳定性； 系统函数的极点位置决定了系统的单位抽样响应的波形，系统函数零点位置只影响冲激响应的幅度和相位，不影响波形。

第七章离散时间系统的Z域分析7.1 学习要求1.熟练掌握信号的Z域分析方法：Z变换的定义、收敛区及基本性质，能够应用长除法和部分分式分解法求Z反变换。

2.掌握序列的傅里叶变换的定义和基本性质，并了解Z变换与拉普拉斯变换、傅里叶变换的关系。

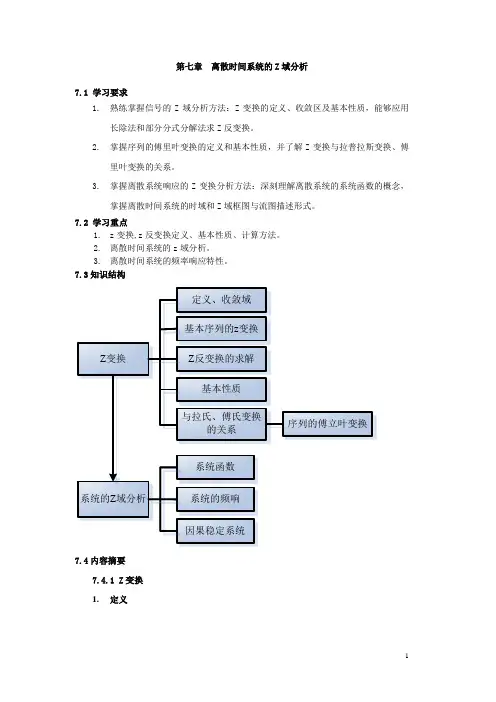
3.掌握离散系统响应的Z变换分析方法：深刻理解离散系统的系统函数的概念，掌握离散时间系统的时域和Z域框图与流图描述形式。

7.2 学习重点1.z变换,z反变换定义、基本性质、计算方法。

2.离散时间系统的z域分析。

3.离散时间系统的频率响应特性。

7.3知识结构7.4内容摘要7.4.1 Z变换1.定义∑∞-∞=-=n nz n x z X )()( 表示为：)()]([z X n x Z =。

2. 收敛域 (1) 有限长序列12(),()0,x n n n n x n n ≤≤⎧=⎨⎩其他当0,021>>n n 时，收敛条件为0>z ；当0,021<<n n 时，收敛条件为∞<z ；当0,021><n n 时，收敛条件为∞<<z 0。

(2) 右边序列11(),()0,x n n n x n n n ≥⎧=⎨<⎩当01>n 时，收敛域为1x R z >，1x R 为最小收敛半径；当01<n 时，收敛域为∞<<z R x 1。

(3) 左边序列2(),()0,x n n n x n n ≤⎧=⎨⎩其他 当02<n ，收敛域为2x R z <，2x R 为最大收敛半径； 当02>n ，收敛域为20x R z <<。

(4) 双边序列双边序列指n 为任意值时,)(n x 皆有值的序列，即左边序列和右边序列之和。

其z 变换：∑∑∑∞=--∞=--∞-∞=-+==1)()()()(n n nnn nzn x zn x zn x z X双边序列的收敛域为一环形区域21x x R z R <<。

X (z) 分子、分母多项式按 z 的降幂排列（如果左边序列则为升幂排列）成下列形式
X (z)
z2
z 2z
1
进行长除
z1 2z2 3z3
z z2 2z 1
z 2 z1
2 z1
2 4z1 2z2
3z1 2z2 3z1 6z2 3z3
4z2 3z3
即 X (z) z1 2z2 3z3 nzn ，所以原函数为 x(n) nu(n) n0
第 7 章 离散信号与系统的z域分析
根据复变函数理论中的柯西积分公式可知
C
z n m 1dz
2
0
j
mn mn
将此结果代入方程式（7.2-9），则方程右边只存在 n m 一项，其余各项均为零。于是式（7.2-9）变为
X (z)zm1dz 2 jx(m) C
(7ቤተ መጻሕፍቲ ባይዱ2-10)
此时，若将式(7.2-10)中的 m 重新用 n 置换，则得
Ai
是极点
Zi
的留数
式(7.2-2)还可表示成
Ai
(z Zi )
X (z) z zZi
X (z)
A0
N i 1
Ai z z Zi
式中 A0 是位于原点的极点的留数
A0
X (z)
z0
b0 a0
Z0 0 (7.2-2) (7.2-3) (7.2-4)
第 7 章 离散信号与系统的z域分析
B(z) A(z)
bM zM aN zN
bM 1zM 1 aN 1z N 1
b1z b0 a1z a0
(7.2-1)
对于单边序列，即 n 0 时，x(n) 0 的序列，其 Z 变换的收敛域为| z | R ，包括 z

《信号与系统》课程实验报告变换。

zz z z z z F 2112)(232+++-=一、实验原理的验证 1、离散系统零极点图实验原理如下：离散系统可以用差分方程描述：∑∑==-=-Mm m Ni i m k f b i k y a 0)()(Z 变换后可得系统函数：NN MM z a z a a z b z b b z F z Y z H ----++++++==......)()()(110110 可以用root 函数可分别求零点和极点。

例7-4 求系统函数零极点图131)(45+-+=z z z z H实验结果如下：2、离散系统的频率特性实验原理如下：离散系统的频率特性可由系统函数求出，既令ωj e z =,函数freqz 可计算频率特性，调用格式是：[H ，W]=freqz(b,a,n)，b 和a 是系统函数分子分母系数，n 是π-0范围内n 个等份点，默认值为512，H 是频率响应函数值，W 是相应频率点； 例7-5 系统函数z z z H 5.0)(-=10个频率点的计算结果为幅频特性曲线相频特性曲线freqz语句直接画图例7-7已知系统函数114/11)1(4/5)(----=z z z H ，画频率响应和零极点图。

零极点图幅频特性曲线相频特性曲线二、已知离散系统的系统函数如下所示：1422)(232+-++=z z z z z H试用MATLAB 实现下列分析过程： （1）求出系统的零极点位置；（2）绘出系统的零极点图，根据零极点图判断系统的稳定性； （3）绘出系统单位响应的时域波形，并分析系统稳定性与系统单位响应时域特性的关系。

（1）由计算结果可知：系统的极点为p0=-3.3028、p1=1、p2=0.3028。

由计算结果可知：系统的零点为z0=1.4142i 、z1=-1.4142i 。

（2）系统的零极点图如下：程序清单如下： a=[1 2 -4 1]; b=[1 0 2]; ljdt(a,b)p=roots(a)q=roots(b)pa=abs(p)由图可知：第一个极点（p0）在单位圆外部，第二个极点（p1）在单位圆上，第三个极点（p2）在单位圆内部，因为有一个极点在单位圆外部，故该系统是不稳定的系统（稳定系统要求极点全部在单位圆内）。

Re s[ F ( z ) z k 1 ] ( z z i ) F ( z ) z k 1
z pi
z zi
若F(z)z k1在z = p处有n 阶极点，则该极点的留数为
n 1 n 1 d ( z p ) F ( z) k 1 Re s[ F ( z ) z ] n 1 z p (n 1)! dz z p
Yf (z)
y[k ] Z 1 Yx ( z) Y f ( z)


16
例： y[k]4y[k1]+4y[k2] = 4(3)ku[k] y[1]=0 ，y[2]=2，求yx [k]、yf [k]、y[k]。
解：
Y(z)4{z1Y(z)y[1]}+4{z2Y(z)+z1y[1]+y[2]}=4F(z)
15
二阶系统响应的Z域求解
Y ( z) a1 y[1] a2 y[2] a2 y[1]z 1 1 a1 z
1
a2 z
2

b0 F b1 z 1 1 a1 z
1
a2 z
2
F ( z)
Yx(z)
a1 y[1] a2 y[2] a2 y[1]z 1 Yx ( z ) 1 a1 z 1 a2 z 2 b0 F b1 z 1 Y f ( z) F ( z) 1 2 1 a1 z a2 z
解：
将 Y f ( z ) 展开成部分分式,得
1.6 0.96 1.44 Yf ( z) 1 2 1 1 (1 2 z ) (1 2 z ) 1 3z 对 Yx ( z ) , Y f ( z ) 进行 z 反变换,即可分别求出系统零输入

实验七 离散系统的z 域分析一、实验目的理解并掌握系统函数的概念; 掌握利用系统函数零极点分析系统的稳定性和频率特性，掌握序列的z 变换及其性质；掌握z 域系统表示和差分方程求解。

二、实验内容1、 利用residuez 函数对)3.0)(6.0()9.05.2()(---=z z z z z F （即)3.0)(6.0(9.05.2)(---=z z z z z F ）进行部分分式展开。

syms zb=[2.5 -0.9 0];a=[1 -0.9 0.18];[R P K]=residuez(b,a);f=0;for i=1:length(R)f=f+R(i)./(1-P(i)*(z^(-1)));end>> ff =2/(1-3/5/z)+1/2/(1-3/10/z)2、设某离散系统的系统函数为：541()341z H z z z +=-+，利用roots 函数求出系统的零极点，并画出系统的零极点图，判断系统是否稳定。

A=[3 -4 0 0 0 1];B=[1 1];sjdt(A,B);m 文件：function [p,q]=sjdt(A,B)%绘制连续系统零极点图程序%A:系统函数分母多项式系数向量%B:系统函数分子多项式系数向量%p:函数返回的系统函数极点位置行向量%q:函数返回的系统函数零点位置行向量p=roots(A);q=roots(B);p=p'; %将极点列向量转置为行向量q=q'; %将零点列向量转置为行向量x=max(abs([p q])); %确定纵坐标范围x=x+0.1;y=x; %确定横坐标范围clfhold onaxis([-x x -y y]); %确定坐标轴显示范围axis('square')plot([-x x],[0 0]) %画横坐标轴plot([0 0],[-y y]) %画纵坐标轴plot(real(p),imag(p),'x') %画极点plot(real(q),imag(q),'o') %画零点title('离散系统零极点图') %标注标题text(0.2,x-0.2,'虚轴')text(y-0.2,0.2,'实轴')3、利用freqz函数画出离散系统0.5()zH zz-=的系统的幅频特性和相频特性曲线。

z
k
cos(
0
k
)
k
z
z2 z2 z cos 2z2 2z cos 0
0
1
2
..........
k
sin 0k
k
z
2z2
z 2
sin 0 z cos 0
1 2
.........
k k
k
z (z )2k kk Nhomakorabea1
五、ZT & DTFT
求和收敛
设f(k)
为因果序列、则
F (e j ) f k e jk
Z eS Ts e e Ts jTs e j
k
F (z) f (k)zk k 0
e Ts
Ts
2 s
S 域中的一点→ → Z 域中的一点；Z 域中的一点→ → S 域中的无穷个点。
S 1 Ln z 1 Ln(e j ) 1 Ln j
Ts
Ts
Ts
Ts
三、收敛域: F (z) f k zk
ak (k) bk (k 1) z z ∣a∣< |z|< |b|
za zb
jIm[z]
|b|
|a|
o
Re[z]
四、常用 z 变换
(k+1) ←→z; (k-1) ←→z-1;……
(k) ←→1 (k) ←→z/(z-1) ←→ - (- k-1)
零、极 点分布
k k z k k 1
F(z)
K1 e j z
z e j
K1 e j z
z e j
若z> , f(k)=2K1kcos(k+)(k)，… …
(3) F(z)有重极点 推导记忆：

第 六 章 离散信号与系统的 Z 域分析引言与线性连续系统的频域分析和复频域分析类似，线性离散系统的频域分析是输入信号分解为基本信号e jΩk 之和,则系统的响应为基本信号的响应之和。

这种方法的数学描述是离散时间傅里叶变换和逆变换。

如果把复指数信号e jΩk 扩展为复指数信号Z k ,Z=re jΩ ,并以Zk 为基本信号， 把输入信号分解为基本信号Z k 之和， 则响应为基本信号Z k 的响应之和。

这种方法的数学描述为Z 变换及其逆变换,这种方法称为离散信号与系统的Z 域分析法.如果把离散信号看成连续时间信号的 抽样值序列，则Z 变换可由拉普拉斯变换引入.因此离散信号与系统的Z 域分析 和连续时间信号与系统的复频域分析有许多相似之处.通过Z 变换，离散时间信 号的卷积运算变成代算,离散时间系统的差分方程变成Z 域的代数方程,因此可 以比较方便的分析系统的响应。

Z 变换从拉普拉斯变换到Z 变换对连续信号f(t)进行理想抽样，即f（t）乘以单位冲击序列δT （t），T 为 抽样间隔，得到抽样信号为f s （t）=f（t）δT （t）= =对fs（t）取双边拉普拉斯变换，得F s （s）=￡[fs（t）]=令z=e sT , 则Fs（s）=F(z) ,得F（z）=因为T为常数,所以通常用f(k)表示f(kT),于是变为F(z)=称为f(k)的双边Z变换,z为复变量。

z和s的关系为:z=e sTs=（1/T）㏑z由复变函数理论,可以得到f(k)= ∮cF(z)z k-1 dz式(7.1-5)称为F(z)的双边Z逆变换(后面讨论).双边Z变换的定义和收敛域§双边 Z 变换的定义对于离散序列f(k)(k=0,±1,±2,┄),函数(z的幂级数)F(z)=称为f(k)的双边Z变换,记为F(z)=Z[f(k)].F(z)又称为f(k)的象函数,f(k)又 称为F(z)的原函数.为了表示方便,f(k)与F(z)之间的对应关系可表示为 f(k)　F(z)§双边 Z 变换的收敛域f(k)的双边Z变换为一无穷级数,因此存在级数是否收敛的问题.只有当 (7.1-6)式的级数收敛,F(z)才存在.F(z)存在或级数收敛的充分条件是　∞在f(k)给定的条件下,式(7.1-6)级数是否收敛取决于z的取值.在z复平面上, 使级数收敛的z取值区域称为F(Z)的收敛域。

7.1.1 z 变换的定义
z变换的由来 —由拉氏变换引出Z变换
采样信号为 : f s (t ) 拉氏变换 : Fs ( s)
sT k
f (t ) (t kT ) f (kT ) (t kT )
k st k





f (kT ) (t kT )e dt
第7章 离散信号与系统的z域分析
7.0 引言
信号与系统的分析方法有时域、变换域两种。
连续系统:时域分析:y(t); 频域分析:Y(jw)→y(t) 复频域分析:Y(s)→y(t) (微分方程) (s) 离散系统:时域分析:y(k);频域分析:Y(jw) →y(k); 复频域分析:Y(z) →y(k) (差分方程) (z)
z 1
z 1
z 1 z a z a
12
z a
m
7.2 Z 变换的性质
序号 1 名称 线性 时域
a1 f1 (k ) a2 f 2 (k )
f (k m) (k m)(m 0) f (k m)
m
z 域（单边） a1 F1 ( z) a2 F2 ( z)
f k
k 0
F ( z)
1
收敛域
k
k
k
z 0 z 1
2பைடு நூலகம்
z z 1 z
3
4
k2 ak ka k
e ak
z 1 z z 1 3 z 1
z za az
z 1 z 1 z a
5
6
z a
2
z a
z ea
7 8
幂级数展开法

实验七离散系统的z域分析与MATLAB实现实验目的：1、掌握离散序列z变换的计算方法。

2、掌握离散系统系统函数零极点的计算方法和零极点图的绘制方法，并能根据零极点图分析系统的因果性和稳定性。

3、掌握利用MATLAB进行z反变换的计算方法。

实验内容：13.1程序：（1）f1=n^2u（n）;syms nzf1=n^2;f1_z=ztrans(f1)f1_z =(z^2 + z)/(z - 1)^3（3）f3=n*exp(-2*n)u（n）syms nzf3=n*exp(-2*n);f3_z=ztrans(f3)f3_z =(z*exp(2))/(z*exp(2) - 1)^213.2程序（2）：syms zX(z）=(2*z^2-z+1)/(z^3+z^2+0.5*z);h=iztrans(X(z）)h =2*kroneckerDelta(n - 1, 0) - 6*kroneckerDelta(n, 0) - (-1)^n*2^(1 - n)*(1 - i)^(n - 1)*3*i + (-1)^n*2^(1 - n)*(1 + i)^(n - 1)*3*i（4）：syms zX(z）=(z^2+0.5*z)/(z-0.5)^3;h=iztrans(X(z）)h =4*(1/2)^n*nchoosek(n - 1, 2) + 2*(1/2)^n + 6*(1/2)^n*(n - 1) 13.4程序（1）：num=[2 0 0];den=[1 3 2];[z,p,k]=tf2zp(num,den)z =p =-2-1k =2所以由程序运行结果可得，该系统的零，极点增益模型如图：实验小结：通过实验我掌握了离散序列z变换的计算方法，掌握了利用MATLAB进行z反变换的计算方法。

学会了用MATLAB 实现传递函数模型与零，极点增益模型的转换。

第七章 离散时间系统的z 域分析1．z 变换是如何提出的？它的作用是什么？z 变换是为分析离散时间系统而提出的一种工程分析方法，它在离散时间系统分析中的地位和作用等价于连续时间系统分析中的拉氏变换。

它可以看作为拉氏变换的推广。

z 变换定义为：()[]nn X z x n z∞-=-∞=∑ ---- 双边z 变换 （1）()[]nn X z x n z ∞-==∑---- 单边z 变换 （2） 其中z 是复变量，Re Im j z z j z re Ω=+=。

而对于取样信号的拉氏变换为()()()() ()() ()stst s s n st n snTn X s x t e dt x nT t nT e dtx nT e t nT dt x nT e δδ∞∞∞---∞-∞=-∞∞∞--∞=-∞∞-=-∞⎡⎤==-⎢⎥⎣⎦⎡⎤=-⎢⎥⎣⎦=∑⎰⎰∑⎰∑（3）如果 [](),x n x nT =令sT z e =，可以发现式（1）和式（3）相同。

2．双边z 变换和单边z 变换时如何定义的？它们的定义域是如何确定的？收敛域的意义是什么？z 变换定义为：()[]nn X z x n z∞-=-∞=∑ ---- 双边z 变换 （1）()[]nn X z x n z ∞-==∑---- 单边z 变换 （2） z 变换收敛域就是使上述级数收敛的所有z 的取值的集合。

根据级数收敛理论，一般我们用根值判别法或比值判别法来确定z 变换收敛域， 其作用是建立序列和z 变换之间的一一对应关系。

根据序列的不同性质，序列z 变换的收敛域各不相同，具体参阅教材Page 297-298 表7-1。

3．z 变换和拉氏变换之间有什么样的关系？具体分析见问题1中的式（1）和（3），根据两式，可以建立分析连续时间系统的拉氏变换的变量s 和分析离散时间系统的z 变换的变量z 之间的映射关系：sT z e =令, j z re s j σωΩ==+， 则有, Tr eT σω=Ω=， 具体见教材Page 300 表7-2 。

z的负幂 z的正幂 0
F ( z ) 是z 的幂级数
1
幂-k中的k指出 f ( k )的位置
级数的系数是 f ( k )
例 7.1 - 1 已知有限长序列f(k)=ε(k+1)-ε(k-2)。求f(k)的双边Z
变换及其收敛域。 解

F ( z)
k 1

f (k ) z k
z z2 F1 ( z ) Z [ f1 (k )] z z 1 z 1
1<|z|<∞
z 1 ( k 2) z z 1 z ( z 1)
2
|z|>1
由序列乘ak性质得
1 1 |z|>1 F2 ( z ) Z [( 1) （k - 2） ] z ( z 1) z ( z + 1)
列双边Z变换的收敛域为|z|>0；有限长反因果序列双边Z变换的收敛域为|z|<∞； 单位序列δ(k)的双边Z变换的收敛域为全Z复平面。
(2) 无限长因果序列双边Z变换的收敛域为|z|>|z0|，z0为复数、虚数或实数， 即收敛域为半径为|z0|的圆外区域。 (3) 无限长反因果序列双边Z变换的收敛域为|z|<|z0|，即收敛域为以|z0|为半 径的圆内区域。 (4) 无限长双边序列双边Z变换的收敛域为|z1|<|z|<|z2|，即收敛域位于以|z1| 为半径和以|z2|为半径的两个圆之间的环状区域。 (5) 不同序列的双边Z变换可能相同，即序列与其双边Z变换不是一一对应 的。序列的双边Z变换连同收敛域一起与序列才是一一对应的。
k k


skT
f (kT ) z k
k

第7章离散时间系统的z 域分析1. z 变换是如何提出的？它的作用是什么？z 变换是为分析离散时间系统而提出的一种工程分析方法, 统分析中的地位和作用等价于连续时间系统分析中的拉氏变换。

氏变换的推广。

Re z j Im z 而对于取样信号的拉氏变换为x( nT)e snT2. 双边z 变换和单边z 变换时如何定义的？它们的定义域是如何确定的？收敛 域的意义是什么？z 变换定义为：X （z ） x[n]z n ----双边z 变换（1）nX(z) x[n]z n----单边 z 变换(2)n 0z 变换收敛域就是使上述级数收敛的所有 z 的取值的集合。

根据级数收敛理 论，一般我们用根值判别法或比值判别法来确定 z 变换收敛域， 其作用是建立序列和z 变换之间的一一一对应关系。

根据序列的不同性质，序列 z 变换的收敛域各不相同，具体参阅教材 Page297-298 表 7-1 oz 变换定义为：X （z ）x[n]z nn----双边z 变换(1)X(z)x[n]z nn 0单边z 变换 (2)X s (s)X s (t)estdt x(nT) (t nT) e stdtx(nT) e st(tnT)dt (3)它在离散时间系 它可以看作为拉re J o其中z 是复变量，z如果 x[n] x(nT),令 ze sT ，可以发现式（1）和式（3）相同3.z变换和拉氏变换之间有什么样的关系？具体分析见问题1中的式（1）和（3）,根据两式，可以建立分析连续时间系统的拉氏变换的变量s和分析离散时间系统的z变换的变量z之间的映射关系:sT令z re j, s j ，则有r e T, T，具体见教材Page 300表7-2 。

4.z逆变换的求解方法有几种？在应用部分分式求解z逆变换时，应注意什么问题？z逆变换的求解方法主要有三种：围线积分法（复变函数理论），幕级数展开法和部分分式展开法。

其中幕级数展开法只适用于单纯的左边序列或右边序列，而且不易得到序列的解析式，因而实际中使用不多；而围线积分法（复变函数理论）和部分分式展开法因其方法的逻辑性较强，适用于各种序列，而且便于得到序列的解析式，所以，最为我们所采纳。