理想气体温标

新概念物理教程热学答案第一章温度1-1在什么温度下,下列一对温标给出相同的读数：（1）华氏温标和摄氏温标；（2）华氏温标和热力学温标；（3）摄氏温标和热力学温标？解：（1）当时，即可由时，解得故在（2）又当时则即解得：故在（3）若则有时，显而易见此方程无解，因此不存在的情况。

1-2定容气体温度计的测温泡浸在水的三相点槽内时，其中气体的压强为50mmHg。

（1）用温度计测量300K的温度时，气体的压强是多少？（2）当气体的压强为68mmHg时，待测温度是多少？解：对于定容气体温度计可知：(2)1-3用定容气体温度计测得冰点的理想气体温度为273.15K，试求温度计内的气体在冰点时的压强与水的三相点时压强之比的极限值。

解：根据已知冰点。

1-4用定容气体温度计测量某种物质的沸点。

原来测温泡在水的三相点时，其中气体的压强；当测温泡浸入待测物质中时，测得的压强值为减为200mmHg时,重新测得,当从,当再抽出一些测温泡中抽出一些气体,使气体使减为100mmHg时,测得.试确定待测沸点的理想气体温度.解：根据从理想气体温标的定义：时,T约为400.5K亦即沸点为400.5K.依以上两次所测数据,作T-P图看趋势得出题1-4图1-5铂电阻温度计的测量泡浸在水的三相点槽内时，铂电阻的阻值为90.35欧姆。

当温度计的测温泡与待测物体接触时，铂电阻的阻值为90.28欧姆。

试求待测物体的温度，假设温度与铂电阻的阻值成正比，并规定水的三相点为273.16K。

解：依题给条件可得则故，1-6在历史上，对摄氏温标是这样规定的：假设测温属性某随温度t 做线性变化即，并规定冰点为设解：和，汽化点为分别表示在冰点和汽化点时某的值，试求上式中的常数a和b。

由题给条件可知由（2）-（1）得将（3）代入（1）式得1-7水银温度计浸在冰水中时，水银柱的长度为4.0cm；温度计浸在沸水中时，水银柱的长度为24.0cm。

（1）在室温时，水银柱的长度为多少？（2）温度计浸在某种沸腾的化学溶液中时，水银柱的长度为25.4cm，试求溶液的温度。

温标2014190102004 航空航天学院王云川1、经验温标经验温标的建立三要素：为了定量地进行温度的测量，必须确定温度的数值表示方法，即温标（1）选择测温物质和测温参量。

即选择某一特定物质的某一随温度变化的属性（表示这种属性的物理量，叫测温参量）来标记温度。

当温度改变时，不仅液体体积会随之变化，物质的其他物理属性，如一定容积气体的压强、一定压强气体的体积、导体的电阻、灯丝颜色、热电偶电动势等都会发生变化。

原则上讲，任一物质的任一物理属性，只要它随温度的改变而单调地变化，都可以被选用来标记温度。

（2）规定测温参量随温度的变化关系。

即要将所选择的测温参量的变化与温度变化联系起来，对测温参量随温度的变化关系作出某种规定，然后根据这个规定来确定温度的数值。

为了简单起见，一般规定测温参量与温度之间呈线性关系。

（3）选择参考点，并规定其数值。

选择便于复现的某个温度点为参考点，并给予它们一定的数值，这样其他各点的温度数值才可以再根据测温参量随温度的变化关系而确定出来。

建立温标必须具备的三个要素当中，前两个为测温依据，后一个为标度方法。

不难看出，这样建立的温标所测温度依赖于测温物质和测温参量的选择。

这种利用特定测温物质的特定测温参量建立的温标统称为经验温标。

经验温标具有相对性，即当我们规定某一测温参量随温度作线性变化而建立起某种经验温标后，再利用这种温标制成的温度计去测量其他测温参量随温度的变化关系时，它就不再是线性的了。

这就是说，根据每种经验温标所进行的温度测量，只是相对于该种温度所赖以建立的测温依据来说才是正确的。

2 、理想气体温标由于经验温标具有相对性，就需要选定某一特定种类的温度计作为标准，来调整其他各种温度计的标度，同时在恒温点的规定与分度不同的温标间建立起某种对应关系，这在建立标准温标之后是很容易进行的。

19 世纪中叶，对气体性质的研究已经很成熟了，建立起了一些气体定律，能够较正确地反映气体膨胀的规律。

引力场中热力学的基本原理罗凌霄（大理大学工程学院，云南大理，671003）摘要：建立了引力场中的理想气体温标，导出引力场中的理想气体的物态方程，重申了玻耳兹曼常量与引力势的函数关系，并给出引力场中温度的微观解释。

给出引力势不随时间改变的情况下，引力势随位置的改变可以忽略的不太大的空间内的热力学第一定律的表述，以及热力学第二定律的表述。

最后，清楚地导出了引力场中的熵概念以及熵增加原理，并且阐明了熵增加原理的适用条件是周围相关环境的引力场不随时间改变。

关键词：引力场；热力学；玻耳兹曼常量；质根动量；热诱变在文献[1]中，我们已经弄清楚，超氢相对基准中玻耳兹曼常量是引力势的函数，超氢绝对基准中玻耳兹曼常量与引力势无关，并且，我们建立了引力场中的黑体辐射理论与恒星辐射理论。

以此为基础，本文要构建引力场中热力学的基本原理。

1、引力场中的平衡态在不受外界拂扰的条件下，宏观性质不随时间变化的状态叫做平衡态。

这里所说的不受外界拂扰，是指外界对系统既不作功，也不传热，并且外界在系统所在处激发的引力势不随时间改变。

2、引力场中的热平衡如果两个各自处于平衡态的热力学系统用导热丝作热接触而不改变状态，那么就说这两个热力学系统处于热平衡。

导热丝由芯线和外壳构成，芯线是良导体，外壳是绝热材料，外壳的内壁是热辐射的全反射膜，在两端芯线稍微突出。

用导热丝对各自处于热平衡的系统A和B作热接触是这样进行的：让导热丝a的一端与系统A接触，另一端伸向系统B，直到稍微超过两个系统间的中界位置。

如果系统A的状态因此发生改变，那么采取措施让它恢复原态。

让导热丝b的一端与系统B接触，另一端伸向系统A，直到稍微超过两个系统间的中界位置。

如果系统B的状态因此发生改变，那么采取措施让它恢复原态。

然后让两根导热丝彼此相邻的两个裸露端接触。

作者简介:罗凌霄(1964—)，男，白族，云南剑川人，大理大学教授，主要从事电磁场理论、数学场论、量子理论和引力理论的研究工作．如果系统A 和B 的状态并不因此而改变，我们就说当初的系统A 和B 处于热平衡。

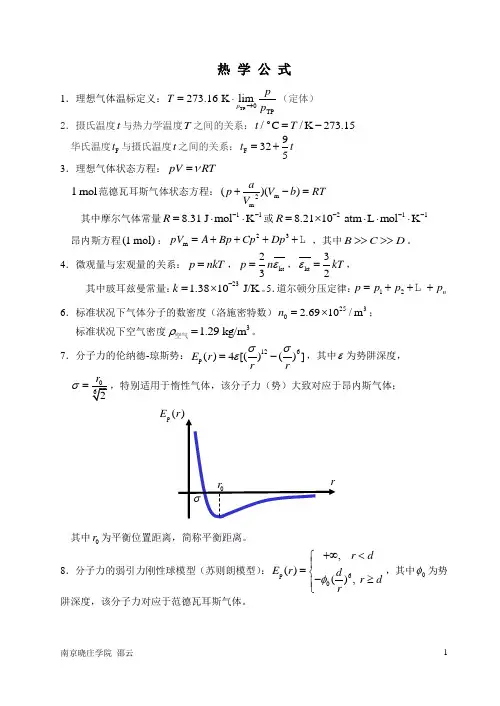
热 学 公 式1．理想气体温标定义：TP 0TP273.16 K limp pT p →=⋅（定体） 2．摄氏温度t 与热力学温度T 之间的关系：o/C /K 273.15t T =- 华氏温度F t 与摄氏温度t 之间的关系：F 9325t t =+ 3．理想气体状态方程：pV RT ν=1 mol 范德瓦耳斯气体状态方程：m 2m()()ap V b RT V +-= 其中摩尔气体常量118.31 J mol K R --=⋅⋅或2118.2110 atm L mol K R ---=⨯⋅⋅⋅ 昂内斯方程(1 mol)：23m pV A Bp Cp Dp =++++，其中B C D >>>>。

4．微观量与宏观量的关系：p nkT =，kt 23p n ε=，kt 32kT ε=， 其中玻耳兹曼常量：231.3810 J/K k -=⨯。

5．道尔顿分压定律：12n p p p p =+++6．标准状况下气体分子的数密度（洛施密特数）2530 2.6910/m n =⨯； 标准状况下空气密度31.29 kg/m ρ=空气。

7．分子力的伦纳德-琼斯势：126p ()4[()()]E r rrσσε=-，其中ε为势阱深度，σ=，特别适用于惰性气体，该分子力（势）大致对应于昂内斯气体；其中0r 为平衡位置距离，简称平衡距离。

8．分子力的弱引力刚性球模型（苏则朗模型）：p 60, ()(), r d E r d r d rφ+∞<⎧⎪=⎨-≥⎪⎩，其中0φ为势阱深度，该分子力对应于范德瓦耳斯气体。

9．麦克斯韦速率分布函数（概率密度）：23/222d ()4π()e d 2πmv kTN m f v v N v kT-==，其简便形式：22()d e d u f v v u -=，其中约化速率p v u v =。

10．三个分子速率的统计平均值：最概然速率：p v ==v ==方均根速率：rms v ===11．麦克斯韦速度分布律：22232()/2d e d d d 2πx y z m v v v kTx y z N m v v v N kT -++⎛⎫= ⎪⎝⎭，其中 x 方向速度分布律：21/2/2d ed 2πxx v mv kTx N m v N kT -⎛⎫= ⎪⎝⎭， 引入约化速度分量px vv ξ=后，上式可简化为2d ()d d x v x x N f v v N ξξ-==。

热力学温标=理想气体温标
热力学温标是一种温度测量系统，它基于热力学第零定律的原理，用于测量物体的温度。

热力学温标与理想气体温标是等价的，它们之间存在一一对应的关系。

热力学温标的基本原理是利用热平衡的性质来定义温度。

根据热力学第零定律，当两个物体处于热平衡时，它们的温度是相等的。

因此，可以通过将物体与一个已知温度的参考物体接触并观察它们是否达到热平衡来测量物体的温度。

理想气体温标是一种基于理想气体性质的温度测量系统。

根据理想气体状态方程PV = nRT，其中P是气体的压强，V 是气体的体积，n是气体的物质量，R是气体常数，T是气体的温度。

理想气体温标的定义是，当理想气体的体积恒定时，气体的压强与温度成正比。

因此，可以通过测量气体的压强来确定其温度。

热力学温标与理想气体温标之间的关系可以通过理想气体状态方程推导得到。

当理想气体的体积恒定时，PV = nRT 可以写为P = kT，其中k是一个常数。

这意味着在等压条件下，理想气体的温度与热力学温标是一致的。

综上所述，热力学温标与理想气体温标是等价的，它们都是基于热平衡和理想气体性质的温度测量系统。

通过测量物体与参考物体的热平衡状态或测量理想气体的压强，可以确定物体的温度。

理想气体温标和热力学温标
理想气体温标和热力学温标是热力学中经常用到的两种温标，它们有什么区别呢？
理想气体温标是以理想气体为基础的温标，它是通过观察理想气体的性质来确定温度的。

理想气体温标的零点是绝对零度，即
-273.15℃，而单位是开尔文(K)。

理想气体温标是绝对温标，意味着它不会受到气体的性质和状态的影响。

因此，理想气体温标是热力学中最基本的温标之一。

而热力学温标是一种更普遍的温标，它不仅仅是基于理想气体的性质来确定温度，还考虑了其他物质的性质。

热力学温标的零点和单位和理想气体温标相同，即绝对零度和开尔文。

但是，热力学温标不仅仅是适用于理想气体，它适用于所有物质，无论是固体、液体还是气体。

总的来说，理想气体温标和热力学温标都是用来测量温度的工具，它们的区别在于理想气体温标基于理想气体的性质来确定温度，而热力学温标则考虑了更广泛的物质性质。

- 1 -。

第1讲 温度和气体分子运动论§1。

1 温度1．1．1、平衡态、状态参量温度是表示物体冷热程度的物理量。

凡是跟温度有关的现象均称为热现象。

热现象是自然界中的一种普遍现象。

热学是研究热现象规律的科学。

热学研究的对象都是由大量分子组成的宏观物体，称为热力学系统或简称系统。

在不受外界影响的条件下，系统的宏观性质不再随时间变化的状态称为平衡态，否则就称为非平衡态。

可见系统平衡态的改变依赖于外界影响(作功、传热)。

系统处于平衡态，所有宏观物理都具有确定的值，我们就可以选择其中几个物理量来描述平衡态，这几个量称为状态参量。

P 、V 、T 就是气体的状态参量。

气体的体积V 是指盛放气体的容器的容积，国际单位制中，体积的单位是m 3。

1m 3=103L=106cm 3气体的压强P 是气体作用在容器的单位面积器壁上的平均压力，单位是p a 。

1atm=76cmHg=1.013⨯105p a1mmHg=133.3p a1．1．2、 温标温度的数值表示法称为温标。

建立温标的三要素是：1、选择某种物质的一个随温度改变发生单调显著变化的属性来标志温度，制作温度计。

例如液体温度计T(V)、电阻温度计T(R)、气体温度计T(P)、T(V)等等。

这种选用某种测温物质的某一测温属性建立的温标称为经验温标。

2、规定固定点，即选定某一易于复现的特定平衡态指定其温度值。

1954年以前，规定冰点为0℃，汽点为100℃，其间等分100份，从而构成旧摄氏温标。

1954年以后，国际上选定水的三相点为基本固定点，温度值规定为273.16K 。

这样0℃与冰点，100℃与汽点不再严格相等，百分温标的概念已被废弃。

3、规定测温属性随温度变化的函数关系。

如果某种温标(例如气体温度计)选定为线性关系，由于不同物质的同一属性或者同一物质的不同属性随温度变化的函数关系不会相同，因而其它的温标就会出现非线性的函数关系。

1．1．3、理想气体温标定容气体温度计是利用其测温泡内气体压强的大小来标志温度的高低的。

理想气体的标准状态
理想气体是指在一定温度和压力下，完全服从理想气体状态方程的气体。

它是理想气体状态方程的基础，也是研究气体性质和行为的重要理论模型。

理想气体的标准状态是指在特定的条件下，气体的状态被规定为标准状态，以便进行实验和计算时的参照。

本文将就理想气体的标准状态进行详细介绍。

首先，理想气体的标准状态包括标准温度和标准压力。

标准温度是指0摄氏度（273.15K），标准压力是指1大气压（101.325千帕）。

在标准状态下，1摩尔的理想气体体积为22.414立方米。

这些标准条件的设定是为了方便科学家们在实验和计算中的使用，使得不同实验和计算结果之间具有可比性。

其次，理想气体的标准状态还包括标准摩尔体积和标准摩尔体积。

标准摩尔体积是指在标准状态下，1摩尔理想气体的体积为22.414立方米，而标准摩尔体积是指在标准状态下，1摩尔理想气体的体积为22.414升。

这些标准条件的设定对于实验室中的气体实验和计算具有重要的指导意义。

最后，理想气体的标准状态在实际应用中有着广泛的意义。

在化学工程、物理实验和工业生产中，科学家们经常需要使用理想气体的标准状态进行实验和计算。

通过对理想气体状态方程的应用，可以更加准确地预测气体的性质和行为，为实际生产和科学研究提供重要的参考依据。

综上所述，理想气体的标准状态是在特定的条件下规定的气体状态，包括标准温度、标准压力、标准摩尔体积和标准摩尔体积。

这些标准条件的设定对于实验和计算具有重要的指导意义，也为科学家们的研究工作提供了重要的参考依据。

希望本文对理想气体的标准状态有所帮助，谢谢阅读。

作者： 曹良腾
作者机构： 四川内江师专
出版物刊名： 龙岩学院学报
页码： 119-120页
主题词： 理想气体温标;热力学温标;热力学第二定律;温度变化;卡诺循环;稀薄气体;放热量;二本;趋近
摘要：<正> 一、问题的提出 量度一物体的质量用天平,量度一物体的温度用温度计,而制定温度计的准则,即温度的数值表示法叫温标。

简言之,温标是温度的标尺。

凡是以某一物质的属性随温度变化为根据而确定的温标,称为经验温标建立在热力学第二定律基础上的温标,叫绝对热力学温标,或开氏温标。

热力学温标不依赖于任何具体的测温物质及测温属性,因此,它是最科学的温标。

理想气体温标,它是依据理想气体的压强(或体积)随温度的线性变化而制定的。

其数学表达式为:。

查理定律，热力学温标，理想气体的状态方程教学目标：1、掌握查理定律，理解气体等容变化的等温线的意义2、理解热力学温标和绝对零度的意义，掌握热力学温度和摄氏温度的换算关系3、掌握理想气体的状态方程教学过程：一、查理定律1、对一定质量的气体：P t =P 0+2730P t=P 0(1+273t ) ⇒ 当t=t 1时, P 1=P 0(1+2731t ) 当t=t 2时, P 2=P 0(1+2732t ) ⇒ ∆P=2730P ∆t, 当∆t =10C 时，∆P=2730P . 2、内容：一定质量的气体，在体积保持不变的情况下，温度每升高或降低10C ，增加或降低的压强等于它在00C 时压强的2731。

P t =P 0+2730P t=P 0(1+273t ) 3、等容线 一定质量的气体，在何种不变的情况下，P-t 的关系图线是：一条一次函数图线（1）截距 P 0（2）斜率 k=2730P =tg α （3）图线与x 轴的交点P t =0=P 0+2730P t ⇒ t=-2730C.结论：一定质量的气体，在不同体积下的等容线是一簇一次函数图线，体积越大，图线越靠近t 轴，但所有图线与t 轴的交点都是-2730C.V 1>V 2二、热力学温标1、热力学温标：也叫绝对温标，由英国的威廉·汤姆逊创立。

热力学温度的零度是-273.150C ，简称为O 开（K ），叫做绝对零度。

热力学温度与摄氏温度间的关系为： T=t+273.15注意：10C1K ，但温度变化10C 和变化1K 是一样的。

2、查理定律引入热力学温标后，查理定律将简化为：11T P =22T P 。

即：一定质量的气体在体积不变的情况下，其压强与热力学温度成正比。

三、理想气体状态方程1、理想气体一、理想气体模型是一种理想化的模型，一种科学的抽象（1）分子本身的大小与它们之间的间距相比可以忽略不计：即分子有质量无大小，可视为质点，表示分子非常稀疏，相互作用力很小。