i第四章目标规划及其图解法
- 格式：pptx
- 大小：520.55 KB
- 文档页数：43
下载文档原格式
合集下载
第四章目标规划
确定获利最大的生产方案。
这是一个单目标规划问题，用线性规划表 示如下
max Z 8 x1 10 x2 2 x1 x2 11 s.t. x1 2 x2 10 x , x 0 1 2
最优方案为
x1 4, x2 3
*
*
实际上工厂在作决策时要考虑到市场等一系列其 他条件。 （1）根据市场信息产品 A销量有下降的趋势，故 考虑产品 A的产量应尽量不大于 B。 （2）超过计划供应的原材料时，需要高价采购， 这就使成本增加，所以原材料有严格限制。 （3）应该尽可能的充分利用设备台时，但尽量 不加班。 （4）应尽可能达到并超过计划利润指标 56元。
优先因子： 目标的重要程度 首先达到的目标赋予优先因子 P1，次位的目 标赋于优先因子 P2,…,并规定 Pk>>Pk+1 k=1,…,K ，的重要程度 j
决策者在原材料供应受严格限制的基础上考虑： P1:产品 B的产量应尽量不低于产品 A的产量； l P2:尽量充分利用设备有效台时，不宜加班； l P3:利润额应尽量不小于 56元。
决策者在原材料供应受严格限制
录音机 资源1：加工 （第一工厂） 2小时 资源2 ：装配试验 （第二工厂） 2.5小时 20元/台 利润 1,500 台 预计销量 8元 月储存成本 第一工厂 2400 18元
收音机 4小时 1.5小时 23元/台 1,000 台 15元
该公司依下列次序为目标的优先 次序，以实现次月的生产与销售目标。 P1 厂内的储存成本不宜超过 23,000 元； P2 录音机销售量应完成 1,500 台； P3 第一，二两工厂的设备应全力运转， 避免有空闲时间，两厂的单位运转成本当作 它们间的权系数。
这个问题的目标规划模型为： min Ζ=P1d3++P2d4 ¯ +P3(6d1 ¯ +5d2 ¯) +P 4d11++P5d5 s.t 2x 1+4x2+d1 ¯ -d1+=2400 2.5x 1+1.5x 2+d2 ¯ -d2+=2800 8x 1+15x 2+d3 ¯ -d3+=23000 x 1 +d 4 ¯ -d4+=1500 x 2 +d5 ¯ -d5+=1000 P3 第一，二两工厂的设备应全力运转 d 1++d11 ¯ -d11+=30 避免有空闲时间，两厂的单位运转成本当 ， P4录音机销售量应完成 第一个工厂的超时作业时间全月份不宜 x 1,x2≥0,d i ¯,di+≥0 (i=1,2,3,4,5,11) P1 23,000 P2 厂内的储存成本不宜超过 1,500 台；元； P5 30 收音机销售量应完成 1,000 台； 作它们间的权系数。 超出 小时；
i第四章 目标规划及其图解法
3x1
10x2 d6 d6 3000
x1, x2 0, di , di 0, (i 1, 2,
目标约束 软约束
, 6)
３．目标规划的目标函数(达成函数)
引入偏差变量使原规划问题中的目标函数变 成了目标约束，那么现在问题的目标是什么呢？
对于满足绝对约束和目标约束的所有解（可行 解），从决策者角度看，判断其优劣的依据是决策 值与目标值的偏差越小越好．从而目标规划的目标 函数就由原目标函数变成的目标约束中偏差变量来 构成．它有三种基本表现形式：
200
4x1
5 x2 2000
3x1 10x2 3000
x1, x2 0, di , di 0,
(i 1, 2,3)
４．优先因子与权系数
目标规划中，当决策者要求实现多个目标时，这
些目标的偏差可能相互替代或抵消，因为我们求的是
所有偏差和最小，而实际问题中的目标之间也有主次、
轻重、缓急之区别．决策者往往有一些最重要的，第
这样根据各个目标的不同要求，确定出总的目标函数
Min Z
(di
d
j
)
i, j
如例4-2
70
x1
x1
120 x2
d1
d
2
d1 d2
45000 250
s.t.9.2x1
x2 d3 d3 200 4 x2 3600
利润希望达
到45000,不
足部分d
越小越好!
4x1
5 x2 2000
一位要求达到的目标，我们赋予它优先因子P1，在它 实现的前提下再去解决次要目标．依次把第二位达到
的目标赋予优先因子P2 ……，并规定Pk » Pk+1，即不 管Pk+1乘以一个多大的正数M，总成立Pk>MPk+1,表示 Pk比Pk+1具有绝对的优先权．因此，不同的优先因子 代表着不同的优先等级．
《目标规划的图解法》课件
目标规划的图解法
本课件介绍目标规划的图解法，包括其简介、基本原理、步骤、补充说明以 及结语。通过图解法帮助读者更好地理解目标规划并应用于实践中。
目标规划的定义
明确目标
目标规划是一种确定和明确组织或个人长期和短期目标的方法。
规划路径
通过目标规划，我们可以制定实现目标所需的路径和步骤。
提高执行力
目标规划有助于提高组织和个人的执行力，实现预期目标。
2
限制条件
考虑到资源、时间和其他限制条件来制定目标。
3
目标权重分配
根据目标的重要性和优先级来分配权重。
图解法的步骤
建立目标模型
明确各个目标之间的 关联，和权重。
填写限制条件
考虑资源和其他限制 条件，并将其纳入目 标规划中。
计算目标权重
根据目标的重要性和 优先级计算权重比例。
目标规划的应用领域
1 个人发展
目标规划可以帮助个人在 职业发展和个人成长方面 制定明确的目标。
2 项目管理
在项目管理中，目标规划 可以帮助规划项目的目标 和实施路径。
3 组织管理
对于组织，目标规划是制 定战略和经营目标的重要 工具。
目标规划的基本原理
1
目标分解
将长期目标分解为具体可行的短期目标。
补充说明
图解法的优点
图解法可以直观地展示目标规划的关系和权重分配，易于理解和传达。
图解法的局限性
图解法可能无法考虑到某些复杂因素和非线性关系。
图解法在实践中的应用
图解法可以应用于项目管理、战略规划、个人成长等多个领域。
结语
目标规划的重要性再强调
通过目标规划，您可以明确目标 并制定实现路径，帮助实现个人 和组织的成功。
本课件介绍目标规划的图解法，包括其简介、基本原理、步骤、补充说明以 及结语。通过图解法帮助读者更好地理解目标规划并应用于实践中。
目标规划的定义
明确目标
目标规划是一种确定和明确组织或个人长期和短期目标的方法。
规划路径
通过目标规划，我们可以制定实现目标所需的路径和步骤。
提高执行力
目标规划有助于提高组织和个人的执行力，实现预期目标。
2
限制条件
考虑到资源、时间和其他限制条件来制定目标。
3
目标权重分配
根据目标的重要性和优先级来分配权重。
图解法的步骤
建立目标模型
明确各个目标之间的 关联，和权重。
填写限制条件
考虑资源和其他限制 条件，并将其纳入目 标规划中。
计算目标权重
根据目标的重要性和 优先级计算权重比例。
目标规划的应用领域
1 个人发展
目标规划可以帮助个人在 职业发展和个人成长方面 制定明确的目标。
2 项目管理
在项目管理中，目标规划 可以帮助规划项目的目标 和实施路径。
3 组织管理
对于组织，目标规划是制 定战略和经营目标的重要 工具。
目标规划的基本原理
1
目标分解
将长期目标分解为具体可行的短期目标。
补充说明
图解法的优点
图解法可以直观地展示目标规划的关系和权重分配，易于理解和传达。
图解法的局限性
图解法可能无法考虑到某些复杂因素和非线性关系。
图解法在实践中的应用
图解法可以应用于项目管理、战略规划、个人成长等多个领域。
结语
目标规划的重要性再强调
通过目标规划，您可以明确目标 并制定实现路径，帮助实现个人 和组织的成功。
目标规划的图解法
解 作图3-3：
(l1 ) (l 2 ) (l3 )
Min Z Pd P d P d 1 1 2 2 3 3
x1 x2 d1 d1 10 2 x1 x2 d 2 d 2 26 x 2 x d d 1 2 3 3 6 x , x 0, d , d 0, (i 1, 2,3) i i 1 2 x2
d2
(l1 ) (l2 ) (l3 ) (l4 ) 最后考虑P3 级，此时 要求目标越小越好， 由图3-2可知R3 为四 按优先级高低，首先 边形CDEF 区域， 考虑P1 级目标，要求 目标越小越好，就在 绝约束的可行解域 △OAB中进一步缩小 为△OAC，记作R1来自Bl3l4
d1
l2
C
d3
s.t
5 x1 10 x2 60 x 2 x d d 0 1 2 1 1 4 x1 4 x2 d 2 d 2 36 再考虑 P2 级目标， 6 x 8 x d d 48 1 2 3 3 x , x 0, d , d要求目标越小越 ( i 1, 2, 3) i i 0, 1 2 好，因而解空间 x2 R2为△OCD 区域
(l1 ) (l2 ) (l3 ) (l4 )
解
将约束方程以直线形式画在图上，这里只使用决策变 量（即 x , x ），偏差变量在画直线时被去掉，直线画好后， 在该直线上标出目标函数中与该直线相关的偏差变量增大时 直线的平移方向（用垂直于直线的箭头来反映）．如图 32．
Min Z Pd 1 1 P 2d2 P 3d3
(l1 )
考虑P2 级目标，由于直线 l2 与R1不相 ( l3 ) 交，所以在R1 内无法使 d 2 0 因此 在不退化P1 级目标时，不可能使P2 级 目标完全满足．这样R2 就缩为一点， d 因为在R1中，使 达到最小的为 A点， 所以：x* = (10 ,0), d
(l1 ) (l 2 ) (l3 )
Min Z Pd P d P d 1 1 2 2 3 3
x1 x2 d1 d1 10 2 x1 x2 d 2 d 2 26 x 2 x d d 1 2 3 3 6 x , x 0, d , d 0, (i 1, 2,3) i i 1 2 x2
d2
(l1 ) (l2 ) (l3 ) (l4 ) 最后考虑P3 级，此时 要求目标越小越好， 由图3-2可知R3 为四 按优先级高低，首先 边形CDEF 区域， 考虑P1 级目标，要求 目标越小越好，就在 绝约束的可行解域 △OAB中进一步缩小 为△OAC，记作R1来自Bl3l4
d1
l2
C
d3
s.t
5 x1 10 x2 60 x 2 x d d 0 1 2 1 1 4 x1 4 x2 d 2 d 2 36 再考虑 P2 级目标， 6 x 8 x d d 48 1 2 3 3 x , x 0, d , d要求目标越小越 ( i 1, 2, 3) i i 0, 1 2 好，因而解空间 x2 R2为△OCD 区域
(l1 ) (l2 ) (l3 ) (l4 )
解
将约束方程以直线形式画在图上，这里只使用决策变 量（即 x , x ），偏差变量在画直线时被去掉，直线画好后， 在该直线上标出目标函数中与该直线相关的偏差变量增大时 直线的平移方向（用垂直于直线的箭头来反映）．如图 32．
Min Z Pd 1 1 P 2d2 P 3d3
(l1 )
考虑P2 级目标，由于直线 l2 与R1不相 ( l3 ) 交，所以在R1 内无法使 d 2 0 因此 在不退化P1 级目标时，不可能使P2 级 目标完全满足．这样R2 就缩为一点， d 因为在R1中，使 达到最小的为 A点， 所以：x* = (10 ,0), d
运筹学第4章上
min z f (d , d )
（2）要求决策值不超过目标值，即正偏差尽可能的小，其构 造形式为：
min z f (d )
（3）要求决策值可以超过目标值，即负偏差尽可能的小，其 构造形式为：
min z f (d )
China University of Mining and Technology
China University of Mining and Technology
-9-
运 筹 学
目标规划的数学模型
如：在引例中,利润的目标值为32，可能目标值会达不到，所 以加上一个负偏差变量d3-≥0，把目标函数变成
3x1 5 x2 d3 32
但是同样，目标值也有可能会超出，所以减去一个正偏差变量 d3+≥0，把目标函数变成
另一种差别是相对的，这些目标具有相同的优先因子，它们 的重要程度可用权系数wj的不同来表示。
-13-
China University of Mining and Technology
运 筹 学
4. 目标函数
目标规划的数学模型
目标函数由于偏差变量、优先因子和权系数的出现，显然其 构造与线性规划时的构造要有所不同. 决策者的目标是要做到决策值与目标值的偏差能够尽可能的 小，因此目标函数应该是一个与偏差有关的函数：
China University of Mining and Technology
运 筹 学
3. 目标的优先级与权系数
不同目标的主次轻重有两种差别：
目标规划的数学模型
一种差别是绝对的，可用优先因子Pj来表示。
只有在高级优先因子对应的目标已满足的基础上，才能考虑较低 级优先因子对应的目标；在考虑低级优先因子对应的目标时，绝不 允许违背已满足的高级优先因子对应的目标。 优先因子间的关系为Pj >> Pj+1 ，即Pj对应的目标比Pj+1对应的目 标有绝对的优先性。
第四章 目标规划1-2
例4.1 某工厂生产两种产品，受到原材料供应和设备工时的限 制.在单件利润等有关数据已知的条件下，要求制订一个获利最 大的生产计划，具体数据见表4-1.
设产品Ⅰ、Ⅱ的产量分别为 x1, x2
，建立线性规划模型
m z = 6x1 +8x2 ax
5x1 +10x2 ≤ 60
4x1 + 4x2 ≤ 40
x1, x2 ≥ 0
解之得最优生产计划为
x1 = 8
x 件， 2 = 2 件，
利润为 zmax = 64 元. 工厂作决策时可能还需根据市场和工厂实际情况， 考虑其它问题，如： （1）由于产品Ⅱ销售疲软，故希望产品Ⅱ的产量不 1 超过产品Ⅰ的一半； （2）原材料严重短缺，原料数量只有60； （3）最好能节约4小时设备工时； （4）计划利润不少于48元.
解：设A、B、C三种产品的产量分别为 ， 单位工时的利润分别为1000/5=200、1440/8=180、 2520/12=210，故单位工时的利润比例为20:18:21， 于是得目标规划模型为：
综上分析，可得目标规划的一般模型 （4.2 ） s.t. （4.3） （4.4） （4.5） （4.6） 其中，式（4.2）是目标函数有L个目标，根据L个目标的优先程度，把它们分成K个 优先等级，即 ， 是权系数， 是正负偏差变量；式 （4.3)是目标约束， 是L个目标的期望值，一般都应同时引入下、 负偏差变量 ，但有时也可根据已知条件只引入单个 或 ；式（4.4） 是目标规划的绝对约束，通常是人力、物力、财力等资源的约束；式（4.5）、 （4.6）是目标规划的非负约束.
二、目标规划的基本概念
1、目标值和偏差变量 目标值:决策者对每一个目标都有一个期望值----或称为理想值. 正偏差变量：表示决策值（实现值）超过目标值 的数量，记为 d + ； 负偏差变量:表示决策值（实现值）未达到目标 值的数量，记为 d − .
第四章多目标规划模型
第四章 多目标规划模型多目标决策问题的理论基础之一是向量优化问题，也称多目标优化问题。
这类问题，从方法论的角度看，它是一个目标函数中具有向量值的数学规划问题；从决策论角度看，它又是决策规则中含有各个目标极值的决策问题。
因此，多目标决策问题属于向量优化问题。
向量优化问题的解与标量优化问题的解是不同的。
标量优化问题对任何两个函数的解，只要比较它们的两个函数值的大小，总可以从中找出一个最优解，且能排出它们的顺序；而多目标优化问题的解都是非劣解，且不是唯一的，究竟谁优谁劣，很难直接作出判断。
非劣解的概念是由经济学家pareto 于1896年提出的。
但是发展为向量优化问题的生成非劣解技术，还是在1951年Kuhn-Tucker 非劣性条件发表以后的事。
由于向量优化问题是在标量优化问题的基础上发展起来的，只要通过适当的途径将向量优化问题转化为标量优化问题，就可以利用求解标量优化问题的现有方法，求解具有一定特征的向量优化问题。
本章主要介绍有关向量优化问题的基本理论，如非劣解概念，特征非裂解的标量优化解法及非劣性的充要条件。
其中提到的许多概念和术语，在本书的后继章节中都是很有用的。
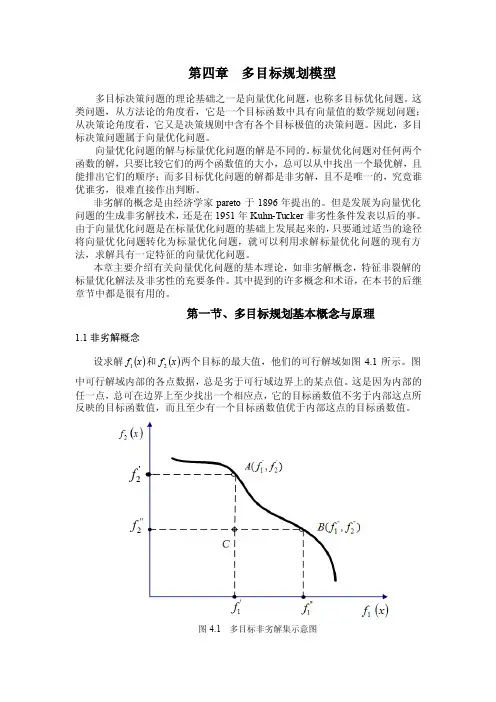
第一节、多目标规划基本概念与原理1.1非劣解概念设求解()x f 1和()x f 2两个目标的最大值，他们的可行解域如图4.1所示。
图中可行解域内部的各点数据，总是劣于可行域边界上的某点值。
这是因为内部的任一点，总可在边界上至少找出一个相应点，它的目标函数值不劣于内部这点所反映的目标函数值，而且至少有一个目标函数值优于内部这点的目标函数值。
图4.1 多目标非劣解集示意图例如，图中的C 点就劣于A 点和B 点之间任一点所反映的目标函数值。
所以，在优选中类似C 点的一些点可以舍去，并将这些可以舍去的解称为劣解。
但是可行域边界上各点所代表的解，就不能直接判断它们的优劣（如A 点、B 点就是这样）。
因为这些点中任一个与其他任一个相比较，总会发现一个目标函数值比其他另一个函数值优越，但又不是两个目标函数值都优越，否则其中的一个作为劣解而舍去。
运筹学课堂PPT4.2目标规划的图解法
x1
,
x2
,
d
j
,
d
j
d1 0
d1
80
(3)
最优解空间：ABCD
(2) C
B
x1
(1) (3)
min
Z
P1d1
P2
(d
2
d
2
)
P3
(d
3
d
3
)
P4d
4
3x1 12
(1)
x2
4 x2 16
复习：两平行直线间的距离公式
Ax By d d C（目标约束）
y
d d 0
Ax By C
d 0 ( x0 , y0 )
d
正负偏差变量中至少有一个零，如：
A2 B2
x Ax By C
Ax By d d C d 0, d 0
Ax By d C
Ax By C d C（在下半平面）
P2d4
P3d
3
P4 (2d1
d
2
)
x1 30 x2 20 / 3
x2
d1 0
d1 0
d
2
25 /
3
d2 0
d
3
680
d
3
0
d
4
0
d4 0
D
E(35/2,15)
(2)
min Z (0, 0, 680, 25 / 3)
F(30,20/3)
A
B
x1
(1)
(4) (3)
4.2 目标规划的图解法
差变量大于零的区域。
(1) (2) (3)
（平行） (4)
(2)
x1
运筹学 第四章 目标规划
二、目标规划模型的建立
1、目标函数的期望值 首先要对每一个目标确定一个希望达到的期望值 ei(i=1,2, …,n) 。根据历史资料、市场需求或上级部门的布 置等来确定。
《运筹学》 第四章 目标规划 Slide 4
2、正负偏差变量 每个目标函数的期望值确定之后，目标的实际值和它的 期望值之间就有正的或负的偏差。 正偏差变量 di+ 表示第i个目标超过期望值的数值；负偏 差变量di- 表示第i个目标未达到期望值的数值。 同一目标，它的取值不可能在超过期望值的同时，又没 有达到期望值，所以在di+ 和di- 中至少有一个必须为零。 di+ ×di-=0 引入正、负偏差变量后，对各个目标建立的目标函数方 n 程。 c x d d E * 原来的目标函数变成了约束条件的一部分，即目标约束 (软约束) ，原来的约束条件称为系统约束(硬约束)。
《运筹学》 第四章 目标规划 Slide 7
5、建立目标规划模型的基本步骤： 1）按生产和工作要求确定各个目标及其优先等级和期望 值； 2）设立决策变量，建立各个约束条件方程； 3）对每个目标引进正、负偏差变量，建立目标约束条件 ，并入已有的约束条件； 4）如果各约束条件之间有矛盾，也可适当引入偏差变量 ； 5）根据各目标的优先等级和权系数写出达成函数。 P110-113 例3.1 ,P117 例3.4 【课堂作业】： 某工厂计划生产甲、乙两种产品，现有的设备资源、每 种产品的技术消耗定额及单位产品的利润如下表所示。
《运筹学》 第四章 目标规划 Slide 3
第一节
目标规划模型
一、目标规划模型的基本思想
P110 例3.1 目标规划的基本思想： 对每一个目标函数引进一个期望值（理想值），但由于 种种条件的限制，这些期望值往往并不都能达到，从而我 们对每个目标引进正、负偏差变量，然后将所有的目标函 数并入原来的约束条件，组成新的约束条件。在这组新的 约束条件下，寻找使各种目标偏差达到最小的方案。
管理运筹学 第四章 目标规划
再来考虑风险约束： 总风险不能超过700， 投资的总风险为 0.5x1＋0.2x2 引入两个变量d1+和d1-，建立等式如下： 0.5x1 +0.2x2=700+d1+-d1根据要求有
min ｛d1+｝
0.5x1 +0.2x2-d1++d1-=700。
再来考虑年收入:
3x1+4x2
引入变量 d2+和d2-，分别表示年收入超过与低于 10000 的数量。于是，第2个目标可以表示为 min ｛d2-｝ 3x1+4x2-d2++d2-=10000。
2. 统一处理目标和约束。
对有严格限制的资源使用建立系统约束，数学形式同线性规划 中的约束条件。如C和D设备的使用限制。
x1 2 x2 40 3x2 24
(3)Ｃ和Ｄ为贵重设备，严格禁止超时使用
对不严格限制的约束，连同原线性规划建模时的目标，均通 过目标约束来表达。 （1）力求使利润指标不低于250元：
本问题中第一个目标的优先权比第二个目标大。即最重要 的目标是满足风险不超过700。分配给第一个目标较高的优先 权P1，分配给第二个目标较低的优先权P2。
Minz= P1（d1+）+P2（d2-） s.t. 20x1＋50x2≤90000 0.5x1 +0.2x2-d1++d1-=700 3x1+4x2-d2++d2-=10000 x1,x2,d1+,d1-,d2+,d2-≥0
现假定： 第1优先级P1——企业利润；
第2优先级P2——Ｉ、II产品的产量保持1:2的比例
第3优先级P3——设备A,B尽量不超负荷工作。其中设备A的重要性 比设备B大三倍。
运筹学第4章
3x15x2d332
综合考虑后，得到结果
3x15x2d3 d3 32 其中 d3 , d3 0
目标规划的数学模型
产品 甲 乙 资源量
可以用同样的方式来处理其它提出的 资源
决策要求：
设备/台时 3
2
18
原料A/吨
1
0
4
（1）要求甲产品产量不大于乙产品产量。 原料B/吨 0 2 12
如：在引例中，利润的目标值为32， 可能目标值会达不到，所以加上一个
产品 资源
甲 乙 资源量
设备/台时 3
2
18
负偏差变量d3-≥0，把目标函数变成
原料A/吨
1
0
4
3x15x2d332
原料B/吨 单位赢利/
0 3
2 5
12
万元
但是同样，目标值也有可能会超出，所以减去一个正偏差变量
d3+≥0，把目标函数变成
A）恰好达到目标值 B）允许超过目标值 C）不允许超过 目标值
构造一个由优先因子和权系数相对应的偏差变量组成的，要求实 现极小化的目标函数.
用目标规划求解问题的过程：
明确问题，列出 目标的优先级和
权系数
构造目标规 划模型
N
满意否？
Y
据此制定出决策方案
目标规划的数学模型
求出满意解 分析各项目标
完成情况
p （3 3）计划利润指标32，并且尽可能达到或超过这个利润指标.
问：如何安排生产可以使得获利最大？
分析：
p（1 1）要求甲产品的产量不大于乙产品的产量；
（1）产量偏差变量
d1 , d1 0
p 2（2）尽可能充分利用设备台时，不希望加班生产；
《管理运筹学》目标规划
第4章 目标规划
7
例4-1用目标规划表示的模型为
min
z
P1d1
P2d 2
P3d
3
P4d 4
P4 d 5
40x1 30x2 50x3 d1 d1 3200
x1
1.5x2
d
2
d
2
0
s.t.
3x1
2x1
x2 2x2
j1 xj 0
j 1,, n
d
k
,
d
k
0
k 1,, K
其中：Pl为第l级优先因子，l=1, …,L; -lk，+lk为分别赋
予第l个目标约束的正负偏差变量的权系数。gk为第k个目 标的预期目标值，k=1, …,K。
第4章 目标规划
9
当目标规划问题中只包含两个决策变量时，可以用图解法 进行求满意解。
目标规划图解法的计算步骤如下：
（1）对所有目标约束，去掉偏差变量，画出相应直线，然后标出偏差 变量变化时直线平移方向。
（2）确定第一优先级P1级各目标的解空间R1。 （3）转到下一个优先级PJ级个目标，确定它的“最佳”解空间RJ。 （4）在求解过程中，若解空间 RJ已缩小为一点，则结束求解过程，因
为此时已没有进一步改进的可能。
（5）重复第（3）步和第（4）步过程，直到解空间缩小为一点，或者 所有L个优先级都已搜索过，求解过程也告结束。
第4章 目标规划
10
例4-2 用图解法求解下列目标规划问题
min
z
目标规划的图解法课件
50 E D
2、先满足P1，OD线段
3、再满足P2，ED线段（满意解） O
50
E (500/11,500/11) ,
d1
d1
d
2
d
2
0
D (360/7,360/7)
,
d1
d1
d
2
0,
d
2
92 / 7
C 100 l2
150
d
2
x1 l1
d
2
l4
第一节 目旳规划旳基本概念与数学模型 一、问题旳提出 二、目旳规划旳基本概念
有关最优解：线性规划是在可行解域内寻找某一点，
使单个目旳到达最优值（最大值或最小值）．而目旳规
划是在可行域内，首先寻找到一种使P1级目旳均满足旳 区域R1，然后再在R1中寻找一种使P2级目旳均满足或尽 最大可能满足旳区域R2（R1），再在R2中寻找一种满 足P3旳各目旳旳区域R3（R2R1），…,如此下去，直 到寻找到一种区域Rk(Rk-1…R1)，满足Pk级旳各目旳， 这个Rk即为所求旳解域，假如某一种Ri (1 i k)已退化 为一点，则计算终止，这一点即为满意解，它只能满足
min
z
P1 (d1
d1 )
P2d
2
s.t 2x1 3x2 300
l1
2x1 1.5x2 180
l 2x2
x1 x2 d1 d1 0
l3
10x1
12 x2
d
2
d
2
1000
1l450
x1,x2
,di
,d
i
0
i 1,2
A
100
l3 d1
B
d1
运筹学第三版之第四章目标规划
,K)
j1
n
aij x j (, )bi
(i 1, 2, , m)
j1
x
j
0
(j
1,2,
, n)
,d
k
,
d
k
0
(k 1, 2,
,K)
（二）、建模的步骤
1、根据要研究的问题所提出的各目标与条件，确定目 标值，列出目标约束与绝对约束；
2、可根据决策者的需要，将某些或全部绝对约束 转化为目标约束。这时只需要给绝对约束加上负偏差 变量和减去正偏差变量即可。
d
3
x1 x1
x2
d
1
d1
0
2 x2
d
2
d
2
10
8 x1
10 x2
d
3
d
3
56
2 x1 x2
11
x12
0,
d
j
.
d
j
0
(j
1.2.3)
C D
min
Z
P1d1
P2
(d
2
d
2
)
P3d
3
d
1
⑴
x1 x1
x2
d1
d
1
0
2 x2
d
2
d
2
10
d1
8 x1
例2、已知一个生产计划的线性规划模型为
max Z 30 x1 12 x2
2 x1 x2 140 (甲资源)
x1
60 (乙资源) x2 100 (丙资源)
x12 0
其中目标函数为总利润，x1,x2 为产品A、B产量。现
有下列目标：
目标规划
１０９ 习题四4.1 分别用图解法和单纯形法求解下述目标规划问题（1） min z ＝p 1（+1d ＋+2d ）＋p 2-3dst. －x 1＋ x 2＋ d －1－ d ＋1＝1－0.5x 1＋ x 2＋ d －2－d ＋2＝23x 1＋3x 2＋ d －3－ d ＋3＝50x 1，x 2≥0；d －i ，d ＋i ≥0（i =1，2，3）（2） min z ＝p 1（2+1d ＋3+2d ）＋p 2-3d ＋p 3+4d st. x 1＋ x 2＋d －1－d ＋1 ＝10x 1 ＋d －2－d ＋2 ＝45x 1＋3x 2＋d －3－d ＋3 ＝56x 1＋ x 2＋d －4－d ＋4 ＝12x 1，x 2≥0；d －i ，d ＋i ≥0（i =1， (4)4.2 考虑下述目标规划问题min z ＝p 1（d ＋1＋d ＋2）＋2p 2d －4＋p 2d －3＋p 3d －1st. x 1 ＋d －1－d ＋1＝20x 2＋d －2－d ＋2＝35－5x 1＋3x 2＋d －3－d ＋3＝220x 1－x 2＋d －4－d ＋4＝60x 1，x 2≥0；d －i ，d ＋i ≥0（i =1， (4)（1）求满意解；（2）当第二个约束右端项由35改为75时，求解的变化；（3）若增加一个新的目标约束：－4x 1＋x 2＋d －5－d ＋5＝8，该目标要求尽量达到目标值，并列为第一优先级考虑，求解的变化；（4）若增加一个新的变量x 3，其系数列向量为（0，1，1，－1）T ，则满意解如何变化？4.3 一个小型的无线电广播台考虑如何最好地来安排音乐、新闻和商业节目时间。
依据法律，该台每天允许广播12小时，其中商业节目用以赢利，每小时可收入250美元，新闻节目每小时需支出40美元，音乐节目每播一小时费用为17.50美元。
法律规定，正常情况下商业节目只能占广播时间的20％，每小时至少安排5分钟新闻节目。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
d 表示利润超过45000元
的数量，d 则表示利润距45000元还差的数量,
d
2
表示
甲产品产量超过250件的部分，……．这样可得三个目
标函数方程
Max Max Min
y1 y2 y2
70 x1 x2
x1
120 x270 x1 x1
120 x2 x2
d1
d
2
d3
d1 d2 d3
9.2x1 4x2 3600
s.t.
34xx11
5x2 2000 10x2 3000
x1, x2 0
对于多目标问题，线性规划很难为其找到最优 方案．极有可能出现：第一个方案使第一目标的结 果优于第二方案，而对于第二目标，第二方案优于 第一方案．就是说很难找到一个方案使所有目标同 时达到最优，特别当约束条件中有矛盾方程时，线 性规划方法是无法解决的．实践中，人们转而采取 “不求最好，但求满意”的策略，在线性规划的基 础上建立一种新的数学规划方法——目标规划．
x1, x2 0
4 1 4 2
4 3 4 4 4 5 4 6
例4-2 某工厂在计划期内要生产甲、乙两种产品， 现有的资源及两种产品的技术消耗定额、单位 利润如表4-1所示．试确定计划期内的生产计划， 使利润最大，同时厂领导为适应市场需求，尽 可能扩大甲产品的生产，减少乙产品的生产．
表4-1 产品的资源、技术消耗定额、单位利润表
s.t
a21x1 a22 x2
a2n xn b2
ak1x1 ck 2 x2 ckn xn bk
x1, x2 , , xn 0
1．决策变量与偏差变量
决策变量也称控制变量，用 x1、x2、…、xn 表示． 在多目标规划问题中，由于目标之间存在冲突或约束条件
中有矛盾方程，我们可以设想降低目标要求、“放松”严格的
绝对约束是指必须严格满足的等式或不等式约束， 也称为系统约束．它对应于线性规划中的约束条件（如 资源、客观条件约束等），不能满足绝对约束的解即为 不可行解，因此也称为硬约束．
d
i
0,
d
i
0 表示第i个目标的实际值未达到目标值
d
i
,
d
i
表示第i个目标的实际值恰好等于目
标值．并且无论发生哪种情况均有:
d
i
d
i
在例4-2中，若提出目标y1的期望值e1= 45000元，y2
的期望值e2=250件，y3的期望值 e3=200件，则可引入偏
差变量
d
i
,
d
i（i
=1，2，3）,
45000 250 200
4
10
d1
,
d1
,
d
2
,
d
2
,
d3
,
d3
0
２． 目标约束与绝对约束
前面通过确定各目标的目标值、引入偏差变量，把 目标函数转化成约束方程，从而并入原约束条件中， 我们称这类具有机动余地的约束为目标约束．如例4-2 的目标函数转化为目标约束（4-10）．因它具有一定 的弹性，一般目标约束不会不满足，只是可能偏差要 大一些，故也称为软约束．
约束条件，即从实际出发，根据经验、历史资料或市场的需求、
上级部门的任务下达等来给每个目标确定一个希望达到的目标
值ei , (i =1，2，…，m)．一般说来，这些值ei 的确定并不要求
十分精确或严格，允许决策的实际值大于或小于ei ．我们称实
际值与目标值的差距为偏差变量．d i用和d
i
表示．
d
i
第四章 目 标 规 划
前面的线性规划问题，研究的都是只有一个目标函 数，若干个约束条件的最优决策问题．然而现实生活 中，衡量一个方案的好坏标准往往不止一个，而且这 些标准之间往往不协调，甚至是相互冲突的，标准的 度量单位也常常各不相同．例如，在资源的最优利用 问题中，除了考虑所得的利润最大，还要考虑使生产 的产品质量好，劳动生产率高，对市场的适应性强等 等．
为正偏差变量——第
i个目标实际值超出目标值的部分．
di 为负偏差变量——第 i 个目标实际值不足目标值的差距
规定
d
和
i
d
i
0
i 1, 2, , m
当目标值确定时，所做的决策只可能出现以下三种情况：即
۞
由
d
i
和d
i
所构成的3种不同组合表示的含义：
d
i
,
d
i
表示第i个目标的实际值超出目标值
目标规划对众多的目标分别确定一个希望实现的 目标值，然后按目标的重要程度（级别）依次进行 考虑与计算，以求得最接近各目标预定数值的方 案．如果某些目标由于种种约束不能完全实现，它 也能指出目标值不能实现的程度以及原因，以供决 策者参考．
第四章 目 标 规 划
第一节 目标规划的基本概念与数学模型 一、问题的提出 二、目标规划的基本概念
分析：这是一个含有两个目标的数学规划问题． 设 x1, x2
分别为采购甲级、乙级原材料的数量（单位：kg）
y1 为花掉的资金，y 2 为所购原料总量．则：
目标函数为： 约束条件有：
Min Max
y1 y2
2x1 x2 x1 x2
2x1 x2 200
x1 x1
x2 50
100
1. 决策变量与偏差变量 ２. 目标约束与绝对约束 ３. 目标规划的目标函数(达成函数) ４. 优先因子与权系数
三、目标规划的数学模型 第二节 目标规划的图解法
第一节 目标规划的基本概念与数学模型
一、问题的提出
例4-1 某生物药厂需在市场上采购某种原料，现市场
上有甲、乙两个等级，单价分别为2千元/kg和1千元 /kg，要求采购的总费用不得超过20万元，购得原料 的总重量不少于100kg，而甲级原料又不得少于50kg， 问如何确定最好的采购方案（即用最少的钱、采购 最多数量的原料）．
二、目标规划的基本概念
多目标规划问题的一般形式如下(简记为：GP1)
Max y1 c11x1 c12 x2 Max y2 c21x1 c22 x2
c1n xn C1X c2n xn C2 X
Max ym cm1x1 cm2 x2 cmn xn Cm X
a11x1 a12 x2 a1n xn b1
甲（每件） 乙（每件） 现有资源
钢 材 （ kg ）
9.2
4
3600
木 材 ( m3 )
4
设备负荷
（台小时）
3
单位产品利润
(元)
70
5
2000
10
3000
120
分析: 设 x1, x2 分别是计划期内甲、乙产品的产
量．则该问题的数学模型为
Max y1 70x1 120x2 Max y2 x1 Min y2 x2