射影面积法求二面角.
- 格式:doc
- 大小:522.50 KB
- 文档页数:8

二面角求法总结一、定义法定义法是求二面角的基本方法,它通过定义二面角的平面角来求解。
具体来说,如果两个平面相交,那么它们会在交线上形成一个角,这个角就是二面角的平面角。
通过找到这个角的两边,我们可以使用三角函数来求解这个角的大小。
二、垂线法垂线法是一种常用的求二面角的方法,它通过找到一个垂直于两个平面的交线的直线,并将这个直线延长到一个已知点,然后使用三角函数来求解这个角的大小。
这个方法的关键在于找到正确的垂线,并且这个垂线应该是垂直于交线的。
三、射影面积法射影面积法是一种利用射影面积定理求解二面角的方法。
通过找到两个平面上的两条射线和它们之间的夹角,我们可以使用射影面积定理来求解这个角的大小。
这种方法需要先找到正确的射线和夹角,然后使用射影面积定理来计算结果。
四、三垂线定理法三垂线定理法是一种利用三垂线定理来求解二面角的方法。
如果一个平面内的直线与另一个平面垂直,那么这个直线与第一个平面的交点与第二个平面的交点的连线与原直线的夹角就是要求的二面角。
这种方法的关键在于找到正确的三垂线定理的应用条件,并且正确地应用三垂线定理来计算结果。
五、角平分线法角平分线法是一种利用角平分线定理来求解二面角的方法。
如果一个平面内的角平分线与另一个平面垂直,那么角平分线与原直线的夹角就是要求的二面角。
这种方法的关键在于找到正确的角平分线的应用条件,并且正确地应用角平分线定理来计算结果。
六、向量法向量法是一种利用向量的数量积和向量积来求解二面角的方法。
通过找到两个平面上的两个向量,我们可以使用向量的数量积和向量积来计算这两个向量的夹角,这个夹角就是要求的二面角。
这种方法的关键在于正确地找到两个向量,并且正确地应用向量的数量积和向量积来计算结果。
七、坐标法坐标法是一种利用坐标系来求解二面角的方法。
通过建立适当的坐标系,我们可以将二面角的问题转化为求解一个几何量的值的问题。
这种方法的关键在于建立正确的坐标系,并且正确地使用代数方法来计算结果。

射影面积法求二面角原理引言:在几何学中,二面角是指由两个平面所夹成的角度,它是空间几何中的基本概念之一。
求解二面角的方法有很多种,其中一种常用的方法是射影面积法。
本文将介绍射影面积法求解二面角的原理和应用。
一、二面角的定义和性质二面角是由两个平面所夹成的角度,可以用来描述两个平面的夹角大小。
二面角有以下性质:1. 二面角的大小范围是0°到180°之间;2. 二面角的大小与两个平面的夹角大小有关,但不仅仅取决于两个平面的夹角;3. 二面角的大小与两个平面的位置有关,即两个平面的相对位置不同,二面角的大小也会有所变化。
二、射影面积法的原理射影面积法是一种常用的求解二面角的方法,它基于以下原理:1. 任意两个平面所夹成的角度可以通过两个平面的射影面积来求解;2. 射影面积是指一个平面在另一个平面上的投影面积,可以用来表示两个平面之间的夹角大小;3. 射影面积可以通过投影公式和向量运算来计算。
三、射影面积法的应用射影面积法在几何学和物理学中有广泛的应用,其中包括以下几个方面:1. 几何学中的角度计算:通过射影面积法可以计算任意两个平面所夹的角度大小,从而求解几何问题;2. 物理学中的力学问题:在力学问题中,二面角可以表示两个力的夹角,通过射影面积法可以计算力的合成和分解;3. 工程学中的结构设计:在结构设计中,二面角可以表示两个构件的夹角,通过射影面积法可以计算结构的稳定性和强度。
四、射影面积法的计算步骤射影面积法的计算步骤如下:1. 确定两个平面的方程;2. 计算两个平面的交线;3. 确定投影方向和投影面积;4. 计算射影面积;5. 根据射影面积计算二面角大小。
五、射影面积法的优缺点射影面积法作为一种求解二面角的方法,具有以下优点:1. 原理简单易懂,计算步骤清晰明确;2. 适用范围广泛,可以应用于多个学科领域;3. 结果准确可靠,能够满足实际需求。
然而,射影面积法也存在一些缺点:1. 计算过程稍复杂,需要一定的数学基础和计算能力;2. 对于一些特殊情况,射影面积法可能无法提供准确的结果;3. 在实际应用中,射影面积法往往需要结合其他方法和技术进行综合分析。

五法求二面角从全国19份高考试卷中我们知道,立体几何题中命有求二面角大小的试题共有12份,并都为分值是12分的大题,足以说明这一知识点在高考中的位置,据有关专家分析,它仍然是2010年高考的重点,因此,我们每位考生必须注意,学会其解题方法,掌握其解题技巧,是十分重要的。
一、 定义法:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。
本定义为解题提供了添辅助线的一种规律。
如例1中从二面角S —AM —B 中半平面ABM 上的一已知点(B )向棱AM 作垂线,得垂足(F );在另一半平面ASM 内过该垂足(F )作棱AM 的垂线(如GF ),这两条垂线(BF 、GF )便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。
例1(2009全国卷Ⅰ理)如图,四棱锥S ABCD -中,底面ABCD 为矩形,SD ⊥底面ABCD,AD =2DC SD ==,点M 在侧棱SC 上,ABM ∠=60°(I )证明:M 在侧棱SC 的中点 (II )求二面角S AM B --的大小。
证(I )略解(II ):利用二面角的定义。
在等边三角形ABM 中过点B作BF AM ⊥交AM 于点F ,则点F 为AM 的中点,过F 点在平面ASM 内作GF AM ⊥,GF 交AS 于G ,连结AC ,∵△ADC ≌△ADS ,∴AS-AC ,且M 是SC 的中点, ∴AM ⊥SC , GF ⊥AM ,∴GF ∥AS ,又∵F 为AM 的中点,∴GF 是△AMS 的中位线,点G 是AS 的中点。
则GFB ∠即为所求二面角. ∵2=SM ,则22=GF ,又∵6==AC SA ,∴2=AM ∵2==AB AM ,060=∠ABM ∴△ABM 是等边三角形,∴3=BF在△GAB 中,26=AG ,2=AB ,090=∠GAB ,∴211423=+=BG FG366232222113212cos 222-=-=⨯⨯-+=⋅-+=∠FB GF BG FB GF BFG ∴二面角S AM B --的大小为)36arccos(-练习1(2008山东)如图,已知四棱锥P -ABCD ,底面ABCD 为菱形,P A ⊥平面ABCD ,60ABC ∠=︒,E ,F 分别是BC , PC 的中点. (Ⅰ)证明:AE ⊥PD ;(Ⅱ)若H 为PD 上的动点,EH 与平面P AD 所成最大角E —AF —C 的余弦值. 分析:第1题容易发现,可通过证AE ⊥AD 后推出AE ⊥平面APD ,使命题获证,而第2题,则首先必须在找到最大角正切值有关的线段计算出各线段的长度之后,考虑到运用在二面角的棱AF 上找到可计算二面角的平面角的顶点S ,和两边SE 与SC ,进而计算二面角的余弦值。

探索求二面角大小的常用方法作者:张学平来源:《科技视界》2013年第31期【摘要】立体几何中的二面角问题是考察学生空间想象能力的的一个重要知识点。
二面角的求解方法很多,本文通过常用实例总结了几种典型的二面角求解方法,并给出了评述。
【关键词】立体几何;二面角;空间想象能力;求解方法二面角问题是立体几何的一个重点也是难点,它的求法很多,且在各种求法中需要充分运用立体几何中的线线、线面、面面关系,教材引进空间向量后解决就更多了,因此,二面角问题具有综合性强,灵活性大的特点,这一内容也自然成为高考的热点,学生需要掌握这一问题的常用方法。
例如:如图1(a)所示,在底面是等腰直角△ABC中,∠B=90°,PA⊥面ABC,且PA=AB=BC. 求二面角B-PC-A的大小。
1 直接法直接作出二面角的平面角来求大小,突出一个“作”。
解法一:如图1(b),过A作AE⊥PB交PB于E,在面PBC内作EF⊥PC交PC于F,连接AF,设PA=PB=PC=a,∵PA⊥面ABC,且CB在面ABC内∴PA⊥BC∵在等腰直角△ABC中, CB⊥AB,且PA∩PB=A∴CB⊥面PAB,且CB在面PBC內∴面PCB⊥面PBA∵在等腰直角△PAB中,AE⊥PB,且PB=面PAB∩面CPB∴AE⊥面PBC,且PC在面PCB内,∴AE⊥PC∵PC⊥EF,且AE∩EF=E∴PC⊥面AEF即∠AFE就是二面角B-PC-A的平面角∴∠AFE=60°故二面角B-PC-A的大小为60°点评:在二面角的棱上任取一点,然后在两个平面内分别作棱的垂线,则这两条直线所成的角即为二面角的平面角,这是利用二面角的定义来作平面角,这种方法叫也做定义法。
2 间接法间接法就是不直接作出二面角的平面角,突出一个“不作”。
方法主要有:1)射影面积法是常用的典型方法,如图1(c),在平面α内有一个平面图形ABC,在平面β内的平面图形OBC为平面图形ABC在平面β内的射影,设二面角的大小为θ,射影图形的面积为S射,原来图形的面积为S原,则可证明cos=S射/S原2)向量法是将求二面角的平面角的大小转化为求两个向量的夹角或补角,如图1(d)。

求解二面角的六种常规方法作者:李淑芸来源:《中学教学参考·理科版》2010年第03期求解二面角问题是高考的热点问题,在近几年的高考中几乎每一年、每一套高考题的立体几何问题都涉及到求二面角的大小问题.然而通过对学生考卷的分析,我们发现这一问题的得分率却并不理想.因此,本文总结了常见的六种求解二面角的方法,希望能给部分读者以帮助.1.定义法是指过二面角的棱上任一点在两个面内分别作垂直于棱的直线,则两直线所构成的角即为二面角的平面角,继而在平面中求出其平面角的一种方法.【例1】如图1,空间四边形ABCD中,AB=BC=CD=DA=a,对角线AC=a,BD=2a,求二面角A—BD—C的大小.图1解:取BD的中点为O,分别连接AO、CO,∵AB=AD,BC=CD.∴AO⊥BD,CO⊥BD.∴∠AOC为二面角A—BD—C的平面角.∵AB=AD=a,BD=2a,∴AO=22a.∵BC=CD=a,BD=2a,∴OC=22a.在△AOC中,OC=22a,OA=22a,AC=a,OA2+OC2=AC2,∴∠AOC=90°,即二面角A—BD—C为直二面角.2三垂线法是指利用三垂线定理,根据“与射影垂直,则也与斜线垂直”的思想构造出二面角的平面角,继而求出平面角的方法.【例2】如图2,二面角α-AB-β的棱AB上有一点C,线段CDα,CD=100,∠BCD=30°,点D 到平面β的距离为253,求二面角α-AB-β的度数.图2解:过D作DE⊥β于E,DF⊥AB于F,连接EF.∵DF⊥AB,EF是DF在β内的射影,∴AB⊥EF(三垂线定理).∴∠DFE为二面角为α-AB-β的平面角.在Rt△DEF中,DF=12CD=50,DE=253,∴sin∠DFE=DEDF=25350=32.∴∠DFE=60°.即二面角α-AB-β的度数为60°.3.垂面法是指用垂直于棱的平面去截二面角,则截面与二面角的两个面必有两条交线,这两条交线构成的角即为二面角的平面角,继而再求出其平面角的一种方法.【例3】如图3,已知SA⊥平面ABC,AB⊥BC,SA=AB,SB=BC,E是SC的中点,DE⊥SC交AC于D,求二面角E-BD-C的大小.图3解:∵BS=BC,SE=EC,∴SC⊥BE,又∵SC⊥DE,∴SC⊥面BDE.∴SC⊥BD.又∵BD⊥SA,∴BD⊥面SAC.∴∠EDC为二面角E-BD-C的平面角.设SA=a,则SB=BC=2a.∵BC⊥AB,SA⊥平面ABC.∴BC⊥SB.∴SC=2a,∠SCD=30°.∴∠EDC=60°,即二面角E-BD-C的大小为60°.4.面积射影法所谓面积射影法,就是根据三角形及其在某一个平面上的射影面积之间的关系,利用cosθ=S射S来计算二面角的一种方法(其中θ为二面角).【例4】在正方体ABCD-A1B1C1D1中,K∈BB1,M∈CC1,且BK=14BB1,CM=34CC1,求平面AKM与ABCD所成角的大小.图4解:连结AC,则由题意可知,△ABC是△AKM在平面AC上的射影.设平面AKM与ABCD所成角为θ,则cosθ=S射S=S△ABCS△AKM.令正方体的棱长为4,∴S△ABC=12AB•A C=12×4×4=8.在△AKM中,AK=12+42=17,AM=42+42+32=41,KM=42+22=20.由海伦公式可知S△AKM=221,∴cosθ=421,θ=arccos421.5.法向量法法向量法是通过求与二面角垂直的两个向量所成的角,继而利用这个角与二面角的平面角相等或互补的关系,求出二面角的一种方法.【例5】如图5,过正方形ABCD的顶点A作PA⊥平面ABCD,设PA=AB=ɑ,求平面PAB 和平面PCD所成的二面角的大小.图5解:以A为射点建立直角坐标系(如图5所示),则P(0,0,a),D(0,a,0),C(a,a,0).设平面PCD的法向量为n=(x,y,z),则n•PD=0,n•CD=0.即(x,y,z)•(0,a,-a)=0,(x,y,z)•(-a,0,0)=0.∴y=-z,x=0.即n=(0,1,-1).又AD成为平面PAB的法向量,而cos〈AD,n〉=(0,a,0)•(0,1,-1)a•2=22,∴AD与n所成的角为45°.因此平面PAB和平面PCD所成的角为45°.6.垂线法是指先利用待定系数法确定垂足,再利用公式求出二面角的大小.【例6】如图6,在四棱锥P—ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC,已知PD=2,CD=2,AE=12,求(1)异面直线PD与EC的距离;(2)二面角E-PC-D的大小.图6解:(1)略.(2)以D为原点,DA、DC、DP分别为x,y,z轴建立空间直角坐标系.作DG⊥PC,可设G(0,y,z).由DG•PC=0得(0,y,z)•(0,2,-2)=0,即z=2y.故可取DG=(0,1,2).作EF⊥PC于F,设F(0,m,n),则EF=(-32,m-12,n).由EF•PC=0,得(-32,m-12,n)•(0,2,-2)=0,即2m-1-2n=0.又由F在PC上得n=-22m+2,故m=1,n=22,EF=(-32,12,22).因EF⊥PC,DG⊥PC,故二面角E-PC-D的平面角θ的大小为向量EF与DG的夹角.故cosθ=DG•EF|DG|•|EF|=22,∴θ=π4.故二面角E-PC-D的大小为π4.(责任编辑金铃)。

射影面积法求二面角原理引言:射影面积法是一种常用于计算几何体二面角的方法,它基于射影面积的概念,通过计算几何体在某一平面上的投影面积来确定二面角的大小。
本文将介绍射影面积法求二面角的原理和应用。
一、射影面积法的基本原理射影面积法是基于几何体在不同平面上的投影面积与几何体二面角之间的关系来进行计算的。
具体而言,我们可以通过在几何体上选择一个合适的平面,将几何体投影到该平面上,然后计算投影面积,最后利用投影面积与二面角之间的关系,求解二面角的大小。
二、射影面积法的步骤1. 选择适当的平面:根据几何体的特点和问题的要求,选择一个合适的平面进行投影。
通常情况下,选择与几何体的某一面垂直的平面可以简化计算过程。
2. 进行投影:将几何体投影到所选择的平面上,得到投影面积。
投影的方法可以根据几何体的形状和问题的要求灵活选择,常用的投影方法包括平行投影和中心投影等。
3. 计算投影面积:根据投影所得到的平面图形的形状和大小,使用几何学方法计算投影面积。
根据平面图形的形状,可以使用不同的计算公式,如矩形的投影面积为底边长度乘以高度,三角形的投影面积为底边长度乘以高度的一半等。
4. 计算二面角:根据投影面积与二面角之间的关系,利用所得到的投影面积计算二面角的大小。
具体的计算方法可以根据几何体的特点和问题的要求选择,常用的计算方法包括使用正弦定理、余弦定理等。
三、射影面积法的应用举例1. 求解四面体的二面角:对于一个四面体,可以选择一个面作为投影面,将四面体投影到该面上。
然后计算投影面积,并利用所得到的投影面积求解四面体的二面角。
2. 求解棱柱的二面角:对于一个棱柱,可以选择柱面作为投影面,将棱柱投影到柱面上。
然后计算投影面积,并利用所得到的投影面积求解棱柱的二面角。
3. 求解球体的二面角:对于一个球体,可以选择一个切面作为投影面,将球体投影到该切面上。
然后计算投影面积,并利用所得到的投影面积求解球体的二面角。
四、射影面积法的优缺点射影面积法作为一种计算几何体二面角的常用方法,具有一定的优点和缺点。

求解二面角的四种基本方法高中数学学习过程中,求解二面角是高考理科高考的必考题型,多种角度,多种方法处理这类问题是一项重要的基本能力,是落实数学核心素养培养的基本方法,在教学过程中有必要对本类型习题进行详尽的介绍和广泛的探索,提升本类问题的处理方式和方法,是多种知识交汇,处理问题的能力的体现,本文根据近年高考题与模拟题中的常见题型,对常用的处理方法进行探究和总结,希望能够找到本类题型的常见处理方法,帮助学生建立良好的处理策略.一、利用定义求解例1. 如图,在直四棱柱1111ABCD A B C D -中,底面ABCD 为菱形,23AC =,12A A BD ==,E 为1BD 中点.求二面角E DC A --的余弦值.分析 过O 作OF CD ⊥,垂足为F ,连OF ,则EFO ∠是二面角E OC A --的平面角.解答过O 作OF CD ⊥,垂足为F ,连OF ,∵1DD ⊥面ABCD ,1//OE DD ,∴OE ⊥面ABCD .∴EFO ∠是二面角E OC A --的平面角.∵1112OE DD ==,3OF =,∴7EF =,217cos EFO ∠=. 故二面角E DC A --的余弦值为217. 说明 二面角是规则图形的面与面之间的角是,采用二面角的定义,直接做出角,利用边长的长度关系找到二面角的平面角之间的边长长度关系,进而求解二面角大小.变式训练1 (2019年天津高考题)如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,PCD △为等边三角形,平面PAC ⊥平面PCD ,PA CD ⊥,2CD =,3AD =,D C O A B求直线AD 与平面PAC 所成角的正弦值.二、利用面积面积射影求解例2. 在三棱锥中P ABC -,,D E 分别为PBC ∆、ABC ∆的重心,若DE ABC ⊥∆面,2PBC ABC S ∆∆=S ,则二面角P BC A --的大小为______.分析 易证DE ∥PA ,则PA ABC ⊥面,则PBC ∆的射影为ABC ∆,此时宜采用“面积射影法”. 解答 设二面角为θ,因为,D E 分别为PBC ∆、ABC ∆的重心,则可得=MD ME DP EA,所以DE ∥PA .又因为DE ABC ⊥面,所以PA ABC ⊥面.因为cos ABC PBC S θ∆∆=S 222==45θ=o . 说明 当题目中涉及斜面三角形面积和相应射影三角形面积时,可采用“面积射影法”求二面角的大小.变式训练2 在等腰直角ABC ∆中,1AB BC ==,M 为AC 的中点,沿BM 把ABC ∆折成二面角,折后A 与C 的距离为62,则二面角C —BM —A 的大小为________. 三、利用三正弦定理求解 例3. (2012年全国新课标卷)在直三棱柱ABC A B C '''-中,12AC BC AA '==,D 是棱AA '的中点,DC BD '⊥.(1)证明:DC BC '⊥;(2)求二面角A BD C ''--的大小.分析 考察面BDC '内的直线DC ',易求90BDC '∠=o ,即2sin 1θ=;取A B ''的中点N ,则C N ABB A '''⊥面,则C DN '∠即为直线DC '与ABB A ''面所成的角,且1sin 2C DN '∠=,即11sin 2θ=,最后代入公式即可求出二面角的大小.解答 因为DA C ''∆和DAC ∆均为等腰直角三角形,所以DC DC '⊥.又因为DC BC '⊥,所以DC DBC '⊥面,从而DC DB '⊥,即2sin sin 901θ==o ;取A B ''的ME D CB A P B B'A'C'A DN中点N ,连接DN ,则C N A B '''⊥.又因为AA C N ''⊥,所以C N ABB A '''⊥面,则C DN '∠即为直线DC '与ABB A ''面所成的角.设2AA a '=,则AC BC a ==,因为2C N a'=,2D C a '=,即11sin sin 2C N C DN CD θ''=∠==.由12sin sin sin θθθ=得1sin 2θ=,又据题意知所求二面角为锐二面角,所以30θ=o .说明 当其中一个半平面内的一条直线与另一个半平面、二面角的棱所成的角的正弦值容易求出时,可采用“三正弦定理法”.变式训练3 已知点O 在二面角AB αβ--的棱上,点P 在平面α内,且60∠=︒POB .若直线PO 与平面β所成的角为45°,则二面角AB αβ--的正弦值为______.四、利用空间向量求解例4. 如图,已知三棱柱111ABC A B C -,平面11A AC C ⊥平面ABC ,90ABC ∠=︒,1130,,,BAC A A AC AC E F ∠=︒==分别是11,AC A B 的中点.(1)证明:EF BC ⊥;(2)求直线EF 与平面1A BC 所成角的余弦值.分析 建立空间直角坐标系,分别求得直线的方向向量和平面的法向量,然后结合线面角的正弦值和同角三角函数基本关系可得线面角的余弦值.解答 (1) 略.(2)在底面ABC 内作EH ⊥AC ,以点E 为坐标原点,EH ,EC ,1EA 方向分别为x ,y ,z 轴正方向建立空间直角坐标系E xyz -.设1EH =,则3AE EC ==1123AA CA ==3,3BC AB ==, 据此可得:()()()1330,3,0,,,0,0,3,3,022A B A C ⎛⎫- ⎪ ⎪⎝⎭,由11AB A B =u u u r u u u u r 可得点1B 的坐标为1333,322B ⎛⎫ ⎪⎝⎭, 利用中点坐标公式可得:333,344F ⎛⎫ ⎪⎝⎭,由于()0,0,0E , 故直线EF 的方向向量为:333,344EF ⎛⎫= ⎪⎝⎭u u u r 设平面1A BC 的法向量为(),,m x y z =u r ,则:()()13333,,330223333,,,,002222m A B x y z x y z m BC x y z x y u u u v v u u u v v ⎧⎛⎫⋅=⋅-=+-=⎪ ⎪ ⎪⎪⎝⎭⎨⎛⎫⎪⋅=⋅-=-+= ⎪⎪ ⎪⎝⎭⎩, 据此可得平面1A BC 的一个法向量为()3,1m =u r ,333,344EF ⎛⎫= ⎪⎝⎭u u u r 此时4cos ,53552EF m EF m EF m ⋅===⨯⨯u u u r u r u u u r u r u u u r u r , 设直线EF 与平面1A BC 所成角为θ,则43sin cos ,,cos 55EF m θθ===u u u r u r .说明 空间向量方法是处理空间中两平面所成角比较通用的方法,建系也是Dz C 1A 1B 1C B A本节要注意的一个重点,合理建系才能比较容易、准确的找到各点坐标,求解法向量,在求解过程中应该充分重视,准确掌握好求解法向量的基本步骤,进一步提升步骤的严谨性,科学性,另,在求解过程中要注意判断二面角是锐角还是钝角,以方便对余弦值的正负进行判断. 解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化,通过严密推理,同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解.变式训练4 已知四棱锥P —ABCD 中,PA ⊥平面,底面ABCD 为菱形,60ABC ∠=o,AB=PA=2,E .F 分别为BC .PD 的中点.求平面PAE 与平面PCD 所成锐二面角的余弦值.(参考答案:3;2. 23π;6 4. 217)。

射影面积法求二面角原理概述:射影面积法是计算二面角的常用方法之一,它基于物体在不同角度下的射影面积的变化来求解二面角。
二面角是指由两个平面所夹的角,它在几何学和计算几何学中有着广泛的应用。
本文将详细介绍射影面积法求解二面角的原理及其应用。
一、射影面积法原理射影面积法通过计算物体在不同角度下的射影面积来求解二面角。
具体步骤如下:1.选择观察点:确定观察点的位置,通常选择观察点位于物体所在平面外部,且与物体的一条边垂直相交。
2.确定观察面:从观察点出发,选择一个平面作为观察面,该平面与物体的一条边垂直相交,并且与观察点所在平面垂直。
3.计算射影面积:在观察面上,以物体的一条边为边界,通过观察点将物体投影到观察面上,计算投影的面积。
4.改变观察角度:保持观察点不变,改变观察面与物体的夹角,重复步骤3,计算不同角度下的射影面积。
5.计算二面角:根据不同角度下的射影面积,利用数学方法求解二面角的大小。
二、射影面积法的应用射影面积法可以应用于多个领域,包括几何学、物理学、计算机图形学等。
以下是该方法的一些具体应用:1.计算物体的空间角:射影面积法可以用于计算物体在空间中所占的角度,例如计算两个平面所夹的角度、计算一个立体角等。
2.三维建模:在计算机图形学中,射影面积法可以用于三维建模和渲染,通过计算物体在不同角度下的射影面积,可以生成真实感的三维模型。
3.物体识别:射影面积法可以应用于物体识别和目标跟踪,通过计算物体在不同角度下的射影面积,可以对物体进行形状和姿态的判断。
4.光线追踪:在光线追踪算法中,射影面积法可以用于计算光线与物体的相交情况,从而实现真实感的光影效果。
总结:射影面积法是一种常用的求解二面角的方法,通过计算物体在不同角度下的射影面积,可以准确地求解二面角的大小。
该方法在几何学、物理学和计算机图形学等领域有着广泛的应用,可以用于计算物体的空间角、三维建模、物体识别和光线追踪等方面。
射影面积法的原理简单易懂,但在具体应用中需要注意选择合适的观察点和观察面,以及正确计算射影面积。
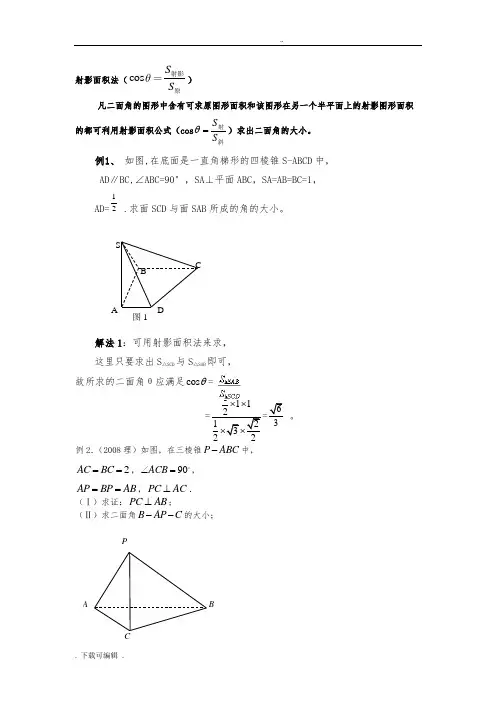
射影面积法(cosS S 射影原)凡二面角的图形中含有可求原图形面积和该图形在另一个半平面上的射影图形面积的都可利用射影面积公式(cos 斜射S S =θ)求出二面角的大小。
例1、 如图,在底面是一直角梯形的四棱锥S-ABCD 中, AD ∥BC,∠ABC=90°,SA ⊥平面ABC ,SA=AB=BC=1,AD=21 .求面SCD 与面SAB 所成的角的大小。
解法1:可用射影面积法来求, 这里只要求出S △SCD 与S △SAB 即可, 故所求的二面角θ应满足cos θ==111212322⨯⨯⨯⨯=6。
例2.(2008理)如图,在三棱锥P ABC -中,2AC BC ==,90ACB ∠=,AP BP AB ==,PC AC ⊥. (Ⅰ)求证:PC AB ⊥;(Ⅱ)求二面角B AP C --的大小;A CBP图1SDCBA解:(Ⅰ)证略(Ⅱ)AC BC =,AP BP =,APC BPC ∴△≌△. 又PC AC ⊥,PC BC ∴⊥. 又90ACB ∠=,即AC BC ⊥,且ACPC C =,BC ∴⊥平面PAC .取AP 中点E .连结BE CE ,. AB BP =,BE AP ∴⊥.EC 是BE 在平面PAC 的射影, CE AP ∴⊥.∴△ACE 是△ABE 在平面ACP 的射影, 于是可求得:2222=+===CB AC AP BP AB ,622=-=AE AB BE ,2==EC AE 则1222121=•=•==∆CE AE S S ACE 射, 3622121=•=•==∆EB AE S S ABE 原 设二面角B AP C --的大小为ϑ,则3331cos ===原射S S ϑ ∴二面角B AP C --的大小为33arccos =ϑ练习1: 如图5,E 为正方体ABCD -A 1B 1C 1D 1的 棱CC 1的中点,求平面AB 1E 和底面A 1B 1C 1D 1所成 锐角的余弦值.(答案:所求二面角的余弦值为cos θ=32).ABE P A 1D 1B 11EDBCA图52. 如图一,在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,2AP AB ==,22BC =,E F ,分别是AD PC ,的中点.(1)证明:PC ⊥平面BEF ;(2)求平面BEF 与平面BAP 夹角的大小. 题(1)解略;题(2)中平面BEF 与平面BAP 夹角即为平面BEF 与平面BAP 所成的锐二面角.方法一:垂面法在图中找到或作出一个与二面角的两个半平面均垂直的平面,此平面截得的图形便是二面角的平面角.如图一:PA ⊥平面ABCD ,BC ⊂平面ABCD ,PA BC ∴⊥.又,BC AB ABPA A ⊥=,BC ∴⊥平面BAP .又BC ⊂平面PBC ,∴平面PBC ⊥平面BAP . 由题(1),PC ⊥平面BEF ,PC ⊂平面BEF ,∴平面PBC ⊥平面BEF . 所以PBF ∠是所求二面角的平面角.222221122,22PB PA AB PF PC AB BC PA =+===++, 2sin ,.24PF PBF PBF PB π∴∠==∠= 即平面BEF 与平面BAP 夹角为4π. 方法二:平移平面法如果两平行平面同时与第三个平面相交,那么这两个平行平面与第三个平面所成的二面角相等或互补.利用此结论可以平移某一平面到合适的位置以便作出二面角的平面角.如图二:取BC 的中点G ,连接,FG EG .,E F 分别是,AD PC 的中点,,EGAB FG PB ∴.又,FG EG G AB PB B ==,∴平面EFG 平面BAP .∴二面角B EF G --的大小就是平面BEF 与平面BAP 夹角的大小.可以证明BFG ∠为二面角B EF G --的平面角,并求出其大小为4π. 方法三:射影法利用公式'cos S Sθ=,其中S 表示二面角的一个半平面某个多边形的面积,'S 表示此多边形在另一个半平面射影的面积,θ表示原图形与射影图形所成的二面角.如图三:取PB 的中点H ,连接,FH AH ,F 为PC 中点, ,FH BC AE BC ∴.由解法一知,BC ⊥平面BAP ,FH ∴⊥平面BAP ,AE ⊥平面BAP ,∴点F 、E 在平面BAP 的射影分别为H 、A . BEF ∴∆在平面BAP 上的射影为BAH ∆. 可以证明BEF ∆和BAH ∆均为直角三角形.1,,2HFBC AEBC HF BC BC ==, ∴四边形HFEA 为平行四边形,EF AE ∴=. 记平面BEF 与平面BAP 夹角为θ,则2cos BAH BEF S S θ∆∆==, 所以4πθ=,即平面BEF 与平面BAP 夹角为4π.3.已知ABC ∆是正三角形,⊥PA 平面ABC 且PA=AB=a,求二面角A-PC-B 的大小。
用射影面积法求二面角在高考中的妙用广西南宁外国语学校隆光诚(邮政编码 530007)立体几何中的二面角是一个非常重要的数学概念,求二面角的大小更是历年高考的热点问题,在每年 全国各省市的高考试题的大题中几乎都出现 •求二面角的方法很多,但是,对无棱二面角,或者不容易作出二面角的平面角时,如何求这个二面角的大小呢?用射影面积法是解决这类问题的捷径,本文以近年高 考题为例说明这个方法在解题中的妙用,以飨读者!定理 已知平面[内一个多边形的面积为 S,它在平面:-内的射影图形的面积为 s ',平面〉和平面一:S所成的二面角的大小为 「则COST - s .S本文仅对多边形为三角形为例证明,其它情形请读者自证 证明:如图,平面 1内的△ ABC 在平面〉的射影AA .1 二于 A , D :, ■ AD 在:.内的射影为A 'D . 又 AD _ BC,BC 二:,.A 'D _ BC (三垂线定理的逆定理)•ZADA 为二面角二一BC —:的平面角.设厶ABC 和厶A ' BC 的面积分别为S 和S ', • ADA '1 'BC AD ' 2 1 S BC AD S2典题妙解下面以近年高考题为例说明上述结论在解题中的妙用 例1如图,已知正方体 ABCD — A i B i C i D i 中,E 是A A i 棱的中点,则 )面BE C i 与面AC 所成的二面角的大小为( + i r B. arctan C. arcta n -2 4 解:连结 人6则厶EBC 1在面AC 内的射影是△ 面积分别为S 和s ,所成的二面角为 A. 45 2 arccos3 ABC ,设它们的 D. D A i ECB设正方体的棱长为 2,则AB = BC = 2 d . BE =*5占6 =2..2,EC ;(2..2)2 12二3.cos^EBG 1 ■ S BE 2 2 2 2BE 2 BG -EG - 2BE BC 1 BC 1 sin EBC 1 =3,S 2 1 . ---- ,sin _ EBC 1 = .10 1 . AB BC 二 2, cos -二 2 2 「cos ^EBC 1 3 ,10二-arccos —. 3 故答案选D. 例2 (04北京)如图,已知四棱锥S —ABCD 的底面是边长为i 的正方形 (1) 求证:BC X SC;(2) 求面ASD 与面BSC 所成的二面角的大小 ; (3) 设棱SA 的中点为M,求异面直线DM 与SB 所成的角的大小. (1)证明:;SD 丄面AC , 几SC 在面AC 内的射影是 SD.又;四边形ABCD 是正方形,BC 面AC , CABBC 丄SC (三垂线定理)COS”AD 2 2(2)解:幕 SD 丄面 AC , CD 面 AC , SD_CD . 又;四边形ABCD 是正方形,.AD _ CD •而 AD SD = D , CD 丄面 ASD. 又 AB //CD , BA 丄面 ASD. .△SBC 在面SAD 的射影是 △SAD ,:._SCB = 90 , BC = 1, SB = 3,. SC.1BC SC -,S^-AD SD =2 2 2(3)解:取AB 的中点E ,连结DE 、ME.AM =MS,AE =EB , ME //SB. .异面直线DM 与SB 所成的角就是• DME1 \/3 : 22ME SB ,DE 二.AD AE =-2 22 2 2MD +ME -DE.cos 二2MD ME解法二:BA _ 面 SAD ,.SB 在面SAD 内的射影是SA.又 AD=SD=1,AM 二MS,. DM _ SA . 而DM 面SAD , . DM - SB (三垂线定理). 所以异面直线 DM 与SB 所成的角的大小为 一.2ABCD 和矩形 ACEF 所在的平面 是线段EF 的中点.1AC ,连结0E.2-EM = AO , EM //A0.-四边形A0EM 是平行四边形, 又;E0二平面BDE ,AM //平面 BDE.(2);四边形ABCD 是正方形,.BD _ AC .又;正方形ABCD 和矩形ACEF 所在的平面互相垂直,EC _ AC ,■ EC _ 面 BD ,从而 EC — BD . 而 AC EC =C , BD _ 面AE . BD 平面 BDF ,-面AE 丄平面BDF.设它们的面积分别为 二 SB 2 - BC 21 . ,cos2兀所以面ASD 与面BSC 所成的二面角的大小为 1,设.DME,52 ,<22 .SA 二.AD 2 SD 2 二、2,MD 二;SA = 所以异面直线DM 与SB 所成的角的大小为 例3 (04浙江)如图,已知正方形互相垂直,AB =、2 , AF = 1 ,M求证:AM //平面BDE ; 求证:面AE 丄平面BDF ; 求二面角 A — DF — B 的大小.证明: 则AO -四边形ACEF 是矩形,EM」EF2从而 AM //E0.S 和s ,所成的二面角为日.C(3)解:BA _ AD, BA _ AF ,AD AF=A BA _ 面ADF ..△BDF在面ADF上的射影是△ADF,设它们的面积分别为S和S',所成的二面角为二. AB = ■■■.'2 ,AF = 1 ,. AD = :. 2, BD = 2, FB = FD = 3 .连结F0,则F0 _ BD, F0 二FB2一B02— 2.1 ' 1 ,2 S' 1S BD ・F0 = - 2, S AD AF , cos2 2 2 S 2故3HT所以二面角 A —DF —B的大小为''.3例4 (08天津)如图,在四棱锥P—ABCD中,底面ABCD是矩形,已知AB = 3,AD = 2,PA = 2,PD = 2、2, PAB = 60 .(1)证明:AD丄平面PAB;(2)求异面直线PC与AD所成的角的大小;3)求二面角P —BD —A的大小.(1)证明:AD 二PA =2,PD =2、2,2 2 2AD PA = PD .PAD =90,即DA _ PA.又:四边形ABCD是正方形,.DA _ AB.而AB PA A , AB、PA 二面PAB,.AD丄平面PAB.(2)AD //BC,.异面直线PC与AD所成的角就是PC与BC所成的角,即• PCB . 在A PAB中,AB = 3 , PA = 2, PD =2.2,/PAB = 60 ,.PB2二PA2AB2- 2PA AB = 7,PB 二7.由(1)得,AD丄平面PAB..CB _ PB,即CBP =90 又BC = AD = 2 ,PBtan PCB =BC 2<7 一PCB = arcta n2所以异面直线PC与AD所成的角的大小为arctan 口(3)作PE _ AB 于E,连结DE. 由(1)知,AD_ PE,而AB AD = A,PE _ 面ABCD.D-△PBD在面ABCD内的射影是A EBD,设它们的面积分别为S和S ,所成的二面角为-.BD = AB2AD2 = 13,AE 二PAcos60 = 1,BE 二AB - AE = 2./ PB2+PD2-BD cos _ BPD2PB PD1S = PB PD sin BPD 2 COS V ■ SS 2 1 ------------------------------------ 2,sin _ BPD = 1 - cos - BPD 2 J455 '2 ,S二1 BE AD =2.24,寸二arccos • 55455 .552.144所以二面角 P — BD —A 的大小为arccos —:——.J55点评:例1和例2中的二面角就是无棱二面角,例3和例4中的二面角虽然是有棱二面角,但是不容易作出二面角的平面角,用定义法解决这两类问题就显得非常繁杂,并且不知如何下手,而另辟溪径,用 射影面积法则是化繁为简,曲径通幽!金指点睛1.( 05全国川)如图,在四棱锥 V — ABCD 中,底面ABCD 是正方形, 底面ABCD.(1)证明:AB 丄平面VAD ;2)求面VAD 与面VDB 所成二面角的大小.2.( 06全国H)如图,在直三棱柱 ABC — A i B i C i 中,AB = BC , D 、 (1)证明: ED 为异面直线BB i 和AC i 的公垂线;(2)设 AA = AC = , 2AB ,求二面角 A - AD - C j 的大小. 3.(07陕西)如图,在底面为直角梯形的四棱锥 PA = 4, AD = 2 , AB = 2 3 , BC = 6.(1)求证:BD 丄平面PAC ;2)求二面角 A — PC — D 的大小.4. (09湖北)如图,四棱柱 S —ABCD 的底面是正方形, SD 丄平面 ABCD , SD = AD = a ,点E 是SD 上的点,且DE a (0v i ) . S(1) 求证:对任意… 0,i 】,都有AC 丄BE ;(2) 若二面角C — AE — D 的大小为60,求■的值.金指点睛的参考答案一 一一一 一D ;1. ( 05全国川)如图,在四棱锥 V — ABCD 中,底面ABCD 是正方形,侧面VAD 是正三角形, 底面ABCD.(1)证明:AB 丄平面VAD ;2)求面VAD 与面VDB 所成二面角的大小.P —ABCD 中,AD //BC ,也ABC = 90 , PA 丄平面 ABCD ,D侧面VAD 是正三角形,平面VAD 丄E 分别为BB i 、AC i 的中点.B iD BEC平面VB(i)证明:取AD的中点E,连结VE.守VA = VD, AE = ED,二VE 丄AD .又;平面VAD丄底面ABCD , VE 平面VAD ,V AC.VE 丄底面ABCD. . VA 在底面ABCD 的射影是AD. AB J_AD , AB 二底面 ABCD , . AB INA (三垂线定理) 而 VA AD =A,VA 、AD 二平面 VAD , 故AB 丄平面VAD.(2)由(1)可知,AB 丄平面VAD ,.△ VBD 在平面VAD 的射影是厶VAD ,设它们的面积分别为 S 和S ',所成的二面角为 -. 设正方形的边长为1,则BD 二、、2,VB =AB 2 • VA 2 = •、2 .2. ( 06全国n)如图,在直三棱柱 ABC — A 1B 1C 1中,AB = BC , D 、E 分别为BB j 、AG 的中点.(1)证明: ED 为异面直线BB 1和AC 1的公垂线;(2)设 AA^ = AC = , 2AB ,求二面角 A — AD —C t 的大小.(1)证明:取AC 的中点F ,连结EF 、BF.1AF = FC, AE = EG , EF // CC 1, EFCC 1. 21在直三棱柱 ABC — AB J G 中,CG _ 面 ABC , CG, CG // BB , DBBB 1 , 2EF //DB , EF= DB , EF _ 面 ABC.■四边形BDEF 是矩形.从而ED _ BB 1 . 在 Rt △ ABD 和 Rt △ C 1B 1D 中,AB 二 C1B, ABD GBD = 90 ,BD 二 BD .Rt △ ABD 也 Rt △ C 1B 1D .AD = C 1 D .而 AE = EC 「 ED _ AC 1所以ED 为异面直线BB 1和AG 的公垂线.(2)解:连结 AB 1. AA =AC a; 2AB, AB =BC,. AC 2 二 AB 2 BC 2.GRA =/CBA =90,即 GB j _ 面 ABB 1A 1-AC 1在面ABB A 1内的射影是 AR ..△AC 1D 在面ABB 1A 1内的射影是△ AB 1D .设它们的面积分别为 设 AB = BC = 1 , S 和s ,所成的二面角为则 AC =CG 二.2,AC^2,B 1D2, AD = . AB 2 BD 2 2 26应—1 J2 , 1 S AC 1 DE , S DB 1 AB 2 2 2312 . COST4=-日=—3所以二面角 A - AD - G 的大小为 . 3 如图,在底面为直角梯形的四棱锥 PA = 4, AD = 2 , AB=2 3 , BC = 6. (1)求证:BD 丄平面PAC ;3.(07陕西) P —ABCD B1D B中, AD //BC , ABC = 90 , PA 丄平面 ABCD ,2 2 2cosVBD.BD BV -VD2BD BV sin . VBD BV7,S 4= 3,si n VB D *1 — coS. VB D=—. 4 1 3 VA VD sin 60 = 2 4 cos —SS.21 21,‘ "rccos77所以面VAD 与面VDB 所成二面角的大小为V21arccos —7B1D BBD B2(2)求二面角 A — PC — D 的大小.(1) 证明:在 Rt △ ABD 和 Rt △ ABC 中,.ABC AD = 2 , AB =23 , BC = 6. AD \'3 AB .t a n ABD , t a n ACB = AB 3 BC =.BAD = 90 ,_V 3 —3 . =90 ,二 NABD =NACB =301 而丛ABD +NDBC .ACB . DBC =90,即 BD _ AC . 又 PA 丄平面 ABCD , BD 平面ABCD ,PA AC =A , PA 、AC 二平面 PAC , 故BD 丄平面PAC. (2) 解:连结 PE.由(1)知,BD 丄平面PAC. .△ PDC 在平面PAC 内的射影是△ PEC ,设它们的面积分别为 PA 丄平面ABCD , BC _ AB , BC _ PB (三垂线定理)PB 二.PA 2 AB 2 =2.7,从而 PC 二 PB 2 BC 2 =8.PA 丄 BD . S 和S ,所成的二面角为日.PD 二 PA 2 AD 2 =2、5,DC 二 AB 2 (BC - AD)2 = 2、7 . ■ - ■ BEC=90 , ACB 二 30 , EC 二 BC cos30 -3 3 .PC 2十PD 2_CD 2 cos CPD = 2PC PDPD sin • CPD,si n N CPD =11 - cos 2 也CPD 4、5 = 2、31,S ‘=1EC PA =6 ..3.2 EC3J93 e 31 ,4. (09湖北)如图,四棱柱上的点,且DE 二・a(1) 求证:对任意■ COS T -— S *3B 93 二 arccos .所以二面角 A — PC — D 的大小 arccos- 一31 31 S —ABCD 的底面是正方形, SD 丄平面 ABCD , SD = AD = a ,点E 是SD(0v 1). 0,11,C 丄BE ; 3. 93(2) 若二面角C — AE — D 的大小为60,求■的值. (1) 证明:连结 BD. ■■四边形ABCD 是正方形,.AC _ BD . 又;SD 丄平面ABCD , SD = a ,点E 是SD 上的点, 且 DE = Z a (0v 人 <1), 护, •点E 在线段SD 上,且不与点 D 重合,因而BE 在平面ABCD 内的射影是BD.- .对任意「三I :0,1 1,都有AC 丄BE (三垂线定理)(2) 解:设 AC BD =O ,连结 EO. ■■ SD 丄平面ABCD ,点E 是SD 上的点,CD 平面ABCD , ■ SD _ CD ., 又;四边形ABCD 是正方形,.AD _ CD . 而SD AD = D , SD 、AD 二面SAD. CE 在平面SAD 内的射影是 AE. ■ △ CAE 在在平面SAD 内的射影是△ DAE.设它们的面积分别为 S 和S ' 「60 . S oyB所成的二面角为二,则CAD 二 a, DE 二 a, AC =、2a,EA 二 EC =a 2 (‘ a)2 =、1 •2 a . 2 42 a .2 EO _ AC,EO 」EA 2 - AO 21 J 1 +2人22 S AC EO a 2,S22解得—,所以■的值为一2. 2 2J ED AD = ] ' a 2,C0S ;-—=22S .1 22=12。

教师: 学生: 年级: 科目: 课次: 时间: 年 月 日 内容: 二面角求解方法总结二面角的作与求求角是每年高考必考内容之一,可以做为选择题,也可作为填空题,时常作为解答题形式出现,重点把握好二面角,它一般出现在解答题中。
下面就对求二面角的方法总结如下:1、定义法:在棱上任取一点,过这点在两个面内分别引棱的垂线,这两条射线所成的角就是二面角的平面角。
2、三垂线定理及逆定理法:自二面角的一个面上的一点向另一个面引垂线,再由垂足向棱作垂线得到棱上的点。
斜足与面上一点连线,和斜足与垂足连线所夹的角即为二面角的平面角。
3、作棱的垂面法:自空间一点作与棱垂直的平面,截二面角的两条射线所成的角就是二面角的平面角。
4、投影法:利用s投影面=s被投影面θcos 这个公式对于斜面三角形,任意多边形都成立,是求二面角的好方法。
尤其对无棱问题5异面直线距离法: EF 2=m 2+n 2+d 2-2mn θcos例1:若p 是ABC ∆所在平面外一点,而PBC ∆和ABC ∆都是边长为2的正三角形,PA=6,求二面角P-BC-A 的大小。
分析:由于这两个三角形是全等的三角形, 故采用定义法解:取BC 的中点E ,连接AE 、PEAC=AB ,PB=PC ∴AE ⊥ BC ,PE ⊥BC∴PEA ∠为二面角P-BC-A 的平面角PCBAE在PAE ∆中AE=PE=3,PA=6∴PEA ∠=900∴二面角P-BC-A 的平面角为900。
例2:已知ABC ∆是正三角形,⊥PA 平面ABC 且PA=AB=a,求二面角A-PC-B 的大小。
[思维]二面角的大小是由二面角的平面角 来度量的,本题可利用三垂线定理(逆)来作 平面角,还可以用射影面积公式或异面直线上两点 间距离公式求二面角的平面角。
解1:(三垂线定理法)取AC 的中点E ,连接BE ,过E 做EF ⊥PC,连接BF ⊥PA 平面ABC ,PA ⊂平面PAC∴平面PAC ⊥平面ABC, 平面PAC 平面ABC=AC∴BE ⊥平面PAC由三垂线定理知BF ⊥PC∴BFE ∠为二面角A-PC-B 的平面角设PA=1,E 为AC 的中点,BE=23,EF=42∴tan BFE ∠=6=EFBE∴BFE ∠=argtan 6解2:(三垂线定理法)取BC 的中点E ,连接AE ,PE 过A 做AF ⊥PE, FM ⊥PC,连接FMAB=AC,PB=PC ∴AE ⊥BC,PE ⊥BC∴ BC ⊥平面PAE,BC ⊂平面PBC∴平面PAE ⊥平面PBC, 平面PAE 平面PBC=PEPC AEF MEPCBAF图1由三垂线定理知AM ⊥PC∴FMA ∠为二面角A-PC-B 的平面角设PA=1,AM=22,AF=721.=PE AE AP∴sin FMA ∠=742=AM AF ∴FMA ∠=argsin742解3:(投影法)过B 作BE ⊥AC 于E,连结PE ⊥PA 平面ABC ,PA ⊂平面PAC∴平面PAC ⊥平面ABC, 平面PAC 平面ABC=AC∴BE ⊥平面PAC∴PEC ∆是PBC ∆在平面PAC 上的射影设PA=1,则PB=PC=2,AB=141=∆PEC S ,47=∆PBC S由射影面积公式得,77cosarg ,77=∴==∆∆θθPBC PEC S S COS , 解4:(异面直线距离法)过A 作AD ⊥PC,BE ⊥PC 交PC 分别于D 、E 设PA=1,则AD=22,PB=PC=2 ∴BE=PC S PBC 21∆=414,CE=42,DE=42由异面直线两点间距离公式得 AB 2=AD 2+BE 2+DE 2-2ADBE θCOS ,θCOS =77cos arg ,77=∴θ PCBAEEPCBA D图3图4[点评]本题给出了求平面角的几种方法,应很好掌握。
射影面积法求二面角.
射影面积法是一种求解二面角大小的方法。
对于图形中含有可求原图形面积和该图形在另一个半平面上的射影图形面积的二面角,可以利用射影面积公式(cosθ=S射/S斜)求得其
大小。
例如,在底面为一直角梯形的四棱锥S-ABCD中,
AD∥BC,∠ABC=90°,SA⊥平面ABC,SA=AB=BC=1,
AD=2.要求面SCD与面SAB所成的角的大小,可以利用射影
面积法,求出S△SCD和S△SAB,然后根据cosθ=S射/S斜
的公式计算出二面角θ的大小。
又如,对于三棱锥P-ABC,其中AC=BC=2,∠ACB=90,AP=BP=AB,PC⊥AC。
要求证PC⊥AB,并求二面角B-AP-
C的大小。
可以通过证明△APC≌△BPC和PC⊥BC,进而推
出PC⊥AB。
然后,利用射影面积法,求得S射和S原,根据cosθ=S射/S原的公式计算出二面角B-AP-C的大小。
练题中,要求求解正方体ABCD-A1B1C1D1的棱CC1的
中点E所在平面AB1E和底面A1B1C1D1所成锐角的余弦值。
根据题目的条件,可以得出CE=1/√2,AE=√3/2,因此S射/S
原=1/3,所求二面角的余弦值为cosθ=2/3.
另一题中,要求在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AP=AB=2,BC=2√2,E,F分别是AD,PC的中点。
由于题目中未给出要求的角的具体信息,无
法进行求解。
二面角大小的几种求法二面角大小的求法中知识的综合性较强,方法的灵活性较大,一般而言,二面角的大小往往转化为其平面角的大小,从而又化归为三角形的内角大小,在其求解过程中,主要是利用平面几何、立体几何、三角函数等重要知识。
求二面角大小的关键是,根据不同问题给出的几何背景,恰在此时当选择方法,作出二面角的平面角,有时亦可直接运用射影面积公式求出二面角的大小。
I.寻找有棱二面角的平面角的方法(定义法、三垂线法、垂面法、射影面积法)一、定义法:利用二面角的平面角的定义,在二面角的棱上取一点(特殊点),过该点在两个半平面内作垂直于棱的射线,两射线所成的角就是二面角的平面角,这是一种最基本的方法。
要注意用二面角的平面角定义的三个“主要特征”来找出平面角。
例空间三条射线CA 、CP 、CB ,∠PCA=∠PCB=60o ,∠ACB=90o ,求二面角B-PC-A 的大小。
解:过PC 上的点D 分别作DE ⊥AC 于E ,DF ⊥BC 于F ,连EF.∴∠EDF 为二面角B-PC-A 的平面角,设CD=a ,∵∠PCA=∠PCB=600,∴CE=CF=2a ,DE=DF=a 3,又∵∠ACB=900,∴EF=,∴∠EDF=31328332222=⋅-+a a a a PB αC AE FD二、三垂线法:已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二面角的平面角。
例在四棱锥P-ABCD 中,ABCD 是平行四边形,PA ⊥平面ABCD ,PA=AB=a ,∠ABC=30°,求二面角P-BC-A 的大小。
解:如图,PA ⊥平面BD ,过A 作AH ⊥BC 于H ,连结PH ,则PH ⊥BC 又AH ⊥BC ,故∠PHA 是二面角P-BC-A 的平面角。
在Rt △ABH 中,AH=ABsin ∠ABC=aSin30°=2a ;在Rt △PHA 中,tan ∠PHA=PA/AH=22aa =,则∠PHA=arctan2.三、垂面法:已知二面角内一点到两个面的垂线时,过两垂线作平面与两个半平面的交线所成的角即为平面角,由此可知,二面角的平面角所在的平面与棱垂直。
例谈求解二面角大小的几种方法解㊀曼㊀㊀房维维(哈尔滨师范大学ꎬ黑龙江哈尔滨150025)摘㊀要:求解二面角大小是高中数学立体几何中的重要内容ꎬ有利于丰富学生的数学知识ꎬ提升数学学科核心素养ꎬ激发学生数学学习的动力ꎬ培养学生的空间想象能力ꎬ所以对于高中生来讲ꎬ如何求解成为了重中之重.本文以普通高中教科书为基础ꎬ例谈运用定义法㊁补形法㊁摄影面积法和向量法求解二面角.关键词:定义法ꎻ补形法ꎻ摄影面积法ꎻ向量法中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)19-0037-04收稿日期:2023-04-05作者简介:解曼(1997.7-)ꎬ女ꎬ硕士研究生ꎬ从事数字教学研究ꎻ房维维(1980.9-)ꎬ女ꎬ硕士ꎬ副教授ꎬ从事数学教学研究.㊀㊀中学数学中的二面角是立体几何的基础概念ꎬ值得学生思考重视ꎬ对于学生而言ꎬ只有在平时学习中多多积累求解二面角的方法ꎬ才能在问题探索中不断提高解题能力ꎬ提高数学核心素养.本文对求解二面角的方法进行归纳和总结ꎬ以供读者借鉴和参考.1定义法在定义法中ꎬ二面角的大小是用二面角的平面角来衡量的ꎬ就是在平面α和平面β的交线l上找一点ꎬ过该点在平面α和平面β内分别作垂直于棱的两条射线.如图1ꎬ射线OA与射线OB所夹的角øAOB就是所求的二面角.在定义法中ꎬ二面角的大小是用二面角的平面角来衡量的.适用范围:定义法是最直接的做法ꎬ它适用于比图1二面角图较明显的两个平面相交图形ꎬ在解题时只需要找出两个平面㊁两个射线及射线夹角即可ꎬ对于不太容易找出射线的图形可以借助辅助线来解决ꎬ如例1中的图形[1].例1㊀如图2ꎬ在三棱锥S-ABC中ꎬøSAB=øSAC=øABC=90ʎꎬSA=ABꎬSB=BCꎬ求二面角A-SC-B的平面角的正弦值.解析㊀如图3ꎬ取SC中点Eꎬ连接BEꎬ因为SB=BCꎬ所以әSBC是等腰三角形.图2㊀例1图㊀㊀㊀㊀㊀图3㊀例1定义法解析由等腰三角形三线合一知BEʅSC.过点A作AFʅSC于点Fꎬ过点E作EMʊAF交AC于点Mꎬ连接BMꎬ此时øMEB就是所求的二面角的平面角.设SA=2ꎬ则AB=2.因为øSAB=90ʎꎬ所以SB=22.因为øABC=90ʎꎬ所以AC=BC2+AB2=23.因为øSAC=90ʎꎬ所以SC=SA2+AC2=4.所以øSCA=30ʎꎬCE=2ꎬEM=233.由面积相等ꎬ知AF=SA ACSC=2ˑ234=3.因为әCEMʐәCFAꎬ所以EMAF=CMCA.所以CM=433ꎬAM=233.在RtәBEC中ꎬBE=BC2-CE2=2.由余弦定理ꎬ知cosøCAB=AC2+AB2-BC22AC AB=12+4-82ˑ23ˑ2=33ꎬBM2=AM2+AB2-2AM ABcosøCAB=129+4-2ˑ233ˑ2ˑ33=249ꎬcosøMEB=ME2+BE2-BM22ME BE=12/9+4-24/92ˑ2ˑ23/3=33.所以sinøMEB=63.所以二面角的正弦值为63.2补形法这种方法也是求解二面角大小的重要方法ꎬ通过补形能够顺利地作出二面角的平面角ꎬ从而整体上把握点㊁线㊁面之间的关系ꎬ与定义法有异曲同工之妙.适用范围:补形法顾名思义适用规则不完整的图形ꎬ利用辅助线将平面的图形完整化ꎬ使之有明确的交线ꎬ然后进行解题[2].例2㊀如图4ꎬ四棱锥P-ABCD中ꎬPAʅ平面ABCDꎬ四边形ABCD是一个直角梯形ꎬ其中PA=AD=CD=1ꎬAB=12ꎬøBAD=øADC=90ʎꎬ求平面PAD和平面PBC所成二面角的余弦值.图4㊀例2图㊀㊀㊀㊀㊀㊀㊀图5㊀例2解析图解析㊀如图5ꎬ延长DA和BC交于一点Eꎬ连接PEꎬ因为AB=12ꎬCD=1ꎬ四边形ABCD是一个直角梯形ꎬ所以ABʊCDꎬCDʅADꎬABʅADꎬAE=AD=1.因为PAʅ平面ABCDꎬ所以PAʅABꎬPAʅADꎬDE=AE+AD=2.所以PE=AE2+PA2=2ꎬPD=PA2+AD2=2.所以DE2=PE2+PD2.即PEʅPD.因为PAɘAD于点Aꎬ所以ABʅ平面PEDꎬCDʅ平面PED.所以CDʅPEꎬCDʅPD.因为PDɘCD于点Dꎬ所以PEʅ平面PCD.所以PEʅPC.又因为PEʅPDꎬ所以øCPD就是平面PAD和平面PBC所成的二面角.因为PC=PD2+CD2=3ꎬ所以cosøCPD=PDPC=63.所以平面PAD和平面PBC所成二面角的余弦值为63.以上是在图形中找二面角的平面角从而求出二面角的大小ꎬ除此之外ꎬ还可以用公式法来求解二面角ꎬ公式法的特点是代入公式中就可直接求出二面角的大小ꎬ使用方便ꎬ下面给出两种用公式求二面角的方法[3].3射影面积法利用公式cosθ=S射S原找出其中一个半平面内的多边形在另一个半平面内的射影ꎬ从而利用射影面积与原来面积的比值求出二面角的大小.适用范围:这种方法适合一个面在另一个面内的投影确定的图形[4]ꎬ对于这种方法我们依旧看例1.解析㊀如图6ꎬ过点B作BDʅAC于点Dꎬ图6㊀例1射影面积法图因为øSAB=øSAC=øABC=90ʎꎬ所以SAʅABꎬSAʅAC.所以SAʅ平面ABC.所以SAʅBD.又因为BDʅACꎬ所以BDʅ平面SAC.所以әSDC是әSBC在平面SAC内的投影.设SA=AB=2ꎬ则SB=BC=22ꎬAC=AB2+BC2=23ꎬDB=AB BCAC=2ˑ2223=263ꎬCD=BC2-BD2=22()2-263æèçöø÷2=433.设二面角A-SC-B的平面角为θꎬ则cosθ=SәSDCSәSBC=DC SA/2BC SB/2=43ˑ2/322ˑ22=33.所以sinθ=63.所以二面角的正弦值为63.4向量法在建立空间直角坐标系后ꎬ找出平面α和平面β的法向量n1ꎬn2ꎬ设二面角为θꎬθɪ0ꎬπ[]ꎬ利用公式cosθ=cos‹n1ꎬn2›=n1 n2n1 n2进行求解ꎬ注意‹n1ꎬn2›与二面角大小的关系ꎬ是相等还是互补ꎬ需要结合图形进行判断ꎬ如图7所示ꎬ当两条法向量的方向相同时ꎬ所成的二面角的平面角θ与法向量夹角大小互补ꎬ即cosθ=-cos‹n1ꎬn2›ꎬ当两条法向量的方向相反时ꎬ如图8所示ꎬ所成的二面角的平面角θ与法向量夹角大小相等ꎬ即cosθ=cos‹n1ꎬn2›.图7㊀两条法向量方向相同时㊀㊀图8㊀两条法向量方向相反时适用范围:向量法适用于所有能作平面直角坐标系的图形ꎬ通过找出两个半平面的法向量进而解出题目.其中ꎬ直角坐标系的建立是基础ꎬ而判断两平面的法向量是相等还是互补是难点和关键[5].例3㊀如图9所示ꎬ正方体ABCD-A1B1C1D1的棱长为1ꎬ求二面角A1-BD-C1的余弦值.图9㊀例9图解析㊀如图9ꎬ以D为坐标原点ꎬDAң的方向为x轴ꎬDCң的方向为y轴ꎬDD1ң的方向为Z轴建立空间直角坐标系ꎬ因为棱长为1ꎬ则D0ꎬ0ꎬ0()ꎬA11ꎬ0ꎬ1()ꎬB1ꎬ1ꎬ0()ꎬC10ꎬ1ꎬ1().所以DA1ң=1ꎬ0ꎬ1()ꎬDBң=1ꎬ1ꎬ0()ꎬDC1ң=0ꎬ1ꎬ1().设平面DA1B的法向量为m=xꎬyꎬz()ꎬ则DA1ңm=0.DBңm=0.{即x+z=0ꎬx+y=0.{所以m=1ꎬ-1ꎬ-1().设平面DBC1的法向量为n=aꎬbꎬc()ꎬ则DBңn=0ꎬDC1ңn=0.{即a+b=0ꎬb+c=0.{所以n=-1ꎬ1ꎬ-1().设平面DA1B和平面DBC1所成的二面角为θꎬ则cosθ=m nm n=13.所以二面角A1-BD-C1的余弦值为13[6].以上就是求解二面角大小的四种方法即相应的例题ꎬ在求解二面角的大小时可以根据不同的题型采取不同的方法ꎬ其中有的题型可以用多种方法来进行解决ꎬ需要视情况而定.参考文献:[1]王永军.精解二面角[J].科学咨询(教育科研)ꎬ2022(03):164-167.[2]吴壁章.浅谈二面角大小的求解方法[J].科教文汇(下旬刊)ꎬ2011(07):109-110.[3]杨竞达.求解二面角的策略初探[J].广西教育学院学报ꎬ2003(05):131-135.[4]王治伟.求解二面角问题的策略[J].数学教学通讯ꎬ2009(12):43-46.[5]张东.从2020年一道高考题谈二面角的求法[J].理科考试研究ꎬ2021ꎬ28(17):17-19.[6]郭兴甫.一道2020年全国高考立体几何题的多解及教学反思[J].理科考试研究ꎬ2021ꎬ28(01):5-9.[责任编辑:李㊀璟]。
立体几何-二面角求解五法一、定义法:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。
本定义为解题提供了添辅助线的一种规律。
如例1中从二面角S —AM —B 中半平面ABM 上的一已知点(B )向棱AM 作垂线,得垂足(F );在另一半平面ASM 内过该垂足(F )作棱AM 的垂线(如GF ),这两条垂线(BF 、GF )便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。
例1如图,四棱锥S ABCD -中,底面ABCD 为矩形,SD ⊥底面ABCD ,2AD =2DC SD ==,点M 在侧棱SC 上,ABM ∠=60°(I )证明:M 在侧棱SC 的中点(II )求二面角S AM B --的大小。
解证(I )略 (II ):利用二面角的定义。
在等边三角形ABM 中过点B 作BF AM ⊥交AM 于点F ,则点F 为AM 的中点,过F 点在平面ASM 内作GF AM ⊥,GF 交AS 于G ,连结AC ,∵△ADC ≌△ADS ,∴AS-AC ,且M 是SC 的中点, ∴AM ⊥SC , GF ⊥AM ,∴GF ∥AS ,又∵F 为AM 的中点, ∴GF 是△AMS 的中位线,点G 是AS 的中点。
则GFB ∠即为所求二面角. ∵2=SM ,则22=GF ,又∵6==AC SA ,∴2=AM ∵2==AB AM ,060=∠ABM ∴△ABM 是等边三角形,∴3=BF在△GAB 中,26=AG ,2=AB ,090=∠GAB , ∴211423=+=BG FGFG366232222113212cos 222-=-=⨯⨯-+=⋅-+=∠FB GF BG FB GF BFG ∴二面角S AM B --的大小为)36arccos(-练习1如图,已知四棱锥P -ABCD ,底面ABCD 为菱形,P A ⊥平面ABCD ,60ABC ∠=︒,E ,F 分别是BC , PC 的中点. (Ⅰ)证明:AE ⊥PD ;(Ⅱ)若H 为PD 上的动点,EH 与平面P AD 所成最大角的正切值为6,求二面角E —AF —C 的余弦值. 分析:第1题容易发现,可通过证AE ⊥AD 后推出AE ⊥平面APD ,使命题获证,而第2题,则首先必须在找到最大角正切值有关的线段计算出各线段的长度之后,考虑到运用在二面角的棱AF 上找到可计算二面角的平面角的顶点S ,和两边SE 与SC ,进而计算二面角的余弦值。
在厶GAB中,AG AB = 2 , GAB 二900,cos —BFG 二GF2 FB2 -BG22GF FB丄3-112 22厂2 32-2 63五法求二面角一、定义法:从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。
本定义为解题提供了添辅助线的一种规律。
如例1中从二面角S—AM —B中半平面ABM上的一已知点(B)向棱AM作垂线,得垂足(F);在另一半平面ASM内过该垂足(F)作棱AM的垂线(如GF),这两条垂线(BF、GF)便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。
例1 (2009全国卷I理)如图,四棱锥S-ABCD中,底面ABCD为矩形,SD _底面ABCD, AD=2DC 二SD =2,点M 在侧棱SC上,.ABM =60°(I)证明:M在侧棱SC的中点(II)求二面角S-AM -B的大小。
证(I)略解(II):利用二面角的定义。
在等边三角形ABM中过点B作BF _ AM交AM于点F,则点F为AM的中点,过F点在平面GF交AS于G ,连结AC ,•••△ AD3A ADS 二AS-AC,且M是SC的中点,••• AML SC, GF 丄AM 二GF// AS,又T F 为AM 的中点,••• 6卩是厶AMS的中位线,点G是AS的中点。
贝U ■ GFB即为所求二面角T SM 二2,则GF SA = AC »6 ,• AM =2T AM 二AB =2, . ABM =60°ABM 是等边三角形,• BF *3练习1 (2008山东)如图,已知四棱锥 P-ABCD ,底面ABCD为菱形,PA 丄平面ABCD ,.ABC =60 ,E , F 分别是BC, PC 的中点.(I )证明:AE 丄PD;(n )若H 为PD 上的动点,EH 与平面RAD 所成最大角的正切值为 —1 2 3 4 5 6,求二面角E — AF — C 的余弦值.2分析:第1题容易发现,可通过证AE 丄AD 后推出AE 丄平 面APD 使命题获证,而第 2题,则首先必须在找到最大 角正切值有关的线段计算出各线段的长度之后,考虑到运用在二面角的棱 AF 上找到可计算二面角的平面角的顶点面角的余弦值。
六种方法求二面角从全国19份高考试卷中我们知道,立体几何题中命有求二面角大小的试题共有12份,并都为分值是12分的大题,足以说明这一知识点在高考中的位置,据有关专家分析,它仍然是2010年高考的重点,因此,我们每位考生必须注意,学会其解题方法,掌握其解题技巧,是十分重要的。
一、 定义法:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。
本定义为解题提供了添辅助线的一种规律。
如例1中从二面角S —AM —B 中半平面ABM 上的一已知点(B )向棱AM 作垂线,得垂足(F );在另一半平面ASM 内过该垂足(F )作棱AM 的垂线(如GF ),这两条垂线(BF 、GF )便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。
例1(2009全国卷Ⅰ理)如图,四棱锥S ABCD -中,底面ABCD 为矩形,SD ⊥底面ABCD,AD =2DC SD ==,点M 在侧棱SC 上,ABM ∠=60°(I )证明:M 在侧棱SC 的中点 (II )求二面角S AM B --的大小。
证(I )略解(II ):利用二面角的定义。
在等边三角形ABM 中过点B作BF AM ⊥交AM 于点F ,则点F 为AM 的中点,过F 点在平面ASM 内作GF AM ⊥,GF 交AS 于G ,连结AC ,∵△ADC ≌△ADS ,∴AS-AC ,且M 是SC 的中点, ∴AM ⊥SC , GF ⊥AM ,∴GF ∥AS ,又∵F 为AM 的中点,∴GF 是△AMS 的中位线,点G 是AS 的中点。
则GFB ∠即为所求二面角. ∵2=SM ,则22=GF ,又∵6==AC SA ,∴2=AM ∵2==AB AM ,060=∠ABM ∴△ABM 是等边三角形,∴3=BF在△GAB 中,26=AG ,2=AB ,090=∠GAB ,∴211423=+=BG FG366232222113212cos 222-=-=⨯⨯-+=⋅-+=∠FB GF BG FB GF BFG ∴二面角S AM B --的大小为)36arccos(-练习1(2008山东)如图,已知四棱锥P -ABCD ,底面ABCD 为菱形,P A ⊥平面ABCD ,60ABC ∠=︒,E ,F 分别是BC , PC 的中点. (Ⅰ)证明:AE ⊥PD ;(Ⅱ)若H 为PD 上的动点,EH 与平面P AD 所成最大角E —AF —C 的余弦值. 分析:第1题容易发现,可通过证AE ⊥AD 后推出AE ⊥平面APD ,使命题获证,而第2题,则首先必须在找到最大角正切值有关的线段计算出各线段的长度之后,考虑到运用在二面角的棱AF 上找到可计算二面角的平面角的顶点S ,和两边SE 与SC ,进而计算二面角的余弦值。
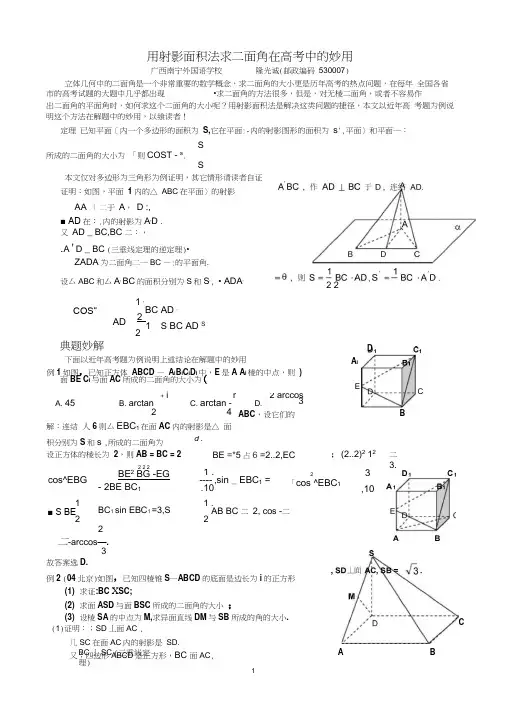
射影面积法(cos
S S 射影原
)
凡二面角的图形中含有可求原图形面积和该图形在另一个半平面上的射影图形面积的都可利用射影面积公式(cos 斜
射S S =
θ)求出二面角的大小。
例1、 如图,在底面是一直角梯形的四棱锥S-ABCD 中, AD ∥BC,∠ABC=90°,SA ⊥平面ABC ,SA=AB=BC=1,
AD=2
1 .求面SCD 与面SAB 所成的角的大小。
解法1:可用射影面积法来求, 这里只要求出S △SCD 与S △SAB 即可, 故所求的二面角θ应满足cos θ=
=
1
112
12322
⨯⨯⨯⨯=
6
3。
例2.(2008北京理)如图,在三棱锥P ABC -中,
2AC BC ==,90ACB ∠=,
AP BP AB ==,PC AC ⊥. (Ⅰ)求证:PC AB ⊥;
(Ⅱ)求二面角B AP C --的大小;
A C
B
P
图1
S
D
C
B
A
解:(Ⅰ)证略
(Ⅱ)AC BC =,AP BP =,APC BPC ∴△≌△. 又PC AC ⊥,PC BC ∴⊥. 又90ACB ∠=,即AC BC ⊥,且AC
PC C =,
BC ∴⊥平面PAC .
取AP 中点E .连结BE CE ,. AB BP =,BE AP ∴⊥.
EC 是BE 在平面PAC 内的射影, CE AP ∴⊥.
∴△ACE 是△ABE 在平面ACP 内的射影, 于是可求得:
2222=+===CB AC AP BP AB ,622=-=AE AB BE ,
2==EC AE 则1222
121=•=•=
=∆CE AE S S ACE 射, 3622
1
21=•=•=
=∆EB AE S S ABE 原 设二面角B AP C --的大小为ϑ,则3
3
3
1cos =
=
=
原
射S S ϑ ∴二面角B AP C --的大小为3
3arccos =ϑ
练习1: 如图5,E 为正方体ABCD -A 1B 1C 1D 1的 棱CC 1的中点,求平面AB 1E 和底面A 1B 1C 1D 1所成 锐角的余弦值.
(答案:所求二面角的余弦值为cos θ=
3
2).
A
C
B
E P A 1
D 1
B 1
1
E
D
B
C
A
图5
2. 如图一,在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,
2AP AB ==,22BC =,E F ,分别是AD PC ,的中点.
(1)证明:PC ⊥平面BEF ;(2)求平面BEF 与平面BAP 夹角的大小. 题(1)解略;题(2)中平面BEF 与平面BAP 夹角即为平面BEF 与平面BAP 所成的锐二面角.
方法一:垂面法
在图中找到或作出一个与二面角的两个半平面均垂直的平面,此平面截得的图形便是二面角的平面角.
如图一:PA ⊥平面ABCD ,BC ⊂平面ABCD ,PA BC ∴⊥.
又
,BC AB AB
PA A ⊥=,BC ∴⊥平面BAP .
又BC ⊂平面PBC ,∴平面PBC ⊥平面BAP . 由题(1),PC ⊥平面BEF ,PC ⊂平面BEF ,∴平面PBC ⊥平面BEF . 所以PBF ∠是所求二面角的平面角.
222221122,22
PB PA AB PF PC AB BC PA =+==
=++, 2sin ,.24
PF PBF PBF PB π
∴∠=
=∠= 即平面BEF 与平面BAP 夹角为
4
π
. 方法二:平移平面法
如果两平行平面同时与第三个平面相交,那么这两个平行平面与第三个平面所成的二面角相等或互补.利用此结论可以平移某一平面到合适的位置以便作出二面角的平面角.
如图二:取BC 的中点G ,连接,FG EG .
,E F 分别是,AD PC 的中点,,EG
AB FG PB ∴.
又
,FG EG G AB PB B ==,
∴平面EFG 平面BAP .
∴二面角B EF G --的大小就是平面BEF 与平面BAP 夹角的大小.
可以证明BFG ∠为二面角B EF G --的平面角,并求出其大小为4
π. 方法三:射影法
利用公式'cos S S
θ=,其中S 表示二面角的一个半平面内某个多边形的面积,'
S 表示
此多边形在另一个半平面射影的面积,θ表示原图形与射影图形所成的二面角.
如图三:取PB 的中点H ,连接,FH AH
,
F 为PC 中点, ,FH BC AE BC ∴.
由解法一知,BC ⊥平面BAP ,
FH ∴⊥平面BAP ,AE ⊥平面BAP ,
∴点F 、E 在平面BAP 内的射影分别为H 、A . BEF ∴∆在平面BAP 上的射影为BAH ∆. 可以证明BEF ∆和BAH ∆均为直角三角形.
1
,,2
HF
BC AE
BC HF BC BC ==
, ∴四边形HFEA 为平行四边形,EF AE ∴=. 记平面BEF 与平面BAP 夹角为θ,则2
cos 2
BAH BEF S S θ∆∆==
, 所以4
πθ=
,即平面BEF 与平面BAP 夹角为
4
π.
3.已知ABC ∆是正三角形,⊥PA 平面ABC 且PA=AB=a,求二面角A-PC-B 的大小。
[思维]二面角的大小是由二面角的平面角 来度量的,本题可利用三垂线定理(逆)来作
E
P
C
B
A
F
平面角,还可以用射影面积公式或异面直线上两点 间距离公式求二面角的平面角。
解1:(三垂线定理法)
取AC 的中点E ,连接BE ,过E 做EF ⊥PC,连接BF ⊥PA 平面ABC ,PA ⊂平面PAC
∴平面
PAC ⊥平面ABC, 平面PAC 平面ABC=AC
∴BE ⊥平面
PAC
由三垂线定理知BF ⊥PC
∴BFE ∠为二面角
A-PC-B 的平面角
设PA=1,E 为AC 的中点,BE=
23,EF=4
2
∴tan BFE ∠=
6=EF
BE
∴BFE ∠=argtan 6
解2:(三垂线定理法)
取BC 的中点E ,连接AE ,PE 过A 做AF ⊥PE, FM ⊥PC,连接
FM
AB=AC,PB=PC ∴
AE ⊥BC,PE ⊥BC
∴ BC ⊥平面PAE,BC ⊂平面PBC
∴
平面PAE ⊥平面PBC, 平面PAE 平面PBC=PE
由三垂线定理知AM ⊥PC
∴FMA ∠为二面角
A-PC-B 的平面角
P
C A
E
F M
图1
图2
设PA=1,AM=
22,AF=7
21
.=PE AE AP
∴sin FMA ∠=
7
42=AM AF ∴FMA ∠=argsin
7
42
解3:(投影法)
过B 作BE ⊥AC 于E,连结PE ⊥PA 平面ABC ,PA ⊂平面PAC
∴平面
PAC ⊥平面ABC, 平面PAC 平面ABC=AC
∴BE ⊥平面
PAC
∴PEC ∆是PBC ∆在平面
PAC 上的射影
设PA=1,则PB=PC=2,AB=1
4
1
=
∆PEC S ,47=
∆PBC S
由射影面积公式得,7
7
cos
arg ,77=∴==
∆∆θθPBC PEC S S COS , 4.在单位正方体1111A B C D ABCD -中, 求二面角1A A C B --的度数。
P
C
B
A
E
图3
一、三垂线法
利用三垂线定理或逆定理构造出二面 角的平面角,进而求解。
解法一. 作1,AO AC ⊥取1A B 的中点M , 连结.OM AM .
1AM A B ⊥
AM BC ⊥ 1A B
BC B =
由三垂线逆定理知
1
OM AC ⊥
AOM ∴∠为所求二面角1A A C B --的平面角 在1Rt A AC 中 111
3AA AC AO AC AC =
⋅=
AM sinAOM AO ∴=
= 60AOM ∴∠= 二.射影法
利用斜面面积和射影面积的关系:S S cos θ=⋅射影斜面 (θ为斜面与射影所成二面角的平面角)直接求解。
解法二、取AC 的中点G ,连结BG
1
1BG AC
BG AA AC
AA A
⊥⊥=
∴ 1A BC 在平面1A AC 上的射影为1A GC
12
Rt
A BC
S =
12244
AGC
Rt
A AG
S
S ==
-= 由 11A GC
Rt
A BC S
S cos θ=⋅ 1
2
cos θ∴=
从而二面角1A A C B --的大小为60。