2-3 割集电压分析法《网络分析与综合》课件

《电网络分析与综合》首先电网络理论是研究电网络（即电路）的基本规律及其分析计算方法的科学，是电工和电子科学与技术的重要理论基础。

“网络分析”与“网络综合”是电网络理论包含的两大主要部分。

本书共十章，第一至六章主要内容为网络分析，第七至十章主要内容为网络综合。

网络分析部分在大学本科电路原理课程的基础上，进一步深入研究电路的基本规律和分析计算方法。

其中，第一章（网络元件和网络的基本性质）包含电网络理论的基本概念与基本定义，是全书的理论基础。

第二、三、四、五章（网络图论和网络方程、网络函数、网络分析的状态变量法、线性网络的信号流图分析法）介绍现代电网络理论中的几类分析电网络的方法。

第六章（灵敏度分析）研究评价电路质量的一个重要性能指标——灵敏度的分析计算方法，为电网络的综合与设计提供必要的工具。

在网络综合部分，除介绍网络综合的基础知识、无源滤波器和有源滤波器综合的基本步骤外，侧重研究得到广泛应用的无源滤波器和有源滤波器的综合方法。

其中，第七、八章（无源网络综合基础、滤波器逼近方法）的内容是进行电网络综合所必须具备的基础知识。

第九章（电抗梯形滤波器综合）对无源LC梯形滤波器的综合方法做了详细介绍。

因为这种滤波器不仅具有优良性能、得到广泛应用，而且在有源RC滤波器以及SC滤波器、SI滤波器等现代滤波器设计中，常以其作为原型滤波器。

第十章（有源滤波器综合基础）在综述有源滤波器基本知识的基础上，介绍几类常用的高阶有源滤波器综合方法。

其中，比较深入地研究了用对无源LC梯形的运算模拟法综合有源滤波器的方法。

第一章主要论述网络的基本元件以及网络和网络与安杰的基本性质。

实际的电路有电气装置、器件连接而成。

在电网络理论中所研究的电路则是实际电路的数学模型，他的基本构造单元时电路元件。

每一个电路元件集中地表征电气装置电磁过程某一方面的性能，用反映这一性能的各变量间关系的方程表示。

电网络的基本变量是电流i、电压u、电荷q、磁通Φ，它们分别对应于电磁场的表征量磁场强度H、电场强度E、电位移D和磁感应强度B。

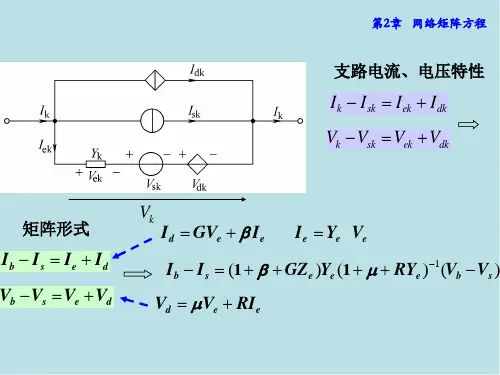
§3-6 割 集 分 析 法一、割集与基本割集1）、割集 割集是支路的集合，它必须满足以下两个条件： （1） 移去该集合中的所有支路，则图被分为两部分。

（2） 当少移去该集合中的任何一条支路，则图仍是连通的。

需要说明的是，在移去支路时，与其相连的结点并不移去。

图G 是一个连通图，如图3－26(a)所示，支路集合{1，5，2}、{1，5，3，6}、{2，5，4，6}均为图G 割集。

将以上割集的支路用虚线表示，分别如图3－26(b)、(c)、(d)所示，不难看出，去掉虚线支路后，各图均被分成了两部分，但是图3－26 图G 及其割集(a)(b)(c)(d)只要少去掉其中的一条虚线支路，图仍然是连通的，故满足割集所要求的条件。

而支路集合{1，5，4，6}、{1，2，3，4，5}不是图G 的割集。

将集合中的支路用虚线表示后如图3－27(a)和(b)所示。

对于图3－27(a)来说，移去支路1、5、4、6后，图虽说被分为两部分（结点①为其中的一部分），但如不移去支路5，图仍被分为两部分；而对于图3－27(b)来说，将支路1、2、3、4、5移去后，图则被分成了三部分，故以上两种支路集合不是割集。

2）、作高斯面确定割集在图G 上作一个高斯面（闭合面），使其包围G 的某些节点，而每条支路只能被闭合面切割一次，去掉与闭合面相切割的支路，图G 将被分为两部分，那么这组支路集合即为图G 的一个割集。

在图G 上画高斯面（闭合面）C 1、C 2、(a)(b)图3－27 非割集说明①②③①②C 3如图3－28所示，对应割集C 1、C 2、C 3的支路集合为{1，5，2}、{1，5，3，6}、{2，5，4，6}。

3）、基本割集基本割集又称单树支割集，即割集中只含一条树支，其余均为连支。

如选支路1、5、3为树支，如图3－29所示，则割集C 1，C 2，C 3为基本割集，基本割集的方向与树支的参考方向一致。

当树选定后，对应的基本割集是唯一确定的。

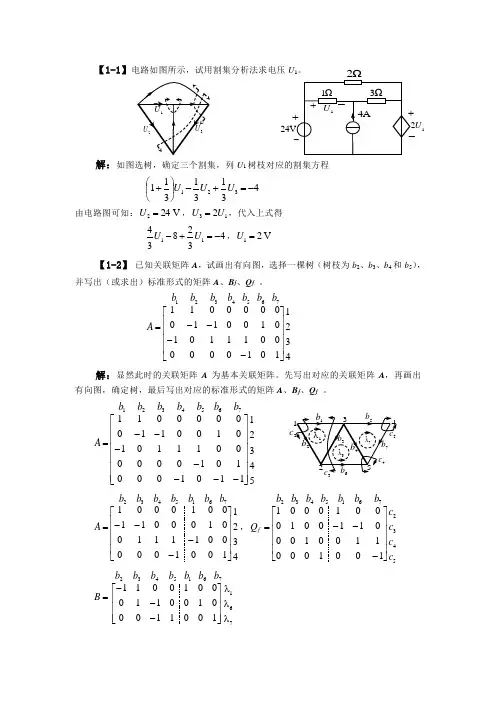
【1-1】电路如图所示，试用割集分析法求电压U 1。

解：如图选树，确定三个割集，列U 1树枝对应的割集方程43131311321-=+-⎪⎭⎫⎝⎛+U U U 由电路图可知：V 242=U ，132U U =，代入上式得43283411-=+-U U ，V 21=U 【1-2】 已知关联矩阵A ，试画出有向图，选择一棵树（树枝为b 2、b 3、b 4和b 5），并写出（或求出）标准形式的矩阵A 、B f 、Q f 。

43211010000001110101001100000011 7654321⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=b b b b b b b A解：显然此时的关联矩阵A 为基本关联矩阵。

先写出对应的关联矩阵A ，再画出有向图，确定树，最后写出对应的标准形式的矩阵A 、B f 、Q f 。

5432111010001010000001110101001100000011 7654321⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------=b b b b b b b A 43211001000001111001000110010001 7615432⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=b b b b b b b A ，543276154321001000110010001100100010001 c c c c b b b b b b b Q f ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=7617615432100110001001100010011 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=b b b b b b b B241Uc【1-3】 电路如图所示，试画出有向图，若选（b 1，b 2，b 5）为树，节点④为参考节点，试写出标准形式的矩阵A 、B f 、Q f 。

解：画出有向图，确定树，写出对应的标准形式的矩阵A 、B f 、Q f 。

321110100011110000011 643521⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=b b b b b b A ，643643521100111010100001011 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=b b b b b b B f 521643521110100101010101001 c c c b b b b b b Q f ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---= 【题2―1】 甲负载对丙负载的相对功率电平比乙负载的绝对功率电平高2N ，能否说明甲负载的绝对功率电平比乙负载的高？为什么？解：不一定，因为：N 2dB dB +=-乙丙甲m p rpN 2dB dB dB +=-乙丙甲m p m p m p N 2dB dB dB +=-丙乙甲m p m p m p显然只有当N 2dB - 丙m p 时，上述论点成立，否则不成立。

第三章：电阻性网络分析的一般方法（节点电压法、网孔电流法）3．1 节点电压法参考点：在电路中任意选择的一点，假设该点的电压为零。

节点电压：其他独立节点与参考点之间的电压。

节点电压法：节点电压法是以节点电压为求解电路的未知量，利用基尔霍夫电流定律和欧姆定律导出（n-1）个独立节点电压为未知量的方程，联立求解，得出各节点电压。

适用范围：结构复杂、非平面电路、独立回路选择麻烦，以及节点少、回路多的电路。

一、节点电压方程式的一般形式步骤：1、选择最佳参考点，标在电路图中。

2、按照节点电压方程的一般形式，根据实际电路直接列出个节点电压方程。

3、联立求解，解出各节点电压。

4、根据节点电压，再求其他待求量。

注意： 1、自电导一定为正，互电导一定为负。

2、方程右边流入节点的电流为正，流出为负。

3、电路中有电压源支路：（1）只有一个电压源支路，把参考节点选在电压源支路的一端，以充分利用已知电压。

（2）有两个以上电压源支路时，对于跨接于两个独立节点之间的电压源支路，一定要假设电流。

或者将电压源与电阻的串联等效成电流源与电阻的并联。

4、电路中含有受控源支路时，一定要写补充方程，即控制量与节点电压的关系式。

例3.3 试用节点电压法求（图8.1）所示电路中的各支路电流。

7 A I（图8.1）解 取节点O 为参考节点, 节点 1、2的节点电压为U 1、U 2, 列出节点方程，得 解之得取各支路电流的参考方向, 如图2.23所示。

根据支路电流与节点电压的关系, 有二、电路中含有理想电压源支路的处理方法例3.4 用节点电压法求（图8.2）所示电路中电流源两端电压u S 和电压源支路中的电流i S 。

解：适当选择参考点，使理想电压源正好跨接在参考点与某一节点之间，该节点电压就是理想电压源的电压。

选择节点4作为参考点，理想电压源正好跨接在参考点与节点之间，各节点电压方程为：节点1： （1/3+1/4）u 1-1/3u 2=-1A7)3121(21321)2111(2121=++-=-+U U U U VU V U 12,621==AU I AU U I AU I 4312332126261612321211===-=-=-====节点1： u2=10V节点1： -1/4 u2+（1/3+1/4）u3=1A联立求解，得：u 1=4V u3=6V电流源两端电压为：u S =u1-u3=-2V八．课堂小结：这节课主要学习了节点电压法的求解过程，在使用节点电压法时，一定要注意电压、电流的参考方向，以及电流源电流的流向。