有限元的matlab编程

matlab 程序2d有限元方法全文共四篇示例，供读者参考第一篇示例：有限元方法是一种数值计算方法，旨在解决工程结构、力学和热力学等领域的复杂问题。

这种方法通过将一个连续的问题离散化为无限多的小单元，然后通过求解每个小单元的方程来逼近整个问题的解。

有限元方法在解决非线性、非定常、多物理场耦合等复杂问题上表现出色，因此在工程领域得到了广泛应用。

2D有限元方法是指在二维平面上建立有限元模型，然后求解其方程得到问题的解。

在MATLAB中，构建2D有限元模型的步骤大致分为三个阶段：几何建模、网格剖分和有限元分析。

首先是几何建模阶段，即对求解问题的几何形状进行建模。

这一步通常通过MATLAB中的绘图函数绘制图形，定义节点和单元信息。

这个阶段的难点在于如何准确表达问题的几何形状和边界条件，因为这将直接影响到后续的网格划分和求解结果的准确性。

接着是网格剖分阶段，即将几何形状离散化为小单元。

在MATLAB中，可以利用自带的网格生成函数或者第三方的网格生成工具箱来生成有限元网格。

网格的质量和密度对求解结果的准确性有很大影响，因此在网格剖分时需要谨慎选择参数和方法。

最后是有限元分析阶段，即对离散化后的有限元模型进行求解。

在MATLAB中，可以利用现成的有限元求解函数来求解线性或非线性方程。

在求解过程中，需要考虑边界条件的处理、材料参数的输入和求解精度的控制等因素，以保证求解的准确性和稳定性。

在实际应用中，2D有限元方法常用于解决板、壳结构的弯曲、扭转、振动等问题，以及流体动力学、电磁场等问题。

MATLAB提供了丰富的工具箱和函数库，使得有限元方法的实现更加简单和高效。

通过合理的建模、网格剖分和求解方法，我们可以快速地解决复杂的工程问题，提高工程设计的效率和精度。

2D有限元方法结合MATLAB工具的应用为工程领域提供了一种高效、准确和可靠的计算方法。

通过不断学习和实践，我们可以更好地利用有限元方法解决实际工程问题，推动工程技术的发展和进步。

一、概述有限元方法是工程学和科学领域中常用的数值分析工具，用于求解复杂的结构力学问题。

在有限元分析中，刚度矩阵是一个重要的概念，它描述了结构的刚度性质，并可以用于求解结构的位移、应力和应变分布。

MATLAB是一款功能强大的数学软件，它提供了丰富的工具和函数，可以用于编程求解有限元刚度矩阵。

本文将介绍如何使用MATLAB编程求解有限元刚度矩阵，并给出详细的步骤和代码示例。

二、有限元刚度矩阵的理论基础有限元分析的基本思想是将一个复杂的结构分解成许多小的单元，每个单元都可以用简单的数学方程描述。

在有限元分析中，每个单元都有一个刚度矩阵，它描述了单元的刚度性质。

结构的总刚度矩阵可以通过合并所有单元的刚度矩阵得到。

总刚度矩阵可以用于求解结构的位移、应力和应变分布，是有限元分析的核心之一。

三、MATLAB编程求解有限元刚度矩阵的步骤在MATLAB中，可以通过以下步骤编程求解有限元刚度矩阵：1. 定义结构的几何形状和材料性质，确定结构的边界条件和加载条件。

2. 将结构分解成有限元单元，根据单元的几何形状和材料性质建立单元的刚度矩阵。

3. 合并所有单元的刚度矩阵，得到结构的总刚度矩阵。

4. 根据边界条件和加载条件，求解结构的位移。

5. 根据结构的总刚度矩阵和位移，计算结构的应力和应变分布。

四、MATLAB编程求解有限元刚度矩阵的代码示例以下是一个简单的MATLAB代码示例，用于求解一维弹簧元的刚度矩阵：```MATLAB定义弹簧元的长度和弹性模量L = 1;E = 1;计算弹簧元的刚度矩阵k = E * A / L;K = [k, -k; -k, k];```以上代码示例中，我们首先定义了弹簧元的长度L和弹性模量E，然后通过公式计算了弹簧元的刚度矩阵K。

这是一个简单的一维情况，实际工程中可能涉及到更复杂的二维、三维情况，但基本的求解步骤是相似的。

五、总结MATLAB是一个强大的数学软件，可以用于编程求解有限元刚度矩阵。

matlab有限元三角形单元编程
在MATLAB中进行有限元分析，可以使用其自带的有限元分析工具箱（FEATool）进行编程。

以下是一个简单的例子，演示如何使用三角形单元进行有限元分析：
1. 打开MATLAB，进入FEATool环境。

2. 创建新的有限元模型。

选择“Model”菜单下的“New Model”选项，进入“Model Builder”界面。

3. 在“Model Builder”界面中，选择“2D Triangle”单元类型，并在绘图区域中绘制出三角形网格。

4. 在“Model Builder”界面中，设置材料属性、边界条件和载荷等参数。

5. 运行有限元分析。

选择“Model”菜单下的“Solve”选项，进行有限元求解。

6. 查看结果。

选择“Model”菜单下的“Results”选项，可以查看位移、应力、应变等结果。

以上是一个简单的例子，演示了如何使用三角形单元进行有限元分析。

在实际应用中，还需要根据具体问题进行详细的建模和计算。

matlab 编写二位静电场有限元程序《MATLAB编写二维静电场有限元程序》在工程领域中，静电场是一个非常重要的概念，它在电力系统、电子设备和传感器等领域都有着广泛的应用。

为了研究和分析静电场的分布情况，有限元方法是一种非常有效的数值计算方法。

本文将探讨如何使用MATLAB编写二维静电场有限元程序，以便更深入地理解这一主题。

一、准备工作在开始编写程序之前，首先需要了解静电场的基本原理和有限元方法的原理。

静电场是由电荷引起的，而有限元方法是一种数值计算方法，用于求解微分方程。

掌握这些理论知识对于编写静电场有限元程序至关重要。

二、程序基本框架1. 定义网格：将二维区域划分为多个小单元，在每个单元内进行计算。

2. 建立有限元方程：根据电场的基本方程和有限元方法，建立离散的数学方程。

3. 求解方程：使用MATLAB的求解器求解离散方程，得到电场分布。

4. 可视化结果：将计算得到的电场分布以图形的形式展现出来，便于分析和理解。

三、具体步骤1. 定义网格：首先需要定义二维区域的网格，在MATLAB中可以使用meshgrid函数来实现。

将区域划分为多个小单元，确定每个单元的节点和连接关系。

2. 建立有限元方程：根据电场的基本方程和有限元方法的原理，建立离散的数学方程。

在二维静电场问题中，通常使用拉普拉斯方程来描述电场分布。

将区域内的拉普拉斯方程离散化，得到线性方程组。

3. 求解方程：利用MATLAB中的矩阵运算和求解器，求解离散化得到的线性方程组，得到每个单元的电场分布。

4. 可视化结果：将计算得到的电场分布以图形的形式展现出来。

可以使用MATLAB的plot函数将电场的大小和方向以矢量图的形式展现出来，也可以使用contour函数将电场的等势线展现出来。

四、个人观点和理解通过编写二维静电场有限元程序，我进一步加深了对静电场和有限元方法的理解。

我也发现了MATLAB强大的数值计算和可视化功能，能够很好地帮助工程师和科研人员进行静电场分析和研究。

题目：使用MATLAB编程实现有限元切线刚度矩阵计算一、引言有限元法是一种用于求解复杂工程问题的数值分析方法，它将连续介质划分为许多小的单元，通过对每个单元进行离散化处理，再用数学方法对这些单元进行组装，最终得到整个结构的解。

在有限元方法中，刚度矩阵是求解结构问题的关键步骤之一，而有限元切线刚度矩阵的计算则是其中的重要内容之一。

本文将介绍如何使用MATLAB编程实现有限元切线刚度矩阵的计算。

二、有限元切线刚度矩阵的基本概念1. 切线刚度矩阵在有限元方法中，切线刚度矩阵是描述结构对外部载荷作用下的应变-应力关系的重要矩阵。

它描述了结构在外部载荷下的变形行为，是求解结构变形和应力的重要工具。

2. 切线刚度矩阵的计算切线刚度矩阵的计算是通过对单元的局部坐标系进行刚度矩阵的求解，并进行坐标变换得到全局坐标系下的切线刚度矩阵。

在实际计算中，需要考虑单元的几何形状、材料性质等因素，以及在单元上施加的外部载荷。

三、MATLAB编程实现有限元切线刚度矩阵的基本步骤1. 单元刚度矩阵的计算我们需要编写MATLAB函数来实现对单元刚度矩阵的计算。

这个函数需要考虑单元的几何形状、材料性质等因素，以及在单元上施加的外部载荷。

通常情况下，我们可以利用数值积分的方法来进行刚度矩阵的计算。

2. 坐标变换矩阵的计算在得到单元刚度矩阵之后，我们需要计算坐标变换矩阵，将单元刚度矩阵从局部坐标系变换到全局坐标系。

这也需要编写一个MATLAB函数来实现坐标变换矩阵的计算。

3. 矩阵组装我们需要将所有单元的切线刚度矩阵组装成整体刚度矩阵。

这通常需要考虑到单元之间的连接关系，以及边界条件等因素。

在MATLAB中，我们可以利用矩阵的组合和相加等运算来实现整体刚度矩阵的计算。

四、编程实例这里我们以一个简单的弹簧-弹簧系统为例，介绍如何使用MATLAB编程实现有限元切线刚度矩阵的计算。

我们需要定义系统的几何形状、材料性质等参数，然后编写MATLAB函数来进行刚度矩阵的计算，坐标变换矩阵的计算，以及矩阵的组装，最终得到整体刚度矩阵，并求解系统的变形和应力。

有限元的MATLAB解法1。

打开MATLAB。

2。

输入“pdetool”再回车，会跳出PDE Toolbox的窗口(PDE意为偏微分方程,是partial differential equations的缩写），需要的话可点击Options菜单下Grid命令，打开栅格.3。

完成平面几何模型：在PDE Toolbox的窗口中，点击工具栏下的矩形几何模型进行制作模型，可画矩形R，椭圆E，圆C，然后在Set formula栏进行编辑并（如双脊波导R1+R2+R3改为RI—R2—R3，设定a、b、s/a、d/b的值从而方便下步设定坐标）用算术运算符将图形对象名称连接起来，若还需要，可进行储存，形成M文件。

4.用左键双击矩形进行坐标设置：将大的矩形left和bottom都设为0，width是矩形波导的X轴的长度，height是矩形波导的y轴的长度,以大的矩形左下角点为原点坐标为参考设置其他矩形坐标。

5。

进行边界设置：点击“Boundary”中的“Boundary Mode”,再点击“Boundary”中的“Specify Boundary Conditions”，选择符合的边界条件,Neumann为诺曼条件,Dirichlet为狄利克雷条件,边界颜色显示为红色.6。

进入PDE模式：点击"PDE"菜单下“PDE Mode”命令，进入PDE 模式，单击“PDE Specification”,设置方程类型,“Elliptic”为椭圆型，“Parabolic”为抛物型，“Hyperbolic"为双曲型，“Eigenmodes"为特征值问题.7。

对模型进行剖分:点击“Mesh”中“Initialize Mesh"进行初次剖分,若要剖的更细,再点击“Refine Mesh”进行网格加密.8。

进行计算：点击“Solve”中“Solve PDE”,解偏微分方程并显示图形解,u值即为Hz或者Ez。

MATLAB源程序（把程序部分复制进入MATLAB，直接运行就可得到结果。

）第1章假定P=-100,L=10m，E=3e11,梁截面是正方形其宽度为h=5e-2m，根据上述数据编制MATLAB程序如下：clearsyms x L EIw='c1'*sin(pi*x/(2*L))+'c2'*sin(3*pi*x/(2*L))+'c3'*sin(5*pi*x/(2*L))+'c4'*sin(7*pi*x/(2*L));kk=int(EI/2*(diff(w,x,2))^2-'P'*w,0,L);[c1,c2,c3,c4]=solve(diff(kk,'c1'),diff(kk,'c2'),diff(kk,'c3'),diff(kk,'c4'),'c1,c2,c3,c4')[c1,c2,c3,c4]根据运行结果得出的[c1,c2,c,3,c4]接着进行下列编程：P=-100;L=10;E=3e11;h=5e-3;I=h^4/12EI=E*I;x=0:L;c1=64*P*L^4/EI/pi^5c2=64/243*P*L^4/EI/pi^5c3=64/3125*P*L^4/EI/pi^5c4=64/16807*P*L^4/EI/pi^5w=c1*sin(pi*x/(2*L))+c2*sin(3*pi*x/(2*L))+c3*sin(5*pi*x/(2*L))+c4*sin(7*pi*x/(2*L))w=1e-4*wplot(x,w,'k','linewidth',2)gridxlabel('L')ylabel('w')y=P*L^3/(3*EI)[y w(10)]假定P=-100,L=10m，E=3e11,梁截面是正方形其宽度为h=5e-2m，根据上述数据编制MATLAB程序如下：clearsyms x EI Lw='c1'*x^2+'c2'*x^3+'c3'*x^4+'c4'*x^5kk=int(EI/2*(diff(w,x,2))^2-'P'*w,0,L)[c1,c2,c3,c4]=solve(diff(kk,'c1'),diff(kk,'c2'),diff(kk,'c3'),diff(kk,'c4'),’c1,c2,c3,c4’)根据运行结果得出的[c1,c2,c,3,c4]接着进行下列编程：P=-100;L=10;EI=1.56e5;x=0:L;c1=1/4*L^2*P/EIc2=-1/6*L*P/EIc3=1/24*P/EIc4=0w=c1*x.^2+c2*x.^3+c3*x.^4+c4*x.^5plot(x,w,'k')gridxlabel('L')ylabel('w')y=P*L^3/(3*EI)[y w(11)]以形函数（Shape Function）为试探函数形函数f1代表左侧节点的位移函数，f2代表右侧节点的位移函数，f3代表左侧节点的斜率函数，f4代表右侧节点的斜率函数。

matlab有限元编程荷载-概述说明以及解释1.引言1.1 概述概述部分的内容可以包括以下内容：有限元方法是一种广泛应用于工程领域的数值计算方法，它通过将复杂的连续体结构分割为一系列简单的子结构，然后利用数学方法为每个子结构建立相应的数学模型，从而得到整个结构的行为特性。

这种分割的过程通常被称为网格划分，而每个子结构则称为有限元。

MATLAB作为一种功能强大的数学软件工具，被广泛应用于有限元方法的编程与分析。

MATLAB提供了大量的工具箱和函数，可以方便地实现有限元方法的各个步骤，包括网格划分、单元构造、边界条件的施加以及结果的可视化分析等。

本文将重点介绍MATLAB在有限元编程中的应用，特别是在荷载分析方面的应用。

荷载分析是有限元分析的核心内容之一，它通过施加不同的荷载条件，分析结构在荷载作用下的变形、位移和应力等。

荷载分析的准确性对于工程设计以及结构安全性的评估至关重要。

文章将首先介绍有限元方法的基本原理，包括对结构的离散化、单元的建立和组装，以及求解过程中的矩阵运算等。

然后，针对荷载分析的特点，将详细介绍MATLAB有限元编程中的荷载处理方法，包括荷载的施加、荷载类型的选择以及荷载与结构响应的耦合关系等。

通过本文的学习，读者可以了解到MATLAB在有限元编程中的应用，并且掌握荷载分析的基本原理和方法。

同时，也可以对MATLAB有限元编程在实际工程问题中的应用进行进一步的探索和研究。

总而言之，本文将为读者提供一个全面而系统的MATLAB有限元编程荷载分析的引导，帮助读者理解有限元方法的基本原理和应用，提高工程设计和结构安全性评估的能力。

1.2 文章结构本文旨在介绍MATLAB在有限元编程中的应用，重点讲解荷载分析的基本原理以及MATLAB有限元编程中的荷载处理方法。

该文章分为引言、正文和结论三个部分。

引言部分对文章进行了概述，包括本文的目的和总结。

在概述中，我们会介绍有限元方法的简要背景和意义，以及MATLAB在该领域中的重要性。

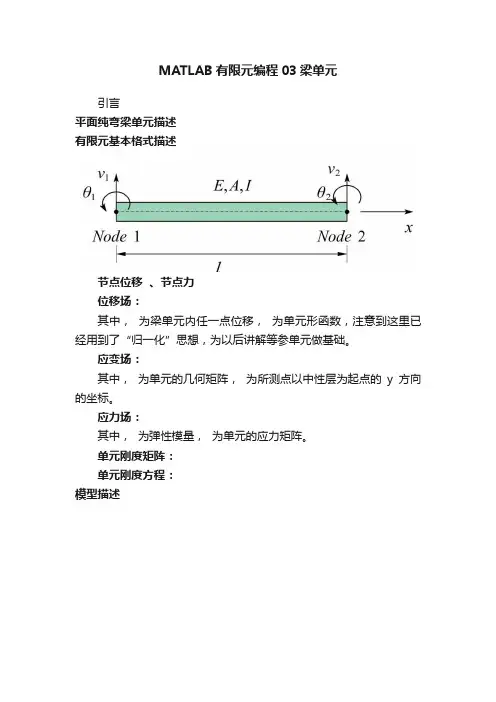
MATLAB有限元编程03梁单元引言平面纯弯梁单元描述有限元基本格式描述节点位移、节点力位移场：其中，为梁单元内任一点位移，为单元形函数，注意到这里已经用到了“归一化”思想，为以后讲解等参单元做基础。

应变场：其中，为单元的几何矩阵，为所测点以中性层为起点的y方向的坐标。

应力场：其中，为弹性模量，为单元的应力矩阵。

单元刚度矩阵：单元刚度方程：模型描述Matlab编程：% 公众号：易木木响叮当，回复梁单元，即可自动获取。

function k =Beam1D2Node_Stiffness(E,I,L)% 直接组装梁单元刚度k = E*I/(L*L*L)*[12 6*L -12 6*L6*L 4*L*L -6*L 2*L*L-12 -6*L 12 -6*L6*L 2*L*L -6*L 4*L*L];function z = Beam1D2Node_Assembly(KK,k,i,j)% 该函数进行整体刚度矩阵的组装% 输入单元刚度矩阵k，单元的节点编号i、j% 输出整体刚度矩阵KKDOF(1)=2*i-1;DOF(2)=2*i;DOF(3)=2*j-1;DOF(4)=2*j;for n1=1:4for n2=1:4KK(DOF(n1),DOF(n2))= KK(DOF(n1),DOF(n2))+k(n1,n2); endendz=KK;function v = Beam1D2Node_Deflection(x,L,u)% 该函数计算单元内某点的挠度% 输入所测点距梁单元左节点的水平距离x% 输入梁单元的长度L，节点位移列阵ue=x/L;N1=1-3*e*e+2*e*e*e;N2=L(e-2*e*e+e*e*e);N3=3*e*e-2*e*e*e;N4=L(e*e*e-e*e);N=[N1,N2,N3,N4];v=N*u% -----------主程序----------------format compactE = 200*10^9;I = 118.6*10^-6;L1 = 5;L2 = 2.5;% cal element stiffnessk1 = Beam1D2Node_Stiffness(E,I,L1);k2 = Beam1D2Node_Stiffness(E,I,L2);% stiffness assemblyKK = zeros(6,6);KK = Beam1D2Node_Assembly(KK,k1,1,2);KK = Beam1D2Node_Assembly(KK,k2,2,3)% cal displacementk = KK(4:6,4:6);p = [39062;-31250;13021];u = k\p% cal node forceU = [0;0;0;u];P = KK*U% cal RFF = [-62500;-52083;-93750;39062;-31250;13021];RF = P-F最终计算得到的支反力、节点位移值与书中解析解一致，可自行验证。