模糊数学例题大全

模糊数学例题大全标题：模糊数学例题大全模糊数学，又称为模糊性数学或者弗晰数学，是一个以模糊集合论为基础的数学分支。

它不仅改变了过去精确数学的观念，而且广泛应用于各个领域，从物理学、生物学到社会科学，甚至。

下面，我们将通过一些具体的例题来展示模糊数学的应用。

例1：模糊逻辑门在经典的逻辑门中，我们使用AND、OR和NOT等操作符来处理布尔值（0或1）。

然而，在现实世界中，很多情况并不是绝对的0或1。

例如，我们可以将“温度高”定义为大于25度，但24度是否算高呢？模糊逻辑门提供了更广泛的定义方式，允许我们使用模糊集合来描述这些边界情况。

例2：模糊聚类分析在统计学中，聚类分析是一种将数据集分类成几个组的方法，其中同一组内的数据点相似度高。

然而，在某些情况下，我们无法用精确的数值来描述数据点的相似度。

这时，模糊聚类分析就派上用场了。

它允许我们使用模糊矩阵来表示数据点之间的相似度，从而更准确地分类数据。

例3：模糊决策树在机器学习中，决策树是一种用于分类和回归的算法。

然而，在某些情况下，我们无法用精确的规则来描述决策过程。

这时，模糊决策树就派上用场了。

它允许我们在决策节点使用模糊规则来代替传统的布尔值规则，从而更好地模拟人类的决策过程。

例4：模糊控制系统在控制系统中，我们通常需要设计一个控制器来控制系统的行为。

然而，在某些情况下，系统的输入和输出并不是绝对的0或1。

这时，模糊控制系统就派上用场了。

它允许我们使用模糊集合来描述系统的输入和输出，从而更准确地控制系统的行为。

例5：模糊图像处理在图像处理中，我们通常需要分类、识别或分割图像中的对象。

然而，在某些情况下，图像中的对象边界并不清晰。

这时，模糊图像处理就派上用场了。

它允许我们使用模糊集合来描述图像中的对象边界，从而更准确地分类、识别或分割图像中的对象。

以上只是模糊数学众多应用的一小部分。

这个领域仍在不断发展，为解决各种复杂的现实问题提供了新的工具和方法。

通过学习模糊数学，我们可以更好地理解和处理那些边界模糊、难以用传统数学方法描述的问题。

模糊数学作业模糊数学1.模糊集合及其运算部分作业：设{}54321,,,,x x x x x U ==16.05.04.05.06.015.04.05.05.05.014.08.04.04.04.014.05.05.08.04.01R ，求8.05.0,R R解：=11101111011110100010111015.0R ，=10000010*******00010001018.0R 2.模糊聚类分析部分作业1）设有模糊相似矩阵如下：??=16.05.06.014.05.04.01R ，试求其传递闭包。

2）模糊聚类问题某高中高二有7个班级，学生成绩的好与差，没有明确的评定界限，并且班级间成绩好坏的表现具有一定的模糊不确定性。

各班级成绩指标值见表1。

表1 7个班4门基础课的成绩指标解：问题的分析：解决上述问题可运用模糊聚类分析方法。

现以7个班级某次其中考试的四门主课成绩为依据，对7个班级成绩好坏的相关程度分类。

设7个班级组成一个分类集合：127(,,,)X x x x =分别代表1班到7班。

每个班级成绩均是四门基础课(语文、数学、英语、综合)作为四项统计指标，即有1234{,,,}ij i i i i X X X X X =这里ij X 表示为第i 个班级的第j 门基础课指标(1,2,,7;1,2,,4)i j ==。

这四项成绩指标为：语文平均成绩1i X ，数学平均成绩2i X ，英语平均成绩3i X ，综合平均成绩4i X 。

问题的解决：1、数据标准化采用极差变换min max minij ijx x X x x -'=-，（1）式中ij x 是第i i 个班级第j 门基础课平均成绩的原始数据，max x 和min x 分别为不同班级的同一门基础课平均成绩的最大值和最小值。

ijX '为第i 个班级第j 门基础课平均成绩指标的标准化数值。

当min ij x x =时，0x '=，当 max ij x x =时，1x '=。

(2.1) 给出下列各个集合的幂集（1） A={1} (2) B={a ，b} (3) C={a ，b ，c} (4) D={1，Ф} (2.2) 设A={a ，b}，B={m ，n}，C=Ф，求：（1）A ⨯B （2）A ⨯C (2.3) X={1，2，3，4，5，6，7}，∈A F (X)，其隶属度)(x A μ如下：1.0)1(=A μ， 3.0)2(=A μ， 8.0)3(=A μ， 1)4(=A μ， 8.0)5(=A μ，3.0)6(=A μ，0)7(=A μ（1） 分别别用查德法、向量法、序偶法表示A ； （2） 求c A ；（3） 指出A 的意义。

(2.4) 已知模糊集 “老年” O 和“年轻”Y 的隶属函数分别为⎪⎩⎪⎨⎧>-+≤≤=--时。

当时。

，当50,])550(1[5000)(12x x x x O μ ⎪⎩⎪⎨⎧≤<-+≤≤=-时。

当时。

，当20025,])525(1[2501)(12x x x x Y μ 试写出模糊集“不老”和“既不老又不年轻”的隶属函数。

(2.5) 设∈C B A ,,F (X)，如下表：求;)(;)(;;ccB A B A B A B A ⋂⋃⋂⋃C B A C B A C B A cc cc⋃⋂⋃⋃⋂⋃)(;)(;)( (2.6) 设X=[0，1]，x x A =)(μ，x x c A -=1)(μ；试证（F (X)，c,,⋂⋃）不满足互补律。

(2.7) 已知∈B A ,F (X)，试证)()(C B A C B A ⋃⋃=⋃⋃ (2.8) 设},,,,{54321x x x x x X =，543213.08.017.02.0x x x x x A ++++=543216.011.017.0x x x x x B ++++=，求B A B A ⋃⋂; (2.9) 任取Fuzzy 集],[X F A ∈ 若存在X x ∈0, 使)1,0()(0∈=a x A μ，证明：对任意][X F B ∈，X B A B A =Φ= ,至少有一个不成立。

3. 证明: (2) 设n m ij n m ij b B a A ××==)(,)(，则ij ij ij ij ij ij ij ij a b a b b a b a B A =∧⇔=∨⇔≤⇔⊆。

即A B A B B A B A =∩⇔=∪⇔⊆(4) 设，则，。

故,)(n m ij a A ×=,)()(n m ij a A ×=λλm n ij T c A ×=)()(λ11)(=⇔≥⇔=λλji ji ij a a c 00)(=⇔<⇔=λλji ji ij a a c T T A A )()(λλ=5. 证明：先用归纳法证A B B A k k o o =，事实上，k =1时成立，设k=n 时成立，即A B B A n n o o =， k=n+1时，B A B B B A B A n n n o o o o o ==+1，A B A B B n n o o o 1+==，故有A B B A k k o o =再证。

事实上，k =1时成立，设k=n 时成立，即k k k B A B A o o =)(n n n B A B A o o =)( k=n+1时， B B A A B A B A B A B A B A n n n n n n o o o o o o o o o o ===+)()()(111++=n n B A o 。

故有k k k B A B A o o =)(6. 证明：用归纳法。

m =1时成立，设m=n 时成立，m=n +1 时，11)()()()()(++∪∪∪=∪∪∪∪=∪∪=∪n n n n A A I A I A A I A I A I A I L o L o 故m=n +1 时成立。

所以有m m A A I A I ∪∪∪=∪L )(8. 证明：设，由A, B 都是模糊自反矩阵，，所以，，n n ij n n ij b B a A ××==)(,)(1,1==ii ii b a 1=∨ii ii b a 1=∧ii ii b a 1)()(=∧≥∧∨ii ii ki ik b a b a ，又，因此有1)(≤∧∨ki ik b a 1)(=∧∨ki ik b a 。

模糊数学八题襄阳纪委程元银1、吃苹果的题目有甲乙二人各自以匀速吃同样大小的苹果。

现在两人同时吃第一口，以后甲吃第二个时，乙也在吃第二个；甲吃第三个时，乙也在吃第三个。

当甲吃第五个时，问乙在吃第几个？这里使用了模糊语言“在……时”，而这是一个连续的过程，所以竟有6个不同的答案。

即甲吃第五个时，乙正在吃第三个、第四个……或第八个。

现在从甲乙都在吃第三个时来分析。

这第三个，也就是大于2而小于3的数。

假如甲吃到2.99（以下都只取两位小数）时，乙吃到2.01，那么甲的速度是乙的1.48倍。

当甲吃第五个吃到4.01时，则乙吃到2.70，应是第三个；甲吃到4.52时，乙吃到3.05，应是第四个；或者甲乙的速度是一样的，则甲吃第五个时，乙也在吃第五个；反过来，若乙的速度是甲的1.48倍，那么当甲吃第五个吃到4.01时，则甲吃到5.93，也就是第六个；甲吃到4.41时，乙吃到6.52，即第七个；甲吃到4.81时，乙吃到7.11，应是第八个。

2、求学校人数某小学有20多个班级，每班平均有60多个学生，而该校共有2000多学生。

上面所说的“多”是一个模糊数，它可以是1—9中间任一数字。

经计算，这20多个班只能是29个班，60多人只能是69人，而2000多学生也只能是2001人。

3、赢了多少钱老陈头2013年打麻将，每次筹码分别为5元、10元、20元或者50元。

全年在固定点打牌赢钱4000多元，在其他地方输钱不到4000元。

上述的4000多元和不到4000元是两个模糊数。

其中4000多元最大可能是4995元，最小可能是4005元；而不到4000元最多会是3995元，最少会是3005元。

那么老陈头全年赢钱最多为1990元，最少为10元。

4、13分钟多于14分钟？老陈头攀登烈士塔山，第一次在山脚下起始时间是8点00分，达到山顶是8点13分；第二次在山脚下起始时间也是8点00分，达到山顶是8点14分。

粗看起来，第二次比第一次多用了1分钟。

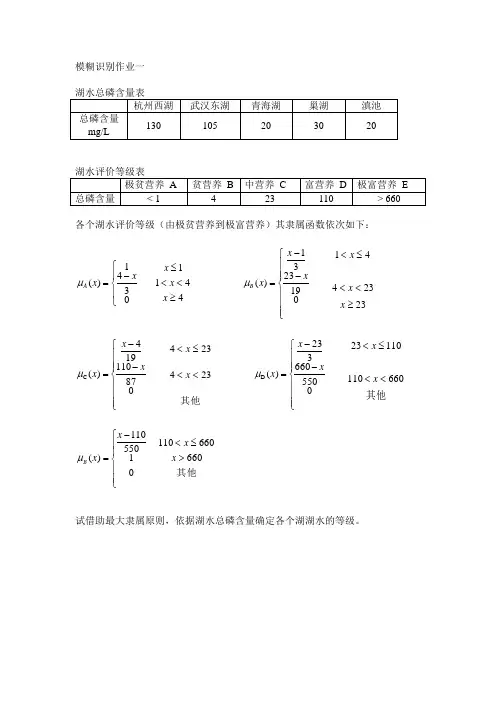
模糊识别作业一各个湖水评价等级（由极贫营养到极富营养）其隶属函数依次如下：44110341)(≥<<≤⎪⎩⎪⎨⎧-=x x x x x A μ ⎪⎪⎪⎩⎪⎪⎪⎨⎧--=0192331)(xx x B μ 2323441≥<<≤<x x x⎪⎪⎪⎩⎪⎪⎪⎨⎧--=087110194)(C x x x μ 其他234234<<≤<x x ⎪⎪⎪⎩⎪⎪⎪⎨⎧--=0550660323)(D xx x μ 其他66011011023<<≤<x x其他66066011001550101)(>≤<⎪⎪⎩⎪⎪⎨⎧-=x x x x B μ试借助最大隶属原则，依据湖水总磷含量确定各个湖湖水的等级。

模糊识别作业二现有茶叶等级标准样品五种：EBA，其中放映茶叶质量的因素CD论域为U，{}条索=U。

假设各个等级的模糊色泽汤色香气滋味净度集为：5.0(=A4.05.03.0)4.06.03.0(B=2.02.02.0)2.01.02.02.0(=C2.0)2.01.01.00(=D1.02.0)1.01.01.00(E1.0=1.01.0)1.01.0现有一样品，其模糊集为：4.0(L=2.0)6.01.05.04.0试依据择近原则确定该样本属于哪一等级。

模糊聚类分析作业一下表表示的是某地区12个县从1981—1990年的降水量，试根据以下数据，按降水量将12个县进行分类。

通过数据标准化，构建模糊相似矩阵，合成模糊等价矩阵，基于模糊等价矩阵，选取适当的λ值，进行模糊聚类分析，给出分类结果。

模糊聚类分析作业二下表是2002年安徽省各地市工业企业效益指标利用C均值进行聚类分析，给出分类结果。

模糊综合评价作业一下表反映的是上海，北京，天津，云南的科技技术进步情况，请进行综合评价，确定这四个地区的排名。

根据相对偏差模糊矩阵评价方法进行综合评价，确定排名。