初二数学 温故班 第七天 乘方和开方

小学数学拓展数学知识认识正数与负数的乘方与开方正数与负数是数学中的基本概念，而乘方与开方则是数学中的重要运算规则。

本文将介绍小学数学中对正数与负数进行乘方与开方的认识和运算方法。

一、正数的乘方正数的乘方是指将一个正数连乘若干次。

具体地说，正数的乘方运算可以通过将这个正数连乘多次来实现，指数表示了连乘的次数。

例如，正数2的乘方可以表示为：2的3次方，即2^3，它等于2×2×2=8。

同样地，正数的乘方还可以表示为小数的乘方和分数的乘方。

例如，正数4的1/2次方表示为4^(1/2)，我们通常将其称为4的平方根，即√4，它等于2。

正数4的1/3次方表示为4^(1/3)，我们通常将其称为4的立方根，即∛4，它约等于1.587。

二、负数的乘方负数的乘方是指将一个负数连乘若干次。

与正数的乘方类似，负数的乘方的指数也表示了连乘的次数。

然而，需要注意的是，当指数为偶数时，负数的乘方结果为正数；当指数为奇数时，负数的乘方结果为负数。

例如，负数-2的乘方，如(-2)^2，表示将-2连乘两次：(-2)×(-2)，结果为正数4。

而(-2)^3表示将-2连乘三次：(-2)×(-2)×(-2)，结果为负数-8。

三、正数与负数的开方开方是乘方的逆运算，即求一个数的平方根、立方根等。

对于正数，它的平方根和立方根都可以求解。

我们可以通过数学运算还原一个数的平方根和立方根。

例如，数值16的平方根是正数4，记作√16=4。

数值27的立方根是正数3，记作∛27=3。

对于负数，它的平方根和立方根则存在一些特殊规律。

我们无法在实数范围内找到一个实数来表示负数的平方根。

因此，负数的平方根通常在数学中被记作虚数。

例如，数值-16的平方根被记作√(-16)=4i，其中i表示虚数单位，满足i^2=-1。

因此，√(-16)=4i。

同样地，负数的立方根可以通过虚数单位来表示。

例如，数值-27的立方根被记作∛(-27)=3√3i。

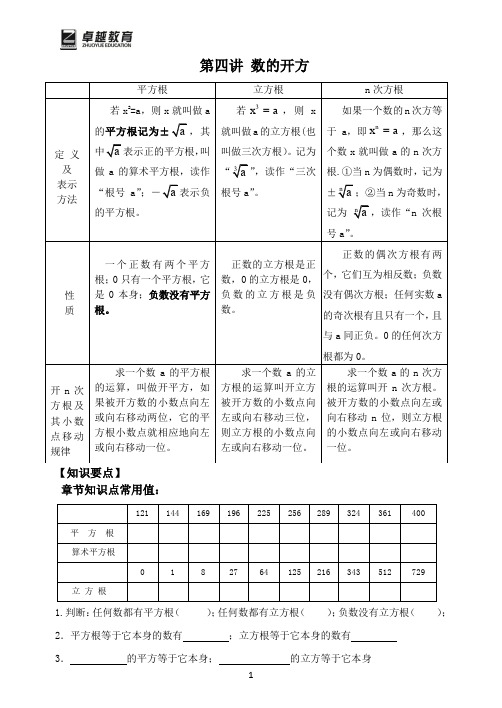
第四讲 数的开方【知识要点】章节知识点常用值：1.判断：任何数都有平方根（ ）；任何数都有立方根（ ）；负数没有立方根（ ）； 2．平方根等于它本身的数有 ；立方根等于它本身的数有 3． 的平方等于它本身； 的立方等于它本身【例1】①求下列各数的平方根及算术平方根：196169， ()25-， 24125， 0.0256②求下列各式的值： 36254+±， 224041-，，③求下列各数的平方根及立方根：164-， 729， 610-【例2】 解下列方程①32)4()1(100-=--x ②22240x x +-=③381250x += ④()31x -=【例3】 1.887= 5.966=35.12=.① 的值。

② 188.7=59.66=，求x 、y 的值。

③ 0.3512=，求x 。

【例4】已知：已知△ABC 的三边长分别为a 、b 、c, 且a 、b 、c 满足 054962=-+-++-c b a a ，试判断△ABC 的形状．【例5】已知0)2(12=-+-ab a ， 求：)2004)(2004(1)2)(2(1)1)(1(11++++++++++b a b a b a ab 的值。

【初试锋芒】1. 有如下命题：①负数没有立方根；②一个实数的立方根不是正数就是负数；③一个正数或负数的立方根和这个数同号，0的立方根是0；④如果一个数的立方根是这个数本身，那么这个数必是1或0。

其中错误的是（ ）A ．①②③B ．①②④C ．②③④D ．①③④2．下面各式无意义的是（ ）A ．2x B ．2- C ．2)2(- D ．32-3的立方根是（ ）A ．±4B ．±2C ．2D ．－2 4．若()225a =-，()335b =-，则a b +的值为（ ）A ．－10B ．0C ．0或－10D ．0，－10或1050=，则x y +=（ ）A ．9B ．10C ．11D ．12 6．若a 是2)3(-的平方根，则3a =( )A ．-3B ．33C ．33±D ．±3 7．若32b -是2—b 的立方根，则（ ）A ．b ＜2B ．b －2C ．b ≤2D ．b 可以是任意数 8．一个自然数的一个平方根是m -，那么紧跟它后面的一个自然数的平方根是（ ） A ．1+m B ．12+m C ．1+±m D ．12+±m92，则a= 。

中班数学学习数字的乘方和开方数学是幼儿园教育中不可或缺的一部分，通过数学学习，幼儿培养了逻辑思维、观察问题和解决问题的能力。

其中，数字的乘方和开方是数学中的重要概念，帮助幼儿理解数字的变化和推理能力的培养。

本文将介绍中班幼儿在数学学习中，如何理解和应用数字的乘方和开方。

一、数字的乘方在中班数学学习中，幼儿会接触到数字的乘方概念。

乘方是指将一个数字作为底数，然后重复乘以自身若干次。

幼儿可以通过实际操作、图形表示和练习题来理解乘方的概念。

1. 实际操作通过实际操作，幼儿可以直观地体验数字的乘方。

例如，教师可以给每个幼儿发放一定数量的小糖果，然后要求他们计算出自己手中小糖果的总数。

通过重复加法操作，幼儿可以发现每次都是将手中的糖果数量乘以相同的倍数，这样就引出了数字的乘方概念。

2. 图形表示图形表示是幼儿学习乘方概念的有效方法。

教师可以通过绘制图形，帮助幼儿理解乘方的含义。

例如，教师可以给幼儿展示一张正方形的图纸，让幼儿计算正方形周长，然后引导幼儿发现周长等于边长乘以4，即4的乘方。

3. 练习题练习题是巩固数字乘方概念的重要途径。

教师可以设计一些简单的乘方计算题，让幼儿进行练习。

通过多次练习，幼儿可逐渐理解数字的乘方，并能够熟练地进行计算。

二、数字的开方除了乘方，中班的幼儿还会接触到数字的开方概念。

开方是乘方的逆运算，即求得一个数的平方根。

幼儿可以通过实际操作、图形表示和游戏活动来理解开方的概念。

1. 实际操作教师可以提供一些平方数的物品，如一个正方形的纸片或棋盘等，要求幼儿找到相应的平方根。

通过实际操作，幼儿可以感受到平方根与平方数之间的关系，从而理解开方的概念。

2. 图形表示通过图形表示，幼儿可以直观地理解开方的含义。

教师可以绘制一些不规则图形，要求幼儿根据图形的面积来计算平方根。

通过观察图形和计算，幼儿可以体会到开方与面积之间的关系。

3. 游戏活动游戏活动可以激发幼儿学习的兴趣，帮助幼儿更好地理解开方。

初二数学知识点归纳临近考试了，各科都会整理好知识点复习。

接下来是小编为大家整理的初二数学知识点归纳，希望大家喜欢!初二数学知识点归纳一第十一章三角形一、知识框架：二、知识概念：1、三角形：由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

2、三边关系：三角形任意两边的和大于第三边，任意两边的差小于第三边。

3、高：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足间的线段叫做三角形的高。

4、中线：在三角形中，连接一个顶点和它对边中点的线段叫做三角形的中线。

5、角平分线：三角形的一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线。

6、三角形的稳定性：三角形的形状是固定的，三角形的这个性质叫三角形的稳定性。

7、多边形：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形。

8、多边形的内角：多边形相邻两边组成的角叫做它的内角。

9、多边形的外角：多边形的一边与它的邻边的延长线组成的角叫做多边形的外角。

10、多边形的对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线。

11、正多边形：在平面内，各个角都相等，各条边都相等的多边形叫正多边形。

12、平面镶嵌：用一些不重叠摆放的多边形把平面的一部分完全覆盖，叫做用多边形覆盖平面，13、公式与性质：⑴三角形的内角和：三角形的内角和为180°⑵三角形外角的性质：性质1：三角形的一个外角等于和它不相邻的两个内角的和。

性质2：三角形的一个外角大于任何一个和它不相邻的内角。

⑶多边形内角和公式：边形的内角和等于·180°⑷多边形的外角和：多边形的外角和为360°。

⑸多边形对角线的条数：①从边形的一个顶点出发可以引条对角线，把多边形分成个三角形。

②边形共有条对角线。

第十二章全等三角形一、知识框架：二、知识概念：1、基本定义：⑴全等形：能够完全重合的两个图形叫做全等形。

⑵全等三角形：能够完全重合的两个三角形叫做全等三角形。