第四强度理论校核
- 格式：doc
- 大小：446.50 KB
- 文档页数：2
下载文档原格式
合集下载
材料力学第五版课后习题答案
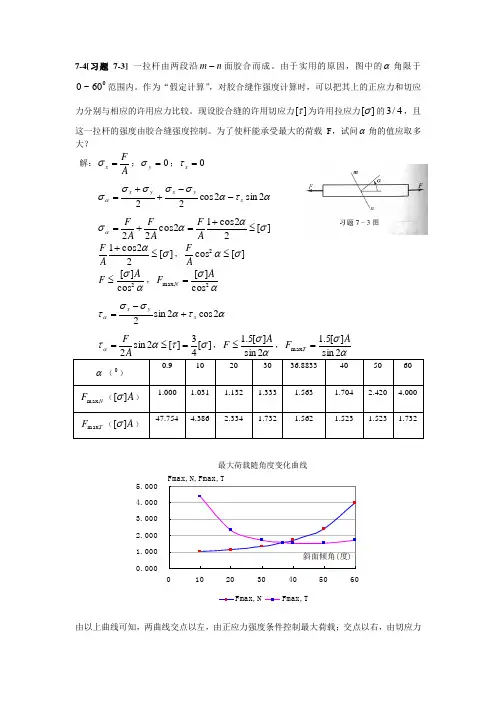
7-4[习题7-3] 一拉杆由两段沿n m -面胶合而成。
由于实用的原因，图中的α角限于060~0范围内。
作为“假定计算”，对胶合缝作强度计算时，可以把其上的正应力和切应力分别与相应的许用应力比较。
现设胶合缝的许用切应力][τ为许用拉应力][σ的4/3，且这一拉杆的强度由胶合缝强度控制。
为了使杆能承受最大的荷载F ，试问α角的值应取多大？ 解：AFx =σ；0=y σ；0=x τ ατασσσσσα2s i n 2c o s 22x yx yx --++=][22cos 12cos 22σαασα≤+=+=A F A F A F ][22cos 1σα≤+A F ，][cos 2σα≤AFασ2cos ][A F ≤，ασ2max,cos ][AF N = ατασστα2c o s 2s i n 2x yx +-=][3][2sin στατα=≤=F ，σ][5.1A F ≤，σ][5.1max,AF T =由切应力强度条件控制最大荷载。
由图中可以看出，当060=α时，杆能承受最大荷载，该荷载为：A F ][732.1max σ=7-6[习题7-7] 试用应力圆的几何关系求图示悬臂梁距离自由端为m 72.0的截面上，在顶面以下mm 40的一点处的最大及最小主应力，并求最大主应力与x 轴之间的夹角。
解：（1）求计算点的正应力与切应力MPa mm mm mm N bh My I My z 55.1016080401072.01012124363=⨯⨯⋅⨯⨯⨯===σMPa mm mm mm N bI QS z z 88.0801608012160)4080(10104333*-=⨯⨯⨯⨯⨯⨯⨯-==τ （2）写出坐标面应力 X （10.55，-0.88）Y （0，0.88）(3) 作应力圆求最大与最小主应力，并求最大主应力与x 轴的夹角 作应力圆如图所示。
从图中按比例尺量得：MPa 66.101=σ MPa 06.03-=σ 0075.4=α7-7[习题7-8] 各单元体面上的应力如图所示。
13-3四个强度理论-材料力学
体，求主应力。 4、强度分析：选择适当的强度理论，计算相当应力，进行
强度计算。
例1 图示几种单元体，分别按第三和第四强度理论 求相当应力（单位MPa)
60
100
（1）
40 100
40
（2）
10
60
30 （3）
例2 直径为d=0.1m的圆杆受力如图,T=7kNm,P=50kN, 为铸铁构
件，[]=40MPa,试用第一强度理论校核杆的强度。
7.7
0
0
所以，此容器不满足第三强度理论。不安全。
第三强度理论（第三相当应力） xd3 1 3
第四强度理论（第四相当应力）
xd 4
1 2
1
2
2
2
3
2
3
1
2
三、强度计算的步骤：
1、外力分析：确定所需的外力。 2、内力分析：画内力图，确定可能的危险面。 3、应力分析：画危险截面应力分布图，确定危险点并画出单元
2
1
2 2
2
3 2
3
1 2
3、实用范围：实用于破坏形式为屈服的构件。
第一、第二强度理论适合于脆性材料； 第三、第四强度理论适合于塑性材料。 1、伽利略1638年提出了第一强度理论； 2、马里奥特1682年提出了第二强度理论；
3、杜奎特（C.Duguet)提出了最大剪应力理论；也有一说是库 伦1773年提出，特雷斯卡1868完善的。
到单向拉伸的强度极限时，构件就发生断裂。
1、破坏判据： 1 b ;( 1 0)
2、强度准则： 1 ; ( 1 0)
3、实用范围：实用于破坏形式为脆断的构件。
强度计算。
例1 图示几种单元体，分别按第三和第四强度理论 求相当应力（单位MPa)
60
100
（1）
40 100
40
（2）
10
60
30 （3）
例2 直径为d=0.1m的圆杆受力如图,T=7kNm,P=50kN, 为铸铁构
件，[]=40MPa,试用第一强度理论校核杆的强度。
7.7
0
0
所以，此容器不满足第三强度理论。不安全。
第三强度理论（第三相当应力） xd3 1 3
第四强度理论（第四相当应力）
xd 4
1 2
1
2
2
2
3
2
3
1
2
三、强度计算的步骤：
1、外力分析：确定所需的外力。 2、内力分析：画内力图，确定可能的危险面。 3、应力分析：画危险截面应力分布图，确定危险点并画出单元
2
1
2 2
2
3 2
3
1 2
3、实用范围：实用于破坏形式为屈服的构件。
第一、第二强度理论适合于脆性材料； 第三、第四强度理论适合于塑性材料。 1、伽利略1638年提出了第一强度理论； 2、马里奥特1682年提出了第二强度理论；
3、杜奎特（C.Duguet)提出了最大剪应力理论；也有一说是库 伦1773年提出，特雷斯卡1868完善的。
到单向拉伸的强度极限时，构件就发生断裂。
1、破坏判据： 1 b ;( 1 0)
2、强度准则： 1 ; ( 1 0)
3、实用范围：实用于破坏形式为脆断的构件。
工程力学第5节 强度理论
max 0
1 3 max 13 2
第三强度理论 建立的强度条件
1 3 s
1 3 [ ]
4、形状改变比能理论（第四强度理论） 这一理论认为形状改变比能是引起材料屈服破 坏的主要因素。即无论什么应力状态，只要构件内 一点处的形状改变比能达到单向应力状态下的极限 值，材料就要发生屈服破坏。经推导可得危险点处 于复杂应力状态的构件发生塑性屈服破坏的条件为
二、四种强度理论 1、最大拉应力理论（第一强度理论） 该理论认为引起材料脆性断裂破坏的因素是最 大拉压力。即无论什么应力状态下，只要构件内一 点处的最大拉压力达到单向应力状态下的极限应力， 材料就要发生脆性断裂。于是危险点处于复杂应力 状态的构件发生脆性断裂破坏的条件为：
1 b
第一强度理论 建立的强度条件
1 b / E 1 1 [1 ( 2 3 )] E
第二强度理论 建立的强度条件
1 ( 2 3 ) b
1 ( 2 3 ) [ ]
3、最大切应力理论（第三强度理论） 这一理论认为最大切应力是引起屈服的主要因 素。即无论什么应力状态，只要最大切应力达到单 向应力状态下的极限切应力，材料就要发生屈服破 坏。于是危险点处于复杂应力状态的构件发生塑性 屈服破坏的条件为：
纵截面上的正应力
2）确定主应力 因t <<D，p 值比 和 小得多，工程计算常忽略。
pD 150106 Pa 2t
1 150MPa 2 75MPa 3 0
3）按照形状改变比能理论校核强度
r 4 1 2 2 3 3 1
2 1 2 2 2 3
第四强度理论校核
第四强度理论校核 Revised by Petrel at 2021
强度校核（第四强度理论）取最危险的截面，合成截面所受正应力、切应力、扭矩，再合成校核强度
，故公式：
：屈服强度：正应力：切应力：挤压强度（起重轨道用）
W可查询机械设计手册（第五版）1-113
...
[：许用屈服强度=[=0.58：许用剪切强度
安全系数：
1.5-2倍（交变应力小，如门铰链）
5-6倍（交变应力大，如电机轴，普通材料取6倍，不锈钢软材料取5倍）
计算实例：
1Cr18Ni9材质的实心轴，轴向力16kN，径向力21kN，截面积1965mm2，无弯矩、转矩，无交变
1Cr18Ni9
，
<
圆轴刚度计算（扭转角度）
G：切变模量E：弹性模量：泊松比：极惯性矩。
管罐结构设计复习
管道部分第一章地下管道一、概述埋地管道的敷设程序①开挖管沟②管段组焊③试压检验④管沟回填二、管道载荷及受力分析1、载荷分类永久载荷、可变载荷、偶然载荷2、薄壁环向应力和轴向应力=2??????=4??3、厚壁管道的应力分析从图中的应力分布曲线可看出，内压引起厚壁圆筒的径向应力和环向应力沿壁厚均是变化的，且两向应力的最大值均在内壁面处，而轴向应力在横截面上则为一个常数三、许用应力与壁厚设计1、管道许用应力计算公式[σ]=K φ??K ——强度设计系数Ф——焊缝系数?——钢管的最低屈服强度2、管道壁厚设计输油管道直管段壁厚设计公式输气管道直管段壁厚设计公式t——温度折减系数注:实际使用壁厚需要加上腐蚀余量3、管材选择目前用于长输管道的钢管主要有无缝钢管和焊缝钢管两种。
(焊缝钢管是发展的主要趋势)焊缝钢管主要有直缝埋弧焊钢管和螺旋缝埋弧焊钢管两大类型:直缝埋弧焊钢管与螺旋缝埋弧焊钢管相比具有焊缝短、成型精度高、残余应力小、错边量小等特点,但受力状况不如螺旋缝埋弧焊钢管好四、地下管道轴向应力与变形1、轴向应力-热应力热应力：与A、L无关，仅与管材、温度、约束条件相关。
2、环向应力的泊松效应注：注意正负号（受拉为正，受压为负）3、埋地管道不同约束情况下的应力分析三种不同的热变形：嵌固段、过渡段、自由段过渡段管道单位长度上的摩擦阻力：平衡条件：fl=???∵∴即出/入土段伸缩变形量为同样长度管段自由伸缩量的一半。
注：自由段长度较短，产生的热变形量可以由垫片等一些设施吸收，而过渡段较长，产生的热变形量则需要固定支墩来吸收。
五、固定支墩的设计计算1、作用和位置把过渡段长度缩减为0的措施。
2、固定支墩的受力平衡推力P与摩擦力f（土壤对支墩抗力T）平衡。
注：上式用于支墩和土壤无相对滑移的情况支墩抗滑移校核条件：T>KΦP3、土压力种类：注：上式用于支墩和土壤有相对滑移的情况4、支墩的倾覆校核5、地耐压校核支墩前边缘对地基的压力最大，以表示，后边缘压力最小，以???表示校核条件：六、管道弯曲应力1、简单弯曲情况下的管道弯曲应力计算（嵌固）管壁外层纤维引起的轴向拉力：2、存在相对位移时的弯曲应力计算如果管道曲率很大（>125），那么???=4??，这时弯曲管道由于内压和温差引起的轴向应力恰好与直线管道相同。
第四强度理论的适用范围
2 0
3
2
2
t 2
27.7
MPa
2
由于梁的材料Q235钢为塑性材料，故用第三或第四 强度理论校核a点的强度。
9
按第三度理论校核
r3 1 3 150 .4 MPa 27.7 MPa 178 .1 MPa
170 MPa r3 178 .1 MPa 1.05 178 .5MPa
M max ya Iz
80103 N m 135103 m 88106 m4
122.7 MPa
t
FS,m
ax
S
* z,a
64.6 MPa
8
Izd
点a处的主应力为
1
2
150.4 MPa
2
x 122.7MPa y 0 t x t 64.6MPa
适用范围： 塑性破坏，拉压屈服极限相同的塑性材料。
应用条件：常温(室温)，静荷载(徐加荷载)，材料 接近于均匀,连续和各向同性。
2
二、第四强度理论的适用范围
第四强度理论即形状改变能密度理论
第四强度理论属于第二类强度理论
研究塑性屈服力学因素
相应的强度条件是：
r4
1 2
1
2 2
(e)
tmax
F S* S,max z,max Izd
200103 N 338106 m3 88106 m4 9103 m
85.4 MPa
t max 85.4 MPa t 100 MPa
所以梁满足切应力强度条件。
材料力学试题带答案B
试卷类型：B 卷一、判断题（判断以下论述的正误，认为正确的就在答题相应位置划“T”，错误的划“F”。
每小题 1分，共10 分）1.材料力学主要研究杆件受力后变形与破坏的规律。
（）2.工程构件正常工作的条件是必须同时满足必要的强度、刚度和稳定性。
（）3.由切应力互等定理可知，在相互垂直平面上，切应力总是成对出现，且数值相等，方向则共同指向该两平面的交线。
（）4.截面法是分析应力的基本方法。
（）5.只有静不定结构才可能有温度应力和装配应力。
（）6.圆轴扭转时，横截面上既有正应力，又有剪应力。
（）7.截面的主惯性矩是截面对通过该点所有轴的惯性矩中的最大值和最小值。
（）8.梁端铰支座处无集中力偶作用，该端的铰支座处的弯矩必为零。
（）9.若集中力作用处，剪力有突变，则说明该处的弯矩值也有突变。
（）10.在平面图形的几何性质中，静矩和惯性积的值可正、可负、也可为零。
（）二、填空题（本题共有10个空，填错或不填均不能得分。
每空2分，共20分）1.基本变形中：轴向拉压杆件横截面上的内力是，扭转圆轴横面上的内力是，平面弯曲梁横截面上的内力是和。
2.图所示铆钉联接件将发生挤压与剪切破坏，铆钉所受剪应力大小为，接触面上的挤压应力为。
(a)(b)PP3.EA称为材料的。
4.图示正方形截面简支梁，若载荷不变而将截面边长增加一倍，则其最大弯曲正应力为原来的倍，最大弯曲剪应力为原来的倍。
5.剪切的胡克定律表明：当应力不超过材料的pτ时，切应力τ与切应变γ成比例关系。
三、单项选择题（从下列各题四个备选答案中选出一个正确答案，并将其代号写在答题纸的相应位置。
答案选错或未选者，该题不得分。
每小题2分，共20分）1.下列结论中，只有哪个是正确的 。
A 材料力学的任务是研究材料的组成分析； B 材料力学的任务是研究各种材料的力学性能；C 材料力学的任务是在保证安全的原则下设计结构的构件；D 材料力学的任务是在即安全又经济的原则下，为设计结构构件提供分析计算的基本理论和方法。
四个强度理论与其相当应力
由于各向同性材料，正应力仅产生线应变，剪应力 仅产生剪 应变。而两种情况下的正应力和剪应力分 别相 等，因此，
其形状改变比能也相等，故两种情况下的危险程度相
等。
σ
σ
τ τ
(a)
(b)
二、定量计算
状态(a):
1
2
2
2
2
3
2
2
2
2
2 0
第2强度理论
—最大伸长 线应变理论
σ r1 σ1
r 2 1 2 3
第二类强度理论
（屈服失效的 理论）
第3强度理论
—最大剪应 力理论
σr3 σ1 σ3
第4强度理论
—形状改变
r4
1 2
1
2 2
2
3 2
解： （1）对于图 (a) 所示的单元体， 由图知 1= 0，2= 3= –100MPa,
100MPa 100MPa
r3 1 3 0 100 100 MPa
(a)
r4
1
2
1
2 2
2
3 2
3
1
2
[ ( )]
r2
1
2
3
(9-2-2)
第 二 类强度理论
三、 最大剪应力理论 (第三强度理论) 根据：当作用在构件上的外力过大时，其危险点处的材料就会 沿最大剪应力所在截面滑移而发生屈服失效。
基本假说： 最大剪应力 max 是引起材料屈服的因素。
四个强度理论的相当应力表达式
aF
Fa
A
B
C
A
B
C
C
A
B
A
B 1
C1
1
3
3
B
C
对图示的纯剪切应力状态，试按强度理论建立纯剪切状
态下的强度条件，并导出剪切许用应力［τ］与拉伸许用
应力［σ］之间的关系。
1＝， 2＝0，3＝
1 单元体纯剪切强度条件
KK
τ
第三强度理论 第四强度理论
第一强度理论 1
2
τ σ
3
[]为材料在单轴拉伸是的许用拉应力。
材料在纯剪切应力状态下的许用剪应力为
τ σ 0.577σ
3
（10-13）
已知铸铁构件上危险点处的应力状态，如图所示。若铸
铁拉伸许用应力为［σ］＋＝30MPa，试校核该点处的强度
是否安全。
第一强度理论
1 ＋
= 100MPa 。试按强度条件选择工字钢的号码。
（a）
200KN
200KN
A C
0.42
1.66
2.50
单位：m 例题 10-3 图
B D
0.42
解：作钢梁的内力图。 C , D 为危险截面
按正应力强度条件选择截面
200KN
A C
0.42
1.66 2.50
取 C 截面计算 Q c = Qmax = 200kN
( 2
3)2
( 3
1)2
rM
1
t
c
3
在大多数应力状态下,脆性材料将发生脆性断裂.因而应选用 第一强度理论;而在大多数应力状态下,塑性材料将发生屈服和剪 断.故应选用第三强度理论或第四强度理论.但材料的破坏形式不 仅取决于材料的力学行为,而且与所处的应力状态,温度和加载速 度有关.实验表明,塑性材料在一定的条件下低温和三向拉伸,会 表现为脆性断裂.脆性材料在三向受压表现为塑性屈服.
材料力学试题有答案
2010—2011材料力学试题及答案 A一、单选题（每小题2分，共10小题，20分）1、 工程构件要正常安全的工作，必须满足一定的条件。
下列除（ ）项，其他各项是必须满足的条件。
A 、强度条件B 、刚度条件C 、稳定性条件D 、硬度条件 2、内力和应力的关系是（ ）A 、内力大于应力B 、内力等于应力的代数和C 、内力是矢量，应力是标量D 、应力是分布内力的集度 3、根据圆轴扭转时的平面假设，可以认为圆轴扭转时横截面（ ）。
A 、形状尺寸不变，直径线仍为直线。
B 、形状尺寸改变，直径线仍为直线。
C 、形状尺寸不变，直径线不保持直线。
D 、形状尺寸改变，直径线不保持直线。
4、建立平面弯曲正应力公式zI My =σ,需要考虑的关系有（ ）。
A 、平衡关系,物理关系，变形几何关系；B 、变形几何关系，物理关系，静力关系；C 、变形几何关系，平衡关系，静力关系；D 、平衡关系, 物理关系，静力关系； 5、利用积分法求梁的变形，不需要用到下面那类条件（ ）来确定积分常数。
A 、平衡条件。
B 、边界条件。
C 、连续性条件。
D 、光滑性条件。
6、图示交变应力的循环特征r 、平均应力m σ、应力幅度a σ分别为（ ）。
A -10、20、10；B 30、10、20；C 31-、20、10； D 31-、10、20 。
7、一点的应力状态如下图所示，则其主应力1σ、2σ、3σ分别为（）。
A 30MPa、100 MPa、50 MPaB 50 MPa、30MPa、-50MPaC 50 MPa、0、-50Mpa、D -50 MPa、30MPa、50MPa8、对于突加载的情形，系统的动荷系数为（）。
A、2B、3C、4D、 59、压杆临界力的大小，（）。
A 与压杆所承受的轴向压力大小有关；B 与压杆的柔度大小有关；C 与压杆材料无关；D 与压杆的柔度大小无关。
10、利用图乘法计算弹性梁或者刚架的位移，要求结构满足三个条件。
以下那个条件不是必须的（）A、EI为常量B、结构轴线必须为直线。
四个强度理论及其相当应力
195MPa
（4）对图d 所示的单元体,计算 r3 ,r4
解：求主应力 由图知 : x=30MPa， y=70MPa， xy= - 40MPa 可求得
70MPa 40MPa
30MP
1 3
30
2
70
30
2
70
2
402
94.72
50 20 5
MPa
5.28
50MPa (d)
2 50 MPa
128MPa
（3）对于图 c 所示的单元体，
70MPa
由图知: 1= 80MPa ， 2= –70MPa , 3= –140MPa
r3 1 3 80 140 220 MPa
80MPa (c)
140MPa
r4
1 2
1
2
2
2
3
2
3
1
2
1 2
80
702
70
1402
140
802
(
2
3)]
即 [σ1 ν (σ 2 σ 3)] σ u
强度条件为:
[ ( )]
r2
1
2
3
(9-2-2)
第 二 类强度理论
三、 最大剪应力理论 (第三强度理论) 根据：当作用在构件上的外力过大时，其危险点处的材料就会 沿最大剪应力所在截面滑移而发生屈服失效。
基本假说： 最大剪应力 max 是引起材料屈服的因素。
例题 9-1 对于图示各单元体，试分别按第三强度理论及第 四 强度理论求相当应力。
解： （1）对于图 (a) 所示的单元体， 由图知 1= 0，2= 3= –100MPa,
100MPa 100MPa
四个强度理论的相当应力表达式
pD ≈ = 90 MPa 4t
( 因为 t «D , 所以 A Dt )
包含直径的纵向截面上的应力
用两个横截面 mm , nn 从圆筒部分 取出
单位长的圆筒研究。
m n
p
m
1
n
由截面法，假想地用 直径平面将取出的单 位长度的圆筒分成两 部分。取下半部分为 研究对象。 包含直径 直径平面
的纵向平
§ 10 - 5 各种强度理论的适用范围及其应用
1、 在三向拉伸应力状态下，会脆断破坏，无论是
脆性或塑性材料，均宜采用最大拉应力理论。 2、对于塑性材料如低C钢，除三轴拉应力状态以外的
复杂应力状态下，都会发生屈服现象，可采用第三、 第四强度理论。
3、 对于脆性材料，在二轴拉应力状态下， 应采用最大拉应力理论。
149.0 MPa
2 3 2
第四强度理论
1 1 2 2 2 3 2 3 1 2 2
141.6MPa
图示为一矩形截面铸铁梁，受两个横向力作用。
（1）从梁表面的A、B、C三点处取出的单元体上，用箭头表示出各个面上的应力。 （2）定性地绘出A、B、C三点的应力圆。 （3）在各点的单元体上，大致地画出主平面的位置和主应力的方向。 （4）试根据第一强度理论，说明（画图表示）梁破坏时裂缝在B、C两点处的走向。
0.25
（ 1＋）
τ
第三强度理论 第四强度理论
3
第二强度理论 －（ ＋ ） 1 2 3
＝
对于铸铁:
1＋
0.8 0.5 0.6
1 3 2
大学工程力学题目与参考答案
工程力学一、判断题：1.力对点之矩与矩心位置有关，而力偶矩则与矩心位置无关。
[ ]2.轴向拉压时无论杆件产生多大的变形，正应力与正应变成正比。
[ ]3.纯弯曲的梁，横截面上只有剪力，没有弯矩。
[ ]4.弯曲正应力在横截面上是均匀分布的。
[ ]5.集中力所在截面上，剪力图在该位置有突变，且突变的大小等于该集中力。
[ ]6.构件只要具有足够的强度，就可以安全、可靠的工作。
[ ]7.施加载荷使低碳钢试件超过屈服阶段后再卸载，材料的比例极限将会提高。
[ ]8.在集中力偶所在截面上，剪力图在该位置有突变。
[ ]9.小柔度杆应按强度问题处理。
[ ]10.应用平面任意力系的二矩式方程解平衡问题时，两矩心位置均可任意选择，无任何限制。
[ ]11.纯弯曲梁横截面上任一点，既有正应力也有剪应力。
[ ]12.最大切应力作用面上无正应力。
[ ]13.平面平行力系有3个独立的平衡方程。
[ ]14.低碳钢试件在拉断时的应力为其强度极限。
[ ]15.若在一段梁上作用着均布载荷，则该段梁的弯矩图为倾斜直线。
[ ]16.仅靠静力学平衡方程，无法求得静不定问题中的全部未知量。
[ ]17.无论杆件产生多大的变形，胡克定律都成立。
[ ]18.在集中力所在截面上，弯矩图将出现突变。
[ ]二、单项选择题：1.图1所示杆件受力，1-1、2-2、3-3截面上轴力分别是 [ ]图1A.0，4F ，3FB.-4F ，4F ，3FC.0，F ，0D.0，4F ，3F2.图2所示板和铆钉为同一材料，已知bs []2[]στ=。
为充分提高材料利用率，则铆钉的直径应该是[ ]图2A.2d δ=B.4d δ=C.4d δπ=D.8d δπ=3.光滑支承面对物体的约束力作用于接触点，其方向沿接触面的公法线 [ ]A.指向受力物体，为压力B.指向受力物体，为拉力C.背离受力物体，为压力D.背离受力物体，为拉力4.一等直拉杆在两端承受轴向拉力作用，若其一半为钢，另一半为铝，则两段的 [ ]A.应力相同，变形相同B.应力相同，变形不同C.应力不同，变形相同D.应力不同，变形不同5.铸铁试件扭转破坏是 [ ]A.沿横截面拉断B.沿45o 螺旋面拉断C.沿横截面剪断D.沿45o 螺旋面剪断6.图2跨度为l的简支梁，整个梁承受均布载荷q时，梁中点挠度是45384CqlwEI，图示简支梁跨中挠度是 [ ]图2A.45768qlEIB.45192qlEIC.451536qlEID.45384qlEI7.塑性材料冷作硬化后，材料的力学性能变化的是 [ ]A.比例极限提高，弹性模量降低B.比例极限提高，塑性降低C.比例极限不变，弹性模量不变D.比例极限不变，塑性不变8.铸铁试件轴向拉伸破坏是 [ ]A.沿横截面拉断B.沿45o斜截面拉断C.沿横截面剪断D.沿45o斜截面剪断9.各向同性假设认为，材料沿各个方向具有相同的 [ ]A.外力B.变形C.位移D.力学性质10.材料不同的两根受扭圆轴，其直径和长度均相同，在扭矩相同的情况下，它们的最大切应力和相对扭转角之间的关系正确的是 [ ]A.最大切应力相等，相对扭转角相等B.最大切应力相等，相对扭转角不相等C.最大切应力不相等，相对扭转角相等D.最大切应力不相等，相对扭转角不相等11.低碳钢试件扭转破坏是 [ ]A.沿横截面拉断B.沿45o螺旋面拉断C.沿横截面剪断D.沿45o螺旋面剪断12.整根承受均布载荷的简支梁，在跨度中间处 [ ]A.剪力最大，弯矩等于零B.剪力等于零，弯矩也等于零C.剪力等于零，弯矩为最大D.剪力最大，弯矩也最大三、填空题：1.圆轴扭转时，横截面上各点的切应力与其到圆心的距离成比。
第四强度理论。
对于 28a 工字钢的截面，查表得
I 7114108 m4
d 0.8510 2 m
I 24.6210 2 m S
最大剪应力为:
Qmax max I d S 200 103 24.62 10 2 0.85 10 2
95.5MPa
2 ' 90MPa
3 ' ' ' 3.6MPa
用第四强度理论校核圆筒内壁的强度
r4
2 2 2 1 [( 1- 2) ( 2 - 3) ( 3- 1) ] 2
150MPa [ ]
所以圆筒内壁的强度满足。
强度理论的一个应用
根据强度理论 , 可以从材料在单轴拉伸时的 可推知 低 C 钢类塑性材料在纯剪切应力状态 下的 纯剪切应力状态下 : 1 = , 2 = 0 , 3 = – 按第三强度理论：
( ) [ ]
[ ] 0.5[ ] 2
[]为材料在单轴拉伸是的许用拉应力。
选用 28a 钢能满足剪应力的强度要求。
腹板与翼缘交界处的的强度校核 取 a 点分析
a
y M
max
a
I
84 106 126.3 149.1MPa 4 7114 10
13.7 6 3 S a 122 13.7 (126.3 2 ) 22310 m *
*
a
Q S
x y
横截面上的应力
假想地，用一垂直于轴线的平面将汽包分成两部分，取右边为 研究对象。n— n面为横截面 。 图（d）研究对象的剖面图，其上的外力为压强 p,合力 P .横截面 上只有正应力
力学题库
8、应力集中：由于截面的突变而导致的局部应力增大的现象。
9、内力：在外力作用下，构件内部各部分间因相对位置的改变而产生的相互作用力。
10、失稳：当压力达到临界压力时，压杆从稳定的平衡状态转变为不稳定的平衡状态，这种现象称为丧失稳定性，简称失稳。
二、选择题（本大题分5小题，每题 2分，共10 分）
1、不属于理论力学研究对象的是。 （B）
2.位移、变形和应变的区别和联系是什么(3分)
3.为什第要提出强度理论(4分)
答：1、改变；不改变。
2、位移是物体的刚体移动，变形是物体大小和形状的改变，而应变则是相对变形。位移时不一定产生变形，而变形时则一定有位移，有变形就有应变。
3、因为复杂应力状态下不可能一一的得出材料的极限应力，因而就没有相应的材料许用应力。因而必须进行材料主要破坏原因的假说，使之与能得出极限应力的简单变形相比较。这些科学的假说就是强度理论.
2、度量梁弯曲后横截面位移的两个基本量是挠度和转角。
3、分析受力构件内力的基本方法是截面法。
4、长度为L，直径为d的等直圆杆两端受一对大小为F的拉力作用，材料的弹性模量为E，则杆的伸长量为 。
5、变形比较法解超静定问题是综合考虑几何、物理、静力平衡三方面进行的。
三、选择题（本大题分5小题，每题2分，共10分）
A：应力圆法；B图乘法；C：截面法。
2、材料力学的主要研究对象是：（ C ）
A：块体；B：板壳；C：杆件。
3、一跨度为l的悬臂梁，受均布荷载q作用，E、IZ都为常数，其最大挠度为：（ B ）
A： ；B： ；C： 。
4、下列命题正确的为：（ C ）
A：胡克定律适用于所有的变形；
B：强度计算时所用的材料许用应力即材料的极限应力；
9、内力：在外力作用下，构件内部各部分间因相对位置的改变而产生的相互作用力。
10、失稳：当压力达到临界压力时，压杆从稳定的平衡状态转变为不稳定的平衡状态，这种现象称为丧失稳定性，简称失稳。
二、选择题（本大题分5小题，每题 2分，共10 分）
1、不属于理论力学研究对象的是。 （B）
2.位移、变形和应变的区别和联系是什么(3分)
3.为什第要提出强度理论(4分)
答：1、改变；不改变。
2、位移是物体的刚体移动，变形是物体大小和形状的改变，而应变则是相对变形。位移时不一定产生变形，而变形时则一定有位移，有变形就有应变。
3、因为复杂应力状态下不可能一一的得出材料的极限应力，因而就没有相应的材料许用应力。因而必须进行材料主要破坏原因的假说，使之与能得出极限应力的简单变形相比较。这些科学的假说就是强度理论.
2、度量梁弯曲后横截面位移的两个基本量是挠度和转角。
3、分析受力构件内力的基本方法是截面法。
4、长度为L，直径为d的等直圆杆两端受一对大小为F的拉力作用，材料的弹性模量为E，则杆的伸长量为 。
5、变形比较法解超静定问题是综合考虑几何、物理、静力平衡三方面进行的。
三、选择题（本大题分5小题，每题2分，共10分）
A：应力圆法；B图乘法；C：截面法。
2、材料力学的主要研究对象是：（ C ）
A：块体；B：板壳；C：杆件。
3、一跨度为l的悬臂梁，受均布荷载q作用，E、IZ都为常数，其最大挠度为：（ B ）
A： ；B： ；C： 。
4、下列命题正确的为：（ C ）
A：胡克定律适用于所有的变形；
B：强度计算时所用的材料许用应力即材料的极限应力；
试按第三和第四强度理论计算单元体的相当应力。图中应力
一、从低碳钢零件中某点取出一单元体，其应力状态如图所示，试按第三和第四强度理论计算单元体的相当应力。
图中应力单位是MPa 。
(1)、40=ασ,40090=+ασ,60=ατ (2)、60=ασ,80090-=+ασ,40-=ατ （1）max min123r313r41004040MPa202σ=100MPa,σ=0MPa,σ=-20MPa σσσ120MPa σ111.3MPa σ+=±=-=-==（2）max min123r313r470.66080MPa90.6σ=70.6MPa,σ=0MPa,σ=-90.6MPa σσσ161.2MPa σ140.0MPa σ=-±=-=-==二、上题中若材料为铸铁，试按第一和第二强度理论计算单元体的相当应力。
图中应力单位是MPa ，泊松比3.0=μ。
（1）r11r2123σσ100MPaσσ(σσ)106.0MPa μ===-+=（2）r11r2123σσ70.6MPaσσ(σσ)97.8MPaμ===-+=α三、图示短柱受载荷kN 251=F 和kN 52=F 的作用，试求固定端截面上角点A 、B 、C 及D 的正应力，并确定其中性轴的位置。
121i 33121260025100150150100101012121.66106.750F F y F zZy zσ---⨯⨯=++⨯⨯⨯⨯=-++1.668.02.58.84MPa1.668.02.53.84MPa1.668.02.512.16MPa 1.668.0 2.57.16MPaA B C D σσσσ=-++==-+-==---=-=--+=--1.66+106.7y +50z ＝0当z ＝0时，31.661015.5mm 106.70y -=⨯= 当y ＝0时，31.661033.3mm 50y -=⨯=四、图示简支梁选用25a 工字钢，受力及尺寸如图。
已知钢材的弹性模量GPa 210=E ，许用应力[]MPa 160=σ，梁的容许挠度为[]500/l f =1cos 41sin 4z y M Fl M Fl αα==3max 6651040.8660.5()62.57MPa 4401.81048.28310y z z y M M W W σ--⨯⨯=+=+=⨯⨯max 3111.42310500f l===⨯<max 40001.4234 5.69mm []8mm 500f f =⨯=<== F z五、手摇绞车如图所示，钢轴的直径mm 20=d ，其许用应力[]MPa 80=σ。
第四强度理论的适用范围
应用条件：常温(室温)，静荷载(徐加荷载)，材料 接近于均匀,连续和各向同性。
2
二、第四强度理论的适用范围
第四强度理论即形状改变能密度理论
第四强度理论属于第二类强度理论
研究塑性屈服力学因素
相应的强度条件是：
r4
1 2
1
2 2
2
3 2
3
1 2
按第三强度理论所得的相当应力r3＝178.1 MPa已略超过 许用正应力[ ]=170 MPa，但超过不到5%，在工程计算中
允许的范围内。所以按第三度理论校核梁在强度方面是安 全的。
10
按第四度理论校核
r4
1 2
1
2 2
2
3 2
3
1 2
(e)
tmax
F S* S,max z,max Izd
200103 N 338106 m3 88106 m4 9103 m
85.4 MPa
t max 85.4 MPa t 100 MPa
所以梁满足切应力强度条件。
6
3. 按强度理论校核 按强度理论校核Mmax和FS,max同时所在横截面上腹板与翼缘
交界处的强度
在Mmax和FS,max同时存在的横截面C稍稍偏左的横截面上， 腹板与翼缘交界点a处，正应力和切应力分别比较接近前面求
得的max和tmax，且该点处于平面应力状态，故需利用强度理
论对该点进行强度校核。
7
从a点取出单元体
在横截面C稍稍偏左的横截面上腹板与翼缘交界点a点处 于平面应力状态
知识点：第三和第四强度理论的应用 一、第三强度理论的适用范围 二、第四强度理论的适用范围 三、第三和第四强度理论的应用
2
二、第四强度理论的适用范围
第四强度理论即形状改变能密度理论
第四强度理论属于第二类强度理论
研究塑性屈服力学因素
相应的强度条件是：
r4
1 2
1
2 2
2
3 2
3
1 2
按第三强度理论所得的相当应力r3＝178.1 MPa已略超过 许用正应力[ ]=170 MPa，但超过不到5%，在工程计算中
允许的范围内。所以按第三度理论校核梁在强度方面是安 全的。
10
按第四度理论校核
r4
1 2
1
2 2
2
3 2
3
1 2
(e)
tmax
F S* S,max z,max Izd
200103 N 338106 m3 88106 m4 9103 m
85.4 MPa
t max 85.4 MPa t 100 MPa
所以梁满足切应力强度条件。
6
3. 按强度理论校核 按强度理论校核Mmax和FS,max同时所在横截面上腹板与翼缘
交界处的强度
在Mmax和FS,max同时存在的横截面C稍稍偏左的横截面上， 腹板与翼缘交界点a处，正应力和切应力分别比较接近前面求
得的max和tmax，且该点处于平面应力状态，故需利用强度理
论对该点进行强度校核。
7
从a点取出单元体
在横截面C稍稍偏左的横截面上腹板与翼缘交界点a点处 于平面应力状态
知识点：第三和第四强度理论的应用 一、第三强度理论的适用范围 二、第四强度理论的适用范围 三、第三和第四强度理论的应用
四大强度理论
第10章强度理论10.1 强度理论的概念构件的强度问题是材料力学所研究的最基本问题之一。
通常认为当构件承受的载荷达到一定大小时，其材料就会在应力状态最危险的一点处首先发生破坏。
故为了保证构件能正常地工作，必须找出材料进入危险状态的原因，并根据一定的强度条件设计或校核构件的截面尺寸。
各种材料因强度不足而引起的失效现象是不同的。
如以普通碳钢为代表的塑性材料，以发生屈服现象、出现塑性变形为失效的标志。
对以铸铁为代表的脆性材料，失效现象则是突然断裂。
在单向受力情况下，出现塑性变形时的屈服点σ和发生断裂时s的强度极限σ可由实验测定。
sσ和bσ统称为失效应力，以安全系数除失效应力得到b许用应力[]σ，于是建立强度条件[]σσ≤可见，在单向应力状态下，强度条件都是以实验为基础的。
实际构件危险点的应力状态往往不是单向的。
实现复杂应力状态下的实验，要比单向拉伸或压缩困难得多。
常用的方法是把材料加工成薄壁圆筒(图10-1)，在内压p 作用下，筒壁为二向应力状态。
如再配以轴向拉力F，可使两个主应力之比等于各种预定的数值。
这种薄壁筒试验除作用内压和轴力外，有时还在两端作用扭矩，这样还可得到更普遍的情况。
此外，还有一些实现复杂应力状态的其他实验方法。
尽管如此，要完全复现实际中遇到的各种复杂应力状态并不容易。
况且复杂应力状态中应力组合的方式和比值又有各种可能。
如果象单向拉伸一样，靠实验来确定失效状态，建立强度条件，则必须对各式各样的应力状态一一进行试验，确定失效应力，然后建立强度条件。
由于技术上的困难和工作的繁重，往往是难以实现的。
解决这类问题，经常是依据部分实验结果，经过推理，提出一些假说，推测材料失效的原因，从而建立强度条件。
图10－1经过分析和归纳发现，尽管失效现象比较复杂，强度不足引起的失效现象主要还是屈服和断裂两种类型。
同时，衡量受力和变形程度的量又有应力、应变和变形能等。
人们在长期的生产活动中，综合分析材料的失效现象和资料，对强度失效提出各种假说。
压力管道强度理论及校核
压力管道强度理论及校核实际工程中，很少有管子仅承受单一的拉压、剪切、扭转或弯曲载荷，而多是两种或多种载荷同时作用，这样就使得应力的求解变得复杂起来。
与简单的拉压、剪切、扭转和弯曲相比，它的难点主要是表现在以下两个方面：其一是管子中各点的应力求解困难。
此时因涉及的未知变量较多，建立的相应静力平衡方程、物理方程和几何方程较多，求解这些方程的计算工作十分浩繁;其二是管子中的各点可能同时承受三个方向的主应力和六个面上的剪应力，这些应力对材料的强度都将产生影响。
此时如何建立与许多应力有关的强度校核公式是十分棘手的，它既不能象简单变形形式那样用单一的强度指标进行判断，又不能对各个应力分别施以判断，这样做也是不现实的。
下面就针对上述两个问题的解决方法进行介绍。
(一)复杂应力状态下的应力求解对于几何形状比较规则的管子，无论它受力多么复杂，都可以按前面所介绍的步骤和方法进行求解。
即首先从管子中取一微元，然后根据受力情况、几何形状、边界条件等分别建立其静力平衡方程、物理方程和几何方程，然后联解方程。
复杂应力状态下的静力平衡方程、物理方程和几何方程型式如下：1、静力平衡方程：ΣFx=0; ΣFy=0; ΣFz=0ΣMx=0; Σmy=o; ΣMz=02、物理方程：3、几何方程：很显然，对于空间几何形状、受力和边界条件复杂的管道系统，要想对每个管道元件建立并求解上面的联合方程确实不是一件容易的事。
但随着电子计算机的应用，这样的计算就不再是难事了。
事实上，目前计算机已广泛应用于这类问题的计算。
对于形状不规则的管道元件，尤其是管道元件局部形状不规则时(如三通分支的根部、对焊法兰颈部弯曲过渡处等)，有时很难通过其平衡方程、物理方程和几何方程求出能满足边界条件的方程解，也就是说其应力将无法通过方程进行求解，此时往往作出一些假设，或根据试验找出一些修正系数来简化计算，从而求出一些工程上尚可使用的近似解。
值得一提的是，随着有限元技术的发展，它在求解复杂情况下的应力分析计算中得到了应用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四强度理论校核
强度校核(第四强度理论)
取 最危险的截面,合成截面所受 正应力、切应力、扭矩,再合成校核强度
:屈服强度
:正应力
,故公式:
:切应力
:挤压强度(起重轨道用)
W 可查询 机械设计手册(第五版)1-113
、、、
[
:许用屈服强度
=[
=0、58 :许用剪切强度
安全系数: 1、5-2 倍(交变应力小,如门铰链) 5-6 倍 (交变应力大,如电机轴,普通材料取 6 倍,不锈钢软材料取 5 倍)
计算实例: 1Cr18Ni9 材质的实心轴,轴向力 16kN,径向力 21kN,截面积 1965mm2,无弯矩、转矩,无交变
1Cr18Ni9
,
< 圆轴刚度计算(扭转角度)
第Hale Waihona Puke 强度理论校核G:切变模量 E:弹性模量 :泊松比 :极惯性矩
强度校核(第四强度理论)
取 最危险的截面,合成截面所受 正应力、切应力、扭矩,再合成校核强度
:屈服强度
:正应力
,故公式:
:切应力
:挤压强度(起重轨道用)
W 可查询 机械设计手册(第五版)1-113
、、、
[
:许用屈服强度
=[
=0、58 :许用剪切强度
安全系数: 1、5-2 倍(交变应力小,如门铰链) 5-6 倍 (交变应力大,如电机轴,普通材料取 6 倍,不锈钢软材料取 5 倍)
计算实例: 1Cr18Ni9 材质的实心轴,轴向力 16kN,径向力 21kN,截面积 1965mm2,无弯矩、转矩,无交变
1Cr18Ni9
,
< 圆轴刚度计算(扭转角度)
第Hale Waihona Puke 强度理论校核G:切变模量 E:弹性模量 :泊松比 :极惯性矩