- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七节 平面曲线的曲率
曲线的弯 与切线的转角有关 曲程度 与曲线的弧长有关 主要内容: 一、 弧微分 二、 曲率及其计算公式 三、 曲率圆与曲率半径
机动 目录 上页
第三章
M
M M
下页
返回
结束
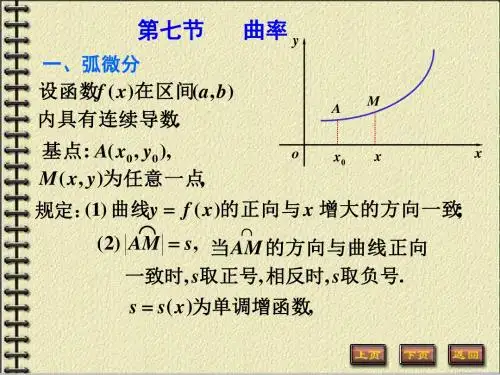
一、 弧微分
在(a , b)内有连续导数, 其图形为 AB, y y f ( x) B 弧长 s AM s( x) M s M M M M A y M x M M x x M M (x) 2 (y ) 2 o a x x b MM x x x 设
这说明椭圆在点 ( a , 0 ) 处曲率 最大.
机动
a
b
目录 上页 下页
a x
返回
结束
三、 曲率圆与曲率半径
设 M 为曲线 C 上任一点 , 在点 M 处作曲线的切线和法线, 在曲线
y
D( , )
C 的凹向一侧法线上取点 D 使 M ( x, y) 1 o x DM R K 把以 D 为中心, R 为半径的圆叫做曲线在点 M 处的
MM y 2 1 ( ) MM x s s( x) lim 1 ( y) 2 x0 x
MM lim 1 x0 M M
机动
目录
上页
下页
返回
结束
2 2 或 ds (dx) (d y ) ds 1 ( y) dx x x(t ) 若曲线由参数方程表示: y y (t ) 2
f (t ) (a 2 b 2 ) sin 2 t 3 令 f (t ) 0 , 得 t 0 , , , , 2 2 2
t
0
2
b2
3 2
2
b2
y b
f (t )
b2
a2
a2
设 0 b a , 则t 0 , , 2 时
f (t ) 取最小值 , 从而 K 取最大值 .
求此缓和曲线在其两个端点 解: 当 x [ 0 , l ] 时, 1 2 l 0 y x 2 Rl 2R 1 y x Rl 1 x K y Rl 显然
处的曲率.
y
R B
o
l
1 3 y x 6 Rl
x
K
x 0
0;
K
x l
1 R
机动
目录
上页
下页
返回
(2) 若曲线方程为 x ( 1 x )
2
3 2
K
y (1 y )
上页 下页 返回
2
3
2
机动
目录
结束
1 3 x 作缓和曲线, 例2. 我国铁路常用立方抛物线 y 6 Rl 其中R是圆弧弯道的半径, l 是缓和曲线的长度, 且 l << R.
则弧长微分公式为 几何意义:
ds x 2 y 2 dt
y
ds M T
dy sin ds
dx cos ; ds
dx o x x dx x
机动 目录 上页 下页 返回 结束
M
T dy
二、曲率及其计算公式
在光滑弧上自点 M 开始取弧段, 其长为 s , 对应切线 转角为 , 定义 弧段 s 上的平均曲率
曲率圆 ( 密切圆 ) , R 叫做曲率半径, D 叫做曲率中心. 在点M 处曲率圆与曲线有下列密切关系: (1) 有公切线; (2) 凹向一致; (3) 曲率相同 .
机动 目录 上页 下页 返回 结束
R
T
设曲线方程为 曲率半径及曲率中心
且
求曲线上点M 处的 的坐标公式 .
设点M 处的曲率圆方程为 故曲率半径公式为
y
D( , )
1 (1 R K y
2 32 y )
C
o
R
M ( x, y)
T
x
, 满足方程组
( x ) ( y ) R y x y
M s R M
可见: R 愈小, 则K 愈大 , 圆弧弯曲得愈厉害 ;
R 愈大, 则K 愈小 , 圆弧弯曲得愈小 .
机动
目录
上页
下页
返回
结束
曲率K 的计算公式 设曲线弧 y f ( x) 二阶可导, 则由
tan y ( 设
得
arctan y
d (arctan y) d x
结束
例3. 求椭圆 解: x a sin t ;
在何处曲率最大?
y b cos t ;
故曲率为
x a cos t y b sin t
2
x 表示对参 数 t 的导数
K
x y x y (x y )
2 2
3
ab
(a sin t b cos t )
K s
点 M 处的曲率
M
M s
d K lim s 0 s ds
注意: 直线上任意点处的曲率为 0 !
机动 目录 上页 下页 返回 结束
例1. 求半径为R 的圆上任意点处的曲率 .
解: 如图所示 ,
s R
1 K lim s 0 s R
2 2 2 2
3 2
K 最大
求驻点:
f (t ) a 2 sin 2 t b 2 cos 2 t 最小
f (t ) 2a 2 sin t cos t 2b cos t sin t (a 2 b 2 ) sin 2 t
机动 目录 上页 下页 返回 结束
计算驻点处的函数值:
求此缓和曲线在其两个端点 说明:
处的曲率.
铁路转弯时为保证行车 平稳安全, 离心力必须
连续变化 , 因此铁道的 曲率应连续变化 .
点击图片任意处播放\暂停
机动 目录 上页 下页 返回 结束
1 3 x 作缓和曲线, 例2. 我国铁路常用立方抛物线 y 6 Rl 其中R是圆弧弯道的半径, l 是缓和曲线的长度, 且 l << R.
) 2 2
d K ds
又 故曲率计算公式为
K
y (1 y )
2 32
当 y 1 时 , 有曲率近似计算公式 K y
机动 目录 上页 下页 返回 结束
说明:
x x(t ) 给出, 则 (1) 若曲线由参数方程 y y (t ) x y x y K 2 2 32 (x y )