河北中考数学复习 第9讲 平面直角坐标系与函数的认识
- 格式:doc
- 大小:134.50 KB
- 文档页数:12

中考复习——平面直角坐标系、一次函数、反比例函数【知识梳理】一、平面直角坐标系1. 坐标平面上的点与 有序实数对 构成一一对应;2. 各象限点的坐标的符号;3. 坐标轴上的点的坐标特征.4. 点P (a ,b )关于x 轴对称的点的坐标为 ;关于y 轴对称的点的坐标为 ;关于原点对称的点的坐标为5.两点之间的距离二、函数的概念1.概念:在一个变化过程中有两个变量x 与y ,如果对于x 的每一个值,y 都有 的值与它对应,那么就说x 是自变量,y 是x 的函数.2.自变量的取值范围: (1)使解析式 (2)实际问题具有 意义3.函数的表示方法; (1) (2) (3) 三、一次函数的概念、图象、性质1.正比例函数的一般形式是 ( ),一次函数的一般形式是 (k≠0). 2. 一次函数y kx b =+的图象是经过( , )和( , )两点的一条直线.4.若两个一次函数解析式中,k 相等,表示两直线 ;若两直线垂直,则 。
5.的大小决定直线的倾斜程度,越大,直线越 ;四、反比例函数的概念、图象、性质1.反比例函数:一般地,如果两个变量x 、y 之间的关系可以表示成y = 或 或 (k 为常数,k≠0)的形式,那么称y 是x 的反比例函数. 2. 反比例函数的图象和性质k >0,b >0k >0,b <0k <0,b >0k <0,21212211P P )0()0()2(y y y P y P -=, ,,,21212211P P )0()0()1(x x x P x P -=, , ,, 3.k 的几何含义:反比例函数y =k x(k≠0)中比例系数k 的几何意义,即过双曲线y =k x(k≠0)上任意一点P 作x 轴、y 轴垂线,设垂足分别为A 、B ,则所得矩形OAPB 的面积为 。
【例题精讲】 例1.函数22y x =-中自变量x 的取值范围是 ;函数y =x 的取值范围是 .例2.已知点(13)A m -,与点(21)B n +,关于x 轴对称,则m = ,n = . 例3.如图,在平面直角坐标系中,点A 的坐标是(10,0),点B 的 坐标为(8,0),点C 、D 在以OA 为直径的半圆M 上,且四边形OCDB 是平行四边形,点C 的坐标为例4.一次函数y=(3a+2)x -(4-b),求满足下列条件的a 、b 的取值范围。
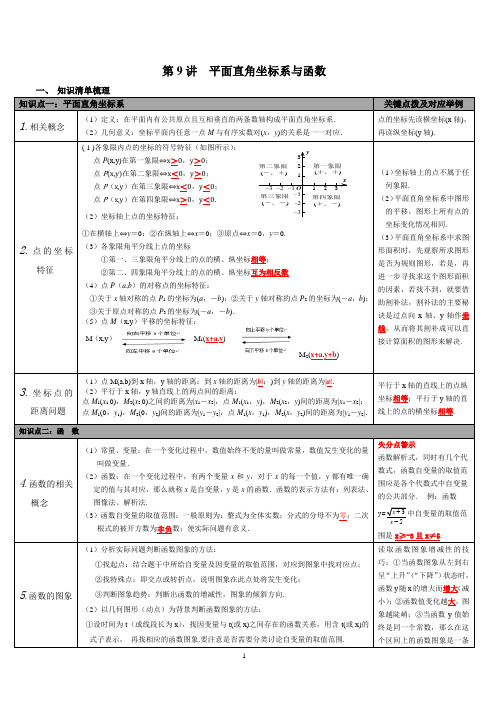




P
(2)坐标轴上点的坐标特征:
①在横轴上⇔y=0;②在纵轴上⇔x=0;③原点⇔x=0,y=0.
(3)各象限角平分线上点的坐标
①第一、三象限角平分线上的点的横、纵坐标相等;
②第二、四象限角平分线上的点的横、纵坐标互为相反数
(4)点P(a,b)的对称点的坐标特征:
①关于x轴对称的点P1的坐标为(a,-b);②关于y轴对称的点P2的坐标为(-a,b);
③关于原点对称的点P3的坐标为
(-a,-b).
(5)点M(x,y)平移的坐标特征:
M(x,y)M1(x+a,y)
M2(x+a,y+b) (2)平面直角坐标系中图形的平移,图形上所有点的坐标变化情况相同(3)平面直角坐标系中求图形面积时,先观察所求图形是否为规则图形,若是,再进一步寻找求这个图形面积的因素,若找不到,就要借助割补法,割补法的主要秘诀是过点向
垂线,从而将其割补成可以直接计算面积的图形来解决
(1)点M(a,b)到x轴,y轴的距离:到x轴的距离为|b|;)到y轴的距离为|a|.
(2)平行于x轴,y轴直线上的两点间的距离:
点M1(x1,0),M2(x2,0)之间的距离为|x1-x2|,点M1(x1,y),M2(x2,y)间的距离为|x1-x2|;点M1(0,y1),M2(0,y2)间的距离为|y1-y2|,点M1(x,y1),M2(x,y2)间的距离为平行于x轴的直线上的点纵坐标相等;平行于
线上的点的横坐标
(一一一) (一一一)–2
–3。
第9讲平面直角坐标系与函数一、教学目标:1.掌握平面直角坐标系中各象限点的坐标特征,会求一个点关于坐标轴和原点对称的点的坐标;会用平面直角坐标系下点的平移规律解决实际问题2.会求一个函数的自变量的取值范围,会根据实际问题情境分析函数的大致图象二、教学重难点:重点:特殊点的坐标特征难点:函数自变量的取值范围及函数值,函数图象的分析三、教学用具:多媒体四、学情分析:“平面直角坐标系”作为“数轴”的进一步发展,实现了认识上从一维空间到二维空间的跨越,构成更广范围内的数形结合、数形互相转化的理论基础。
是今后学习函数、函数与方程、函数与不等式关系的必要知识。
五、教学方法:启发引导法、归纳分析六、教学资源:课本、PPT七、教学过程:考点一平面直角坐标系及点的坐标特征平面直角坐标系的有关概念在平面内由两条互相垂直、原点重合的数轴组成平面直角坐标系,水平的数轴为x轴或①,竖直方向的数轴为y轴或②,两坐标轴的交点为平面直角坐标系的原点坐标轴上的点x轴、y轴上的点不属于任何象限对应关系坐标平面内的点与有序实数对是③对应的平面内点P(x,y)的坐标特征(1)各象限内点的坐标的特征:点P(x, y)在第一象限⇔④点P(x, y)在第二象限⇔⑤点P(x, y)在第三象限⇔⑥点P(x, y)在第四象限⇔⑦(2)坐标轴上点的坐标的特征:点P(x, y)在x轴上⇔⑧点P(x, y)在y轴上⇔⑨;点P(x, y)既在x轴上,又在y轴上⇔x,y同为0,即点P的坐标为(0, 0)平行于坐标轴的直线上的点的坐标特征(1)平行于x轴(或垂直于y轴)的直线上的点的纵坐标相同,横坐标为不相等的实数(2)平行于y轴(或垂直于x轴)的直线上的点的横坐标相同,纵坐标为不相等的实数各象限的角平分线上的点的坐标特征(1)第一、三象限的角平分线上的点:第一、三象限的角平分线上的点的横、纵坐标⑩(2)第二、四象限的角平分线上的点:第二、四象限的角平分线上的点的横、纵坐标【思政元素】:通过复习平面直角坐标系知识,介绍法国数学家笛卡尔在数学中的卓越贡献,激发学生学习数学的热情,树立远大的学习目标考点二点到坐标轴的距离到x轴的距离点P(a,b)到x轴的距离等于点P的①即到y轴的距离点P(a,b)到y轴的距离等于点P的②即到原点的距离点P(a,b)到坐标原点的距离为考点三平面直角坐标系中的平移与对称点的坐标用坐标表示平移平移规律在平面直角坐标系中,将点(x,y)向右(或向左)平移a个单位长度,可以得到对应点①(或②);将点(x,y)向上(或向下)平移b个单位长度,可以得到对应点③(或④)某点的对称点的坐标关于x轴对称点P(x,y)关于x 轴对称的点P 1的坐标为规律可简记为:关于谁对称谁不变,另一个变号,原点对称都变号关于y轴对称点P(x,y)关于y轴对称的点P2的坐标为关于原点对称点P(x,y)关于原点对称的点P3的坐标为考点四函数的有关概念1.常量与变量:在一个变化过程中,我们称数值发生①的量为变量,数值始终②的量为常量.如s=vt,当v一定时,v是常量,s,t都是变量.2.函数的概念:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与之对应,我们就说x是自变量,y是x的函数.3.自变量的取值范围:(1)函数解析式有意义的条件;(2)实际问题有意义的条件.4.函数值:对于一个函数,如果当自变量x=a时,因变量y=b,那么b叫做自变量的值为a时的函数值.5.函数的三种表示法:③法、④法和⑤法.6.描点法画函数图象的一般步骤:(1)⑥; (2)⑦; (3)⑧.例1.点A(3,-2)关于x轴对称的点的坐标是; 关于y轴对称的点的坐标是; 关于原点对称的点的坐标是; 把点A向左平移2个单位,再向下平移3个单位得到的点的坐标是; 把点A绕着原点顺时针旋转90°后的点的坐标是.探究三函数图象例2如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的( )A.乙前4秒行驶的路程为48米B.在0到8秒内甲的速度每秒增加4米/秒C.两车到第3秒时的路程相等D.在4至8秒内甲的速度都大于乙的速度【思政元素】:生活中的行车安全,注意遵守道路交通规则,不超速,文明行车例3.[2017·北京] 小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图②所示.下列叙述正确的是()A.两人从起跑线同时出发,同时到达终点B.小苏跑全程的平均速度大于小林跑全程的平均速度C.小苏前15 s跑过的路程大于小林前15 s跑过的路程D.小林在跑最后100 m的过程中,与小苏相遇2次例4.[2017·丽水] 在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象.下列说法错误的是( )A.乙先出发的时间为0.5小时B.甲的速度是80千米/小时C.甲出发0.5小时后两车相遇D.甲到B地比乙到A地早小时八、布置作业:九、板书设计:平面直角坐标系与函数1.知识点2.例题十、教学反思:。
第三章函数第9讲平面直角坐标系与函数的认识1. (2019,河北)一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km/h,水流速度为5 km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s 关于t的函数图象大致是(C)A B C D【解析】航行过程分三段,且第二段停留,此时s值不变,即图象与x轴平行,故选项D错误.无论速度快慢,路程都随时间的增大而增大,所以第一、三段图象都应是向上的趋势,故选项A错误.从甲地到乙地顺水航行,从乙地返回到甲地逆水航行,所以第一段图象比第三段倾斜程度更陡一些,故选项B错误,选项C正确.2. (2019,河北)如图,在矩形中截取两个相同的圆柱的上、下底面,剩余的矩形作为圆柱的侧面,刚好能组合成圆柱.设矩形的长和宽分别为y和x,则y关于x的函数图象大致是(A)第2题图A B C D【解析】由题意,得y-x2=π2x,即y=⎝⎛⎭⎪⎫π2+12x.3. (2019,河北,导学号5892921)如图,在梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12,动点P从点A出发,沿折线AD→DC→CB以每秒1个单位长度的速度运动到点B停止.设运动时间为t s ,y =S △EPF ,则y 关于t 的函数图象大致是(A)第3题图A B C D【解析】 在Rt △ADE 中,AD =AE 2+DE 2=13.在Rt △CFB 中,BC =BF 2+CF 2=13.①当点P 在AD 上运动时,如答图①,过点P作PM ⊥AB 于点M ,则PM = AP·sin A =1213t ,此时y =12EF ·PM =3013t ,为一次函数.②当点P 在DC 上运动时,y = 12EF ·DE =30.③当点P 在BC 上运动时,如答图②,过点P 作PN ⊥AB 于点N ,则PN=BP·sin B =1213 (AD +CD +BC -t)=12(31-t )13,则y =12EF ·PN =30(31-t )13,为一次函数.综上可得选项A 的图象符合. 第3题答图平面直角坐标系与点的坐标特征例1 (2019,枣庄)在平面直角坐标系中,将点A(-1,-2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为(B)A. (-3,-2)B. (2,2)C. (-2,2)D. (2,-2)【解析】点A(-1,-2)向右平移3个单位长度得到点B(2,-2),点B关于x轴的对称点B′的坐标为(2,2).针对训练1(2019,沈阳)在平面直角坐标系中,点B的坐标是(4,-1),点A与点B关于x轴对称,则点A的坐标是(A)A. (4,1)B. (-1,4)C. (-4,-1)D. (-1,-4)【解析】关于x轴对称的点,横坐标相等,纵坐标互为相反数.函数图象的判断与分析例2 (2019,达州)如图,在物理课上,老师将挂在弹簧测力计下端的铁块浸没于水中,然后缓慢匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧测力计的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的图象大致是(D)例2题图A B C D【解析】铁块完全浸没在水中时,y应是重力与浮力的差,且保持不变;铁块从露出水面到完全离开水面的过程中,所受浮力减小,故y值增大;铁块完全离开水面后,y值等于重力,保持不变.针对训练2(2019,衢州)星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(km)与时间t(min)之间的关系如图所示,则上午8:45小明离家的距离是 1.5 km.训练2题图【解析】分析图象,可知图书馆距小明家2 km,他回程的速度是2÷20=0.1(km/min),所以上午8:45他距家2-0.1×5=1.5(km).函数自变量的取值范围例3 (2019,恩施州)函数y=2x+1x-3的自变量x的取值范围是( x≥-12且x≠3).【解析】 使式子有意义的条件是⎩⎪⎨⎪⎧2x +1≥0,x -3≠0.解得x≥-12且x≠3. 针对训练3 (2019,岳阳)函数y =x -3中,自变量x 的取值范围是(C)A. x >3B. x ≠3C. x ≥3D. x ≥0【解析】 根据二次根式有意义的条件,得x -3≥0.解得x≥3.一、 选择题1. (2019,十堰模拟)下列说法中,正确的是(D)A. 点P (3,2)到x 轴的距离是3B. 在平面直角坐标系中,点(2,-3)和点(-2,3)表示同一个点C. 若y =0,则点M (x ,y )在y 轴上D. 在平面直角坐标系中,第三象限内点的横坐标与纵坐标同号【解析】 A . 点P(3,2)到x 轴的距离是2,故此选项错误.B . 在平面直角坐标系中,点(2,-3)和点(-2,3)表示不同的点,故此选项错误.C . 若y =0,则点M(x ,y)在x 轴上,故此选项错误.D . 在平面直角坐标系中,第三象限内点的横坐标与纵坐标同为负号,故此选项正确.2. 如果点P (x -4,2x +6)在平面直角坐标系的第二象限内,那么x 的取值范围在数轴上可表示为(C)A B C D【解析】 ∵点P 在第二象限,∴⎩⎪⎨⎪⎧x -4<0,2x +6>0.解得-3<x<4.3. (2019,成都)在平面直角坐标系中,点P(-3,-5)关于原点对称的点的坐标是(C)A. (3,-5)B. (-3,5)C. (3,5)D. (-3,-5)【解析】关于原点对称的两点,横坐标和纵坐标分别互为相反数.4. (2019,石家庄27中模拟)将点A(-1,2)向左平移3个单位长度得到点B,则点B关于y轴的对称点C的坐标是(B)A. (-4,-2)B. (4,2)C. (-2,2)D. (2,-2)【解析】点A向左平移3个单位长度,则横坐标减3,纵坐标不变,即B(-4,2).关于y轴对称的两点,纵坐标相等,横坐标互为相反数,即C(4,2).5. (2019,扬州改编)在平面直角坐标系的第四象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是(B)A. (3,-4)B. (4,-3)C. (-4,3)D. (-3,4)【解析】点到x轴的距离等于纵坐标的绝对值,点到y轴的距离等于横坐标的绝对值.点在第四象限,横坐标是正数,纵坐标是负数.6. (2019,昆山一模)在平面直角坐标系中,点P(x,-x2-4x-3)所在的象限不可能是(A)A. 第一象限B. 第二象限C. 第三象限D. 第四象限【解析】 ∵-x 2-4x -3=-(x +2)2+1,∴当x>0时,-(x +2)2+1<-3<0.∴点P 所在的象限不可能是第一象限.7. (2019,内江)已知函数y =x +1x -1,则自变量x 的取值范围是(B) A. -1<x <1B. x ≥-1且x ≠1C. x ≥-1D. x ≠1【解析】 根据二次根式、分式有意义的条件,得⎩⎪⎨⎪⎧x +1≥0,x -1≠0.解得x≥-1且x ≠1.8. 如图,一个函数的图象由射线BA 、线段BC 、射线CD 组成,其中点A (-1,2),B (1,3),C (2,1),D (6,5),则此函数(A)第8题图A. 当-1<x <1时,y 随x 的增大而增大B. 当-1<x <1时,y 随x 的增大而减小C. 当1<x <2时,y 随x 的增大而增大D. 当2<x <6时,y随x 的增大而减小【解析】 观察图象的变化趋势可得结论.9. (2019,潍坊)如图,菱形ABCD 的边长是4 cm ,∠B =60°,动点P 以1 cm/s 的速度自点A 出发沿AB 方向运动至点B 停止,动点Q 以2 cm/s 的速度自点B 出发沿折线BCD 运动至点D 停止.若点P ,Q 同时出发运动了t s ,记△BPQ 的面积为S cm 2,下面图象中能表示S 与t 之间的函数关系的是(D)第9题图A B C D【解析】 当0≤t<2时,S =12×2t ·32×(4-t)=-32t 2+23t.当2≤t≤4时,S =12×4×32·(4-t)=-3t +4 3 .只有选项D 的图象符合.10. 定义新运算:a *b =⎩⎨⎧a -1(a ≤b ),-a b (a >b 且b ≠0),则函数y =3*x 的图象大致是(B) A B C D【解析】 根据新运算,可知y =3*x =⎩⎨⎧3-1(3≤x ),-3x (3>x 且x≠0).①当x≥3时,此函数解析式为y =2,函数图象在第一象限,是以(3,2)为端点平行于x 轴的射线,故可排除选项C ,D .②当x<3且x≠0时,此函数是反比例函数,图象位于第二、四象限,可排除选项A .11. (2019,石家庄新华区二模)定义新运算:a ⊕b =⎩⎪⎨⎪⎧|a |+b (a ≤b ),b -a 2(a >b ),则函数y =x ⊕1的图象大致是(A) A B C D【解析】 根据新运算,可知y =x ⊕1=⎩⎪⎨⎪⎧||x +1(x≤1),1-x 2(x >1).①当x>1时,此函数解析式为y =1-x 2,函数图象在第四象限.②当x≤1时,此函数解析式为y =1+||x ,图象在第一、二象限.二、 填空题12. (2019,新疆)点(-1,2)所在的象限是第 二 象限.【解析】 横坐标是负数、纵坐标是正数的点在第二象限.13. (2019,临安)点P (3,-4)到x 轴的距离是 4 .【解析】 点到x 轴的距离等于纵坐标的绝对值.14. (2019,宿迁)在平面直角坐标系中,将点(3,-2)先向右平移2个单位长度,再向上平移3个单位长度,则所得的点的坐标是 (5,1) .【解析】 由题意,得所得点的坐标为(3+2,-2+3),即(5,1).15. (2019,枣庄,导学号5892921)如图①,点P 从△ABC 的顶点B 出发,沿B →C →A 匀速运动到点A ,图②是点P 运动时,线段BP 的长度y 随时间x 变化的关系图象,其中M 为曲线部分的最低点,则△ABC 的面积是 12 .第15题图【解析】 根据图象可知点P 在BC 上运动时,BP 的长度不断增大,且BP 的最大值为5,即BC =5.∵M 是曲线部分的最低点,∴此时BP 最短,即当BP ⊥AC 时,BP =4.∴由勾股定理,可知此时PC =3.∵图象的曲线部分是轴对称图形,∴此时PA =3.∴AC =6.∴S △ABC =12×4×6=12.三、 解答题16. (2019,嘉兴)小红帮弟弟荡秋千(如图①),秋千离地面的高度h (m)与摆动时间t (s)之间的关系如图②所示.(1)根据函数的定义,请判断变量h 是否为关于t 的函数?(2)结合图象回答:①求当t =0.7时,h 的值,并说明它的实际意义;②秋千摆动第一个来回需多少时间?第16题图【思路分析】 (1)根据图象和函数的定义可以解答.(2)①根据函数图象可以解答本题.②根据函数图象中的数据可以解答本题.解:(1)由图象,可知对于每一个摆动时间t ,h 都有唯一确定的值与其对应,∴变量h 是关于t 的函数.(2)①由函数图象,可知当t =0.7时,h =0.5.它的实际意义是当摆动时间为0.7 s 时,秋千离地面的高度是0.5 m.②由图象,可知秋千摆动第一个来回需2.8 s.1. (2019,潍坊)在平面内,由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O 称为极点;从点O 出发引一条射线Ox 称为极轴;线段OP 的长度称为极径,点P 的极坐标就可以用线段OP 的长度以及从Ox 转动到OP 的角度(规定逆时针方向转动角度为正)来确定,即P (3,60°)或P (3,-300°)或P (3,420°)等,则点P 关于点O 成中心对称的点Q 的极坐标表示不正确的是(D)第1题图A. Q (3,240°)B. Q (3,-120°)C. Q (3,600°)D. Q (3,-500°)【解析】 ∵P(3,60°)或P(3,-300°)或P(3,420°),点P 与点Q 关于点O 成中心对称,∴点Q 的极坐标为(3,240°)或(3,-120°)或(3,600°)等.2. (2019,石家庄43中三模,导学号5892921)在平面直角坐标系xOy 中,点A 的坐标为(1,0),P 是第一象限内任意一点,连接PO ,P A .若∠POA =m °,∠P AO =n °,则我们把(m °,n °)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).(1)点⎝ ⎛⎭⎪⎫12,32的“双角坐标”为 (60°,60°) ; (2)若m ≤n ,则点P 到y 轴的距离d 的取值范围为( d ≥12 ).【解析】 (1) ∵P ⎝ ⎛⎭⎪⎫12,32 ,OA =1,∴tan ∠POA =3212=3, tan ∠PAO =321-12= 3.∴∠POA =60°,∠PAO =60°,即点⎝ ⎛⎭⎪⎫12,32的“双角坐标”为(60°,60°).(2)当m =n 时,点P 在线段OA 的垂直平分线上,此时点P 到y 轴的距离d =12.当m<n ,即∠POA<∠PAO时,点P 在直线x =12的右侧,此时点P 到y 轴的距离d>12.综上所述,d≥12.。