2013年高考数学总复习_4-2_同角三角函数的基本关系及诱导公式课件_新人教B版

2013年高考第一轮复习数学北师(江西版)理第四章4.2 同角三角函数的基本关系及三角函数的诱导公式考纲要求1．理解同角三角函数的基本关系式：sin 2α＋cos 2α＝1，sin αcos α＝πtan π2k αα⎛⎫≠ ⎪⎝⎭＋(k ∈Z ))．2．能利用单位圆中的三角函数线推导出π2α±，π±α的正弦、余弦、正切的诱导公式，并能灵活运用．知识梳理1．同角三角函数的基本关系式 (1)平方关系：__________； (2)商数关系：__________； (3)倒数关系：__________. 2．诱导公式总口诀为：奇变偶不变，符号看象限，其中“奇”“偶”是指“k ·π2±α(k ∈Z )”中k 的奇偶性；“符号”是指把任意角α看作锐角时，原函数值的符号．即α＋k ·2π(k ∈Z )，－α，π±α的三角函数值，等于α的同名函数值，前面加上一个把α看成__________时原函数值的符号；π2±α的正弦(余弦)函数值，分别等于α的余弦(正弦)函数值，前面加上一个把α看成锐角时原函数值的符号．1．已知cos(α－π)＝－513，且α是第四象限角，则sin α＝( )．A ．－1213B ．1213C ．±1213D ．5122．已知sin x ＝2cos x ，则sin 2x ＋1＝( )．A ．65B ．95C ．43D ．533．已知α是第四象限角，tan α＝－512，则sin α等于( )．A ．15B ．－15C ．513D ．－5134．已知sin α＋3cos α3cos α－sin α＝5，则sin 2α－sin αcos α的值是________．思维拓展1．有人说sin(k π－α)＝sin(π－α)＝sin α(k ∈Z )，你认为正确吗？提示：不正确．当k ＝2n (n ∈Z )时，sin(k π－α)＝sin(2n π－α)＝sin(－α)＝－sin α；当k ＝2n ＋1(n ∈Z )时，sin(k π－α)＝sin[(2n ＋1)·π－α]＝sin(2n π＋π－α)＝sin(π－α)＝sin α.2．“符号看象限”中，符号是否与α的大小有关？提示：无关，只是把α从形式上看作锐角，从而2k π＋α(k ∈Z )，π＋α，－α，π－α，π2－α，π2＋α分别是第一，三，四，二，一，二象限的角．一、同角三角函数关系式的应用【例1－1】已知tan α＝14，则cos 2α＋sin 2α的值为__________．【例1－2】已知α是三角形的内角，且sin α＋cos α＝15.(1)求tan α的值；(2)把1cos 2α－sin 2α用tan α表示出来，并求其值． 方法提炼1．利用sin 2α＋cos 2α＝1可以实现角α的正弦、余弦的互化，利用sin αcos α＝tan α⎝ ⎛⎭⎪⎫α≠k π＋π2，k ∈Z 可以实现角α的弦切互化．2．注意公式逆用及变形应用：1＝sin 2α＋cos 2α，sin 2α＝1－cos 2α，cos 2α＝1－sin 2α.请做[针对训练]1二、诱导公式的应用 【例2－1】化简：sin(540°－x )tan(900°－x )·1tan(450°－x )tan(810°－x )·cos(360°－x )sin(－x )＝__________.【例2－2】化简：cos(π＋θ)cos θ[cos(π－θ)－1]＋cos(θ－2π)sin ⎝ ⎛⎭⎪⎫θ－3π2cos(θ－π)－sin ⎝⎛⎭⎪⎫3π2＋θ.【例2－3】已知cos(π＋α)＝－12，且α是第四象限角，计算：sin[α＋(2n ＋1)π]＋sin[α－(2n ＋1)π]sin(α＋2n π)·cos (α－2n π)(n ∈Z )．方法提炼利用诱导公式化简求值时的原则为：1．“负化正”，运用公式三将任意负角的三角函数化为任意正角的三角函数．2．“大化小”，利用公式一将大于360°的角的三角函数化为0°到360°的三角函数，利用公式二将大于180°的角的三角函数化为0°到180°的三角函数．3．“小化锐”，利用公式六将大于90°的角化为0°到90°的角的三角函数．4．“锐求值”，得到0°到90°的三角函数后，若是特殊角直接求得，若是非特殊角可由计算器求得．请做[针对训练]2三、sin x ±cos x 与方程思想【例3】已知sin θ－cos θ＝12，求：(1)sin θcos θ；(2)sin 3θ－cos 3θ；(3)sin 4θ＋cos 4θ.方法提炼1．已知a sin x ＋b cos x ＝c 可与sin 2x ＋cos 2x ＝1联立，求得sin x ，cos x ，一般此法不常用，原因是计算麻烦．2．sin x ＋cos x ，sin x －cos x ，sin x cos x 之间的关系为：(sin x ＋cos x )2＝1＋2sin x cos x ，(sin x －cos x )2＝1－2sin x cos x ，(sin x ＋cos x )2＋(sin x －cos x )2＝2.因此已知上述三个代数式中的任意一个代数式的值可求其余两个代数式的值．请做[针对训练]3考情分析从近几年的高考试题来看，同角三角函数的基本关系和诱导公式中是高考的热点，题型既有选择题、填空题，又有解答题．主要考查诱导公式在三角函数式求值，化简的过程中与同角三角函数的关系式，和差角公式及倍角公式的综合应用，在考查基本运算的同时，注重考查等价转化的思想方法．预测2013年高考仍将以诱导公式为主要考点，重点考查考生的运算能力与恒等变形能力．针对训练 1．(2011重庆高考，文12)若cos α＝－35，且α∈⎝⎛⎭⎪⎫π，3π2，则tan α＝__________.2．已知A ＝sin(k π＋α)sin α＋cos(k π＋α)cos α(k ∈Z )，则A 的值构成的集合是__________．3．已知关于x 的方程2x 2－(3＋1)x ＋m ＝0的两根为sin θ和cos θ，θ∈(0,2π)，求m 的值．参考答案基础梳理自测 知识梳理1．(1)sin 2α＋cos 2α＝1(2)tan α＝sin αcos α⎝ ⎛⎭⎪⎫α≠k π＋π2，k ∈Z(3)tan α·cot α＝12．sin α －sin α －sin α sin α cos αcos α cos α －cos α cos α －cos α sin α －sin α tan α tan α －tan α －tan α 锐角3．0 π6 π4 π3 π2 2π3 56ππ 3π2 0 12 22 32 1 32 120 －1 132 22 12 0 －12－32 －1 0 0 331 3 不存在 － 3 －33不存在基础自测1．A 解析：cos(α－π)＝－cos α＝－513，cos α＝513.sin α＝±1－cos 2α＝±1213，∵α是第四象限角，∴sin α＝－1213.2．B 解析：∵sin 2x ＋cos 2x ＝1，∴sin 2x ＋⎝ ⎛⎭⎪⎫12sin x 2＝1，∴sin 2x ＝45，∴sin 2x ＋1＝95.3．D 解析：由tan α＝sin αcos α＝－512，sin 2α＋cos 2α＝1及α是第四象限角，解得sin α＝－513.4．25 解析：由sin α＋3cos α3cos α－sin α＝5得，tan α＋33－tan α＝5，即tan α＝2.所以sin 2α－sin αcos α＝sin 2α－sin αcos αsin 2α＋cos 2α＝tan 2α－tan αtan 2α＋1＝25. 考点探究突破【例1－1】1617 解析：cos 2α＋sin 2α＝1－2sin 2α＋sin 2α＝cos 2α＝cos 2αcos 2α＋sin 2α＝11＋tan 2α＝1617. 【例1－2】解：(1)联立方程 ⎩⎪⎨⎪⎧ sin α＋cos α＝15，sin 2α＋cos 2α＝1.①②由①得cos α＝15－sin α，将其代入②.整理得25sin 2α－5sin α－12＝0. ∵α是三角形的内角，∴⎩⎪⎨⎪⎧sin α＝45，cos α＝－35.∴tan α＝－43.(2)1cos 2α－sin 2α＝sin 2α＋cos 2αcos 2α－sin 2α＝sin 2α＋cos 2αcos 2αcos 2α－sin 2αcos 2α＝tan 2α＋11－tan 2α.∵tan α＝－43， ∴1cos 2α－sin 2α＝tan 2α＋11－tan 2α＝⎝ ⎛⎭⎪⎫－432＋11－⎝ ⎛⎭⎪⎫－432＝－257. 【例2－1】sin x 解析：原式＝sin(180°－x )tan(180°－x )·1tan(90°－x )tan(90°－x )·cos x－sin x＝sin x－tan x ·ta n x ·tan x ⎝ ⎛⎭⎪⎫－1tan x ＝sin x . 【例2－2】解：原式＝－cos θcos θ(－cos θ－1)＋cos θcos θ(－cos θ)＋cos θ＝11＋cos θ＋11－cos θ＝2sin 2θ. 【例2－3】解：∵cos(π＋α)＝－12.∴－cos α＝－12，cos α＝12.则sin[α＋(2n ＋1)π]＋sin[α－(2n ＋1)π]sin(a ＋2n π)·cos (α－2n π)＝sin(2n π＋π＋α)＋sin(－2n π－π＋α)sin(2n π＋α)·cos (－2n π＋α)＝sin(π＋α)＋sin(－π＋α)sin α·cos α＝－sin α－sin(π－α)sin α·cos α＝－2sin αsin αcos α＝－2cos α＝－4.【例3】解：(1)∵sin θ－cos θ＝12，∴(sin θ－cos θ)2＝14，即sin 2θ－2sin θcos θ＋cos 2θ＝14.由平方关系sin 2θ＋cos 2θ＝1，可得sin θcos θ＝38.(2)sin 3θ－cos 3θ＝(sin θ－cos θ)(sin 2θ＋cos θsin θ＋cos 2θ)．由平方关系及sin θ－cos θ＝12，可得sin 3θ－cos 3θ＝12×⎝⎛⎭⎪⎫1＋38＝1116.(3)由(sin 2θ＋cos 2θ)2＝sin 4θ＋2sin 2θ·cos 2θ＋cos 4θ＝1，可得sin 4θ＋cos 4θ＝1－2sin 2θ·cos 2θ＝1－2×964＝2332.演练巩固提升 针对训练1．43 解析：由1＋tan 2α＝1cos 2α，则tan 2α＝169.又因α∈⎝ ⎛⎭⎪⎫π，3π2，故tan α＞0，则tan α＝43.2．{－2,2} 解析：当k 为偶数时，A ＝sin αsin α＋cos αcos α＝2；k 为奇数时，A ＝－sin αsin α－cos αcos α＝－2.3．解：由韦达定理可知⎩⎪⎨⎪⎧sin θ＋cos θ＝3＋12，sin θcos θ＝m 2.①②由①式平方得1＋2sin θcos θ＝2＋32，∴sin θcos θ＝34，由②得m 2＝34.∴m ＝32.。

第2讲 同角三角函数的基本关系与诱导公式 最新考纲考向预测1.理解同角三角函数的基本关系式sin 2x ＋cos 2x ＝1，sin xcos x ＝tan x .2.借助单位圆的对称性，利用定义推导出诱导公式⎝ ⎛⎭⎪⎫α±π2，α±π的正弦、余弦、正切. 命题趋势 考查利用同角三角函数的基本关系、诱导公式解决条件求值问题，常与三角恒等变换相结合起到化简三角函数关系的作用，强调利用三角公式进行恒等变形的技巧以及基本的运算能力.核心素养数学运算1．同角三角函数的基本关系 (1)平方关系：sin 2x ＋cos 2x ＝1．(2)商数关系：tan x ＝sin x cos x ⎝ ⎛⎭⎪⎫其中x ≠k π＋π2，k ∈Z .2．三角函数的诱导公式 组数 一 二 三 四 五 六 角 α＋2k π (k ∈Z ) π＋α －α π－α π2－α π2＋α 正弦 sin α －sin__α －sin__α sin__α cos__α cos__α 余弦 cos α －cos__α cos__α －cos__α sin__α －sin__α正切tan αtan__α－tan__α－tan__α常用结论1．诱导公式的记忆口诀“奇变偶不变，符号看象限”，其中的奇、偶是指π2的奇数倍和偶数倍，变与不变指函数名称的变化．2．同角三角函数的基本关系式的几种变形 (1)sin 2α＝1－cos 2α＝(1＋cos α)(1－cos α)；cos 2α＝1－sin 2α＝(1＋sin α)(1－sin α)； (sin α±cos α)2＝1±2sin αcos α. (2)sin α＝tan αcos α⎝ ⎛⎭⎪⎫α≠π2＋k π，k ∈Z .(3)sin 2α＝sin 2αsin 2α＋cos 2α＝tan 2αtan 2α＋1；cos 2α＝cos 2αsin 2α＋cos 2α＝1tan 2α＋1.常见误区1．同角三角函数的基本关系式及诱导公式要注意角的范围对三角函数符号的影响，尤其是利用平方关系求三角函数值，进行开方时要根据角的范围，判断符号后，正确取舍．2．注意求值与化简后的结果一般要尽可能有理化、整式化．1．判断正误(正确的打“√”，错误的打“×”) (1)对任意的角α，β，都有sin 2α＋cos 2β＝1.( ) (2)若α∈R ，则tan α＝sin αcos α恒成立．( )(3)sin(π＋α)＝－sin α成立的条件是α为锐角．( ) (4)若cos(n π－θ)＝13(n ∈Z )，则cos θ＝13.( ) 答案：(1)× (2)× (3)× (4)×2．(易错题)已知cos(π＋α)＝23，则tan α＝( ) A ．52 B ．255 C ．±52D ．±255解析：选C.因为cos(π＋α)＝23， 所以cos α＝－23，则α为第二或第三象限角，所以sin α＝±1－cos 2α＝±53.所以tan α＝sin αcos α＝±53－23＝±52. 3．已知sin αcos α＝12，则tan α＋1tan α＝( ) A ．2 B ．12 C ．－2D ．－12解析：选A.tan α＋1tan α＝sin αcos α＋cos αsin α＝sin 2α＋cos 2αsin αcos α＝112＝2.4．sin 2 490°＝________；cos ⎝ ⎛⎭⎪⎫－52π3＝________．解析：sin 2 490°＝sin(7×360°－30°)＝－sin 30°＝－12.cos ⎝ ⎛⎭⎪⎫－52π3＝cos 52π3＝cos ⎝ ⎛⎭⎪⎫16π＋π＋π3＝cos ⎝ ⎛⎭⎪⎫π＋π3＝－cos π3＝－12. 答案：－12 －125．化简cos ⎝ ⎛⎭⎪⎫α－π2sin ⎝ ⎛⎭⎪⎫52π＋α·cos(2π－α)的结果为________．解析：原式＝sin αcos α·cos α＝sin α. 答案：sin α同角三角函数的基本关系式 角度一 “知一求二”问题(2020·北京市适应性测试)已知α是第四象限角，且tan α＝－34，则sinα＝( )A ．－35 B.35 C.45 D ．－45 【解析】 因为tan α＝sin αcos α＝－34， 所以cos α＝－43sin α ①.sin 2α＋cos 2α＝1 ②，由①②得sin 2α＝925，又α是第四象限角，所以sin α<0，则sin α＝－35，故选A.【答案】 A利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形．同角三角函数的基本关系本身是恒等式，也可以看作是方程，对于一些题，可利用已知条件，结合同角三角函数的基本关系列方程组，通过解方程组达到解决问题的目的．角度二 sin α，cos α的齐次式问题已知tan αtan α－1＝－1，求下列各式的值：(1)sin α－3cos αsin α＋cos α；(2)sin 2α＋sin αcos α＋2. 【解】 由已知得tan α＝12. (1)sin α－3cos αsin α＋cos α＝tan α－3tan α＋1＝－53.(2)sin 2α＋sin αcos α＋2＝sin 2α＋sin αcos αsin 2α＋cos 2α＋2＝tan 2α＋tan αtan 2α＋1＋2＝⎝ ⎛⎭⎪⎫122＋12⎝ ⎛⎭⎪⎫122＋1＋2＝135.关于sin α与cos α的齐n 次分式或齐二次整式的化简求值的解题策略已知tan α，求关于sin α与cos α的齐n次分式或齐二次整式的值．角度三sin α±cos α，sin αcos α之间的关系已知α∈(－π，0)，sin α＋cos α＝1 5.(1)求sin α－cos α的值；(2)求sin 2α＋2sin2α1－tan α的值．【解】(1)由sin α＋cos α＝1 5，平方得sin2α＋2sin αcos α＋cos2α＝1 25，整理得2sin αcos α＝－24 25.所以(sin α－cos α)2＝1－2sin αcos α＝49 25.由α∈(－π，0)，知sin α<0，又sin α＋cos α>0，所以cos α>0，则sin α－cos α<0，故sin α－cos α＝－7 5.(2)sin 2α＋2sin2α1－tan α＝2sin α（cos α＋sin α）1－sin αcos α＝2sin αcos α（cos α＋sin α）cos α－sin α＝－2425×1575＝－24175.sin α±cos α与sin αcos α关系的应用技巧(1)通过平方，sin α＋cos α，sin α－cos α，sin αcos α之间可建立联系，若令sin α＋cos α＝t ，则sin αcos α＝t 2－12，sin α－cos α＝±2－t 2(注意根据α的范围选取正、负号)．(2)对于sin α＋cos α，sin α－cos α，sin αcos α这三个式子，可以知一求二．1．(2020·河南六市一模)已知cos ⎝ ⎛⎭⎪⎫π2＋α＝35，且α∈⎝ ⎛⎭⎪⎫π2，3π2，则tan α＝( )A ．43 B ．34 C ．－34D ．±34解析：选B.因为cos ⎝ ⎛⎭⎪⎫π2＋α＝35，所以sin α＝－35.又α∈⎝ ⎛⎭⎪⎫π2，3π2，所以cos α＝－1－sin 2α＝－45，所以tan α＝sin αcos α＝34.2．已知tan α＝－34，则sin α(sin α－cos α)＝( ) A.2125 B.2521 C.45D.54解析：选 A.sin α(sin α－cos α)＝sin 2α－sin αcos α＝sin 2α－sin αcos αsin 2α＋cos 2α＝tan 2α－tan αtan 2α＋1，将tan α＝－34代入得原式＝⎝ ⎛⎭⎪⎫－342－⎝ ⎛⎭⎪⎫－34⎝ ⎛⎭⎪⎫－342＋1＝2125.3．(一题多解)已知sin α－cos α＝2，α∈(0，π)，则tan α＝( ) A ．－1 B ．－22 C ．22D ．1解析：选A.方法一：由⎩⎨⎧sin α－cos α＝2，sin 2α＋cos 2α＝1，得2cos 2α＋22cos α＋1＝0，即(2cos α＋1)2＝0， 所以cos α＝－22.又α∈(0，π)，所以α＝3π4， 所以tan α＝tan 3π4＝－1.方法二：因为sin α－cos α＝2， 所以2sin ⎝ ⎛⎭⎪⎫α－π4＝2，所以sin ⎝ ⎛⎭⎪⎫α－π4＝1.因为α∈(0，π)，所以α＝3π4，所以tan α＝－1.法三：由sin α－cos α＝2得1－sin 2α＝2，所以sin 2α＝－1. 设sin α＋cos α＝t ，所以1＋sin 2α＝t 2，所以t ＝0.由⎩⎨⎧sin α－cos α＝2，sin α＋cos α＝0得sin α＝22，cos α＝－22， 所以tan α＝－1.诱导公式的应用(1)sin(－1 200°)cos 1 290°＝________．(2)已知角θ的顶点在坐标原点，始边与x 轴正半轴重合，终边在直线3x －y ＝0上，则sin ⎝ ⎛⎭⎪⎫3π2＋θ＋2cos （π－θ）sin ⎝ ⎛⎭⎪⎫π2－θ－sin （π－θ）等于________．【解析】 (1)原式＝－sin 1 200°cos 1 290° ＝－sin(3×360°＋120°)cos(3×360°＋210°) ＝－sin 120°cos 210°＝－sin(180°－60°)cos(180°＋30°) ＝sin 60°cos 30°＝32×32＝34.(2)由题意可知tan θ＝3，原式＝－cos θ－2cos θcos θ－sin θ＝－31－tan θ＝32.【答案】 (1)34 (2)32【引申探究】 (变问法)若本例(2)的条件不变，则cos ⎝ ⎛⎭⎪⎫π2＋θ－sin （－π－θ）cos ⎝ ⎛⎭⎪⎫11π2－θ＋sin ⎝ ⎛⎭⎪⎫9π2＋θ＝________．解析：由题意可知tan θ＝3， 原式＝－sin θ＋sin （π＋θ）cos ⎝ ⎛⎭⎪⎫6π－π2－θ＋sin ⎝ ⎛⎭⎪⎫4π＋π2＋θ ＝－sin θ－sin θcos ⎝ ⎛⎭⎪⎫π2＋θ＋sin ⎝ ⎛⎭⎪⎫π2＋θ＝－2sin θ－sin θ＋cos θ＝2tan θtan θ－1＝2×33－1＝3.答案：3(1)诱导公式用法的一般思路①化负为正，化大为小，化到锐角为止；②角中含有加减π2的整数倍时，用公式去掉π2的整数倍． (2)常见的互余和互补的角①常见的互余的角：π3－α与π6＋α；π3＋α与π6－α；π4＋α与π4－α等； ②常见的互补的角：π3＋θ与2π3－θ；π4＋θ与3π4－θ等．1．已知sin ⎝ ⎛⎭⎪⎫α－π3＝13，则cos ⎝ ⎛⎭⎪⎫α＋π6的值是( )A ．－13 B.13 C.223 D ．－223解析：选A.因为sin ⎝ ⎛⎭⎪⎫α－π3＝13，所以cos ⎝ ⎛⎭⎪⎫α＋π6＝cos ⎣⎢⎡⎦⎥⎤π2＋⎝ ⎛⎭⎪⎫α－π3＝－sin ⎝ ⎛⎭⎪⎫α－π3＝－13.2．(多选)已知A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α，则A 的值可以是( )A ．3B ．－3C ．1D ．－1解析：选AD.由已知可得，当k 为偶数时，A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α＝sin αsin α＋cos αcos α＋tan αtan α＝3；当k 为奇数时，A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α＝－sin αsin α＋－cos αcos α＋tan αtan α＝－1，所以A 的值可以是3或－1.故答案为AD.同角三角函数的基本关系式与诱导公式的综合应用(2020·湖北宜昌一中期末)已知α是第三象限角，且cos α＝－1010. (1)求tan α的值；(2)化简并求cos （π－α）2sin （－α）＋sin ⎝ ⎛⎭⎪⎫π2＋α的值．【解】 (1)因为α是第三象限角，cos α＝－1010， 所以sin α＝－1－cos 2α＝－31010，所以tan α＝sin αcos α＝3.(2)原式＝－cos α－2sin α＋cos α＝cos α2sin α－cos α＝12tan α－1，由(1)知tan α＝3，所以原式＝12×3－1＝15.求解诱导公式与同角关系综合问题的基本思路和化简要求基本 思路①分析结构特点，选择恰当公式； ②利用公式化成单角三角函数；③整理得最简形式化简 要求①化简过程是恒等变换；②结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值1．已知sin ⎝ ⎛⎭⎪⎫5π2＋α＝35，所以tan α的值为( )A ．－43B ．－34C ．±43D ．±34解析：选C.sin ⎝ ⎛⎭⎪⎫5π2＋α＝sin ⎝ ⎛⎭⎪⎫π2＋α＝cos α＝35，所以sin α＝±45，tan α＝sin αcos α＝±43.2．已知tan(π－α)＝－23，且α∈⎝ ⎛⎭⎪⎫－π，－π2，则cos （－α）＋3sin （π＋α）cos （π－α）＋9sin α的值为( )A ．－15B ．－37 C.15 D.37解析：选 A.因为tan(π－α)＝－23，所以tan α＝23，所以cos （－α）＋3sin （π＋α）cos （π－α）＋9sin α＝cos α－3sin α－cos α＋9sin α＝1－3tan α－1＋9tan α＝1－2－1＋6＝－15，故选A.[A 级 基础练]1．(多选)已知x ∈R ，则下列等式恒成立的是( ) A ．sin(－x )＝sin x B ．sin ⎝ ⎛⎭⎪⎫3π2－x ＝cos xC ．cos ⎝ ⎛⎭⎪⎫π2＋x ＝－sin xD ．cos(x －π)＝－cos x解析：选CD.sin(－x )＝－sin x ，故A 不成立；sin ⎝ ⎛⎭⎪⎫3π2－x ＝－cos x ，故B 不成立；cos ⎝ ⎛⎭⎪⎫π2＋x ＝－sin x ，故C 成立；cos(x －π)＝－cos x ，故D 成立．2．(多选)若sin α＝45，且α为锐角，则下列选项中正确的有( )A ．tan α＝43 B ．cos α＝35 C ．sin α＋cos α＝85D ．sin α－cos α＝－15解析：选AB.因为sin α＝45，且α为锐角， 所以cos α＝1－sin 2α＝1－⎝ ⎛⎭⎪⎫452＝35，故B 正确， 所以tan α＝sin αcos α＝4535＝43，故A 正确，所以sin α＋cos α＝45＋35＝75≠85，故C 错误， 所以sin α－cos α＝45－35＝15≠－15，故D 错误．3．已知角α是第二象限角，且满足sin ⎝ ⎛⎭⎪⎫5π2＋α＋3cos(α－π)＝1，则tan(π＋α)＝( )A ． 3B ．－ 3C ．－33D ．－1解析：选B.由sin ⎝ ⎛⎭⎪⎫5π2＋α＋3cos(α－π)＝1，得cos α－3cos α＝1，所以cos α＝－12， 因为角α是第二象限角，所以sin α＝32， 所以tan(π＋α)＝tan α＝sin αcos α＝－ 3.4．已知f (α)＝sin （2π－α）cos ⎝ ⎛⎭⎪⎫π2＋αcos ⎝ ⎛⎭⎪⎫－π2＋αtan （π＋α），则f ⎝ ⎛⎭⎪⎫π3＝( ) A ．12 B ．22 C ．32D ．－12解析：选A.f (α)＝sin （2π－α）cos ⎝ ⎛⎭⎪⎫π2＋αcos ⎝ ⎛⎭⎪⎫－π2＋αtan （π＋α）＝－sin α·（－sin α）sin α·tan α＝sin 2αsin α·sin αcos α＝cos α，则f ⎝ ⎛⎭⎪⎫π3＝cos π3＝12.5．已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上一点A (2sin α，3)(sin α≠0)，则cos α＝( )A ．12B ．－12C ．32D ．－32解析：选A.由三角函数定义得tan α＝32sin α，即sin αcos α＝32sin α，得3cos α＝2sin 2α＝2(1－cos 2α)，解得cos α＝12或cos α＝－2(舍去)．故选A.6．计算：sin 11π6＋cos 10π3的值为________．解析：原式＝sin ⎝ ⎛⎭⎪⎫2π－π6＋cos ⎝ ⎛⎭⎪⎫3π＋π3＝－sin π6－cos π3＝－12－12＝－1.答案：－17．已知sin ⎝ ⎛⎭⎪⎫－π2－αcos ⎝ ⎛⎭⎪⎫－7π2＋α＝1225，且0＜α＜π4，则sin α＝________，cos α＝________．解析：sin ⎝ ⎛⎭⎪⎫－π2－αcos ⎝ ⎛⎭⎪⎫－7π2＋α＝－cos α·(－sin α)＝sin αcos α＝1225.因为0＜α＜π4，所以0＜sin α＜cos α.又因为sin 2α＋cos 2α＝1，所以sin α＝35，cos α＝45.答案：35 45 8．化简1－2sin 40°cos 40°cos 40°－1－sin 250°＝________． 解析：原式＝sin 240°＋cos 240°－2sin 40°cos 40°cos 40°－cos 50°＝|sin 40°－cos 40°|sin 50°－sin 40°＝|sin 40°－sin 50°|sin 50°－sin 40°＝sin 50°－sin 40°sin 50°－sin 40°＝1.答案：19．已知sin(3π＋α)＝2sin ⎝ ⎛⎭⎪⎫3π2＋α，求下列各式的值：(1)sin α－4cos α5sin α＋2cos α；(2)sin 2α＋sin 2α.解：由已知得sin α＝2cos α. (1)原式＝2cos α－4cos α5×2cos α＋2cos α＝－16.(2)原式＝sin 2α＋2sin αcos αsin 2α＋cos 2α＝sin 2α＋sin 2αsin 2α＋14sin 2α＝85.10．已知角θ的终边与单位圆x 2＋y 2＝1在第四象限交于点P ，且点P 的坐标为⎝ ⎛⎭⎪⎫12，y .(1)求tan θ的值；(2)求cos ⎝ ⎛⎭⎪⎫π2－θ＋cos （θ－2π）sin θ＋cos （π＋θ）的值．解：(1)由θ为第四象限角，终边与单位圆交于点P ⎝ ⎛⎭⎪⎫12，y ，得⎝ ⎛⎭⎪⎫122＋y 2＝1，y <0，解得y ＝－32，所以tan θ＝－3212＝－ 3.(2)因为tan θ＝－3， 所以cos ⎝ ⎛⎭⎪⎫π2－θ＋cos （θ－2π）sin θ＋cos （π＋θ）＝sin θ＋cos θsin θ－cos θ＝tan θ＋1tan θ－1＝－3＋1－3－1＝2－ 3. [B 级 综合练]11．(多选)已知角θ的终边与坐标轴不重合，式子1－sin 2（π＋θ）化简的结果为－cos θ，则( )A ．sin θ>0，tan θ>0B ．sin θ<0，tan θ>0C ．sin θ<0，tan θ<0D ．sin θ>0，tan θ<0解析：选BD.1－sin 2（π＋θ）＝1－sin 2θ＝cos 2θ＝|cos θ|＝－cos θ，所以cos θ<0，角θ的终边落在第二或三象限，所以sin θ>0，tan θ<0或sin θ<0，tan θ>0，故选BD.12．(2020·陕西汉中月考)已知角α为第二象限角，则cos α·1＋sin α1－sin α＋sin 2α1＋1tan 2α＝( )A ．1B ．－1C ．0D ．2解析：选B.因为角α为第二象限角，所以sin α>0，cos α<0，所以cos α 1＋sin α1－sin α＝cos α（1＋sin α）2cos 2α＝cos α·1＋sin α|cos α|＝－1－sin α，sin 2α1＋1tan 2α＝sin 2α1＋cos 2αsin 2α＝sin 2αsin 2α＋cos 2αsin 2α＝sin 2α1sin 2α＝sin 2α⎪⎪⎪⎪⎪⎪1sin α＝sin α，所以cos α1＋sin α1－sin α＋sin 2α1＋1tan 2α＝－1－sin α＋sin α＝－1.故选B.13．是否存在α∈⎝ ⎛⎭⎪⎫－π2，π2，β∈()0，π使等式sin(3π－α)＝2cos ⎝ ⎛⎭⎪⎫π2－β，3cos(－α)＝－2cos(π＋β)同时成立？若存在，求出α，β的值；若不存在，请说明理由．解：假设存在角α，β满足条件． 由已知条件可得⎩⎨⎧sin α＝2sin β，①3cos α＝2cos β，②由①2＋②2，得sin 2α＋3cos 2α＝2.所以sin 2α＝12，所以sin α＝±22.因为α∈⎝ ⎛⎭⎪⎫－π2，π2，所以α＝±π4. 当α＝π4时，由②式知cos β＝32， 又β∈(0，π)，所以β＝π6，此时①式成立； 当α＝－π4时，由②式知cos β＝32，又β∈(0，π)， 所以β＝π6，此时①式不成立，故舍去． 所以存在α＝π4，β＝π6满足条件． 14．在△ABC 中，(1)求证：cos 2A ＋B 2＋cos 2 C2＝1；(2)若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫3π2＋B tan(C －π)＜0，求证：△ABC 为钝角三角形．证明：(1)在△ABC 中，A ＋B ＝π－C ， 所以A ＋B 2＝π2－C2，所以cos A ＋B 2＝cos ⎝ ⎛⎭⎪⎫π2－C 2＝sin C 2，所以cos 2A ＋ B 2＋cos 2C2＝1.(2)若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫3π2＋B tan(C －π)＜0，所以(－sin A )(－cos B )tan C ＜0， 即sin A cos B tan C ＜0.因为在△ABC 中，0＜A ＜π，0＜B ＜π，0＜C ＜π且sin A ＞0， 所以⎩⎨⎧cos B ＜0，tan C ＞0或⎩⎨⎧cos B ＞0，tan C ＜0，所以B 为钝角或C 为钝角，所以△ABC 为钝角三角形．[C 级 创新练]15．(2020·山东肥城统考)公元前6世纪，古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图，发现黄金分割比例为5－12≈0.618，这一数值也可以表示为m ＝2sin 18°.若m 2＋n ＝4，则m n2cos 227°－1＝( )A ．4B ．3C ．2D ．1解析：选C.因为m ＝2sin 18°，且m 2＋n ＝4，所以n ＝4－m 2＝4－4sin 218°＝4(1－sin 218°)＝4cos 218°，所以m n2cos 227°－1＝2sin 18°4cos 218°cos 54°＝4sin 18°cos 18°sin 36°＝2.故选C.16．已知α，β∈(0，2π)且α<β，若关于x 的方程(x ＋sin α)(x ＋sin β)＋1＝0有实数根，则代数式3sin ⎝ ⎛⎭⎪⎫π2＋α＋cos ⎝ ⎛⎭⎪⎫3π2－β2－sin （π－α）cos ⎝ ⎛⎭⎪⎫3π2＋β＝________．解析：整理方程(x ＋sin α)(x ＋sin β)＋1＝0得x 2＋x (sin α＋sin β)＋sin αsin β＋1＝0.由题意得Δ＝(sin α＋sin β)2－4sin αsin β－4≥0， 即(sin α－sin β)2≥4①.因为－1≤sin α≤1，－1≤sin β≤1，所以sin α－sin β∈[－2，2]，从而(sin α－sin β)2≤4②.由①②得sin α－sin β＝±2，所以⎩⎨⎧sin α＝1，sin β＝－1或⎩⎨⎧sin α＝－1，sin β＝1.因为α，β∈(0，2π)且α<β，所以α＝π2，β＝3π2，即⎩⎨⎧sin α＝1，sin β＝－1.因此3sin ⎝ ⎛⎭⎪⎫π2＋α＋cos ⎝ ⎛⎭⎪⎫3π2－β2－sin （π－α）cos ⎝ ⎛⎭⎪⎫3π2＋β＝3cos α－sin β2－sin αsin β＝12＋1＝13.答案：13第2讲 同角三角函数的基本关系与诱导公式 最新考纲考向预测1.理解同角三角函数的基本关系式sin 2x ＋cos 2x ＝1，sin xcos x ＝tan x .2.借助单位圆的对称性，利用定义推导出诱导公式⎝ ⎛⎭⎪⎫α±π2，α±π的正弦、余弦、正切. 命题趋势 考查利用同角三角函数的基本关系、诱导公式解决条件求值问题，常与三角恒等变换相结合起到化简三角函数关系的作用，强调利用三角公式进行恒等变形的技巧以及基本的运算能力.核心素养数学运算1．同角三角函数的基本关系 (1)平方关系：sin 2x ＋cos 2x ＝1．(2)商数关系：tan x ＝sin x cos x ⎝ ⎛⎭⎪⎫其中x ≠k π＋π2，k ∈Z .2．三角函数的诱导公式 组数 一 二 三 四 五 六 角 α＋2k π (k ∈Z ) π＋α －α π－α π2－α π2＋α 正弦 sin α －sin__α －sin__α sin__α cos__α cos__α 余弦 cos α －cos__α cos__α －cos__α sin__α －sin__α正切tan αtan__α－tan__α－tan__α常用结论1．诱导公式的记忆口诀“奇变偶不变，符号看象限”，其中的奇、偶是指π2的奇数倍和偶数倍，变与不变指函数名称的变化．2．同角三角函数的基本关系式的几种变形 (1)sin 2α＝1－cos 2α＝(1＋cos α)(1－cos α)；cos 2α＝1－sin 2α＝(1＋sin α)(1－sin α)； (sin α±cos α)2＝1±2sin αcos α. (2)sin α＝tan αcos α⎝ ⎛⎭⎪⎫α≠π2＋k π，k ∈Z .(3)sin 2α＝sin 2αsin 2α＋cos 2α＝tan 2αtan 2α＋1；cos 2α＝cos 2αsin 2α＋cos 2α＝1tan 2α＋1.常见误区1．同角三角函数的基本关系式及诱导公式要注意角的范围对三角函数符号的影响，尤其是利用平方关系求三角函数值，进行开方时要根据角的范围，判断符号后，正确取舍．2．注意求值与化简后的结果一般要尽可能有理化、整式化．1．判断正误(正确的打“√”，错误的打“×”) (1)对任意的角α，β，都有sin 2α＋cos 2β＝1.( ) (2)若α∈R ，则tan α＝sin αcos α恒成立．( )(3)sin(π＋α)＝－sin α成立的条件是α为锐角．( ) (4)若cos(n π－θ)＝13(n ∈Z )，则cos θ＝13.( ) 答案：(1)× (2)× (3)× (4)×2．(易错题)已知cos(π＋α)＝23，则tan α＝( ) A ．52 B ．255 C ．±52D ．±255解析：选C.因为cos(π＋α)＝23， 所以cos α＝－23，则α为第二或第三象限角，所以sin α＝±1－cos 2α＝±53.所以tan α＝sin αcos α＝±53－23＝±52. 3．已知sin αcos α＝12，则tan α＋1tan α＝( ) A ．2 B ．12 C ．－2D ．－12解析：选A.tan α＋1tan α＝sin αcos α＋cos αsin α＝sin 2α＋cos 2αsin αcos α＝112＝2.4．sin 2 490°＝________；cos ⎝ ⎛⎭⎪⎫－52π3＝________．解析：sin 2 490°＝sin(7×360°－30°)＝－sin 30°＝－12.cos ⎝ ⎛⎭⎪⎫－52π3＝cos 52π3＝cos ⎝ ⎛⎭⎪⎫16π＋π＋π3＝cos ⎝ ⎛⎭⎪⎫π＋π3＝－cos π3＝－12. 答案：－12 －125．化简cos ⎝ ⎛⎭⎪⎫α－π2sin ⎝ ⎛⎭⎪⎫52π＋α·cos(2π－α)的结果为________．解析：原式＝sin αcos α·cos α＝sin α. 答案：sin α同角三角函数的基本关系式 角度一 “知一求二”问题(2020·北京市适应性测试)已知α是第四象限角，且tan α＝－34，则sinα＝( )A ．－35 B.35 C.45 D ．－45 【解析】 因为tan α＝sin αcos α＝－34， 所以cos α＝－43sin α ①.sin 2α＋cos 2α＝1 ②，由①②得sin 2α＝925，又α是第四象限角，所以sin α<0，则sin α＝－35，故选A.【答案】 A利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形．同角三角函数的基本关系本身是恒等式，也可以看作是方程，对于一些题，可利用已知条件，结合同角三角函数的基本关系列方程组，通过解方程组达到解决问题的目的．角度二 sin α，cos α的齐次式问题已知tan αtan α－1＝－1，求下列各式的值：(1)sin α－3cos αsin α＋cos α；(2)sin 2α＋sin αcos α＋2. 【解】 由已知得tan α＝12. (1)sin α－3cos αsin α＋cos α＝tan α－3tan α＋1＝－53.(2)sin 2α＋sin αcos α＋2＝sin 2α＋sin αcos αsin 2α＋cos 2α＋2＝tan 2α＋tan αtan 2α＋1＋2＝⎝ ⎛⎭⎪⎫122＋12⎝ ⎛⎭⎪⎫122＋1＋2＝135.关于sin α与cos α的齐n 次分式或齐二次整式的化简求值的解题策略已知tan α，求关于sin α与cos α的齐n次分式或齐二次整式的值．角度三sin α±cos α，sin αcos α之间的关系已知α∈(－π，0)，sin α＋cos α＝1 5.(1)求sin α－cos α的值；(2)求sin 2α＋2sin2α1－tan α的值．【解】(1)由sin α＋cos α＝1 5，平方得sin2α＋2sin αcos α＋cos2α＝1 25，整理得2sin αcos α＝－24 25.所以(sin α－cos α)2＝1－2sin αcos α＝49 25.由α∈(－π，0)，知sin α<0，又sin α＋cos α>0，所以cos α>0，则sin α－cos α<0，故sin α－cos α＝－7 5.(2)sin 2α＋2sin2α1－tan α＝2sin α（cos α＋sin α）1－sin αcos α＝2sin αcos α（cos α＋sin α）cos α－sin α＝－2425×1575＝－24175.sin α±cos α与sin αcos α关系的应用技巧(1)通过平方，sin α＋cos α，sin α－cos α，sin αcos α之间可建立联系，若令sin α＋cos α＝t ，则sin αcos α＝t 2－12，sin α－cos α＝±2－t 2(注意根据α的范围选取正、负号)．(2)对于sin α＋cos α，sin α－cos α，sin αcos α这三个式子，可以知一求二．1．(2020·河南六市一模)已知cos ⎝ ⎛⎭⎪⎫π2＋α＝35，且α∈⎝ ⎛⎭⎪⎫π2，3π2，则tan α＝( )A ．43 B ．34 C ．－34D ．±34解析：选B.因为cos ⎝ ⎛⎭⎪⎫π2＋α＝35，所以sin α＝－35.又α∈⎝ ⎛⎭⎪⎫π2，3π2，所以cos α＝－1－sin 2α＝－45，所以tan α＝sin αcos α＝34.2．已知tan α＝－34，则sin α(sin α－cos α)＝( ) A.2125 B.2521 C.45D.54解析：选 A.sin α(sin α－cos α)＝sin 2α－sin αcos α＝sin 2α－sin αcos αsin 2α＋cos 2α＝tan 2α－tan αtan 2α＋1，将tan α＝－34代入得原式＝⎝ ⎛⎭⎪⎫－342－⎝ ⎛⎭⎪⎫－34⎝ ⎛⎭⎪⎫－342＋1＝2125.3．(一题多解)已知sin α－cos α＝2，α∈(0，π)，则tan α＝( ) A ．－1 B ．－22 C ．22D ．1解析：选A.方法一：由⎩⎨⎧sin α－cos α＝2，sin 2α＋cos 2α＝1，得2cos 2α＋22cos α＋1＝0，即(2cos α＋1)2＝0， 所以cos α＝－22.又α∈(0，π)，所以α＝3π4， 所以tan α＝tan 3π4＝－1.方法二：因为sin α－cos α＝2， 所以2sin ⎝ ⎛⎭⎪⎫α－π4＝2，所以sin ⎝ ⎛⎭⎪⎫α－π4＝1.因为α∈(0，π)，所以α＝3π4，所以tan α＝－1.法三：由sin α－cos α＝2得1－sin 2α＝2，所以sin 2α＝－1. 设sin α＋cos α＝t ，所以1＋sin 2α＝t 2，所以t ＝0.由⎩⎨⎧sin α－cos α＝2，sin α＋cos α＝0得sin α＝22，cos α＝－22， 所以tan α＝－1.诱导公式的应用(1)sin(－1 200°)cos 1 290°＝________．(2)已知角θ的顶点在坐标原点，始边与x 轴正半轴重合，终边在直线3x －y ＝0上，则sin ⎝ ⎛⎭⎪⎫3π2＋θ＋2cos （π－θ）sin ⎝ ⎛⎭⎪⎫π2－θ－sin （π－θ）等于________．【解析】 (1)原式＝－sin 1 200°cos 1 290° ＝－sin(3×360°＋120°)cos(3×360°＋210°) ＝－sin 120°cos 210°＝－sin(180°－60°)cos(180°＋30°) ＝sin 60°cos 30°＝32×32＝34.(2)由题意可知tan θ＝3，原式＝－cos θ－2cos θcos θ－sin θ＝－31－tan θ＝32.【答案】 (1)34 (2)32【引申探究】 (变问法)若本例(2)的条件不变，则cos ⎝ ⎛⎭⎪⎫π2＋θ－sin （－π－θ）cos ⎝ ⎛⎭⎪⎫11π2－θ＋sin ⎝ ⎛⎭⎪⎫9π2＋θ＝________．解析：由题意可知tan θ＝3， 原式＝－sin θ＋sin （π＋θ）cos ⎝ ⎛⎭⎪⎫6π－π2－θ＋sin ⎝ ⎛⎭⎪⎫4π＋π2＋θ ＝－sin θ－sin θcos ⎝ ⎛⎭⎪⎫π2＋θ＋sin ⎝ ⎛⎭⎪⎫π2＋θ＝－2sin θ－sin θ＋cos θ＝2tan θtan θ－1＝2×33－1＝3.答案：3(1)诱导公式用法的一般思路①化负为正，化大为小，化到锐角为止；②角中含有加减π2的整数倍时，用公式去掉π2的整数倍． (2)常见的互余和互补的角①常见的互余的角：π3－α与π6＋α；π3＋α与π6－α；π4＋α与π4－α等； ②常见的互补的角：π3＋θ与2π3－θ；π4＋θ与3π4－θ等．1．已知sin ⎝ ⎛⎭⎪⎫α－π3＝13，则cos ⎝ ⎛⎭⎪⎫α＋π6的值是( )A ．－13 B.13 C.223 D ．－223解析：选A.因为sin ⎝ ⎛⎭⎪⎫α－π3＝13，所以cos ⎝ ⎛⎭⎪⎫α＋π6＝cos ⎣⎢⎡⎦⎥⎤π2＋⎝ ⎛⎭⎪⎫α－π3＝－sin ⎝ ⎛⎭⎪⎫α－π3＝－13.2．(多选)已知A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α，则A 的值可以是( )A ．3B ．－3C ．1D ．－1解析：选AD.由已知可得，当k 为偶数时，A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α＝sin αsin α＋cos αcos α＋tan αtan α＝3；当k 为奇数时，A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α＝－sin αsin α＋－cos αcos α＋tan αtan α＝－1，所以A 的值可以是3或－1.故答案为AD.同角三角函数的基本关系式与诱导公式的综合应用(2020·湖北宜昌一中期末)已知α是第三象限角，且cos α＝－1010. (1)求tan α的值；(2)化简并求cos （π－α）2sin （－α）＋sin ⎝ ⎛⎭⎪⎫π2＋α的值．【解】 (1)因为α是第三象限角，cos α＝－1010， 所以sin α＝－1－cos 2α＝－31010，所以tan α＝sin αcos α＝3.(2)原式＝－cos α－2sin α＋cos α＝cos α2sin α－cos α＝12tan α－1，由(1)知tan α＝3，所以原式＝12×3－1＝15.求解诱导公式与同角关系综合问题的基本思路和化简要求基本 思路①分析结构特点，选择恰当公式； ②利用公式化成单角三角函数；③整理得最简形式化简 要求①化简过程是恒等变换；②结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值1．已知sin ⎝ ⎛⎭⎪⎫5π2＋α＝35，所以tan α的值为( )A ．－43B ．－34C ．±43D ．±34解析：选C.sin ⎝ ⎛⎭⎪⎫5π2＋α＝sin ⎝ ⎛⎭⎪⎫π2＋α＝cos α＝35，所以sin α＝±45，tan α＝sin αcos α＝±43.2．已知tan(π－α)＝－23，且α∈⎝ ⎛⎭⎪⎫－π，－π2，则cos （－α）＋3sin （π＋α）cos （π－α）＋9sin α的值为( )A ．－15B ．－37 C.15 D.37解析：选 A.因为tan(π－α)＝－23，所以tan α＝23，所以cos （－α）＋3sin （π＋α）cos （π－α）＋9sin α＝cos α－3sin α－cos α＋9sin α＝1－3tan α－1＋9tan α＝1－2－1＋6＝－15，故选A.[A 级 基础练]1．(多选)已知x ∈R ，则下列等式恒成立的是( ) A ．sin(－x )＝sin x B ．sin ⎝ ⎛⎭⎪⎫3π2－x ＝cos xC ．cos ⎝ ⎛⎭⎪⎫π2＋x ＝－sin xD ．cos(x －π)＝－cos x解析：选CD.sin(－x )＝－sin x ，故A 不成立；sin ⎝ ⎛⎭⎪⎫3π2－x ＝－cos x ，故B 不成立；cos ⎝ ⎛⎭⎪⎫π2＋x ＝－sin x ，故C 成立；cos(x －π)＝－cos x ，故D 成立．2．(多选)若sin α＝45，且α为锐角，则下列选项中正确的有( )A ．tan α＝43 B ．cos α＝35 C ．sin α＋cos α＝85D ．sin α－cos α＝－15解析：选AB.因为sin α＝45，且α为锐角， 所以cos α＝1－sin 2α＝1－⎝ ⎛⎭⎪⎫452＝35，故B 正确， 所以tan α＝sin αcos α＝4535＝43，故A 正确，所以sin α＋cos α＝45＋35＝75≠85，故C 错误， 所以sin α－cos α＝45－35＝15≠－15，故D 错误．3．已知角α是第二象限角，且满足sin ⎝ ⎛⎭⎪⎫5π2＋α＋3cos(α－π)＝1，则tan(π＋α)＝( )A ． 3B ．－ 3C ．－33D ．－1解析：选B.由sin ⎝ ⎛⎭⎪⎫5π2＋α＋3cos(α－π)＝1，得cos α－3cos α＝1，所以cos α＝－12， 因为角α是第二象限角，所以sin α＝32， 所以tan(π＋α)＝tan α＝sin αcos α＝－ 3.4．已知f (α)＝sin （2π－α）cos ⎝ ⎛⎭⎪⎫π2＋αcos ⎝ ⎛⎭⎪⎫－π2＋αtan （π＋α），则f ⎝ ⎛⎭⎪⎫π3＝( ) A ．12 B ．22 C ．32D ．－12解析：选A.f (α)＝sin （2π－α）cos ⎝ ⎛⎭⎪⎫π2＋αcos ⎝ ⎛⎭⎪⎫－π2＋αtan （π＋α）＝－sin α·（－sin α）sin α·tan α＝sin 2αsin α·sin αcos α＝cos α，则f ⎝ ⎛⎭⎪⎫π3＝cos π3＝12.5．已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上一点A (2sin α，3)(sin α≠0)，则cos α＝( )A ．12B ．－12C ．32D ．－32解析：选A.由三角函数定义得tan α＝32sin α，即sin αcos α＝32sin α，得3cos α＝2sin 2α＝2(1－cos 2α)，解得cos α＝12或cos α＝－2(舍去)．故选A.6．计算：sin 11π6＋cos 10π3的值为________．解析：原式＝sin ⎝ ⎛⎭⎪⎫2π－π6＋cos ⎝ ⎛⎭⎪⎫3π＋π3＝－sin π6－cos π3＝－12－12＝－1.答案：－17．已知sin ⎝ ⎛⎭⎪⎫－π2－αcos ⎝ ⎛⎭⎪⎫－7π2＋α＝1225，且0＜α＜π4，则sin α＝________，cos α＝________．解析：sin ⎝ ⎛⎭⎪⎫－π2－αcos ⎝ ⎛⎭⎪⎫－7π2＋α＝－cos α·(－sin α)＝sin αcos α＝1225.因为0＜α＜π4，所以0＜sin α＜cos α.又因为sin 2α＋cos 2α＝1，所以sin α＝35，cos α＝45.答案：35 45 8．化简1－2sin 40°cos 40°cos 40°－1－sin 250°＝________． 解析：原式＝sin 240°＋cos 240°－2sin 40°cos 40°cos 40°－cos 50°＝|sin 40°－cos 40°|sin 50°－sin 40°＝|sin 40°－sin 50°|sin 50°－sin 40°＝sin 50°－sin 40°sin 50°－sin 40°＝1.答案：19．已知sin(3π＋α)＝2sin ⎝ ⎛⎭⎪⎫3π2＋α，求下列各式的值：(1)sin α－4cos α5sin α＋2cos α；(2)sin 2α＋sin 2α.解：由已知得sin α＝2cos α. (1)原式＝2cos α－4cos α5×2cos α＋2cos α＝－16.(2)原式＝sin 2α＋2sin αcos αsin 2α＋cos 2α＝sin 2α＋sin 2αsin 2α＋14sin 2α＝85.10．已知角θ的终边与单位圆x 2＋y 2＝1在第四象限交于点P ，且点P 的坐标为⎝ ⎛⎭⎪⎫12，y .(1)求tan θ的值；(2)求cos ⎝ ⎛⎭⎪⎫π2－θ＋cos （θ－2π）sin θ＋cos （π＋θ）的值．解：(1)由θ为第四象限角，终边与单位圆交于点P ⎝ ⎛⎭⎪⎫12，y ，得⎝ ⎛⎭⎪⎫122＋y 2＝1，y <0，解得y ＝－32，所以tan θ＝－3212＝－ 3.(2)因为tan θ＝－3， 所以cos ⎝ ⎛⎭⎪⎫π2－θ＋cos （θ－2π）sin θ＋cos （π＋θ）＝sin θ＋cos θsin θ－cos θ＝tan θ＋1tan θ－1＝－3＋1－3－1＝2－ 3. [B 级 综合练]11．(多选)已知角θ的终边与坐标轴不重合，式子1－sin 2（π＋θ）化简的结果为－cos θ，则( )A ．sin θ>0，tan θ>0B ．sin θ<0，tan θ>0C ．sin θ<0，tan θ<0D ．sin θ>0，tan θ<0解析：选BD.1－sin 2（π＋θ）＝1－sin 2θ＝cos 2θ＝|cos θ|＝－cos θ，所以cos θ<0，角θ的终边落在第二或三象限，所以sin θ>0，tan θ<0或sin θ<0，tan θ>0，故选BD.12．(2020·陕西汉中月考)已知角α为第二象限角，则cos α·1＋sin α1－sin α＋sin 2α1＋1tan 2α＝( )A ．1B ．－1C ．0D ．2解析：选B.因为角α为第二象限角，所以sin α>0，cos α<0，所以cos α 1＋sin α1－sin α＝cos α（1＋sin α）2cos 2α＝cos α·1＋sin α|cos α|＝－1－sin α，sin 2α1＋1tan 2α＝sin 2α1＋cos 2αsin 2α＝sin 2αsin 2α＋cos 2αsin 2α＝sin 2α1sin 2α＝sin 2α⎪⎪⎪⎪⎪⎪1sin α＝sin α，所以cos α1＋sin α1－sin α＋sin 2α1＋1tan 2α＝－1－sin α＋sin α＝－1.故选B.13．是否存在α∈⎝ ⎛⎭⎪⎫－π2，π2，β∈()0，π使等式sin(3π－α)＝2cos ⎝ ⎛⎭⎪⎫π2－β，3cos(－α)＝－2cos(π＋β)同时成立？若存在，求出α，β的值；若不存在，请说明理由．解：假设存在角α，β满足条件． 由已知条件可得⎩⎨⎧sin α＝2sin β，①3cos α＝2cos β，②由①2＋②2，得sin 2α＋3cos 2α＝2.所以sin 2α＝12，所以sin α＝±22. 因为α∈⎝ ⎛⎭⎪⎫－π2，π2，所以α＝±π4. 当α＝π4时，由②式知cos β＝32，又β∈(0，π)，所以β＝π6，此时①式成立；当α＝－π4时，由②式知cos β＝32，又β∈(0，π)，所以β＝π6，此时①式不成立，故舍去．所以存在α＝π4，β＝π6满足条件．14．在△ABC 中，(1)求证：cos 2A ＋B 2＋cos 2 C 2＝1；(2)若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫3π2＋B tan(C －π)＜0，求证：△ABC 为钝角三角形． 证明：(1)在△ABC 中，A ＋B ＝π－C ，所以A ＋B 2＝π2－C 2，所以cos A ＋B 2＝cos ⎝ ⎛⎭⎪⎫π2－C 2＝sin C 2， 所以cos 2A ＋ B 2＋cos 2C 2＝1.(2)若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫3π2＋B tan(C －π)＜0， 所以(－sin A )(－cos B )tan C ＜0，即sin A cos B tan C ＜0.因为在△ABC 中，0＜A ＜π，0＜B ＜π，0＜C ＜π且sin A ＞0，所以⎩⎨⎧cos B ＜0，tan C ＞0或⎩⎨⎧cos B ＞0，tan C ＜0， 所以B 为钝角或C 为钝角，所以△ABC 为钝角三角形．[C 级 创新练]15．(2020·山东肥城统考)公元前6世纪，古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图，发现黄金分割比例为5－12≈0.618，这一数值也可以表示为m ＝2sin 18°.若m 2＋n ＝4，则m n 2cos 227°－1＝( ) A ．4 B ．3 C ．2 D ．1解析：选C.因为m ＝2sin 18°，且m 2＋n ＝4，所以n ＝4－m 2＝4－4sin 218°＝4(1－sin 218°)＝4cos 218°，所以m n 2cos 227°－1＝2sin 18°4cos 218°cos 54°＝4sin 18°cos 18°sin 36°＝2.故选C.16．已知α，β∈(0，2π)且α<β，若关于x 的方程(x ＋sin α)(x ＋sin β)＋1＝0有实数根，则代数式3sin ⎝ ⎛⎭⎪⎫π2＋α＋cos ⎝ ⎛⎭⎪⎫3π2－β2－sin （π－α）cos ⎝ ⎛⎭⎪⎫3π2＋β＝________． 解析：整理方程(x ＋sin α)(x ＋sin β)＋1＝0得x 2＋x (sin α＋sin β)＋sin αsin β＋1＝0.由题意得Δ＝(sin α＋sin β)2－4sin αsin β－4≥0，即(sin α－sin β)2≥4①.因为－1≤sin α≤1，－1≤sin β≤1，所以sin α－sin β∈[－2，2]，从而(sin α－sin β)2≤4②.由①②得sin α－sin β＝±2，所以⎩⎨⎧sin α＝1，sin β＝－1或⎩⎨⎧sin α＝－1，sin β＝1.因为α，β∈(0，2π)且α<β，所以α＝π2，β＝3π2，即⎩⎨⎧sin α＝1，sin β＝－1. 因此3sin ⎝ ⎛⎭⎪⎫π2＋α＋cos ⎝ ⎛⎭⎪⎫3π2－β2－sin （π－α）cos ⎝ ⎛⎭⎪⎫3π2＋β＝3cos α－sin β2－sin αsin β＝12＋1＝13. 答案：13。

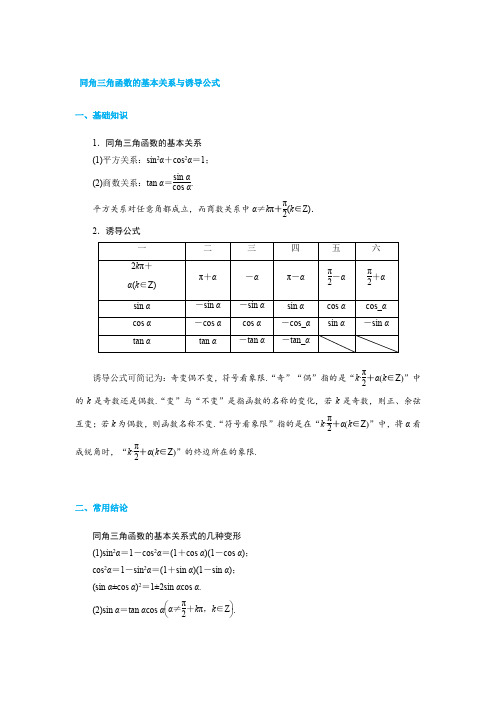
同角三角函数的基本关系与诱导公式一、基础知识1．同角三角函数的基本关系 (1)平方关系：sin 2α＋cos 2α＝1； (2)商数关系：tan α＝sin αcos α.平方关系对任意角都成立，而商数关系中α≠k π＋π2(k ∈Z)．2．诱导公式诱导公式可简记为：奇变偶不变，符号看象限.“奇”“偶”指的是“k ·π2＋α(k ∈Z )”中的k 是奇数还是偶数.“变”与“不变”是指函数的名称的变化，若k 是奇数，则正、余弦互变；若k 为偶数，则函数名称不变.“符号看象限”指的是在“k ·π2＋α(k ∈Z )”中，将α看成锐角时，“k ·π2＋α(k ∈Z )”的终边所在的象限.二、常用结论同角三角函数的基本关系式的几种变形 (1)sin 2α＝1－cos 2α＝(1＋cos α)(1－cos α)； cos 2α＝1－sin 2α＝(1＋sin α)(1－sin α)； (sin α±cos α)2＝1±2sin αcos α. (2)sin α＝tan αcos α⎝⎛⎭⎫α≠π2＋k π，k ∈Z .考点一 三角函数的诱导公式[典例] (1)已知f (α)＝cos ⎝⎛⎭⎫π2＋αsin ⎝⎛⎭⎫3π2－αcos (－π－α)tan (π－α)，则f ⎝⎛⎭⎫－25π3的值为________． (2)已知cos ⎝⎛⎭⎫π6－α＝23，则sin ⎝⎛⎭⎫α－2π3＝________. [解析] (1)因为f (α)＝cos ⎝⎛⎭⎫π2＋αsin ⎝⎛⎭⎫3π2－αcos (－π－α)tan (π－α) ＝－sin α(－cos α)(－cos α)⎝⎛⎭⎫－sin αcos α＝cos α， 所以f ⎝⎛⎭⎫－25π3＝cos ⎝⎛⎭⎫－25π3＝cos π3＝12. (2)sin ⎝⎛⎭⎫α－2π3＝－sin ⎝⎛⎭⎫2π3－α＝－sin ⎣⎡⎦⎤π－⎝⎛⎭⎫π3＋α＝－sin ⎝⎛⎭⎫π3＋α＝－sin ⎣⎡⎦⎤π2－⎝⎛⎭⎫π6－α＝－cos ⎝⎛⎭⎫π6－α＝－23. [答案] (1)12 (2)－23[题组训练]1.已知tan α＝12，且α∈⎝⎛⎭⎫π，3π2，则cos ⎝⎛⎭⎫α－π2＝________. 解析：法一：cos ⎝⎛⎭⎫α－π2＝sin α，由α∈⎝⎛⎭⎫π，3π2知α为第三象限角， 联立⎩⎪⎨⎪⎧tan α＝sin αcos α＝12，sin 2α＋cos 2α＝1，解得5sin 2α＝1，故sin α＝－55.法二：cos ⎝⎛⎭⎫α－π2＝sin α，由α∈⎝⎛⎭⎫π，3π2知α为第三象限角，由tan α＝12，可知点(－2，－1)为α终边上一点，由任意角的三角函数公式可得sin α＝－55. 答案：－552. sin(－1 200°)·cos 1 290°＋cos(－1 020°)·sin(－1 050°)＋tan 945°＝________.解析：原式＝sin(－3×360°－120°)cos(3×360°＋180°＋30°)＋cos(－3×360°＋60°) sin(－3×360°＋30°)＋tan(2×360°＋180°＋45°)＝sin 120°cos 30°＋cos 60°sin 30°＋tan 45°＝34＋14＋1＝2. 答案：23.已知tan ⎝⎛⎭⎫π6－α＝33，则tan ⎝⎛⎭⎫5π6＋α＝________. 解析：tan ⎝⎛⎭⎫5π6＋α＝tan ⎝⎛⎭⎫π－π6＋α＝tan ⎣⎡⎦⎤π－⎝⎛⎭⎫π6－α＝－tan ⎝⎛⎭⎫π6－α＝－33. 答案：－33考点二 同角三角函数的基本关系及应用[典例] (1)若tan α＝2，则sin α＋cos αsin α－cos α＋cos 2α＝( )A.165 B ．－165C.85D ．－85(2)已知sin αcos α＝38，且π4<α<π2，则cos α－sin α的值为( )A.12 B ．±12C ．－14D ．－12[解析] (1)sin α＋cos αsin α－cos α＋cos 2α＝sin α＋cos αsin α－cos α＋cos 2αsin 2α＋cos 2α ＝tan α＋1tan α－1＋1tan 2α＋1，将tan α＝2代入上式，则原式＝165.(2)因为sin αcos α＝38，所以(cos α－sin α)2＝cos 2α－2sin αcos α＋sin 2α＝1－2sin αcos α＝1－2×38＝14，因为π4<α<π2，所以cos α<sin α，即cos α－sin α<0，所以cos α－sin α＝－12.[答案] (1)A (2)D[题组训练]1．(2018·甘肃诊断)已知tan φ＝43，且角φ的终边落在第三象限，则cos φ＝( )A.45 B ．－45C.35D ．－35解析：选D 因为角φ的终边落在第三象限，所以cos φ<0，因为tan φ＝43，所以⎩⎪⎨⎪⎧sin 2φ＋cos 2φ＝1，sin φcos φ＝43，cos φ<0，解得cos φ＝－35.2．已知tan θ＝3，则sin 2θ＋sin θcos θ＝________. 解析：sin 2θ＋sin θcos θ＝sin 2θ＋sin θcos θsin 2θ＋cos 2θ＝tan 2θ＋tan θtan 2θ＋1＝32＋332＋1＝65.答案：653．已知sin α＋3cos α3cos α－sin α＝5，则sin 2α－sin αcos α＝________.解析：由已知可得sin α＋3cos α＝5(3cos α－sin α)， 即sin α＝2cos α，所以tan α＝sin αcos α＝2， 从而sin 2α－sin αcos α＝sin 2α－sin αcos αsin 2α＋cos 2α＝tan 2α－tan αtan 2α＋1＝22－222＋1＝25.答案：254．已知－π<α<0，sin(π＋α)－cos α＝－15，则cos α－sin α的值为________．解析：由已知，得sin α＋cos α＝15，sin 2α＋2sin αcos α＋cos 2α＝125， 整理得2sin αcos α＝－2425.因为(cos α－sin α)2＝1－2sin αcos α＝4925，且－π<α<0，所以sin α<0，cos α>0， 所以cos α－sin α>0，故cos α－sin α＝75.答案：75[课时跟踪检测]A 级1．已知x ∈⎝⎛⎭⎫－π2，0，cos x ＝45，则tan x 的值为( ) A.34 B ．－34C.43D ．－43解析：选B 因为x ∈⎝⎛⎭⎫－π2，0，所以sin x ＝－1－cos 2x ＝－35，所以tan x ＝sin x cos x ＝－34. 2．(2019·淮南十校联考)已知sin ⎝⎛⎭⎫α－π3＝13，则cos ⎝⎛⎭⎫α＋π6的值为( ) A ．－13B.13C.223D ．－223解析：选A ∵sin ⎝⎛⎭⎫α－π3＝13，∴cos ⎝⎛⎭⎫α＋π6＝cos ⎣⎡⎦⎤π2＋⎝⎛⎭⎫α－π3＝－sin ⎝⎛⎭⎫α－π3＝－13. 3．计算：sin 11π6＋cos 10π3的值为( ) A ．－1 B ．1 C ．0D.12－32解析：选A 原式＝sin ⎝⎛⎭⎫2π－π6＋cos ⎝⎛⎭⎫3π＋π3 ＝－sin π6－cos π3＝－12－12＝－1.4．若sin (π－θ)＋cos (θ－2π)sin θ＋cos (π＋θ)＝12，则tan θ的值为( )A ．1B ．－1C ．3D ．－3解析：选D 因为sin (π－θ)＋cos (θ－2π)sin θ＋cos (π＋θ)＝sin θ＋cos θsin θ－cos θ＝12，所以2(sin θ＋cos θ)＝sin θ－cos θ， 所以sin θ＝－3cos θ，所以tan θ＝－3.5．(2018·大庆四地六校调研)若α是三角形的一个内角，且sin ⎝⎛⎭⎫π2＋α＋cos ⎝⎛⎭⎫3π2＋α＝15，则tan α的值为( )A ．－43B ．－34C ．－43或－34D ．不存在解析：选A 由sin ⎝⎛⎭⎫π2＋α＋cos ⎝⎛⎭⎫3π2＋α＝15， 得cos α＋sin α＝15，∴2sin αcos α＝－2425<0.∵α∈(0，π)，∴sin α>0，cos α<0， ∴sin α－cos α＝1－2sin αcos α＝75，∴sin α＝45，cos α＝－35，∴tan α＝－43.6．在△ABC 中，3sin ⎝⎛⎭⎫π2－A ＝3sin(π－A )，且cos A ＝－3cos(π－B )，则△ABC 为( ) A ．等腰三角形 B ．直角三角形 C ．等腰直角三角形D ．等边三角形解析：选B 将3sin ⎝⎛⎭⎫π2－A ＝3sin(π－A )化为3cos A ＝3sin A ，则tan A ＝33，则A ＝π6，将cos A ＝－3cos(π－B )化为 cos π6＝3cos B ，则cos B ＝12，则B ＝π3，故△ABC 为直角三角形．7．化简：1－cos 22θcos 2θtan 2θ＝________.解析：1－cos 22θcos 2θtan 2θ＝sin 22θcos 2θ·sin 2θcos 2θ＝sin 2θ.答案：sin 2θ8．化简：cos ⎝⎛⎭⎫α－π2sin ⎝⎛⎭⎫5π2＋α·sin(α－π)·cos(2π－α)＝________. 解析：原式＝cos ⎝⎛⎭⎫π2－αsin ⎝⎛⎭⎫2π＋π2＋α·(－sin α)·cos α＝sin αsin ⎝⎛⎭⎫π2＋α·(－sin α)·cos α ＝sin αcos α·(－sin α)·cos α＝－sin 2α. 答案：－sin 2α9．sin 4π3·cos 5π6·tan ⎝⎛⎭⎫－4π3的值为________． 解析：原式＝sin ⎝⎛⎭⎫π＋π3·cos ⎝⎛⎭⎫π－π6·tan ⎝⎛⎭⎫－π－π3 ＝⎝⎛⎭⎫－sin π3·⎝⎛⎭⎫－cos π6·⎝⎛⎭⎫－tan π3 ＝⎝⎛⎭⎫－32×⎝⎛⎭⎫－32×(－3)＝－334.答案：－33410．(2019·武昌调研)若tan α＝cos α，则1sin α＋cos 4α＝________.解析：tan α＝cos α⇒sin αcos α＝cos α⇒sin α＝cos 2α，故1sin α＋cos 4α＝sin 2α＋cos 2αsin α＋cos 4α＝sin α＋cos 2αsin α＋cos 4α＝sin α＋sin αsin α＋sin 2α＝sin 2α＋sin α＋1＝sin 2α＋cos 2α＋1＝1＋1＝2.答案：211．已知α为第三象限角，f (α)＝sin ⎝⎛⎭⎫α－π2·cos ⎝⎛⎭⎫3π2＋α·tan (π－α)tan (－α－π)·sin (－α－π).(1)化简f (α)；(2)若cos ⎝⎛⎭⎫α－3π2＝15，求f (α)的值． 解：(1)f (α)＝sin ⎝⎛⎭⎫α－π2·cos ⎝⎛⎭⎫3π2＋α·tan (π－α)tan (－α－π)·sin (－α－π)＝(－cos α)·sin α·(－tan α)(－tan α)·sin α＝－cos α.(2)∵cos ⎝⎛⎭⎫α－3π2＝15， ∴－sin α＝15，从而sin α＝－15.又∵α为第三象限角，∴cos α＝－1－sin 2α＝－265，∴f (α)＝－cos α＝265.12．已知sin α＝255，求tan(α＋π)＋sin ⎝⎛⎭⎫5π2＋αcos ⎝⎛⎭⎫5π2－α的值．解：因为sin α＝255>0，所以α为第一或第二象限角．tan(α＋π)＋sin ⎝⎛⎭⎫5π2＋αcos ⎝⎛⎭⎫5π2－α ＝tan α＋cos αsin α＝sin αcos α＋cos αsin α＝1sin αcos α.①当α为第一象限角时，cos α＝1－sin 2α＝55， 原式＝1sin αcos α＝52.②当α为第二象限角时，cos α＝－1－sin 2α＝－55， 原式＝1sin αcos α＝－52.综合①②知，原式＝52或－52.B 级1．已知sin α＋cos α＝12，α∈(0，π)，则1－tan α1＋tan α＝( )A ．－7 B.7 C.3D ．－3解析：选A 因为sin α＋cos α＝12，所以(sin α＋cos α)2＝1＋2sin αcos α＝14，所以sin αcos α＝－38，又因为α∈(0，π)，所以sin α>0，cos α<0，所以cos α－sin α<0，因为(cos α－sin α)2＝1－2sin αcos α＝1－2×⎝⎛⎭⎫－38＝74，所以cos α－sin α＝－72， 所以1－tan α1＋tan α＝1－sin αcos α1＋sin αcos α＝cos α－sin αcos α＋sin α＝－7212＝－7.2．已知θ是第一象限角，若sin θ－2cos θ＝－25，则sin θ＋cos θ＝________.解析：∵sin θ－2cos θ＝－25，∴sin θ＝2cos θ－25，∴⎝⎛⎭⎫2cos θ－252＋cos 2θ＝1， ∴5cos 2θ－85cos θ－2125＝0，即⎝⎛⎭⎫cos θ－35⎝⎛⎭⎫5cos θ＋75＝0. 又∵θ为第一象限角，∴cos θ＝35，∴sin θ＝45，∴sin θ＋cos θ＝75.答案：753．已知关于x 的方程2x 2－(3＋1)x ＋m ＝0的两根分别是sin θ和cos θ，θ∈(0,2π)，求： (1)sin 2θsin θ－cos θ＋cos θ1－tan θ的值； (2)m 的值；(3)方程的两根及此时θ的值． 解：(1)原式＝sin 2θsin θ－cos θ＋cos θ1－sin θcos θ＝sin 2θsin θ－cos θ＋cos 2θcos θ－sin θ ＝sin 2θ－cos 2θsin θ－cos θ＝sin θ＋cos θ. 由条件知sin θ＋cos θ＝3＋12， 故sin 2θsin θ－cos θ＋cos θ1－tan θ＝3＋12.(2)由已知，得sin θ＋cos θ＝3＋12，sin θcos θ＝m2，因为1＋2sin θcos θ＝(sin θ＋cos θ)2， 所以1＋2×m 2＝⎝ ⎛⎭⎪⎫3＋122，解得m ＝32. (3)由⎩⎪⎨⎪⎧sin θ＋cos θ＝3＋12，sin θcos θ＝34，得⎩⎨⎧sin θ＝32，cos θ＝12或⎩⎨⎧sin θ＝12，cos θ＝32.又θ∈(0,2π)，故θ＝π3或θ＝π6.故当sin θ＝32，cos θ＝12时，θ＝π3； 当sin θ＝12，cos θ＝32时，θ＝π6.。