圆的期末复习检测试题(提高卷)

小学数学六年级上（圆）专项复习卷（含答案）北师大版姓名：__________ 班级：__________考号：__________题号一二三四五总分评分一、单选题（共8题；共16分）1. ( 2分) 用同样长的铁丝围成一个正方形和一个圆，（）的面积大。

A. 圆B. 正方形C. 一样大D. 无法判断2. ( 2分) 圆的半径扩大到原来的4倍，它的周长将扩大到原来的（）倍。

A. 4B. 8C. 16D. 123. ( 2分) 下图中，O是大圆的圆心，小圆的面积是大圆的（）。

A. B. C. D.4. ( 2分) 如果大圆的周长是小圆周长的2倍，那么，大圆面积是小圆面积的（）倍。

A. 2B. 4C. 85. ( 2分) 笑笑在边长3cm的正方形中画了一个最大的圆，求这个圆的周长是多少？正确列式是（）A. 3.14×3B. 3.14×（3÷2）2C. 3.14×（3÷2）6. ( 2分) 半圆的周长用字母表示是（）A. c=πdB. c=πrC. c=πr+2r7. ( 2分) 一个半径为3cm的半圆，周长是（）。

A. 18.84cmB. 24.84cmC. 15.42cmD. 21.84cm8. ( 2分) 下面公式可以求出半圆周长的是（）。

A. πrB. π（r +2）C. （π+2）r二、判断题（共5题；共10分）9. ( 2分) 半圆的面积是它圆面积的一半，半圆的周长是它圆周长的一半。

（）10. ( 2分) 所有圆的半径都相等，直径也都相等。

（）11. ( 2分) 周长相等的长方形、正方形与圆，正方形的面积最大。

（）12. ( 2分) 把圆形纸片对折，打开后得到的折痕不一定通过圆心。

（）13. ( 2分) 同一个圆上的所有点到圆心的距离都相等。

（）三、填空题（共5题；共20分）14. ( 2分) 一张光盘的刻录面为环形，内圆的直径是4厘米，外圆的直径是12厘米，这张光盘刻录面的面积是平方厘米。

小学数学六年级上（圆）专项复习卷————北师大版姓名：__________ 班级：__________考号：__________题号一二三四总分评分一、单选题（共13题；共26分）1.在《九章算术》中提出把割圆术作为计算圆的周长、面积以及圆周率的基础的我国古代数学家是（）。

A. 刘徽B. 祖冲之C. 杨辉2.把一个周长为12.56cm的圆剪成两个半圆形，每个半圆形的周长是（）cm。

A. 12.56B. 6.28C. 10.28D. 25.123.圆的半径由3cm增加到6cm，这个圆的面积增加了（）cm2。

A. 3πB. 6πC. 9πD. 27π4.一个钟表的分针长10厘米，从2时走到5时，分针针尖走过了（）厘米。

A. 31.4B. 62.8C. 15.75.下图中，从M到N走路线①和路线②的结果是（）。

A. 路线①远B. 路线②远C. 同样远6.半圆的半径是r，半圆的周长是（）。

A. πrB. πr+rC. πr+2r7.一个圆环，大圆的半径是2米，小圆的半径是1米，圆环的面积是（）。

A. 3.14平方米B. 9.42平方米C. 12.56平方米8.如图中，大圆的周长与两个小圆的周长比较，（）A. 一样长B. 大圆的周长长C. 大圆的周长短D. 无法比较9.大小两个圆半径的比是3：2，那么大圆和小圆面积的比是（）A. 3：2B. 6：4C. 9：4D. 无法确定10.我国古代建筑中常用到“外圆内方”的图案，下图中圆的直径是20厘米，正方形的面积是多少？列式正确的是（）。

A. 20×20B. 20×（20÷2）÷2C. 20×（20÷2）÷2×211.如图，用三张边长都是8厘米的正方形铁皮，分别剪下甲、乙、丙三种不同规格的圆片，剩下的铁皮（）.A. 甲最多B. 乙最多C. 丙最多D. 同样多12.用同样长的铁丝围成平面图形，（）形的面积最大A. 正方形B. 长方形C. 圆形13.在一个长10分米，宽7分米的硬纸板里裁剪半径是3分米的圆，可以剪（）。

“圆”期末复习试题一．选择题（共18小题）1．小明不慎把家里的圆形镜子打碎了，其中三块碎片如图所示，三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是（）A．①B．②C．③D．均不可能2．对下列生活现象的解释其数学原理运用错误的是（）A．把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理B．木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中，垂线段最短”的原理C．将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理D．将车轮设计为圆形是运用了“圆的旋转对称性”的原理3．如图，AB是⊙O的直径，弦CD⊥AB于点E，∠CDB=30°，⊙O的半径为5cm，则圆心O到弦CD的距离为（）A．cm B．3cm C．3cm D．6cm4．如图，在⊙O中，=，∠AOB=40°，则∠ADC的度数是（）A．40°B．30°C．20°D．15°5．如图，在⊙O中，若点C是的中点，∠A=50°，则∠BOC=（）A．40°B．45°C．50°D．60°6．把一张圆形纸片按如图所示方式折叠两次后展开，图中的虚线表示折痕，则的度数是（）A．120°B．135°C．150°D．165°7．如图，已知AC是⊙O的直径，点B在圆周上（不与A、C重合），点D在AC的延长线上，连接BD交⊙O于点E，若∠AOB=3∠ADB，则（）A．DE=EB B．DE=EB C．DE=DO D．DE=OB8．如图，已知AB是⊙O的直径，∠D=40°，则∠CAB的度数为（）A．20°B．40°C．50°D．70°9．如图，点A、B、C是圆O上的三点，且四边形ABCO是平行四边形，OF⊥OC交圆O 于点F，则∠BAF等于（）A．12.5° B．15°C．20°D．22.5°10．如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（）A．B．2 C．D．11．在公园的O处附近有E、F、G、H四棵树，位置如图所示（图中小正方形的边长均相等）现计划修建一座以O为圆心，OA为半径的圆形水池，要求池中不留树木，则E、F、G、H四棵树中需要被移除的为（）A．E、F、G B．F、G、H C．G、H、E D．H、E、F12．在RT△ABC中，∠C=90°，BC=3cm，AC=4cm，以点C为圆心，以2.5cm为半径画圆，则⊙C与直线AB的位置关系是（）A．相交 B．相切 C．相离 D．不能确定13．以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是（）A．B．C．D．14．已知等边三角形的内切圆半径，外接圆半径和高的比是（）A．1：2：B．2：3：4 C．1：：2 D．1：2：315．如图，将正六边形ABCDEF放置在直角坐标系内，A（﹣2，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过2016次翻转之后，点C的坐标是（）A．（4032，0）B．（4032，2）C．（4031，）D．（4033，）16．如图，PA、PB是⊙O的切线，切点分别为A、B，若OA=2，∠P=60°，则的长为（）A．πB．πC．D．17．如图，AB为⊙O的直径，AB=6，AB⊥弦CD，垂足为G，EF切⊙O于点B，∠A=30°，连接AD、OC、BC，下列结论不正确的是（）A．EF∥CD B．△COB是等边三角形C．CG=DG D．的长为π18．如图，已知一块圆心角为270°的扇形铁皮，用它作一个圆锥形的烟囱帽（接缝忽略不计），圆锥底面圆的直径是60cm，则这块扇形铁皮的半径是（）A．40cm B．50cm C．60cm D．80cm二．填空题（共6小题）19．如图，A，B，C，D是⊙O上的四个点，∠C=110°，则∠BOD=度．20．如图，在△ABC中，AB=AC=10，以AB为直径的⊙O与BC交于点D，与AC交于点E，连OD交BE于点M，且MD=2，则BE长为．21．在Rt△ABC中，∠C=90°，BC=3，AC=4，点P在以C为圆心，5为半径的圆上，连结PA，PB．若PB=4，则PA的长为．22．如图，半圆O的直径AB=2，弦CD∥AB，∠COD=90°，则图中阴影部分的面积为．23．已知圆锥的底面半径是2，母线长是4，则圆锥的侧面积是．24．若一个圆锥的底面圆半径为3cm，其侧面展开图的圆心角为120°，则圆锥的母线长是cm．三．解答题（共6小题）25．已知AB是半径为1的圆O直径，C是圆上一点，D是BC延长线上一点，过点D的直线交AC于E点，且△AEF为等边三角形（1）求证：△DFB是等腰三角形；（2）若DA=AF，求证：CF⊥AB．26．已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED=EC．（1）求证：AB=AC；（2）若AB=4，BC=2，求CD的长．27．如图，AB是⊙O的直径，弦CD⊥AB于点E，且CD=24，点M在⊙O上，MD经过圆心O，联结MB．（1）若BE=8，求⊙O的半径；（2）若∠DMB=∠D，求线段OE的长．28．如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD 的垂直平分线交BC于点E，交BD于点F，连接DE．（1）判断直线DE与⊙O的位置关系，并说明理由；（2）若AC=6，BC=8，OA=2，求线段DE的长．29．如图，AB为⊙O的直径，点E在⊙O上，C为的中点，过点C作直线CD⊥AE于D，连接AC、BC．（1）试判断直线CD与⊙O的位置关系，并说明理由；（2）若AD=2，AC=，求AB的长．30．如图，△ABC中，∠ACB=90°，D为AB上一点，以CD为直径的⊙O交BC于点E，连接AE交CD于点P，交⊙O于点F，连接DF，∠CAE=∠ADF．（1）判断AB与⊙O的位置关系，并说明理由；（2）若PF：PC=1：2，AF=5，求CP的长．九年级上圆期末复习试题参考答案与试题解析一．选择题（共18小题）1．（2016秋•南京期中）小明不慎把家里的圆形镜子打碎了，其中三块碎片如图所示，三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是（）A．①B．②C．③D．均不可能【解答】解：第①块出现两条完整的弦，作出这两条弦的垂直平分线，两条垂直平分线的交点就是圆心，进而可得到半径的长．故选A．2．（2016•永州）对下列生活现象的解释其数学原理运用错误的是（）A．把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理B．木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中，垂线段最短”的原理C．将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理D．将车轮设计为圆形是运用了“圆的旋转对称性”的原理【解答】解：A、把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理，正确；B、木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“两点确定一条直线”的原理，故错误；C、将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理，正确；D、将车轮设计为圆形是运用了“圆的旋转对称性”的原理，正确，故选B．3．（2016•黔南州）如图，AB是⊙O的直径，弦CD⊥AB于点E，∠CDB=30°，⊙O的半径为5cm，则圆心O到弦CD的距离为（）A．cm B．3cm C．3cm D．6cm【解答】解：连接CB．∵AB是⊙O的直径，弦CD⊥AB于点E，∴圆心O到弦CD的距离为OE；∵∠COB=2∠CDB（同弧所对的圆周角是所对的圆心角的一半），∠CDB=30°，∴∠COB=60°；在Rt△OCE中，OC=5cm，OE=OC•cos∠COB，∴OE=cm．故选A．4．（2016•济宁）如图，在⊙O中，=，∠AOB=40°，则∠ADC的度数是（）A．40°B．30°C．20°D．15°【解答】解：连接CO，如图：∵在⊙O中，=，∴∠AOC=∠AOB，∵∠AOB=40°，∴∠AOC=40°，∴∠ADC=∠AOC=20°，故选C．5．（2016•兰州）如图，在⊙O中，若点C是的中点，∠A=50°，则∠BOC=（）A．40°B．45°C．50°D．60°【解答】解：∵∠A=50°，OA=OB，∴∠OBA=∠OAB=50°，∴∠AOB=180°﹣50°﹣50°=80°，∵点C是的中点，∴∠BOC=∠AOB=40°，故选A．6．（2016•舟山）把一张圆形纸片按如图所示方式折叠两次后展开，图中的虚线表示折痕，则的度数是（）A．120°B．135°C．150°D．165°【解答】解：如图所示：连接BO，过点O作OE⊥AB于点E，由题意可得：EO=BO，AB∥DC，可得∠EBO=30°，故∠BOD=30°，则∠BOC=150°，故的度数是150°．故选：C．7．（2016•杭州）如图，已知AC是⊙O的直径，点B在圆周上（不与A、C重合），点D 在AC的延长线上，连接BD交⊙O于点E，若∠AOB=3∠ADB，则（）A．DE=EB B．DE=EB C．DE=DO D．DE=OB【解答】解：连接EO．∵OB=OE，∴∠B=∠OEB，∵∠OEB=∠D+∠DOE，∠AOB=3∠D，∴∠B+∠D=3∠D，∴∠D+∠DOE+∠D=3∠D，∴∠DOE=∠D，∴ED=EO=OB，故选D．8．（2016•娄底）如图，已知AB是⊙O的直径，∠D=40°，则∠CAB的度数为（）A．20°B．40°C．50°D．70°【解答】解：∵∠D=40°，∴∠B=∠D=40°．∵AB是⊙O的直径，∴∠ACB=90°，∴∠CAB=90°﹣40°=50°．故选C．9．（2016•泰安）如图，点A、B、C是圆O上的三点，且四边形ABCO是平行四边形，OF ⊥OC交圆O于点F，则∠BAF等于（）A．12.5° B．15°C．20°D．22.5°【解答】解：连接OB，∵四边形ABCO是平行四边形，∴OC=AB，又OA=OB=OC，∴OA=OB=AB，∴△AOB为等边三角形，∵OF⊥OC，OC∥AB，∴OF⊥AB，∴∠BOF=∠AOF=30°，由圆周角定理得∠BAF=∠BOF=15°，故选：B．10．（2016•安徽）如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（）A．B．2 C．D．【解答】解：∵∠ABC=90°，∴∠ABP+∠PBC=90°，∵∠PAB=∠PBC，∴∠BAP+∠ABP=90°，∴∠APB=90°，∴点P在以AB为直径的⊙O上，连接OC交⊙O于点P，此时PC最小，在RT△BCO中，∵∠OBC=90°，BC=4，OB=3，∴OC==5，∴PC=OC﹣OP=5﹣3=2．∴PC最小值为2．故选B．11．（2016•宜昌）在公园的O处附近有E、F、G、H四棵树，位置如图所示（图中小正方形的边长均相等）现计划修建一座以O为圆心，OA为半径的圆形水池，要求池中不留树木，则E、F、G、H四棵树中需要被移除的为（）A．E、F、G B．F、G、H C．G、H、E D．H、E、F【解答】解：∵OA==，∴OE=2＜OA，所以点E在⊙O内，OF=2＜OA，所以点F在⊙O内，OG=1＜OA，所以点G在⊙O内，OH==2＞OA，所以点H在⊙O外，故选A12．（2016•湘西州）在RT△ABC中，∠C=90°，BC=3cm，AC=4cm，以点C为圆心，以2.5cm为半径画圆，则⊙C与直线AB的位置关系是（）A．相交 B．相切 C．相离 D．不能确定【解答】解：过C作CD⊥AB于D，如图所示：∵在Rt△ABC中，∠C=90°，AC=4，BC=3，∴AB==5，∵△ABC的面积=AC×BC=AB×CD，∴3×4=5CD，∴CD=2.4＜2.5，即d＜r，∴以2.5为半径的⊙C与直线AB的关系是相交；故选A．13．（2016•泸州）以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是（）A．B．C．D．【解答】解：如图1，∵OC=1，∴OD=1×sin30°=；如图2，∵OB=1，∴OE=1×sin45°=；如图3，∵OA=1，∴OD=1×cos30°=，则该三角形的三边分别为：、、，∵（）2+（）2=（）2，∴该三角形是以、为直角边，为斜边的直角三角形，∴该三角形的面积是××=，故选：D．14．（2016•东平县二模）已知等边三角形的内切圆半径，外接圆半径和高的比是（）A．1：2：B．2：3：4 C．1：：2 D．1：2：3【解答】解：图中内切圆半径是OD，外接圆的半径是OC，高是AD，因而AD=OC+OD；在直角△OCD中，∠DOC=60°，则OD：OC=1：2，因而OD：OC：AD=1：2：3，所以内切圆半径，外接圆半径和高的比是1：2：3．故选D．15．（2016•宛城区一模）如图，将正六边形ABCDEF放置在直角坐标系内，A（﹣2，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过2016次翻转之后，点C的坐标是（）A．（4032，0）B．（4032，2）C．（4031，）D．（4033，）【解答】解：∵正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，∴每6次翻转为一个循环组循环，∵2016÷6=336，∴经过2016次翻转为第336循环，点C在开始时的位置，∵A（﹣2，0），∴AB=2，∴翻转前进的距离=2×2016=4032，如图，过点C作CG⊥x于G，则∠CBG=60°，∴AG=2×=1，BG=2×=，∴OG=4032+1=4033，∴点B的坐标为（4033，）．故选D．16．（2016•长春）如图，PA、PB是⊙O的切线，切点分别为A、B，若OA=2，∠P=60°，则的长为（）A．πB．πC．D．【解答】解：∵PA、PB是⊙O的切线，∴∠OBP=∠OAP=90°，在四边形APBO中，∠P=60°，∴∠AOB=120°，∵OA=2，∴的长l==π，故选C17．（2016•昆明）如图，AB为⊙O的直径，AB=6，AB⊥弦CD，垂足为G，EF切⊙O于点B，∠A=30°，连接AD、OC、BC，下列结论不正确的是（）A．EF∥CD B．△COB是等边三角形C．CG=DG D．的长为π【解答】解：∵AB为⊙O的直径，EF切⊙O于点B，∴AB⊥EF，又AB⊥CD，∴EF∥CD，A正确；∵AB⊥弦CD，∴=，∴∠COB=2∠A=60°，又OC=OD，∴△COB是等边三角形，B正确；∵AB⊥弦CD，∴CG=DG，C正确；的长为：=π，D错误，故选：D．18．（2016•东营）如图，已知一块圆心角为270°的扇形铁皮，用它作一个圆锥形的烟囱帽（接缝忽略不计），圆锥底面圆的直径是60cm，则这块扇形铁皮的半径是（）A．40cm B．50cm C．60cm D．80cm【解答】解：∵圆锥的底面直径为60cm，∴圆锥的底面周长为60πcm，∴扇形的弧长为60πcm，设扇形的半径为r，则=60π，解得：r=40cm，故选A．二．填空题（共6小题）19．（2016•葫芦岛）如图，A，B，C，D是⊙O上的四个点，∠C=110°，则∠BOD=140度．【解答】解：∵A，B，C，D是⊙O上的四个点，∠C=110°，∴四边形ABCD是圆内接四边形，∴∠C+∠A=180°，∴∠A=70°，∵∠BOD=2∠A，∴∠BOD=140°，故答案为：140．20．（2016•雅安）如图，在△ABC中，AB=AC=10，以AB为直径的⊙O与BC交于点D，与AC交于点E，连OD交BE于点M，且MD=2，则BE长为8．【解答】解：连接AD，如图所示：∵以AB为直径的⊙O与BC交于点D，∴∠AEB=∠ADB=90°，即AD⊥BC，∵AB=AC，∴BD=CD，∵OA=OB，∴OD∥AC，∴BM=EM，∴CE=2MD=4，∴AE=AC﹣CE=6，∴BE==；故答案为：8．21．（2015•义乌市）在Rt△ABC中，∠C=90°，BC=3，AC=4，点P在以C为圆心，5为半径的圆上，连结PA，PB．若PB=4，则PA的长为3或．【解答】解：连结CP，PB的延长线交⊙C于P′，如图，∵CP=5，CB=3，PB=4，∴CB2+PB2=CP2，∴△CPB为直角三角形，∠CBP=90°，∴CB⊥PB，∴PB=P′B=4，∵∠C=90°，∴PB∥AC，而PB=AC=4，∴四边形ACBP为矩形，∴PA=BC=3，在Rt△APP′中，∵PA=3，PP′=8，∴P′A==，∴PA的长为3或．故答案为3或．22．（2016•宁波）如图，半圆O的直径AB=2，弦CD∥AB，∠COD=90°，则图中阴影部分的面积为．【解答】解：∵弦CD∥AB，∴S△ACD=S△OCD，∴S阴影=S扇形COD=•π•=×π×=．故答案为：．23．（2016•盐城）已知圆锥的底面半径是2，母线长是4，则圆锥的侧面积是8π．【解答】解：底面半径是2，则底面周长=4π，圆锥的侧面积=×4π×4=8π．24．（2016•孝感）若一个圆锥的底面圆半径为3cm，其侧面展开图的圆心角为120°，则圆锥的母线长是9cm．【解答】解：设母线长为l，则=2π×3解得：l=9．故答案为：9．三．解答题（共6小题）25．（2016•株洲）已知AB是半径为1的圆O直径，C是圆上一点，D是BC延长线上一点，过点D的直线交AC于E点，且△AEF为等边三角形（1）求证：△DFB是等腰三角形；（2）若DA=AF，求证：CF⊥AB．【解答】解：（1）∵AB是⊙O直径，∴∠ACB=90°，∵△AEF为等边三角形，∴∠CAB=∠EFA=60°，∴∠B=30°，∵∠EFA=∠B+∠FDB，∴∠B=∠FDB=30°，∴△DFB是等腰三角形；（2）过点A作AM⊥DF于点M，设AF=2a，∵△AEF是等边三角形，∴FM=EM=a，AM=a，在Rt△DAM中，AD=AF=2a，AM=，∴DM=5a，∴DF=BF=6a，∴AB=AF+BF=8a，在Rt△ABC中，∠B=30°，∠ACB=90°，∴AC=4a，∵AE=EF=AF=2a，∴CE=AC﹣AE=2a，∴∠ECF=∠EFC，∵∠AEF=∠ECF+∠EFC=60°，∴∠CFE=30°，∴∠AFC=∠AFE+∠EFC=60°+30°=90°，∴CF⊥AB．26．（2016•宁夏）已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED=EC．（1）求证：AB=AC；（2）若AB=4，BC=2，求CD的长．【解答】（1）证明：∵ED=EC，∴∠EDC=∠C，∵∠EDC=∠B，∴∠B=∠C，∴AB=AC；（2）方法一：解：连接AE，∵AB为直径，∴AE⊥BC，由（1）知AB=AC，∴BE=CE=BC=，∵△CDE∽△CBA，∴，∴CE•CB=CD•CA，AC=AB=4，∴•2=4CD，∴CD=．方法二：解：连接BD，∵AB为直径，∴BD⊥AC，设CD=a，由（1）知AC=AB=4，则AD=4﹣a，在Rt△ABD中，由勾股定理可得：BD2=AB2﹣AD2=42﹣（4﹣a）2在Rt△CBD中，由勾股定理可得：BD2=BC2﹣CD2=（2）2﹣a2∴42﹣（4﹣a）2=（2）2﹣a2整理得：a=，即：CD=．27．（2016•金乡县一模）如图，AB是⊙O的直径，弦CD⊥AB于点E，且CD=24，点M 在⊙O上，MD经过圆心O，联结MB．（1）若BE=8，求⊙O的半径；（2）若∠DMB=∠D，求线段OE的长．【解答】解：（1）设⊙O的半径为x，则OE=x﹣8，∵CD=24，由垂径定理得，DE=12，在Rt△ODE中，OD2=DE2+OE2，x2=（x﹣8）2+122，解得：x=13．（2）∵OM=OB，∴∠M=∠B，∴∠DOE=2∠M，又∠M=∠D，∴∠D=30°，在Rt△OED中，∵DE=12，∠D=30°，∴OE=4．28．（2016•三明）如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．（1）判断直线DE与⊙O的位置关系，并说明理由；（2）若AC=6，BC=8，OA=2，求线段DE的长．【解答】解：（1）直线DE与⊙O相切，理由如下：连接OD，∵OD=OA，∴∠A=∠ODA，∵EF是BD的垂直平分线，∴EB=ED，∴∠B=∠EDB，∵∠C=90°，∴∠A+∠B=90°，∴∠ODA+∠EDB=90°，∴∠ODE=180°﹣90°=90°，∴直线DE与⊙O相切；（2）连接OE，设DE=x，则EB=ED=x，CE=8﹣x，∵∠C=∠ODE=90°，∴OC2+CE2=OE2=OD2+DE2，∴42+（8﹣x）2=22+x2，解得：x=4.75，则DE=4.75．29．（2016•漳州）如图，AB为⊙O的直径，点E在⊙O上，C为的中点，过点C作直线CD⊥AE于D，连接AC、BC．（1）试判断直线CD与⊙O的位置关系，并说明理由；（2）若AD=2，AC=，求AB的长．【解答】解：（1）相切，连接OC，∵C为的中点，∴∠1=∠2，∵OA=OC，∴∠1=∠ACO，∴∠2=∠ACO，∴AD∥OC，∵CD⊥AD，∴OC⊥CD，∴直线CD与⊙O相切；（2）方法1：连接CE，∵AD=2，AC=，∵∠ADC=90°，∴CD==，∵CD是⊙O的切线，∴CD2=AD•DE，∴DE=1，∴CE==，∵C为的中点，∴BC=CE=，∵AB为⊙O的直径，∴∠ACB=90°，∴AB==3．方法2：∵∠DCA=∠B，易得△ADC∽△ACB，∴=，∴AB=3．30．（2016•泰州）如图，△ABC中，∠ACB=90°，D为AB上一点，以CD为直径的⊙O交BC于点E，连接AE交CD于点P，交⊙O于点F，连接DF，∠CAE=∠ADF．（1）判断AB与⊙O的位置关系，并说明理由；（2）若PF：PC=1：2，AF=5，求CP的长．【解答】解：（1）AB是⊙O切线．理由：连接DE、CF．∵CD是直径，∴∠DEC=∠DFC=90°，∵∠ACB=90°，∴∠DEC+∠ACE=180°，∴DE∥AC，∴∠DEA=∠EAC=∠DCF，∵∠DFC=90°，∴∠FCD+∠CDF=90°，∵∠ADF=∠EAC=∠DCF，∴∠ADF+∠CDF=90°，∴∠ADC=90°，∴CD⊥AD，∴AB是⊙O切线．（2）∵∠CPF=∠CPA，∠PCF=∠PAC，∴△PCF∽△PAC，∴=，∴PC2=PF•PA，设PF=a．则PC=2a，∴4a2=a（a+5），∴a=，∴PC=2a=．。

人教版六年级数学上册第五单元同步复习卷圆时间:70分钟满分:100分+10分一、冷静思考认真填。

(24分)1.如图，点O是( ),线段OA 是( ),线段BC是( ),当OA=6cm时，这个圆的直径是( )cm。

2.用圆规画一个直径是8cm 的圆，圆规两脚张开的距离是( )cm, 所画的圆的周长是( )cm, 面积是( )cm²。

3.张大伯用长12.56m的篱笆正好围成一个圆形的菜园，菜园的面积是( )m²。

4.如图所示，半圆的周长是( )cm, 面积是( )cm²,梯形的面积是( )cm²。

5.一个圆的半径扩大到原来的5倍，直径就扩大到原来的( )倍，周长就扩大到原来的( )倍，面积就扩大到原来的( )倍。

6.便民饭店有一种圆形餐桌，桌面的周长是502.4cm, 它的上面配有一个半径比桌面半径小20cm的圆形玻璃转盘，这个转盘的面积是( )cm²。

7.一张周长是40 cm的正方形铁皮，要剪下一个最大的圆，这个圆的直径是( )cm, 周长是( )cm, 面积是( )cm²; 剩余的面积是( )cm²。

8.如图，把一个圆沿半径剪开分成若干等份，拼成一个近似的长方形。

已知拼成的长方形的宽是5 cm, 长是( )cm。

9.一只挂钟的分针长10 cm, 经过15分钟，分针的针尖走过( )cm; 分针扫过的部分是一个( )形，面积是( )cm²。

10.如图，把两个横截面半径都是10cm的圆柱用铁丝紧紧捆在一起，如果捆绑处忽略不计，需要用铁丝( )cm。

二、反复比较精心选。

(10分)11.经过一点可以画( )个圆。

A.1B.2C.3D.无数12.下列图形中的涂色部分，( )是扇形。

13.在一个周长是62.8m的圆形花坛的圆心处安装喷灌装置，安装射程( )m的装置最合适。

A.20B.15C.10D.514.周长相等的圆、正方形和长方形，面积最大的是( )。

一、填空题（每空1分，共10分）1. 圆的半径是5cm，那么圆的直径是______cm。

2. 一个圆的周长是31.4cm，那么这个圆的半径是______cm。

3. 圆的面积公式是S=______，其中r表示______。

4. 一个圆的半径增加了2cm，那么这个圆的面积增加了______cm²。

5. 圆的面积与半径的关系是：半径增加a倍，面积增加______倍。

6. 一个圆的直径是12cm，那么这个圆的周长是______cm。

7. 圆的面积公式推导过程中，我们运用了______的方法。

8. 一个圆的半径是4cm，那么这个圆的面积是______cm²。

9. 一个圆的面积是50.24cm²，那么这个圆的半径是______cm。

10. 一个圆的直径是8cm，那么这个圆的周长是______cm。

二、选择题（每题2分，共10分）1. 下列哪个图形的面积可以用圆的面积公式计算？A. 正方形B. 长方形C. 三角形D. 圆2. 圆的面积公式中，S表示什么？A. 圆的半径B. 圆的直径C. 圆的面积D. 圆的周长3. 圆的面积与半径的关系是：A. 面积与半径成正比B. 面积与半径成反比C. 面积与半径平方成正比D. 面积与半径平方成反比4. 下列哪个图形的周长可以用圆的周长公式计算？A. 正方形B. 长方形C. 三角形D. 圆5. 圆的周长公式中，C表示什么？A. 圆的半径B. 圆的直径C. 圆的面积D. 圆的周长6. 下列哪个图形的面积可以用圆的面积公式计算？A. 正方形B. 长方形C. 三角形D. 圆7. 圆的面积公式推导过程中，我们运用了什么方法？A. 移动法B. 剪拼法C. 平移法D. 对折法8. 一个圆的半径是6cm，那么这个圆的面积是：A. 36cm²B. 37.68cm²C. 38.16cm²D. 39.84cm²9. 一个圆的面积是113.04cm²，那么这个圆的半径是：A. 4cmB. 5cmC. 6cmD. 7cm10. 一个圆的直径是14cm，那么这个圆的周长是：A. 35.84cmB. 36cmC. 36.56cmD. 37.68cm三、计算题（每题5分，共15分）1. 计算下列各题的面积：（1）半径为3cm的圆的面积。

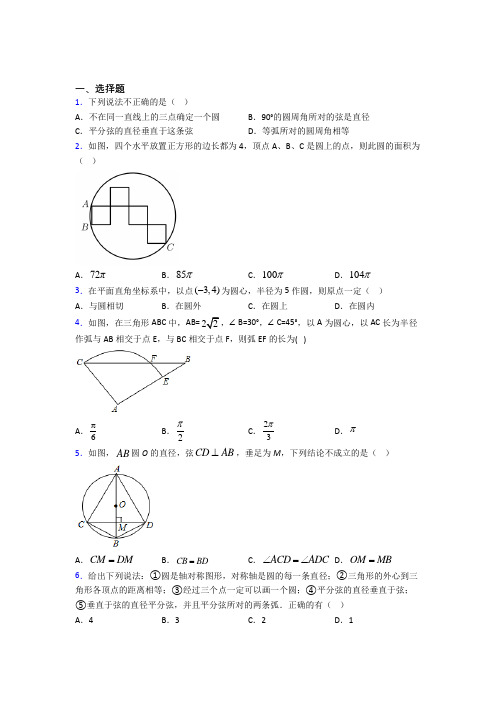
一、选择题1．下列说法不正确的是（ ）A ．不在同一直线上的三点确定一个圆B ．90°的圆周角所对的弦是直径C ．平分弦的直径垂直于这条弦D ．等弧所对的圆周角相等 2．如图，四个水平放置正方形的边长都为4，顶点A 、B 、C 是圆上的点，则此圆的面积为（ ）A ．72πB ．85πC ．100πD ．104π 3．在平面直角坐标系中，以点()3,4-为圆心，半径为5作圆，则原点一定（ ） A ．与圆相切 B ．在圆外 C ．在圆上 D ．在圆内 4．如图，在三角形ABC 中，AB=22，∠B=30°，∠C=45°，以A 为圆心，以AC 长为半径作弧与AB 相交于点E ，与BC 相交于点F ，则弧EF 的长为( )A ．6πB ．2πC ．23πD ．π5．如图，AB 圆O 的直径，弦CD AB ⊥，垂足为M ，下列结论不成立的是（ ）A ．CM DM =B ．CB BD =C ．ACD ADC ∠=∠ D ．OM MB = 6．给出下列说法：①圆是轴对称图形，对称轴是圆的每一条直径；②三角形的外心到三角形各顶点的距离相等；③经过三个点一定可以画一个圆；④平分弦的直径垂直于弦；⑤垂直于弦的直径平分弦，并且平分弦所对的两条弧．正确的有（ ）A ．4B ．3C ．2D ．17．如图，正六边形ABCDEF 内接于O ，过点O 作OM ⊥弦BC 于点M ，若O 的半径为4，则弦心距OM 的长为（ ）A ．23B ．3C ．2D ．22 8．若圆锥的底面半径为5cm ，侧面积为265cm π，则该圆锥的高是（ ） A ．13cm B ．12cm C ．11cmD ．10cm 9．如图，在等边ABC 中，点O 在边AB 上，O 过点B 且分别与边AB BC 、相交于点D 、E ，F 是AC 上的点，判断下列说法错误的是（ ）A ．若EF AC ⊥，则EF 是O 的切线 B ．若EF 是O 的切线，则EF AC ⊥ C ．若32BE EC =，则AC 是O 的切线 D ．若BE EC =，则AC 是O 的切线 10．已知O 的半径为5，若4PO =，则点P 与O 的位置关系是（ ） A ．点P 在O 内 B ．点P 在O 上 C ．点P 在O 外 D ．无法判断 11．如图，O 的半径为5，弦AB 的长为8，M 是弦AB 上的一个动点，则线段OM 可取的整数值有（ ）个A ．1B ．2C ．3D ．4 12．如图，AB 为O 的弦，半径OC 交AB 于点D ，AD DB =，5OC =，3OD =，则AB 的长为（ ）A ．8B ．6C ．4D ．213．如图，在菱形ABCD 中，60A ∠=︒ ，3AB = ，A ，B 的半径分别为2和1，P ，E ，F 分别是CD 边、A 和B 上的动点，则PE PF +的最小值是（ ）A ．333-B ．2C ．3D ．33 14．如图，MN 是半径为1的⊙O 的直径，点A 在⊙O 上，∠AMN=30°，点B 为劣弧AN 的中点，P 是直径MN 上一动点，则PA+PB 的最小值为（ ）A ．2B ．1C ．2D ．22 15．下列说法中，正确的是（ ） A ．三点确定一个圆B ．在同圆或等圆中，相等的弦所对的圆周角相等 C ．平分弦的直径垂直于弦D ．在同圆或等圆中，相等的圆心角所对的弦相等二、填空题16．ABC 是边长为5的等边三角形，点D 在ABC 的外部且30BDC ∠=︒，则AD 的最大值是______．17．如图，⊙O 是ABC 的外接圆，64A ∠=︒，则OBC ∠=______°．18．如图，O 的半径为6，AB 、CD 是互相垂直的两条直径，点P 是O 上任意一点，过点P 作PM AB ⊥于M ，PN CD ⊥于N ，点Q 是MN 的中点，当点P 沿着圆周从点D 逆时针方向运动到点C 的过程中，当∠QCN 度数取最大值时，线段CQ 的长为______．19．如图，,PA PB 切⊙O 于,A B ，点C 在AB 上，DE 切⊙O 于C ，10cm,PO =⊙O 的半径为6cm ，则PDE △的周长是_________cm ．20．如图，已知正方形ABCD 的边长为2，点M 和N 分别从B 、C 同时出发，以相同的速度沿BC 、CD 方向向终点C 和D 运动．连接AM ，BN 交于点P ，则PC 长的最小值为____________．21．一点到O 上的最近距离为3cm ，最远距离为11cm ，则这圆的半径是______． 22．如图，已知BD 是⊙O 的直径，点A ，C 在⊙O 上，58AOB ∠=，B 是弧AC 的中点，则BDC ∠的度数为___________．23．在矩形ABCD 中，43AB =6BC =，若点P 是矩形ABCD 上一动点，要使得60APB ∠=︒，则AP 的长为__________．24．如图，在平面直角坐标系xOy 中，A （8，0），⊙O 半径为3，B 为⊙O 上任意一点，P 是AB 的中点，则OP 的最小值是____．25．如图，ABC 是等边三角形，180BAD BCD ∠+∠=︒，8BD =，2CD =，则AD =________．26．在半径为4cm 的圆中，长为4cm 的弦所对的圆周角的度数为________三、解答题27．如图，在△ABC 中，以AB 为直径的⊙O 交AC 于点M ，弦MN ∥BC 交AB 于点E ，且ME ＝NE ＝3．（1）求证：BC 是⊙O 的切线；（2）若AE ＝4，求⊙O 的直径AB 的长度．28．如图，在直角坐标系中，A （0，4）、B （4，4）、C （6，2），（1）写出经过A 、B 、C 三点的圆弧所在圆的圆心M 的坐标：______； （2）判断点()5,2D -与圆M 的位置关系．29．如图，在平面直角坐标系中，点A 的坐标为()3,2-，点B 的坐标为()0,2． （1）画出将绕点O 顺时针旋转90后的图形，记为A OB ''△；（2）在题（1）旋转过程中线段OA 扫过的面积为_______（直接写出答案）30．如图，在33⨯的网格中有一个圆，请仅用无刻度直尺作图（保留画图痕迹）．（1）在图1中，圆过格点A ，B ，请作出圆心O ；（2）在图2中，⊙O 的两条弦AB CD =，请作一个45圆周角．。

圆期末复习题及答案一、选择题（每题2分，共10分）1. 圆的周长公式是（）。

A. C=πdB. C=2πrC. C=πrD. C=2r答案：B2. 半径为r的圆的面积公式是（）。

A. A=πr²B. A=2πrC. A=πrD. A=r²答案：A3. 圆的直径是半径的（）倍。

A. 2B. πC. 1/2D. 1/π答案：A4. 圆的半径增加一倍，面积增加（）倍。

A. 2B. 3C. 4D. π答案：C5. 圆的周长与直径的比值是（）。

A. πB. 2πC. 1/πD. 1答案：A二、填空题（每题2分，共10分）1. 圆的周长是其直径的________倍。

答案：π2. 半径为3厘米的圆的面积是________平方厘米。

答案：28.263. 圆的直径是半径的________倍。

答案：24. 圆的面积公式是________。

答案：πr²5. 圆的周长公式是________。

答案：2πr 或πd三、计算题（每题5分，共20分）1. 已知圆的半径为5厘米，求其周长和面积。

答案：周长为31.4厘米，面积为78.5平方厘米。

2. 已知圆的直径为8厘米，求其周长和面积。

答案：周长为25.12厘米，面积为50.24平方厘米。

3. 已知圆的周长为18.84厘米，求其半径。

答案：半径为3厘米。

4. 已知圆的面积为12.56平方厘米，求其半径。

答案：半径为2厘米。

四、简答题（每题5分，共20分）1. 圆的周长和半径之间有什么关系？答案：圆的周长是其半径的2π倍。

2. 圆的面积和半径之间有什么关系？答案：圆的面积是其半径的平方乘以π。

3. 为什么圆的周长和直径的比值是一个常数？答案：因为圆的周长和直径的比值定义了圆周率π，它是一个固定不变的数学常数。

4. 圆的半径增加时，其面积如何变化？答案：圆的面积随着半径的增加而增加，且增加的倍数是半径增加倍数的平方。

单元测试(四) 圆(时间：45分钟总分：100分）一、选择题(每小题3分，共30分)1.如图，A 、B 、C 是⊙O 上的三点，且∠ABC ＝70°，则∠AOC 的度数是( )A.35°B.140°C.70°D.70°或140°2.如图，⊙O 的直径AB=8，点C 在⊙O 上，∠ABC=30°，则AC 的长是( )A.2B.22C.23D.43.如图，在△ABC 中，AB=BC=2，以AB 为直径的⊙O 与BC 相切于点B ，则AC 等于()A.2B.3C.22D.23 4.如图，PA ，PB 是⊙O 的切线，A ，B 是切点，点C 是劣弧AB 上的一个点，若∠P=40°，则∠ACB 的度数是( )A.80°B.110°C.120°D.140°5.如图，A 、B 是⊙O 上两点，若四边形ACBO 是菱形，⊙O 的半径为r ，则点A 与点B 之间的距离为( )A.2rB.3rC.rD.2r6.在Rt △ABC 中，∠C=90°，AC=12，BC=5，将△ABC 绕边AC 所在直线旋转一周得到圆锥，则该圆锥的侧面积是( )A.25πB.65πC.90πD.130π7.下列四个命题：①等边三角形是中心对称图形；②在同圆或等圆中，相等的弦所对的圆周角相等；③三角形有且只有一个外接圆；④垂直于弦的直径平分弦所对的两条弧.其中真命题的个数有( )A.1个B.2个C.3个D.4个8.如图，AB 是⊙O 的直径，CD 是弦，AB ⊥CD ，垂足为点E ，连接OD 、CB 、AC ，∠DOB=60°，EB=2,那么CD 的长为( )A.3B.23C.33D.439.如图，Rt △AB ′C ′是Rt △ABC 以点A 为中心逆时针旋转90°而得到的，其中AB=1，BC=2，则旋转过程中弧CC ′的长为( )A.25πB.25πC.5πD.5π10.如图所示，直线CD 与以线段AB 为直径的圆相切于点D ，并交BA 的延长线于点C ，且AB=2，AD=1，P 点在切线CD 上移动.当∠APB 的度数最大时，∠ABP 的度数为( )A.15°B.30°C.60°D.90°二、填空题(每小题4分，共24分)11.在⊙O 中，已知半径长为3，弦AB 长为4，那么圆心O 到AB 的距离为_____12.如图，点A、B、C、D分别是⊙O上四点，∠ABD=20°，BD是直径，则∠ACB=_____13.如图，水平放置的圆柱形排水管道的截面直径是1 m，其中水面的宽AB为0.8 m，则排水管内水的深度为_____14.小明用图中所示的扇形纸片作一个圆锥的侧面，已知扇形的半径为5 cm，弧长是6πcm，那么这个圆锥的高是_____15.如图，在Rt△ABC中，∠C=90°，∠A=60°，BC=4 cm，以点C为圆心，以3 cm长为半径作圆，则⊙C与AB的位置关系是_____16.如图，四边形OABC是菱形，点B，C在以点O为圆心的弧EF上，且∠1＝∠2，若扇形OEF的面积为3π，则菱形OABC的边长为_____三、解答题(共46分)17.(8分)在⊙O中，直径AB⊥CD于点E，连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数.18.(8分)如图，四边形ABCD是矩形，以AD为直径的⊙O交BC边于点E、F，AB=4，AD=12.求线段EF的长.19.(10分)如图，AB是⊙O的切线，B为切点，圆心在AC上，∠A=30°，D为弧BC的中点.(1)求证:AB=BC；(2)求证:四边形BOCD是菱形.20.(10分)如图，Rt△ABC中，∠ABC=90°，以AB为直径作半圆⊙O交AC与点D，点E为BC的中点，连接DE.(1)求证：DE是半圆⊙O的切线；(2)若∠BAC=30°，DE=2，求AD的长.21.(10分)在ABCD中，AB=10，∠ABC=60°，以AB为直径作⊙O，边CD切⊙O于点E.(1)求圆心O到CD的距离；(2)求由弧AE，线段AD，DE所围成的阴影部分的面积.(结果保留π和根号)参考答案一、选择题(每小题3分，共30分)1.B2.D3.C4.B5.B6.B7.B8.D9.A 10.B二、填空题(每小题4分，共24分)11.5. 12.70°. 13.0.2m. 14.4 cm. 15.相交. 16.3.三、解答题(共46分)∵∠AOC=2∠D，∴∠EOF=∠AOC=2∠D.在四边形FOED中，∠CFD+∠D+∠DEO+∠FOE=360°，∴90°+∠D+90°+2∠D=360°，∴∠D=60°.17.18.作OM ⊥BC 于M ，连接OE.∴ME=MF=21EF. ∵AD=12，∴OE=6.在矩形ABCD 中，OM ⊥BC ，∴OM=AB=4.在△OEM 中，∠OME=90°，∴ME=25.∴EF=2ME=45.19.(1)∵AB 是⊙O 的切线，∴∠OBA=90°，∠AOB=90°-30°=60°. ∵OB=OC ，∴∠OBC=∠OCB.∵∠AOB=∠OBC+∠OCB ，∴∠OCB=30°=∠A.∴AB=BC.(2)连接OD 交BC 于点M.∵D 是弧BC 的中点，∴OD 垂直平分BC.∵在Rt △OMC 中，∠OCM=30°，∴OC=2OM=OD.∴OM=DM.∴四边形BOCD 是平行四边形.又BO=CO ，∴四边形BOCD 是菱形.20(1)连接OD 、OE 、BD ，∵AB 为圆O 的直径，∴∠ADB=∠BDC=90°.在Rt △BDC 中，E 为斜边BC 的中点，∴DE=BE.在△OBE 和△ODE 中，O B=OD,OE=OE,BE=DE.∴△OBE ≌△ODE(SSS).∴∠ODE=∠ABC=90°.∴DE 为圆O 的切线.(2)在Rt △ABC 中，∠BAC=30°，∴BC=21AC. ∵BC=2DE=4，∴AC=8.又∵∠C=60°，DE=EC ，∴△DEC 为等边三角形，即DC=DE=2.∴AD=AC-DC=6. 21.(1)连接OE,∵CD 切⊙O 于点E ，∴OE ⊥CD.∵AB 是⊙O 的直径，OE 是⊙O 的半径，∴OE=OA=5. 即圆心O 到CD 的距离是5.(2)过点A 作AF ⊥CD ，垂足为F.∵四边形ABCD 是平行四边形，∴∠B=∠D=60°，AB ∥CD. ∵OE ⊥CD ，∴OA=OE=AF=EF=5.在Rt △ADF 中，∠D=60°，A F=5，∴DF=335.∴DE=5+335. 在直角梯形AOED 中，OE=5，OA=5，DE=5+335， ∴S 梯形AOED =21×(5+5+335)×5=25+3625. ∵∠AOE=90°，∴S 扇形OAE =41×π×52=425π. ∴S 阴影=S 梯形AOED -S 扇形OAE =25+3625-425π.。

初三期末圆试题及答案一、选择题（每题3分，共30分）1. 圆的半径为r，则圆的周长为（）A. 2πrB. πrC. 2rD. 4πr答案：A2. 圆的直径为d，则圆的面积为（）A. πd²B. π(d/2)²C. πdD. π(d²/4)答案：B3. 圆心角为90°的扇形面积是整个圆面积的（）A. 1/4B. 1/2C. 3/4D. 1/8答案：A4. 圆的半径扩大到原来的2倍，则面积扩大到原来的（）A. 2倍B. 4倍C. 8倍D. 16倍答案：C5. 一个圆的半径为5cm，圆心到圆上任意一点的距离为（）A. 5cmB. 10cmC. 15cmD. 不确定答案：A6. 两圆相切时，它们的圆心距等于（）A. 两圆半径之和B. 两圆半径之差C. 两圆半径之积D. 两圆半径之商答案：A7. 圆的切线垂直于（）A. 圆心B. 圆心到切点的连线C. 切点到圆心的连线D. 圆的半径答案：B8. 圆的内接四边形对角互补，这是因为（）A. 圆周角定理B. 切线长定理C. 圆内接四边形定理D. 圆心角定理答案：C9. 圆的外切四边形对边之和相等，这是因为（）A. 圆周角定理B. 切线长定理C. 圆内接四边形定理D. 圆心角定理答案：B10. 圆的切线与半径垂直，这是因为（）A. 圆周角定理B. 切线长定理C. 圆内接四边形定理D. 圆心角定理答案：D二、填空题（每题3分，共30分）11. 圆的周长公式为：C = ________。

答案：2πr12. 圆的面积公式为：A = ________。

答案：πr²13. 圆的直径是半径的______倍。

答案：214. 圆的半径是直径的______倍。

答案：1/215. 圆的切线垂直于经过切点的______。

答案：半径16. 圆的内接四边形对角互补，这是因为圆内接四边形的对角线互相平分，且对角线所对的弧相等，所以对角互补。

答案：对角线互相平分17. 圆的外切四边形对边之和相等，这是因为外切四边形的对边分别与圆相切，且切线长定理告诉我们，从圆外一点引出的两条切线长度相等。

圆的复习题和答案一、选择题1. 圆的周长公式是：A. C = πdB. C = 2πrC. C = πrD. C = πd + 2r答案：B2. 圆的面积公式是：A. A = πr²B. A = πd²C. A = π(d/2)²D. A = πr²/2答案：A3. 圆的直径是半径的：A. 2倍B. 1/2倍C. π倍D. 不能确定答案：A4. 圆的半径增加1倍，面积增加多少倍？A. 1倍B. 2倍C. 4倍D. π倍答案：C二、填空题1. 如果一个圆的半径为 \( r \) ，那么它的直径 \( d \) 等于\( \_\_\_\_\_\_\_\_\_\_\_ \) 。

答案：\( 2r \)2. 圆的周长与半径成正比，比例系数是 \( \_\_\_\_\_\_\_\_\_\_\_ \) 。

答案：\( 2π \)3. 一个圆的半径是5厘米，那么它的周长是\( \_\_\_\_\_\_\_\_\_\_\_ \) 厘米，面积是\( \_\_\_\_\_\_\_\_\_\_\_ \) 平方厘米。

答案：周长是 \( 2π \times 5 = 10π \) 厘米，面积是 \( π \times 5^2 = 25π \) 平方厘米。

三、简答题1. 描述圆心角、弧长、半径之间的关系。

答案：圆心角的度数与弧长和半径之间存在一个固定的关系。

如果圆心角的度数为 \( θ \)（以弧度为单位），弧长为 \( l \)，半径为 \( r \)，那么它们之间的关系可以表示为 \( l = rθ \)。

2. 解释什么是圆的内接多边形，并且说明它与圆的关系。

答案：圆的内接多边形是指所有顶点都位于同一个圆上的多边形。

对于一个圆的内接多边形，它的每条边都是圆的弦，每个角都是圆心角的一部分，且所有边的长度之和等于圆的周长。

四、计算题1. 已知一个圆的周长是 \( 12π \) 厘米，求它的半径。