常用数学符号大全
- 格式:doc
- 大小:203.00 KB
- 文档页数:5

常用数学符号,用时直接复制常用数学符号,用时直接复制1 几何符号Dⅷⅶ↋ↆↄ▣ADE2 代数符号ⅴⅸⅹ~ⅼↅↇↈↃⅵↀ3运算符号×÷ⅳ±4集合符号ⅻⅺⅰ5特殊符号ⅲπ(圆周率)6推理符号|a| ↂ▣ⅶⅺⅻↅↆ±ↈↇⅰⅬⅭⅮⅯ↖↗↘↙ⅷⅸⅹ&; §←↑→↓↔↕↖↗ΓΔΘΛΞΟΠΣΦΧΨΩαβγδεδεζηθικλμνπξζηυθχψωⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹⅰⅱⅲ↚ⅳⅴⅵ↛ⅶ↜ⅷⅸⅹⅺⅻⅼⅽⅾⅿↀↁↂↃↄ↝ↅↆↇↈ↞↟↉↊⊕↋↠℃指数0123:º¹²³符号意义ⅵ无穷大PI 圆周率|x| 函数的绝对值ⅻ集合并ⅺ集合交ↈ大于等于ↇ小于等于ↆ恒等于或同余ln(x) 自然对数lg(x) 以2为底的对数log(x) 常用对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数{x} 小数部分x - floor(x)ⅼf(x)δx 不定积分ⅼ[a:b]f(x)δx a到b的定积分[P] P为真等于1否则等于0ⅲ[1ↇkↇn]f(k) 对n进行求和,可以拓广至很多情况如:ⅲ[n is prime][n < 10]f(n)ⅲⅲ[1ↇiↇjↇn]n^2lim f(x) (x->?) 求极限f(z) f关于z的m阶导函数C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除nmn m与n互质a ⅰ A a属于集合A#A 集合A中的元素个数ⅭⅯ↋●★☆■☇『』▤◣◥▢Ψ※◤◥Ⅾ№Ⅼ㊣ⅲ〖〗@μδω□ⅽ〒※ⅾぷⅱ卐▂▃▅▆█▓【】▣ⅳⅺ¤々☇☈ⅵㄨↆ↘↙▂▃▄▅▆▇█┗┛╰☆╮。
![数学符号[宝典]](https://uimg.taocdn.com/a93f74c2370cba1aa8114431b90d6c85ec3a8834.webp)
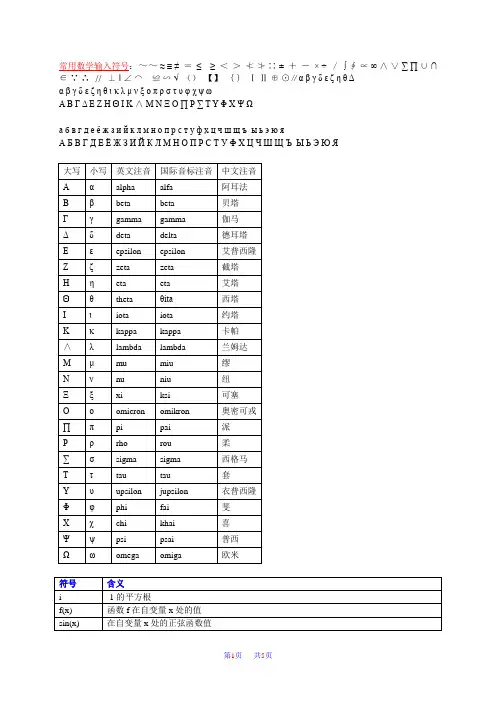
1、希腊字母:α——阿尔法β——贝塔γ——伽马Γ——德尔塔μ——可sei ψ——可赛ω——奥秘噶κ——米哟ι——南木打ζ——西格玛η——套θ——fai2、数学运算符:ⅲ—连加号ⅱ—连乘号ⅻ—并ⅺ—补ⅰ—属于ⅿ—因为ⅾ—所以ⅳ—根号‖—平行—垂直ⅶ—角—弧↋—圆ⅴ—正比于ⅵ—无穷ⅼ—积分Ↄ—约等ↆ—恒等3、三角函数:sin—赛因cos—考赛因tan—叹近体cot—考叹近体sec—赛看近体csc —考赛看近体序号大写小写英文注音国际音标注音中文注音1 Α α alpha a:lf 阿尔法2 Β β beta bet 贝塔3 Γ γ gamma ga:m 伽马4 Γ δ delta delt 德尔塔5 Δ ε epsilon ep`silon 伊普西龙6 Ε δ zeta zat 截塔7 Ζ ε eta eit 艾塔8 Θ ζ thet ζit 西塔9 Η η iot aiot 约塔10 Θ θ kappa kap 卡帕11 Ι ι lambda lambd 兰布达12 Κ κ mu mju 缪13 Λ λ nu n ju 纽14 Μ μ xi ksi 克西15 Ν ν omicron omik`ron 奥密克戎16 Ξ π pi pai 派17 Ο ξ rho rou 肉18 Π ζ sigma `sigma 西格马19 Ρ η tau tau 套20 υ upsilon jup`silon 宇普西龙21 Φ θ phi fai 佛爱22 Σ χ chi phai 西23 Τ ψ psi psai 普西24 Υ ω omega o`miga 欧米伽希腊字母的正确读法是什么?1 Α α alpha a:lf 阿尔法2 Β β beta bet 贝塔3 Γ γ gamma ga:m 伽马4 Γ δ delta delt 德尔塔5 Δ ε epsilon ep`silon 伊普西龙6 Ε δ zeta zat 截塔7 Ζ ε eta eit 艾塔8 Θ ζ thet ζit 西塔9 Η η iot aiot 约塔10 Κ θ kappa kap 卡帕11 ⅸι lambda lambd 兰布达12 Μ κ mu mju 缪13 Ν λ nu nju 纽磁阻系数14 Ξ μ xi ksi 克西15 Ο ν omicron omik`ron 奥密克戎16 ∏ π pi pai 派17 Ρ ξ rho rou 肉18 ∑ ζ sigma `sigma 西格马19 Σ η tau tau 套20 Τ υ upsilon jup`silon 宇普西龙21 Φ θ phi fai 佛爱22 Υ χ chi phai 西23 Φ ψ psi psai 普西角速;24 Χ ω omega o`miga 欧米伽希腊字母读法Αα:阿尔法AlphaΒβ:贝塔BetaΓγ:伽玛GammaΓδ:德尔塔DelteΔε:艾普西龙Epsilonδ :捷塔ZetaΕε:依塔EtaΘζ:西塔ThetaΗη:艾欧塔IotaΚθ:喀帕Kappaⅸι:拉姆达LambdaΜκ:缪MuΝλ:拗NuΞμ:克西XiΟν:欧麦克轮Omicron∏π:派PiΡξ:柔Rho∑ζ:西格玛SigmaΣη:套TauΤυ:宇普西龙UpsilonΦθ:fai PhiΥχ:器ChiΦψ:普赛PsiΧω:欧米伽Omega数学符号大全各种符号的英文读法'exclam'='!''at'='@''numbersign'='#''dollar'='$''percent'='%''caret'='^''ampersand'='&''asterisk'='*''parenleft'='(''parenright'=')''minus'='-''underscore'='_''equal'='=''plus'='+''bracketleft'='''braceright'='}''semicolon'=';''colon'=':''quote'=''''doublequote'='"''backquote'=''''tilde'='~''backslash'='\''bar'='|''comma'=',''less'='<''period'='.''greater'='>''slash'='/''question'='?''space'=' '~~~~~~~~~~~~~~~~~~~~~~。 hyphen 连字符' apostrophe 省略号;所有格符号— dash 破折号‘ ’single quotation marks 单引号“ ”double quotation m arks 双引号( ) parentheses 圆括号square brackets 方括号Angle bracket{} Brace《》French quotes 法文引号;书名号... ellipsis 省略号¨ tandem colon 双点号" ditto 同上‖ parallel 双线号/ virgule 斜线号& ampersand = and~ swung dash 代字号§ section; division 分节号Ⅾ arrow 箭号;参见号+ plus 加号;正号- minus 减号;负号ª plus or minus 正负号× is multiplied by 乘号÷ is divided by 除号= is equal to 等于号ↅ is not equal to 不等于号ↆ is equivalent to 全等于号ↄ is equal to or approximately equal to 等于或约等于号Ↄ is approximately equal to 约等于号< is less than 小于号> is more than 大于号↉ is not less than 不小于号↊ is not more than 不大于号ↇ is less than or equal to 小于或等于号ↈ is more than or equal to 大于或等于号% per cent 百分之…‟ per mill 千分之…ⅵ infinity 无限大号ⅴ varies as 与…成比例ⅳ (square) root 平方根ⅿ since; b ecause 因为ⅾ hence 所以ↁ equals, as (proportion) 等于,成比例ⅶ angle 角 semicircle 半圆↋ circle 圆◈ circumference 圆周π pi 圆周率△ triangle 三角形 perpendicular to 垂直于ⅻ union of 并,合集ⅺ intersection of 交,通集ⅼ the integral of …的积分ⅲ (sigma) summation of 总和© degree 度† minute 分‡ second 秒#number …号‣ Celsius system 摄氏度@ at 单价x'是x prime(比如转置矩阵)x"是x double-prime数学符号大全1 几何符号ⅷⅶ↋ↆↄ△‖2 代数符号ⅴⅸⅹ~ⅼↅↇↈↃⅵↀ3运算符号×÷ⅳª4集合符号ⅻⅺⅰⅰↇↈ⊆⊂5特殊符号ⅲπ(圆周率)6推理符号|a| ↂ△ⅶⅺⅻↅↆªↈↇⅰⅬⅭⅮⅯ↖↗↘↙ⅷⅸⅹ&; §←↑→↓↔↕↖↗ΓΓΘΛΞΟΠΦΥΦΧαβγδεδεζηθικλμνπξζηυθχψωⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫ﹪﹫ﹰﹱﹲﹳⅰⅱⅲ↚ⅳⅴⅵ↛ⅶ↜ⅷⅸⅹⅺⅻⅼⅽⅾⅿↀↁↂↃↄ↝ↅↆↇↈ↞↟↉↊?↋↠‣上述符号所表示的意义和读法(中英文参照)+plus 加号;正号-minus 减号;负号±plus or minus 正负号×is multiplied by 乘号÷is divided by 除号=is equal to 等于号≠ is not equal to 不等于号≡ is equivalent to 全等于号ↄis approximately equal to 约等于≈ is approximately equal to 约等于号<is less than 小于号>is more than 大于号≤ is less than or equal to 小于或等于≥ is more than or equal to 大于或等于%per cent 百分之…∞ infinity 无限大号√ (square) root 平方根X squared X的平方X cubed X的立方ⅿsince; because 因为ⅾhence 所以ⅶangle 角semicircle 半圆↋circle 圆○ circumference 圆周△triangle 三角形perpendicular to 垂直于ⅻintersection of 并,合集∩ union of 交,通集∫ the integral of …的积分∑ (sigma) summation of 总和°degree 度′ minute 分〃second 秒#number …号@at 单价符号意义ⅵ无穷大PI 圆周率|x| 函数的绝对值ⅻ集合并ⅺ集合交ↈ大于等于ↇ小于等于ↆ恒等于或同余ln(x) 自然对数lg(x) 以2为底的对数log(x) 常用对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数{x} 小数部分 x - floor(x)ⅼf(x)δx 不定积分ⅼ[a:b]f(x)δx a到b的定积分[P] P为真等于1否则等于0ⅲ[1ↇkↇn]f(k) 对n进行求和,可以拓广至很多情况如:ⅲ[n is prime][n < 10]f(n)ⅲⅲ[1ↇiↇjↇn]n^2lim f(x) (x->?) 求极限f(z) f关于z的m阶导函数C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除nmn m与n互质a ⅰ A a属于集合A#A 集合A中的元素个数ⅰⅱⅲⅳⅵⅶ↜ⅷⅸⅹⅺⅻⅼⅽⅾⅿↂↃↄↅↆↇↈ↞↟?↋ •数学符号大全收藏运算符: ± × ÷ ↀ∫ ⅽↆↄ≈ ↂⅴ↝≠ ↆ≤ ≥ ↞↟↉↊/√ ‰ ∑ ∏ &关系运算符:ⅸⅹ集合符号:ⅻⅺⅰ↜⊆序号:←↑→↓↔↕↖↗ⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫ﹪﹫ﹰﹱﹲﹳ≈㈠㈡㈢㈣㈤㈥㈦㈧㈨㈩其它:~ ± × ÷ ∑ⅻⅺⅰ√ⅷⅶ↋ↆↄ≈ↂ≠↉↊≤≥∞ⅿⅾ☈☇‣⦅‰☆★○●◉◇◆□■△▲ⅮⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫ*ΟαβγδεζηθικλμνξποστυφχψωΑ Β Γ Δ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Ωα β γ δ ε ζ η θ ι κ λ μ μ ν ξ π ο σ τ υ φ χψ ωⅬⅭⅮⅯ↖↗↘↙∞ ⅾⅿↀↁ° ′ ″ ‣▝↠△↋ⅶⅷ〓〔〈〉《》「」『』〕〖【】()[]{}ﹶ§ № •#&@☆★○● ◉△▲◇◆□ ■〒▙▛▚▘☇☈ⅬⅭⅮⅯ↖↗↘↙ⅰ∏∑↠∕√ⅴ∞↛ⅶ↜ⅷⅸⅹⅺⅻ∫ⅽⅾⅿↀↁↂ≈ↄ↝≠ↆ≤≥↞↟↉↊﹞﹟﹠﹡﹢﹣﹤﹥﹦﹨﹩!﹖﹗"#$%&'*\^_`|~⦅⦆ﹴ。「▝↋▔▕■□▲△▖▗◆◇◈◉●▘▙▚▛★☆▜☇☈、。

数学符号大全及意义数学符号是数学领域中的重要工具,它们用来表示数学概念、关系和运算,是数学语言中不可或缺的一部分。
在数学中,有许多常用的符号,它们代表着不同的数学概念和意义。
本文将为大家介绍一些常见的数学符号及其意义,希望能够帮助大家更好地理解和运用这些符号。
1. 加号(+)。
加号是数学中最基本的运算符号之一,它表示两个数相加的运算。
例如,3+5=8,表示3加5的结果是8。
2. 减号(-)。
减号也是常见的运算符号,表示两个数相减的运算。
例如,7-4=3,表示7减去4的结果是3。
3. 乘号(×)。
乘号表示两个数相乘的运算。
例如,2×6=12,表示2乘以6的结果是12。
4. 除号(÷)。
除号表示两个数相除的运算。
例如,8÷2=4,表示8除以2的结果是4。
5. 等号(=)。
等号用来表示两个数或表达式相等的关系。
例如,2+3=5,表示2加3的结果等于5。
6. 小于号(<)和大于号(>)。
小于号和大于号分别表示数学中的小于和大于关系。
例如,3<5表示3小于5,5>2表示5大于2。
7. 求和符号(∑)。
求和符号用来表示对一组数进行求和的运算。
例如,∑(i=1 to 5) i,表示对1到5的所有整数进行求和。
8. 开方符号(√)。
开方符号表示对一个数进行开方运算。
例如,√9=3,表示对9进行开方的结果是3。
9. π(圆周率)。
π是一个代表圆周率的数学常数,它的值约为3.14159。
在数学中,π经常用来表示圆的周长和面积等概念。
10. Σ(求和)。
Σ是希腊字母中的一个,表示求和的意思。
在数学中,Σ常用来表示对一组数进行求和的运算。
11. ∫(积分)。
积分符号用来表示对一个函数进行积分运算。
在微积分中,积分是一个重要的概念,它常常用来求函数的面积、体积等。
12. ∞(无穷大)。
无穷大符号表示一个数值是无穷大的概念。
在数学中,无穷大常常用来表示某些极限值或者数列的趋势。

常用数学符号大全及意义1.加号(+):表示两个数的和,通常用来表示加法运算。
2.减号(-):表示两个数的差,通常用来表示减法运算。
3.乘号(×):表示两个数的乘积,通常用来表示乘法运算。
4.除号(÷):表示两个数的商,通常用来表示除法运算。
5.等于号(=):表示两个数相等,通常用来表示等式或者表达式的结果。
6.大于号(>):表示左边的数大于右边的数,通常用来表示一种比较关系。
7.小于号(<):表示左边的数小于右边的数,通常用来表示一种比较关系。
8.大于等于号(≥):表示左边的数大于等于右边的数,通常用来表示一种比较关系。
9.小于等于号(≤):表示左边的数小于等于右边的数,通常用来表示一种比较关系。
10.不等于号(≠):表示左边的数不等于右边的数,通常用来表示一种比较关系。
11.竖线(|):一般用来分隔字符串,表示分割。
12.加上等于号(+=):在原有基础上加上一定量,通常用来表示赋值运算。
13.减去等于号(-=):在原有基础上减去一定量,通常用来表示赋值运算。
14.乘以等于号(*=):在原有基础上乘以一定量,通常用来表示赋值运算。
15.除以等于号(/=):在原有基础上除以一定量,通常用来表示赋值运算。
16.幂运算符(^):表示一个数的n次方,通常用来表示乘方运算。
17.三角函数符(sin,cos,tan):分别表示正弦、余弦、正切函数。
18.根号(√):表示求n次方根的运算,通常用来表示开方运算。
19.百分号(%):表示一个数字的百分比,即该数字与100的比例。
20.逻辑运算符(&&,||):&&代表“与”,||代表“或”,都是常用的逻辑运算符。

数学中常用的符号
数学中常用的符号有很多,以下列举一些常见的:
1. 数字:0, 1, 2, 3, 4, 5, 6, 7, 8, 9
2. 基本运算符号:
- 加法:+
- 减法:-
- 乘法:*
- 除法:/
- 等于:=
- 不等于:≠
- 大于:>
- 小于:<
- 大于等于:≥
- 小于等于:≤
3. 数学函数符号:
- 圆周率:π
- 开根号:√
- 绝对值:| |
- 平方:²
- 立方:³
- 对数:log
4. 集合符号:
- 元素属于:∈
- 元素不属于:∉
- 空集:∅
- 子集:⊆
- 真子集:⊂
5. 集合运算符号:
- 并集:∪
- 交集:∩
- 补集:'
- 差集:\
- 符号集合:ℝ(实数集),ℕ(自然数集),ℤ(整数集),ℚ(有理数集),S(复数集)
6. 三角函数符号:
- 正弦:sin
- 余弦:cos
- 正切:tan
7. 极限符号:
- 极限:lim
8. 微积分符号:
- 导数:d/dx
- 积分:∫
- 偏导数:∂/∂x
9. 概率统计符号:
- 同等于:≈
- 和:Σ
- 均值:μ
- 方差:σ²
10. 集合论符号:
- 内含于:⊂
- 并集:⋃
- 交集:⋂
- 全集:U
- 子集:⊆
以上只是一些常见的符号,实际中还有很多其他符号,如矩阵符号、微分方程符号等。
数学中的符号非常丰富,灵活运用可以简洁地表示数学概念和运算关系。


常用单位数学符号集合大全1. 算术运算符加号(+):表示两个数相加减号():表示两个数相减乘号(× 或):表示两个数相乘除号(÷ 或 /):表示两个数相除等于号(=):表示两个数相等2. 比较运算符大于号(>):表示一个数大于另一个数小于号(<):表示一个数小于另一个数大于等于号(≥):表示一个数大于或等于另一个数小于等于号(≤):表示一个数小于或等于另一个数不等于号(≠):表示两个数不相等3. 分数与根号分数(/):表示两个数相除,如 3/4根号(√):表示求一个数的平方根,如√4 = 24. 指数与对数指数(^ 或):表示一个数的乘方,如 2^3 = 8对数(log):表示求一个数的对数,如 log10(100) = 2 5. 函数符号正弦函数(sin):表示求一个角的正弦值余弦函数(cos):表示求一个角的余弦值正切函数(tan):表示求一个角的正切值反正弦函数(arcsin 或 asin):表示求一个数的反正弦值反余弦函数(arccos 或 acos):表示求一个数的反余弦值反正切函数(arctan 或 atan):表示求一个数的反正切值6. 微积分符号导数('):表示求一个函数的导数,如 f'(x)积分(∫):表示求一个函数的不定积分,如∫f(x)dx极限(lim):表示求一个函数的极限,如lim(x→0)f(x)7. 集合符号属于(∈):表示一个元素属于某个集合,如x ∈ A不属于(∉):表示一个元素不属于某个集合,如 x ∉ A空集(∅):表示一个不包含任何元素的集合并集(∪):表示两个集合的并集,如 A ∪ B交集(∩):表示两个集合的交集,如 A ∩ B8. 其他符号无穷大(∞):表示一个无限大的数虚数单位(i):表示虚数单位,如√1求和(Σ):表示求一个序列的和,如Σn = 1^∞ an求积(Π):表示求一个序列的积,如Πn = 1^∞ an9. 矩阵和向量符号矩阵([a_{ij}]):表示一个由数字组成的矩形阵列,如[a_{11} a_{12}; a_{21} a_{22}]向量(<a_1, a_2, , a_n>):表示一个由数字组成的有序序列,如 <1, 2, 3>转置(^T):表示一个矩阵的转置,如 A^T矩阵乘法(A B):表示两个矩阵的乘积,如 A B = C矩阵加法(A + B):表示两个矩阵的加法,如 A + B = C矩阵减法(A B):表示两个矩阵的减法,如 A B = C矩阵的行列式(det(A)):表示一个矩阵的行列式,如 det(A)矩阵的逆(A^{1}):表示一个矩阵的逆,如 A^{1}10. 几何符号平行(∥):表示两条线段或直线平行,如AB ∥ CD垂直(⊥):表示两条线段或直线垂直,如AB ⊥ CD相似(~):表示两个几何图形相似,如△ABC ~ △DEF全等(≅):表示两个几何图形全等,如△ABC ≅ △DEF圆(O):表示一个圆,如 O弧(⌒):表示圆的一部分,如AB⌒角(∠):表示一个角,如∠ABC11. 概率与统计符号概率(P):表示某个事件发生的概率,如 P(A)期望值(E):表示随机变量的期望值,如 E(X)方差(Var):表示随机变量的方差,如 Var(X)标准差(σ):表示随机变量的标准差,如σ(X)累积分布函数(CDF):表示随机变量的累积分布函数,如 F(x)概率密度函数(PDF):表示随机变量的概率密度函数,如 f(x) 12. 逻辑符号与(∧):表示两个条件同时成立,如 A ∧ B或(∨):表示两个条件中至少有一个成立,如 A ∨ B非(¬):表示对一个条件取反,如¬A包含(⊆):表示一个集合是另一个集合的子集,如 A ⊆ B等价(≡):表示两个表达式等价,如 A ≡ B13. 其他常用符号平方(^2):表示一个数的平方,如 2^2 = 4立方(^3):表示一个数的立方,如 2^3 = 8平方根(√):表示求一个数的平方根,如√4 = 2立方根(∛):表示求一个数的立方根,如∛8 = 2求和(Σ):表示求一个序列的和,如Σn = 1^∞ an求积(Π):表示求一个序列的积,如Πn = 1^∞ an14. 复数符号复数(a + bi):表示一个由实部和虚部组成的复数,如 3 + 4i共轭复数(a bi):表示一个复数的共轭复数,如 3 4i模长(|a + bi|):表示一个复数的模长,如 |3 + 4i| = 5辐角(arg(a + bi)):表示一个复数的辐角,如 arg(3 + 4i) ≈ 0.92715. 三角函数符号正弦函数(sin):表示求一个角的正弦值,如sin(θ)余弦函数(cos):表示求一个角的余弦值,如cos(θ)正切函数(tan):表示求一个角的正切值,如tan(θ)余切函数(cot):表示求一个角的余切值,如cot(θ)正割函数(sec):表示求一个角的正割值,如sec(θ)余割函数(csc):表示求一个角的余割值,如csc(θ)16. 不等式符号大于号(>):表示一个数大于另一个数,如 a > b小于号(<):表示一个数小于另一个数,如 a < b大于等于号(≥):表示一个数大于或等于另一个数,如 a ≥ b小于等于号(≤):表示一个数小于或等于另一个数,如 a ≤ b不等于号(≠):表示两个数不相等,如a ≠ b17. 几何符号平行(∥):表示两条线段或直线平行,如AB ∥ CD垂直(⊥):表示两条线段或直线垂直,如AB ⊥ CD相似(~):表示两个几何图形相似,如△ABC ~ △DEF全等(≅):表示两个几何图形全等,如△ABC ≅ △DEF圆(O):表示一个圆,如 O弧(⌒):表示圆的一部分,如AB⌒角(∠):表示一个角,如∠ABC18. 概率与统计符号概率(P):表示某个事件发生的概率,如 P(A)期望值(E):表示随机变量的期望值,如 E(X)方差(Var):表示随机变量的方差,如 Var(X)标准差(σ):表示随机变量的标准差,如σ(X)累积分布函数(CDF):表示随机变量的累积分布函数,如 F(x)概率密度函数(PDF):表示随机变量的概率密度函数,如 f(x)19. 逻辑符号与(∧):表示两个条件同时成立,如 A ∧ B或(∨):表示两个条件中至少有一个成立,如 A ∨ B非(¬):表示对一个条件取反,如¬A包含(⊆):表示一个集合是另一个集合的子集,如 A ⊆ B 等价(≡):表示两个表达式等价,如 A ≡ B20. 其他常用符号平方(^2):表示一个数的平方,如 2^2 = 4立方(^3):表示一个数的立方,如 2^3 = 8平方根(√):表示求一个数的平方根,如√4 = 2立方根(∛):表示求一个数的立方根,如∛8 = 2求和(Σ):表示求一个序列的和,如Σn = 1^∞ an求积(Π):表示求一个序列的积,如Πn = 1^∞ an。
常用数学输入符号:~~≈ ≡ ≠ =≤≥ <>≮≯∷ ±+-× ÷/∫ ∮∝∞ ∧∨∑ ∏ ∪∩ ∈∵∴//⊥‖ ∠⌒≌∽√()【】{}ⅠⅡ⊕⊙∥αβγδεζηθΔαβγδεζηθικλμνξοπρστυφχψωΑΒΓΔΕΖΗΘΙΚ∧ΜΝΞΟ∏Ρ∑ΤΥΦΧΨΩабвгдеёжзийклмнопрстуфхцчшщъыьэюяАБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯexp(x) 在自变量x处的指数函数值,常被写作e xa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数a x同a^xlog b a 以b为底a的对数;b log b a = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值,其值等于1/cos xcsc x 余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin yacos x y,余弦函数反函数在x处的值,即x = cos yatan x y,正切函数反函数在x处的值,即x = tan yacot x y,余切函数反函数在x处的值,即x = cot yasec x y,正割函数反函数在x处的值,即x = sec yacsc x y,余割函数反函数在x处的值,即x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在其上部。

常用数学符号大全作者:佚名 文章来源:zx98 点击数:15616 更新时间:2012-9-51:18:431、几何符号 ABCD-1A 1B 1C 1D⊥ ∥ ∠ ⌒ ⊙ ≡ ≌ △2、代数符号∝ ∧ ∨ ~ ∫ ≠ ≤ ≥ ≈ ∞ ∶3、运算符号如加号(+),减号(-),乘号(×或·),除号(÷或/),两个集合的并集(∪),交集(∩),根号(√),对数(log ,lg ,ln ),比(:),微分(dx ),积分(∫),曲线积分(∮)等。
4、集合符号 ()[]()[]{}∩∪ ∩ Φ ⊆⊇ ∉ ∈ ⊂ ⊃≠⊂ ≠⊃5、特殊符号∑ π(圆周率)6、推理符号|a| ⊥ ∽ △ ∠ ∩ ∪ ≠ ≡ ± ≥ ≤ ∈ ←↑ → ↓ ↖ ↗ ↘ ↙ ∥ ∧ ∨&; §① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩Γ Δ Θ Λ Ξ Ο Π Σ Φ Χ Ψ Ωα β γ δ ε ζ η θ ι κ λ μ νξ ο π ρ σ τ υ φ χ ψ ωⅠ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻ(Ⅰ)(Ⅱ)(Ⅲ)ⅰ ⅱ ⅲ ⅳ ⅴ ⅵ ⅶ ⅷ ⅸ ⅹ∈ ∏ ∑ ∕ √ ∝ ∞ ∟ ∠ ∣ ∥ ∧ ∨ ∩ ∪ ∫ ∮∴ ∵ ∶ ∷ ∽ ≈ ≌ ≒ ≠ ≡ ≤ ≥ ≦ ≧ ≮ ≯ ⊕ ⊙ ⊥⊿ ⌒ ℃指数0123:o1237、数量符号如:i,2+i,a,x,自然对数底e,圆周率π。
8、关系符号如“=”是等号,“≈”是近似符号,“≠”是不等号,“>”是大于符号,“<”是小于符号,“≥”是大于或等于符号(也可写作“≮”),“≤”是小于或等于符号(也可写作“≯”),。
“→ ”表示变量变化的趋势,“∽”是相似符号,“≌”是全等号,“∥”是平行符号,“⊥”是垂直符号,“∝”是成正比符号,(没有成反比符号,但可以用成正比符号配倒数当作成反比)“∈”是属于符号,“??”是“包含”符号等。

常用数学符号大全、关系代数符号1、几何符号⊥∥∠⌒⊙≡≌△2、代数符号∝∧∨~∫≠≤≥≈∞∶3、运算符号如加号(+),减号(-),乘号(×或·),除号(÷或/),两个集合的并集(∪),交集(∩),根号(√),对数(log,lg,ln),比(:),微分(dx),积分(∫),曲线积分(∮)等。
4、集合符号∪∩∈5、特殊符号∑π(圆周率)6、推理符号|a| ⊥∽△∠∩∪≠≡±≥≤∈←↑→↓↖↗↘↙∥∧∨&; §①②③④⑤⑥⑦⑧⑨⑩ΓΔΘΛΞΟΠΣΦΧΨΩαβγδεζηθικλμνξοπρστυφχψωⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹ∈∏∑∕√∝∞∟∠∣∥∧∨∩∪∫∮∴∵∶∷∽≈≌≒≠≡≤≥≦≧≮≯⊕⊙⊥⊿⌒℃指数0123:o1237、数量符号如:i,2+i,a,x,自然对数底e,圆周率π。
8、关系符号如“=”是等号,“≈”是近似符号,“≠”是不等号,“>”是大于符号,“<”是小于符号,“≥”是大于或等于符号(也可写作“≮”),“≤”是小于或等于符号(也可写作“≯”),。
“→”表示变量变化的趋势,“∽”是相似符号,“≌”是全等号,“∥”是平行符号,“⊥”是垂直符号,“∝”是成正比符号,(没有成反比符号,但可以用成正比符号配倒数当作成反比)“∈”是属于符号,“??”是“包含”符号等。
9、结合符号如小括号“()”中括号“[]”,大括号“{}”横线“—”10、性质符号如正号“+”,负号“-”,绝对值符号“| |”正负号“±”11、省略符号如三角形(△),直角三角形(Rt△),正弦(sin),余弦(cos),x的函数(f(x)),极限(lim),角(∠),∵因为,(一个脚站着的,站不住)∴所以,(两个脚站着的,能站住)总和(∑),连乘(∏),从n个元素中每次取出r个元素所有不同的组合数(C(r)(n) ),幂(A,Ac,Aq,x^n)等。

2024年常用数学符号总结随着时间的推移,数学符号在不断发展和演变。
在2024年,我们可以预见一些常用的数学符号将继续被广泛使用。
以下是对2024年常用数学符号的总结,展示了它们的含义和用法。
1. = (等于号):表示两个量相等,也可用于方程中的解等式。
例:2 + 3 = 52. + (加号):用于表示两个数相加。
例:4 + 6 = 103. - (减号):用于表示两个数相减。
例:8 - 3 = 54. × 或 * (乘号):用于表示两个数相乘。
例:2 × 7 = 14 或 3 * 4 = 125. ÷ 或 / (除号):用于表示两个数相除。
例:10 ÷ 2 = 5 或 12 / 3 = 46. % (百分号):表示百分数。
例如,12%表示12的百分之一。
例:20% = 0.2 或0.2 × 100 = 207. < (小于号):表示一个数小于另一个数。
例:5 < 108. > (大于号):表示一个数大于另一个数。
例:10 > 59. ≤ (小于等于号):表示一个数小于或等于另一个数。
例:4 ≤ 510. ≥ (大于等于号):表示一个数大于或等于另一个数。
例:5 ≥ 411. ≠ (不等于号):表示两个数不相等。
例:3 ≠ 712. π (圆周率):表示圆的周长与直径的比值,约为3.14159。
例:C = 2πr13. √ (平方根):表示一个数的平方根。
例:√16 = 414. ^ (指数符号):表示一个数的幂。
例:2^3 = 815. ∑ (求和符号):表示对一系列数求和。
例:∑x 表示对所有x进行求和。
16. ∫ (积分符号):表示对一个函数进行积分。
例:∫f(x)dx 表示对函数f(x)进行积分。
17. ∞ (无穷大):表示趋于无穷大的数。
例:lim(x→∞) f(x) 表示当x趋于无穷大时,函数f(x)的极限。
18. ∈ (属于符号):表示一个元素属于一个集合。
常⽤数学符号⼤全⼤写⼩写英⽂注⾳国际⾳标注⾳中⽂注⾳Ααalpha alfa阿⽿法Ββbeta beta贝塔Γγgamma gamma伽马Δδdeta delta德⽿塔Εεepsilon epsilon艾普西隆Ζζzeta zeta截塔Ηηeta eta艾塔Θθthetaθita西塔Ιιiota iota约塔Κκkappa kappa卡帕∧λlambda lambda兰姆达Μµmu miu缪Ννnu niu纽Ξξxi ksi可塞Οοomicron omikron奥密可戎∏πpi pai派Ρρrho rou柔∑σsigma sigma西格马Ττtau tau套Υυupsilon jupsilon⾐普西隆Φφphi fai斐Χχchi khai喜Ψψpsi psai普西Ωωomega omiga欧⽶公式输⼊符号≈≡≠=≤≥<>≮≯∷±+-×÷/∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒⊙≌∽√:plus(positive正的)-:minus(negative负的)*:multiplied by乘以;乘上÷:divided by除以=:be equal to相等≈:be approximately equal to 约等于,近似等于():round brackets(parenthesis)圆括号[]:square brackets⽅括号{}:braces花括号n. 背带;吊带(brace的复数)∵:because∴:therefore adv. 因此;所以≤:less than or equal to≥:greater than or equal to∞:infinity n. ⽆穷;⽆限⼤;⽆限距LOG n X:logx to the base nx n:the nth power of x功率;⼒量;能⼒;政权;势⼒;[数] 幂f(x):the function of x函数dx:differential of xadj. 微分的;差别的;特异的n. 微分;差别x y:x plus y(a b):bracket a plus b bracket closeda=b: a equals b与…相同a≠b: a isn't equal to ba>b : a is greater than ba>>b: a is much greater than ba≥b: a is greater than or equal to ba≥b: a is greater than or equal to bx→∞:approaches infinity 接近⽆穷⼤x2:x squarex3:x cube√ ̄x:the square root of x平⽅根3√ ̄x:the cube root of x⽴⽅根3‰:three permilln∑i=1xi:the summation of x where x goes from 1to nn∏i=1xi:the product of x sub i where I goes from 1to n∫ab:integral betweens a and b1.基本符号+- × ÷(/)2.分数号/3.正负号±4.相似全等∽≌5.因为所以∵∴6.判断类= ≠ <≮(不⼩于)>≯(不⼤于)7.集合类∈(属于)∪(并集)∩(交集)8.求和符号∑9.n次⽅符号¹(⼀次⽅) ²(平⽅) ³(⽴⽅)⁴(4次⽅)ⁿ(n次⽅)10.下⾓标₁₂₃₄ (如A₁B₂C₃D₄效果如何?)11.或与⾮的'⾮'¬12.导数符号(备注符号)′〃13.度° ℃14.任意∀15.推出号⇒16.等价号⇔17.包含被包含⊆⊇⊂⊃18.导数∫∬19.箭头类↗↙↖↘↑↓↔↕↑↓→←20.绝对值|21.弧⌒22.圆⊙ 11.或与⾮的'⾮'12.导数符号(备注符号)′〃13.度° ℃14.任意∀15.推出号⇒16.等价号⇔17.包含被包含⊆⊇⊂⊃18.导数∫∬19.箭头类↗↙↖↘↑↓↔↕↑↓→←20.绝对值|21.弧⌒22.圆。
(完整版)常用数学符号大全1. 加号(+):表示两个数相加,例如 2 + 3 = 5。
2. 减号():表示两个数相减,例如 5 3 = 2。
3. 乘号(×):表示两个数相乘,例如2 × 3 = 6。
4. 除号(÷):表示两个数相除,例如6 ÷ 2 = 3。
5. 等号(=):表示两个数或表达式相等,例如 2 + 3 = 5。
6. 不等号(≠):表示两个数或表达式不相等,例如2 + 3 ≠ 4。
7. 大于号(>):表示一个数大于另一个数,例如 5 > 3。
8. 小于号(<):表示一个数小于另一个数,例如 3 < 5。
9. 大于等于号(≥):表示一个数大于或等于另一个数,例如 5 ≥ 3。
10. 小于等于号(≤):表示一个数小于或等于另一个数,例如3 ≤ 5。
11. 分数线(/):用于表示分数,例如 1/2 表示一半。
12. 开方号(√):用于表示求一个数的平方根,例如√9 = 3。
13. 乘方号(^):用于表示求一个数的幂,例如 2^3 = 8。
14. 求和号(∑):用于表示求和,例如∑(i=1 to n) i 表示求从 1 到 n 的和。
15. 积分号(∫):用于表示求定积分,例如∫(f(x)dx) 表示求函数 f(x) 在某个区间上的定积分。
16. 对数号(log):用于表示求对数,例如 log10(100) = 2。
17. 三角函数符号(sin、cos、tan):用于表示求三角函数的值,例如sin(30°) = 0.5。
18. 倒数符号(1/x):用于表示求一个数的倒数,例如 1/2 =0.5。
19. 无穷大符号(∞):表示无穷大,例如lim(x→∞) f(x) 表示求函数 f(x) 当 x 趋向于无穷大时的极限。
(完整版)常用数学符号大全1. 矩阵符号([ ]):用于表示矩阵,例如 [1 2; 3 4] 表示一个 2x2 的矩阵。
数学符号大全1、几何符号ⅷⅶ↋ↆↄ△2、代数符号ⅴⅸⅹ~ⅼↅↇↈↃⅵↀ3、运算符号如加号(+),减号(-),乘号(³或²),除号(÷或/),两个集合的并集(ⅻ),交集(ⅺ),根号(ⅳ),对数(log,lg,ln),比(:),微分(dx),积分(ⅼ),曲线积分(ⅽ)等。
4、集合符号ⅻⅺ5、特殊符号ⅲπ(圆周率)6、推理符号|a| ↂ△ⅶⅺⅻↅↆ±ↈↇⅰⅬⅭⅮⅯ↖↗↘↙ⅷⅸⅹ&; §←↑→↓↔↕↖↗ΓΔΘΛΞΟΠΣΦΧΨΩαβγδεδεζηθικλμνπξζηυθχψωⅠ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻⅰ ⅱ ⅲ ⅳ ⅴ ⅵ ⅶ ⅷ ⅸ ⅹⅰⅱⅲ↚ⅳⅴⅵ↛ ⅶ↜ⅷⅸⅹⅺⅻⅼⅽⅾⅿↀↁↂↃↄ↝ↅↆↇↈ↞↟↉↊⊕↋↠℃指数0123:o1237、数量符号如:i,2+i,a,x,自然对数底e,圆周率π。
8、关系符号如“=”是等号,“Ↄ”是近似符号,“ↅ”是不等号,“>”是大于符号,“<”是小于符号,“ↈ”是大于或等于符号(也可写作“↉”),“ↇ”是小于或等于符号(也可写作“↊”),。
“Ⅾ ”表示变量变化的趋势,“ↂ”是相似符号,“ↄ”是全等号,“ⅷ”是平行符号,“”是垂直符号,“ⅴ”是成正比符号,(没有成反比符号,但可以用成正比符号配倒数当作成反比)“ⅰ”是属于符号,“??”是“包含”符号等。
9、结合符号如小括号“()”中括号“[]”,大括号“{}”横线“—”10、性质符号如正号“+”,负号“-”,绝对值符号“| |”正负号“±”11、省略符号如三角形(△),直角三角形(Rt△),正弦(sin),余弦(cos),x的函数(f(x)),极限(lim),角(ⅶ),ⅿ因为,ⅾ所以,总和(ⅲ),连乘(ⅱ),从n个元素中每次取出r个元素所有不同的组合数(C (r)(n) ),幂(A,Ac,Aq,x^n)等。
12、排列组合符号C-组合数A-排列数N-元素的总个数R-参与选择的元素个数!-阶乘,如5!=5³4³3³2³1=120C-Combination- 组合A-Arrangement-排列13、离散数学符号├ 断定符(公式在L中可证)╞ 满足符(公式在E上有效,公式在E上可满足)┐ 命题的“非”运算ⅸ 命题的“合取”(“与”)运算ⅹ 命题的“析取”(“或”,“可兼或”)运算Ⅾ 命题的“条件”运算A<=>B 命题A 与B 等价关系A=>B 命题 A与 B的蕴涵关系A* 公式A 的对偶公式wff 合式公式iff 当且仅当Ⅽ 命题的“与非” 运算(“与非门” )Ⅿ 命题的“或非”运算(“或非门” )□ 模态词“必然”◇ 模态词“可能”θ空集ⅰ 属于(??不属于)P(A)集合A的幂集|A| 集合A的点数R^2=R○R [R^n=R^(n-1)○R] 关系R的“复合”(或下面加ↅ)真包含ⅻ 集合的并运算ⅺ 集合的交运算- (~)集合的差运算〡限制[X](右下角R) 集合关于关系R的等价类A/ R 集合A上关于R的商集[a] 元素a 产生的循环群I (i大写) 环,理想Z/(n) 模n的同余类集合r(R) 关系 R的自反闭包s(R) 关系的对称闭包CP 命题演绎的定理(CP 规则)EG 存在推广规则(存在量词引入规则)ES 存在量词特指规则(存在量词消去规则)UG 全称推广规则(全称量词引入规则)US 全称特指规则(全称量词消去规则)R 关系r 相容关系R○S 关系与关系的复合domf 函数的定义域(前域)ranf 函数的值域f:XⅮY f是X到Y的函数GCD(x,y) x,y最大公约数LCM(x,y) x,y最小公倍数aH(Ha) H 关于a的左(右)陪集Ker(f) 同态映射f的核(或称 f同态核)[1,n] 1到n的整数集合d(u,v) 点u与点v间的距离d(v) 点v的度数G=(V,E) 点集为V,边集为E的图W(G) 图G的连通分支数k(G) 图G的点连通度△(G) 图G的最大点度A(G) 图G的邻接矩阵P(G) 图G的可达矩阵M(G) 图G的关联矩阵C 复数集N 自然数集(包含0在内)N* 正自然数集P 素数集Q 有理数集R 实数集Z 整数集Set 集范畴Top 拓扑空间范畴Ab 交换群范畴Grp 群范畴Mon 单元半群范畴Ring 有单位元的(结合)环范畴Rng 环范畴CRng 交换环范畴R-mod 环R的左模范畴mod-R 环R的右模范畴Field 域范畴Poset 偏序集范畴上述符号所表示的意义和读法(中英文参照)+加号;正号°度′分〃秒#…号@ at 单价- 减号;负号±正负号³乘号÷除号=等于号ↅ不等于号ↆ全等于号ↄ 约等于Ↄ约等于号<小于号>大于号ↇ小于或等于ↈ大于或等于%百分之…ⅵ无限大号ⅳ (square) root 平方根ⅿ因为ⅾ 所以ⅶ 角 半圆↋ 圆○圆周△ 三角形 垂直于ⅻ 并,合集ⅺ交,通集ⅼ…的积分ⅲ总和常用数学符号大全2010-10-31 19:44:301 几何符号ⅷⅶ↋≡ↄ△2 代数符号ⅴⅸⅹ~∫≠≤≥≈∞ↀ3运算符号×÷√±4集合符号ⅻ∩ⅰ5特殊符号∑π(圆周率)6推理符号|a| ↂ△ⅶ∩ⅻ≠≡±≥≤ⅰ←↑→↓↖↗↘↙ⅷⅸⅹ&; §←↑→↓↔↕↖↗ΓΔΘΛΞΟΠΣΦΧΨΩαβγδεδεζηθικλμνπξζηυθχψωⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹⅰ∏∑∕√ⅴ∞∟ ⅶ↜ⅷⅸⅹ∩ⅻ∫ⅽⅾⅿↀↁↂ≈ↄ↝≠≡≤≥↞↟↉↊⊕↋↠℃指数0123:o123上述符号所表示的意义和读法(中英文参照)+加号;减号;负号±正负号×乘号÷除号=等于号≠不等于号≡全等于号ↄ约等于≈约等于号<小于号>大于号≤小于或等于≥大于或等于%百分之…∞无限大号√平方根X X的平方X的立方∞ 无穷大PI 圆周率|x| 函数的绝对值ⅻ集合并∩ 集合交≥ 大于等于≤ 小于等于≡ 恒等于或同余ln(x) 自然对数lg(x) 以2为底的对数log(x) 常用对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数{x} 小数部分x - floor(x)∫f(x)δx 不定积分∫[a:b]f(x)δx a到b的定积分[P] P为真等于1否则等于0∑[1≤k≤n]f(k) 对n进行求和,可以拓广至很多情况如:∑[n is prime][n < 10]f(n)∑∑[1≤i≤j≤n]n^2lim f(x) (x->?) 求极限f(z) f关于z的m阶导函数C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除nmn m与n互质a ⅰA a属于集合A#A 集合A中的元素个数∑(n=p,q)f(n) 表示f(n)的n从p到q逐步变化对f(n)的连加和,如果f(n)是有结构式,f(n)应外引括号;∑(n=p,q ; r=s,t)f(n,r) 表示∑(r=s,t)[∑(n=p,q)f(n,r)],如果f(n,r)是有结构式,f(n,r)应外引括号;∏(n=p,q)f(n) 表示f(n)的n从p到q逐步变化对f(n)的连乘积, 如果f(n)是有结构式,f(n)应外引括号;∏(n=p,q ; r=s,t)f(n,r) 表示∏(r=s,t)[∏(n=p,q)f(n,r)],如果f(n,r)是有结构式,f(n,r)应外引括号;lim(x→u)f(x) 表示f(x) 的x 趋向u 时的极限,如果f(x)是有结构式,f(x)应外引括号;lim(y→v ; x→u)f(x,y) 表示lim(y→v)[lim(x→u)f(x,y)],如果f(x,y)是有结构式,f(x,y)应外引括号;∫(a,b)f(x)dx 表示对f(x) 从x=a 至x=b 的积分,如果f(x)是有结构式,f(x)应外引括号;∫(c,d ; a,b)f(x,y)dxdy 表示∫(c,d)[∫(a,b)f(x,y)dx]dy,如果f(x,y)是有结构式,f(x,y)应外引括号;∫(L)f(x,y)ds 表示f(x,y) 在曲线L 上的积分,如果f(x,y)是有结构式,f(x,y)应外引括号;∫∫(D)f(x,y,z)dζ 表示f(x,y,z) 在曲面D 上的积分,如果f(x,y,z)是有结构式,f(x,y,z)应外引括号;ⅽ(L)f(x,y)ds 表示f(x,y) 在闭曲线L 上的积分,如果f(x,y)是有结构式,f(x,y)应外引括号;ⅽⅽ(D)f(x,y,z)dζ 表示f(x,y,z) 在闭曲面 D 上的积分,如果f(x,y)是有结构式,f(x,y)应外引括号;ⅻ(n=p,q)A(n) 表示n从p到q之A(n)的并集,如果A(n)是有结构式,A(n)应外引括号;ⅻ(n=p,q ; r=s,t)A(n,r) 表示ⅻ(r=s,t)[ⅻ(n=p,q)A(n,r)],如果A(n,r)是有结构式,A(n,r)应外引括号;∩(n=p,q)A(n) 表示n从p到q逐步变化对A(n)的交集,如果A(n)是有结构式,A(n)应外引括号;∩(n=p,q ; r=s,t)A(n,r) 表示∩(r=s,t)[∩(n=p,q)A(n,r)],如果A(n,r)是有结构式,A(n,r)应外引括号。
数学中各种符号
1. 包含加法、减法、乘法和除法的四则运算符号如下: - 加法: +
- 减法: -
- 乘法: ×
- 除法: ÷
2. 常用的表示不等式的符号如下:
- 大于: >
- 小于: <
- 大于等于: ≥
- 小于等于: ≤
3. 数学中常见的数学关系符号如下:
- 等于: =
- 不等于: ≠
- 约等于: ≈
4. 表示数学集合的符号如下:
- 属于: ∈
- 不属于: ∉
- 子集: ⊆
- 真子集: ⊂
- 并集: ∪
- 交集: ∩
- 差集: \ (即集合减法)
5. 常见的几何符号如下:
- 角度: °
- 平行: ∥
- 垂直: ⊥
- 相似: ~
- 等边: ≌
- 直径: ⌀
6. 数学函数符号如下:
- 幂运算: ^
- 求和: Σ
- 积分: ∫
- 极限: lim
- 开方: √
- 绝对值: | |
7. 数字表示的符号:
- 底数: b (常用于对数)
- 自然对数: ln
- 对数: log
8. 常见的集合符号:
- 空集: ∅
- 整数集: ℤ
- 有理数集: ℚ
- 实数集: ℝ
- 自然数集: ℕ
这些符号都是数学中常用的,用于表示各种数学概念和运算。
常用数学输入符号:≈ ≡ ≠ =≤≥ <>≮≯∷ ±+-× ÷/∫ ∮∝∞ ∧∨∑ ∏ ∪∩ ∈∵∴//⊥‖ ∠⌒≌∽√()【】{}ⅠⅡ⊕⊙∥αβγδεζηθΔ
αβγδεζηθικλμνξοπρστυφχψω
ΑΒΓΔΕΖΗΘΙΚ∧ΜΝΞΟ∏Ρ∑ΤΥΦΧΨΩ
абвгдеёжзийклмнопрстуфхцчшщъыьэюя
АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
exp(x) 在自变量x处的指数函数值,常被写作e x
a^x a的x次方;有理数x由反函数定义
ln x exp x 的反函数
a x同a^x
log b a 以b为底a的对数;b log b a = a
cos x 在自变量x处余弦函数的值
tan x 其值等于sin x/cos x
cot x 余切函数的值或cos x/sin x
sec x 正割含数的值,其值等于1/cos x
csc x 余割函数的值,其值等于1/sin x
asin x y,正弦函数反函数在x处的值,即x = sin y
acos x y,余弦函数反函数在x处的值,即x = cos y
atan x y,正切函数反函数在x处的值,即x = tan y
acot x y,余切函数反函数在x处的值,即x = cot y
asec x y,正割函数反函数在x处的值,即x = sec y
acsc x y,余割函数反函数在x处的值,即x = csc y
θ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时
i, j, k 分别表示x、y、z方向上的单位向量
(a, b, c) 以a、b、c为元素的向量
(a, b) 以a、b为元素的向量
(a, b) a、b向量的点积
a•b a、b向量的点积
(a•b)a、b向量的点积
|v| 向量v的模
|x| 数x的绝对值
Σ表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在其上部。
如j从1到
100 的和可以表示成:。
这表示1 + 2 + … + n
M 表示一个矩阵或数列或其它
|v> 列向量,即元素被写成列或可被看成k×1阶矩阵的向量
<v| 被写成行或可被看成从1×k阶矩阵的向量
dx 变量x的一个无穷小变化,dy, dz, dr等类似
ds 长度的微小变化
ρ变量(x2 + y2 + z2)1/2或球面坐标系中到原点的距离
r 变量(x2 + y2)1/2或三维空间或极坐标中到z轴的距离
|M| 矩阵M的行列式,其值是矩阵的行和列决定的平行区域的面积或体积
||M|| 矩阵M的行列式的值,为一个面积、体积或超体积
det M M的行列式
M-1矩阵M的逆矩阵
v×w 向量v和w的向量积或叉积
θvw向量v和w之间的夹角
A•B×C标量三重积,以A、B、C为列的矩阵的行列式
u w在向量w方向上的单位向量,即w/|w|
df 函数f的微小变化,足够小以至适合于所有相关函数的线性近似
df/dx f关于x的导数,同时也是f的线性近似斜率
f ' 函数f关于相应自变量的导数,自变量通常为x
∂f/∂x y、z固定时f关于x的偏导数。
通常f关于某变量q的偏导数为当其它几个变量固定时df 与dq的比值。
任何可能导致变量混淆的地方都应明确地表述
(∂f/∂x)|r,z保持r和z不变时,f关于x的偏导数
grad f 元素分别为f关于x、y、z偏导数[(∂f/∂x), (∂f/∂y), (∂f/∂z)] 或(∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k;
的向量场,称为f的梯度
∇向量算子(∂/∂x)i + (∂/∂x)j + (∂/∂x)k, 读作"del"
∇f f的梯度;它和u w的点积为f在w方向上的方向导数
∇•w向量场w的散度,为向量算子∇同向量w的点积, 或(∂w x/∂x) + (∂w y/∂y) + (∂w z/∂z) curl w 向量算子∇同向量w 的叉积
∇×w w的旋度,其元素为[(∂f z/∂y) - (∂f y/∂z), (∂f x/∂z) - (∂f z/∂x), (∂f y/∂x) - (∂f x/∂y)]
∇•∇拉普拉斯微分算子:(∂2/∂x2) + (∂/∂y2) + (∂/∂z2)
f "(x) f关于x的二阶导数,f '(x)的导数
d2f/dx2f关于x的二阶导数
f(2)(x) 同样也是f关于x的二阶导数
f(k)(x) f关于x的第k阶导数,f(k-1) (x)的导数
T 曲线切线方向上的单位向量,如果曲线可以描述成r(t), 则T = (dr/dt)/|dr/dt|
ds 沿曲线方向距离的导数
κ曲线的曲率,单位切线向量相对曲线距离的导数的值:|dT/ds|
N dT/ds投影方向单位向量,垂直于T
B 平面T和N的单位法向量,即曲率的平面
τ曲线的扭率:|dB/ds|
g 重力常数
F 力学中力的标准符号
k 弹簧的弹簧常数
p i第i个物体的动量
H 物理系统的哈密尔敦函数,即位置和动量表示的能量
{Q, H} Q, H的泊松括号
以一个关于x的函数的形式表达的f(x)的积分
函数f 从a到b的定积分。
当f是正的且 a < b 时表示由x轴和直线y = a, y = b 及在这
些直线之间的函数曲线所围起来图形的面积
L(d) 相等子区间大小为d,每个子区间左端点的值为f的黎曼和
R(d) 相等子区间大小为d,每个子区间右端点的值为f的黎曼和
M(d) 相等子区间大小为d,每个子区间上的最大值为f的黎曼和
m(d) 相等子区间大小为d,每个子区间上的最小值为f的黎曼和
公式输入符号
≈≡≠=≤≥<>≮≯∷±+-×÷/∫∮∝∞∧∨∑∏∪∩∈∵∴//⊥‖∠⌒⊙≌∽√
引理→Lemma
是辅助定理(auxiliary theorem),是为了叙述主要的定理而事先叙述的基本概念(concept)、基本原理(principle)、基本规则(rule)、基本特性(property).
推理→Deduce,Deduction
是证明的过程(proving),逻辑推理的过程(logic reasoning),也就是前提推演(derive,deduce)出一个定理(theorem)的过程(process,procedure).
公理(Axiom)是不需要证明的立论、陈述(statement),例如:过一点可画无数条直线;过两点只可画一条直线。
定理(theorem)是理论(theory)的核心,在科学上,定律(Law)是不可以证明的,是无法证明的。
从定律出发,得出一系列的定理,通常我们又将定理称为公式(formula),它们是物理量跟物理量(physical quantity)之间的关系,是一种恒等式关系(identity),不同于普通的方程(equation),普通的方程是有条件的成立(conditional equation),如x+2=5,只有x=3才能满足。
如电磁学上的高斯定理指的是电荷分布与电场强度分布的关系。
数学上的Law指的是运算规则,如分配律、结合律、交换律、传递律等等,theorem指的也是量与量(variable)之间的关系,如勾股定理、相交弦定理等等。
微积分中高斯定理,是将电磁场中的高斯定理进一步理论化,变成面积分与体积分之间的关系。
由定理、运算规则,加以拓展,形成理论。