2020九年级数学上册二次函数应用题讲义(新版)新人教版

第二十二章二次函数22．1 二次函数的图象和性质22．1.1 二次函数1．设一个正方形的边长为x，则该正方形的面积y＝_______，其中变量是____，____是____的函数．2．一般地，形如y＝ax2＋bx＋c(_________________)的函数，叫做二次函数，其中x是自变量，a，b，c分别为二次项系数、一次项系数、常数项．知识点1：二次函数的定义1．下列函数是二次函数的是( )A．y＝2x＋1B．y＝－2x＋1 C．y＝x2＋2 D．y＝0.5x－22．下列说法中，正确的是()A．二次函数中，自变量的取值范围是非零实数B．在圆的面积公式S＝πr2中，S是r的二次函数C．y＝12(x－1)(x＋4)不是二次函数D．在y＝1－2x2中，一次项系数为13．若y＝(a＋3)x2－3x＋2是二次函数，则a的取值范围是_________．4．已知二次函数y＝1－3x＋2x2，则二次项系数a＝_____，一次项系数b＝_____，常数项c＝_______．5．已知两个变量x，y之间的关系式为y＝(a－2)x2＋(b＋2)x－3.(1)当_________时，x，y之间是二次函数关系；(2)当_______________时，x，y之间是一次函数关系．6．已知两个变量x，y之间的关系为y＝(m－2)x m2－2＋x－1，若x，y之间是二次函数关系，求m的值．知识点2：实际问题中的二次函数的解析式7．某商店从厂家以每件21元的价格购进一批商品，该商品可以自行定价．若每件商品售价为x元，则可卖出(350－10x)件商品，那么商品所赚钱数y元与售价x元的函数关系式为( )A．y＝－10x2－560x＋7350 B．y＝－10x2＋560x－7350C．y＝－10x2＋350x＋7350 D．y＝－10x2＋350x－73508．某车的刹车距离y(m)与开始刹车时的速度x(m/s)之间满足二次函数y＝120x2(x＞0)，若该车某次的刹车距离为5 m，则开始刹车时的速度为()A．40 m/s B．20 m/s C．10 m/s D．5 m/s9．某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y＝_________．10．多边形的对角线条数d与边数n之间的关系式为____________，自变量n的取值范围是_______________；当d＝35时，多边形的边数n＝__________．11．如图，有一个长为24米的篱笆，一面利用墙(墙的最大长度a为10米)围成的中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S平方米．(1)求S与x的函数关系式；(2)如果要围成面积为45平方米的花圃，AB的长为多少米？12．已知二次函数y＝x2－2x－2，当x＝2时，y＝________；当x＝_______时，函数值为1.13．边长为4 m的正方形中间挖去一个边长为x(m)(x＜4)的小正方形，剩余的四方框的面积为y(m2)，则y与x之间的函数关系式为________________，它是_________函数．14．设y＝y1－y2，y1与x成正比例，y2与x2成正比例，则y与x的函数关系是( ) A．正比例函数B．一次函数C．二次函数D．以上都不正确15．某种正方形合金板材的成本y(元)与它的面积成正比，设边长为x厘米，当x＝3时，y＝18，那么当成本为72元时，边长为( )A．6厘米B．12厘米C．24厘米D．36厘米16．某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形，抽屉底面周长为180 cm，高为20 cm.设底面的宽为x，抽屉的体积为y时，求y与x之间的函数关系式．(材质及其厚度等暂忽略不计)17．某商店经营一种小商品，进价为2.5元，据市场调查，销售单价是13.5元时，平均每天销售量是500件，而销售单价每降低1元，平均每天就可以多售出100件．假定每件商品降价x元，商店每天销售这种小商品的利润是y元，请写出y与x之间的函数关系式，并注明x的取值范围．18．一块矩形的草坪，长为8 m，宽为6 m，若将长和宽都增加x m，设增加的面积为y m2.(1)求y与x的函数关系式；(2)若使草坪的面积增加32 m2，求长和宽都增加多少米？22．1.2 二次函数y ＝ax 2的图象和性质1．由解析式画函数图象的步骤是________、________、_________． 2．一次函数y ＝kx ＋b(k ≠0)的图象是__________． 3．二次函数y ＝ax 2(a ≠0)的图象是一条_______，其对称轴为_____轴，顶点坐标为_______． 4．抛物线y ＝ax 2与y ＝－ax 2关于_____轴对称．抛物线y ＝ax 2，当a ＞0时，开口向____，顶点是它的最______点；当a ＜0时，开口向_______，顶点是它的最______点，随着|a|的增大，开口越来越______．知识点1：二次函数y ＝ax 2的图象及表达式的确定1．已知二次函数y ＝x 2，则其图象经过下列点中的( )A ．(－2，4)B ．(－2，－4)C ．(2，－4)D ．(4，2) 2．2_______________(2)将表格中的空格补全．3．已知二次函数y ＝ax 2的图象经过点A(－1，－13)．(1)求这个二次函数的解析式并画出其图象； (2)请说出这个二次函数的顶点坐标、对称轴．知识点2：二次函数y ＝ax 2的图象和性质4．对于函数y ＝4x 2，下列说法正确的是( )A ．当x ＞0时，y 随x 的增大而减小B ．当x ＜0时，y 随x 的增大而减小C ．y 随x 的增大而减小D ．y 随x 的增大而增大5．已知点(－1，y 1)，(2，y 2)，(－3，y 3)都在函数y ＝x 2的图象上，则( )A ．y 1＜y 2＜y 3B ．y 1＜y 3＜y 2C ．y 3＜y 2＜y 1D ．y 2＜y 1＜y 36．已知二次函数y ＝(m －2)x 2的图象开口向下，则m 的取值范围是_________．7．二次函数y＝－12x2的图象是一条开口向_______的抛物线，对称轴是________，顶点坐标是_________；当x______时，y随x的增大而减小；当x＝0时，函数y有_______(填“最大”或“最小”)值是_______．8．如图是一个二次函数的图象，则它的解析式为_________，当x＝_____时，函数图象的最低点为__________．9．已知二次函数y＝mxm2－2.(1)求m的值；(2)当m为何值时，二次函数有最小值？求出这个最小值，并指出x取何值时，y随x的增大而减小；(3)当m为何值时，二次函数的图象有最高点？求出这个最高点，并指出x取何值时，y随x的增大而增大．10．二次函数y ＝15x 2和y ＝5x 2，以下说法：①它们的图象都是开口向上；②它们的对称轴都是y 轴，顶点坐标都是原点(0，0)；③当x ＞0时，它们的函数值y 都是随着x 的增大而增大；④它们开口的大小是一样的．其中正确的说法有( ) A ．1个 B ．2个 C ．3个 D ．4个11．已知a ≠0，同一坐标系中，函数y ＝ax 与y ＝ax 2的图象有可能是( )12．如图是下列二次函数的图象：①y ＝ax 2；②y ＝bx 2；③y ＝cx 2；④y ＝dx 2.比较a ，b ，c ，d 的大小，用“＞”连接为_______________．（第12题图) （第14题图)13．当a ＝________时，抛物线y ＝ax 2与抛物线y ＝－4x 2关于x 轴对称；抛物线y ＝－7x 2关于x 轴对称所得抛物线的解析式为___________；当a ＝_______时，抛物线y ＝ax 2与抛物线y ＝－2x 2的形状相同． 14．已知二次函数y ＝2x 2的图象如图所示，将x 轴沿y 轴向上平移2个单位长度后与抛物线交于A ，B 两点，则△AOB 的面积为________． 15．已知正方形的周长为C(cm )，面积为S(cm 2)．(1)求S 与C 之间的函数关系式； (2)画出所示函数的图象；(3)根据函数图象，求出S ＝1 cm 2时正方形的周长； (4)根据列表或图象的性质，求出C 取何值时S ≥4 cm 2?16．二次函数y＝ax2与直线y＝2x－1的图象交于点P(1，m)．(1)求a，m的值；(2)写出二次函数的表达式，并指出x取何值时，y随x的增大而增大；(3)指出抛物线的顶点坐标和对称轴．17．如图，抛物线y＝x2与直线y＝2x在第一象限内有一个交点A.(1)你能求出A点坐标吗？(2)在x轴上是否存在一点P，使△AOP为等腰三角形？若存在，请你求出点P的坐标；若不存在，请说明理由．22．1.3 二次函数y ＝a(x －h)2＋k 的图象和性质22.1.3.1 二次函数y ＝ax 2＋k 的图象和性质1．二次函数y ＝ax 2＋k 的图象是一条_________．它与抛物线y ＝ax 2的________相同，只是________不同，它的对称轴为________轴，顶点坐标为________．2．二次函数y ＝ax 2＋k 的图象可由抛物线y ＝ax 2__ ___得到，当k ＞0时，抛物线y ＝ax 2向上平移_______个单位得y ＝ax 2＋k ；当k ＜0时，抛物线y ＝ax 2向________平移|k|个单位得y ＝ax 2＋k.知识点1：二次函数y ＝ax 2＋k 的图象和性质 1．抛物线y ＝2x 2＋2的对称轴是___，顶点坐标是_____，它与抛物线y ＝2x 2的形状_____．2．抛物线y ＝－3x 2－2的开口向______，对称轴是_______，顶点坐标是_________．3．若点(x 1，y 1)和(x 2，y 2)在二次函数y ＝－12x 2＋1的图象上，且x 1＜x 2＜0，则y 1与y 2的大小关系为_________．4．对于二次函数y ＝x 2＋1，当x ＝______时，y 最______＝____；当x______时，y 随x 的增大而减小；当x______时，y 随x 的增大而增大． 5．已知二次函数y ＝－x 2＋4.(1)当x 为何值时，y 随x 的增大而减小？ (2)当x 为何值时，y 随x 的增大而增大？(3)当x 为何值时，y 有最大值？最大值是多少？ (4)求图象与x 轴、y 轴的交点坐标．知识点2：二次函数y ＝ax 2＋k 与y ＝ax 2之间的平移6．将二次函数y ＝x 2的图象向上平移1个单位，则平移后的抛物线的解析式是_______． 7．抛物线y ＝ax 2＋c 向下平移2个单位得到抛物线y ＝－3x 2＋2，则a ＝_____，c ＝_____．8．在同一个直角坐标系中作出y ＝12x 2，y ＝12x 2－1的图象． (1)分别指出它们的开口方向、对称轴以及顶点坐标；(2)抛物线y ＝12x 2－1与抛物线y ＝12x 2有什么关系？知识点3：抛物线y ＝ax 2＋k 的应用9．如图，小敏在某次投篮中，球的运动路线是抛物线y ＝－15x 2＋3.5的一部分．若命中篮圈中心，则她与篮底的距离l 是( B )A ．3.5 mB ．4 mC ．4.5 mD ．4.6 m10．如果抛物线y ＝x 2＋2向下平移1个单位，那么所得新抛物线的解析式是( )A ．y ＝(x －1)2＋2B ．y ＝(x ＋1)2＋2C ．y ＝x 2＋1D ．y ＝x 2＋311．已知y ＝ax 2＋k 的图象上有三点A(－3，y 1)，B(1，y 2)，C(2，y 3)，且y 2＜y 3＜y 1，则a 的取值范围是( )A ．a ＞0B ．a ＜0C ．a ≥0D ．a ≤012．已知抛物线y ＝－x 2＋2与x 轴交于A ，B 两点，与y 轴交于C 点，则△ABC 的面积为_______． 13．若抛物线y ＝ax 2＋c 与抛物线y ＝－4x 2＋3关于x 轴对称，则a ＝_____，c ＝_______．14．如图，在平面直角坐标系中，抛物线y ＝ax 2＋3与y 轴交于A ，过点A 作与x 轴平行的直线交抛物线y ＝13x 2于点B ，C ，则BC 的长度为_______．15．直接写出符合下列条件的抛物线y ＝ax 2－1的函数关系式：(1)经过点(－3，2)；(2)与y ＝12x 2的开口大小相同，方向相反；(3)当x 的值由0增加到2时，函数值减少4.16．把y ＝－12x 2的图象向上平移2个单位．(1)求新图象的解析式、顶点坐标和对称轴； (2)画出平移后的函数图象；(3)求平移后的函数的最大值或最小值，并求对应的x 的值．17．已知抛物线的对称轴是y 轴，顶点坐标是(0，2)，且经过(1，3)，求此抛物线的解析式．18．若二次函数y＝ax2＋c，当x取x1，x2(x1≠x2)时，函数值相等，则当x取x1＋x2时，函数值为( )A．a＋c B．a－c C．－c D．c19．廊桥是我国古老的文化遗产，如图所示是一座抛物线形廊桥的示意图．已知抛物线对应的函数关系式为y＝－140x2＋10，为保护廊桥的安全，在该抛物线上距水面AB高为8米的点E，F处要安装两盏警示灯，求这两盏灯的水平距离．(5≈2.24，结果精确到1米)22.1.3.2 二次函数y ＝a(x －h)2的图象和性质1．二次函数y ＝a(x －h)2的图象是______，它与抛物线y ＝ax 2的_____相同，只是____不同；它的对称轴为直线_______，顶点坐标为________．2．二次函数y ＝a(x －h)2的图象可由抛物线y ＝ax 2________得到，当h ＞0时，抛物线y＝ax 向______平移h 个单位得y ＝a(x －h)2; 当h ＜0时，抛物线y ＝ax 2向_________平移|h|个单位得y ＝a(x －h)2.知识点1：二次函数y ＝a(x －h)2的图象 1．将抛物线y ＝－x 2向左平移2个单位后，得到的抛物线的解析式是( )A ．y ＝－(x ＋2)2B ．y ＝－x 2＋2C ．y ＝－(x －2)2D ．y ＝－x 2－22．抛物线y ＝－3(x ＋1)2不经过的象限是( )A ．第一、二象限B ．第二、四象限C ．第三、四象限D ．第二、三象限3．已知二次函数y ＝a(x －h)2的图象是由抛物线y ＝－2x 2向左平移3个单位长度得到的，则a ＝_________，h ＝________.4．在同一平面直角坐标系中，画出函数y ＝x 2，y ＝(x ＋2)2，y ＝(x －2)2的图象，并写出对称轴及顶点坐标．知识点2：二次函数y ＝a(x －h)2的性质5．二次函数y ＝15(x －1)2的最小值是( )A ．－1B ．1C ．0D ．没有最小值6．如果二次函数y ＝a(x ＋3)2有最大值，那么a___0，当x ＝___时，函数的最大值是___．7．对于抛物线y ＝－13(x －5)2，开口方向____，顶点坐标为______，对称轴为________．8．二次函数y ＝－5(x ＋m)2中，当x ＜－5时，y 随x 的增大而增大，当x ＞－5时，y 随x 的增大而减小，则m ＝_______，此时，二次函数的图象的顶点坐标为________，当x ＝____时，y 取最_____值，为_____．9．已知A(－4，y 1)，B(－3，y 2)，C(3，y 3)三点都在二次函数y ＝－2(x ＋2)2的图象上，则y 1，y 2，y 3的大小关系为_____________．10．已知抛物线y ＝a(x －h)2，当x ＝2时，有最大值，此抛物线过点(1，－3)，求抛物线的解析式，并指出当x 为何值时，y 随x 的增大而减小．11．顶点为(－6，0)，开口向下，形状与函数y ＝12x 2的图象相同的抛物线的解析式是( ) A ．y ＝12(x －6)2 B ．y ＝12(x ＋6)2 C ．y ＝－12(x －6)2 D ．y ＝－12(x ＋6)212．平行于x 轴的直线与y ＝a(x －2)2的一个交点坐标为(－1，2)，则另一个交点坐标为( )A ．(1，2)B ．(1，－2)C ．(5，2)D ．(－1，4)13．在同一直角坐标系中，一次函数y ＝ax ＋c 和二次函数y ＝a(x ＋c)2的图象大致为( )14．已知二次函数y ＝3(x －a)2的图象上，当x ＞2时，y 随x 的增大而增大，则a 的取值范围是_________．15．已知一条抛物线与抛物线y ＝－12x 2＋3形状相同，开口方向相反，顶点坐标是(－5，0)，则该抛物线的解析式是____________．16．已知抛物线y ＝a(x －h)2的对称轴为x ＝－2，且过点(1，－3)．(1)求抛物线的解析式；(2)画出函数的图象；(3)从图象上观察，当x 取何值时，y 随x 的增大而增大？当x 取何值时，函数有最大值(或最小值)?17．已知一条抛物线的开口方向和形状大小与抛物线y ＝－8x 2都相同，并且它的顶点在抛物线y ＝2(x ＋32)2的顶点上．(1)求这条抛物线的解析式；(2)求将(1)中的抛物线向左平移5个单位后得到的抛物线的解析式；(3)将(2)中所求抛物线关于x 轴对称，求所得抛物线的解析式．18．如图，在Rt △OAB 中，∠OAB ＝90°，O 为坐标原点，边OA 在x 轴上，OA ＝AB＝1个单位长度，把Rt △OAB 沿x 轴正方向平移1个单位长度后得△AA 1B 1.(1)求以A 为顶点，且经过点B 1的抛物线的解析式；(2)若(1)中的抛物线与OB 交于点C ，与y 轴交于点D ，求点D ，C 的坐标．22.1.3.3 二次函数y ＝a(x －h)2＋k 的图象和性质1．抛物线y ＝a(x －h)2＋k 与y ＝ax 2形状_____，位置_____，把抛物线y ＝ax 2向上(下)和向左(右)平移，可以得到抛物线y ＝a(x －h)2＋k ，平移的方向、距离要根据________，_________的值来决定．2．抛物线y ＝a(x －h)2＋k 有如下特点：①当a ＞0时，开口向________；当a ＜0时，开口向________；②对称轴是直线_______；③顶点坐标是_________．知识点1：二次函数y ＝a(x －h)2＋k 的图象1．抛物线y ＝(x －1)2－3的对称轴是( )A ．y 轴B ．直线x ＝－1C ．直线x ＝1D ．直线x ＝－32．抛物线y ＝(x ＋2)2＋1的顶点坐标是( )A ．(－2，1)B ．(－2，－1)C ．(2，1)D ．(2，－1)3．把抛物线y ＝－2x 2先向右平移1个单位长度，再向上平移2个单位长度后，所得函数的表达式为( )A ．y ＝－2(x ＋1)2＋2B ．y ＝－2(x ＋1)2－2C ．y ＝－2(x －1)2＋2D ．y ＝－2(x －1)2－24．写出下列抛物线的开口方向、对称轴及顶点坐标：(1)y ＝3(x －1)2＋2 (2)y ＝－13(x ＋1)2－5.知识点2：二次函数y ＝a(x －h)2＋k 的性质5．在函数y ＝(x ＋1)2＋3中，y 随x 的增大而减小，则x 的取值范围为( )A ．x ＞－1B ．x ＞3C ．x ＜－1D ．x ＜36．如图，在平面直角坐标系中，抛物线的解析式为y ＝－2(x －h)2＋k ，则下列结论正确的是( )A ．h ＞0，k ＞0B ．h ＜0，k ＞0C ．h ＜0，k ＜0D ．h ＞0，k ＜0（第6题图) （第9题图)7．一小球被抛出后，距离地面的高度h(米)和飞行时间t(秒)满足函数关系式h ＝－5(t －1)2＋6，则小球距离地面的最大高度是( )A ．1米B ．5米C ．6米D ．7米8．用长度一定的绳子围成一个矩形，如果矩形的一边长x(m )与面积y(m 2)满足函数关系式y ＝－(x －12)2＋144(0＜x ＜24)，则该矩形面积的最大值为__ ___．9．如图是二次函数y ＝a(x ＋1)2＋2图象的一部分，该图象在y 轴右侧与x 轴交点的坐标是__ ___．10．已知抛物线y ＝a(x －3)2＋2经过点(1，－2)．(1)求a 的值；(2)若点A(m ，y 1)，B(n ，y 2)(m ＜n ＜3)都在该抛物线上，试比较y 1与y 2的大小．11．将抛物线y ＝－2x 2＋1向右平移1个单位，再向上平移2个单位后所得到的抛物线为( )A ．y ＝－2(x ＋1)2－1B ．y ＝－2(x ＋1)2＋3C ．y ＝－2(x －1)2＋1D ．y ＝－2(x －1)2＋312．已知二次函数y ＝3(x －2)2＋1.下列说法：①其图象的开口向下；②其图象的对称轴为直线x ＝－2；③其图象顶点坐标为(2，－1)；④当x ＜2时，y 随x 的增大而减小．则其中说法正确的有( )A ．1个B ．2个C ．3个D ．4个13．二次函数y ＝a(x ＋m)2＋n 的图象如图，则一次函数y ＝mx ＋n 的图象经过( )A ．第一、二、三象限B ．第一、二、四象限C ．第二、三、四象限D ．第一、三、四象限14．设A(－2，y 1)，B(1，y 2)，C(2，y 3)是抛物线y ＝－(x ＋1)2＋a 上三点，则y 1，y 2，y 3的大小关系为( )A ．y 1＞y 2＞y 3B ．y 1＞y 3＞y 2C ．y 3＞y 2＞y 1D ．y 3＞y 1＞y 215．二次函数y ＝a(x ＋k)2＋k ，无论k 为何实数，其图象的顶点都在( )A ．直线y ＝x 上B ．直线y ＝－x 上C ．x 轴上D ．y 轴上16．把二次函数y ＝a(x －h)2＋k 的图象先向左平移2个单位，再向上平移4个单位，得到二次函数y ＝12(x ＋1)2－1的图象． (1)试确定a ，h ，k 的值；(2)指出二次函数y ＝a(x －h)2＋k 的开口方向、对称轴和顶点坐标．17．某广场中心标志性建筑处有高低不同的各种喷泉，其中一支高度为1米的喷水管喷出的抛物线水柱最大高度为3米，此时距喷水管的水平距离为12米，求在如图所示的平面直角坐标系中抛物线水柱的解析式．(不要求写出自变量的取值范围)18．已知抛物线y ＝－(x －m)2＋1与x 轴的交点为A ，B(B 在A 的右边)，与y 轴的交点为C.(1)写出m ＝1时与抛物线有关的三个正确结论；(2)当点B 在原点的右边，点C 在原点的下方时，是否存在△BOC 为等腰三角形的情形？若存在，求出m 的值；若不存在，请说明理由．22．1.4 二次函数y＝ax2＋bx＋c的图象和性质22.1.4.1 二次函数y＝ax2＋bx＋c的图象和性质1．二次函数y＝ax2＋bx＋c(a≠0)通过配方可化为y＝a(x＋b2a)2＋4ac－b24a的形式，它的对称轴是_______，顶点坐标是_______．如果a＞0，当x＜－b2a时，y随x的增大而_______，当x＞－b2a时，y随x的增大而_______；如果a＜0，当x＜－b2a时，y随x的增大而______，当x＞－b2a时，y随x的增大而_______．2．二次函数y＝ax2＋bx＋c(a≠0)的图象与y＝ax2的图象_________，只是______不同；y ＝ax2＋bx＋c(a≠0)的图象可以看成是y＝ax2的图象平移得到的，对于抛物线的平移，要先化成顶点式，再利用“_____________________”的规则来平移．知识点1：二次函数y＝ax2＋bx＋c(a≠0)的图象和性质1．已知抛物线y＝ax2＋bx＋c的开口向下，顶点坐标为(2，－3)，那么该二次函数有( ) A．最小值－3B．最大值－3 C．最小值2 D．最大值22．将二次函数y＝x2－2x＋3化为y＝(x－h)2＋k的形式，结果为( )A．y＝(x＋1)2＋4 B．y＝(x＋1)2＋2 C．y＝(x－1)2＋4 D．y＝(x－1)2＋2 3．若抛物线y＝x2－2x＋c与y轴的交点为(0，－3)，则下列说法不正确的是( ) A．抛物线开口向上B．抛物线的对称轴是x＝1C．当x＝1时，y的最大值为－4 D．抛物线与x轴的交点为(－1，0)，(3，0) 4．抛物线y＝x2＋4x＋5的顶点坐标是_______．5．已知二次函数y＝－2x2－8x－6，当______时，y随x的增大而增大；当x＝______时，y有最_______值是_____．知识点2：二次函数y＝ax2＋bx＋c(a≠0)的图象的变换6．抛物线y＝－x2＋2x－2经过平移得到y＝－x2，平移方法是( )A．向右平移1个单位，再向下平移1个单位B．向右平移1个单位，再向上平移1个单位C．向左平移1个单位，再向下平移1个单位D．向左平移1个单位，再向上平移1个单位7．把抛物线y＝x2＋bx＋c的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式为y＝x2－3x＋5，则( )A．b＝3，c＝7 B．b＝6，c＝3 C．b＝－9，c＝－5 D．b＝－9，c＝21 8．如图，抛物线y＝ax2－5ax＋4a与x轴相交于点A，B，且过点C(5，4)．(1)求a的值和该抛物线顶点P的坐标；(2)请你设计一种平移的方法，使平移后抛物线的顶点落在第二象限，并写出平移后抛物线的解析式．9．已知抛物线y ＝ax 2＋bx ＋c(a ≠0)与x 轴交于A ，B 两点．若点A 的坐标为(－2，0)，抛物线的对称轴为直线x ＝2，则线段AB 的长为______．10．二次函数y ＝2x 2＋mx ＋8的图象如图所示，则m 的值是( )A ．－8B ．8C ．±8D ．6（第10题图) （第12题图)11．已知二次函数y ＝－12x 2－7x ＋152.若自变量x 分别取x 1，x 2，x 3，且0＜x 1＜x 2＜x 3，则对应的函数值y 1，y 2，y 3的大小关系正确的是( )A ．y 1＞y 2＞y 3B ．y 1＜y 2＜y 3C ．y 2＞y 3＞y 1D ．y 2＜y 3＜y 112．已知二次函数y ＝ax 2＋bx ＋c(a ＜0)的图象如图，当－5≤x ≤0时，下列说法正确的是( )A ．有最小值－5，最大值0B ．有最小值－3，最大值6C ．有最小值0，最大值6D ．有最小值2，最大值613．如图，抛物线y ＝ax 2＋bx 和直线y ＝ax ＋b 在同一坐标系内的图象正确的是( )14．已知二次函数y ＝x 2－2kx ＋k 2＋k －2.(1)当实数k 为何值时，图象经过原点？(2)当实数k 在何范围取值时，函数图象的顶点在第四象限内？15．当k 分别取－1，1，2时，函数y ＝(k －1)x 2－4x ＋5－k 都有最大值吗？请写出你的判断，并说明理由；若有，请求出最大值．16．已知二次函数y ＝x 2－2mx ＋m 2－1.(1)当二次函数的图象经过坐标原点O(0，0)时，求二次函数的解析式；(2)如图，当m ＝2时，该抛物线与y 轴交于点C ，顶点为D ，求C ，D 两点的坐标；(3)在(2)的条件下，x 轴上是否存在一点P ，使得PC ＋PD 最短？若P 点存在，求出P 点坐标；若P 点不存在，请说明理由．22.1.4.2 用待定系数法求二次函数的解析式用待定系数法求二次函数的解析式的几种常见的形式：(1)三点式：已知图象上的三个点的坐标，可设二次函数的解析式为______________．(2)顶点式：已知抛物线的顶点坐标(h ，k)及图象上的一个点的坐标，可设二次函数的解析式为__________________．以下有三种特殊情况：①当已知抛物线的顶点在原点时，我们可设抛物线的解析式为____________；②当已知抛物线的顶点在y 轴上或以y 轴为对称轴，但顶点不一定是原点时，可设抛物线的解析式为_________________；③当已知抛物线的顶点在x 轴上，可设抛物线的解析式为_____________，其中(h ，0)为抛物线与x 轴的交点坐标．(3)交点式：已知抛物线与x 轴的两个交点坐标(x 1，0)，(x 2，0)及图象上任意一点的坐标，可设抛物线的解析式为_____________________．知识点1：利用“三点式”求二次函数的解析式1．由表格中信息可知，2( )A .y ＝x 2－C ．y ＝x 2－3x ＋3 D ．y ＝x 2－4x ＋82．已知二次函数y ＝ax 2＋bx ＋c 的图象经过点(－1，0)，(0，－2)，(1，－2)，则这个二次函数的解析式为_________________．3．已知二次函数y ＝ax 2＋bx ＋c ，当x ＝0时，y ＝1；当x ＝－1时，y ＝6；当x ＝1时，y＝0.求这个二次函数的解析式．知识点2：利用“顶点式”求二次函数的解析式4．已知某二次函数的图象如图所示，则这个二次函数的解析式为( )A ．y ＝2(x ＋1)2＋8 B ．y ＝18(x ＋1)2－8C ．y ＝29(x －1)2＋8D ．y ＝2(x －1)2－85．已知抛物线的顶点坐标为(4，－1)，与y 轴交于点(0，3)，求这条抛物线的解析式．知识点3：利用“交点式”求二次函数的解析式6．如图，抛物线的函数表达式是( )A ．y ＝12x 2－x ＋4B ．y ＝－12x 2－x ＋4 C ．y ＝12x 2＋x ＋4 D ．y ＝－12x 2＋x ＋47．已知一个二次函数的图象与x 轴的两个交点的坐标分别为(－1，0)和(2，0)，与y 轴的交点坐标为(0，－2)，求这个二次函数的解析式．8．抛物线的图象如图所示，根据图象可知，抛物线的解析式可能是( )A ．y ＝x 2－x －2B ．y ＝－12x 2－12x ＋2C ．y ＝－12x 2－12x ＋1D ．y ＝－x 2＋x ＋29．二次函数y ＝－x 2＋bx ＋c 的图象的最高点是(－1，－3)，则b ，c 的值分别是( )A ．b ＝2，c ＝4B ．b ＝2，c ＝－4C ．b ＝－2，c ＝4D ．b ＝－2，c ＝－410．抛物线y ＝2从上表可知)① 抛物线与x 轴的一个交点为(3，0)；② 函数y ＝ax 2＋bx ＋c 的最大值为6；③ 抛物线的对称轴是x ＝0.5；④在对称轴左侧，y 随x 增大而增大．11．已知抛物线y ＝ax 2＋bx ＋c(a ≠0)的对称轴为x ＝1，且抛物线经过A(－1，0)，B(0，－3)两点，则这条抛物线的解析式为_________________．12．将二次函数y ＝(x －1)2＋2的图象沿x 轴对折后得到的图象的解析式为_______________．13．设抛物线y ＝ax 2＋bx ＋c(a ≠0)过A(0，2)，B(4，3)，C 三点，其中点C 在直线x ＝2上，且点C 到抛物线对称轴的距离等于1，则抛物线的函数解析式为_______________________．14．已知二次函数的图象的对称轴为x ＝1，函数的最大值为－6，且图象经过点(2，－8)，求此二次函数的表达式．15．已知二次函数的图象经过点(0，3)，(－3，0)，(2，－5)，且与x 轴交于A ，B 两点．(1)试确定此二次函数的解析式；(2)判断点P(－2，3)是否在这个二次函数的图象上？如果在，请求出△PAB 的面积；如果不在，试说明理由．16．若两个二次函数图象的顶点、开口方向都相同，则称这两个二次函数为“同簇二次函数”．(1)请写出两个为“同簇二次函数”的函数；(2)已知关于x的二次函数y1＝2x2－4mx＋2m2＋1和y2＝ax2＋bx＋5，其中y1的图象经过点A(1，1)，若y1＋y2与y1为“同簇二次函数”，求函数y2的解析式，并求出当0≤x≤3时，y2的最大值．专题训练(三) 用待定系数法求二次函数解析式一、已知三点求解析式1．已知二次函数的图象经过(1，0)，(2，0)和(0，2)三点，则该函数的解析式是( )A ．y ＝2x 2＋x ＋2B ．y ＝x 2＋3x ＋2C ．y ＝x 2－2x ＋3D ．y ＝x 2－3x ＋2 2．如图，二次函数y ＝ax 2＋bx ＋c 的图象经过A ，B ，C 三点，求出抛物线的解析式．二、已知顶点或对称轴求解析式3．在直角坐标平面内，二次函数的图象顶点为A(1，－4)，且过点B(3，0)，求该二次函数的解析式．4．已知抛物线经过两点A(1，0)，B(0，3)，且对称轴是直线x ＝2，求其解析式．三、已知抛物线与x 轴的交点求解析式5．已知抛物线与x 轴的交点是A(－2，0)，B(1，0)，且经过点C(2，8)，则该抛物线的解析式为_______________．6．如图，抛物线y ＝－x 2＋bx ＋c 与x 轴的两个交点分别为A(1，0)，B(3，0)，求这条抛物线的解析式．四、已知几何图形求解析式7．如图，在平面直角坐标系xOy 中，边长为2的正方形OABC 的顶点A ，C 分别在x 轴、y 轴的正半轴上，二次函数y ＝－23x 2＋bx ＋c 的图象经过B ，C 两点．求该二次函数的解析式．五、已知面积求解析式8．直线l过点A(4，0)和B(0，4)两点，它与二次函数y＝ax2的图象在第一象限内交于点P，若S△AOP＝92，求二次函数关系式．六、已知图形变换求解析式9．已知抛物线C1：y＝ax2＋bx＋c经过点A(－1，0)，B(3，0)，C(0，－3)．(1)求抛物线C1的解析式；(2)将抛物线C1向左平移几个单位长度，可使所得的抛物线C2经过坐标原点，并写出C2的解析式．七、运用根与系数的关系求解析式10．已知抛物线y＝－x2＋2mx－m2－m＋2.(1)直线l：y＝－x＋2是否经过抛物线的顶点；(2)设该抛物线与x轴交于M，N两点，当OM·ON＝4，且OM≠ON时，求出这条抛物线的解析式．22．2 二次函数与一元二次方程22.2.1 二次函数与一元二次方程之间的关系1．一元二次方程ax 2＋bx ＋c ＝0的实数根，就是二次函数y ＝ax 2＋bx ＋c ，当_______时，自变量x 的值，它是二次函数的图象与x 轴交点的___________．2．抛物线y ＝ax 2＋bx ＋c 与x 轴交点个数与一元二次方程ax 2＋bx ＋c ＝0根的判别式的关系：①当b 2－4ac ＜0时，抛物线与x 轴_______交点；②当b 2－4ac ＝0时，抛物线与x 轴有__________交点；③当b 2－4ac ＞0时，抛物线与x 轴有_________交点．知识点1：二次函数与一元二次方程1．抛物线y ＝－3x 2－x ＋2与坐标轴的交点个数是( )A ．3B ．2C ．1D ．02．如图，已知抛物线与x 轴的一个交点A(2，0)，对称轴是x ＝－1，则该抛物线与x 轴的另一个交点的坐标是( )A ．(－2，0)B ．(－3，0)C ．(－4，0)D ．(－5，0)3．抛物线y ＝x 2＋6x ＋m 与x 轴只有一个公共点，则m 的值为________．4．绿茵场上，足球运动员将球踢出，球的飞行高度h(米)与前行距离s(米)之间的关系为h＝45s －2125s 2，那么当足球落地时距离原来的位置有_______米．知识点2：利用二次函数求一元二次方程的近似解5．根据下列表格的对应值，判断方程ax 2＋bx ＋c ＝0(a ≠0，a ，b ，c 为常数)一个解的范围是( )A .2＜C ．2.24＜x ＜2.25 D ．2.25＜x ＜2.266．用图象法求一元二次方程2x 2－4x －1＝0的近似解．知识点3：二次函数与不等式7．二次函数y＝x2－x－2的图象如图所示，则函数值y＜0时x的取值范围是() A．x＜－1 B．x＞2 C．－1＜x＜2 D．x＜－1或x＞2(第7题图) (第8题图)8．如图是二次函数y＝ax2＋bx＋c的部分图象，由图象可知不等式ax2＋bx＋c＜0的解集是( )A．－1＜x＜5 B．x＞5 C．x＜－1且x＞5 D．x＜－1或x＞5 9．已知二次函数2则当y＜5时，_________10．已知函数y＝x2＋2x－3，当x＝m时，y＜0，则m的值可能是( )A．－4B．0C．2D．311．2)的根的个数是( )x 5.17 5.18 5.19 5.20ax2＋bx＋c 0.02 －0.01 0.02 0.04A.012．抛物线y＝ax2＋bx＋c的图象如图，则关于x的方程ax2＋bx＋c－2＝0的情况是( )A．有两个不相等的实数根B．有两个异号的实数根C．有两个相等的实数根D．没有实数根13．抛物线y＝2(x＋3)(x－2)与x轴的交点坐标分别为_______________．14．(1)用配方法把二次函数y＝x2－4x＋3化成y＝(x－h)2＋k的形式；(2)在直角坐标系中画出y＝x2－4x＋3的图象；(3)若A(x1，y1)，B(x2，y2)是函数y＝x2－4x＋3图象上的两点，且x1＜x2＜1，请比较y1，y2的大小关系；(直接写结果)(4)把方程x2－4x＋3＝2的根在函数y＝x2－4x＋3的图象上表示出来．15．二次函数y＝ax2＋bx＋c(a≠0)的图象如图，根据图象解答下列问题：(1)写出方程ax2＋bx＋c＝0的两个根；(2)写出y随x的增大而减小的自变量x的取值范围；(3)若方程ax2＋bx＋c＝k有两个不相等的实数根，求k的取值范围．17．已知抛物线y＝ax2＋bx＋c(a＞0)的图象与x轴交于A(x1，0)，B(x2，0)(x1＜x2)两点，与y轴交于点C，x1，x2是方程x2＋4x－5＝0的两根．(1)若抛物线的顶点为D，求S△ABC∶S△ACD的值；(2)若∠ADC＝90°，求二次函数的解析式．22.2.2 二次函数y ＝ax 2＋bx ＋c 的图象与字母系数的关系抛物线y ＝ax 2＋bx ＋c 的图象与字母系数a ，b ，c 之间的关系： (1) ①当a ＞0时，开口__________，②当a ＜0时，开口__________；(2) ①若对称轴在y 轴的左边，则a ，b________，②若对称轴在y 轴的右边，则a ，b______； (3) ①若抛物线与y 轴的正半轴相交，则c_____0，②若抛物线与y 轴的负半轴相交，则c____0， ③若抛物线经过原点，则c_____0；(4) ①当x ＝1时，y ＝ax 2＋bx ＋c ＝a ＋b ＋c ；②当x ＝－1时，y ＝ax 2＋bx ＋c ＝a －b ＋c ； ③ 当x ＝2时，y ＝ax 2＋bx ＋c ＝4a ＋2b ＋c ；④当x ＝－2时，y ＝ax 2＋bx ＋c ＝4a －2b ＋c ；…；(5) ①当对称轴x ＝1时，x ＝－b2a ＝1，所以－b ＝2a ，此时2a ＋b ＝0;②当对称轴x ＝－1时，x ＝－b2a ＝－1，所以b ＝2a ，此时2a －b ＝0； (6) ①b 2－4ac ＞0⇔二次函数与横轴有两个交点；②b 2－4ac ＝0⇔二次函数与横轴有一个交点； ③b 2－4ac ＜0⇔二次函数与横轴无交点．知识点1：二次函数图象与字母系数的关系1．二次函数y ＝ax 2＋bx ＋c 的图象如图所示，则下列关系式错误的是( )A ．a ＞0B ．c ＞0C ．b 2－4ac ＞0D ．a ＋b ＋c ＞0(第1题图) (第2题图) (第4题图)2．二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象如图所示，下列结论正确的是( )A ．a ＜0B ．b 2－4ac ＜0C ．当－1＜x ＜3时，y ＞0D ．－b2a ＝13．二次函数y ＝x 2＋bx ＋c 中，若b ＋c ＝0，则它的图象一定过点( )A ．(1，－1)B ．(－1，1)C ．(－1，－1)D ．(1，1)4．二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象如图所示，若M ＝a ＋b －c ，N ＝4a －2b ＋c ，P ＝2a －b ，则M ，N ，P 中，值小于0的数有( )A ．3个B ．2个C ．1个D ．0个。

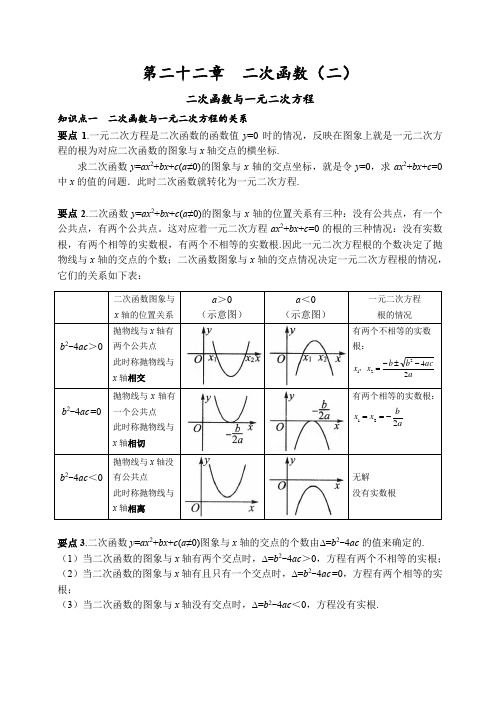
第二十二章二次函数（二）二次函数与一元二次方程知识点一二次函数与一元二次方程的关系要点1.一元二次方程是二次函数的函数值y=0时的情况，反映在图象上就是一元二次方程的根为对应二次函数的图象与x轴交点的横坐标.求二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点坐标，就是令y=0，求ax2+bx+c=0中x的值的问题．此时二次函数就转化为一元二次方程.要点2.二次函数y=ax2+bx+c(a≠0)的图象与x轴的位置关系有三种：没有公共点，有一个公共点，有两个公共点。

这对应着一元二次方程ax2+bx+c=0的根的三种情况：没有实数根，有两个相等的实数根，有两个不相等的实数根.因此一元二次方程根的个数决定了抛物线与x轴的交点的个数；二次函数图象与x轴的交点情况决定一元二次方程根的情况，它们的关系如下表：要点3.二次函数y=ax2+bx+c(a≠0)图象与x轴的交点的个数由∆=b2-4ac的值来确定的.（1）当二次函数的图象与x轴有两个交点时，∆=b2-4ac＞0，方程有两个不相等的实根；（2）当二次函数的图象与x轴有且只有一个交点时，∆=b2-4ac=0，方程有两个相等的实根；（3）当二次函数的图象与x轴没有交点时，∆=b2-4ac＜0，方程没有实根.课堂练习1.在平面直角坐标系xOy中，二次函数y=x2-4x的图象与x轴的交点坐标是（）A.(0，0)B.(4，0)C.(4，0)、(0，0)D.(2，0)、(-2，0)2.已知关于x的一元二次方程ax2+bx+c=0有两个相等的实数根，则抛物线y=ax2+bx+c与x轴的交点个数是（）A.0B.1C.2D.33.若函数y=kx2-6x+3的图象与x轴有交点，则k的取值范围是（）A.k<3B.k<3且k≠0C.k≤3D.k≤3且k≠04.已知抛物线y=ax2+bx+c(a≠0)的部分图象如图所示，那么关于x的一元二次方程ax2+bx+c=0的两个解为（）A.-1，3B.-2，3C.1，3D.3，45.二次函数y=x2-6x-7的图象与x轴的交点坐标是，与y轴的交点坐标是.6.已知抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1，0)，B(5，0)，则一元二次方程ax2+bx+c =0(a≠0)的根是.7.若二次函数y=x2+bx的图象的对称轴是经过点(2，0)且平行与y轴的直线，则关于x的方程x2+bx=5的解为（）A.x1=0，x2=4B.x1=1，x2=5C.x1=1，x2=-5D. x1=-1，x2=58.已知抛物线y=2(k+1)x2+4kx+2k-3，求k为何值时，抛物线与x轴有两个交点、有唯一交点、没有交点.9.已知关于x 的一元二次方程：x 2-(t -1)x +t -2=0. （1）求证：对于任意实数t ，方程都有实数根；（2）当t 为何值时，二次函数y =x 2-(t -1)x +t -2的图象与x 轴的两个交点的横坐标互为相反数？请说明理由.知识点二 抛物线与x 轴两交点之间的距离 要点1.抛物线与x 轴两交点之间的距离公式：若抛物线y =ax 2+bx +c (a ≠0)与x 轴两交点为A (x 1，0)，B (x 2，0)由于x 1、x 2是方程ax 2+bx +c =0的两个根，.有2121acx x a b x x =-=+，则结合两点之间的距离公式：22)()(B A B A x x y y AB -+-=（勾股定理）.a a acb a ca b x x x x x x x x AB ∆=-=-⎪⎭⎫ ⎝⎛-=-+=-=-=444)()(222122122121.课堂练习1.已知抛物线y =43x 2415-x +3经过与x 轴相交于A ，B 两点，与y 轴相交于C 点，顶点为D 点，分别求出△ABC 和△ABD 的面积.知识点三利用二次函数的图象求一元二次方程的近似解要点1.我们可以利用二次函数的图象求一元二次方程的解.由于作图或观察可能有误差，由图象求得的解一般是近似的.利用二次函数的图象求一元二次方程的近似解的一般步骤如下：（1）作出二次函数y=ax2+bx+c(a≠0)的图象，由图象确定与x轴交点的个数，即方程解的个数；（2）观察图象与x轴的交点在哪两个数之间，即确定交点的横坐标的取值范围；（3）在两个数之间取值估计，并用计算器估算近似解近似解出现在对应y值正负交替的地方.当x由x1到x2，对应的y值出现y1>0，y2<0(或y1<0<y2)时，则x1，x2中必有一个是方程的近似解.再比较|y1|和|y2|，若|y1|<|y2|，则x1是方程的近似解；若|y1|>|y2|则x2是方程的近似解.利用二次函数的图象求一元二次方程的近似解的常用方法如下表：方法步骤结论方法一直接作出二次函数y=ax2+bx+c(a≠0)的图象图象与x轴的交点的横坐标就是方程ax2+bx+c=0(a≠0)的根方法二先将一元二次方程变为ax2+bx=-c(a≠0)，再在同一直角坐标系中画出抛物线y=ax2+bx和直线y=-c两图象交点的横坐标就是方程ax2+bx+c=0(a≠0)的根方法三先将一元二次方程化为ax2=-bx-c(a≠0)移项后得再在同一直角坐标系中画出抛物线y=ax2和直线y=-bx-c两图象交点的横坐标就是方程ax2+bx+c=0(a≠0)的根课堂练习1.已知二次函数y=x2-2x-3.（1）请你将函数解析式化成y=a(x-h)2+k的形式，并在平面直角坐标系中画出y=x2-2x-3的图象（2）利用（1）中的图象结合图象变换表示x2-2x-1=0的根，要求保留作图痕迹，指出方程的图形意义.2.如图，点A （2.18，-0.51），B （2.68，0.54），在二次函数y ＝ax 2+bx +c （a ≠0）的图象上，则方程ax 2+bx +c ＝0的一个近似值可能是（ ） A.2.18 B.2.68C.-0.51D.2.453.根据下列表格的对应值，判断ax 2+bx +c =0（a ≠0，a ，b ，c 为常数）的一个解x 的取值范围是 .知识点四 二次函数与一元二次不等式的关系要点1.二次函数y =ax 2+bx +c (a ≠0)与一元二次不等式ax 2+bx +c >0(a ≠0)及ax 2+bx +c <0(a ≠0)之间的关系如下(x 1<x 2)： （1）a ＜0时：判别式a >0抛物线y =ax 2+bx +c 与x 轴的交点不等式ax 2+bx +c >0 的解集 不等式ax 2+bx +c <0的解集△＞01x x <或2x x > 12x x x <<△＝01x x ≠（或2x x ≠）无解△＜0全体实数 无解x 3.23 3.24 3.25 3.26 ax 2+bx +c-0.06-0.020.030.09（2）a＜0时：利用二次函数y=ax2+bx+c(a≠0)的图象解不等式：不等式ax2+bx+c>0(a≠0)的解集是二次函数y=ax2+bx+c(a≠0)的图象位于x轴上方的所有点的横坐标.不等式ax2+bx+c<0(a≠0)的解集是二次函数y=ax2+bx+c(a≠0)的图象位于x轴下方的所有点的横坐标；当二次函数y=ax2+bx+c(a≠0)的函数值y>0时，其自变量x的取值范围是不等式ax2+bx+c>0的解集；当二次函数y=ax2+bx+c(a≠0)的函数值y<0时，其自变量x的取值范围是不等式ax2+bx+c<0的解集.要点2.利用二次函数图象解一元二次不等等式的步骤：（1）将一元二次不等式化为ax2+bx+c>0(或<0)的形式；（2）明确二次项系数a的正负、对称轴在y轴哪侧，并计算b2-4ac的值；（3）作出不等式对应的二次函数y=ax2+bx+c(a≠0)的草图；（4）二次函数在x轴上方的图象对应的函数值大于零，在x轴下方的图象对应的函数值小于零.课堂练习1.解不等式-x2+5x+3>7.2.已知二次函数y=x2-4x+3.（1）求出该二次函数图象的顶点坐标和对称轴；（2）在坐标系中画出该函数的图象；（3）根据图象直接写出不等式x2-4x+3>0的解集.3.已知二次函数y=-x2+2x+3.（1）求其开口方向、对称轴、顶点坐标，并画出这个函数的图象；（2）根据图象，直接写出；①当函数值y为正数时，自变量x的取值范围；②当-2＜x＜2 时，函数值y的取值范围．4.函数y=ax2+2ax+m(a<0)的图象过点(2，0)，则使函数值y<0成立的x的取值范围是（）A.x<-4或x>2B.-4<x<2C.x<0或x>2D.0<x<2。

第6讲二次函数的应用知识定位讲解用时：3分钟A、适用范围：人教版初三，基础偏上B、知识点概述：本讲义主要用于人教版初三新课，本节课我们主要学习二次函数在实际问题以及几何图形中的应用，重点掌握常见的几类二次函数题型的分析过程和处理方法。

本节课的部分内容属于中考常考知识点，同时也是中考难点之一，需要同学们灵活运用二次函数解析式及图像性质解决实际问题、代数问题和几何问题的综合能力。

知识梳理讲解用时：15分钟二次函数的应用题型（1）利润问题在商品经营活动中，经常会遇到求最大利润，最大销量等问题，解此类题的关键是通过题意，确定出二次函数的解析式，然后再通过配方的方式确定其最大值；实际问题中自变量x的取值要使实际问题有意义，因此在求二次函数的最值时，一定要注意自变量x的取值范围。

（2）几何图形中的最值问题几何图形中的二次函数问题常见的有：几何图形中面积的最值以及动态几何中的最值的讨论；求解二次函数与面积结合的问题时，基本方法上与利润最大化是相同的，也是通过配方的方式求解相关面积的最值，当然也需要注意自变量的取值范围；而与利润最大化问题不同的是，面积问题中可能会涉及到三角形、四边形或者圆等图形，也可能会出现动点与面积相结合的类型，变化较多。

课堂精讲精练【例题1】某体育用品商店购进一批滑板，每块滑板利润为30元，一星期可卖出80块，商家决定降价促销，根据市场调查，每降价1元，则一星期可多卖出4块，设每块滑板降价x元，商店一星期销售这种滑板的利润是y元，则y与x之间的函数表达式为。

【答案】y=﹣4x2+40x+2400【解析】本题考查了根据实际问题抽象出二次函数关系式，设每块滑板降价x元，商店一星期销售这种滑板的利润是y元，则y与x之间的函数表达式为：y=（30﹣x）（80+4x）=﹣4x2+40x+2400．讲解用时：3分钟解题思路：设每块滑板降价x元，则销售利润为=销量×每件利润进而得出答案。

教学建议：利用利润=销量×每件商品利润，进而得出利润与定价之间的函数关系式。

面积问题有些实际问题并不直接表现出抛物线，却把二次函数相关的知识隐含在其中，我们可以用二次函数来解决面积问题例1、爷爷退休后在乡下养鸡，他用长为50米的篱笆围成一个养鸡场，养鸡场的一面靠墙（墙的最大长度为20米）。

问如何围，才能使养鸡场的面积最大？请你帮爷爷设计一下，并说明理由例2、小李同学帮奶奶养鸭，想用篱笆围成一个周长为60米的矩形场地，矩形面积S（单位：平方米）随矩形一边长x（单位：米）的变化而变化．（1）求S与x之间的函数关系式，并写出自变量x的取值范围；（2）当x是多少时，矩形场地面积S最大？最大面积是多少？1、如图1，用长为18米的篱笆（虚线部分）和两面墙围成矩形苗圃。

（1）设矩形的一边长为x（米），面积为y（平方米），求y关于x的函数关系式（2）当x为何值时，所围成的苗圃面积最大？最大面积是多少？2、卢爷爷要围成一个矩形花圃．花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成．围成的花圃是如图所示的矩形ABCD．设AB边的长为x米．矩形ABCD的面积为S平方米．（1）求S与x之间的函数关系式（不要求写出自变量x的取值范围）（2）当x为何值时，S有最大值？并求出最大值．3、用长为20cm的铁丝，折成一个矩形，设它的一边长为xcm，面积为ycm2。

(1)求出y与x的函数关系式。

（2）当边长x为多少时，矩形的面积最大，最大面积是多少？4、将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长做成一个正方形．(1)要使这两个正方形的面积之和等于17cm2，那么这段铁丝剪成两段后的长度分别是多少?(2)两个正方形的面积之和可能等于12cm2吗? 若能，求出两段铁丝的长度；若不能，请说明理由．5、在城市开展的环境创优活动中，某居民小区要在一块靠墙（墙长15米）的空地上修建一个矩形花园ABCD，花园的一边靠墙，另三边用总长为40m的栅栏围成，若设花园靠墙的一边长为x(m)，花园的面积为y(m2)。

二次函数一．知识梳理1、定义：只含有一个未知数，且未知数最高次数为2的方程叫做一元二次方。

一元二次方程的标准式：ax2+bx+c=0 （a≠0）其中： ax2叫做二次项， bx叫做一次项， c叫做常数项a是二次项系数，b是一次项系数2、一元二次方程根的判别式（二次项系数不为0）：“△”读作德尔塔，在一元二次方程ax2+bx+c=0 （a≠0）中△=b2-4ac△=b2-4ac>0 <====> 方程有两个不相等的实数根，即：x1,x2△=b2-4ac=0 <====> 方程有两个相等的实数根，即：x1=x2△=b2-4ac<0 <====> 方程没有实数根。

注：“<====>” 是双向推导，也就是说上面的规律反过来也成立，如：告诉我们方程没有实数根，我们便可以得出△<03、一元二次方程根与系数的关系（二次项系数不为0;△≥0），韦达定理。

ax2+bx+c=0 （a≠0）中，设两根为x1,x2,那么有：因为：ax2+bx+c=0 （a≠0）化二次项系数为1可得，所以：韦达定理也描述为：两根之和等于一次项系数的相反数，两根之积等于常数项。

注意：（1）在一元二次方程应用题中，如果解出来得到的是两个根，那么我们要根据实际情况判断是否应舍去一个跟。

5、一元二次方程的求根公式：注：任何一元二次方程都能用求根公式来求根，虽然使用起来较为复杂，但非常有效。

一、求二次函数的三种形式：1. 一般式：y=ax 2+bx+c ，（已知三个点）顶点坐标（－2b a，244ac b a -）2.顶点式：y=a （x －h ）2+k ，（已知顶点坐标对称轴）顶点坐标（h ，k ）3.交点式：y=a(x- x 1)(x- x 2)，（有交点的情况）与x 轴的两个交点坐标x 1，x 2对称轴为221x x h +=二、a b c 作用分析│a │的大小决定了开口的宽窄，│a │越大，开口越小，│a │越小，开口越大，a ，b 的符号共同决定了对称轴的位置，当b=0时，对称轴x=0，即对称轴为y 轴，当a ，b同号时，对称轴x=－2b <0，即对称轴在y 轴左侧，当a ，b•异号时，对称轴x=－2ba>0，即对称轴在y 轴右侧，c•的符号决定了抛物线与y 轴交点的位置，c=0c<0时，与y•轴交于负半轴，以上a ，b ，c 的符号与图像的位置是共同作用的，也可以互相推出．二．专题精练专题一：二次函数与一元二次方程的关系本专题主要涉及根据二次函数的图象求一元二次方程的近似根，由图象判断一元二次方程根的情况，由一元二次方程根的情况判断抛物线与x 轴的交点个数等，题型主要填空题、选择题和解答题.考点1.根据二次函数的自变量与函数值的对应值，确定方程根的范围一元二次方程ax 2+bx+c=0就是二次函数y=ax 2+bx+c 当函数y 的值为0时的情况. 例1 根据下列表格中二次函数y=ax 2+bx+c 的自变量x 与函数值y 的对应值，判断方程ax 2+bx+c=0（a ≠0,a,b,c,为常数）的一个解x 的范围是（ ）Ａ．6 6.17x << Ｂ．6.17 6.18x << Ｃ．6.18 6.19x <<Ｄ．6.19 6.20x <<抛物线 顶点坐标 对称轴 位置 开口方向 增减性 最值y=ax2+bx+c(a>0)y=ax 2+bx+c(a<0)由a,b 和c 的符号确定由a,b 和c 的符号确定 a>0,开口向上a<0,开口向下在对称轴的左侧,y 随着x 的增大而减小. .在对称轴的左侧,y 随着x 的增大而增大. 在.⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22abx 2-=直线abx 2-=直线考点2.根据二次函数的图象确定所对应的一元二次方程的根.二次函数y=ax 2+bx+c 的图象与x 轴的交点有三种情况：有两个交点、一个交点、没有交点；当二次函数y=ax 2+bx+c 的图象与x 轴有交点时，交点的横坐标就是当y=0时自变量x 的值，即一元二次方程ax 2+bx+c=0的根.例2 已知二次函数y=-x 2+3x+m 的部分图象如图1所示，则关于x 的一元二次方程-x 2+3x+m=0的解为________.考点3.抛物线的交点个数与一元二次方程的根的情况当二次函数y=ax 2+bx+c 的图象与x 轴有两个交点时，则一元二次方程ax 2+bx+c=0有两个不相等的实数根；当二次函数y=ax 2+bx+c 的图象与x 轴有一个交点时，则一元二次方程ax 2+bx+c=0有两个相等的实数根；当二次函数y=ax 2+bx+c 的图象与x 轴没有交点时，则一元二次方程ax 2+bx+c=0没有实数根.反之亦然.例3 在平面直角坐标系中，抛物线21y x =-与x 轴的交点的个数是（ ）专项练习31.抛物线y=kx 2-7x-7的图象和x 轴有交点，则k 的取值范围是________.2.已知二次函数22y x x m =-++的部分图象如图2所示，则关于x 的一元二次方程220x x m -++=的解为 ．3.已知函数2y ax bx c =++的图象如图3所示，那么关于x 的方程220ax bx c +++= 的根的情况是（ ）A.无实数根B.有两个相等实数根C.有两个异号实数根D.有两个同号不等实数根4. 二次函数2(0)y ax bx c a =++≠的图象如图4所示，根据图象解答下列问题：（1）写出方程20ax bx c ++=的两个根． （2）写出不等式20ax bx c ++>的解集．图2图1（3）写出y 随x 的增大而减小的自变量x 的取值范围．（4）若方程2ax bx c k ++=有两个不相等的实数根，求k 的取值范围．专题二、探究几何图形中的二次函数关系【例11】在梯形ABCD 中，AD BC ∥，6AB DC AD ===，60ABC ∠=o，点E F，分别在线段AD DC ，上（点E 与点A D ，不重合），且120BEF ∠=o，设AE x =，DF y =．（1）求y 与x 的函数表达式；（2）当x 为何值时，y 有最大值，最大值是多少课堂检测1、二次函数342++=x x y 的图像可以由二次函数2x y =的图像平移而得到，下列平移正确的是（ ）A ．先向左平移2个单位，再向上平移1个单位B ．先向左平移2个单位，再向下平移1个单位;C ．先向右平移2个单位，再向上平移1个单位D ．先向右平移2个单位，再向下平移1个单位2、在平面直角坐标系中，如果抛物线y ＝2x 2不动，而把x 轴、y 轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是（ ） A ．y ＝2(x －2)2+ 2 B ．y ＝2(x + 2)2－2 C ．y ＝2(x －2)2－2D ．y ＝2(x + 2)2+ 2Ａ ＥＤ ＦＣＢO xy1-1A 3、二次函数21(4)52y x =-+的开口方向、对称轴、顶点坐标分别是（ ） A ．向上、直线x=4、（4，5） B ．向上、直线x=-4、（-4，5） C ．向上、直线x=4、（4，-5） D ．向下、直线x=-4、（-4，5） 4、二次函数c bx ax y ++=2的图象如图所示，则下列关系式不正确的是（ ）A 、a ＜0B 、abc ＞0C 、c b a ++＞0D 、ac b 42-＞05、函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是 （ ）6、二次函数2(0)y ax bx c a =++≠的图象如图4所示， 则下列说法不正确的是（ ） A ．240b ac -> B ．0a >C ．0c >D ．02ba-<7、如图是二次函数y ＝ax 2＋bx ＋c 图象的一部分，图象过点A （－3，0），对称轴为x ＝－1．给出四个结论：①b 2＞4ac ；②2a ＋b =0；③a －b ＋c =0；④5a ＜b ．其中正确结论是（ ）． A ．②④ B ．①④ C ．②③ D ．①③8、已知关于x 的函数同时满足下列三个条件：①函数的图象不经过第二象限；②当2<x 时，对应的函数值0<y ；③当2<x 时，函数值y 随x 的增大而增大．你认为符合要求的函数的解析式可以是： （写出一个即可）．9、如右图，抛物线n x x y ++-=52经过点)0,1(A ，与y 轴交于点B. （1）求抛物线的解析式；（2）P 是y 轴正半轴上一点，且△PAB 是等腰三角形，试求点P 的坐标...《专题五。

灵活运用三种解析式求二次函数二次函数有三种解析式：一般式、顶点式、交点式 ①一般式：y=ax 2+bx+c （a ≠0） ②顶点式：y=a(x-h)2+k （a ≠0） ③交点式：y=a(x-x 1)(x-x 2) （a ≠0）定理：二次函数y=ax 2+bx+c 可以转化为y=a(x-x 1)(x-x 2)其中x 1、x 2是二次函数与x 轴交点的横坐标，这个式子叫做二次函数的交点式 证明：提出来把a acx a b x a y cbx ax y )(22++=++=21x xx x -- 使用十字相乘法检验：2.x x x =，acx x x x ==--2121)).(( （使用了韦达定理） 交叉相乘后相加：x aba b x x x x xx xx =--=+-=-+-).()()()(2121 （使用了韦达定理）满足十字相乘法的要求∴二次函数y=ax 2+bx+c 可以转化为y=a(x-x 1)(x-x 2)，其中x 1、x 2是二次函数与x 轴交点的横坐标例1、根据条件求二次函数的解析式（1）抛物线过（-1，-6）、（1，-2）和（2，3）三点 （2）抛物线过（－1，0），（3，0），（1，－5）三点（3）抛物线的顶点坐标为（-1，-1），且与y 轴交点的纵坐标为-3 （4）抛物线在x 轴上截得的线段长为4，且顶点坐标是（3，－2）总结：尽量用______式、______式，迫不得已才用______式1、已知抛物线经过点（1，0），（-5，0），且顶点纵坐标为29，这个二次函数的解析式＿＿＿＿＿＿＿＿＿2、已知二次函数y=ax 2+bx+c 的图象交x 轴于A 、B 两点，交y 轴于C 点，且△ABC 是直角三角形，请写出一个符合要求的二次函数解析式________________3、二次函数y= ax2+bx+c，x=－2时y=－6,x=2时y=10,x=3时y=24,求此函数的解析式。

人教版九年级数学第22章二次函数 22.1 二次函数讲义合作探究探究点1 二次函数的概念情景激疑我们知道形如b k b kx y ,(+=是常数,k ≠0)的式子是一次函数，那么什么样的函数是二次函数呢?判断二次函数又需要消足哪些条件?知识讲解一般地，形如c b a c bx ax y ,,(2++=是常数,a ≠0)的函数，叫做二次函数。

其中，x 是自变量,a,b,c 分别是函数解析式的次项系数、一次项系数和常数项，如73,23,32222+-=+=+-=x y x x y x x y 等都是二次函数。

（1）c b a c bx ax y ,,(2++=是常数,a ≠0)叫做二次函数的-般式任何一个二次函数的解析式都可以化为c b a c bx ax y ,,(2++=是常数,a ≠0)的形式.(2)在二次函数c b a c bx ax y ,,(2++=是常数,a ≠0)中，a 必須不等于O,因为若a=0的话，此式子则变为c bx y +=的形式，就不是二次函数了.(3)在二次函数c b a c bx ax y ,,(2++=是常数,a ≠0)中,若y=0.则二次函数可以转化为一元二次方程)0(02≠=++a c bx ax 典例剖析例1 下列哪些函数是二次函数?解析 判断一个函数是不是二次函数，先把关系式化简 整理，再分三个步骤来判断:(1)看它的等号两边是否都是整式，如果不都是整式，则必不是二次函数:(2)当它的等号两边都号林式时，再看它是否含有自变量的二次式，如果含有自变量的二安式，那就可能是二次函数，否则就不是:(3)看它的二次项系数是否为0,如果不为0，那就是二次函教.只要按上述三步来分析。

即可作出正确判断.答案 ①③④是二次函数.⑤不一定是二次函数，只有当a ≠0时，才是二次函数②不是整式，故不是二次函数，易错警示二次涵数关系式的等号两边都是整式.答案 (1)设一次购买x 只.才能以最低价购买，则有0.1(x-10)=20-16,解这个方程得x=50.答:一次至少买50只，才能以最低价购买。

二次函数之数形结合法我国著名数学家华罗庚曾说过：数缺形时少直观，形少数时难入微。

数形结合百般好，隔裂分家万事休。

“数”与“形”反映了事物两个方面的属性。

我们认为，数形结合，主要指的是数与形之间的一一对应关系。

数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而实现优化解题途径的目的。

例题讲解：例1、如图，抛物线y=x2-2x-3与x轴交于A、B两点，与y轴交于C点，求当y<0时，x的取值范围例2、抛物线y=x 2-2x+3过__________象限；抛物线y=-x 2-4x+9过__________象限例3、若A （1,413y -），B （2,45y -），C （3,41y ）为二次函数245y x x =+-的图象上的三点，则1,y 2,y 3y 的大小关系是( ) A 、123y y y <<B 、213y y y <<C 、312y y y <<D 、132y y y <<例4、直线y=mx+n 和抛物线y=ax 2+bx+c 在同一坐标系中的位置如图所示，那么不等式mx+n ＜ax 2+bx+c ＜0的解集是 ．课堂练习1、函数y=2x 2-3x+4经过的象限是（ ） A.一、二、三象限 B.一、二象限 C.三、四象限 D.一、二、四象限2、已知抛物线2y ax bx =+，当00a b ><，时，它的图象经过( )A.一、二、三象限B.一、二、四象限 C ．一、三、四象限 D.一、二、三、四象限.3、不论x 为何值，函数()20y ax bx c a =++≠的值恒大于0的条件是( ) A.0a >，0∆> B.00a >∆<， C.00a <∆<， D.00a <∆>，4、二次函数()21212y x k x =--+，当1x >时，y 随着x 的增大而增大，当1x <时，y 随着x 的增大而减小，则 k 的值应取（ ）A 、12B 、11C 、10D 、95、若一次函数y=ax+b 的图象经过第二、三、四象限，则二次函数y=ax 2+bx 的图象只可能是( )6、已知二次函数c bx ax y ++=2，且0<a ，0>+-c b a ，则一定有（ ） A. 042>-ac b B. 042=-ac bC. 042<-ac bD. ac b 42-≤07、已知函数y=x 2－2x －2的图象如图所示，根据其中提供的信息，可求得使y ≥1成立的x 的取值范围是 （ ） A 、－1≤x ≤3 B 、－3≤x ≤1 C 、x ≥－3 D 、x ≤－1或x ≥38、已知二次函数221,1=++>当时，y随x的增大而增大，则m的取值范围是______________ y x mx x9、已知二次函数2y ax x=-+与二次函数285=-+共顶点，若直线y=x+b与这两个抛物线恰好有三243y x x个公共点，则b的值为______________10、已知二次函数y=3（x﹣1）2+k的图象上三点A（2，y1），B（3，y2），C（﹣4，y3），则y1、y2、y3的大小关系是12、点A（2，y1）、B（3，y2）是二次函数y=-（x﹣1）2+2的图象上两点，则y1y213、对于二次函数y=x2+mx+1，当0＜x≤2时的函数值总是非负数，则实数m的取值范围为（）A．m≥﹣2B．﹣4≤m≤﹣2C．m≥﹣4D．m≤﹣4或m≥﹣214、已知函数y=x2-2x-1，当0>x时，求使y≥2的x的取值范围15、二次函数c bx ax y ++=2的图象过A(-3,0),B(1,0),C(0,3),点D 在函数图象上，点C 、D 是二次函数图象上的一对对称点，一次函数图象过点B 、D ，求 （1）一次函数和二次函数的解析式（2）写出使一次函数值大于二次函数值的x 的取值范围.16、二次函数y= ax 2+bx+c ，当x ＜6时y 随x 的增大而减小，x ＞6时y 随x 的增大而增大，其最小值为－12，其图象与x 轴的交点的横坐标是8，求此函数的解析式。

二次函数的图象和性质例题讲解：例1、在平面直角坐标系中画出y=x2、y=-x2、y=2x2、y=-2x2的图象y=x2表格：x -2 -1 0 1 2 yy=-x2表格：x -2 -1 0 1 2 yy=2x2表格：x -2 -1 0 1 2 yy=-2x2表格：x -2 -1 0 1 2 y通过画图我们可以得出二次函数y=ax 2的性质：1、二次函数的图象叫做_________，是__________图形；顶点坐标是______，对称轴是__________2、a>0，开口向_____；a<0，开口向_____3、|a|越大，开口越____；|a|越小，开口越____例2、抛物线215y x =-不具有的性质是（ ） A.开口向下 B.对称轴是y 轴 C.与y 轴不相交 D.最高点是坐标原点例3、如图所示,在同一坐标系中,作出①23x y = ②221x y = ③2x y =的图象则图象从里到外的三条抛物线对应的函数依次是 (填序号)例4、下列说法错误的是（ ）A ．二次函数y=3x 2中，当x>0时，y 随x 的增大而增大B ．二次函数y=－6x 2中，当x=0时，y 有最大值0C ．a 越大图象开口越小，a 越小图象开口越大D ．不论a 是正数还是负数，抛物线y=ax 2(a ≠0)的顶点一定是坐标原点思考：对于二次函数y=ax 2+bx+c(a ≠0)，既然a 控制抛物线的开口，那么b 和c 控制什么呢？知识点三：函数的图象和性质知识回顾：函数平移法则:_______________________________例1、将y=2x 2向右平移3个单位，再上移1个单位，所得新的抛物线的解析式为__________，顶点坐标是__________，对称轴是__________再看更一般的情况：将y=ax 2向右平移h 个单位，再上移k 个单位，所得新的抛物线解析式为_________________________________叫做二次函数的顶点式，顶点坐标（ ， ） ， 对称轴是_________________总结：要确定二次函数的顶点和对称轴，可用配方法把它配成顶点式，再根据平移的思想判断出来例2、求二次函数y=x 2-2x+4的顶点坐标和对称轴 例3、求二次函数y=-x 2-4x-6的顶点坐标和对称轴例4、抛物线22-=x y 的顶点坐标为（ ）A ．（2，0）B ．（-2，0）C ．（0，2）D ．（0，-2）例5、抛物线2(1)3y x =-+的对称轴是（ ） A 、直线1x =B 、直线3x =C 、直线1x =-D 、直线3x =-例6、抛物线 y ＝-2(x ＋1)2＋3的顶点坐标是1、函数y=-x 2-4x+3图象顶点坐标是（ ） A.（2，-7） B.（-2，7） C.（-2，-7）D.（2， 7）2、抛物线()12212++=x y 的顶点坐标是（ ） A ．（2，1） B ．（-2，1） C ．（2，-1） D ．（-2，-1）3、 y=(x －1)2＋2的对称轴是直线（ ）A ．x=－1B ．x=1C ．y=－1D ．y=14、抛物线y=x 2-2x+1的对称轴是 ( )A 、直线x=1B 、直线x=-1C 、直线x=2D 、直线x=-25、二次函数的最小值是（ ）．A 、2B 、1C 、－3D 、236、抛物线3)2(2+-=x y 的对称轴是（ ） A. 直线3-=x B. 直线3=x C. 直线2-=x D. 直线2=x7、抛物线y=2(x-3)2的顶点在( )A. 第一象限B. 第二象限C. x 轴上D. y 轴上2(1)2y x =++8、函数y=x 2-2x+3的图象的顶点坐标是( )A. (1，-4)B.(-1，2)C. (1，2)D.(0，3)9、将二次函数322+-=x x y 配方成k h x y +-=2)(的形式，则y=______________________10、对于2)3(22+-=x y 的图象下列叙述正确的是（ ）A 、顶点坐标为(－3，2)B 、对称轴为y=3C 、当3≥x 时y 随x 增大而增大D 、当3≥x 时y 随x 增大而减小11、用配方法把y ＝-x 2＋4x ＋5化为y ＝a(x-h)2＋k 的形式为y ＝ ，其开口方向 ，对称轴为 ，顶点坐标为12、若将二次函数y=x 2-2x+3配方为y=(x-h)2+k 的形式，则y=___________13、已知抛物线y= -2（x+3）²+5，如果y 随x 的增大而减小，那么x 的取值范围是_______定理：二次函数y=ax 2+bx+c(a ≠0）的顶点坐标是24(,)24b ac b a a --，对称轴是直线2b x a=-222222222222222证明：y =ax +bx +cby =a(x +x)+c(把a 提出来)a b b by =a[x +x +()-()]+c(配方法：加上一次项系数一半的平方）a 2a 2a b b y =a[(x +)-]+c（配成完全平方公式）2a 4a b b y =a(x +)-+c（乘法分配律）2a 4ab 4ac -b b 4ac -b y =a(x +)+（通分、合并，-+c =)2a 4a4a 4a由二次函数顶点式y =a(x -h)+k 得h =222b 4ac -b -，k =2a 4ab 4ac -b b∴二次函数y =ax +bx +c 的顶点坐标是(-,)，对称轴是直线x =-2a 4a 2a例7、抛物线942++=x x y 的顶点坐标是___________，对称轴是 ，有最____值______例8、二次函数y=mx 2-2mx-1+m 的顶点坐标是___________，对称轴是例9、已知抛物线y=x 2－8x ＋c 的顶点在x 轴上，则c 的值是（ ） A ．16 B ．－4 C ．4 D ．8例10、二次函数y=(x －3)(x ＋2)的图象的对称轴是（ ） A ．x=3 B ．x=－2 C ．x=12- D ．x=1214、抛物线221y x x =--+的顶点在（ ）A 、 第一象限B 、第二象限C 、第三象限D 、第四象限15、若0b <，则二次函数21y x bx =+-的图象的顶点在（ ） A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限16、已知二次函数2y ax bx =+的图象经过点11A -（，），则ab 有 ( ) A 、最小值0 B 、最大值 1 C 、最大值2 D 、有最小值14-17、抛物线251222+-=x x y 的开口方向 ，顶点坐标是18、将 y ＝x 2－2x ＋3 化成 y ＝a (x －h)2＋k 的形式，则 y ＝＿＿＿＿19、函数x x y +-=22有最_____值，最值为_______20、若抛物线y ＝x 2－bx ＋9的顶点在x 轴上，则b 的值为_____21、二次函数y=x 2-2x+1的对称轴方程是______________22、如果抛物线2y ax bx c 与y 轴交于点A (0,2)，它的对称轴是1x ，那么ac b23、函数2y x px q 的图象是以3,2为顶点的一条抛物线，这个二次函数的表达式为24、二次函数有最小值为1，当0x 时，1y ，它的图象的对称轴为1x ，则函数的关系式为_________25、已知二次函数215222y x x =+-，求出抛物线的顶点坐标、对称轴、最小值26、直接写出下列函数的开口方向、顶点坐标、对称轴，最值 （1）12212+-=x x y （2）2832-+-=x x y （3）4412-+-=x x y27、请写出一个二次函数的解析式，满足：图象的开口向下，对称轴是直线x=﹣1，且与y 轴的交点在x 轴的下方，那么这个二次函数的解析式可以为28、请你写出函数2)1(+=x y 与12+=x y 具有的一个共同性质：_______________29、有一个二次函数的图象，三位同学分别说出它的一些特点：甲：对称轴是直线4 x；乙：与x轴两个交点的横坐标都是整数；丙：与y轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式：_______________30、已知二次函数的图象开口向上，且与y轴的正半轴相交，请你写出一个满足条件的二次函数的解析式：_____________________。

对于二次函数()20y ax bx c a =++>（max y 表示y 的最大值，min y 表示y 的最小值） ⑴ 若自变量x 的取值范围为全体实数，如图①，函数在顶点处2bx a=-时，取到最值． ⑵ 若2bm x n a<-≤≤，如图②，当x m =，max y y =；当x n =，min y y =． ⑶ 若2bm x n a-<≤≤，如图③，当x m =，min y y =；当x n =，max y y =． ⑷ 若m x n ≤≤，且2b m n a -≤≤，22b b n m a a +>--如图④，当2bx a=-，min y y =； 当x n =，max y y =．知识互联网思路导航二次函数的应用题型一：二次函数的最值x=-b 2ax=-b 2a x=-b 2a x=-2a ④③②①【引例】 ⑴ 若x 为任意实数，求函数221y x x =-+的最小值；⑵ 若12x ≤≤，求221y x x =-+的最大值、最小值； ⑶ 若01x ≤≤，求221y x x =-+的最大值、最小值； ⑷ 若20x -≤≤，求221y x x =-+的最大值、最小值； ⑸ 若x 为整数，求函数221y x x =-+的最小值．【解析】 ⑴ 套用求最值公式（建议教师讲配方法）：当112224b x a -=-=-=⨯时，y 的最小值是24748ac b a -=． ⑵ 由图象可知：当12x ≤≤时，函数221y x x =-+单调递增，当1x =时，y 最小，且21112y =⨯-+=，当2x =时，y 最大，且222217y =⨯-+=．⑶ 由图象可知：当01x ≤≤时，函数221y x x =-+是先减后增，∴当14x =，y 最小，且78y =．∵当0x =时，20011y =⨯-+=；当1x =时， 211121y =⨯-+=>， ∴当1x =时，y 最大，且2y =．⑷ 由函数图象开口向上，且120<4x -≤≤，故当2x =-时，y 取最大值为11，当0x =时，y 取最小值为1．⑸ ∵112224b x a -=-=-=⨯，当0x =时，y 取最小值为1．【点评】 由此题我们可以得到：求二次函数2(0)y ax bx c a =++≠在给定区域内的最值，得看抛物线顶点横坐标2bx a=-是否在给定区域内．若在，则在顶点处取到一个最值，若不在，则在端点处取得最大值和最小值（其实求出端点值和顶点值，这三个值中最大的为最大值，最小的为最小值）．【例1】 ⑴ 已知实数x y ，满足2330x x y ++-=，则x y +的最大值为 ．⑵ 当331012x +-≤≤时，二次函数223y x x =--的最小值为（ ） A ．4- B ．154- C ．12- D ．12（昌平二模）例题精讲典题精练【解析】 ⑴ 4．提示：233y x x =--+，令()222314q x y x x x =+=--+=-++，当1x =-，q 的最大值为4．本题属于x 为全体实数，求二次函数的最值，配方法要熟练掌握．⑵ B ．提示：二次函数的对称轴为1122b x a =-=>，且抛物线的开口向上，故12x =时，y 的最小值为154-．【例2】如图，平面直角坐标系中，矩形OABC 的边OA 在y 轴的正半轴上，OC 在x 轴的正半轴上，已知()04A ，、()50C ，．作AOC ∠的平分线交AB 于点D ，连接CD ，过点D 作DE CD ⊥交OA 于点E ． ⑴求点D 的坐标；⑵求证：ADE BCD △≌△；⑶抛物线2424455y x x =-+经过点A 、C ，连接AC ．探索：若点P 是x 轴下方抛物线上一动点，过点P 作平行于y 轴的直线交AC 于点M ．是否存在点P ，使线段MP 的长度有最大值？若存在，求出点P 的坐标；若不存在，请说明理由．(2012西宁)【解析】⑴ 证明：∵OD 平分AOC ∠，∴AOD DOC ∠=∠， ∵四边形AOCB 是矩形， ∴AB OC ∥．∴ADO DOC ∠=∠， ∴AOD ADO ∠=∠．∴OA AD =（等角对等边）．∴D 点坐标为()44，． ⑵ 解：∵四边形AOCB 是矩形 ∴90OAB B ∠=∠=︒，BC OA =． ∵OA AD =， ∴AD BC =． ∵ED DC ⊥， ∴90EDC ∠=︒．∴90ADE BDC ∠+∠=︒． ∵90BDC BCD ∠+∠=︒， ∴ADE BCD ∠=∠． 在ADE △和BCD △中， DAE B AD BCADE BCD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ADE BCD △≌△（ASA ） ⑶ 解：存在．∵二次函数解析式为：2424455y x x =-+，点P 是抛物线上一动点， ∴设P 点坐标为2424455t t t ⎛⎫-+ ⎪⎝⎭，设AC 所在直线函数关系式为y kx b =+，()04A ，、()50C ，， ∴4540b k =⎧⎨+=⎩ ∴454k b ⎧=-⎪⎨⎪=⎩． ∴AC 所在直线函数解析式为：445y x =-+．∵PM y ∥轴，∴445M t t ⎛⎫-+ ⎪⎝⎭，．2424444555PM t t t ⎛⎫⎛⎫=--++-+ ⎪ ⎪⎝⎭⎝⎭2445t t =-+24255554t t ⎛⎫=--++ ⎪⎝⎭245552t ⎛⎫=--+ ⎪⎝⎭∴当52t =时，5PM =最大值． ∴所求的P 点坐标为532⎛⎫- ⎪⎝⎭，．【例3】 如图，有长为30米的篱笆，围成中间隔有一道篱笆的长方形的花圃，且花圃的长可借用一段墙体（墙体的最大可用长度10a =米）， 当AB 为多少米时，围成的花圃面积最大．（人大附练习题） 【解析】 设AB 长为x 米，则花圃的面积()()()2223033303103575S x x x x x x x =-=-+=--=--+显然0303100x x <-⎧⎨>⎩≤解得20103x <≤，当203x =时，max 2003S =（平方米）.【例4】如图，已知抛物线经过点()10A -，、()30B ，、()03C ，三点． （1）求抛物线的解析式．（2）点M 是线段BC 上的点（不与B ，C 重合），过M 作MN y ∥轴交抛物线于N ，若点M 的横坐标为m ，请用m 的代数式表示MN 的长．（3）在（2）的条件下，连接NB 、NC ，是否存在m ，使BNC △的面积最大？若存在，求m 的值；若不存在，说明理由． (2012黔东南州) 【解析】（1）设抛物线的解析式为：()1y a x =+()3x -，则：()01a +()033-=，1a =-； ∴抛物线的解析式：()()21323y x x x x =-+-=-++．（2）设直线BC 的解析式为：y kx b =+，则有： 303k b b +=⎧⎨=⎩， 解得13k b =-⎧⎨=⎩；故直线BC 的解析式：3y x =-+．已知点M 的横坐标为m ，则()3M m m -+，、()223N m m m -++，； ∴故()()22233303N m m m m m m =-++--+=-+<<．（3）如图；∵()1122BNC MNC MNB S S S MN OD DB MN OB =+=+=⋅△△△，∴()()213327332032228BNC S m m m m m ⎛⎫=-+⋅=--+<< ⎪⎝⎭△； ∴当32m =时，BNC △的面积最大，最大值为278．典题精练题型二：二次函数综合应用xyNMOCBA【例5】如图1，在平面直角坐标系xOy 中，直线l ：34y x m =+与x 轴、y 轴分别交于点A 和 点B (0，1-)，抛物线212y x bx c =++经过点B ，且与直线l 的另一个交点为C (4，n )． (1) 求n 的值和抛物线的解析式；(2) (2) 点D 在抛物线上，且点D 的横坐标为t （0< t <4）．DE ∥y 轴交直线l 于点E ，点F 在直线l 上，且四边形DFEG 为矩形（如图2）．若矩形DFEG 的周长为p ，求p 与t 的函数关系式以及p 的最大值． （2013西城一模）【解析】（1）∵直线l ：34y x m =+经过点B （0，1-）， ∴1m =-.∴直线l 的解析式为314y x =-. ∵直线l ：314y x =-经过点C （4，n ）， ∴34124n =⨯-=. ∵抛物线212y x bx c =++经过点C （4，2）和点B （0，1-），∴21244,21.b c c ⎧=⨯++⎪⎨⎪-=⎩ 解得5,41.b c ⎧=-⎪⎨⎪=-⎩ ∴抛物线的解析式为21524y x =- （2）∵直线l ：314y x =-与x ∴点A 的坐标为（43，0）.∴OA=43.在Rt △OAB 中，OB=1，∴AB 53=.∵DE ∥y 轴， ∴∠OBA =∠FED .∵矩形DFEG 中，∠DFE =90°， ∴∠DFE =∠AOB =90°.∴△OAB ∽△FDE .∴OA OB ABFD FE DE==. ∴45OA FD DE DE AB =⋅=，35OB FE DE DE AB =⋅=.∴p =2(FD+ FE )=43142()555DE DE ⨯+=.∵D （t ，215124t t --），E （t ，314t -），且04t <<，∴223151(1)(1)24242DE t t t t t =----=-+.∴22141728(2)5255p t t t t =⨯-+=-+.∵2728(2)55p t =--+，且705-<，∴当2t =时，p 有最大值528.【例6】如图，在平面直角坐标系xOy 中，四边形ABCD 是菱形，顶点A 、C 、D 均在坐标轴上，且5AB =，4sin 5B =．（1）求过A 、C 、D 三点的抛物线的解析式；（2）记直线AB 的解析式为1y mx n =+，（1）中抛物线的解析式为22y ax bx c =++，求当12y y <时，自变量x 的取值范围；（3）设直线AB 与（1）中抛物线的另一个交点为E ，P 点为抛物线上A 、E 两点之间的一个动点，当P 点在何处时，PAE △的面积最大？并求出面积的最大值．（2012攀枝花）【解析】（1）∵四边形ABCD 是菱形，∴5AB AD CD BC ====，4sin sin 5B D -=；Rt OCD △中，sin 4OC CD D =⋅=，3OD =；2OA AD OD =-=，即：()20A -，、()54B -，、()04C ，、()30D ，； 设抛物线的解析式为：()2y a x =+()3x -，得：()234a ⨯-=，23a =-；∴抛物线：222433y x x =-++．（2）由()20A -，、()54B -，得直线AB ：14835y x =--； 由（1）得：2222433y x x =-++，则：2483322433y x y x x ⎧=--⎪⎪⎨⎪=-++⎪⎩， 解得：1120x y =-⎧⎨=⎩，225283x y =⎧⎪⎨=-⎪⎩；由图可知：当12y y <时，25x -<<． （3）∵12APE S AE h =⋅△， ∴当P 到直线AB 的距离最远时，ABC S △最大；若设直线L AB ∥，则直线L 与抛物线有且只有一个交点时，该交点为点P ； 设直线L ：43y x b =-+，当直线L 与抛物线有且只有一个交点时，24224333x b x x -+=-++，且0=△； 求得：112b =，即直线L ：41132y x =-+； 可得点3722P ⎛⎫⎪⎝⎭，．由（2）得：2853E ⎛⎫- ⎪⎝⎭，，则直线PE ：1193y x =-+； 则点27011F ⎛⎫ ⎪⎝⎭，，4911AF OA OF =+=；∴PAE △的最大值：1492873432113212PAE PAF AEF S S S ⎛⎫=+=⨯⨯+= ⎪⎝⎭△△△．综上所述，当3722P ⎛⎫ ⎪⎝⎭，时，PAE △的面积最大，为34312．【例7】如图，在平面直角坐标系中，直线112y x =+与抛物线23y ax bx =+-交于A ，B 两点， 点A 在x 轴上，点B 的纵坐标为3．点P 是直线AB 下方的抛物线上一动点（不与A ，B 重合），过点P 作x 轴的垂线交直线AB 与点C ，作PD AB ⊥于点D ⑴求a ，b 及sin ACP ∠的值 ⑵设点P 的横坐标为m①用含m 的代数式表示线段PD 的长，并求出线段PD 长的最大值；②连接PB ，线段PC 把PDB △分成两个三角形，是否存在适合的m 值，使这两个三角形的面积之比为9:10？若存在，直接写出m 值；若不存在，说明理由．(2012河南) 【解析】⑴ 由1102x +=，得到2x =-，∴(20)A -，由1132x +=，得到4x =， ∴(43)B ，． ∵23y ax bx =+-经过A ，B 两点，22(2)230,4430a b a b ⎧-⋅--=⎪⎨⋅+-=⎪⎩∴1122a b ==-，． 设直线A ，B 与y 轴交于点E ，则(01)E ，∵PC y ∥轴，∴ACP AEO ∠=∠． ∴25sin sin 5OA ACP AEO AE ∠=∠=== ⑵ 由⑴可知抛物线的解析式为211322y x x =-- ∴211322P m m m ⎛⎫-- ⎪⎝⎭，，112C m m ⎛⎫+ ⎪⎝⎭，2211111342222PC m m m m m ⎛⎫=+---=-++ ⎪⎝⎭在Rt PCD △中，sin PD PC ACP =⋅∠212542m m ⎛⎫=-++ ⎪⎝⎭yxPOABCD21)m =-+∵0< ∴当1m =时，PD． ②存在满足条件的m 值，52m =或329．分别过点D ，B 作DF PC ⊥，垂足分别为F ，G ．在Rt PDF △中，21(28).5DF m m ==--- 又4,BG m =- ∴21(28)2545PCDPBCm m S DF m S BG m ---+===-△△ 当29510PCD PBC S m S +==△△时． 解得52m =． 当21059PCD PBCS m S +==△△时，解得329m =．A 讲训练1. ⑴ 已知实数x ，y 满足方程()()224233213x x y y ++++=，则x y += .⑵ 若实数a ，b 满足21a b +=，则2227a b +的最小值是 .【解析】 ⑴ 43-.⑵ 2.训练2. 已知a b 、均为整数，直线b ax y +=与三条抛物线,32+=x y 762++=x x y 和542++=x x y 交点的个数分别是2,1,0，若.62222的最大值，求y x x ay bx +=+（大兴期末）【解析】 由题意得：22236745x ax bx x ax b x x ax b+=+++=+++=+∵方程有两个不相等的实根，方程有两个相等实根，方程无实根.∴2122234120124808440a b a a b a a b ∆=+->∆=-++=∆=-+-< 由2∆得24(128)b a a =--+代入得222212(128)084(128)0a a a a a a a ⎧---+>⎪⎨----+<⎪⎩解此不等式组，得533a <<因为a 是整数，所以有2a =于是412b =，得3b = ∴2,3a b == ∴22326x y x +=22632x x y -=∵226302x x y -=≥∴2630x x -≥ ∴(2)0x x -≥020x x ⎧⎨-⎩≥≥或020x x ⎧⎨-⎩≤≤ ∴02x ≤≤设222222631193(3)2222x x Z x y x x x x -=+=+=-+=--+思维拓展训练(选讲)∴当3x ≤时，函数Z 随x 的增大而增大， ∴当2x =时，=4Z 最大值即当2x =时，22x y +有最大值4.训练3. 如图，抛物线c bx x y ++-=2与x 轴交于(10)A ，,(30)B -，两点， ⑴ 求该抛物线的解析式；⑵ 设⑴中的抛物线交y 轴于C 点，在该抛物线的对称轴上是否存在点Q ，使得△QAC 的周长最小？若存在，求出Q 点的坐标；若不存在，请说明理由.⑶ 在⑴中的抛物线上的第二象限上是否存在一点P ，使△PBC 的面积最大？若存在，求出点P 的坐标及△PBC 的面积最大值.若没有，请说明理由.【解析】⑴将A (1，0)，(30)B -，代2y x bx c =-++中得 10930b c b c -++⎧⎨--+=⎩＝ ∴23b c =-⎧⎨=⎩∴抛物线解析式为：223y x x =--+⑵存在. 理由如下：由题知A 、B 两点关于抛物线的对称轴1x =-对称 ∴直线BC 与1x =-的交点即为Q 点， 此时△AQC 周长最小 ∵223y x x =--+∴C 的坐标为：(0，3) 直线BC 解析式为：3y x =+ Q 点坐标即为13x y x =-⎧⎨=+⎩的解 ∴12x y =-⎧⎨=⎩ ∴Q (－1，2)⑶答：存在. 理由如下：设P 点2(23) (30)x x x x --+-<<，∵92BPC BOC BPCO BPCO S S S S ∆∆=-=-四边形四边形 若BPCO S 四边形有最大值，则BPC S ∆就最大， ∴BPE BPCO PEOC S S S ∆+Rt 四边形直角梯形＝11()22BE PE OE PE OC =⋅++ ＝2211(3)(23)()(233)22x x x x x x +--++---++ ＝233927()2228x -+++当32x =-时，BPCO S 四边形最大值＝92728+∴BPC S ∆最大＝9279272828+-=当32x =-时，215234x x --+=∴点P 坐标为315( )24-，训练4. 已知抛物线2y x bx =+，且在x 轴的正半轴上截得的线段长为4，对称轴为直线x c =．过点A 的直线绕点(0)A c ，旋转，交抛物线于点()B x y ，，交y 轴负半轴于点C ，过点C 且平行于x 轴的直线与直线x c =交于点D ，设AOB △的面积为1S ，ABD △的面积为2S ． ⑴ 求这条抛物线的顶点的坐标；⑵ 判断1S 与2S 的大小关系，并说明理由．(大兴二模) 【解析】 ⑴∵ 抛物线y =x 2+bx ，在x 轴的正半轴上截得的线段的长为4，可知对称轴为直线x =2． ∴ A (2，0)，设图象与x 轴的另一个交点E 的坐标为 (4，0)， ∴ 抛物线为 y = x 2 +b x 经过点E (4，0) ．∴4b =- ，∴24y x x =-．∴ 顶点坐标为（2，－4）．⑵ S 1与S 2的大小关系是：S 1 = S 2 理由如下： 设经过点A （2，0）的直线为y=kx+b (k ≠0)．∴ 0 =2k +b ．∴ k =21-b ． ∴ y =b x b+-2． ∴ 点B 1的坐标为（x 1 ，b x b+-12）， 点B 2的坐标为（x 2 ，b x b+-22）．当交点为B 1时，b x bb x b S -=+-⨯⨯=11122221， 12221x b S -⨯⨯=b x bx b -=--=112)2(2． 21S S =∴．当交点为B 2时， b x bb x b S +-=+-⨯⨯=22122221 22122-⨯⨯=x b S =b x bx b +-=--=222)2(2． ∴ S 1 = S 2．综上所述，S 1 = S 2．B 讲训练1. 如图，一面利用墙，用篱笆围成的矩形花圃ABCD 的面积为2m S ，平行于墙的BC 边长为m x ．⑴若墙可利用的最大长度为10m ，篱笆长为24m ，花圃中间用一道篱笆隔成两个小矩形，求S 与x 之间的函数关系式．⑵在⑴的条件下，围成的花圃的面积为245m 时，求AB 的长．能否围成面积比245m 更大的花圃？如果能，应该怎样围？如果不能，请说明理由．⑶若墙可利用最大长度为40m ，篱笆长77m ，中间用n 道篱笆隔成小矩形，且当这些小矩形为正方形和x 为正整数时，请直接写出一组满足条件的x 、n 的值．【解析】 ⑴ 由题意得：2241833x S x x x -=⋅=-+，()010x <≤⑵ 由218453S x x =-+=解得：115x =（舍去），29x = ∴9x =时，2453xAB -== 又()22118124833S x x x =-+=--+，()010x <≤又∵103a =-<，抛物线的开口向下∴当10x =米时，S 最大为1403平方米 ∴平行于院墙的一边长大于9且小于等于10时，就能围成面积比45平方米更大的花圃．⑶ ∵()2771x x n n +⋅+=+()040x <≤，即12771x n ⎛⎫+= ⎪+⎝⎭又∵n 为自然数时，12231n <++≤ ∴7723x<≤ ∴22538.53x <≤检验：当33x =，2n =；当35x =，4n =；当38x =，37n =．训练2. 已知a b 、均为整数，直线b ax y +=与三条抛物线,32+=x y 762++=x x y 和542++=x x y 交点的个数分别是2,1,0，若.62222的最大值，求y x x ay bx +=+（大兴期末）【解析】 由题意得：22236745x ax bx x ax b x x ax b+=+++=+++=+∵方程有两个不相等的实根，方程有两个相等实根，方程无实根.∴2122234120124808440a b a a b a a b ∆=+->∆=-++=∆=-+-< 由2∆得24(128)b a a =--+代入得222212(128)084(128)0a a a a a a a ⎧---+>⎪⎨----+<⎪⎩ 解此不等式组，得533a <<因为a 是整数，所以有2a = 于是412b =，得3b = ∴2,3a b == ∴22326x y x += 22632x x y -=∵226302x x y -=≥∴2630x x -≥ ∴(2)0x x -≥020x x ⎧⎨-⎩≥≥或020x x ⎧⎨-⎩≤≤ ∴02x ≤≤设222222631193(3)2222x x Z x y x x x x -=+=+=-+=--+∴当3x ≤时，函数Z 随x 的增大而增大， ∴当2x =时，=4Z 最大值即当2x =时，22x y +有最大值4.训练3. 如图，在平面直角坐标系xOy 中，已知二次函数2+2y ax ax c =+的图像与y 轴交于点(03)C ，，与x 轴交于A 、B 两点，点B 的坐标为(30)-，⑴ 求二次函数的解析式及顶点D 的坐标；⑵点M 是第二象限内抛物线上的一动点，若直线OM 把四边形ACDB 分成面积为1:2的两部分，求出此时点M 的坐标； ⑶ 点P 是第二象限内抛物线上的一动点，问：点P 在何处时CPB △的面积最大？最大面积是多少？并求出 此时点P的坐标.（东城二模） 【解析】 ⑴ 由题意，得：3,960.c a a c =⎧⎨-+=⎩解得：1,3.a c =-⎧⎨=⎩所以，所求二次函数的解析式为：223y x x =--+顶点D 的坐标为(14)-，⑵ 易求四边形ACDB 的面积为9. 可得直线BD 的解析式为y=2x+6设直线OM 与直线BD 交于点E ，则△OBE 的面积可以为3或6.①当1=9=33OBE S ⨯△时，易得E 点坐标(22)-，，直线OE 的解析式为y x =-.设M 点坐标()x x -，，y xOMEDCB A2122 3.).x x x x x -=--+==舍∴M② 当1=9=63OBE S ⨯△时，同理可得M 点坐标．∴ M 点坐标为(14)-，⑶如图，连接OP ，设P 点的坐标为(),m n ， 因为点P 在抛物线上，所以232n m m =-+-， 所以PB PO OPB OB S S S S =+-△C △C △△C 111()222OC m OB n OC OB =⋅-+⋅-⋅()339332222m n n m =-+-=--()22333273.2228m m m ⎛⎫=-+=-++ ⎪⎝⎭因为3<0m -<，所以当32m =-时，154n =.CPB △的面积有最大值27.8所以当点P 的坐标为315(,)24-时，CPB △的面积有最大值，且最大值为27.8训练4. 已知：如图，在平面直角坐标系xOy 中，边长为的等边ABC △随着顶点A 在抛物线2y x =-上运动而运动，且始终有BC ∥x 轴．⑴ 当顶点A 运动至与原点重合时，顶点C 是否在该抛 物线上？⑵ABC △在运动过程中有可能被x 轴分成两部分，当上下两部分的面积之比为1∶8（即:1:8S S =上部分下部分）时，求顶点A 的坐标；⑶ABC △在运动过程中，当顶点B 落在坐标轴上时，直接写出顶点C 的坐标．【解析】 ⑴ 当顶点A 运动至与原点重合时，设BC 与y 轴交于点D ，如图所示．∵BC ∥x 轴，BC=AC=32，∴CD =，3=AD ． ∴C 点的坐标为)3,3(-． ∵当3=x 时，23y =--．∴当顶点A 运动至与原点重合时，顶点C 在抛物线上．⑵ 过点A 作AD BC ⊥于点D ，设点A 的坐标为（x，2x -）． ∵:1:8S S =上部分下部分，∴23()AD x =-． ∵等边ABC △的边长为 ∴sin603AD AC =⋅︒=．∴23()3x -=．∴210x --=． 解方程，得 =x 2．∴顶点A的坐标为2,1)或2,1)．⑶当顶点B 落在坐标轴上时，顶点C 的坐标为0)、0)、6)-．题型一 二次函数的最值 巩固练习【练习1】 某商店销售一种进价为20元/双的手套，经调查发现，该种手套每天的销售量w (双) 与销售单价x (元)满足280w x =-+(20≤x ≤40),设销售这种手套每天的利润为y （元）. ⑴ 求y 与x 之间的函数关系式；⑵ 当销售单价定为多少元时, 每天的利润最大？最大利润是多少？（海淀期末）【解析】 ⑴(20)(280)(20)y w x x x =-=-+-221201600x x =-+-.⑵22(30)200y x =--+.∵2040x ≤≤, a =-2<0,∴当30x =时，200y =最大值.答：当销售单价定为每双30元时，每天的利润最大，最大利润为200元.【练习2】 已知2221x y +=，求225x y +的最大值和最小值. 【解析】 222215552292525222222510x x y x x x x ⎛⎫⎛⎫+=+-=-++=--+⎪ ⎪⎝⎭⎝⎭∵22210y x =-≥，∴11x -≤≤当25x =时，取到最大值为2910；当1x =-时，取到最小值为2-.【练习3】 已知：关于x 的一元二次方程22(2)0x n m x m mn +-+-=①.⑴ 求证：方程①有两个实数根；⑵ 若10m n --=，求证方程①有一个实数根为1；⑶ 在⑵的条件下，设方程①的另一个根为a . 当2x =时，关 于m 的函数1y nx am =+与()2222y x a n m x m mn =+-+-的图 象交于点A 、B （点A 在点B 的左侧），平行于y 轴的直线l 与 1y 、2y 的图象分别交于点C 、D . 当l 沿AB 由点A 平移到点B 时，求CD 的最大值.【解析】 ⑴ 证明：()()22224n m m mn n ∆=---=.∵20n ≥，∴0∆≥.∴方程①有两个实数根.⑵ 解：由10m n --=，得1m n -=当x =1时，等号左边212n m m mn =+-+-复习巩固my 12344321-1-2-3-3-2-1O()121210n m m m n n m m n m =+-+-=+-+=+-=.等号右边=0. ∴左边=右边.∴ x =1是方程①的一个实数根.⑶ 解：由求根公式，得22m n nx -±=.x =m 或x m n =- ∵1m n -=， ∴ a =m .当x =2时，y 1=2n +m 2=2（m -1）+m 2= m 2 +2m -2，y 2=22+ 2m （n -m -m ）+m （m -n ）=4 +2m （-1-m ）+m 224m m =--+. 如图，当l 沿AB 由点A 平移到点B 时，CD = y 2-y 1=2336m m --+=-3（m +12）2 +274由 y 1=y 2，得m 2 +2m -2=-2m 2-m +4.解得m =-2或m =1. ∴ m A =-2，m B =1. ∵-2<12-<1，∴当m =12-时，CD 取得最大值274.题型二 二次函数综合应用 巩固练习【练习4】 如图，抛物线2(1)y x k =++与x 轴交于A 、B 两点，与y轴交于点(03)C -，．⑴ 求抛物线的对称轴及k 的值；⑵ 在抛物线的对称轴上存在一点P ，使得PA PC +的值最 小，求此时点P 的坐标；⑶ 设点M 是抛物线上的一动点，且在第三象限．当M 点 运动到何处时，△AMB 的面积最大？求出△AMB 的最大面 积及此时点M 的坐标.（平谷一模）【解析】 ⑴ 抛物线2(1)y x k =++的对称轴为：直线1x =-．Q 抛物线2(1)y x k =++过点(03)C -，，则23(01)k -=++， 4k ∴=-． ⑵ 如下图，根据两点之间线段最短可知，当P 点在线段AC 上就可使PA PC +的值最小．又因为P 点要在对称轴上，所以P 点应为线段AC 与对称轴直线1x =-的交点．由⑴可知，抛物线的表达式为：22(1)423y x x x =+-=+-．令0y =，则2230x x +-=．解得：1231x x =-=，．则点A B 、的坐标分别是(30)A -，、(10)B ，． 设直线AC 的表达式为y kx b =+，则303k b b -+=⎧⎨=-⎩，. 解得 13.k b =-⎧⎨=-⎩，所以直线AC 的表达式为3y x =--． 当1x =-时，(1)32y =---=-. 所以，此时点P 的坐标为(12)--，．⑶ 依题意得：当点M 运动到抛物线的顶点时，AMB △的 面积最大．由抛物线表达式2(1)4y x =+-可知，抛物线的顶点坐标为(14)--，． ∴点M 的坐标为(14)--，．AMB △的最大面积1(31)482AMB S =⨯+⨯=△．【练习5】 如图, 已知抛物线经过坐标原点O 及)0,32(-A ，其 顶点为B (m ,3),C 是AB 中点，点E 是直线OC 上的一 个动点 (点E 与点O 不重合)，点D 在y 轴上, 且EO =ED .⑴ 求此抛物线及直线OC 的解析式；⑵ 当点E 运动到抛物线上时, 求BD 的长；⑶ 连接AD , 当点E 运动到何处时，△AED 的面积为433，请直接写出此时E 点的坐标.（海淀期末）【解析】 ⑴∵ 抛物线过原点和A (0-)，∴ 抛物线对称轴为3-=x . ∴ B (3).设抛物线的解析式为2(3y a x =+. ∵ 抛物线经过(0, 0), ∴330a += . ∴1a =- .∴3)3(2++-=x y 2.y x =--∵ C 为AB 的中点, A (0-)、B (3)， 可得 C (32) .可得直线OC 的解析式为x y 33-=. ⑵连结OB . 依题意点E 为抛物线x x y 322--=与直线x y 33-=的交点（点E 与点O 不重合）.由2,y x y x ⎧=⎪⎨⎪=--⎩， 解得5,3x y ⎧=⎪⎪⎨⎪=⎪⎩ 或0,0.x y =⎧⎨=⎩（不合题意，舍）.∴ E（53） 过E 作EF ⊥y 轴于F , 可得OF =53，∵ OE =DE ，EF ⊥y 轴， ∴ OF=DF .∴ DO =2OF =103.∴ D (0, 10).∴ BD=⑶E 点的坐标为(32)或12-).。