线性模型参数的估计理论(陈希孺[等]著)思维导图

R2 = 1-
(yi -
i )2 = 1-
残差平方和
(yi - y)2
总偏差平方和
①和②的R2分别为0.7325和0.9983
R2越大 ，表示残差平方和越小 ，即模型的拟合效果越好； R2越小 ，表示残差平方和越大 ，即模型的拟合效果越差. 显然0≤R2 ≤1 ， R2越接近1 ，则线性回归刻画的效果越好.
2 ≈ 0 .669, Q 2 =
2 ≈ 0 .004
Q2明显小于Q1 ，说明非线性回归方程的拟合效果 要优于线性回归方程.
探究新知
思考 ：对于通过创纪录时间预报世界纪录的问题 ，我们建立了两个回归模型， 得到了两个回归方程 ，你能判断哪个回归方程拟合的精度更好吗？
（3) 利用决定系数R2刻画回归效果.
1.残差等于观测值减预测值 = y -
2.残差的平方和越小越好； 3.原始数据中的可疑数据往往是残差绝对值过大的数据； 4. 对数据刻画效果比较好的残差图特征:残差点比较均匀的集 中在水平带状区域内 .
一般地, 建立经验回归方程后,通常需要对模型刻画数据的效 果进行分析.借助残差分析还可以对模型进行改进,使我们能根据改 进模型作出更符合实际的预测与决策.
探究新知
思考: 儿子身高与父亲身高的关系 ，运用残差分析所得的一元线性回归模型的 有效性吗？
: 作图时纵坐标为残差, 横坐标可以选为样本编号, 或身高数据 或体重估计值等 ，这样作出的图形称为残差图 .
探究新知
为了使数据更加直观 ，用父亲身高作为横坐标 ，残差作为 纵坐标 ，可以画出残差图 ，如下图所示：
再根据求解线性回归模型的方法求出a, b. 求解线性回归模型的方法求出a, b.
1.残差平方和

下面讨论更为一般的情况。 假设在t1, t2, …, tm时刻对Y及X的观测值序列已经被我们获得，并且用
y(i), x1(i), x2(i), x3(i), … i = 1,2, …, m 来表示这些观测数据。显然，可以用 m 个方程组来表示量测数据与估计值之间的关系
⎧ y(1) = θ1x1(1) +θ 2 x2 (1) +L+θ n xn (1)
从图中可看到，前两条线都仅能满足两个点的要求，而对其它点的误差都很大，其 6 个点的 误差平方累计分别为 0.49 和 0.42。第三条线能满足三个点的要求，但误差平方累计更大，为 1.58。 显然我们需要找到一条更为理想的直线来取得较小的误差。例如图中的红色短划线，它的方程 为 y=1.697 + 0.294x，误差平方累计为 0.25。这条线是怎样得到的呢？它是用最小二乘法得到的。
z
−2
，在其输入端加入 M 序列输入后
所得到的输出输入数据见下表，请利用这些数据辨识出系统的传递函数的系数。
k
1
2
3
4
5
6
7
8
9
10
输入 u
1
0
1
1
0
0
1
1
1
0
输出 y -0.45 -0.01
1.15
2.56
1.92
-0.30 -0.80 0.91 2.92 2.40
解： 已知系统阶数 n=2，有 4 个未知数。将式（4.4）展开 y(k) = −a1 y(k −1) − a2 y(k − 2) + b0u(k) + b1u(k −1) 根据要求，观测次数 N>2n+1，取 N 为 6，k=3

E(β XX1Xε -β )(β XX1Xε -β )
E X X 1 X ε ε X X X 1 X X 1 X E ε ε ( ) X X X 1
X X 1 X E2 I ( n ) X X X 1 2 X X 1
三、 参数估计量的性质
性质1 βˆ 是随机向量y的一个线性变换。
β ˆ (XX)-1Xy 性质2 βˆ 是β的无偏估计。
E(βˆ ) E ((X X)-1 Xy) (X X)-1XE(y) (X X)-1XE( Xβε) (X X)-1X Xββ
性质 3 D（βˆ )=σ 2(X′X)-1
Lxx
x 2
Lxx

2
L xx

性质四（高斯-马尔可夫定理）
在假设 E( y) X ，D( y) 2In 下， 的任一线性函数 的 最小方差线性无偏估计为 ˆ ，其中 是任一不为零的 p 1 维向量， ˆ 是 最小二乘估计。 证明：（1）ˆ ( X X )1 X y 是 y 的线性函数，所以是线性估计。
D(β ˆ)coβ vˆ,β (ˆ)
E(β ˆ(Eβ ˆ)β (ˆEβ ˆ))E(β ˆ(β )β (ˆβ ))
EXX1XyβXX1Xyβ


EXX1X(Xβ ε )β XX1X(Xβ ε )β
在正态假定下:
y～N(Xβ, 2In)
E(y)=Xβ
var(y)= 2In
3. 多元线性回归方程的解释
例1
y表示空调机的销售量,
x1表示空调机的价格, x2表示消费者可用于支配的收入。
y=β0+β1x1+β2x2+ε

，得到的数据如下表所示.
编号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
下面，我们用散点图对上面的数据进行分析。
新知讲解
问题1 这是上述的数据画出来的散点图，你发现了什么？
如图所示.可以发现，散点大致分布在一条
从左下角到右上角的直线附近，表明儿子
身高和父亲身高线性相关.
利用统计软件，求得样本相关系数为 ≈
. ，表明儿子身高和父亲身高正线性
相关，且相关程度较高.
如母亲身高、生活环境、饮食习惯等作为随机误差，得到刻画两个
变量之间关系的线性回归模型.其中，随机误差是一个随机变量.
概念生成
用表示父亲身高，表示儿子身高，表示随机误差.假定随机误差
的均值为，方差为与父亲身高无关的定值 ，则它们之间的关系
= + + ，
可以表示为
() = ，() = .
的没有线性相关关系；当||＝时，成对数据都落在一条直线上.
新课导入
通过前面的学习，我们已经了解到，根据成对样本数据的散点图和样本相关
系数，可以推断两个变量是否存在相关关系、是正相关还是负相关，以及线
性相关程度的强弱等.
进一步地，如果能像建立函数模型刻画两个变量之间的确定性关系那样，通
过建立适当的模型刻画两个随机变量的相关关系，那么我们就可以利用这个

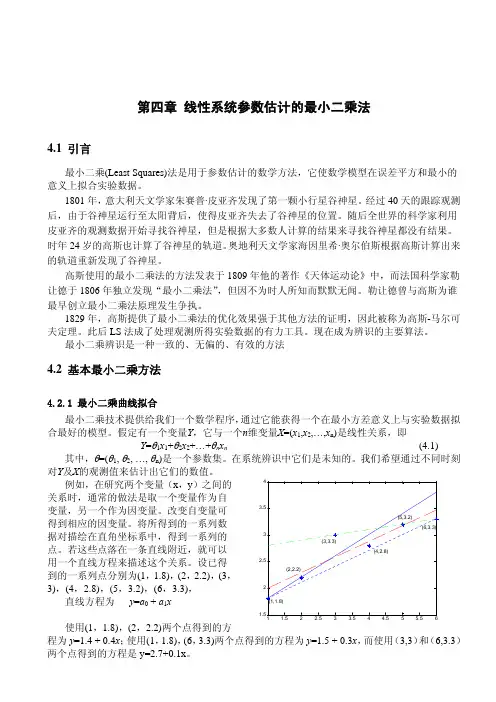
文章编号:1002—1566(2004)01—0077—04广义线性模型(九)陈希孺(中国科学院研究生院,北京100039)摘要:本讲座是广义线性模型这个题目的一个比较系统的介绍。

主要分3部分:建模、统计分析与模型选择和诊断。

写作时依据的主要参考资料是L .F ahrmeir 等人的《M ultivariate Statistical M od -eling Based o n Generalized Linear M odels 》。

关键词:广义线性模型;建模;统计分析;模型选择和诊断中图分类号:O212文献标识码:AGeneralized Linear ModelsCHEN Xi -ru(Graduate school of Chinese academia of science ,Beijing 100039,China )A bstract :This set of articles gives an introduction to generalized linear models .T hey can be divided into three parts ;M odel building ,statistical inference and M odel diagnostics .The presentation is mainly based on L .Fahrmeir et al .《M ultivariate Statistical M odeling Based on G eneralized Linear M odels 》.Key words :g eneralized linear models ;model building ;statistical inference ;model diagnostics3.2　模型选择(一)从若干个备选模型中选取一个模型选择包含以下一些方面·因变量Y 分布的选择;·联系函数的选择;·自变量的选择;·z (x )的选择。

5
2024/11/25
P(Y 65 X 80) P(Y 70 X 80) P(Y 75 X 80) 1 .
5
5
第6页/共25页
• 对于同一等级收入水平，消费支出Y的平均值称
为条件期望，记为E（Y｜X）。
例如: E(Y X 80) 55 1 60 1 65 1 70 1 75 1 65 55555
身高的趋势，而矮个子父母的子女身高有高于其父母身
高的趋势，结论：父母所生子女有回归于人类平均身高 的趋势，故某人种的平均身高是相当稳定的。
——见1889年F.Gallton的论文《普用回归定律》。
回归的含义：任何变异的东西总有趋向于一般、平稳 的势头。
后来人们将此种方法普遍用于寻找变量之间的规律 。
1997 1904 8651 645.1429 3151 1962.851 -58.85057 -3.09%
2024/11/2平5 均百分误差在10%以内，表第明22页是/共一25个页 拟合得比较好的模型
21
拟合优度R2
1、作业记录
2.估计结果：系数、标准误差、 T统计量、显著性水平prob
残差标准差SE
边际消费<消费与收 入的比重。
y
y y
实际上消费与收入之间的关系式并不是准确的。 原因在于：
（1）消费还受到除收入以外的因素的影响； （2）线性关系是一种近似关系； （3）收入、消费数据也是一个近似 。
2024/11/25
3
第4页/共25页
• 为了更准确、符合实际地描述消费与收 入间的关系，必须引入随机误差μ。
随机扰动项是不可观察的，但可通过残差 （实际值与拟合值的差）进行估计。
2024/11/25
9

2
i =1
n
=b
2
( x - x)
i
i =1
n
2
n
2b ( xi - x )( yi y ) + ( yi y ) .
2
i =1
i =1
上式是关于b的二次函数，因此要使Q取得最小值，
当且仅当b的取值为 n
( xi - x )( yi y )

bˆ = i =1 n
.
2
( xi - x )
174.943
171.587
174.104
170.748
181.655
173.256
179.977
173.256
169.909
168.231
181.655
174.104
166.553
179.977
残差/cm
1.057
4.413
−4.104
−0.748
3.345
2.735
−1.977
0.735
0.091
−0.231
−3.655
−2.104
−1.553
2.023
为了使数更加直观，用父亲身高作为横坐标，残差作
为纵坐标，可以画出残差图，如下图所示.
残差 / cm
5
4
3
2
1
0 160 165
-1
-2
-3
-4
-5
170
175
180
父亲身高 / cm
185
观察残差表可以看到，残差有正有负，残差的绝对值
最大是4.413. 观察残差的散点图可以发现，残差比较均匀
i =1
综上，当a, b的取值为

编号 胸径/cm 树高/cm
1 2 3 4 5 6 7 8 9 10 11 12 18.1 20.1 22.2 24.4 26.0 28.3 29.6 32.4 33.7 35.7 38.3 40.2 18.8 19.2 21.0 21.0 22.1 22.1 22.4 22.6 23.0 24.3 23.9 24.7
yˆ2 0.4264398 ln(t 1895) 11.8012653.
②
在同一坐标系中画出成对数据散点图、非线性经验回归方程②的图象(蓝色) 以及经验回归方程①的图象(红色)，如图(5)所示. 我们发现，散点图中各散点都 非常靠近②的图象，表明非线性经验回归方程②对于原始数据的拟合效果远远 好于经验回归方程①.
问题人”. 下表给
出了1968年之前男子短跑100m世界纪录产生的年份和世界纪录的数据. 试
根据这些成对数据，建立男子短跑100m世界纪录关于纪录产生年份的经验
回归方程.
编号
12345678
年份
1896 1912 1921 1930 1936 1956 1960 1968
两个经验回归方程的残差(精确到0.001)如下表所示.
编号
t
eˆ uˆ
1 1896 0.591 -0.001
2 1912 -0.284 0.007
3
4
1921 1930
-0.301 -0.218
-0.012 0.015
5 1936 -0.196 -0.018
6 1956 0.111 0.052
7 1960 0.092 -0.021
i 1
i 1
∴ R2 1 0.01318 0.9991. 14.6784
0.025 2.31

X
i
i
可见，在满足一系列基本假设的情况下，模
型结构参数的最大或然估计量与普通最小二乘估 计量是相同的。
15
但是，随机误差项的方差的估计量是不同的。
解或然方程

s
2 m
L*
=
n
2s
2 m
+
1
2s
4 m
S(Yi
bˆ0
bˆ1 X i )2
=
0
即可得到sm2 的最大或然估计量为：
sˆ
2 m
22
3、有效性：在所有线性无偏估计量中，最 小二乘参数估计量具有最小方差。
23
（1）先求bˆ0 和bˆ1 的方差
Var(bˆ ) = Var( k Y ) =
1
ii
k 2Var(b
i
0
+b X
1i
+
m
i
)
=


x
i
x2
i

2
s
2 m

=
s
2 m
Sx2
i
Var(bˆ ) = Var w Y
条件 ，当
Q
对
b$ 0
、
b$ 1
的一阶偏导数为
0 时， Q 达到最小。即
Q

bˆ0 Q
bˆ1
=0 =0



(bˆ0 (bˆ0 +
+ bˆ1 bˆ1 X
X i
i

Yi) Yi) X
=
i
0 =
0

S Yi = nbˆ0 + bˆ1S X i

大多数有序模型是按下述机制产生 : 有一个( 或几个 , 此处只考虑一个的情形) 明显或潜在 ( 1. 70)
此处 Y 记样品的序值( 勿与前面的 Y = ( Y( ) ′ 混淆) 。 而 U 则是从该样品测 1), …, Y ( q) 得的值 。 例如 , 学生的考试成绩分不及格( 1) , 中( 2) , 良( 3) , 优( 4) 4 个等级 , U 为其考试分数 。
+x′ β r P( Y > r | x )= 1 -F ( θ β)= exp( - eθ ) r + x′

( 1. 76) ( 1. 77)
因此 log ( -log P ( Y > r |x ) )= θ β r + x′ 3 . 极大值分布模型 F 为极大值分布 : F( t) = exp( -e -t ) ,有 P( Y ≤ r |x )= exp( -e ) -log ( -log P ( Y ≤ r | x) )= θ β r + x′ 78) 知
年龄 吸烟史 从不吸 以前吸 现在吸 结果( 人数) 正常 边缘 不正常 577 192 682 27 20 46 4 15 47 7 3 11 0 7 27
〈40
调查某大学心理系即将毕业的学生对照工作前景的预 从不吸 164 期反应分 3 种 : 1. 不预期能找到合适工作 。 2 . 不清楚 。 3 . 40 -59 以前吸 145 预期毕业后可立即找到工作 。 数据 : 现在吸 245 的变量 U 及门限 -∞=θ 0 <θ 1 <… <θ k -1 <θ k =∞, 而定 Y = r , 当且仅当 θ r1 <U ≤θ r , r =1, …, k
( 四) 状态有序的情况 在旅行交通工具的例中 , 火车 、 汽车 、 轮船 、 飞机等状态 , 可以认为是 “ 无序” 的 。 一则因为 对其优劣次序的看法因人而异 , 二则即使同一个人 , 在不同情况下的排序也不同 。 在有些问题 中 , 目标状态有公认的优劣次序 , 如病情分 1 、 2、 3 期 , 产品品质分 1 、 2、 3 和等外等等级 , 都是公 认的由好到不好的次序 。 注意 : 即使在这种场合 , 其序号( 1 , 2 , …) 也无数量意义 。 例 1. 7 呼吸测验 : 目标 Y 分 3 状态 : 正常 、 边缘 、 不正 常 。 自变量 2 个 : 年龄 , 分〈40 和 40 -59 两级 , 吸烟史 : 分 “ 从不吸烟” 、 “以前级” 、 “ 现在吸” 3 级 , 数据 : 例 1. 8 找工作前景的调查

常用模型知识点总结图一、线性回归模型1.1. 简介线性回归是一种基本的回归分析方法，它用于建立因变量和一个或多个自变量之间的线性关系。

在线性回归模型中，我们假设因变量与自变量之间的关系是线性的，具体表达为：y = β0 + β1x1 + β2x2 + ... + βnxn + ε。

其中，y是因变量，x1, x2, ..., xn是自变量，β0是截距项，β1, β2, ..., βn是各自变量对应的系数，ε是残差项。

1.2. 模型的拟合与评价线性回归模型的拟合通常使用最小二乘法，即最小化残差平方和来估计模型参数。

评价模型通常可以使用R方值、调整R方值、均方差等指标来评估模型的拟合程度和预测能力。

1.3. 模型的应用线性回归模型适用于连续型因变量和定量型自变量之间的关系分析，可以用于价格预测、销售预测、生产量预测等领域。

二、逻辑回归模型2.1. 简介逻辑回归是一种用于解决分类问题的模型，它使用线性回归模型与逻辑函数的组合来进行分类。

逻辑回归模型的表达式可以表示为：p = 1 / (1 + e^(-z))，其中p为事件发生的概率，z为线性函数的和。

2.2. 模型的拟合与评价逻辑回归模型的拟合通常使用极大似然估计，即最大化事件发生的概率来估计模型参数。

评价模型通常可以使用准确率、召回率、精确率、F1值等指标来评估模型的分类能力。

2.3. 模型的应用逻辑回归模型适用于二分类和多分类问题，可以用于垃圾邮件过滤、信用评分、疾病预测等领域。

三、决策树模型3.1. 简介决策树是一种基于树形结构进行决策的模型，它通过特征选择和分裂节点的方式来建立分类或回归模型。

决策树模型的构建过程可以分为特征选取、节点分裂和剪枝三个步骤，其中特征选取通常使用信息增益、基尼系数等指标来选择。

3.2. 模型的拟合与评价决策树模型的拟合通常使用递归划分和修剪的方法来构建树结构，以最小化模型的复杂度和最大化模型的泛化能力。

评价模型通常可以使用准确率、召回率、精确率、F1值等指标来评估模型的分类能力。

§2.2 一元线性回归模型的参数估计
一、一元线性回归模型的基本假设 二、参数的普通最小二乘估计（OLS） 三、参数估计的最大或然法(ML) * 四、最小二乘估计量的性质 五、参数估计量的概率分布及随机干扰项方差的估计
11/18/2019
1
单方程计量经济学模型分为两大类： 线性模型和非线性模型
•线性模型中，变量之间的关系呈线性关系 •非线性模型中，变量之间的关系呈非线性关系
以上假设也称为线性回归模型的经典假设或 高斯（Gauss）假设，满足该假设的线性回归 模型，也称为经典线性回归模型（Classical Linear Regression Model, CLRM）。
11/18/2019
7
另外，在进行模型回归时，还有两个暗含的 假设：
假设5：随着样本容量的无限增加，解释变 量X的样本方差趋于一有限常数。即
11/18/2019
11
顺便指出 ，记 yˆi Yˆi Y
则有 可得
yˆi (ˆ0 ˆ1 X i ) (ˆ0 ˆ1 X e )

ˆ1 ( X i

X
)

1 n
ei
yˆi ˆ1xi
（**）
（**）式也称表示对均值 的离差。
11/18/2019
17
例2.2.1：在上述家庭可支配收入-消费支出例中，对 于所抽出的一组样本数，参数估计的计算可通过下面的 表2.2.1进行。
表 2.2.1 参数估计的计算表
Xi
Yi
xi
yi
xi yi
x i2
y
2 i
X
2 i
Yi 2
1 2 3 4 5 6 7 8 9 10 求和 平均

用Y表示男子短跑100m的世界纪录, t表示纪录产生的年份, 利用
一元线性回归模型
Y bx a e

2
E
(
e
)

0,
D
(
e
)

σ

来刻画世界纪录和世界纪录产生年份之间的关系. 根据最小二乘法,
由表中的数据得到经验回归方程为
yˆ1 0.02033743t 49.76913031
2
ˆ
(
y

y
)
i i
i 1
n
2
(
y

y
)
i
i 1
R2越大，说明模型拟合效果越好.
探究新知
建立非线性经验回归模型的基本步骤：
1.确定研究对象，明确哪个是解释变量，哪个是响应变量；
2.由经验确定非线性经验回归方程的模型；
3.通过变换，将非线性经验回归模型转化为线性经验回归模型；
4.按照公式计算经验回归方程中的参数，得到经验回归方程；
以及非线性经验回归方程②的图象(蓝色).
12.0
11.5
我们发现，散点图
中各散点都非常靠
近②的图像, 表明非
线性经验回归方程
②对于原始数据的
拟合效果远远好于
经验回归方Leabharlann ①.记录 / syˆ 1 = -0.02033743t + 49.76913031
11.0
10.5
10.0
9.5
1890 1900 1910
的经验回归直线，以及经验回归方程②所对应的经验回归曲线，得到下图.
显然绿色散点散布在蓝色
经验回归曲线的附近，远离

x6
8
10
12
y23
5
6
(1)请画出上表数据的散点图；
解 散点图如图所示.
x6
8
10
12
y23
5
6
(2)请根据上表提供的数据，用最小二乘法求出 y 关于 x 的经验回归方程y^
＝b^ x＋a^ ；
解 x ＝6＋8＋410＋12＝9， y ＝2＋3＋4 5＋6＝4，
4
x2i ＝62＋82＋102＋122＝344，
之间的随机 误差 .
例1 判断下列变量间哪些能用函数模型刻画，哪些能用回归模型刻画？ (1)某公司的销售收入和广告支出； (2)某城市写字楼的出租率和每平米月租金； (3)航空公司的顾客投诉次数和航班正点率； (4)某地区的人均消费水平和人均国内生产总值(GDP)； (5)学生期末考试成绩和考前用于复习的时间； (6)一辆汽车在某段路程中的行驶速度和行驶时间； (7)正方形的面积与周长.
i＝1
4
xiyi＝6×2＋8×3＋10×5＋12×6＝158，
i＝1
b^ ＝15384－4－4×4×9×924＝2104＝0.7，a^ ＝ y －b^ x ＝4－0.7×9＝－2.3，
故经验回归方程为y^ ＝x－2.3.
(3)试根据求出的经验回归方程，预测记忆力为9的同学的判断力.
n
xiyi－n x y
编号
1
2
3
4
5
6
7
父亲身高 174 170 173 169 182 172 180
儿子身高 176 176 170 170 185 176 178
编号
8 9 10 11 12 13 14
父亲身高 172 168 166 182 173 164 180

精品PPT课件----第十次课 一元线性回 归中的参数估计
51、山气日夕佳，飞鸟相与还。 52、木欣欣以向荣，泉涓涓而始流。
53、富贵非吾愿，帝乡不可期。 54、雄发指危冠，猛气冲长缨。 55、土地平旷，屋舍俨然，有良田美 池桑竹 之属， 阡陌交 通，鸡 犬相闻 。
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
70

性相关时，我们如何对成对样本数据建立一个模型进行预测？
提示
为了对两个变量线性相关关系进行预测，我们通常建立一元线性
回归模型进行预测．
新知探究
生活经验告诉我们，儿子身高与父亲身高存在正线性相关关系，即父亲的身高较
高时，儿子的身高通常也较高. 为了进一步研究两者之间的关系，有人调查了14
名男大学生的身高及其父亲的身高，得到的数据如表所示.
数作为所求直线的斜率和截距
.
上面这些方法虽然有一定的道理，但比较难操作，我们需要另辟蹊径.
思考4：为什么要假设E(e)=0，而不假设它为某个不
为0的常数？
因为随机误差表示大量已知和未知的影响因素之和，因为
误差是随机的，即取各种正负误差的可能性一样，它们会
相互抵消，所以随机误差的期望值应为0.
E (e) 0, E (Y ) bx a.
新知探究
用x表示父亲身高，Y表示儿子身高，e表示随机误差.
新知探究
用x表示父亲身高，Y表示儿子身高，e表示随机误差.
则它们之间的关系可以表示为下面的一元线性回归模型：
理解为
Y bx a e
E (Y ) bx a

2
E (e) 0, D(e)
思考7：你能结合上述身高案例解释模型中产生随机误差项e的原因吗？
(1)存在其他可能影响儿子身高Y的因素，如母亲身高、生活环境、饮食习惯
为bxi+a，即该子总体的均值与父亲身高是线性函数关系。
思考6：父亲身高为xi的某一名男大学生，他的身高yi一定为bxi+a吗？
yi不一定为bxi+a，yi=bxi+a+ei，bxi+a是子总体的均值，yi只是该子总体中的一个样本值