年高考数学试题知识分类大全排列组合二项式

近五年全国高考试题分类—排列组合二项式部分1.(2018·浙江高考T16)从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字, 一共可以组成 个没有重复数字的四位数.(用数字作答)2.(2018·全国卷I 高考理科·T15)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有 种.(用数字填写答案)3.(2018·全国Ⅲ高考理科·T5)(x 2+2x )5的展开式中x 4的系数为( )A .10B .20C .40D .804.(2018·天津高考理科·T10)在(x 2√x )5的展开式中,x 2的系数为 . 5.(2018·浙江高考T14)二项式(√x 3+12x )8的展开式的常数项是 .6.(2017·甲卷理·T6)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有 ( ) A.12种 B.18种 C.24种 D.36种7.(2017·浙江高考·T16)从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有 种不同的选法.(用数字作答) 8.(2017·天津高考理科·T14)用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有 个.(用数字作答)9.(2017·全国丙卷·理科·T4)(x+y)(2x-y)5的展开式中x 3y 3的系数为 ( ) A.-80 B.-40 C.40 D.8010.(2017·全国乙卷理科·T6)211x ⎛⎫+ ⎪⎪⎝⎭(1+x)6展开式中x 2的系数为 ( )A.15B.20C.30D.3511.(2017·山东高考理科·T11)已知(1+3x)n 的展开式中含有x 2项的系数是54,则n= 12.(2016·四川高考理科T4)用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为( ) A.24 B.48 C.60 D.7213.(2016·四川高考理科·T2)设i 为虚数单位,则(x+i)6的展开式中含x 4的项为 ( )A.-15x 4B.15x 4C.-20ix 4D.20ix 414.(2016·全国卷Ⅰ高考理科·T14)(2x+5的展开式中,x 3的系数是 .(用数字填写答案)15.(2016·山东高考理科·T12)若521ax ⎛⎫+ ⎝的展开式中x 5的系数是-80,则实数a= .16.(2016·天津高考理科·T10)821x x ⎛⎫- ⎪⎝⎭的展开式中x 7的系数为 .(用数字作答)17.(2016·北京高考理科·T10)在(1-2x)6的展开式中,x 2的系数为 .(用数字作答) 18.(2015·新课标全国卷Ⅰ理科·T10)(x 2+x+y)5的展开式中,x 5y 2的系数为 ( ) A.10B.20C.30D.6019.(2015·湖北高考理科·T3)已知(1+x)n 的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为 ( ) A.212B.211C.210D.2920. (2015·陕西高考理科·T4)二项式(x+1)n(n ∈N +)的展开式中x 2的系数为15,则n=( )A.4B.5C.6D.721.（2015·安徽高考理科·T11）371()x x+的展开式中5x 的系数是 （用数字填写答案）22. (2015·广东高考理科·T9)在(√x -1)4的展开式中,x 的系数为 .23. (2015·北京高考理科·T9)在(2+x)5的展开式中,x 3的系数为 (用数字作答). 24.(2015·四川高考理科·T11)在(2x-1)5的展开式中,含x 2的项的系数是 (用数字填写答案). 25.(2015·全国卷Ⅱ理科)(a+x)(1+x)4的展开式中x 的奇数次幂项的系数之和为32,则a= .26.(2015·山东高考理科·T11)观察下列各式:0014C =；011334C C +=；01225554C C C ++=；0123377774C C C C +++=；……，照此规律，当n *∈N 时，012121212121n n n n n C C C C -----++++= .27.(2015·天津高考理科·T12)在(x-14x )6的展开式中,x 2的系数为 .28. （2015·重庆高考理科·Ｔ12）53x ⎛ ⎝的展开式中8x 的系数是_________（用数字作答）.29.(2015·福建高考理科·T11)的展开式中，的系数等于 （用数字作答）30. (2015·广东高考理科·T4)袋中共有15个除了颜色外完全相同的球,其中有10个 白球,5个红球.从袋中任取2个球,所取的2个球中恰有1个白球,1个红球的概率为 ( ) A.1B.2111C.1021D.52131.(2015四川高考理科)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有( ) A.144个B.120个C.96个D.72个32. (2015·湖北高考理科·T9)已知集合A={(x,y)|x 2+y 2≤1,x,y ∈Z},B={(x,y)||x|≤2,|y|≤2,x,y ∈Z},定义集合A ⊕B={(x 1+x 2,y 1+y 2)|(x 1,y 1)∈A,(x 2,y 2)∈B},则A ⊕B 中元素的个数为 ( ) A.77B.49C.45D.3033. (2015·广东高考理科·T12)某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了 条毕业留言.(用数字作答)34.(2014·广东高考理科)设集合A={(x 1,x 2,x 3,x 4,x 5)|x i ∈{-1,0,1},i=1,2,3,4,5},那么集合A 中满足条件“1≤|x 1|+|x 2|+|x 3|+|x 4|+|x 5|≤3”的元素个数为 ( ) A.60B.90C.120D.13035.（2014·福建高考理科·Ｔ10）用a 代表红球，b 代表蓝球，c 代表黑球，由加法原理及乘法原理，从1个红球和1个篮球中取出若干个球的所有取法可由()()b a ++11的展开式ab b a +++1表示出来，如：“1”表示一个球都不取、“a ”表示取出一个红球，面“ab ”用表示把红球和篮球都取出来.以此类推，下列各式中，其展开式可用来表示从5个无区别的红球、5个有区别的蓝球、5个有区别的黑球中取出若干个球，且所有的篮球都取出或都不取出的所有取法的是()52x +2xA. ()()()555432111c b a a a a a +++++++ B.()()()554325111c b b b b b a +++++++C. ()()()554325111c b b b b b a +++++++ D.()()()543255111c c c c c b a +++++++36.（2014·浙江高考理科·Ｔ5）在46)1()1(y x ++的展开式中，记nm y x 项的系数为),(n m f ，则=+++)3,0(2,1()1,2()0,3(f f f f ）（ ）A.45B.60C.120D. 21037. （2014·辽宁高考理科·Ｔ6）6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为()144()120()72()24A B C D38.（2014·安徽高考理科·Ｔ8）从正方体六个面的对角线中任取两条作为一对，其中所成的角为的共有（ ）A.24对B.30对C.48对D.60对39.（2014·四川高考理科·Ｔ6）六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有（ ） A.192 B.216 C.240 D.288 40. （2014·湖北高考理科·Ｔ2）若二项式7)2(x a x +的展开式中31x的系数是84，则实数a ＝ A. 2 B. 34 C.1 D.4241. （2014·湖南高考理科·Ｔ4）的展开式中的系数是( )A ．－20B ．－5C ．5D ．2042.（2014·浙江高考理科·Ｔ5）在46)1()1(y x ++的展开式中，记nm y x 项的系数为),(n m f ，则=+++)3,0(2,1()1,2()0,3(f f f f ）（ ）A.45B.60C.120D. 21043.（2014·四川高考理科·Ｔ2）在6)1(x x +的展开式中，含3x 项的系数为（ ）A.30B.20C.15D.10 44.（2014·山东高考理科·Ｔ14）若24()b ax x+的展开式中3x 项的系数为20，则22a b +的最小值为 .45 (2014·新课标全国卷Ⅱ高考理科数学·T13) ()10x a +的展开式中,x 7的系数为15,则a= .(用数字填写答案)60︒51(2)2x y -23x y1. 【命题意图】考查排列组合的简单应用.【解析】分类讨论:第一类:不含0的,按照分步乘法计数原理: C 52C 32A 44=10×3×24=720;第二类:包含0的,按照分步乘法计数原理: C 52C 31A 31A 33=10×3×3×6=540,所以一共有1260个没有重复数字的四位数. 答案:12602.【解题指南】本题是一道关于组合计数的题目,并且在涉及至多至少问题时多采用间接法,间接法是得出选3人的选法总数,利用总的减去没有女生入选的选法种数,该题还可以用直接法,分别求出有1位女生和有2位女生入选分别有多少种选法,之后相加求解.【解析】方法一:根据题意,没有女生入选有C 43=4种选法,从6名学生中任意选3人有C 63=20种选法,故至少有1位女生入选的选法共有20-4=16种.方法二:恰有1位女生,有C 21C 42=12种,恰有2位女生,有C 22C 41=4种,所以不同的选法共有12+4=16种.3.【命题意图】本题设计与二项式定理、二项式特定项相关的问题,考查二项式定理应用,考查运算求解能力和方程的思想,体现了数学运算的核心素养.试题难度:易.【解析】选C .展开式的通项公式为T r +1=C 5r (x 2)5-r (2x )r =2r C 5r x 10-3r,令10-3r =4可得r =2,则x 4的系数为22C 52=40.4. 【命题意图】本题考查二项式定理、二项式某项的系数,考查考生应用二项式定理解决与二项式某项有关的问题,考查考生的逻辑推理能力与运算求解能力.【解析】因为(x 2√x)5的第r +1项T r +1=C 5r x 5-r(2√x )r=(-1)r 2-rC 5r x 10-3r 2,令10-3r 2=2,解得r =2,即T 3=T 2+1=(-1)22-2C 52x 2=52x 2.所以在(x 2√x )5的展开式中,x 2的系数为52.答案:525. 【命题意图】考查二项式定理的展开.【解析】通项公式为T r +1=C 8r (√x 3)8-r (12x )r =C 8r 2-rx 8-4r 3,由8-4r =0得r =2,所以常数项为C 822-2=7.答案:76. 【命题意图】考查排列组合的知识,意在考查学生对排列组合概念的理解能力以及计算能力.【解析】选 D.由题意4项工作分配给3名志愿者,分配方式只能为(2,1,1),所以安排方式有24C·33A=36(种).7. 【命题意图】本题主要考查排列与组合问题.【解析】由题意可知,只选1名女生的选法有13112643C C C C =480种,选2名女生的选法有211643C C C =180种,所以选法总数为480+180=660种.答案:6608. 【命题意图】本题考查有条件限制的排列组合问题.【解析】分两种情况:第一种:四位数都不是偶数的个数为:45A =120,第二种:四位数中有一位为偶数的个数为113445C C A =960,则共有1 080个. 答案:1 0809. 【命题意图】本题考查二项式定理,考查学生的运算求解能力.【解析】选C.由二项式定理可得,原式展开式中含x 3y 3的项为: x ·35C (2x)2(-y)3+y ·25C (2x)3(-y)2=-40x 3y 3+80x 3y 3=40x 3y 3,故展开式中x 3y 3的系数为40.10. 【命题意图】主要考查乘积形式的二项式的系数问题,突出考查二项式定理的应用.【解析】选C.211x ⎛⎫+ ⎪⎪⎝⎭(1+x)6展开式中含x 2的项为1·26C x 2+21x·46C x 4=30x 2,故x 2的系数为30.【反思总结】对于两个二项式乘积的问题,第一个二项式中的每项乘以第二个二项式的每项,分析好含x 2的项共有几项,进行求和.这类问题的易错点主要是未能分析清楚构成这一项的具体情况,尤其是两个二项式展开式中的r 不同.11. 【命题意图】本题考查二项式展开式中通项公式的应用,意在考查考生的运算求解能力.【解析】2nC (3x)2=54x 2,即()12n n -=6,解得n=4.答案:412. 【解题指南】根据排列组合公式及分步乘法计数原理求解.【解析】选D.由题意,要组成没有重复数字的五位奇数,则个位数应该为1,3,5,其他位置共有44A 种,所以其中奇数的个数为344A =72.13. 【解题指南】利用二项式定理展开,复数的运算.【解析】选A.二项式()6x i +展开的通项T r+1=r 6C x 6-r i r ,则其展开式中含x 4的项是当6-r=4,即r=2,则展开式中含x 4的项为26C x 4i 2=-15x 4.14. 【解析】设展开式的第k+1项为T k+1,k ∈{0,1,2,3,4,5},所以5521555(2)2kkkk k kk T C C xx ---+==当5-2k =3时,k=4,即T 5=5445425C x 2--=10x 3.答案:1015. 【解题指南】写出二项式的通项T r+1=()1n r212n 2r rr 2rr 2nnC ax()C xn rax-----=,利用x 5的系数求出实数a的值.【解析】写出二项式的通项T r+1=()1n r212n 2r rr 2rr 2nnCax ()C xn rax-----=,这里n=5,令10-52r=5,则r=2,所以25C a 3=-80,所以a=-2.答案:-216. 【解题指南】写出通项公式T r+1,找到含有x 7的项,计算系数.【解析】821x x ⎛⎫- ⎪⎝⎭的展开式的通项T r+1=()r8rr2r 163881C x C 1x ()r r x --⎛⎫-- ⎪=⎝⎭⋅,令16-3r=7,则r=3.当r=3时,()353281C x x ⎛⎫- ⎪⎝⎭⋅ =-56x 7,所以x 7的系数为-56. 答案:-5617. 【解题指南】利用二项展开式的通项T r+1=r n C a n-r b r 求解.【解析】(1-2x)6的展开式的通项为T r+1=r C 6(-2x)r, 所以T 3=26C (-2x)2=60x 2. 所以,x 2的系数为60. 答案:6018. 【解析】选C.在(x 2+x+y)5的5个因式中,2个取因式中x 2,剩余的3个因式中1个取x,其余因式取y,故x 5y 2的系数为=30.19. 【解题指南】利用二项式系数的性质.二项式系数之和为2n .奇数项的二项式系数和等于偶数项的二项式系数和. 【解析】选D.37=nn，n=3+7=10,二项式系数之和为210.奇数项的二项式系数和等于偶数项的二项式系数和,所以奇数项的二项式系数和为29.20. 【解题指南】在二项展开式的通项公式中,令x 的幂指数等于2,从而求得n 的值.【解析】选 C.二项式(x+1)n(n ∈N +)展开式的通项公式为T r+1=C n r x n-r,令n-r=2,则C n r=15,解之得r=4,n=6,故C 正确.21. 【解题指南】利用二项展开式定理计算。

排列组合与二项式定理（1）【基本知识】1.甲班有四个小组，每组10人，乙班有3个小组，每组15人，现要从甲、乙两班中选1人担任校团委部，不同的选法种数为 852．6人站成一排，甲、乙 、丙三人必须站在一起的排列种数为 1444．用二项式定理计算59.98，精确到1的近似值为（ 99004 ）5．若2)nx 的项是第8项，则展开式中含1x的项是第 9项6．从4名男生和3名女生中选出4人参加某个座谈会，若这4人中必须既有男生又有女生，则不同的选法共有 34种7．已知8()a x x-展开式中常数项为1120，其中实数a 是常数，则展开式中各项系数的和是 1或288．某城市新修建的一条道路上有12盏路灯，为了节省用电而又不能影响正常的照明，可以熄灭其中的3盏灯，但两端的灯不能熄灭，也不能熄灭相邻的两盏灯，则熄灯的方法有 38A 种9．设34550500150(1)(1)(1)(1)x x x x a a x a x ++++++++=+++L L ，则3a 的值是 451C10．不同的五种商品在货架上排成一排，其中甲、乙两种必须排在一起，丙、丁两种不能排在一起，则不同的排法种数共有____24______．11．102(2)(1)x x +-的展开式中10x 的系数为____179______．（用数字作答）若1531-++++n n n n n C C C C ΛΛ=32，则n = 612．用0，1，2，3，4组成没有重复数字的全部五位数中，若按从小到大的顺序排列，则数字12340应是第____10_____个数。

13、体育老师把9个相同的足球放入编号为1、2、3的三个箱子里，要求每个箱子放球的个数不少于其编号，则不同的放法有___10___种。

三、解答题15、已知n 展开式中偶数项的二项式系数之和为256，求x 的 系数．【解】由二项式系数的性质：二项展开式中偶数项的二项式系数之和为2n －1，得n =9，由通项92923199C (C (2)r rrrrr r r T x---+==-g g g ，令92123r r --=，得r =3，所以x 的二项式为39C =84， 而x 的系数为339C (2)84(8)672-=⨯-=-g．16、有5名男生，4名女生排成一排：（1）从中选出3人排成一排，有多少种排法？（2）若男生甲不站排头，女生乙不站在排尾，则有多少种不同的排法？ （3）要求女生必须站在一起，则有多少种不同的排法？ （4）若4名女生互不相邻，则有多少种不同的排法？【解】（1）39504A = （2）287280 （3）17280 （4）211217．从7个不同的红球，3 个不同的白球中取出4个球，问：（1）有多少种不同的取法？（2）其中恰有一个白球的取法有多少种？ （3）其中至少有现两个白球的取法有多少种？ 【解】（1）210 （2）105 （3）7018、 已知n展开式中偶数项二项式系数和比()2na b +展开式中奇数项二项式系数和小120，求：（1）n展开式中第三项的系数;（2）()2na b +展开式的中间项。

高考数学知识点专题精讲与知识点突破排列、组合、二项式、概率一、分类计数原理和分步计数原理：分类计数原理：如果完成某事有几种不同的方法，这些方法间是彼此独立的，任选其中一种方法都能达到完成此事的目的，那么完成此事的方法总数就是这些方法种数的和。

分步计数原理：如果完成某事，必须分成几个步骤，每个步骤都有不同的方法，而—个步骤中的任何一种方法与下一步骤中的每一个方法都可以连接，只有依次完成所有各步，才能达到完成此事的目的，那么完成此事的方法总数就是这些方法种数的积。

区别：如果任何一类办法中的任何一种方法都能完成这件事，则选用分类计数原理，即类与类之间是相互独立的，即“分类完成”；如果只有当n 个步骤都做完，这件事才能完成，则选用分步计数原理，即步与步之间是相互依存的，连续的，即“分步完成”。

二、排列与组合：（1）排列与组合的区别和联系：都是研究从一些不同的元素中取出n 个元素的问题； 区别：前者有顺序，后者无顺序。

（2）排列数、组合数： 排列数的公式：)()!(!)1()2)(1(n m m n n m n n n n A m n ≤-=+---= 注意：①全排列：n ； ②记住下列几个阶乘数，1！=1，2！=2，3！=6，4！=24，5！=120，6！=720；排列数的性质：①11--=m n m n nA A （将从n 个不同的元素中取出)(n m m ≤个元素，分两步完成：第一步从n 个元素中选出1个排在指定的一个位置上；第二步从余下1-n 个元素中选出1-m 个排在余下的1-m 个位置上）②m n m n m n A mA A 111---+=（将从n 个不同的元素中取出)(n m m ≤个元素，分两类完成：第一类：个元素中含有a ，分两步完成：第一步将a 排在某一位置上，有m 不同的方法。

第二步从余下1-n 个元素中选出1-m 个排在余下的1-m 个位置上）即有11--m n mA 种不同的方法。

高考数学试题分类汇编---- 排列组合二项式定理一． 选择题：1.（全国一3）512x ⎛⎫+ ⎪⎝⎭的展开式中2x 的系数为（ C ） A ．10 B ．5 C ．52 D ．12.（全国一12）将1，2，3填入33⨯的方格中，要求每行、每列都没有重复数字，下面是一种填法，则不同的填写方法共有（ B ） A ．6种 B ．12种 C ．24种 D ．48种3.（全国二9）44)1()1(x x +-的展开式中x 的系数是（ A ）A ．4-B ．3-C ．3D ．44.（安徽卷7）设88018(1),x a a x a x +=+++则0,18,,a a a 中奇数的个数为（ A ） A ．2 B ．3 C ．4 D ．55.（安徽卷12）12名同学合影，站成前排4人后排8人，现摄影师要从后排8人中抽2人调整到前排，若其他人的相对顺序不变，则不同调整方法的总数是 ( C )A ． 2686C AB ． 2283C A C ．2286C AD ．2285C A6.（福建卷9)某班级要从4名男士、2名女生中选派4人参加某次社区服务，如果要求至少有1名女生，那么不同的选派方案种数为AA.14B.24C.28D.487.（湖北卷9）从5名男生和5名女生中选3人组队参加某集体项目的比赛，其中至少有一名女生入选的组队方案数为BA.100B.110C.120D.1808.（湖南卷8）某市拟从4个重点项目和6个一般项目中各选2个项目作为本年度启动的项目，则重点项目A 和一般项目B 至少有一个被选中的不同选法种数是( C )A ．15B ．45C ．60D ．759.（江西卷8）10101(1)(1)x x++展开式中的常数项为 D A ．1 B ．1210()C C ．120C D ．1020C10.（辽宁卷7）4张卡片上分别写有数字1，2，3，4，从这4张卡片中随机抽取2张，则取出的2张卡片上的数字之和为奇数的概率为（ C ）A ．13B ．12C ．23D ．3411.（辽宁卷10）一生产过程有4道工序，每道工序需要安排一人照看．现从甲、乙、丙等6名工人中安排4人分别照看一道工序，第一道工序只能从甲、乙两工人中安排1人，第四道工序只能从甲、丙两工人中安排1人，则不同的安排方案共有（ B ）A ．24种B ．36种C ．48种D ．72种12.(浙江卷6）在)5)(4)(3)(2)(1(-----x x x x x 的展开式中，含4x 的项的系数是（A ）-15 （B ）85 （C ）-120 （D ）27413.（重庆卷10)若(x +12x)n 的展开式中前三项的系数成等差数，则展开式中x 4项的系数为B(A)6 (B)7 (C)8 (D)9 二． 填空题：1.（全国二14）从10名男同学，6名女同学中选3名参加体能测试，则选到的3名同学中既有男同学又有女同学的不同选法共有 种（用数字作答）4202.（北京卷12）5231x x ⎛⎫+ ⎪⎝⎭的展开式中常数项为 ；各项系数之和为 ．（用数字作答）10， 323.（福建卷13）（x +1x）9展开式中x 2的系数是 .（用数字作答）84 4.（湖南卷13）记n x x )12(+的展开式中第m 项的系数为m b ，若432b b =，则n =__________.55.（辽宁卷15）6321(1)x x x ⎛⎫++ ⎪⎝⎭展开式中的常数项为 ．356.（陕西卷14）72(1)x -的展开式中21x的系数为 84 ．(用数字作答) 7.（陕西卷16）某地奥运火炬接力传递路线共分6段，传递活动分别由6名火炬手完成．如果第一棒火炬手只能从甲、乙、丙三人中产生，最后一棒火炬手只能从甲、乙两人中产生，则不同的传递方案共有 96 种．（用数字作答）．8.（四川卷13）()()34121x x +-展开式中x 的系数为______2_________。

“排列、组合、二项式、概率、统计”复习资料一、基础知识和方法梳理 （一）排列组合 1．计数两原理：分类计数原理：完成一件事情，有n 类方法，在第1类方法中又有m 1种不同的方式可以完成这件事情，在第2类方法中，又有m 2种方式，……第n 类方法中有m n 种方式可以完成，那么要完成这件事情的方法共有：n m m m N +++= 21分步计数原理：完成一件事情，需要分成n 步完成，在第1步中，有m 1种不同的方式可以完成这一步，在第2步中，有m 2种方式，……第n 步中，有m n 种方式可以完成这一步，那么要完成这件事情的方法共有：n m m m N ⨯⨯⨯= 21 2．排列：从n 个不同元素中取出m （m ≤n ）个元素，按照一定的顺序排成一列，叫做从n 个不同元素中取出m 个元素的一个排列。

排列数)!(!)1()1(m n n m n n n A mn -=+--=3．组合：从n 个不同的元素中不重复选取m 个元素组成一组，与顺序无关； 组合公式：)!(!!!)1()1(m n m n m m n n n C mn -=+--=；组合数性质：m n n m n C C -=，mn m n m n C C C 11+-=+4．排列组合常用方法：分类讨论法：将0,1,2,3,4五个数字可以组成多少个无重复数字的五位偶数？间接法：100件产品含有5件次品，从中任取5件，则至少含有一件次品的取法有多少种？ 捆绑、插空法：将3本语文书，3本数学书，2本英语书排成一排，数学书必须排在一起，英语书不能相邻，则有多少中排列方式？特殊元素特殊位置优先考虑法：例如，将0,1,2,3可以组成多少个无重复数字的四位数 分组法：将5个苹果分给甲、乙、丙三人，每人至少一个苹果，有多少种分配方案？ 隔板法：例如，将10个相同的小球装入3个编号为1,2,3的盒子(每次要把10个球装完),要求每个盒子里球的个数不少盒子的编号数,这样的装法总数有多少种？ 等可能性法：六个字母a 、r 、r 、r 、b 、c 排成一排，有多少种排列方式？（二）二项式定理1．二项式定理：nn n r r n r n n n n n n b C b a C b a C a C b a +++++=+-- 110)(，其中rn C 为第1+r 项的二项式系数，=-nb a )(2．通项公式：rr n r n r b a C T -+=1,),1,0(n r =3．二项式定理的性质： （1）对称性，二项式系数是关于2n对称 （2）增减性与最大值，当n 为偶数时，二项式系数最大项为第12+n项，最大值为2nn C当n 为奇数时，二项式系数最大项为第121+-n 项和第121++n 项，最大值为2121+-=n n n n C C （3）二项式系数之和nn n n n C C C 210=+++奇数项与偶数项的二项式系数之和相等131202-=++=++n n n n n C C C C（三）概率1．概率的定义：在大量重复进行同一试验时事件A 发生的频率nm总是接近于某个常数p ，这时就把这个常数叫做事件A 的概率，记做)(A P ．2．事件的和A+B ：表示事件A 和B 至少有一个发生； 事件的积A ×B ：表示事件A 和B 同时发生B A B A B A B A ⋅=++=⋅,3．常见的几种类型的概率计算：（1）等可能事件：可预知的有限个结果，且每个结果出现的可能性相同 计算方法：nm A P =)( （2）互斥事件：在一次试验中，事件A 发生了，则事件B 一定不会发生，事件B 发生了，事件A 不可能发生互斥事件有一个发生的概率计算方法：)()()(B P A P B A P +=+， 特殊的，对立事件：1)()(=+A P A P（3）相互独立事件：在一次试验中，事件A 发生与否对事件B 发生的概率没有影响，同理，事件B 发生与否对事件A 发生的概率没有影响，若A 与B 是独立事件，则A 与B ，A 与B ，A 与B 都是独立事件 独立事件同时发生的概率的计算方法：)()()(B P A P B A P ⋅=⋅（4）n 次独立重复事件恰有k 次发生的概率：kn k k n n p p C k P --=)1()(4．关于两个事件常见的概率计算：（若21)(,)(p B P p A P ==）5．注意事项（1）等可能事件的概率中，基本事件数目的计算可以分化得细致一点或粗略一点，这样虽然形式上有所差别，结果往往是一样的，通常有这样一些不同考虑：“整体考虑或局部考虑” 、“元素可辨或不可辨” 、“元素放回或不放回” 、“元素有序或无序”.（2）重视几种概率类型的混合，注意概率加法、乘法的混合运算，适当注意概率类型的突破. （3）准确理解文字（生活）语言，如“至少”、“至多”、“都”、“不都”、“都不”、“恰有几个”、“有几个”，“只有第几次”、“第几次”，“直到第几次”等等，然后等价转化为数学（概率）语言，并注意表述规范.（四）统计1．离散型随机变量的定义：若随机试验的结果可以用一个变量表示，这个变量叫做随机变量。

排列组合二项式定理知识点及例题1．排列的概念：从n 个不同元素中，任取m （m n ≤）个元素（这里的被取元素各不相同）按照一定的顺序．．．．．排成一列，叫做从n 个不同元素中取出m 个元素的一个排列．．．．2．排列数的定义：从n 个不同元素中，任取m （m n ≤）个元素的所有排列的个数叫做从n 个元素中取出m 元素的排列数，用符号m n A 表示3．排列数公式：(1)(2)(1)m n A n n n n m =---+ （,,m n N m n *∈≤） 4 阶乘：!n 表示正整数1到n 的连乘积，叫做n 的阶乘规定0!1=．5．排列数的另一个计算公式：m n A =!()!n n m - 组合概念：从n 个不同元素中取出m ()m n ≤个元素并成一组，叫做从n 个不同元素中取出m 个元素的一个组合7．组合数的概念：从n 个不同元素中取出m ()m n ≤个元素的所有组合的个数，叫做从n 个不同元素中取出m 个元素的组合数．．．．用符号mn C 表示． 8．组合数公式：(1)(2)(1)!m mn nm m A n n n n m C A m ---+== 或)!(!!m n m n C m n-=,,(n m N m n ≤∈*且9.组合数的性质1：m n n m n C C -=．规定：10=n C ；10.组合数的性质2：m n C 1+＝m n C +1-m n C C n 0+C n 1+…+C n n =2n11.二项式展开公式：(a+b)n =C n 0a n +C n 1a n-1b+…+C n k a n-k b k +…+C n n b n 12.通项公式：二项式展开式中第k+1项的通项公式是T k+1=C n k a n-k b k题型讲解例1 分别求出符合下列要求的不同排法的种数（1）6名学生排3排，前排1人，中排2人，后排3人； （2）6名学生排成一排，甲不在排头也不在排尾；（3）从6名运动员中选出4人参加4×100米接力赛，甲不跑第一棒， 乙不跑第四棒；（4）6人排成一排，甲、乙必须相邻； （5）6人排成一排，甲、乙不相邻；（6）6人排成一排，限定甲要排在乙的左边，乙要排在丙的左边（甲、 乙、丙可以不相邻）解：（1）分排坐法与直排坐法一一对应，故排法种数为72066=A（2）甲不能排头尾，让受特殊限制的甲先选位置，有14A 种选法，然后其他5人选，有55A 种选法，故排法种数为4805514=A A（3）有两棒受限制，以第一棒的人选来分类：①乙跑第一棒，其余棒次则不受限制，排法数为35A ；②乙不跑第一棒，则跑第一棒的人有14A 种选法，第四棒除了乙和第一棒选定的人外，也有14A 种选法，其余两棒次不受限制，故有221414A A A 种排法，由分类计数原理，共有25224141435=+A A A A 种排法（4）将甲乙“捆绑”成“一个元”与其他4人一起作全排列共有2405522=A A 种排法（5）甲乙不相邻，第一步除甲乙外的其余4人先排好；第二步，甲、乙选择已排好的4人的左、右及之间的空挡插位，共有2544A A （或用6人的排列数减去问题（2）后排列数为48024066=-A ）（6）三人的顺序定，实质是从6个位置中选出三个位置，然后排按规定的顺序放置这三人，其余3人在3个位置上全排列，故有排法1203336=A C 种点评：排队问题是一类典型的排列问题，常见的附加条件是定位与限位、相邻与不相邻 例2 假设在100件产品中有3件是次品，从中任意抽取5件，求下列抽取方法各多少种？ （1）没有次品；（2）恰有两件是次品；（3）至少有两件是次品解：（1）没有次品的抽法就是从97件正品中抽取5件的抽法，共有64446024597=C 种 （2）恰有2件是次品的抽法就是从97件正品中抽取3件，并从3件次品中抽2件的抽法，共有44232023397=C C 种 （3）至少有2件次品的抽法，按次品件数来分有二类：第一类，从97件正品中抽取3件，并从3件次品中抽取2件，有32973C C 种 第二类从97件正品中抽取2件，并将3件次品全部抽取，有23973C C 种按分类计数原理有4469763329723397=+C C C C 种点评：此题是只选“元”而不排“序”的典型的组合问题，附加的条件是从不同种类的元素中抽取，应当注意：如果第（3）题采用先从3件次品抽取2件（以保证至少有2件是次品），再从余下的98件产品中任意抽取3件的抽法，那么所得结果是46628839823=C C 种，其结论是错误的，错在“重复”：假设3件次品是A 、B 、C ，第一步先抽A 、B 第二步再抽C 和其余2件正品，与第一步先抽A 、C （或B 、C ），第二步再抽B （或A ）和其余2件正品是同一种抽法，但在算式39823C C 中算作3种不同抽法例3 求证：①m n m n m n A mA A =+---111 ；②12112++-+=++m n m n m n m n C C C C证明：①利用排列数公式 左()()()()1!1!1!!n m n n m n m -⋅-=+---()()()()1!1!!n m n m n n m --+⋅-==-()==-m n A m n n !!右另一种证法：（利用排列的定义理解）从n 个元素中取m 个元素排列可以分成两类：①第一类不含某特殊元素a 的排列有mn A 1-第二类含元素a 的排列则先从()1-n 个元素中取出()1-m 个元素排列有11--m n A 种，然后将a 插入，共有m 个空档，故有11--⋅m n A m 种，因此m n m n m n A A m A =⋅+---111②利用组合数公式 左()()()()()!!2!11!1!1!m n m n m n m n m n m n -++--+--+=()()()()()()()[]11211!1!1!+-+++++--⋅+-+m n m m m m n m n m n m n ＝()()()()()()()==+-++=+++-+=++12!1!1!212!1!1!m n C m n m n n n m n m n 右另法：利用公式111---+=m n m n m n C C C 推得 左()()==+=+++=+++++-+1211111m n n n m n m n m n m n m n C C C C C C C 右 点评：证明排列、组合恒等式通常利用排列数、组合数公式及组合数基本性质例4 已知f 是集合{}d c b a A ,,,=到集合{}2,1,0=B 的映射 （1）不同的映射f 有多少个？（2）若要求()()()()4=+++d f c f b f a f 则不同的映射f 有多少个？ 分析：（1）确定一个映射f ，需要确定d c b a ,,,的像（2）d c b a ,,,的象元之和为4，则加数可能出现多种情况，即4有多种分析方案，各方案独立且并列需要分类计算解：（1）A 中每个元都可选0,1,2三者之一为像，由分步计数原理，共有433333=⋅⋅⋅个不同映射（2）根据d c b a ,,,对应的像为2的个数来分类，可分为三类：第一类：没有元素的像为2，其和又为4，必然其像均为1，这样的映射只有一个；第二类：一个元素的像是2，其余三个元素的像必为0,1,1，这样的映射有121314=P C 个； 第三类：二个元素的像是2，另两个元素的像必为0，这样的映射有624=C 个由分类计数原理共有1+12+6=19（个）点评：问题（1）可套用投信模型：n 封不同的信投入m 个不同的信箱，有nm 种方法；问题（2）的关键结合映射概念恰当确定分类标准，做到不重、不漏【例题解析】例1 完成下列选择题与填空题（1）有三个不同的信箱，今有四封不同的信欲投其中，则不同的投法有种。

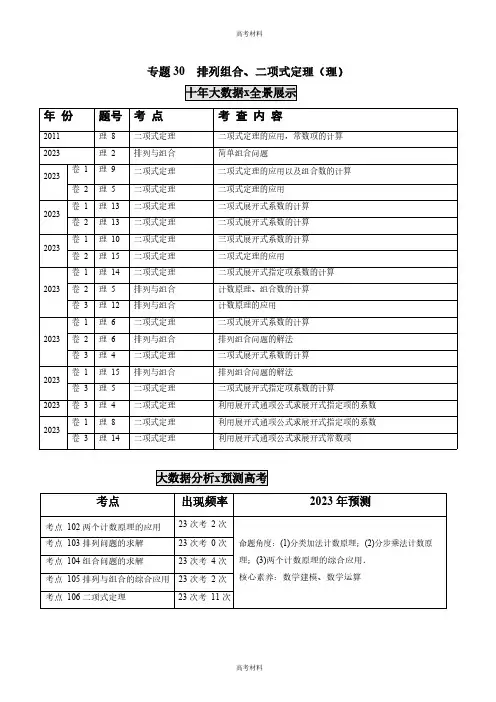
专题 30 排列组合、二项式定理（理）年 份题号 考 点考 查 内 容2011 理 8 二项式定理 二项式定理的应用，常数项的计算 2023 理 2排列与组合 简单组合问题卷 1 理 9 二项式定理 二项式定理的应用以及组合数的计算 2023卷 2理 5 二项式定理 二项式定理的应用 卷 1 理 13 二项式定理 二项式展开式系数的计算2023卷 2 理 13 二项式定理 二项式展开式系数的计算 卷 1 理 10 二项式定理 三项式展开式系数的计算2023卷 2 理 15 二项式定理 二项式定理的应用卷 1 理 14 二项式定理 二项式展开式指定项系数的计算 卷 2 理 5 排列与组合 计数原理、组合数的计算2023卷 3理 12 排列与组合 计数原理的应用 卷 1 理 6 二项式定理 二项式展开式系数的计算 卷 2 理 6 排列与组合 排列组合问题的解法2023卷 3理 4 二项式定理 二项式展开式系数的计算 卷 1 理 15 排列与组合 排列组合问题的解法2023 卷 3 理 5 二项式定理 二项式展开式指定项系数的计算2023卷 3 理 4 二项式定理 利用展开式通项公式求展开式指定项的系数 卷 1 理 8 二项式定理 利用展开式通项公式求展开式指定项的系数2023 卷 3理 14二项式定理利用展开式通项公式求展开式常数项考点出现频率2023 年预测考点 102 两个计数原理的应用 23 次考 2 次 考点 103 排列问题的求解 23 次考 0 次 考点 104 组合问题的求解23 次考 4 次 考点 105 排列与组合的综合应用 23 次考 2 次 考点 106 二项式定理23 次考 11 次命题角度：(1)分类加法计数原理；(2)分步乘法计数原 理；(3)两个计数原理的综合应用．核心素养：数学建模、数学运算考点102 两个计数原理的应用1．(2023 全国II 理)如图，小明从街道的E 处出发，先到F 处与小红会合，再一起到位于G 处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为A．24 B．18 C．12 D．9（答案）B（解析）由题意可知E →F 有6 种走法，F →G 有3 种走法，由乘法计数原理知，共有6 ⨯ 3 = 18 种走法，应选B．2．(2023 新课标理1 理)4 位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活动的概率为A.18B.3824 - 2 7C.58D.78（答案）D（解析）P ==．24 83．(2023 湖北理)回文数是指从左到右读与从右到左读都一样的正整数．如22，121，3443，94249 等．显然2位回文数有9 个：11，22，33，…，99．3 位回文数有90 个：101，111，121，…，191，202，…，999．则(Ⅰ)4 位回文数有个；(Ⅱ) 2n +1 (n ∈N+) 位回文数有个．（解析）(Ⅰ)4 位回文数只用排列前面两位数字，后面数字就可以确定，但是第—位不能为0，有9(1~9)种情况，第二位有10(0~9)种情况，所以4 位回文数有9 ⨯10 = 90 种．答案：90(Ⅱ)解法一：由上面多组数据研究发觉，2n +1 位回文数和2n + 2 位回文数的个数相同，所以可以算出2n + 2位回文数的个数．2n + 2 位回文数只用看前n +1位的排列情况，第—位不能为0 有9 种情况，后面n 项每项有10 种情况，所以个数为9 ⨯10n ．解法二：可以看出2 位数有9 个回文数，3 位数90 个回文数。

摆列组合及二项式定理【基本知识点】1. 分类计数和分步计数原理的观点2．摆列的观点：从n 个不同元素中，任取m（m n ）个元素（这里的被取元素各不同样）按照一．定．的．顺．序．排成一列，叫做从n 个不同元素中拿出m 个元素的一．个．排．列．3．摆列数的定义：从n 个不同元素中，任取m （m n ）个元素的全部摆列的个数叫做从n个元素中拿出m 元素的摆列数，用符号mA 表示nm4．摆列数公式：A n(n 1)(n 2)L (n m 1) （m,n N ,m n）n5.阶乘：n!表示正整数1 到n 的连乘积，叫做n 的阶乘规定0! 1．6．摆列数的另一个计算公式：mA =nn! (n m)!7.组合观点：从n 个不同元素中拿出m m n 个元素并成一组，叫做从n 个不同元素中取出m 个元素的一个组合8．组合数的观点：从n 个不同元素中拿出m m n 个元素的全部组合的个数，叫做从n 个不同元素中拿出m 个元素的组．合．数．．用符号mC 表示．n9.组合数公式：mA n(n 1)(n 2)L (n m 1)m nCn mA m!m或 C m nm!(n!n m)!(n, m N ,且m n)10.组合数的性质1：m n m 0C n C ．规定：C 1 ；n n11.组合数的性质2：mCn 1 ＝m m 1C +C Cn nn n n0+C1+⋯ +C n=20+C1+⋯ +C n=2n12. 二项式睁开公式： (a+b) n=C0a n+C1a n-1 b+⋯ +C k a n-k b k+⋯ +C n bnn n n n13．二项式系数的性质：n(a b) 睁开式的二项式系数是C ，n1C ，n2C ，⋯，nnC ．nrC 能够当作以r为自变量的函数nf (r ) ，定义域是{0,1,2, L ,n} ，（1）对称性．与首末两头“等距离”的两个二项式系数相等（∵m n mC C ）．n nn（2）增减性与最大值：当n是偶数时，中间一项C 2 获得最大值；当n是奇数时，中间两项nn 1 n 12 C ，n2C 获得最大值．n（3）各二项式系数和：∵n 1 r r n(1 x) 1 C x L C x L x ，n n令x 1，则n 0 1 2 r n2 C C C L C L Cn n n n n【常有考点】一、可重复的摆列求幂法：重复摆列问题要划分两类元素：一类能够重复，另一类不可以重复，把不可以重复的元素看作“客”，能重复的元素看作“店”，则经过“住店法”可顺利解题，在这种问题使用住店办理的策略中，重点是在正确判断哪个底数，哪个是指数（1）有 4 名学生报名参加数学、物理、化学比赛，每人限报一科，有多少种不同的报名方法？（2）有 4 名学生参加抢夺数学、物理、化学比赛冠军，有多少种不同的结果？（3）将 3 封不同的信投入 4 个不同的邮筒，则有多少种不同投法？【分析】：（1）43 （2）34 （3）4 3二．相邻问题捆绑法：题目中规定相邻的几个元素捆绑成一个组，看作一个大元素参加排列.（4）A, B,C, D, E 五人并排站成一排，假如A, B 一定相邻且B 在A的右侧，那么不同的排法种数有【分析】：把A,B视为一人，且B 固定在A的右侧，则此题相当于4 人的全摆列，4A4 24种（5）3 位男生和 3 位女生共 6 位同学站成一排，若男生甲不站两头， 3位女生中有且只有两位女生相邻，则不同排法的种数是（）A. 360B. 188C. 216D. 96【分析】：间接法 6 位同学站成一排， 3 位女生中有且只有两位女生相邻的排法有，2 2 2 2C A A A =432 种3 24 2此中男生甲站两头的有 1 2 2 2 2A C A A A =144 ，切合条件的排法故共有 2882 3 2 3 2三．相离问题插空法：元素相离（即不相邻）问题，可先把无地点要求的几个元素全摆列，再把规定的相离的几个元素插入上述几个元素的空位和两头 . （6）七人并排站成一行，假如甲乙两个一定不相邻，那么不同的排法种数是【分析】：除甲乙外，其他 5 个摆列数为 5A 种，再用甲乙去插 6 个空位有52A 种，不同的排6法种数是 5 2A5 A6 3600 种（7）书架上某层有 6 本书，新买3 本插进去，要保持原有 6 本书的次序，有种不同的插法（详细数字作答）【分析】： 1 1 1A A A =5047 8 9（8）马路上有编号为1，2，3⋯， 9 九只路灯，现要关掉此中的三盏，但不可以关掉相邻的二盏或三盏，也不可以关掉两头的两盏，求知足条件的关灯方案有多少种？【分析】：把此问题看作一个排对模型，在 6盏亮灯的 5 个缝隙中插入 3盏不亮的灯 3C 种方5 法, 所以知足条件的关灯方案有 10 种.四．元素剖析法（地点剖析法）：某个或几个元素要排在指定地点，可先排这个或几个元素；再排其他的元素。

专题56 排列、组合与二项式定理（知识梳理）一、分类加法计数原理和分步乘法计数原理1、分类加法计数原理：完成一件事情，有n 类办法，在第1类办法中有1m 种不同的方法，在第2类办法中有2m 种不同的方法…在第n 类办法中有n m 种不同的方法。

那么完成这件事共有n m m m M +⋅⋅⋅++=21种不同的方法。

例1-1．一蚂蚁沿着长方体的棱，从的一个顶点爬到相对的另一个顶点的最近路线共有多少条？2、分步乘法计数原理：完成一件事情，需要分成n 个步骤，做第1步有1m 种不同的方法，做第2步有2m 种不同的方法…做第n 步有n m 种不同的方法。

那么完成这件事共有n m m m M ⨯⋅⋅⋅⨯⨯=21种不同的方法。

例1-2．如图，要给地图A 、B 、C 、D 四个区域分别涂上3种不同颜色中的某一种，允许同一种颜色使用多次，但相邻区域必须涂不同的颜色，不同的涂色方案有多少种？3、理解分类加法计数原理与分步乘法计数原理异同点：①相同点：都是完成一件事的不同方法种数的问题。

②不同点：分类加法计数原理针对的是“分类”问题，完成一件事要分为若干类，各类的方法相互独立，各类中的各种方法也相对独立，用任何一类中的任何一种方法都可以单独完成这件事，是独立完成；而分步乘法计数原理针对的是“分步”问题，完成一件事要分为若干步，各个步骤相互依存，完成任何其中的一步都不能完成该件事，只有当各个步骤都完成后，才算完成这件事，是合作完成。

4、计数原理的解题步骤(1)指明要完成一件什么事，并依事件特点确定是“分n 类”还是“分n 步”；(2)求每“类”或每“步”中不同方法的种数；(3)利用“相加”或“相乘”得到完成事件的方法总数；(4)作答。

5、从m 个不同元素中，每次取出n 个元素，元素可以重复出现，按照一定的顺序排成一排，那么第一、第二……第n 位上选取元素的方法都是m 个，所以从m 个不同元素中，每次取出n 个元素可重复排列数n m m m m =⋅⋅⋅⋅。

十年高考真题分类汇编（2010—2019）数学专题13 排列组合与二项式定理一、选择题1.(2019·全国3·理T4)(1+2x2)(1+x)4的展开式中x3的系数为( )A.12B.16C.20D.24【答案】A【解析】(1+2x2)(1+x)4的展开式中x3的系数为+2=4+8=12.故选A.2.(2018·全国3·理T5) 的展开式中x4的系数为( )A.10B.20C.40D.80【答案】C【解析】由展开式知T r+1=(x2)5-r(2x-1)r=2r x10-3r.当r=2时,x4的系数为22=40.3.(2017·全国1·理T6)(1+x)6展开式中x2的系数为( )A.15B.20C.30D.35【答案】C【解析】(1+x)6的二项展开式通项为T r+1=x r,(1+x)6的展开式中含x2的项的来源有两部分,一部分是1×x2=15x2,另一部分是x4=15x2,故(1+x)6的展开式中含x2的项为15x2+15x2=30x2,其系数是30.4.(2017·全国3·理T4)(x+y)(2x-y)5的展开式中x3y3的系数为()A.-80B.-40C.40D.80【答案】C【解析】(2x-y)5的展开式的通项公式T r+1=(2x)5-r(-y)r.当r=3时,x(2x-y)5的展开式中x3y3的系数为×22×(-1)3=-40;当r=2时,y(2x-y)5的展开式中x3y3的系数为×23×(-1)2=80.故展开式中x3y3的系数为80-40=40.5.(2017·全国2·理T6)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有()A.12种B.18种C.24种D.36种【答案】D【解析】先把4项工作分成3份有种情况,再把3名志愿者排列有种情况,故不同的安排方式共有=36种,故选D.6.(2016·四川·理T2)设i为虚数单位,则(x+i)6的展开式中含x4的项为()A.-15x4B.15x4C.-20i x4D.20i x4【答案】A【解析】二项式(x+i)6展开的通项T r+1=x6-r i r,则其展开式中含x4是当6-r=4,即r=2,则展开式中含x4的项为x4i2=-15x4,故选A.7.(2016·全国2·理T5)如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为()A.24B.18C.12D.9【答案】B【解析】由题意知,小明从街道的E处出发到F处的最短路径有6条,再从F处到G处的最短路径有3条,则小明到老年公寓可以选择的最短路径条数为6×3=18,故选B.8.(2016·全国3·理T12)定义“规范01数列”{a n}如下:{a n}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,a k中0的个数不少于1的个数.若m=4,则不同的“规范01数列”共有()A.18个B.16个C.14个D.12个【答案】C【解析】由题意知a1=0,a8=1,则满足题意的a1,a2,…,a8的可能取值如下:综上可知,不同的“规范01数列”共有14个.9.(2016·四川·理T4)用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为()A.24B.48C.60D.72【答案】D【解析】要组成没有重复数字的五位奇数,则个位数应该为1,3,5中的一个,其他位置共有种排法,所以其中奇数的个数为3=72,故选D.10.(2015·四川·理T6)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有()A.144个B.120个C.96个D.72个【答案】B【解析】当首位数字为4,个位数字为0或2时,满足条件的五位数有个;当首位数字为5,个位数字为0或2或4时,满足条件的五位数有个.故满足条件的五位数共有=(2+3)=5×4×3×2×1=120个.故选B.11.(2015·全国1·理T10)(x2+x+y)5的展开式中,x5y2的系数为()A.10B.20C.30D.60【答案】C【解析】(x2+x+y)5=[(x2+x)+y]5的展开式通项为T r+1=(x2+x)5-r y r(r=0,1,2,…,5).由题意,y的幂指数为2,故r=2.对应的项为(x2+x)3y2=10(x2+x)3y2.记(x2+x)3的展开式通项为T s+1=(x2)3-s x s=x6-s(s=0,1,2,3),由题意令6-s=5,得s=1.故所求项的系数为10=30.12.(2015·陕西·理T4)二项式(x+1)n(n∈N*)的展开式中x2的系数为15,则n=()A.7B.6C.5D.4【答案】B【解析】(x+1)n的展开式通项为T r+1=x n-r.令n-r=2,即r=n-2.则x2的系数为=15,解得n=6,故选B.13.(2015·湖北·理T3)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( )A.212B.211C.210D.29【答案】D【解析】由条件知,∴n=10.∴(1+x)10中二项式系数和为210,其中奇数项的二项式系数和为210-1=29.14.(2014·大纲全国·理T5)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有()A.60种B.70种C.75种D.150种【答案】C【解析】从6名男医生中选出2名有种选法,从5名女医生中选出1名有种选法,故共有×5=75种选法,选C.15.(2014·辽宁·理T6)6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为()A.144B.120C.72D.24【答案】D【解析】插空法.在已排好的三把椅子产生的4个空档中选出3个插入3人即可.故排法种数为=24.故选D.16.(2014·四川·理T6)六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有()A.192种B.216种C.240种D.288种【答案】B【解析】(1)当最左端排甲的时候,排法的种数为;(2)当最左端排乙的时候,排法种数为.因此不同的排法的种数为=120+96=216.17.(2014·重庆·理T9)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是()A.72B.120C.144D.168【答案】B【解析】第1步,先排歌舞类节目,有=6种排法,排好后有4个空位.第2步,排另3个节目,因为3个歌舞节目不相邻,则中间2个空位必须安排2个节目.分两类情况:①中间两个空位安排1个小品类节目和1个相声节目,有=4种排法,最后一个小品类节目排两端,有2种方法.共有6×4×2=48种排法.②中间两个空位安排2个小品类节目,有=2种排法,排好后有6个空位,选1个将相声类节目排上,有6种排法.共有6×2×6=72种排法.所以一共有48+72=120种排法.18.(2014·四川·理T2)在x(1+x)6的展开式中,含x3项的系数为( )A.30B.20C.15D.10【答案】C【解析】含x3的项是由(1+x)6展开式中含x2的项与x相乘得到,又(1+x)6展开式中含x2的项的系数为=15, 故含x3项的系数是15.19.(2014·湖南·理T4) 的展开式中x2y3的系数是( )A.-20B.-5C.5D.20【答案】A【解析】由已知,得T r+1=(-2y)r=(-2)r x5-r y r(0≤r≤5,r∈Z),令r=3,得T4=(-2)3x2y3=-20x2y3.20.(2014·浙江·理T5)在(1+x)6(1+y)4的展开式中,记x m y n项的系数为f(m,n),则f(3,0)+f(2,1)+f(1,2)+f(0,3)=( )A.45B.60C.120D.210【答案】C【解析】∵(1+x)6展开式的通项公式为T r+1=x r,(1+y)4展开式的通项公式为T h+1=y h,∴(1+x)6(1+y)4展开式的通项可以为x r y h.∴f(m,n)=.∴f(3,0)+f(2,1)+f(1,2)+f(0,3)==20+60+36+4=120.故选C.21.(2013·全国1·理T9)设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b.若13a=7b,则m=( )A.5B.6C.7D.8【答案】B【解析】由题意可知,a=,b=,∵13a=7b,∴13·=7·,即,解得m=6.故选B.22.(2013·山东·理T10)用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为()A.243B.252C.261D.279【答案】B【解析】构成所有的三位数的个数为=900,而无重复数字的三位数的个数为=648,故所求个数为900-648=252,应选B.23.(2013·全国2·理T5)已知(1+ax)(1+x)5的展开式中x2的系数为5,则a=()A.-4B.-3C.-2D.-1【答案】D【解析】因为(1+x)5的二项展开式的通项为x r(0≤r≤5,r∈Z),则含x2的项为x2+ax·x=(10+5a)x2,所以10+5a=5,a=-1.24.(2013·辽宁·理T7)使 (n∈N*)的展开式中含有常数项的最小的n为( )A.4B.5C.6D.7【答案】B【解析】展开式中的第r+1项为(3x)n-r3n-r,若展开式中含常数项,则存在n∈N*,r∈N,使n-r=0,故最小的n值为5,故选B.25.(2013·大纲全国·理T7)(1+x)8(1+y)4的展开式中x2y2的系数是( )A.56B.84C.112D.168【答案】D【解析】因为(1+x)8的展开式中x2的系数为,(1+y)4的展开式中y2的系数为,所以x2y2的系数为=168.故选D.26.(2012·湖北·理T5)设a∈Z,且0≤a<13,若512 012+a能被13整除,则a=( )A.0B.1C.11D.12【答案】D【解析】∵512 012可化为(52-1)2 012,其二项式系数为T r+1=522 012-r·(-1)r.故(52-1)2 012被13除余数为·(-1)2 012=1,则当a=12时,512 012+12被13整除.27.(2012·安徽·理T7)(x2+2) 的展开式的常数项是( )A.-3B.-2C.2D.3【答案】D【解析】通项为T r+1=(-1)r=(-1)r.令10-2r=2或0,此时r=4或5.故(x2+2)的展开式的常数项是(-1)4×+2×(-1)5×=3.28.(2012·全国·理T2)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有()A.12种B.10种C.9种D.8种【答案】A【解析】将4名学生均分为2个小组共有=3种分法,将2个小组的同学分给两名教师带有=2种分法,最后将2个小组的人员分配到甲、乙两地有=2种分法,故不同的安排方案共有3×2×2=12种.29.(2012·辽宁·理T5)一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种数为()A.3×3!B.3×(3!)3C.(3!)4D.9!【答案】C【解析】完成这件事可以分为两步,第一步排列三个家庭的相对位置,有种排法;第二步排列每个家庭中的三个成员,共有种排法.由乘法原理可得不同的坐法种数有,故选C.30.(2012·安徽·理T10)6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品.已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为()A.1或3B.1或4C.2或3D.2或4【答案】D【解析】6人之间互相交换,总共有=15种,而实际只交换了13次,故有2次未交换.不妨设为甲与乙、丙与丁之间未交换或甲与乙、甲与丙之间未交换,当甲与乙、丙与丁之间未交换时,甲、乙、丙、丁4人都收到4份礼物;当甲与乙、甲与丙之间未交换时,只有乙、丙两人收到4份礼物,故选D.31.(2011·全国·理T8) 的展开式中各项系数的和为2,则该展开式中常数项为( )A.-40B.-20C.20D.40【答案】D【解析】令x=1得(1+a)(2-1)5=2,∴a=1.原式=x·,故常数项为x·(2x)2(2x)3=-40+80=40.32.(2010·山东·理T8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位,节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有()A.36种B.42种C.48种D.54种【答案】B【解析】若乙排在第二位,则有种方案;若乙不排在第二位,则乙只能排在第三、四、五位,此时共有种方案,故共有=42(种).二、填空题1.(2019·天津·理T10)（2x-8的展开式中的常数项为【答案】28【解析】T r+1=(2x)8-r（r=·28-r·（-r·x8-4r.需8-4r=0,r=2.常数项为26（-2=26=28.2.(2018·天津·理T10)在的展开式中,x2的系数为.【答案】【解析】展开式的通项为T r+1=x5-r.令5-=2,可得r=2.所以的展开式中的x2的系数为.3.(2018·浙江·T14)二项式的展开式的常数项是.【答案】7【解析】通项为T r+1=,当r=2时,=0.故展开式的常数项为=7.4.(2018·上海·T3)在(1+x)7的二项展开式中,x2项的系数为(结果用数值表示).【答案】21【解析】由(1+x)7的二项展开式的通项,得(1+x)7的二项展开式的x2项的系数为=21.5.(2018·全国1·理T15)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有种.(用数字填写答案)【答案】16【解析】方法一:①恰有1位女生时,有=12种选法.②恰有2位女生时,有=4种选法.故不同的选法共有12+4=16种.方法二:6人中选3人共有种选法,3人全是男生时有种选法,所以至少有1位女生入选时有=16种选法.6.(2018·浙江·T16)从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成个没有重复数字的四位数.(用数字作答)【答案】1260【解析】分两类:第一类:从0,2,4,6中取到0,则没有重复数字的四位数有=540;第二类:从0,2,4,6中不取0,则没有重复数字的四位数有=720.所以没有重复数字的四位数共有540+720=1260种.7.(2017·山东·理T11)已知(1+3x)n的展开式中含有x2项的系数是54,则n= .【答案】4【解析】二项展开式的通项T r+1=(3x)r=3r··x r,令r=2,得32·=54,解得n=4.8.(2017·浙江·T13)已知多项式(x+1)3(x+2)2=x5+a1x4+a2x3+a3x2+a4x+a5,则a4= ,a5= .【答案】16 4【解析】由二项式展开式可得通项公式为x3-r x2-m2m,分别取r=3,m=1和r=2,m=2可得a4=4+12=16,令x=0可得a5=13×22=4.9.(2017·天津·理T14)用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有个.(用数字作答)【答案】1080【解析】①没有一个数字是偶数的四位数有=120个;②有且只有一个数字是偶数的四位数有=960个.所以至多有一个数字是偶数的四位数有120+960=1 080个.10.(2017·浙江·T16)从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有种不同的选法.(用数字作答)【答案】660【解析】由题意可得,总的选择方法为种方法,其中不满足题意的选法有种方法,则满足题意的选法有=660种.11.(2016·全国1·理T14)(2x+)5的展开式中,x3的系数是.(用数字填写答案)【答案】10【解析】二项式的通项公式T r+1=(2x)5-r25-r,令5-=3,解得r=4,故x3的系数为×25-4=10.12.(2016·天津·理T10) 的展开式中x7的系数为.(用数字作答)【答案】-56【解析】展开式通项为T r+1=(x2)8-r=(-1)r x16-3r,令16-3r=7,得r=3,所以展开式中x7的系数为(-1)3=-56.13.(2015·广东·理T12)某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了条毕业留言.(用数字作答)【答案】1560【解析】共有=40×39=1 560条毕业留言.14.(2015·天津·理T12)在的展开式中,x2的系数为.【答案】【解析】由题意知T r+1=x6-r··x6-2r·.令6-2r=2,可得r=2.故所求x2的系数为.15.(2015·重庆·理T12)的展开式中x8的系数是(用数字作答).【答案】【解析】展开式的通项公式T r+1=·(x3)5-r··2-r·(r=0,1,2,…,5).令15-r=8,得r=2,于是展开式中x8项的系数是·2-2=.16.(2015·全国2·理T15)(a+x)(1+x)4的展开式中x的奇数次幂项的系数之和为32,则a= .【答案】3【解析】∵(1+x)4=x4+x3+x2+x+x0=x4+4x3+6x2+4x+1,∴(a+x)(1+x)4的奇数次幂项的系数为4a+4a+1+6+1=32,∴a=3.17.(2014·安徽·理T13)设a≠0,n是大于1的自然数, 的展开式为a0+a1x+a2x2+…+a n x n.若点A i(i,a i)(i=0,1,2)的位置如图所示,则a= .【答案】3【解析】由题意得a1==3,∴n=3a;a2==4,∴n2-n=8a2.将n=3a代入n2-n=8a2得9a2-3a=8a2,即a2-3a=0,解得a=3或a=0(舍去).∴a=3.18.(2014·北京·理T13)把5件不同产品摆成一排.若产品A与产品B相邻,且产品A与产品C不相邻,则不同的摆法有种.【答案】36【解析】产品A,B相邻时,不同的摆法有=48种.而A,B相邻,A,C也相邻时的摆法为A在中间,C,B在A的两侧,不同的摆法共有=12(种).故产品A与产品B相邻,且产品A与产品C不相邻的不同摆法有48-12=36(种).19.(2014·全国1·理T13)(x-y)(x+y)8的展开式中x2y7的系数为.(用数字填写答案)【答案】-20【解析】(x+y)8的通项公式为T r+1=x8-r y r(r=0,1,…,8,r∈Z).当r=7时,T8=xy7=8xy7,当r=6时,T7=x2y6=28x2y6,所以(x-y)(x+y)8的展开式中含x2y7的项为x·8xy7-y·28x2y6=-20x2y7,故系数为-20.20.(2014·全国2·理T13)(x+a)10的展开式中,x7的系数为15,则a= .(用数字填写答案)【答案】【解析】设展开式的通项为T r+1=x10-r a r,令r=3,得T4=x7a3,即a3=15,得a=.21.(2013·浙江·理T11)设二项式的展开式中常数项为A,则A= .【答案】-10【解析】T r+1=)5-r··(-1)r·=(-1)r=(-1)r.令15-5r=0,得r=3,所以A=(-1)3=-=-10.22.(2013·北京·理T12)将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是.【答案】96【解析】分给同一人的2张参观券连号的情况共有12,23,34,45四种情况,从4人中选一人得到连号参观券,有4种方法.其余3张分给3人可以全排列,有种方法,所以不同的分法有4=96种.23.(2013·大纲全国·理T14)6个人排成一行,其中甲、乙两人不相邻的不同排法共有种.(用数字作答)【答案】480【解析】先排除甲、乙外的4人,方法有种,再将甲、乙插入这4人形成的5个间隔中,有种排法,因此甲、乙不相邻的不同排法有=480(种).24.(2013·浙江·理T14)将A,B,C,D,E,F六个字母排成一排,且A,B均在C的同侧,则不同的排法共有种(用数字作答).【答案】480【解析】按C的位置分三类情况:①当C在第一或第六位时,有=120种排法;②当C在第二或第五位时,有=72种排法;③当C在第三或第四位时,有=48种排法.所以共有2×(120+72+48)=480种排法.25.(2012·福建·理T11)(a+x)4的展开式中x3的系数等于8,则实数a= .【答案】2【解析】∵T r+1=a r x4-r,∴当4-r=3,即r=1时,T2=·a·x3=4ax3=8x3.故a=2.26.(2012·浙江·理T14)若将函数f(x)=x5表示为f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,其中a0,a1,a2,…,a5为实数,则a3= .【答案】10【解析】由x5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5可得,可解得27.(2012·大纲·理T15)若的展开式中第3项与第7项的二项式系数相等,则该展开式中的系数为.【答案】56【解析】∵,∴n=8.T r+1=x8-r x8-2r,当8-2r=-2时,r=5.∴系数为=56.28.(2011·北京·理T12)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有个.(用数字作答)【答案】14【解析】可用排除法,这个四位数每一位上的数字只能是2或3,则共有24个,而这其中要求数字2或3至少出现一次,所以全是2和全是3不满足,即满足要求的四位数有24-2=14个.。

高考数学专题命题解读1.高考对排列组合的考查，重点是特殊元素与特殊位置、两元素相邻或不相邻、分组、分配等问题。

题型一般与生活实际联系紧密。

2.高考对二项式定理的考查，重点是二项展开基本定理考查特定项、系数、二项式系数等问题，同时会涉及到赋值法的应用。

命题分析2024年高考新高考Ⅰ卷的排列组确定所有可能结果，其实Ⅰ卷的题目也其中逻辑推理能力比较重要，而且都是试题精讲一、填空题1．（2024新高考Ⅱ卷·14）在如图的则共有种选法，在所有符合上述要求的考数学真题题型分类解析08排列组合与二项式定理考向 点是特殊或不相一般与生重点是二特定项的时会涉及排列组合202202202202二项式定理 202排列组合是体现在概率中的，后续专题会体现出来。

题目也可以采用列举法，这两题考查的方向偏向于与实且都是压轴题。

预计2025年高考还是主要考查排列组合图的4×4方格表中选4个方格，要求每行和每列均恰要求的选法中，选中方格中的4个数之和的最大值是解析解析 式定理式定理考查统计2023·新高考Ⅰ卷，13 2022·新高考Ⅱ卷，5 2023·新高考Ⅱ卷，3 2024·新高考Ⅱ卷，14 2022·新高考Ⅰ卷，13 。

Ⅱ卷考查了通过列举来于与实际生活联系在一起；列组合的应用，题型多变。

列均恰有一个方格被选中，大值是．【答案答案】】 24 112【分析分析】】由题意可知第一由题意可知第一、、二、三、四列分别有4、3、2、1个方格可选个方格可选；；利用列举法写出所有的可能结果利用列举法写出所有的可能结果，，即可求解.【详解详解】】由题意知由题意知，，选4个方格个方格，，每行和每列均恰有一个方格被选中每行和每列均恰有一个方格被选中，， 则第一列有4个方格可选个方格可选，，第二列有3个方格可选个方格可选，， 第三列有2个方格可选个方格可选，，第四列有1个方格可选个方格可选，， 所以共有432124×××=种选法种选法；；每种选法可标记为(,,,)a b c d ，a b c d ,,,分别表示第一分别表示第一、、二、三、四列的数四列的数字字， 则所有的可能结果为则所有的可能结果为：： (11,22,33,44),(11,22,34,43),(11,22,33,44),(11,22,34,42),(11,24,33,43),(11,24,33,42)， (12,21,33,44),(12,21,34,43),(12,22,31,44),(12,22,34,40),(12,24,31,43),(12,24,33,40)， (13,21,33,44),(13,21,34,42),(13,22,31,44),(13,22,34,40),(13,24,31,42),(13,24,33,40)， (15,21,33,43),(15,21,33,42),(15,22,31,43),(15,22,33,40),(15,22,31,42),(15,22,33,40)，所以选中的方格中所以选中的方格中，，(15,21,33,43)的4个数之和最大个数之和最大，，为152********+++=. 故答案为故答案为：：24；112 【点睛点睛】】关键点点睛关键点点睛：：解决本题的关键是确定第一解决本题的关键是确定第一、、二、三、四列分别有4、3、2、1个方格可选个方格可选，，利用列举法写出所有的可能结果.一、单选题1．（2022新高考Ⅱ卷·5）有甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演，若甲不站在两端，丙和丁相邻，则不同排列方式共有（ ） A ．12种B ．24种C ．36种D ．48种【答案答案】】B【分析分析】】利用捆绑法处理丙丁利用捆绑法处理丙丁，，用插空法安排甲用插空法安排甲，，利用排列组合与计数原理即可得解【详解详解】】因为丙丁要在一起因为丙丁要在一起，，先把丙丁捆绑先把丙丁捆绑，，看做一个元素看做一个元素，，连同乙连同乙，，戊看成三个元素排列,有3!种排列方式；为使甲不在两端为使甲不在两端，，必须且只需甲在此三个元素的中间两个位置任选一个位置插入必须且只需甲在此三个元素的中间两个位置任选一个位置插入，，有2种插空方式种插空方式；；注意到丙丁两人的顺序可交换注意到丙丁两人的顺序可交换，，有2种排列方式种排列方式，，故安排这5名同学共有名同学共有：：3!2224××=种不同的排列方式种不同的排列方式，，故选故选：：B 2．（2023新高考Ⅱ卷·3）某学校为了解学生参加体育运动的情况，用比例分配的分层随机抽样方法作抽样调查，拟从初中部和高中部两层共抽取60名学生，已知该校初中部和高中部分别有400名和200名学生，则不同的抽样结果共有（ ）．A ．4515400200C C ⋅种B ．2040400200C C ⋅种C ．3030400200C C ⋅种D ．4020400200C C ⋅种二、填空题3．（2022新高考Ⅰ卷·13）81()y x y x −+的展开式中26x y 的系数为（用数字作答）．修2门或3门课，并且每类选修课至少选修1门，则不同的选课方案共有种（用数字作答）． 【答案答案】】64【分析分析】】分类讨论选修2门或3门课门课，，对选修3门，再讨论具体选修课的分配再讨论具体选修课的分配，，结合组合数运算求解.【详解详解】（】（1）当从8门课中选修2门，则不同的选课方案共有144116C C =种；（2）当从8门课中选修3门，①若体育类选修课1门，则不同的选课方案共有1244C C 24=种； ②若体育类若体育类选修课选修课2门，则不同的选课方案共有2144C C 24=种；综上所述综上所述：：不同的选课方案共有16242464++=种. 故答案为故答案为：：64.一、排列与排列数1、定义：从n 个不同元素中取出()m m n ≤个元素排成一列，叫做从n 个不同元素中取出m 个元素的一个排列．从n 个不同元素中取出()m m n ≤个元素的所有排列的个数，叫做从n 个不同元素中取出m 个元素的排列数，用符号mn A 表示．2、排列数的公式：()()()()!121!mnn A n n n n m n m =−−−+=− ． 特例：当m n =时，()()!12321m n A n n n n ==−−⋅⋅ ；规定：0!1=． 3、排列数的性质：①11m m n n A nA −−=；②111mm m n n n n A A A n m n m+−==−−；③111m m m n n n A mA A −−−=+．二、组合与组合数1、定义：从n 个不同元素中取出()m m n ≤个元素并成一组，叫做从n 个不同元素中取出m 个元素的一个组合．从n 个不同元素中取出()m m n ≤个元素的所有组合的个数，叫做从n 个不同元素中取出m 个元素的组合数，用符号mn C 表示．2、组合数公式及其推导求从n 个不同元素中取出m 个元素的排列数m n A ，可以按以下两步来考虑： 第一步，先求出从这n 个不同元素中取出m 个元素的组合数m n C ； 第二步，求每一个组合中m 个元素的全排列数m n A ； 根据分步计数原理，得到m m m n n m A C A =⋅；因此()()()121!m mn nm m n n n n m A C A m −−−+== ．这里n ，m N +∈，且m n ≤，这个公式叫做组合数公式．因为()!!m n n A n m =−，所以组合数公式还可表示为：()!!!m n n C m n m =−．特例：01n n n C C ==．注意：组合数公式的推导方法是一种重要的解题方法！在以后学习排列组合的混合问题时，一般都是按先取后排（先组合后排列）的顺序解决问题．公式(1)(2)(1)C !m n n n n n m m −−⋅⋅⋅−+=常用于具体数字计算，!C !()!m n n m nm =−常用于含字母算式的化简或证明．3、组合数的主要性质：①m n m n n C C −=；②11m m mn n n C C C −++=．4、组合应用题的常见题型：①“含有”或“不含有”某些元素的组合题型 ②“至少”或“最多”含有几个元素的题型三、排列和组合的区别组合：取出的元素地位平等，没有不同去向和分工． 排列：取出的元素地位不同，去向、分工或职位不同．注意：排列、组合都是研究事物在某种给定的模式下所有可能的配置数目问题，它们之间的主要区别在于是否要考虑选出元素的先后顺序，不需要考虑顺序的是组合问题，需要考虑顺序的是排列问题．排列是在组合的基础上对入选的元素进行排队，因此，分析解决排列组合综合问题的基本思维是“先组合，后排列”．四、二项式展开式的特定项二项式展开式的特定项、、特定项的系数问题1、二项式定理一般地，对于任意正整数，都有：011()()n n n r n r r n n n n n n a b C a C a b C a b C b n N −−∗+=+++++∈ ，这个公式所表示的定理叫做二项式定理，等号右边的多项式叫做的二项展开式．式中的r n r r n C a b −做二项展开式的通项，用1r T +表示，即通项为展开式的第1r +项：1r n r r r n T C a b −+=， 其中的系数r n C （r =0，1，2，…，n ）叫做二项式系数，2、二项式()n a b +的展开式的特点：①项数：共有1n +项，比二项式的次数大1；②二项式系数：第1r +项的二项式系数为r n C ，最大二项式系数项居中；③次数：各项的次数都等于二项式的幂指数n ．字母a 降幂排列，次数由n 到0；字母b 升幂排列，次 数从0到n ，每一项中，a ，b 次数和均为n ；④项的系数：二项式系数依次是012r n n n n n n C C C C C ⋅⋅⋅⋅⋅⋅，，，，，，，项的系数是a 与b 的系数（包括二项式系数）．3、两个常用的二项展开式：①（）②4、二项展开式的通项公式二项展开式的通项：1r n r r r n T C a b −+=()0,1,2,3,,r n =…公式特点：①它表示二项展开式的第1r +项，该项的二项式系数是；②字母b 的次数和组合数的上标相同； ③a 与b 的次数之和为n ．n n b a )(+011()(1)(1)n n n r r n r r n n n n n n n a b C a C a b C a b C b −−−=−++−⋅++−⋅ *N n ∈122(1)1n r r n n n n x C x C x C x x +=++++++ r n C注意：①二项式()n a b +的二项展开式的第r +1项和()n b a +的二项展开式的第r +1项是有区别的，应用二项式定理时，其中的a 和b 是不能随便交换位置的．②通项是针对在()n a b +这个标准形式下而言的，如()n a b −的二项展开式的通项是（只需把b −看成b 代入二项式定理）．五、二项式展开式中的最值问题1、二项式系数的性质①每一行两端都是1，即0n n n C C =；其余每个数都等于它“肩上”两个数的和，即11m m mn n n C C C −+=+． ②对称性每一行中，与首末两端“等距离”的两个二项式系数相等，即m n m n n C C −=．③二项式系数和令1a b ==，则二项式系数的和为0122r n n n n n n n C C C C C ++++++= ，变形式1221r n n n n n n C C C C +++++=− ．④奇数项的二项式系数和等于偶数项的二项式系数和在二项式定理中，令11a b ==−，，则0123(1)(11)0n n n n n n n n C C C C C −+−++−=−= ，从而得到：0242132111222r r nn n n n n n n n C C C C C C C +−++⋅⋅⋅++⋅⋅⋅=++++⋅⋅⋅=⋅= ． ⑤最大值：如果二项式的幂指数n 是偶数，则中间一项12n T +的二项式系数2n nC 最大；如果二项式的幂指数n 是奇数，则中间两项12n T +，112n T +的二项式系数12n nC−，12n nC+相等且最大．2、系数的最大项求()n a bx +展开式中最大的项，一般采用待定系数法．设展开式中各项系数分别为121n A A A +⋅⋅⋅，，，，设第1r +项系数最大，应有112r r r r A A A A +++≥ ≥ ，从而解出r 来．六、二项式展开式中系数和有关问题常用赋值举例：1、设， 二项式定理是一个恒等式，即对a ，b 的一切值都成立，我们可以根据具体问题的需要灵活选取a ，b 的值．①令，可得：②令11a b ==，，可得：，即：（假设为偶数），再结合①可得：．r n r rnC a b −r n r r n C b a −1(1)r r n r rr nT C a b −+=−()011222nn n n r n r r n nn nn n n a b C a C a b C a b C a b C b −−−+=++++++ 1a b ==012n nn n n C C C =+++ ()012301nnn n n n n C C C C C =−+−+− 02131n n n n n n n n C C C C C C −+++=+++ n 0213112n n n n n n n n n C C C C C C −−+++=+++=2、若121210()n n n n n n f x a x a x a x a x a −−−−=+++++ ，则①常数项：令0x =，得0(0)a f =．②各项系数和：令1x =，得0121(1)n n f a a a a a −=+++++ ． ③奇数项的系数和与偶数项的系数和（i ）当n 为偶数时，奇数项的系数和为024(1)(1)2f f a a a +−+++= ；偶数项的系数和为135(1)(1)2f f a a a −−+++=． （可简记为：n 为偶数，奇数项的系数和用“中点公式”，奇偶交错搭配） （ii ）当n 为奇数时，奇数项的系数和为024(1)(1)2f f a a a −−+++= ；偶数项的系数和为135(1)(1)2f f a a a +−+++=．（可简记为：n 为奇数，偶数项的系数和用“中点公式”，奇偶交错搭配） 若1210121()n n n n f x a a x a x a x a x −−=+++++ ，同理可得．注意：常见的赋值为令0x =，1x =或1x =−，然后通过加减运算即可得到相应的结果． 【排列组合常用结论排列组合常用结论】】一、解决排列组合综合问题的一般过程1、认真审题，确定要做什么事；2、确定怎样做才能完成这件事，即采取分步还是分类或是分步与分类同时进行，弄清楚分多少类及多少步；3、确定每一步或每一类是排列（有序）问题还是组合（无序）问题，元素总数是多少及取出多少个元素；4、解决排列组合综合性问题，往往类与步交叉，因此必须掌握一些常用的解题策略．二、常见排列组合类型及解法1、如图，在圆中，将圆分n 等份得到n 个区域1M ，2M ，3M ， ，(2)n M n …，现取(2)k k …种颜色对这n个区域涂色，要求每相邻的两个区域涂不同的两种颜色，则涂色的方案有(1)(1)(1)n n k k −−+−种．2、错位排列公式1(1)(1)!!inn i D n n =−=+⋅∑ 3、数字排列问题的解题原则、常用方法及注意事项（1）解题原则：排列问题的本质是“元素”占“位子”问题，有限制条件的排列问题的限制条件主要表现在某元素不排在某个位子上，或某个位子不排某些元素，解决该类排列问题的方法主要是按“优先”原则，即优先排特殊元素或优先满足特殊位子，若一个位子安排的元素影响到另一个位子的元素个数时，应分类讨论． 4、定位、定元的排列问题，一般都是对某个或某些元素加以限制，被限制的元素通常称为特殊元素，被限制的位置称为特殊位置．这一类问题通常以三种途径考虑：（1）以元素为主考虑，这时，一般先解决特殊元素的排法问题，即先满足特殊元素，再安排其他元素； （2）以位置为主考虑，这时，一般先解决特殊位置的排法问题，即先满足特殊位置，再考虑其他位置； （3）用间接法解题，先不考虑限制条件，计算出排列总数，再减去不符合要求的排列数．5、解决相邻问题的方法是“捆绑法”，其模型为将n 个不同元素排成一排，其中某k 个元素排在相邻位置上，求不同排法种数的方法是：先将这k 个元素“捆绑在一起”，看成一个整体，当作一个元素同其他元素一起排列，共有11n k n k A −+−+种排法；然后再将“捆绑”在一起的元素“内部”进行排列，共有k k A 种排法．根据分步乘法计数原理可知，符合条件的排法共有11n k nk kk A A −+−+⋅种． 6、解决不相邻问题的方法为“插空法”，其模型为将n 个不同元素排成一排，其中某k 个元素互不相邻（1k n k ≤−+），求不同排法种数的方法是：先将（n k −）个元素排成一排，共有n kn k A −−种排法；然后把k 个元素插入1n k −+个空隙中，共有1k n k A −+种排法．根据分步乘法计数原理可知，符合条件的排法共有n k n k A −−·1k n k A −+种．一、单选题1．（2024·重庆·三模）重庆某高校去年招收学生来自成渝地区2400人，除成渝外的西部地区2000人，中部地区1400人，东部地区1800人，港澳台地区400人.学校为了解学生的饮食习惯，拟选取40人作样本调研，为保证调研结果的代表性，则从该校去年招收的成渝地区学生中不同的抽样结果种数为（ ）A ．402400CB ．242400C C ．122400CD ．102400C2．（2024·北京·三模）已知x的二项式系数之和为64，则其展开式的常数项为（ ）A ．240−B ．240C ．60D ．60−的票价分别对应球场三个不同的区域，五位球迷相约看球赛，则五人中恰有三人在同一区域的不同座位方式共有（ ）A ．30种B ．60种C ．120种D ．240种【答案答案】】C【分析分析】】依题意依题意，，先将在同一区域的三个先将在同一区域的三个人选出并选定区域人选出并选定区域人选出并选定区域，，再对余下的两人分别在其它两个区域进行选择，由分步乘法计数原理即得.【详解详解】】要使五人中恰有三人在同一区域要使五人中恰有三人在同一区域，，可以分成三步完成可以分成三步完成：： 第一步第一步，，先从五人中任选三人先从五人中任选三人，，有35C 种方法种方法；； 第二步再选这三人所在的区域第二步再选这三人所在的区域，，有13C 种方法种方法；；第三步第三步，，将另外两人从余下的两个区域里任选将另外两人从余下的两个区域里任选，，有1122C C ⋅种方法.由分步乘法计数原理由分步乘法计数原理，，共有31115322C C C C 120⋅⋅⋅=种方法.故选:C.4．（2024·四川成都·三模）成实外教育集团自2000年成立以来，一直行走在民办教育的前端，致力于学生的全面发展，对学生的教育视为终身己任，在教育事业上砥砺前行，永不止步.截至目前，集团已开办29所K-12学校和两所大学，其中高中教育学校有11所.集团拟召开综合考评会.经考评后，11所学校得分互不相同，现从中任选3所学校的代表交流发言，则排名为第一名或第五名的学校代表去交流发言的概率为（ ） A ．2455B ．2855C ．811D ．2755 【答案答案】】D【分析分析】】利用古典概率结合组合数的计算求解即可. 【详解详解】】从11所学校中任选3所学校共有种311C 165=选法. 其中排名为第一名或第五名的学校其中排名为第一名或第五名的学校，，可以分为三种情况可以分为三种情况：：第一类第一类：：只含有排名为第一名的学校的有29C 36=种选法种选法；；邻的条件下，数字2，4，6也相邻的概率为（ ） A ．310B ．35C ．110D ．156．（2024·新疆喀什·三模）21x x ++展开式中，3x 的系数为（ ）A ．20B ．30C ．25D ．40【答案答案】】B【分析分析】】分不含2x 项和含有一个2x 项两种情况求解项两种情况求解．．【详解详解】】25(1)++x x 展开式中展开式中，，3x 的项为33212133554C 1C C 130x x x x ⋅+⋅⋅=，则3x 的系数为30． 故选故选：：B ．7．（2024·新疆·三模）西安、洛阳、北京、南京和开封并称中国的五大古都.某旅游博主为领略五大古都之美，决定用两个月的时间游览完五大古都，且每个月只游览五大古都中的两个或三个（五大古都只游览一次），则恰好在同一个月游览西安和洛阳的概率为（ ）A ．15B ．25C ．12D ．35【答案答案】】B【分析分析】】求出事件的总数以及目标事件的数量求出事件的总数以及目标事件的数量，，再用古典再用古典概型计算即可概型计算即可..【详解详解】】将古都分成2个、3个两组个两组，，再在两个月安排旅游顺序再在两个月安排旅游顺序，，故事件总数为2252C A 20⋅=，分2个古都组中含西安个古都组中含西安、、洛阳洛阳，，或3个古都组中含西安个古都组中含西安、、洛阳洛阳，，故恰好在同一个月游览西安和洛阳的事件8．（2024·北京·三模）在2221x x −−的展开式中，5x 项的系数为（ ） A ．144−B ．16−C ．16D ．144【答案答案】】C【分析分析】】写出()()552112x x −=−−的展开式通项，即可列式求解.【详解详解】】()()552112x x −=−−，其展开式通项公式为()15C 2rr r T x +=−−，0,1,2,3,4,5r =，所以所求5x 项的系数为()()353555C 22C 2806416−−+−=−=，故选故选：： C ． 9．（2024·河北秦皇岛·三模）三人被邀请参加同一个时间段的两个晚会，若两个晚会都必须有人去，去几人自行决定，且每人最多参加一个晚会，则不同的去法有（ ） A ．8种B ．12种C ．16种D ．24种【答案答案】】B【分析分析】】根据参加晚会的人数分类讨论根据参加晚会的人数分类讨论，，利用排列组合数求解即可.【详解详解】】第一种情况第一种情况，，只有两人参加晚会只有两人参加晚会，，有23A 6=种去法种去法；； 第二种情况第二种情况，，三人参加晚会三人参加晚会，，有2232C A 6=种去法种去法，，共12种去法.故选故选：：B10．（2024·安徽芜湖·三模）已知A 、B 、C 、D 、E 、F 六个人站成一排，要求A 和B 不相邻，C 不站两端，则不同的排法共有（ ）种A ．186B ．264C ．284D ．336【答案答案】】D【分析分析】】先考虑A 和B 不相邻的排法不相邻的排法，，再考虑A 和B 不相邻不相邻，，且C 站两端的情况站两端的情况，，相减后得到答案. 【详解详解】】先考虑A 和B 不相邻的排法不相邻的排法，，将C 、D 、E 、F 四个人进行全排列四个人进行全排列，，有44A 种情况种情况，，C 、D 、E 、F 四个人之间共有5个空个空，，选择2个排A 和B ，有25A 种情况种情况，，故有4245480A A =种选择种选择，，再考虑A 和B 不相邻不相邻，，且C 站两端的情况站两端的情况，， 先从两端选择一个位置安排C ，有12C 种情况种情况，， 再将D 、E 、F 三个人进行全排列三个人进行全排列，，有33A 种情况最后D 、E 、F 三个人之间共有4个空个空，，选择2个排A 和B ，有24A 种情况种情况，，故有132234C A A 144=种情况种情况，，则要求A 和B 不相邻不相邻，，C 不站两端不站两端，，则不同的安排有480144336−=种情况. 故选故选：：D 11．（2024·浙江绍兴·三模）在()()()()()123x x x x a x b +++++的展开式中，含4x 项的系数是10，则()2log a b +=（ ）A ．0B ．1C ．2D ．4【答案答案】】C【分析分析】】在()()()()()123x x x x a x b +++++的展开式中含4x 的项即从5个因式中取4个x ，1个常数项即可写出含4x 的项的项，，则可得出答案.【详解详解】】根据二项展开式可知含4x 项即从5个因式中取4个x ，1个常数项即可写出含4x 的项；所以含4x 的项是()4412310a b x x ++++=，可得4a b +=；即可得()22log log 42a b +==. 故选故选：：C 12．（2024·湖北荆州·三模）已知()202422024012202431a a x a x a x x =+++−+L ，则122024a a a +++L 被3除的余数为（ ）A ．3B ．2C ．1D ．0【答案答案】】D【分析分析】】先对二项展开式中的x 进行赋值进行赋值，，得出101212202441a a a +++=− ，再将10124看作()101231+进行展开，再利用二项展开式特点分析即得.【详解详解】】令0x =，得01a =，令1x =，得202401220242a a a a ++++= ， 两式相减两式相减，，202410121220242141a a a +++=−=− ，因为()101210120101211011101110121012101210121012431C 3C 3C 3C =+=++++ ，其中01012110111011101210121012C 3C 3C 3+++L 被3整除整除，，所以10124被3除的余数为1， 综上综上，，122024a a a +++L 能被3整除整除．． 故选故选：：D.二、多选题13．（2024·山西临汾·三模）在82x 的展开式中（ ） A ．所有奇数项的二项式系数的和为128 B ．二项式系数最大的项为第5项 C ．有理项共有两项D ．所有项的系数的和为8314．（2024·江西南昌·三模）已知12x x − 的展开式中二项式系数的最大值与+a x x的展开式中1x 的系数相等，则实数a 的值可能为（ ）A B ．D ．15．（2024·山西·三模）已知函数2120121241f x x a a x a x a x =−=+++⋅⋅⋅+，则（ ）A ．333124C a =×B ．()f x 展开式中，二项式系数的最大值为612CC ．12123123a a a a +++⋅⋅⋅+=D ．()5f 的个位数字是1【答案答案】】BD【分析分析】】对于A ：根据二项展开式分析求解根据二项展开式分析求解；；对于B ：根据二项式系数的性质分析求解根据二项式系数的性质分析求解；；对于C ：利用赋值法值法，，令0x =、1x =即可得结果即可得结果；；对于D ：因为()()125201f =−，结合二项展开式分析求解.【详解详解】】对于选项A ：()1241x −的展开式的通项为()()()12121211212C 4114C ,0,1,2,,12rr rr r rr r T x x r −−−+=⋅−=−⋅⋅⋅=⋅⋅⋅，令9r =，可得()93933334121214C 4C T x x =−⋅⋅⋅=−×⋅， 所以333124C a =−×，故A 错误错误；；对于选项B ：因为12n =为偶数为偶数，，可知二项式系数的最大值为612C ，故B 正确正确；； 对于选项C ：令0x =，可得01a =；令1x =，可得12012123a a a a +++⋅⋅⋅+=； 所以121231231a a a a +++⋅⋅⋅+=−，故C 错误错误；；对于选项D ：因为()()125201f =−，且()12201−的展开式的通项为()12112C 201,0,1,2,,12kkk k T k −+=⋅⋅−=⋅⋅⋅， 可知当0,1,2,,11k =⋅⋅⋅，1k T +均为20的倍数的倍数，，即个位数为0， 当12k =时，131T =，所以()5f 的个位数字是1，故D 正确正确；； 故选故选：：BD.三、填空题16．（2024·山东烟台·三模）614x展开式的中间一项的系数为.胜杰，江新林3人）顺利打开“家门”，欢迎远道而来的神舟十八号航天员乘组（叶光富、李聪、李广苏3人）入驻“天宫”．随后，两个航天员乘组拍下“全家福”，共同向全国人民报平安．若这6名航天员站成一排合影留念，叶光富不站最左边，汤洪波不站最右边，则不同的排法有． 【答案答案】】504【分析分析】】本题考查排列中分类加法计数原理和分步乘法计数原理.根据题目要求根据题目要求，，分两类进行讨论分两类进行讨论，，第一类叶光富在最右侧叶光富在最右侧，，第二类叶光富不在最右侧.然后根据分类加法计数原理相加即可得到答案. 【详解详解】】根据叶光富不站最左边根据叶光富不站最左边，，可以分为两种情况可以分为两种情况：：第一种情况第一种情况：：叶光富站在最右边叶光富站在最右边，，此时剩余的5人可以进行全排列人可以进行全排列，，共有55A 120=种排法.第二种情况第二种情况：：叶光富不站在最右边叶光富不站在最右边，，根据题目条件叶光富不站最左边根据题目条件叶光富不站最左边，，此时叶光富有4种站法.根据题目条件汤洪波不站在最右边件汤洪波不站在最右边，，可知杨洪波只有4种站法.剩余的4人进行全排列,共有4444A 384××=种排法种排法，，由分类加法计数原理可知由分类加法计数原理可知，，总共有120384504+=种排法种排法．． 故答案为故答案为：：504 18．（2024·福建福州·三模）421x x +−的展开式中常数项为．4，1，5，9进行某种排列得到密码．若排列时要求相同数字不相邻，且相同数字之间一个数字，则小明可以设置的不同密码种数为． 【答案答案】】96【分析分析】】利用捆绑法即可求解.【详解详解】】从3，4，5，9中选择一个数字放入两个1之间之间，，将其与两个1看作一个整体看作一个整体，，与剩下元素全排列与剩下元素全排列，，故不同的密码个数为1444C A 96=，故答案为故答案为：：96 20．（2024·河北衡水·三模）()()7222x y x y +−的展开式中46x y 的系数为（用数字作答）【答案答案】】35−【分析分析】】根据题意根据题意，，结合二项式的展开式的性质结合二项式的展开式的性质，，准确计算准确计算，，即可求解.【详解详解】】由题意由题意，，多项式()()7222x y x y +−的展开式中含有46x y 的项为的项为：：()()()265262524677C 2C 35x x y y xy x y ⋅⋅−+⋅−=−，所以46x y 的系数为35−． 故答案为故答案为：：35−.21．（2024·河南·三模）若()*nn∈N 的展开式中存在常数项，则n 的值可以是（写出一个值即可）场为女双，一场为男女混双），每名选手只参加1场表演赛，则所有不同的安排方法有种. 【答案答案】】4050【分析分析】】先考虑两对混双的组合先考虑两对混双的组合，，再从余下4名男选手和4名女选手各有3种不同的配对方法组成两对男双组合双组合，，两对女双组合双组合，，利用分步乘法原理可求得结果. 【详解详解】】先考虑两对混双的组合有22662C C ⋅种不同的方法种不同的方法，，余下4名男选手和4名女选手各有3种不同的配对方法组成两对男双组合对方法组成两对男双组合，，两对女双组合双组合，，故共有22662C C 334050⋅××=.故答案为故答案为：：4050。

高三数学排列组合与二项式定理试题答案及解析1.三张卡片的正反面分别写有1和2,3和4,5和6,若将三张卡片并列,可得到不同的三位数(6不能作9用)的个数为()A．8B．6C．14D．48【答案】D【解析】方法一:第一步,选数字.每张卡片有两个数字供选择,故选出3个数字,共有23=8(种)选法.第二步,排数字.要排好一个三位数,又要分三步,首先排百位,有3种选择,由于排出的三位数各位上的数字不可能相同,因而排十位时有2种选择,排个位只有一种选择.故能排出3×2×1=6(个)不同的三位数.由分步乘法计数原理知共可得到8×6=48(个)不同的三位数.方法二:第一步,排百位有6种选择,第二步,排十位有4种选择,第三步,排个位有2种选择.根据分步乘法计数原理,共可得到6×4×2=48(个)不同的三位数.2.设、、为整数，若和被除得余数相同，则称和对模同余，记.若，且，则的值可以为（）A．B．C．D．【答案】A【解析】，因此除的余数为，即，因此的值可以为，故选A.【考点】1.二项式定理；2.数的整除性3.5名志愿者到3个不同的地方参加义务植树，则每个地方至少有一名志愿者的方案共有____种．【答案】150【解析】将5名志愿者分到3个不同的地方参加义务植树，且每个地方至少有一名志愿者，则分配至3地的人数模式只有“1、1、3”与“1、2、2”这两种模式.设这3地分别为甲、乙、丙.(1)当分配的人数模式是“1、1、3”时，即甲、乙、丙3地中有一地是3个人，其他两地都只有1人,则共有（种）.即先从三地中选一地是分配3个人的，再从5名志愿者中选三人派到该地.剩余2人再分配至其余两地.(2) 当分配的人数模式是“1、2、2”时,即甲、乙、丙3地中有一地是1个人，其他两地都有2人,则共有（种）.即先从三地中选一地是只分配1个人的，再从5名志愿者中选1人派到该地.剩余4人再选出2人分配至其余两地中的某地，那剩余2人即是最后一地所得.综上所述，共有60+90=150种方案.【考点】排列与组合4.如图是网络工作者经常用来解释网络运作的蛇形模型：数字1出现在第1行；数字2，3出现在第2行；数字6，5，4（从左至右）出现在第3行；数字7，8，9，10出现在第4行；依次类推，则（1）按网络运作顺序第n行第一个数字（如第2行第一个数字为2，第3行第一个数字为4，…）是；（2）第63行从左至右的第4个数应是．【答案】（1）。

历年(2019-2024)全国高考数学真题分类(排列组合与二项式定理)汇编考点01 排列组合综合1．（2024∙全国甲卷∙高考真题）甲、乙、丙、丁四人排成一列，则丙不在排头，且甲或乙在排尾的概率是（ ） A ．14 B ．13C ．12D ．232．（2023∙全国甲卷∙高考真题）现有5名志愿者报名参加公益活动，在某一星期的星期六、星期日两天，每天从这5人中安排2人参加公益活动，则恰有1人在这两天都参加的不同安排方式共有（ ） A ．120B ．60C ．30D ．203．（2023∙全国甲卷∙高考真题）某校文艺部有4名学生，其中高一、高二年级各2名．从这4名学生中随机选2名组织校文艺汇演，则这2名学生来自不同年级的概率为（ ）A ．16B ．13C ．12D ．234．（2023∙全国乙卷∙高考真题）甲乙两位同学从6种课外读物中各自选读2种，则这两人选读的课外读物中恰有1种相同的选法共有（ ） A ．30种B ．60种C ．120种D ．240种5．（2023∙全国新Ⅱ卷∙高考真题）某学校为了解学生参加体育运动的情况，用比例分配的分层随机抽样方法作抽样调查，拟从初中部和高中部两层共抽取60名学生，已知该校初中部和高中部分别有400名和200名学生，则不同的抽样结果共有（ ）． A ．4515400200C C ⋅种 B ．2040400200C C ⋅种C ．3030400200C C ⋅种D ．4020400200C C ⋅种6．（2022∙全国新Ⅱ卷∙高考真题）有甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演，若甲不站在两端，丙和丁相邻，则不同排列方式共有（ ） A ．12种B ．24种C ．36种D ．48种7．（2022∙全国新Ⅰ卷∙高考真题）从2至8的7个整数中随机取2个不同的数，则这2个数互质的概率为（ ）A ．16B ．13C ．12D ．238．（2021∙全国乙卷∙高考真题）将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训，每名志愿者只分配到1个项目，每个项目至少分配1名志愿者，则不同的分配方案共有（ ） A ．60种B ．120种C ．240种D ．480种9．（2021∙全国甲卷∙高考真题）将3个1和2个0随机排成一行，则2个0不相邻的概率为（ ） A ．0.3B ．0.5C ．0.6D ．0.810．（2021∙全国甲卷∙高考真题）将4个1和2个0随机排成一行，则2个0不相邻的概率为（ ）A ．13B ．25C ．23D ．4511．（2020∙海南∙高考真题）要安排3名学生到2个乡村做志愿者，每名学生只能选择去一个村，每个村里至少有一名志愿者，则不同的安排方法共有（ ）A ．2种B ．3种C ．6种D ．8种12．（2020∙山东∙高考真题）6名同学到甲、乙、丙三个场馆做志愿者，每名同学只去1个场馆，甲场馆安排1名，乙场馆安排2名，丙场馆安排3名，则不同的安排方法共有（ ）A ．120种B ．90种C ．60种D ．30种13．（2019∙全国∙高考真题）我国古代典籍《周易》用“卦”描述万物的变化．每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻“——”和阴爻“— —”，如图就是一重卦．在所有重卦中随机取一重卦，则该重卦恰有3个阳爻的概率是A ．516B ．1132C ．2132D ．1116考点02 二项式定理综合1．（2024∙北京∙高考真题）在(4x 的展开式中，3x 的系数为（ ） A ．6B ．6-C ．12D ．12-2．（2022∙北京∙高考真题）若443243210(21)x a x a x a x a x a -=++++，则024a a a ++=（ ）A ．40B ．41C ．40-D ．41-3．（2020∙北京∙高考真题）在52)-的展开式中，2x 的系数为（ ）． A ．5-B ．5C ．10-D ．104．（2020∙全国∙高考真题）25()()x x y x y ++的展开式中x 3y 3的系数为（ ）A ．5B ．10C ．15D ．205．（2019∙全国∙高考真题）（1+2x 2）（1+x ）4的展开式中x 3的系数为 A ．12 B ．16 C ．20 D ．24参考答案考点01 排列组合综合1．（2024∙全国甲卷∙高考真题）甲、乙、丙、丁四人排成一列，则丙不在排头，且甲或乙在排尾的概率是（ ） A ．14 B ．13C ．12D ．23【答案】B【详细分析】解法一：画出树状图，结合古典概型概率公式即可求解.解法二：分类讨论甲乙的位置，结合得到符合条件的情况，然后根据古典概型计算公式进行求解. 【答案详解】解法一：画出树状图，如图，由树状图可得，甲、乙、丙、丁四人排成一列，共有24种排法， 其中丙不在排头，且甲或乙在排尾的排法共有8种， 故所求概率81=243P =. 解法二：当甲排在排尾，乙排第一位，丙有2种排法，丁就1种，共2种； 当甲排在排尾，乙排第二位或第三位，丙有1种排法，丁就1种，共2种；于是甲排在排尾共4种方法，同理乙排在排尾共4种方法，于是共8种排法符合题意；基本事件总数显然是44A 24=，根据古典概型的计算公式，丙不在排头，甲或乙在排尾的概率为81243=. 故选：B2．（2023∙全国甲卷∙高考真题）现有5名志愿者报名参加公益活动，在某一星期的星期六、星期日两天，每天从这5人中安排2人参加公益活动，则恰有1人在这两天都参加的不同安排方式共有（ ） A ．120B ．60C ．30D ．20【详细分析】利用分类加法原理，分类讨论五名志愿者连续参加两天公益活动的情况，即可得解. 【答案详解】不妨记五名志愿者为,,,,a b c d e ，假设a 连续参加了两天公益活动，再从剩余的4人抽取2人各参加星期六与星期天的公益活动，共有24A 12=种方法，同理：,,,b c d e 连续参加了两天公益活动，也各有12种方法， 所以恰有1人连续参加了两天公益活动的选择种数有51260⨯=种. 故选：B.3．（2023∙全国甲卷∙高考真题）某校文艺部有4名学生，其中高一、高二年级各2名．从这4名学生中随机选2名组织校文艺汇演，则这2名学生来自不同年级的概率为（ ）A ．16B ．13C ．12D ．23【答案】D【详细分析】利用古典概率的概率公式，结合组合的知识即可得解.【答案详解】依题意，从这4名学生中随机选2名组织校文艺汇演，总的基本事件有24C 6=件， 其中这2名学生来自不同年级的基本事件有1122C C 4=，所以这2名学生来自不同年级的概率为4263=. 故选：D.4．（2023∙全国乙卷∙高考真题）甲乙两位同学从6种课外读物中各自选读2种，则这两人选读的课外读物中恰有1种相同的选法共有（ ） A ．30种 B ．60种 C ．120种 D ．240种【答案】C【详细分析】相同读物有6种情况，剩余两种读物的选择再进行排列，最后根据分步乘法公式即可得到答案.【答案详解】首先确定相同得读物，共有16C 种情况，然后两人各自的另外一种读物相当于在剩余的5种读物里，选出两种进行排列，共有25A 种，根据分步乘法公式则共有1265C A 120⋅=种，故选：C.5．（2023∙全国新Ⅱ卷∙高考真题）某学校为了解学生参加体育运动的情况，用比例分配的分层随机抽样方法作抽样调查，拟从初中部和高中部两层共抽取60名学生，已知该校初中部和高中部分别有400名和200名学生，则不同的抽样结果共有（ ）． A ．4515400200C C ⋅种 B ．2040400200C C ⋅种C ．3030400200C C ⋅种D ．4020400200C C ⋅种【详细分析】利用分层抽样的原理和组合公式即可得到答案. 【答案详解】根据分层抽样的定义知初中部共抽取4006040600⨯=人，高中部共抽取2006020600⨯=， 根据组合公式和分步计数原理则不同的抽样结果共有4020400200C C ⋅种. 故选：D.6．（2022∙全国新Ⅱ卷∙高考真题）有甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演，若甲不站在两端，丙和丁相邻，则不同排列方式共有（ ） A ．12种 B ．24种C ．36种D ．48种【答案】B【详细分析】利用捆绑法处理丙丁，用插空法安排甲，利用排列组合与计数原理即可得解【答案详解】因为丙丁要在一起，先把丙丁捆绑，看做一个元素，连同乙，戊看成三个元素排列,有3!种排列方式；为使甲不在两端，必须且只需甲在此三个元素的中间两个位置任选一个位置插入，有2种插空方式；注意到丙丁两人的顺序可交换，有2种排列方式，故安排这5名同学共有：3!2224⨯⨯=种不同的排列方式， 故选：B7．（2022∙全国新Ⅰ卷∙高考真题）从2至8的7个整数中随机取2个不同的数，则这2个数互质的概率为（ ）A ．16B ．13C ．12D ．23【答案】D【详细分析】由古典概型概率公式结合组合、列举法即可得解.【答案详解】从2至8的7个整数中随机取2个不同的数，共有27C 21=种不同的取法，若两数不互质，不同的取法有：()()()()()()()2,4,2,6,2,8,3,6,4,6,4,8,6,8，共7种， 故所求概率2172213P -==. 故选：D.8．（2021∙全国乙卷∙高考真题）将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训，每名志愿者只分配到1个项目，每个项目至少分配1名志愿者，则不同的分配方案共有（ ） A ．60种 B ．120种 C ．240种 D ．480种【答案】C【详细分析】先确定有一个项目中分配2名志愿者，其余各项目中分配1名志愿者，然后利用组合，排列，乘法原理求得.【答案详解】根据题意，有一个项目中分配2名志愿者，其余各项目中分配1名志愿者，可以先从5名志愿者中任选2人，组成一个小组，有25C 种选法；然后连同其余三人，看成四个元素，四个项目看成四个不同的位置，四个不同的元素在四个不同的位置的排列方法数有4！种，根据乘法原理，完成这件事，共有2 54!240C⨯=种不同的分配方案，故选：C.【名师点评】本题考查排列组合的应用问题，属基础题，关键是首先确定人数的分配情况，然后利用先选后排思想求解.9．（2021∙全国甲卷∙高考真题）将3个1和2个0随机排成一行，则2个0不相邻的概率为（） A．0.3 B．0.5 C．0.6 D．0.8【答案】C【详细分析】利用古典概型的概率公式可求概率.【答案详解】解：将3个1和2个0随机排成一行，可以是：00111,01011,01101,01110,10011,10101,10110,11001,11010,11100，共10种排法，其中2个0不相邻的排列方法为：01011,01101,01110,10101,10110,11010，共6种方法，故2个0不相邻的概率为6=0.6 10，故选：C.10．（2021∙全国甲卷∙高考真题）将4个1和2个0随机排成一行，则2个0不相邻的概率为（）A．13B．25C．23D．45【答案】C【答案详解】将4个1和2个0随机排成一行，可利用插空法，4个1产生5个空，若2个0相邻，则有155C=种排法，若2个0不相邻，则有2510C=种排法，所以2个0不相邻的概率为102 5103=+.故选：C.11．（2020∙海南∙高考真题）要安排3名学生到2个乡村做志愿者，每名学生只能选择去一个村，每个村里至少有一名志愿者，则不同的安排方法共有（）A．2种 B．3种 C．6种 D．8种【答案】C【详细分析】首先将3名学生分成两个组，然后将2组学生安排到2个村即可.【答案详解】第一步，将3名学生分成两个组，有12323C C=种分法第二步，将2组学生安排到2个村，有222A=种安排方法所以，不同的安排方法共有326⨯=种 故选：C【名师点评】解答本类问题时一般采取先组后排的策略.12．（2020∙山东∙高考真题）6名同学到甲、乙、丙三个场馆做志愿者，每名同学只去1个场馆，甲场馆安排1名，乙场馆安排2名，丙场馆安排3名，则不同的安排方法共有（ ）A ．120种B ．90种C ．60种D ．30种【答案】C【详细分析】分别安排各场馆的志愿者，利用组合计数和乘法计数原理求解. 【答案详解】首先从6名同学中选1名去甲场馆，方法数有16C ； 然后从其余5名同学中选2名去乙场馆，方法数有25C ； 最后剩下的3名同学去丙场馆.故不同的安排方法共有126561060C C ⋅=⨯=种.故选：C【名师点评】本小题主要考查分步计数原理和组合数的计算，属于基础题.13．（2019∙全国∙高考真题）我国古代典籍《周易》用“卦”描述万物的变化．每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻“——”和阴爻“— —”，如图就是一重卦．在所有重卦中随机取一重卦，则该重卦恰有3个阳爻的概率是A ．516B ．1132C ．2132D ．1116【答案】A【详细分析】本题主要考查利用两个计数原理与排列组合计算古典概型问题，渗透了传统文化、数学计算等数学素养，“重卦”中每一爻有两种情况，基本事件计算是住店问题，该重卦恰有3个阳爻是相同元素的排列问题，利用直接法即可计算．【答案详解】由题知，每一爻有2种情况，一重卦的6爻有62情况，其中6爻中恰有3个阳爻情况有36C ，所以该重卦恰有3个阳爻的概率为3662C =516，故选A ．【名师点评】对利用排列组合计算古典概型问题，首先要详细分析元素是否可重复，其次要详细分析是排列问题还是组合问题．本题是重复元素的排列问题，所以基本事件的计算是“住店”问题，满足条件事件的计算是相同元素的排列问题即为组合问题．考点02 二项式定理综合1．（2024∙北京∙高考真题）在(4x 的展开式中，3x 的系数为（ ） A ．6 B ．6- C ．12 D ．12-【答案】A【详细分析】写出二项展开式，令432r-=，解出r 然后回代入二项展开式系数即可得解.【答案详解】(4x 的二项展开式为(()()442144C C 1,0,1,2,3,4r rrr rr r T x xr --+==-=，令432r-=，解得2r =， 故所求即为()224C 16-=. 故选：A.2．（2022∙北京∙高考真题）若443243210(21)x a x a x a x a x a -=++++，则024a a a ++=（ ）A ．40B ．41C ．40-D ．41-【答案】B【详细分析】利用赋值法可求024a a a ++的值. 【答案详解】令1x =，则432101a a a a a ++++=， 令=1x -，则()443210381a a a a a -+-+=-=， 故420181412a a a +++==， 故选：B.3．（2020∙北京∙高考真题）在52)-的展开式中，2x 的系数为（ ）． A ．5- B ．5C ．10-D ．10【答案】C【详细分析】首先写出展开式的通项公式，然后结合通项公式确定2x 的系数即可.【答案详解】)52展开式的通项公式为：()()55215522r rrrr r r T CC x--+=-=-，令522r -=可得：1r =，则2x 的系数为：()()11522510C -=-⨯=-. 故选：C.【名师点评】二项式定理的核心是通项公式，求解此类问题可以分两步完成：第一步根据所给出的条件(特定项)和通项公式，建立方程来确定指数(求解时要注意二项式系数中n 和r 的隐含条件，即n ，r 均为非负整数，且n ≥r ，如常数项指数为零、有理项指数为整数等)；第二步是根据所求的指数，再求所求解的项．4．（2020∙全国∙高考真题）25()()x x y xy ++的展开式中x 3y 3的系数为（ ）A ．5B ．10C ．15D ．20【答案】C【详细分析】求得5()x y +展开式的通项公式为515rrrr T C xy -+=（r N ∈且5r ≤），即可求得2y x x ⎛⎫+ ⎪⎝⎭与5()x y +展开式的乘积为65r rr C xy -或425r r r C x y -+形式，对r 分别赋值为3，1即可求得33x y 的系数，问题得解.【答案详解】5()x y +展开式的通项公式为515r rr r T C xy -+=（r N ∈且5r ≤）所以2y x x ⎛⎫+ ⎪⎝⎭的各项与5()x y +展开式的通项的乘积可表示为：56155r rrr rrr xT xC xy C xy --+==和22542155r r rr r r r T C x y xC y y y x x --++==在615rrr r xT C xy -+=中，令3r =，可得：33345xT C x y =，该项中33x y 的系数为10，在42152r r r r T C x x y y -++=中，令1r =，可得：521332T C y x x y =，该项中33x y 的系数为5所以33x y 的系数为10515+= 故选：C【名师点评】本题主要考查了二项式定理及其展开式的通项公式，还考查了赋值法、转化能力及详细分析能力，属于中档题.5．（2019∙全国∙高考真题）（1+2x 2）（1+x ）4的展开式中x 3的系数为 A ．12 B ．16 C ．20 D ．24【答案】A【详细分析】本题利用二项展开式通项公式求展开式指定项的系数．【答案详解】由题意得x 3的系数为314424812C C +=+=，故选A ．【名师点评】本题主要考查二项式定理，利用展开式通项公式求展开式指定项的系数．。

排列组合二项式定理知识点以及典型例题总结考纲要求:1.知道分类计数原理与分步计数原理的区别，会用两个原理分析和解决一些简单的问题2.知道排列和组合的区别和联系，记住排列数和组合数公式，能用它们解决一些简单的应3.知道一些组合数性质的应用.4.了解二项式定理及其展开式5.记住二项式展开式的通项公式，并能够运用它求展开式中指定的项6.了解二项式系数的性质，能够利用二项式展开式的通项公式求出展开式中二项式系数最大的项.7.了解二项式的展开式中二项式系数与项的系数的区别知识点一：计数原理1.分类加法计数原理如果完成一件事，有n类办法，在第1类办法中有m1种不同的方法，在第2类办法中有m2种不同的方法，…，在第n类办法中有m n种不同的方法，那么完成这件事共有N＝m1＋m2＋…＋m n种不同的方法．两个基本计数原理的区别：分类计数原理——每一类办法都能把事单独完成；分步计数原理——缺少任何一个步骤都无法把事完成．2.分步乘法计数原理如果完成一件事，需分成n个步骤，做第1步有m1种不同的方法，做第2步有m2种不同的方法，…，做第n步有m n种不同的方法，那么完成这件事共有N＝m1·m2·…·m n种不同的方法．知识点二：排列1.排列的定义：一般地，从n个不同的元素中，任取m(m≤n)个元素，按照一定顺序排成一列，叫作从n个不同元素中取出m 个元素的一个排列．如果m ＜n ，这样的排列叫作选排列．如果m ＝n ，这样的排列叫作全排列．2. 排列数的定义：从n 个不同元素中取出m (m ≤n )个元素的所有排列的个数，叫作从n 个不同元素中取出m 个元素的排列数，用符号P mn 表示．3. 排列数的公式： (1) P m n ＝n ·(n －1)·(n －2)·…·(n －m ＋1)；(2) P m n ＝()!!n n m -； 规定：0！＝1.知识点三：组合1.组合的定义：一般地，从n 个不同元素中，任取m (m ≤n )个元素并成一组，叫做从n 个不同元素中取出m 个元素的一个组合．2.组合数的定义：从n 个不同元素中取出m (m ≤n )个元素的所有组合的个数，叫做从n 个不同元素中取出m 个元素的组合数，用符号C mn 表示．3. 组合数公式： (1)()()()121P C P !m mn n m n n n n n m m ---+==(2)()!C !!m n n m n m =-(n ，m ∈N ＋，且m ≤n ) 4. 组合数性质：(1) C =C m n m n n -；(2) 111C +C C mm m n n n +++=知识点四：二项式定理1. 二项式定理(a ＋b )n ＝011222C C C C C n n n m n m nn n n n n n a a b a b a b b ---++++++， n ∈N ＋其中C m n (m ＝0，1，2，…，n )叫做二项式系数；T m ＋1＝C m n m m n a b -叫做二项式展开式的通项公式．2. 二项式系数的性质：(1)每一行的两端都是1，其余每一个数都是它“肩上”两个数的和；(2)在二项展开式中，与首末两端“等距离”的两项的二项式系数相等，即C C r n r n n -=(3)如果二项式的幂指数n 是偶数，那么中间一项即第12n +项的系数最大；如果二项式的幂指数n 是奇数，那么中间两项即第12n +项和第32n +项的二项式系数相等且最大； (4)(a ＋b )n 的二项式系数之和为2n ，即012C C C ++C ++C m n n n n n n ++＝2n ； (5)(a ＋b )n 的二项展开式中，奇数项的二项式系数之和等于偶数项的二项式系数之和，都等12n -，024C C C +n n n ++135C +C C n n n =++12n -=.题型一 分类加法计数原理例1 一个盒子里有4个不同的红球，3个不同的黄球和5个不同的蓝球．从盒子中任取一个球，有多少种不同的取法？分析：盒子中取出一个球就可以完成任务，所以考察分类加法计数原理.解答：从盒子中任取一个球，共有三类方案：第一类方案，从4个不同的红球中任取一球，有4种方法；第二类方案，从3个不同的黄球中任取一球，有3种方法；第三类方案，从5个不同的蓝球中任取一球，有5种方法．所以，选一个班担任升旗任务的方法共有：12+10+10=32（种）题型二分步乘法计数原理例2 一个盒子里有4个不同的红球，7个不同的黄球和5个不同的蓝球．从盒子中取红球、黄球和蓝球各一个，有多少种不同的取法？分析：盒子中各取出一个球需要分三步，所以考察分步乘法计数原理.解答：完成这件事需要分三步．第一步，从4个不同的红球中任取一球，有4种方法；第二步，从3个不同的黄球中任取一球，有3种方法；第三步，从5个不同的蓝球中任取一球，有5种方法．由分步乘法计数原理，从盒子中取红球、黄球和蓝球各一个共有⨯⨯435=60种不同的取法．例3 邮政大厅有4个邮筒，现将三封信逐一投入邮筒，共有多少种投法？分析：三封信逐一投入邮筒分成三个步骤，每个步骤投一封信，分别均有4种方法．解答：应用分步计数原理，投法共有44464⨯⨯=种．题型三分类分步混合运算例4 一个盒子里有4个不同的红球，7个不同的黄球和5个不同的蓝球．从盒子中任取2个颜色不同的球，有多少种不同的取法？分析分类计数原理与分步计数原理混合使用的问题，一般要“先分类，后分步”.解答：可按所选两球的颜色分为如下3类．第1类：红球、黄球各一个，有4×7＝28种选法；第2类：红球、蓝球各一个，有4×5＝20种选法；第3类：黄球、蓝球各一个，有7×5＝35种选法．根据分类计数原理，不同的选法种数为N ＝28＋20＋35＝83(种)．知识点二 排列题型一 排列数公式的运用例5 已知221P P n n +-＝10，则n 的值为( ). A ．4 B ．5 C ．6 D ．7解答：由221P P n n +-＝10，得(n ＋1)n －n (n －1)＝10，解得n ＝5.故选B .题型二 排列的运用例6 小华准备从7本世界名著中任选3本，分别送给甲、乙、丙3位同学，每人1本，共有多少种选法？分析 选出3本不同的书，分别送给甲乙丙3位同学，书的不同排序，结果是不同的.因此选法的种数是从7个不同元素中取出3个元素的排列数.解答：不同的送法的种数是 37P 765210=⨯⨯=．即共有210种不同送法．题型三 某元素一定在某位置例7 4名男生和3名女生排成一排照相，分别按下列要求，求各有多少种不同的排法．（1）男生甲一定在中间位置；（2）男生甲不在中间位置.分析 本题是有限制条件的排列问题，若有特殊元素优先考虑特殊元素，若有特殊位置，优先考虑特殊位置.（1）分两步完成：第一步，男生站在中间位置，有一种排法；第二步，排其他的元素，共有66P 种排法.所以，男生甲一定在中间位置共有661P 720⨯=种排法.（2）分两步完成：第一步，男生不在中间位置，有5种排法；第二步，排其他的元素，共有66P 种排法.所以，男生甲一定在中间位置共有665P 3600⨯=种排法. 题型四 某几个元素相邻例8 4名男生和3名女生排成一排照相，同学甲、乙相邻有多少种排法？分析：解决“相邻”问题采用的是“捆绑法”解答：第一步，把甲、乙看成一个元素，与其他5人共6个元素进行全排列；第二步，甲、乙二人进行全排列．即6262P P ＝720×2＝1440(种)．题型五 某几个元素不相邻例9 4名男生和3名女生排成一排照相，同学甲、乙不相邻有多少种排法？分析：解决“不相邻”问题采用的是“插空法”.解答：第一步，把甲、乙之外的5名同学进行全排列；第二步，在5名同学之间或两端共6个空中插入甲、乙两名同学．即5256P P ＝120×30＝3600(种)． 例10 4名男生和3名女生排成一排照相，男女同学相间排列，有多少种排法？ 分析：“相间”是特殊的“不相邻”问题解答：第一步，男生全排列，有44P 种排法；第二步，女生全排列，有33P 种排法；第三步，相间插入有2中插入方法．即男女同学相间排列，有4343P P 2576⨯=种种排法．题型六 数字的排列问题例11 用数字0，1，2，3，4组成没有重复数字的三位数，求：(1)组成的三位数的个数；(2)组成的三位数中偶数的个数；分析：对数字进行排列时，如果数字中含有0，应区别对待．因为0作为特殊元素，不能在首位出现．解答：(1)应采用特殊位置优先法．因为0不能为首位(百位)，所以首位的排法有14P 种，其他两位是从剩余的4个数字中选2个的一个排列，有24P 种，所以共有1244P P ＝48(种)．(2)由于0的存在，应分两类：第一类个位是0，有24P 个；第二类，个位不是0，先确定个位，从2，4中选一个，有12P 种，再确定首位，有13P 种，剩余的一位是从3个数中选1个，有13P 种．所以共有21114233P P P P +＝30(种)． 知识点三 组合题型一 组合的应用例12 学校组织一项活动，要从5名男同学，3名女同学中选4名．共有多少种选法？ 分析: 从5名男同学，3名女同学中选4名, 选出的4名同学任务是一样的，因此选法的种数是从8个不同元素中取出4个元素的组合数. 解答：不同的选法种数是488765C 704321⨯⨯⨯==⨯⨯⨯种. 题型二 一定包含或一定不包含某元素例13 学校组织一项活动，要从5名男同学，3名女同学中选4名．（1）若甲同学必须去，有多少种选法？（2）若甲同学一定不去，有多少种选法？分析：若甲同学必须去，再从其他7人中选3人即可．解答：（1）共有37765C 321⨯⨯=⨯⨯＝35种选法． 分析：若甲同学一定不去，从其他7人中选4人即可．解答：（2）共有47C 35=种选法．题型三 至多、至少问题例14 学校组织一项活动，要从5名男同学，3名女同学中选4名．若男生甲、女生乙至少有一个被选中，有多少种选法？分析：至多、至少问题从正面解，一般情况先分类，再求解.当从正面求解困难时，可从对立面求解.解答：方法一 男生甲、女生乙至少有一个被选中，分成两类：第一类 男生甲、女生乙只有一个人被选中，有1326C C 260120=⨯=种选法； 第二类 男生甲、女生乙都被选中，有2226C C 21530=⨯=种选法.所以，男生甲、女生乙至少有一个被选中，共有120+30=150种不同的选法.题型四 组合数性质的的相关计算例15 若44511C C C n n n --=+，求n .分析：考察组合数的性质111C +C C m m m n nn +++=；C =C m n m n n-. 解答：45511C +C =C ,n n n --∴45C =C ,n n∴n ＝4＋5＝9.题型四 排列、组合混合应用例16 从6名男生和5名女生中选出3名男生和2名女生排成一行，有多少种不同排法? 分析:可以首先将男生选出，再将女生选出，然后对选出的5名学生排序．解 不同排法的总数为32565565454C C P 543212400032121⨯⨯⨯⋅⋅=⨯⨯⨯⨯⨯⨯=⨯⨯⨯（种）． 知识点四 二项式定理题型一 求二项式展开式的指定项例17 求二项式103x x ⎛⎫- ⎪⎝⎭的展开式中第4项. 分析：.二项式103x x ⎛⎫- ⎪⎝⎭的展开式第4项，则n 的值为10，m 的值为3，可直接用二项式的通项T m ＋1＝C m n m m n a b -求解.解答：T 4＝T 3＋1＝337103C x x ⎛⎫- ⎪⎝⎭＝－3240x 4， ∴第4项是－3240x 4.. 例18 求二项式103x x ⎛⎫- ⎪⎝⎭的展开式中含x 6的项. 分析：二项式103x x ⎛⎫- ⎪⎝⎭的展开式中含x 6的项，则n 的值为10，m 的值未知.此类问题应先写出二项式的通项，结合条件“含x 6的项”确定出m 的值.从而求出含x 6的项.解答: ∵T m ＋1＝()1010210103C 3C m m m mm m x x x --⎛⎫-=- ⎪⎝⎭， 令10－2m ＝6，得m ＝2.∴含x 6的项为T 3＝T 2＋1＝(－3)2210C x 6＝405x 6. 例19 在二项式103x x ⎛⎫- ⎪⎝⎭的展开式，求： (1)常数项；(2)二项式系数最大的项．分析：（1）求常数项，因为不知道m 的值，要根据“常数项”之一条件确定m 的值.所以，与例18过程相似；（2）可计算出第10162+=项为二项式系数最大的项，其实就是求第6项，所以与例17过程相似.解答：（1）∵T m ＋1＝()1010210103C 3C m m m mm m x x x --⎛⎫-=- ⎪⎝⎭， 10－2m ＝0，即m ＝5.∴展开式的第6项是常数项，即T 6＝T 5＋1＝5555510103C =(3)C x x ⎛⎫-- ⎪⎝⎭＝－61236. （2）∵n ＝10，∴展开式有11项，中间一项的二项式系数最大，中间一项为第6项． ∴T 6＝T 5＋1＝5555510103C =(3)C x x ⎛⎫-- ⎪⎝⎭＝－61236. 题型二 求二项式展开式的某一项系数与某一项的二项式系数.例20 求92)x -（的二项展开式中6x 的系数和该项的二项式系数． 分析：二项展开式中某项的的系数与这一项二项式系数是两个不同的概念. 某项的系数是除字母外的所有数乘积的结果，某项的二项式系数是该项的组合数，和其他无关. 解答： 92)x -（的展开式的通项公式为99199C (2)C (1)2m m m m m m m m T x x --+=-=-⋅⋅ 由9－m =6,得m ＝3．即二项展开式中含6x 的项为第4项．故这一项的系数是3339987C (1)2(8)672321⨯⨯⨯-⨯=⨯-=-⨯⨯．该项的二项式系数为39987C 84321⨯⨯==⨯⨯. 题型三 二项式各项系数和与二项式系数和例21 在(1－x )5的二项展开式中，各项系数和为____________；所有项的二项式系数之和为____________.分析：在二项式中令式子中的字母为1，可得各项系数和；所有项的二项式系数之和为2n ，即012C C C ++C ++C m n n n n n n ++＝2n ，故所有项的二项式系数之和只和n 有关.解答：在(1－x )5中，令x =1，可得各项系数和为0.(1－x )5的二项式系数之和为25=32.。

高中数学知识要点(y àodi ǎn)重温〔21〕排列组合及二项式定理1. 熟悉排列数、组合数的计算公式；理解排列数、组合数的一些性质：①， 由此可得：，，为相应的数列求和创造了条件； ②；③，由此得：；[举例] =___________解析：原式=；记，数列{}的前19项和即为所求。

记数列{n a }的前项和为；该数列的求和方法有很多种，但都比拟烦琐，这里介绍用组合数性质求解：注意到2)1(+=n n a n =， ==== …==1330；[稳固1]设且，那么等于 〔 〕 〔A 〕〔B 〕 〔C 〕 〔D 〕 [稳固2] 的展开式中第9项、第10项、第11项的二项式系数成等差数列，那么n=____2．解排列组合应用题首先要明确需要完成的事件是什么；其次要辨析完成该事件的过程：分类相加〔每一类方法都能HY 地完成这件事〕，分步相乘〔每一步都不能完成事件，只有各个步骤都完成了，才能完成事件〕；较为复杂的事件往往既要分类，又要分步〔每一类方法又都需分步施行〕；分类讨论是研究排列组合问题的重要思想方法之一，分类时要选定讨论对象、确保不重不漏。

[举例] 设集合I={1,2,3,4,5}，选择I的两个(liǎnɡɡè)非空子集A和B，要使B中最小的数大于A中的最大数，那么不同的选择方法一共有：〔〕种A．50种 B．49种 C．48种 D．47种解析：此题要完成的事件是：构造集合I的两个非空子集；要求：B中最小的数大于A中的最大数；显然B中的最小数不可能是1，以下分类：① B中的最小数是2，B中可以有{2，3，4，5}中的1个元素、2个元素、3个元素或者4个元素，所有可能的情况有：=8种，此时A只有{1}这1种；集合A、B都确定了，才算完成事件，∴完成事件有8×1=8中方法；② B中的最小数是3，B中可以有{3，4，5}中的1个元素、2个元素或者3个元素，所有可能的情况有：=4种，此时A中可以有{1，2}中的有1个元素或者2个元素，有=3种，∴完成事件有4×3=12种方法；③ B中的最小数是4，B中可以有{4，5}中的1个元素或者2个元素，所有可能的情况有2种，此时A中可以有{1，2，3}中的有1个元素、2个元素或者3个元素，有=7种，∴完成事件有2×7=14种方法；④ B中的最小数是5，只有{5}这1种，此时A中可以有{1，2，3，4}中的有1个元素、2个元素、3个元素或者4个元素，有=15种，∴完成事件有1×15=15种方法；故完成事件的方法总数为：8+12+14+15=49，选B。