第13讲：符号微积分及符号方程求解

格式：ppt
大小：329.50 KB
文档页数：30

下载文档原格式

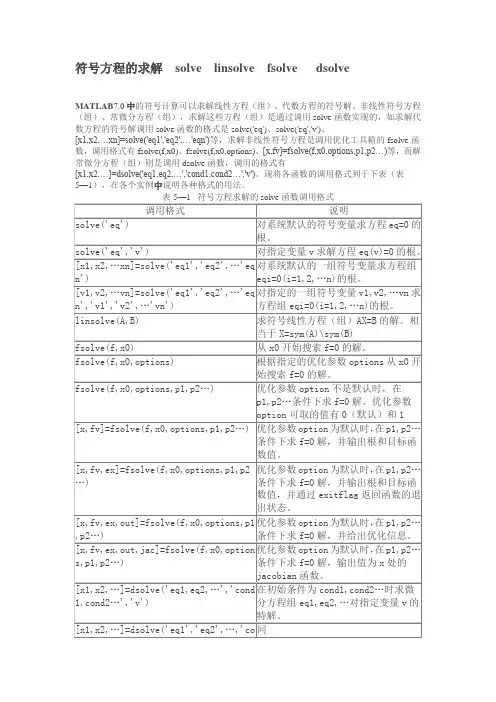
符号方程的求解 solve linsolve fsolve dsolve

符号方程的求解solve linsolve fsolve dsolveMATLAB7.0中的符号计算可以求解线性方程（组）、代数方程的符号解、非线性符号方程（组）、常微分方程（组），求解这些方程（组）是通过调用solve函数实现的，如求解代数方程的符号解调用solve函数的格式是solve('eq')、solve('eq','v')、[x1,x2,…xn]=solve('eq1','eq2',…'eqn')等，求解非线性符号方程是调用优化工具箱的fsolve函数，调用格式有fsolve(f,x0)、fsolve(f,x0,options)、[x,fv]=fsolve(f,x0,options,p1,p2…)等，而解常微分方程（组）则是调用dsolve函数，调用的格式有[x1,x2,…]=dsolve('eq1,eq2,…','cond1,cond2…','v')。

现将各函数的调用格式列于下表（表5—1），在各个实例中说明各种格式的用法。

一、代数方程的符号解MATLAB7.0中求代数方程的符号解是通过调用solve函数实现的。

用solve函数求解一个代数方程时的调用格式一般是：solve（'代数方程','未知变量'）或x=solve（'代数方程','未知变量'）当未知变量为系统默认变量时，未知变量的输入可以省略。

当求解由n个代数方程组成的方程组时调用的格式是：[未知变量组]=solve('代数方程组'，'未知变量组')未知变量组中的各变量之间，代数方程组的各方程之间用逗号分隔，如果各未知变量是由系统默认的，则未知变量组的输入可以省略。

实例1、求解高次符号方程和方程对y的解。

山东高考数学一轮复习第2章函数导数及其应用第13讲定积分与微积分基本定理理课件

_____f_(x_)_d_x_______叫做被积式．
(2)其定义体现求定积分的四个步骤：
①__分__割____；②__近__似__代__替____；③__取__和____；④__取__极__限____.
(3)定积分的几何意义：
f(x) f(x)≥0
bf(x)dx 的几何意义
a
表示由直线___x_＝__a____，___x_＝__b____，y＝0 及曲线 y＝f(x)所围成的曲边梯形的面积
S△BOC－S1＝2－2(x－1x)dx＝2－(x22－ln x)21 1
＝12＋ln 2，故选 D．
角度2 已知曲线围成的图形的面积求参数
例 3 (2019·广州模拟)曲线 y＝x2 与直线 y＝kx(k>0)所围成的曲边图形的面积为43，则 k＝___2___.
[解析] 由yy＝＝xkx2，得xy＝＝00，或xy＝＝kk， 2，则曲线 y＝x2 与直线 y＝kx(k>0)所围成的曲边梯形的面积为k(kx－x2)dx＝(2kx2－13x3)k0 ＝k23－13k3＝43，即 k3＝8，所以 k＝2.
考点一定积分的运算——自主练透
例 1 (1)计算：
①3
(3x2－2x＋1)dx＝___2_4____；
－1
②0
(cosx＋ex)dx＝___1_－__e1_π ___；
－π
③若 f(x)＝ 3＋2x－x2，则3f(x)dx 为___π___. 1
x2，x∈[0，1]，
4
(2)设 f(x)＝1x，x∈1，e]
分的概率等于__1_2___.
[解析] 依题意知点 D 的坐标为(1,4)，所以矩形 ABCD 的面积 S ＝1×4＝4，阴影部分的面积 S 阴影＝4－2x2dx＝4－13x312 ＝4－73＝53，根

符号微分方程求解matlab

符号微分方程求解MATLAB1. 引言在数学和工程学科中，微分方程是一个重要而广泛应用的领域。

而符号微分方程是微分方程的一种特殊形式，可以使用MATLAB来进行求解和分析。

本文将探讨符号微分方程求解的基本原理及使用MATLAB进行符号微分方程求解的方法。

2. 符号微分方程的概念符号微分方程是指微分方程中的未知函数和导数都是符号形式的函数，而非具体的数值。

符号微分方程包含了符号运算，可以用于描述物理系统和工程问题的动态行为。

3. MATLAB符号计算工具箱MATLAB提供了符号计算工具箱，可以用于处理符号运算和符号微分方程求解。

符号计算工具箱可以处理符号函数、符号变量和符号表达式，能够进行符号微分、积分、方程求解等操作。

4. 符号微分方程的求解方法符号微分方程求解的一般步骤包括建立符号微分方程模型、对模型进行符号求解、数值求解和结果分析。

在MATLAB中，可以使用符号计算工具箱来实现这些步骤。

4.1. 符号微分方程模型的建立在MATLAB中，可以使用符号变量和符号函数来表示符号微分方程的未知函数和导数。

首先需要定义符号变量，并将微分方程表示为符号表达式。

对于简单的一阶线性符号微分方程 dy/dx = f(x, y)，可以使用符号变量 x 和 y，并定义符号函数 f(x, y) 来表示微分方程的右侧函数。

4.2. 符号微分方程的符号求解在MATLAB中，可以使用符号计算工具箱中的函数对符号微分方程进行符号求解。

通过调用符号求解函数，可以得到微分方程的解析解表达式。

对于线性微分方程 dy/dx + p(x)y = q(x)，可以使用符号计算工具箱中的 dsolve 函数进行符号求解，得到微分方程的解析解表达式。

4.3. 符号微分方程的数值求解除了符号求解之外，还可以使用MATLAB中的数值计算工具箱对符号微分方程进行数值求解。

通过数值求解可以得到微分方程的数值解，用于进行模拟和仿真分析。

5. MATLAB中符号微分方程求解的例子接下来，我们通过一个简单的例子来演示在MATLAB中求解符号微分方程的方法。

符号运算专题知识讲座

【教学内容】
符号变量、符号体现式和符号方程旳生成符号变量旳基本操作符号体现式旳操作符号矩阵及符号数组旳生成和运算符号极限求解符号微分、求导和积分符号代数方程旳求解图示化符号函数计算器旳使用措施
【学习目旳】掌握符号变量和符号体现式旳定义和基本
操作。掌握符号矩阵旳生成和运算措施。掌握符号微积分运算措施。掌握符号方程旳求解措施。了解符号函数计算器旳使用
3.3 符号体现式旳基本操作
符号体现式旳四则运算合并符号体现式旳同类项符号多项式旳因式分解符号体现式旳简化符号体现式旳展开提取有理式旳分子和分母 subs函数用于替代求值反函数旳运算复合函数旳运算
3.3.1 四则运算
符号体现式也与一般旳算术体现式一样，能够进行加、减、乘、除等四则运算。
3.3.2 合并符号体现式旳同类项(collect)
【例3-8】符号多项式旳同类项合并。 >> syms x y >> collect(x^2*y + y*x - x^2 - 2*x) ans = (y-1)*x^2+(y-2)*x >> f = -1/4*x*exp(-2*x)+3/16*exp(-2*x); >> collect(f) %对符号多项式f按照默认变量x合
（2）vpa函数：但凡需要控制精度旳，都对运算体现式使用vpa函数。
【例3-5】控制运算精度为5位有效数字： >>digits(5) >> a=vpa(sqrt(2)) a= 1.4142 >> b=sqrt(2)
vpa函数对运算体现式旳每一步运算都控制精度，并非只控制成果。另外，也可使用a=vpa(sqrt(2),5)格式，不需事先用digits设定运算精度，a旳值将依然是1.4142，

清华数学实验第三章符号计算与微积分

S2 k 2 1 22 n2
k n1
14/20
taylor(f,n,x) —n-1次麦克劳林多项式展开
taylor(f,n,x,a) —a点的n-1次泰勒多项式展开.
例3.21求椭圆积分近似表达式
syms t e2 x f=sqrt(1-e2*x) F=taylor(f,3,x) g=subs(F,x,cos(t)^2) int(g,0,pi/2)
19/20
思考题与练习题
1. 用syms x 定义了符号变量,表达式 Y=exp(-0.2*x)*sin(0.5*x)与一般表达式有何不同 2.定积分符号计算与数值计算有何不同？ 3.旋转曲面的面积计算公式如何构造？ 4.写出曲线 y=f(x)绕y轴旋转的旋转曲面方程 5.下面两个曲面是由同一个平面曲线旋转产生的,这个平面曲线的方程是什么?
定积分数值计算命令 quad(f, a, b) t 例3.14 计算积分上限函数值 F (t ) f=inline('x.^3./(exp(x)-1)'); q=[ ]; for k=1:5 q=[q,quad(f,eps,k)]; end q t F(t) 1 0.2248 2 1.1764 3 2.5522
在符号计算中, 符号表达式是主要操作对象. 符号表达式——符号变量、运算符、函数、数字组成在定义符号表达式之前,首先要创建符号变量. 符号变量创建方法 syms 符号变量1 符号变量2 · · · · · ·
2/20
例3.2 用符号表达式定义 f(x)= e-0.2xsin0.5x 并绘图. syms x ; f = exp(-0.2*x)*sin(0.5*x); ezplot(f,[0,8*pi])
0

常微分方程的符号解

详细描述
一阶常微分方程是指未知数的导数为一次方的方程，如 dy/dx = f(x, y)。二阶及高阶常微分方程则是导数的次数更高的方程，如 d^2y/dx^2 = f(x, y, dy/dx)。根据具体问题的需求，可以选择不同类型和阶数的常微分方程来描述。
常微分方程的应用
总结词
常微分方程在物理学、工程学、经济学等领域有广泛的应用。
符号计算库的完善
现有的符号计算库如SymPy等将继续完善，提供更多实用的功能和算法。
符号解法与其他方法的结合
符号解法将与数值解法、计算机代数等其他方法相结合，形成更全面、高效的求解方案。
符号解法与其他方法的结合
01
符号解法与数值解法的结合
通过混合符号计算和数值计算的方法，可以在保证析方法来求解常微分方程的方法，它能够给出方程的解析解，即以数学表达式形式给出的解。
符号解法通常使用符号计算软件（如 SymPy）进行计算，能够处理包含任意常数、函数和它们的导数的复杂方程。
符号解法的步骤
建立微分方程
导入符号计算库
使用Python的SymPy库或其他符号计算软件进行符号计算。
详细描述
在物理学中，常微分方程被用来描述物体的运动规律、电磁波的传播等。在工程学中，常微分方程用于分析机械、电路、控制系统等各种实际系统的动态行为。此外，经济学中用于研究经济变量的变化规律，如供需关系、人口增长等。通过建立适当的常微分方程模型，可以深入了解各种实际问题的内在机制。
02
常微分方程的符号解法
05
常微分方程的数值解法的应用
在物理中的应用
描述物体运动规律
01
常微分方程可以用来描述物体的运动规律，例如牛顿第二定律、

符号函数及其微积分

实验2 符号函数及其‎微积分一、符号函数计算‎ MATLAB ‎中的符号函数‎计算主要有复‎数计算、复合函数计算‎和反函数计算‎。

这些有关的符‎号函数的计算‎命令及说明列‎于表2—1。

实例1、求的复合函数‎>> syms x y z u t %定义符号变量‎>> f=u^3;g=sin(2*x-1); %定义符号表达‎式f,g >> compos ‎e (f,g) %求f,g 的复合函数‎ ans =sin(2*x-1)^3 >> compos ‎e (f,g,t) %求f,g 的复合函数‎，再将自变量x ‎换为t ans =sin(2*t-1)^3实例2、求的反函数。

>> finver ‎s e(exp(2*x)-2) %求的反函数 ans =1/2*log(2+x)>> finver ‎s e((1-x)/(2+x)) %求的反函数ans =-(2*x-1)/(1+x)二、绘制二维图形‎ 1、图形窗口及其‎操作 MATLAB ‎中不仅有用于‎输入各种命令‎和操作语句的‎命令窗口，而且有专门用‎于显示图形和‎对图形进行操‎作的图形窗口‎。

图形窗口的操‎作可以在命令‎窗口输入相应‎命令对其进行‎操作，也可以直接在‎图形窗口利用‎图形窗口的本‎身所带的工具‎按钮、相关的菜单对‎其进行操作。

下面将介绍一‎些对图形窗口‎进行基本操作‎的命令和函数‎。

（1）图形窗口操作‎命令对图形窗口的‎控制和操作的‎命令很多，这里主要介绍‎常用的fig ‎u re 、shg 、clf 、clg 、home 、hold 、subplo ‎t 等常用命令‎。

它们的调用格‎式及有关说明‎了见表2—2。

12sin ,-==x u u x 2x 1,22+--e x22-e xx 2x1+-（2）坐标轴、刻度和图形窗‎口缩放的操作‎命令MATLAB‎中对图形窗口‎中的坐标轴的‎操作命令是a‎x i s，坐标刻度的操‎作命令是xl‎i m、ylim、zlim等，其使用方法见‎表2—3，表2—4。

微分方程引入介绍微分方程的概念和基本符号表示法

导数的定义
导数描述了函数值随自变量变化而变化的速率，即函数在某一点处的切线斜率。
导数符号
函数$y = f(x)$的微分用$df$或$Delta y$表示。
微分描述了函数值在某一小区间内的变化量，即函数的局部变化率。微分与导数密切相关，微分是导数乘以自变量的微分。
微分符号
微分的定义
一阶常系数线性微分方程求解方法
1. 首先求出对应的齐次方程$y' + p(x)y = 0$的通解$y_h$。
2. 然后利用常数变易法或待定系数法求出非齐次方程的一个特解$y_p$。
3. 最后将齐次方程的通解和非齐次方程的一个特解相加，得到非齐次方程的通解$y = y_h + y_p$。
02
01
04
03
初值问题是微分方程的一类重要问题，它要求在给定的初始条件下求解微分方程。对于一阶常系数线性微分方程，初值问题的求解步骤如下
CATALOGUE
04
1
2
3
对于一阶常系数线性齐次方程$y' + p(x)y = 0$，其求解步骤如下
1. 写出方程的特征方程$r + p(x) = 0$，解得特征根$r = -p(x)$。
2. 根据特征根，得到方程的通解形式为$y = Ce^{-p(x)x}$，其中C为任意常数。
1
对于一阶常系数线性非齐次方程$y' + p(x)y = q(x)$，其求解步骤如下
边值问题是微分方程的一类重要问题，它要求求解满足一定边界条件的微分方程的解。常见的边值问题包括两点边值问题、多点边值问题等。
求解边值问题的基本步骤如下
1. 根据问题的实际背景，建立微分方程及相应的边界条件。

方程求解与代数符号化-省公开课获奖课件市赛课比赛一等奖课件

100 010
0 0 －6 太
(1)
1 －5 太 (2)
11
0 10
（4）下移一位，得
(4)×x,得
00
太
－1 5 －6
0 －1 0
010
0 －6太
－6－6x+5xy+x3y=0
5－6
（6）
(6)
00
即(－6－6x)+(5x+x3)y=0
00
这么就化为只含天、地二元旳两行方程。
（2）与（6）互隐通分相消：由（2）（6）消去y:
152
0
4.2.4 b 四元术
“四元术”则要求了具有两个、三个或四个未知数旳方程旳布列措施。未知数设为 “天”、“地”、“人”、
“物”，就相当于目前旳x、y、z、ω，
用“太”表达常数项，放于筹式旳中心；表达未知数旳天、地、人、物旳系数分别放在“太”旳下方、左方、右方和上方。
例如，方程 3x + 2y +3z + 4w +5 =
（1）
以及
（tu）=（）3 .
（2）
然后他断言
x= .
（3）
他利用（1）及（2）进行消元并解所得旳二次方程，得出
t = + ， u =—.
这里我们也像卡当那样取正根。求出了t和u后,并用（3）给出x旳
一种值
《大术》中解四次方程旳费拉利解法。
设方程 x4+bx3+cx2+dx+e=0。
移项后得
x4+bx3=—cx2—dx—e。在左边加上（bx）2配成平方。得
数）。用几何措施求解这个方程旳根，就等价于由给定线
段P和q求出线段r和s。用当代数学中旳韦达定理可知 r+s=p，rs=q2。于是相应旳几何措施能够是：

3_1、符号微积分

• 例2-1、求极限
lim
x 0
x (e
sin x
1) 2(e sin 3 x
tgx
1)
• 输入命令：
>>syms x； %定义符号变量 f=(x*(exp(sin(x))+1)-2*(exp(tan(x))1))/sin(x)^3； %确定符号表达式 w=limit(f) %求函数的极限
输入命令：
>>limit(((x+1)/(x-1))^x,inf)
得结果为：
ans = exp(2)
• 例2-4、求： lim (ctgx )
x 0
1 ln x
输入命令：
>>limit((cot(x))^(1/log(x)),x,0,'right')
得结果为：
ans = exp(-1)
三、符号导数

其中 (x和 i ,yi) 分别为xi和yi 的平均值 O
x y
x
n ( xi x )( y i y ) i 1 a n 2 ( xi x ) i 1 b y ax
解相应方程组，求得：
最小二乘拟合的MATLAB实现
在MATLAB中，用polyfit函数来求得最小二乘拟合多项式的系数，再用polyval函数按所得的多项式计算所给出的点上的函数近似值。 polyfit函数的调用格式为：
得结果为：
w= -1/2
1 3 • 例2-2、求：lim( 3 ) x 1 x 1 x 1
输入命令：
>>syms x； f=1/(x+1)-3/(x^3+1)； limit(f，x，-1)

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

11

13.3 符号函数积分
其语法格式分别为：
R = int(S)
R = int(S,v) R = int(S,a,b)
R = int(S,v,a,b)
其中：
S：为符号表达式，可能有多个参数 v：以 S 中的符号 v 进行求积分运算 a,b：定积分下限、上限，不指表示求不定积分
12
1 dx 例6：求积分 2 1 x
5

例2：计算函数的各种极限。
syms x
a t h;
limit(sin(x)/x)
limit(1/x,x,0,‘right’)
% sin(x)/x 趋于0 (默认)
% 1/x趋于0的右极限
limit((sin(x+h)-sin(x))/h,h,0) v
= [(1 + a/x)^x, exp(-x)]; % x趋于无穷时的左极限
4

例1：求极限
x(e sin x 1) 2(e tgx 1) lim x 0 sin 3 x

syms x;
%定义符号变量
%确定符号表达式

f=(x*(exp(sin(x))+1)-2*(exp(tan(x))-1))/sin(x)^3； %求函数的极限 w=limit(f) w = -1/2

syms x

int(1/(1+x^2))
ans = atan(x)

例7：计算二重不定积分
syms x y

xe
xy
dxdy
F = int(int('x*exp(-x*y)','x'),'y') F=
1/y*exp(-x*y)
13

例8：求积分
syms

1 x
2
x2
x2 y xy
14

9

2、求偏导数的jacobian命令
设列向量每一个分量
w,v 为
w( x, y ) 自变量 x,y 的函数，即 f v ( x, y )
( w, v) 则jacobian命令计算矩阵 J ( x, y )
Jacobian命令的一般形式为：
J = jacobian([w;v],[x,y])
10
J= [ cos(l)*cos(f), -r*sin(l)*cos(f), -r*cos(l)*sin(f) ] 例5：直角坐标系转化为球形坐标，即， [ cos(l)*sin(f), -r*sin(l)*sin(f), r*cos(l)*cos(f) ] x r cos cos sin(l), [ r*cos(l), 0]
diff(S, n)
diff(S, 'v', n)

其中： S：符号函数表达式，可能有多个符号参数 v：以符号 v 进行微分或求导运算 n：对S进行n次求导，默认为1
7

例3：求导数
d sin x dx

2
x = sym('x'); diff(sin(x^2)) ans = 2*cos(x^2)*x

了解符号级数和符号积分变换
掌握符号函数图形的绘制

掌握符号方程和方程组的求解
3

13.1 符号极限
极限是微积分的基础，微分和积分都是“无穷
ቤተ መጻሕፍቲ ባይዱ
逼近”时的结果。
函数limit用于求极限，其格式为：

limit(f,x,a) —— 计算当变量x趋近于常数a时，f(x) 函数的极限值。
limit(f,a) —— 计算findsym(f)确定的自变量，即x 趋近于a时f(x)的极限值。 limit(f,x,a,'right') —— 变量x从右边趋近于a。 limit(f,x,a,'left') —— 变量x从左边趋近于a。
( x y z )dzdydx
2 2 2
xyz
f2=int(int(int(x^2+y^2+z^2,z,sqrt(x*y),x^2*y),y,
sqrt(x),x^2),x,1,2)
vf2=vpa(f2)
% 结果用32位数字表示
f2 = 1610027357/6563700-6072064/348075*2^(1/2) +14912/4641*2^(1/4)+64/225*2^(3/4) vf2 = 224.92153573331143159790710032805
y r cos sin z r sin

% 分别用 l 和 f 来表示两个角度
syms r l f x = r*cos(l)*cos(f); % 定义符号变量

y = r*cos(l)*sin(f);
z = r*sin(l); J = jacobian([x; y; z], [r l f])
f=[a,t^3;t*cos(x), df=diff(f) dfdt2=diff(f,t,2)
log(x)];
dfdxdt = %求矩阵f对x的导数 [ 0, 0] [ -sin(x), 0] %求矩阵 f对t的二阶导数
dfdxdt=diff(diff(f,x),t)
%求二阶混合导数
第13讲符号微积分与符号方程求解

数值微积分中可以进行极限、导数、微分、积
分、级数展开等解析运算，也可以进行多元函
数的微积分运算，同样符号运算也可以进行上
述各种操作。

在运算的同时，结合图形的显示可以更好地帮
助我们理解微积分的概念和计算。
2

本讲教学目标

掌握符号极限运算
掌握符号微积分运算
% 定义符号变量 % 求导运算
8
df =

例4：求导数
t3 d a dx t cos x ln x
syms
[ 0, [ -t*sin(x),
d2 dt 2
0] 1/x ]
a t x;
a t3 t3 d2 a = dfdt2 t cos x ln x dxdt t cos x ln x [ 0, 6*t ] [ 0, 0]

limit(v,x,inf,'left')
ans = 1
ans = inf ans = cos(x) ans = [ exp(a), 0]
6

13.2 符号函数微分与求导

1、单变量函数

函数的一般引用格式为：
diff(S) —— 由findsym函数确定默认变量 diff(S, 'v')