第二类换元法

第二类换元法三角代换
第二类换元法是高等数学中的重要内容，它可以帮助我们解决许多复杂的积分问题。

其中，三角代换是第二类换元法的一种常见形式，它可以将一个积分式子中的三角函数转化为代数函数，从而使积分更加容易求解。

三角代换的基本形式是：假设我们的积分式子中包含一个三角函数，例如sin(x)或cos(x)，我们可以通过将x用另外一个三角函数代替，从而将原积分式子中的三角函数转化为代数函数。

常见的三角代换包括sin(x)代换、cos(x)代换、tan(x/2)代换等。

具体来说，对于sin(x)代换，我们可以将x表示为sin(t)，然后将积分式子中的所有x项用sin(t)表示，从而将原积分式子转化为只含有t和代数函数的式子。

类似地，对于cos(x)代换，我们可以将x表示为cos(t)，然后将积分式子中的所有x项用cos(t)表示，从而将原积分式子转化为只含有t和代数函数的式子。

对于tan(x/2)代换，我们可以将x表示为2arctan(t)，然后将积分式子中的所有x 项用2arctan(t)表示，从而将原积分式子转化为只含有t和代数函数的式子。

通过三角代换，我们可以将原本复杂的三角函数积分转化为简单的代数函数积分，从而大大简化了求解的难度。

因此，掌握第二类换元法三角代换是高等数学学习中的重要内容。

- 1 -。

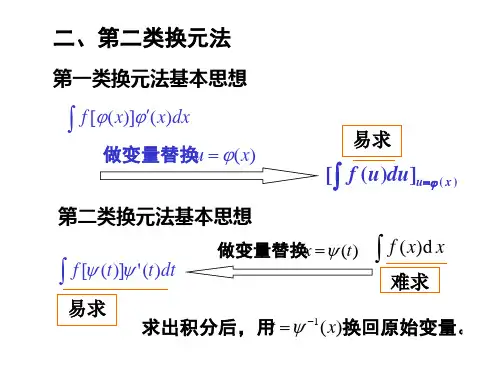
§4.2 换元积分法（第二类）Ⅰ 授课题目（章节）：§4.2 换元积分法 （第二类换元积分法） Ⅱ 教学目的与要求：1.了解第二类换元法的基本思想2.掌握几种典型题的第二类换元积分法解法 Ⅲ 教学重点与难点：重点：第二换元法中的三角代换及根式代换 难点：积分后的结果进行反代换 Ⅳ 讲授内容：第一类换元积分法的思想是：在求积分()g x dx ⎰时, 如果函数g (x )可以化为[()]()f x x ϕϕ'的形式, 那么()()[()]()[()]()()u x g x dx f x x dx f x d x f u du ϕϕϕϕϕ='==⎰⎰⎰⎰()F u C =+[()]F x C ϕ=+所以第一换元积分法体现了“凑”的思想.把被积函数凑出形如[()]()f x x ϕϕ'函数来.对于某些函数第一换元积分法无能为力，例如⎰-dx x a 22.对于这样的无理函数的积分我们就得用今天要学习的第二类换元积分法。

第二类换元的基本思想是选择适当的变量代换)(t x ψ=将无理函数()f x 的积分()f x dx ⎰化为有理式[()]()f t t ψψ'的积分[()]()f t t dt ψψ'⎰。

即()[()]()f x dx f t t dt ψψ'=⎰⎰若上面的等式右端的被积函数[()]()f t t ψψ'有原函数()t Φ，则[()]()()f t t dt t C ψψ'=Φ+⎰,然后再把()t Φ中的t 还原成1()x ψ-，所以需要一开始的变量代换)(t x ψ=有反函数。

定理2 设)(t x ψ=是单调、可导的函数，且0)(≠ψ't ，又设)()]([t t f ψ'ψ有原函数()t Φ，则⎰⎰+ψΦ=+Φ=ψ'ψ=-C x C t dt t t f dx x f )]([)()()]([)(1分析 要证明1()[()]f x dx x C ψ-=Φ+⎰，只要证明1[()]x ψ-Φ的导数为()f x ，1[()]d d dt x dx dt dx ψ-ΦΦ=⋅ ， ?dt dx=证明 )(t x ψ=Θ单调、可导，∴()x t ψ=存在反函数)(1x t -=ψ，且)(11t dtdx dx dt ψ'== 11[()][()]()()()d d dt x f t t f x dx dt dx t ψψψψ-Φ'Φ=⋅=='Q)]([1x -ψΦ∴是)(x f 是一个原函数⎰+ψΦ=-C x dx x f )]([)(1.第二换元法，常用于如下基本类型 类型1：被积函数中含有22x a -（0>a ）,可令t a x sin =（并约定(,)22t ππ∈-）则t a x a cos 22=-，tdx a dx cos =，可将原积分化作三角有理函数的积分.例1 求⎰-dx x a 22)0(>a解 令t a x sin = ，(,)22t ππ∈-，则t a x a cos 22=- tdt a dx cos = 22cos cos a x dx a ta tdt ∴-=⎰⎰22211(cos 2)sin 22224a a a t dt t t C =+=++⎰22222sin cos arcsin 2222a a a x x t t t C a x C a =++=+-+. 借助下面的辅助三角形把sin t ，cos t 用x 表示.例2 求⎰-dx xx 224解 令t x sin 2=，(,)22t ππ∈-，则t x cos 242=-，tdt dx cos 2=2224sin 1cos22cos =42cos 24t t tdt dt t x-∴=⋅-⎰⎰ =(22cos2)2sin 2t dt t t C -=-+⎰ 222sin cos 2arcsin422x xt t t C x C =-+=--+类型2：被积函数中含有)0(22>+a x a 可令 t axtan = 并约定(,)22t ππ∈-，则t a x a sec 22=+；tdt a dx 2sec = ；可将原积分化为三角有理函数的积分.例3 求⎰+22ax dx )0(>a解 令t a x tan =，)2,2(ππ-∈t ，则22sec x a a t +=，2sec dx a tdt = 22sec tdt x a∴=+⎰⎰ln sec tan t t C =++22221lnln x a xC x x a C a a+=++=+++.例4 求⎰+224xxdx解 令t x tan 2=，)2,2(ππ-∈t 242sec x t +=，tdt dx 2sec 2=22222sec 4tan 2sec 4t dt t t xx ∴=⋅+⎰1cos 22sin 2cos 1sec 14tan 4t t tt dt dt t ==⎰⎰2221cos 111114sin 4sin 4sin 4sin 4t x dt d t C C t t t x+===-⋅+=-⋅+⎰⎰ 例5求⎰+22)9(x dx（分母是二次质因式的平方）解 令t x tan 3=，则t x 22sec 99=+， tdt dx 2sec 3=222243sec 1cos (9)81sec 27dx t dt tdt x t ==+⎰⎰⎰111(1cos 2)cos 2cos 2254545454254t t t dt tdt td t =+=+=+⨯⎰⎰⎰ 11sin 2sin cos 542545454t t t t t C =+=++⨯ 2113arctan 543549x x C x =+⋅++练习： 求221(25)dx x x -+⎰（第二换元积分法分）解 22222])1(2[)52(-+=+-x x x ，令t x tan 21=-)2,2(ππ-∈t 则 222442sec 11(1cos 2)sin cos (25)2sec 161616dx t t dt t dt t t C x x t ==+=++-+⎰⎰⎰21111arctan 162825x x C x x --=+⋅+-+ 类型 3 被积分函数中含有22a x - )0(>a ，当a x ≥时，可令t a x sec =，并约定(0,)2t π∈，则t a a x tan 22=-，sec tan dx a t tdt =，当a x -≤时，可令x u -=，则a u ≥，可将原积分化为三角有理函数的积分。

定积分是微积分中的重要概念，通过定积分我们可以求解曲线与坐标轴之间的面积、体积以及质心等问题。

在求解定积分时，换元法是一种常用且有效的方法。

换元法分为第一类换元法和第二类换元法，它们在不同类型的积分计算中发挥着重要作用。

下面我们将分别介绍这两种换元法的原理和应用。

一、第一类换元法1.1 换元法简介第一类换元法，又称代换法或变量代换法，是对定积分中被积函数中的变量进行替换，将原来的积分变为更容易求解的积分。

其基本思想是通过引入适当的新变量，将被积函数中的复杂部分转化为简单的形式，从而便于积分计算。

1.2 换元法的步骤（1）寻找合适的变量替换：根据被积函数的形式和特点，选择适当的新变量代替原来的变量。

（2）计算新变量的微分：对新变量进行微分，求出新变量的微分表达式。

（3）将被积函数用新变量表示：将原来的积分中的被积函数用新变量表示出来，得到新的积分形式。

（4）进行积分计算：对新的积分形式进行计算，得出最终结果。

1.3 换元法的应用第一类换元法常用于代换型积分，如含有根式、三角函数等形式的积分。

通过合适的变量替换，可以将原积分化为简单的形式，从而便于求解。

二、第二类换元法2.1 换元法简介第二类换元法，又称参数代换法或极坐标代换法，是通过引入参数来替换被积函数中的自变量，从而实现对原积分的简化。

这种换元法常用于解决平面曲线和曲面的面积、弧长以及质心等问题。

2.2 换元法的步骤（1）引入参数：选择适当的参数替换自变量，通常选择直角坐标系下的参数形式或极坐标系下的参数形式。

（2）表达被积函数：将原来的被积函数用参数表示出来，并求出新的被积函数。

（3）进行积分计算：对新的被积函数进行积分计算，得出最终结果。

2.3 换元法的应用第二类换元法常用于参数型积分，如平面曲线、曲面以及柱面体的面积、弧长和质心的计算。

通过引入参数替换自变量，可以将原积分化为简单的形式，从而便于求解。

三、第一类换元法和第二类换元法的比较3.1 适用范围（1）第一类换元法适用于一般的代换型积分，如含有根式、三角函数等形式的积分；（2）第二类换元法适用于参数型积分，如平面曲线、曲面以及柱面体的面积、弧长和质心的计算。

第二类换元法常见类型总结摘要：一、第二类换元法简介二、第二类换元法常见类型1.单一变量换元2.多元变量换元3.参数换元4.逆换元三、应用实例及解题步骤四、注意事项与技巧五、总结与展望正文：一、第二类换元法简介第二类换元法是数学分析中的一种方法，主要用于求解复杂数学问题。

它通过对变量进行替换，将原问题转化为更简单的问题，从而达到求解原问题的目的。

第二类换元法不同于第一类换元法，它是在积分过程中进行的，可以有效地简化积分的计算过程。

二、第二类换元法常见类型1.单一变量换元单一变量换元是指在积分过程中，将一个较难处理的变量替换为一个容易处理的变量。

这种换元方法可以降低问题的难度，使积分过程更加简洁。

例如，在积分过程中，我们可以将复杂的函数形式换成简单的形式，从而提高积分效率。

2.多元变量换元多元变量换元是指在积分过程中，将多个变量替换为一个新的变量。

这种换元方法可以简化积分过程，使得问题更容易处理。

例如，在多变量函数的积分中，我们可以通过换元将多个变量合并为一个新变量，从而降低问题的复杂度。

3.参数换元参数换元是指在积分过程中，将一个或多个变量替换为参数。

这种换元方法可以使积分过程更加直观，有助于发现积分公式。

例如，在积分过程中，我们可以通过参数换元法，将复杂的函数形式转换为简单的形式，进而求解问题。

4.逆换元逆换元是指在积分过程中，将替换过的变量重新替换回原变量。

这种换元方法在求解问题时，可以恢复原变量的值。

例如，在积分过程中，我们可以通过逆换元法，将换元后的积分结果转换回原变量，从而得到最终的积分结果。

三、应用实例及解题步骤以下以一个具体实例来说明第二类换元法的应用：例：求积分∫(x^2 + 3x + 2)dx解：1.选择换元变量：令u = x^2 + 3x + 2，则原函数可以表示为∫u dx。

2.求出原函数：对u 求导得到du = 2x + 3，所以原函数为F(u) = 1/2 *u^2 + 3/2 * u + C。

第二类换元法证明第二类换元法是微积分中的一种重要方法，它可以将一个复杂的积分转化为一个更简单的形式，从而更容易求解。

在本文中，我们将探讨第二类换元法的原理和应用。

第二类换元法的原理是将积分中的自变量替换为一个新的变量，从而使积分变得更容易求解。

具体来说，我们可以将自变量替换为一个函数的导数，这样就可以将积分转化为一个更简单的形式。

例如，考虑以下积分：$$\int \frac{1}{x^2+1}dx$$我们可以使用第二类换元法，将$x$替换为$tan\theta$，从而得到：$$\int \frac{1}{x^2+1}dx=\int \frac{1}{tan^2\theta+1}sec^2\theta d\theta$$这个积分可以通过简单的代数运算和三角函数的性质来求解，最终得到：$$\int \frac{1}{x^2+1}dx=arctan(x)+C$$这个例子展示了第二类换元法的原理和应用。

通过将自变量替换为一个新的变量，我们可以将积分转化为一个更简单的形式，从而更容易求解。

除了上述例子，第二类换元法还可以应用于其他类型的积分，例如： $$\int \frac{1}{\sqrt{1-x^2}}dx$$我们可以使用$x=sin\theta$来进行替换，从而得到：$$\int \frac{1}{\sqrt{1-x^2}}dx=\int \frac{1}{cos\theta}d\theta$$这个积分可以通过简单的代数运算和三角函数的性质来求解，最终得到：$$\int \frac{1}{\sqrt{1-x^2}}dx=arcsin(x)+C$$通过这些例子，我们可以看到第二类换元法的强大之处。

它可以将一个复杂的积分转化为一个更简单的形式，从而更容易求解。

在实际应用中，我们可以根据积分的形式来选择合适的换元方法，从而更加高效地求解积分。

第二类换元法是微积分中的一种重要方法，它可以将一个复杂的积分转化为一个更简单的形式，从而更容易求解。