hash散列表的解决冲突——开放定址法(线性探索再散列法)
- 格式:doc
- 大小:34.50 KB
- 文档页数:3

第9章查找一、选择题1.顺序查找一个共有n个元素的线性表,其时间复杂度为(),折半查找一个具有n个元素的有序表,其时间复杂度为()。
【*,★】A.O(n)B. O(log2n)C. O(n2)D. O(nlog2n)2.在对长度为n的顺序存储的有序表进行折半查找,对应的折半查找判定树的高度为()。
【*,★】A.nB. ⌊log2n⌋C. ⌊log2(n+1)⌋D. ⌈log2(n+1)⌉3.采用顺序查找方式查找长度为n的线性表时,平均查找长度为()。
【*】A.nB. n/2C. (n+1)/2D. (n-1)/24.采用折半查找方法检索长度为n的有序表,检索每个元素的平均比较次数()对应判定树的高度(设高度大于等于2)。
【**】A.小于B. 大于C. 等于D. 大于等于5.已知有序表(13,18,24,35,47,50,62,83,90,115,134),当折半查找值为90的元素时,查找成功的比较次数为()。
【*】A. 1B. 2C. 3D. 46.对线性表进行折半查找时,要求线性表必须()。
【*】A.以顺序方式存储B. 以链接方式存储C.以顺序方式存储,且结点按关键字有序排序D. 以链接方式存储,且结点按关键字有序排序7.顺序查找法适合于存储结构为()的查找表。
【*】A.散列存储B. 顺序或链接存储C. 压缩存储D. 索引存储8.采用分块查找时,若线性表中共有625个元素,查找每个元素的概率相同,假设采用顺序查找来确定结点所在的块时,每块应分()个结点最佳。
【**】A.10B. 25C. 6D. 6259.从键盘依次输入关键字的值:t、u、r、b、o、p、a、s、c、l,建立二叉排序树,则其先序遍历序列为(),中序遍历序列为()。
【**,★】A.abcloprstuB. alcpobsrutC. trbaoclpsuD. trubsaocpl10.折半查找和二叉排序树的时间性能()。
【*】A.相同B. 不相同11.一棵深度为k的平衡二叉树,其每个非终端结点的平衡因子均为0,则该树共有()个结点。

哈希表——线性探測法、链地址法、查找成功、查找不成功的平均长度⼀、哈希表1、概念哈希表(Hash Table)也叫散列表,是依据关键码值(Key Value)⽽直接进⾏訪问的数据结构。
它通过把关键码值映射到哈希表中的⼀个位置来訪问记录,以加快查找的速度。
这个映射函数就做散列函数。
存放记录的数组叫做散列表。
2、散列存储的基本思路以数据中每⼀个元素的keywordK为⾃变量。
通过散列函数H(k)计算出函数值,以该函数值作为⼀块连续存储空间的的单元地址,将该元素存储到函数值相应的单元中。
3、哈希表查找的时间复杂度哈希表存储的是键值对,其查找的时间复杂度与元素数量多少⽆关。
哈希表在查找元素时是通过计算哈希码值来定位元素的位置从⽽直接訪问元素的,因此,哈希表查找的时间复杂度为O(1)。
⼆、经常使⽤的哈希函数1. 直接寻址法取keyword或者keyword的某个线性函数值作为哈希地址,即H(Key)=Key或者H(Key)=a*Key+b(a,b为整数),这样的散列函数也叫做⾃⾝函数.假设H(Key)的哈希地址上已经有值了,那么就往下⼀个位置找,知道找到H(Key)的位置没有值了就把元素放进去.2. 数字分析法分析⼀组数据,⽐⽅⼀组员⼯的出⽣年⽉,这时我们发现出⽣年⽉的前⼏位数字⼀般都同样,因此,出现冲突的概率就会⾮常⼤,可是我们发现年⽉⽇的后⼏位表⽰⽉份和详细⽇期的数字区别⾮常⼤,假设利⽤后⾯的⼏位数字来构造散列地址,则冲突的⼏率则会明显减少.因此数字分析法就是找出数字的规律,尽可能利⽤这些数据来构造冲突⼏率较低的散列地址.3. 平⽅取中法取keyword平⽅后的中间⼏位作为散列地址.⼀个数的平⽅值的中间⼏位和数的每⼀位都有关。
因此,有平⽅取中法得到的哈希地址同keyword的每⼀位都有关。
是的哈希地址具有较好的分散性。
该⽅法适⽤于keyword中的每⼀位取值都不够分散或者较分散的位数⼩于哈希地址所须要的位数的情况。

【学习总结】哈希表:哈希函数构造;哈希表解决地址冲突的⽅法⼩结散列函数构造⽅法:1.直接定址法:H(key) = a*key + b2.除留余数法:H(key) = key % p(p为不⼤于散列表表长,但最接近或等于表长的质数p)3.数字分析法:选取r进制数数码分布较为均匀的若⼲位作为散列地址4.平⽅取中法:取关键字的平⽅值的中间⼏位作为散列地址5.折叠法:将关键字分割成位数相同的⼏部分,然后取这⼏部份的叠加和作为散列地址处理冲突的⽅法:1.开放定址法(闭哈希表):在冲突的哈希地址的基础上进⾏处理,得到新的地址值。
Hi = (H(key)+di) % m(m表⽰散列表表长,di为增量序列)1)线性探测法:dii=1,2,3,…,m-12)⼆次探测法:di=12,-12,22,-22,…,k2,-k2 ( k<=m/2 )冲突发⽣时,以原哈希地址为中⼼,在表的左右进⾏跳跃式探测,⽐较灵活。
3)伪随机数法:di=伪随机数序列。
具体实现时,应建⽴⼀个伪随机数发⽣器,(如i=(i+p) % m),并给定⼀个随机数做起点。
线性探测再散列的优点是:只要哈希表不满,就⼀定能找到⼀个不冲突的哈希地址,⽽⼆次探测再散列和伪随机探测再散列则不⼀定。
注:在开放定址的情形下,不能随便物理删除表中已有元素,若删除元素将会截断其他具有相同散列地址的元素的查找地址。
若想删除⼀个元素,给它做⼀个删除标记,进⾏逻辑删除。
2.链地址法、拉链法(开哈希表)将所有哈希地址为i的元素构成⼀个称为同义词链的单链表,并将单链表的头指针存在哈希表的第i个单元中,因⽽查找、插⼊和删除主要在同义词链中进⾏。
链地址法适⽤于经常进⾏插⼊和删除的情况。
3.再哈希法:同时构造多个不同的哈希函数,发⽣冲突时,使⽤其他哈希函数求值。
这种⽅法不易产⽣聚集,但增加了计算时间。
4.建⽴公共溢出区:将哈希表分为基本表和溢出表两部分,凡是和基本表发⽣冲突的元素,⼀律填⼊溢出表概述哈希法⼜称散列法、杂凑法以及关键字地址计算法等,相应的表称为哈希表。

第1章绪论一、选择题1. 算法的时间复杂度取决于( C )A.问题的规模 B. 待处理数据的初态 C. A和B2.计算机算法指的是(C),它必须具备(B)这三个特性。
(1) A.计算方法 B. 排序方法 C. 解决问题的步骤序列 D. 调度方法(2) A.可执行性、可移植性、可扩充性 B. 可执行性、确定性、有穷性C. 确定性、有穷性、稳定性D. 易读性、稳定性、安全性3.从逻辑上可以把数据结构分为( C )两大类。
A.动态结构、静态结构 B.顺序结构、链式结构C.线性结构、非线性结构 D.初等结构、构造型结构4.以下与数据的存储结构无关的术语是( D )。
A.循环队列 B. 链表 C. 哈希表 D. 栈5.在下面的程序段中,对x的赋值语句的频度为( C )FOR i:=1 TO n DOFOR j:=1 TO n DOx:=x+1;A. O(2n) B.O(n) C.O(n2) D.O(log2n)6.连续存储设计时,存储单元的地址( A )。
A.一定连续 B.一定不连续 C.不一定连续 D.部分连续,部分不连续二、判断题1. 数据元素是数据的最小单位。
( F ) 【山东师范大学 2001 一、1 (2分)】2. 记录是数据处理的最小单位。
( F )3.数据的物理结构是指数据在计算机内的实际存储形式。
( T )【山东师范大学2001 一、2(2分)】4. 在顺序存储结构中,有时也存储数据结构中元素之间的关系。
( F )5. 顺序存储方式的优点是存储密度大,且插入、删除运算效率高。
( F )三、填空1.数据的物理结构包括的表示和的表示。
2. 对于给定的n个元素,可以构造出的逻辑结构有(1),(2),(3),_(4)四种。
3.数据的逻辑结构是指。
4.一个数据结构在计算机中称为存储结构。
5.数据结构中评价算法的两个重要指标是6.已知如下程序段FOR i:= n DOWNTO 1 DO {语句1}BEGINx:=x+1;{语句2}FOR j:=n DOWNTO i DO {语句3}y:=y+1; {语句4}END;语句1执行的频度为(1);语句2执行的频度为(2);语句3执行的频度为(3);语句4执行的频度为(4)。

第9章查找一、选择题1.顺序查找一个共有n个元素的线性表,其时间复杂度为(),折半查找一个具有n个元素的有序表,其时间复杂度为()。
【*,★】A.O(n)B. O(log2n)C. O(n2)D. O(nlog2n)2.在对长度为n的顺序存储的有序表进行折半查找,对应的折半查找判定树的高度为()。
【*,★】A.nB.C.D.3.采用顺序查找方式查找长度为n的线性表时,平均查找长度为()。
【*】A.nB. n/2C. (n+1)/2D. (n-1)/24.采用折半查找方法检索长度为n的有序表,检索每个元素的平均比较次数()对应判定树的高度(设高度大于等于2)。
【**】A.小于B. 大于C. 等于D. 大于等于5.已知有序表(13,18,24,35,47,50,62,83,90,115,134),当折半查找值为90的元素时,查找成功的比较次数为()。
【*】A. 1B. 2C. 3D. 46.对线性表进行折半查找时,要求线性表必须()。
【*】A.以顺序方式存储B. 以链接方式存储C.以顺序方式存储,且结点按关键字有序排序D. 以链接方式存储,且结点按关键字有序排序7.顺序查找法适合于存储结构为()的查找表。
【*】A.散列存储B. 顺序或链接存储C. 压缩存储D. 索引存储8.采用分块查找时,若线性表中共有625个元素,查找每个元素的概率相同,假设采用顺序查找来确定结点所在的块时,每块应分()个结点最佳。
【**】A.10B. 25C. 6D. 6259.从键盘依次输入关键字的值:t、u、r、b、o、p、a、s、c、l,建立二叉排序树,则其先序遍历序列为(),中序遍历序列为()。
【**,★】A.abcloprstuB. alcpobsrutC. trbaoclpsuD. trubsaocpl10.折半查找和二叉排序树的时间性能()。
【*】A.相同B. 不相同11.一棵深度为k的平衡二叉树,其每个非终端结点的平衡因子均为0,则该树共有()个结点。

哈希表处理冲突的方法哈希表是一种常见的数据结构,用于实现快速查找和插入操作。
它通过将关键字映射到数组的特定位置来存储数据。
然而,当两个或多个关键字映射到同一个位置时,就会发生冲突。
为了解决冲突,哈希表采用了多种方法。
1. 链地址法(Chaining):在哈希表中的每个位置上维护一个链表或链表数组。
如果发生冲突,新的数据将被添加到链表的末尾。
这种方法可以处理任意数量的冲突,但需要额外的空间来存储链表。
2. 开放地址法(Open Addressing):在哈希表中的每个位置上存储一个数据,并通过探测序列来处理冲突。
探测序列是一个确定的规则,用于寻找下一个可用的位置。
常见的探测方法包括线性探测(Linear Probing),二次探测(Quadratic Probing)和双重散列(Double Hashing)。
这种方法不需要额外的存储空间,但可能会导致聚集现象,即连续的冲突会增加查找的时间复杂度。
3. 再哈希法(Rehashing):当发生冲突时,重新计算关键字的哈希值,并将数据存储在计算得到的新位置上。
这种方法需要额外的存储空间来保存原始数据,但可以避免聚集现象,并减少冲突的概率。
4. 建立公共溢出区(Primary Clustering):将哈希表分为两个区域,一个区域用于存储主要数据,另一个区域用于存储冲突的数据。
当发生冲突时,将数据存储在冲突区域中。
这种方法可以减少聚集现象的发生,但需要额外的存储空间来存储冲突数据。
5. 完全散列(Perfect Hashing):在构建哈希表时,通过一系列算法和数据预处理,使得每个关键字都映射到唯一的位置,从而避免冲突。
这种方法需要较高的计算成本和空间消耗,但可以实现最佳的查找和插入性能。
以上所述的方法都是常见的哈希表处理冲突的方式。
在选择合适的方法时,需要考虑数据的特点、内存限制和性能需求等因素。

哈希表处理冲突的⼏种⽅式1、链地址法指把所有的冲突关键字存储在⼀个线性链表中,这个链表由其散列地址唯⼀标识。
2、开放定址法开放地址法通常需要有三种⽅法:线性探测、⼆次探测、再哈希法。
线性探测线性探测⽅法就是线性探测空⽩单元。
当数据通过哈希函数计算应该放在700这个位置,但是700这个位置已经有数据了,那么接下来就应该查看701位置是否空闲,再查看702位置,依次类推。
当哈希表越来越满时聚集越来越严重,这导致产⽣⾮常长的探测长度,后续的数据插⼊将会⾮常费时。
线性探测就是使⽤算术取余的⽅法计算余数,当产⽣冲突时就通过线性递增的⽅法进⾏探测,⼀直到数组的位置为空,插⼊数据项即可。
⼆次探测⼆次探测是过程是x+1,x+4,x+9,以此类推。
⼆次探测的步数是原始位置相隔的步数的平⽅。
⼆次探测可以消除在线性探测中产⽣的聚集问题,但是⼆次探测还是会产⽣⼀种更明确更细的聚集。
⼆次聚集的产⽣是在⼆次探测的基础上产⽣的现象。
例如N个数据经hash函数计算后都映射到到数组下标10,探测第⼆个数字需要以⼀步长,第三个数字需要以4步长为单位,第四个数字则需要以九为步长。
好在⼆次探测并不常⽤,解决聚集问题还是有⼀种更好的办法:再哈希法。
再哈希法再哈希是把关键字⽤不同的哈希函数再做⼀遍哈希化,⽤这个结果作为步长,对指定的关键字,探测的步长是不变的,可以说不同的关键字可以使⽤不同的步长,并且步长可以控制。
⼀般来说,再哈希函数可以采⽤以下这种:stepSize=constant-(key%constant);3、再散列法当发⽣冲突时,利⽤另⼀个哈希函数再次计算⼀个地址。
直到冲突不再发⽣。
4、建⽴⼀个公共溢出区⼀旦由哈希函数得到的地址冲突,就都填⼊溢出表。

以下是列举收集来的三个题目,三个题目是同一个意思,一,利用线性探测法构造散列表(用除余法来得出散列地址,用开放地址法解决同义词问题)题目:已知一组关键字为(26,36,41,38,44,15,68,12,06,51),用除余法构造散列函数,用线性探查法解决冲突构造这组关键字的散列表。
解答:为了减少冲突,通常令装填因子α<l。
这里关键字个数n=10,不妨取m=13,此时α≈0.77,散列表为T[0..12],散列函数为:h(key)=key%13。
由除余法的散列函数计算出的上述关键字序列的散列地址为(0,10,2,12,5,2,3,12,6,12)。
前5个关键字插入时,其相应的地址均为开放地址,故将它们直接插入T[0],T[10),T[2],T[12]和T[5]中。
当插入第6个关键字15时,其散列地址2(即h(15)=15%13=2)已被关键字41(15和41互为同义词)占用。
故探查h1=(2+1)%13=3,此地址开放,所以将15放入T[3]中。
当插入第7个关键字68时,其散列地址3已被非同义词15先占用,故将其插入到T[4]中。
当插入第8个关键字12时,散列地址12已被同义词38占用,故探查hl=(12+1)%13=0,而T[0]亦被26占用,再探查h2=(12+2)%13=1,此地址开放,可将12插入其中。
类似地,第9个关键字06直接插入T[6]中;而最后一个关键字51插人时,因探查的地址12,0,1,…,6均非空,故51插入T[7]中。
二、题目:已知一个线性表(38,25,74,63,52,48),假定采用h(k)=k%6计算散列地址进行散列存储,若用线性探测的开放定址法处理冲突,则在该散列表上进行查找的平均查找长度为()。
A. 1.5B. 1.7C. 2D. 2.32、解题过程:(1)计算h(k):38%6 = 2 25%6 = 1 74%6 = 2 63%6 = 3 52%6 = 4 48%6 = 0(2)定址:把不冲突的和冲突的全部列出来即可地址:0 1 2 3 4 51、线性表第1个元素(38):38(第1 次不冲突)2、线性表第2个元素(25):25(第1次不冲突)3、线性表第3个元素(74):74(第1 次冲突,地址+ 1)4、线性表第3个元素(74):74(第2 次不冲突)5、线性表第4个元素(63):63(第1 次冲突,地址+ 1)6、线性表第4个元素(63):63(第2 次不冲突)7、线性表第5个元素(52):52(第1 次冲突,地址+ 1)8、线性表第5个元素(52):52(第2 次不冲突)9、线性表第6个元素(48):48(第1次不冲突)经过上述定址过程,线性表中的各个元素都有了唯一的地址。

线性探测再散列https:///qq_19446965/article/details/102290770哈希表⼜称散列表。
哈希表存储的基本思想是:以数据表中的每个记录的关键字 k为⾃变量,通过⼀种函数H(k)计算出函数值。
把这个值解释为⼀块连续存储空间(即数组空间)的单元地址(即下标),将该记录存储到这个单元中。
在此称该函数H为哈希函数或散列函数。
按这种⽅法建⽴的表称为哈希表或散列表。
处理冲突的⽅法:开放寻址法:Hi=(H(key) + di) MOD m, i=1,2,…, k(k<=m-1),其中H(key)为散列函数,m为散列表长,di为增量序列,可有下列三种取法:1.di=1,2,3,…, m-1,称线性探测再散列;2.di=1^2, -1^2, 2^2,-2^2, 3^2, …, ±(k)^2,(k<=m/2)称⼆次探测再散列;3.di=伪随机数序列,称伪随机探测再散列。
再散列法:Hi=RHi(key), i=1,2,…,k. RHi均是不同的散列函数,即在同义词产⽣地址冲突时计算另⼀个散列函数地址,直到冲突不再发⽣,这种⽅法不易产⽣“聚集”,但增加了计算时间;链地址法(拉链法):将所有关键字为同义词的记录存储在同⼀线性链表中;设哈希表长为14,哈希函数是H(key)=key%11,表中已有数据的关键字为15,38,61,84共四个,现要将关键字为49的结点加到表中,⽤⼆次探测再散列法解决冲突,则放⼊的位置是( ) 【南京理⼯⼤学 2001 ⼀、15 (1.5分)】A.8 B.3 C.5 D.9答案为A,为什么我计算出来是D呢?我的计算步骤如下:15,38,61,84⽤哈希函数H(key)=key%11计算后得地址:4,5,6,749计算后为5,发⽣冲突.⽤⼆次探测再散列法解决冲突:1:(key+1^2)%11=(49+1)%11=6,仍然发⽣冲突.2:(key-1^2)%11=(49-1)%11=4,仍然发⽣冲突.3:(key+2^2)%11=(49+4)%11=9,不再发⽣冲突.得出结果为D。

散列表冲突处理方案散列表(Hash Table)是一种重要的数据结构,它能够快速地进行插入、查找和删除等操作。
然而,在实际应用中,冲突(Collision)是散列表中常见的问题之一。
本文将介绍散列表冲突处理的几种常见方案,以及它们的优缺点。
一、开放定址法开放定址法是一种解决冲突的常见方法。
其原理是,当发生冲突时,通过一定的探测序列找到下一个可用的空槽,将待插入的元素放入该槽内。
常用的探测序列有线性探测、二次探测以及双重散列等。
1. 线性探测线性探测是最简单的开放定址法策略。
当发生冲突时,直接往后查找下一个空槽,并将待插入元素放入该槽内。
即使数组中只有少数位置被占用,线性探测也可能导致长时间的查找。
此外,线性探测容易产生一次聚集(Primary Clustering)现象,即冲突后的元素倾向于聚集在一起,进一步影响散列表的性能。
2. 二次探测二次探测对线性探测进行了改进。
当发生冲突时,根据一个二次探测序列进行查找下一个空槽,并将待插入元素放入该槽内。
二次探测的探测序列可以是平方探测、斐波那契探测等。
相比线性探测,二次探测能够减少聚集现象,但仍然存在聚集的问题。
3. 双重散列双重散列是一种更为高效的开放定址法策略。
当发生冲突时,通过计算另一个散列函数的值,并将其与原始散列值相加,得到下一个空槽的位置。
双重散列能够更好地解决聚集问题,提高散列表的性能。
二、链表法链表法是另一种常见的散列表冲突处理方案。
基本思想是,将散列得到的相同索引值的元素存储在同一个链表中。
当插入元素时,只需要将其插入到对应索引位置的链表尾部即可。
链表法对于散列冲突的处理效果较好,但在插入和查找操作上需要额外的链表遍历开销。
三、再散列法再散列法是一种结合链表法和开放定址法的冲突处理方法。
当发生冲突时,使用一个新的散列函数对待插入的元素进行再散列,并将其放入新的散列位置。
再散列法能够在一定程度上减少冲突的概率,提高散列表的性能。
综上所述,散列表冲突处理的方案有开放定址法、链表法以及再散列法等。
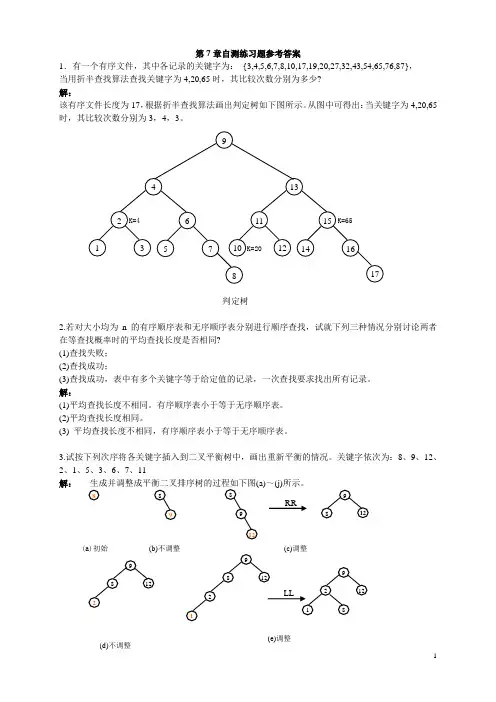
第7章自测练习题参考答案1.有一个有序文件,其中各记录的关键字为: {3,4,5,6,7,8,10,17,19,20,27,32,43,54,65,76,87}, 当用折半查找算法查找关键字为4,20,65时,其比较次数分别为多少? 解:该有序文件长度为17,根据折半查找算法画出判定树如下图所示。
从图中可得出:当关键字为4,20,65时,其比较次数分别为3,4,3。
2.若对大小均为n 的有序顺序表和无序顺序表分别进行顺序查找,试就下列三种情况分别讨论两者在等查找概率时的平均查找长度是否相同? (1)查找失败; (2)查找成功;(3)查找成功,表中有多个关键字等于给定值的记录,一次查找要求找出所有记录。
解:(1)平均查找长度不相同。
有序顺序表小于等于无序顺序表。
(2)平均查找长度相同。
(3) 平均查找长度不相同,有序顺序表小于等于无序顺序表。
3.试按下列次序将各关键字插入到二叉平衡树中,画出重新平衡的情况。
关键字依次为:8、9、12、2、1、5、3、6、7、11解:~(j)所示。
RR(b)不调整 (a)初始 (d)不调整(e)调整4.已知长度为12的表:(Jan,Feb,Mar,Apr,May,Jun,Jul,Aug,Sep,Oct,Nov,Dec )。
(1) 试按表中元素的顺序,依次插入一棵初始为空的二叉树;试画出插入完成之后的二叉排序树,并求其在等查找概率情况下查找成功的平均查找长度。
(2)若对表中元素先进行排序构成有序表,试求在等查找概率情况下对此有序表进行二分查找时查找(f)调整(g)不调整(h)不调整(i)调整(j)调整成功的平均查找长度。
解:(1) 二叉排序树如下图所示。
平均查找长度SAL=(1*1+2*2+3*3+3*4+2*5+1*6)/12=42/12=3.5(2) 对有序表(Apr,Aug,Dec,Feb,Jan,Jul,Jun,Mar,May,Nov,Oct,Sep)进行二分查找时,其判定树如下图所示,所以平均查找长度SAL=(1*1+2*2+4*3+5*4)/12=37/12≈3.085.在题图7-1所示的3阶B-树中,删除关键字37,试画出删除过程。
线性探测法在开放定址算法⾥,线性探测法是散列解决冲突的⼀种⽅法,当hash⼀个关键字时,发现没有冲突,就保存关键字,如果出现冲突,则就探测冲突地址下⼀个地址,依次按照线性查找,直到发现有空地址为⽌,从⽽解决冲突,例如关键字集合{7、8、30、11、18、9、14},散列函数为:H(key) = (keyx3) MOD 7,设装填因⼦(元素个数/散列表长度)为0.7,那么散列表的长度为 10。
关键字(key)集合存放位置分别为:783011189140365560由表格知道,这⾥的7和14、30和9、11和18出现了位置存放冲突。
存放key=7时,散列表长度为10的表中其实没有冲突,因为7是第⼀个存在到表中的key,所以⼀定不会有冲突的,所以7对应散列表的地址0。
8、30、11存放的地址分别是3、 6 、5,但是到了key=18时候,发现存放的地址为5,⽽地址5已经存放了key=11,这时发⽣了地址冲突。
根据线性探测法,算法会探测地址5的下⼀个地址,即地址6,⽽此时地址6已经存放了key=30,程序继续探测下⼀个地址,发现地址7位空,此时把key=18存放到地址7处。
以此类推,最后得出的散列表为:最后集合存放位置012345678971481130189成功查找率:(1+1+1++1+3+3+2)/ 7不成功查找率计算查找不成功的次数就直接找关键字到第⼀个地址上关键字为空的距离即可,但根据哈希函数地址为MOD7,因此初始只可能在0~6的位置。
等概率情况下,查找0~6位置查找失败的查找次数为: 地址0,到第⼀个关键字为空的地址2的距离为3,因此查找不成功的次数为3. 地址1,到第⼀个关键为空的地址2的距离为2,因此查找不成功的次数为2.地址2,到第⼀个关键为空的地址2的距离为1,因此查找不成功的次数为1.地址3,到第⼀个关键为空的地址4的距离为2,因此查找不成功的次数为2.地址4,到第⼀个关键为空的地址4的距离为1,因此查找不成功的次数为1.地址5,到第⼀个关键为空的地址2(注意不是地址9,因为初始只可能在0~6之间,因此循环回去)的距离为5,因此查找不成功的次数为5.地址6,到第⼀个关键为空的地址2(注意不是地址9,因为初始只可能在0~6之间,因此循环回去)的距离为4,因此查找不成功的次数为4.不成功查找率:(3+2+1+2+1+5+4)/7。
第9章查找9.1知识点:静态查找表一、填空题1.在数据的存放无规律而言的线性表中进行检索的最佳方法是。
2.查找表是由构成的集合。
3.若对查找表只做“查询某个特定的数据元素是否在查找表中”和“查询某个特定的数据元素的各种属性”操作,则称此类查找表为。
若在查找过程中同时插入查找表中不存在的数据元素,或者从查找表中删除已存在的某个数据元素,则称此类查找表为。
4.在n个记录的有序顺序表中进行折半查找,最大的比较次数为。
5.是顺序查找的一种改进方法,又称索引顺序查找,具体实现为将一个主表分成n个子表,要求子表之间元素是按,而子表中元素可以无序的,用每个子表最大关键字和指示块中第一个记录在表中位置建立。
6.分块查找的时间复杂度是。
7.顺序查找n个元素的顺序表,若查找成功,则比较关键字的次数最多为次;当使用监视哨时,若查找失败,则比较关键字的次数为次。
8.由于查找运算的主要运算是关键字的比较,所以通常把______________作为衡量一个查找算法效率优劣的标准。
它的计算公式为________________________________________。
二、选择题1.()在表长为n的链表中进行顺序查找,它的平均查找长度为()。
A. ASL=nB. ASL=(n+1)/2C. ASL=+1D. ASL≈log2(n+1)-12.()采用折半查找方法查找长度为n的线性表时,平均时间复杂度为()。
A.O(n2)B.O(nlogn)C.O(n)D.O(logn)3.()折半查找有序表(4,6,10,12,20,30,50,70,88,100)。
若查找表中元素58,则它将依次与表中()比较大小,查找结果是失败。
A.20,70,30,50 B.30,88,70,50 C.20,50 D.30,88,504.()有序线性表(a1,a2,a3,…,a256)是从小到大排列的,对一个给定的值k,用二分法检索表中与k相等的元素,在查找不成功的情况下,最多需要检索()次。
利⽤线性探测法解决hash冲突问题背景 有⼀种数据结构,叫做散列表,还有⼀些称之为“字典”(dict)、“映射”(map)、“哈希”(hash)。
这种数据结构有个特点,⼀般情况下,能在O(1)时间内根据关键字找到要查询的信息(进⾏⼀次或者很少次⽐较),这是因为散列表的底层⼀般会使⽤数组实现,利⽤“散列函数”或者称为“hash函数”,可以计算出该元素应该存到哪个位置,能够让所有的元素均匀分布在数组中,下⼀次查找的时候,根据散列函数计算出对应的位置,就能找到元素。
但是存在⼀个问题,没有完美的hash函数也就是说⽬前不能确定某个元素的位置,且不重复!也就是说,散列可能会存在冲突,⽐如某个元素通过散列函数计算,确定应该存在下标5的位置,下⼀次再来⼀个元素,计算后发现还是存在下标为5的位置,此时就出现了冲突。
出现hash冲突后,有多种⽅式可以解决冲突,⽐如开放地址法、链地址法(拉链法),本⽂主要介绍开放地址法的⼀种——线性探测法。
线性探测法的定义 根据维基百科对线性探测法的介绍,摘抄如下:线性探测是⼀种开放寻址的策略。
在这些策略⾥,散列表的每个单元都存储⼀对键值对。
当散列函数对⼀个给定值产⽣⼀个键,并且这个键指向散列表中某个已经被另⼀个键值对所占⽤的单元时,线性探测⽤于解决此时产⽣的冲突:查找散列表中离冲突单元最近的空闲单元,并且把新的键插⼊这个空闲单元。
同样的,查找也同插⼊如出⼀辙:从散列函数给出的散列值对应的单元开始查找,直到找到与键对应的值或者是找到空单元。
讲的通俗⼀点,就是发现蹲坑的时候发现坑已经被占了,就找后⾯⼀个坑,如果后⾯⼀个坑空闲,则占⽤这个空闲的坑;如果后⾯⼀个坑也被占了,则⼀直往后⾯的坑进⾏遍历,直到找到空闲的坑,否则就⼀直憋着。
线性探测法的插⼊过程图解 ⽬前有⼀个长度为8的数组,选择的hash函数是 e.key%8,这个8是指数组的长度(容量),当数组长度发⽣变化,hash函数也应该变化。
解决hash冲突的几种方法
当哈希函数无法将数据映射到预期的地址时,就会发生哈希冲突。
哈希冲突可能会导致数据在散列表中的位置不正确,从而导致访问失败或性能下降。
下面是几种常见的解决哈希冲突的方法:
1. 开放地址法:当发生哈希冲突时,开放地址法会尝试在散列表的其他地方查找数据。
这种方法可以通过在散列表中创建一个额外的地址空间来解决哈希冲突,从而提高散列表的性能和效率。
2. 链表法:链表法会在散列表中创建一组指针,这些指针指向包含相同关键字的数据节点。
这种方法可以有效地解决哈希冲突,并且可以在较短的时间内找到数据。
3. 置换法:当发生哈希冲突时,置换法会将数据重新放置到散列表的其他地方。
这种方法可能会导致散列表的效率和性能下降,因此通常只用于非常简单的哈希表应用场景。
4. 哈希函数优化:为了提高哈希表的效率和性能,可以使用一些优化技术,例如使用非线性哈希函数、减少哈希函数的计算复杂度、使用前缀哈希函数等。
这些技术可以有效地减少哈希冲突的发生,从而提高散列表的访问效率和性能。
5. 哈希表结构选择:选择合适的哈希表结构也可以提高哈希表的效率和性能。
例如,使用链表哈希表、有序哈希表等结构可以更好地处理哈希冲突,从而提高散列表的效率和性能。
解决哈希冲突的方法有很多种,每种方法都有其优缺点和适用范围。
在选择哈希冲突解决方法时,应该根据具体应用场景和数据特点进行选择,以实现最佳的性能和效率。
详解数据结构之散列(哈希)表1.散列表查找步骤散列表,最有用的基本数据结构之一。
是根据关键码的值直接进行访问的数据结构,散列表的实现常常叫做散列(hasing)。
散列是一种用于以常数平均时间执行插入、删除和查找的技术,下面我们来看一下散列过程。
我们的整个散列过程主要分为两步:1.通过散列函数计算记录的散列地址,并按此散列地址存储该记录。
就好比麻辣鱼,我们就让它在川菜区,糖醋鱼,我们就让它在鲁菜区。
但是我们需要注意的是,无论什么记录我们都需要用同一个散列函数计算地址,然后再存储。
2.当我们查找时,我们通过同样的散列函数计算记录的散列地址,按此散列地址访问该记录。
因为我们存和取的时候用的都是一个散列函数,因此结果肯定相同。
刚才我们在散列过程中提到了散列函数,那么散列函数是什么呢?我们假设某个函数为f,使得存储位置= f (key) ,那样我们就能通过查找关键字不需要比较就可获得需要的记录的存储位置。
这种存储技术被称为散列技术。
散列技术是在通过记录的存储位置和它的关键字之间建立一个确定的对应关系 f ,使得每个关键字key 都对应一个存储位置f(key)。
见下图这里的 f 就是我们所说的散列函数(哈希)函数。
我们利用散列技术将记录存储在一块连续的存储空间中,这块连续存储空间就是我们本文的主人公------散列(哈希)上图为我们描述了用散列函数将关键字映射到散列表。
但是大家有没有考虑到这种情况,那就是将关键字映射到同一个槽中的情况,即f(k4) = f(k3) 时。
这种情况我们将其称之为冲突,k3 和k4 则被称之为散列函数 f 的同义词,如果产生这种情况,则会让我们查找错误。
幸运的是我们能找到有效的方法解决冲突。
首先我们可以对哈希函数下手,我们可以精心设计哈希函数,让其尽可能少的产生冲突,所以我们创建哈希函数时应遵循以下规则:1.必须是一致的。
假设你输入辣子鸡丁时得到的是在看,那么每次输入辣子鸡丁时,得到的也必须为在看。
线性探测法解决哈希冲突的一种方法哈希表是一种常用的数据结构,用于存储和查找数据。
但由于哈希函数的性质,不同的数据可能会映射到同一个哈希值上,这就导致了哈希冲突的问题。
本文将介绍线性探测法作为一种解决哈希冲突的方法。
一、哈希表和哈希冲突哈希表是一种依靠哈希函数进行存储和查找操作的数据结构。
其核心思想是将关键字通过哈希函数映射到一个固定的位置上,即哈希地址。
然而,由于哈希函数的可能性有限,不同的关键字可能会映射到同一个哈希地址上,即发生哈希冲突。
二、线性探测法的原理线性探测法是一种简单而常用的解决哈希冲突的方法。
其基本原理是当发生哈希冲突时,顺序地查找下一个空槽位,直到找到一个空槽位或者查满整个哈希表。
具体的步骤如下:1. 根据哈希函数计算关键字的哈希地址。
2. 若该地址处为空槽位,则直接将关键字插入到此位置。
3. 若该地址处已被其他关键字占据,则顺序地查找下一个槽位,直到找到一个空槽位或者查满整个哈希表。
4. 将关键字插入到找到的空槽位上。
三、线性探测法的实现为了实现线性探测法,我们需要使用一个数组来存储哈希表,同时还需要定义一个哈希函数来计算关键字的哈希地址。
下面是一个简单的线性探测法的实现示例:```pythonclass LinearProbingHash:def __init__(self, size):self.size = sizeself.hash_table = [None] * sizedef hash_function(self, key):return key % self.sizedef insert(self, key):index = self.hash_function(key)while self.hash_table[index] is not None:index = (index + 1) % self.sizeself.hash_table[index] = keydef search(self, key):index = self.hash_function(key)while self.hash_table[index] != key:index = (index + 1) % self.sizeif self.hash_table[index] is None:return Nonereturn index```以上代码中,我们使用一个大小为size的数组作为哈希表,其中每个槽位上存放的是关键字。
以下是列举收集来的三个题目,三个题目是同一个意思,
一,利用线性探测法构造散列表(用除余法来得出散列地址,用开放地址法解决同义词问题)题目:已知一组关键字为(26,36,41,38,44,15,68,12,06,51),用除余法构造散列函数,用线性探查法解决冲突构造这组关键字的散列表。
解答:为了减少冲突,通常令装填因子α<l。
这里关键字个数n=10,不妨取m=13,此时α≈0.77,散列表为T[0..12],散列函数为:h(key)=key%13。
由除余法的散列函数计算出的上述关键字序列的散列地址为(0,10,2,12,5,2,3,12,6,12)。
前5个关键字插入时,其相应的地址均为开放地址,故将它们直接插入T[0],T[10),T[2],T[12]和T[5]中。
当插入第6个关键字15时,其散列地址2(即h(15)=15%13=2)已被关键字41(15和41互为同义词)占用。
故探查h1=(2+1)%13=3,此地址开放,所以将15放入T[3]中。
当插入第7个关键字68时,其散列地址3已被非同义词15先占用,故将其插入到T[4]中。
当插入第8个关键字12时,散列地址12已被同义词38占用,故探查hl=(12+1)%13=0,而T[0]亦被26占用,再探查h2=(12+2)%13=1,此地址开放,可将12插入其中。
类似地,第9个关键字06直接插入T[6]中;而最后一个关键字51插人时,因探查的地址12,0,1,…,6均非空,故51插入T[7]中。
二、题目:
已知一个线性表(38,25,74,63,52,48),假定采用h(k)=k%6计算散列地址进行散列存储,若用线性探测的开放定址法处理冲突,则在该散列表上进行查找的平均查找长度为()。
A. 1.5
B. 1.7
C. 2
D. 2.3
2、解题过程:
(1)计算h(k):38%6 = 2 25%6 = 1 74%6 = 2 63%6 = 3 52%6 = 4 48%6 = 0
(2)定址:把不冲突的和冲突的全部列出来即可
地址:0 1 2 3 4 5
1、线性表第1个元素(38):38(第1 次不冲突)
2、线性表第2个元素(25):25(第1次不冲突)
3、线性表第3个元素(74):74(第1 次冲突,地址+ 1)
4、线性表第3个元素(74):74(第2 次不冲突)
5、线性表第4个元素(63):63(第1 次冲突,地址+ 1)
6、线性表第4个元素(63):63(第2 次不冲突)
7、线性表第5个元素(52):52(第1 次冲突,地址+ 1)
8、线性表第5个元素(52):52(第2 次不冲突)
9、线性表第6个元素(48):48(第1次不冲突)
经过上述定址过程,线性表中的各个元素都有了唯一的地址。
2.3、结果
线性表中的6 个元素,经过9次定址,
在该散列表上进行查找的平均查找长度为:9/6 = 1.5, 答案选:A
三、哈希表查找不成功怎么计算?
解答:先建好表,然后可以算出每个位置不成功时的比较次数之和,再除以表空间个数!
例如:散列函数为hash(x)=x MOD 13,用线性探测,建立了哈希表之后,如何求查找不成功时的平均查找长度!?
地址:0 1 2 3 4 5 6 7 8 9 10 11 12
数据:39 12 28 15 42 44 6 25 --36 -38
成功次数: 1 3 1 2 2 1 1 9 1 1
不成功次数:9 8 7 6 5 4 3 2 1 1 2 1 10
查找成功时的平均查找长度:ASL=(1+3+1+2+2+1+1+9+1+1)/10 =2.2
查找不成功时的平均查找长度:ASL=(9+8+7+6+5+4+3+2+1+1+2+1+10)/13=4.54
说明:
第n个位置不成功时的比较次数为,第n个位置到第1个没有数据位置的距离。
至少要查询多少次才能确认没有这个值。
(1)查询hash(x)=0,至少要查询9次遇到表值为空的时候,才能确认查询失败。
(2)查询hash(x)=1,至少要查询8次遇到表值为空的时候,才能确认查询失败。
(3)查询hash(x)=2,至少要查询7次遇到表值为空的时候,才能确认查询失败。
(4)查询hash(x)=3,至少要查询6次遇到表值为空的时候,才能确认查询失败。
(5)查询hash(x)=4,至少要查询5次遇到表值为空的时候,才能确认查询失败。
(6)查询hash(x)=5,至少要查询4次遇到表值为空的时候,才能确认查询失败。
(7)查询hash(x)=6,至少要查询3次遇到表值为空的时候,才能确认查询失败。
(8)查询hash(x)=7,至少要查询2次遇到表值为空的时候,才能确认查询失败。
(9)查询hash(x)=8,至少要查询1次遇到表值为空的时候,才能确认查询失败。
(10)查询hash(x)=9,至少要查询1次遇到表值为空的时候,才能确认查询失败。
(11)查询hash(x)=10,至少要查询2次遇到表值为空的时候,才能确认查询失败。
(12)查询hash(x)=11,至少要查询1次遇到表值为空的时候,才能确认查询失败。
(13)查询hash(x)=12,至少要查询10次遇到表值为空(循环查询顺序表)的时候,才能确认查询失败。