小学奥数应用题讲义 7-浓度问题

浓度问题六年级应用题奥数浓度问题是数学中的一个重要概念，在奥数竞赛中也经常涉及到。

在六年级时，学生已经开始学习有关浓度的知识并且能够应用于解决问题。

下面，我将给出几个典型的浓度问题，并进行详细的解答。

浓度问题通常涉及到溶液的配制和稀释。

在许多实际问题中，我们需要根据所需浓度来配制溶液，或者根据已知溶液的浓度来计算稀释后的浓度。

这样的问题都可以通过使用浓度公式来解决。

要理解浓度公式，首先需要明确溶液的浓度是指溶质在溶液中所占的比例或者质量。

通常，浓度可以用溶质的质量或者浓度与溶液总质量的比值来表示。

为了方便计算，常用百分数或者摩尔浓度来表示溶液的浓度。

以下是一些常见的浓度问题。

问题一：小明需要配制一种质量浓度为30%的盐水溶液，他有100克的盐。

他需要加入多少毫升的水？解答：要计算所需的水的体积，我们需要知道溶质（盐）的质量和溶液（盐水）的质量。

根据浓度的定义，30%的盐水表示100克溶液中含有30克的盐。

设所需水的体积为V。

根据溶液的质量定义，溶液的质量等于溶质的质量加上溶剂（水）的质量。

所以，总质量为100克（盐） + V克（水）。

根据质量浓度的定义，浓度等于溶质的质量与溶液的总质量的比值。

所以，30%的盐水的质量浓度等于30克（盐）/（100克（盐） + V克（水））。

根据上述条件，我们可以列出方程：30克/（100克+ V克） = 0.3通过移项，并转化为通分的形式，可以得到：30克= 0.3 ×（100克+ V克）化简方程，可以得到：30克= 30克+ 0.3V0.3V = 0克V = 0克/ 0.3V = 0克根据方程计算结果可知，所需的水的体积为0毫升。

这意味着小明选择的盐的量已经达到了饱和，无需再加入水。

问题二：小红有一瓶质量浓度为20%的葡萄糖溶液，她需要制作100毫升质量浓度为10%的葡萄糖溶液。

她应该加入多少毫升的水？解答：要计算所需的水的体积，我们需要知道已知溶液（20%的葡萄糖溶液）的质量和所需溶液（10%的葡萄糖溶液）的质量。

小学奥数浓度问题高难版简介本文档将为小学奥数学生介绍浓度问题的高难度版。

浓度问题是数学中的一个重要概念，对于培养学生的逻辑思维和推理能力非常有帮助。

问题描述设有两种液体A和B，液体A的浓度为m%，液体B的浓度为n%。

现在要将m升液体A和n升液体B混合在一起，得到一种新的液体C。

问：液体C的浓度为多少？解题思路1. 首先，我们要知道液体的浓度是表示溶质在溶剂中的比例。

因此，设液体C的浓度为c%。

2. 液体A的浓度为m%，表示液体A中溶质的质量占总质量的百分比。

3. 液体B的浓度为n%，表示液体B中溶质的质量占总质量的百分比。

4. 液体C中液体A的质量为m升乘以液体A的浓度m%，液体C中液体B的质量为n升乘以液体B的浓度n%。

5. 因此，液体C中液体A的质量占总质量的百分比为(m * m%) / ((m * m%) + (n * n%))，液体C中液体B的质量占总质量的百分比为(n * n%) / ((m * m%) + (n * n%))。

6. 液体C的浓度为液体C中溶质的质量占总质量的百分比，即c% = [(m * m%) + (n * n%)] / (m + n)。

示例假设液体A的浓度为20%，液体B的浓度为30%。

现在要将4升液体A和6升液体B混合在一起，求混合后液体C的浓度。

解题步骤：1. 液体A的浓度m% = 20%，液体B的浓度n% = 30%。

2. 液体A的数量m = 4升，液体B的数量n = 6升。

3. 液体C的浓度c% = [(m * m%) + (n * n%)] / (m + n) = [(4 * 20%) + (6 * 30%)] / (4 + 6) = 22%。

4. 因此，混合后液体C的浓度为22%。

总结通过本文档的介绍，我们了解了浓度问题的高难度版。

掌握了解题的思路和步骤后，我们可以运用这些知识解决更复杂的浓度问题。

希望本文档对小学奥数学生的学习有所帮助。

【#小学奥数# 导语】奥数是奥林匹克数学竞赛的简称。

1934年—1935年，前苏联开始在列宁格勒和莫斯科举办中学数学竞赛，并冠以数学奥林匹克竞赛的名称，1959年在布加勒斯特举办第一届国际数学奥林匹克竞赛。

以下是?无忧考网整理的《小学生奥数浓度问题五篇》相关资料，希望帮助到您。

1.小学生奥数浓度问题1、有甲乙两只桶，甲桶盛了半桶水，乙桶盛了不到半桶纯酒精，先将甲桶的水倒入乙桶，倒入的容量与乙桶的酒精量相等；再将乙桶的溶液倒入甲桶，倒入的容量与甲桶剩下的水相等；再将甲桶的溶液倒入乙桶，倒入的容量与乙桶剩下的溶液量相等；再将乙桶的溶液倒入甲桶，倒入的容量与甲桶剩下的溶液量相等。

此时，恰好两桶溶液的数量相等，求些时甲，乙两桶酒精溶液的浓度比。

2、甲桶中装有10升纯酒精，乙桶中装有6升纯酒精与8升水的混合物，丙桶中装有10升水，现在先从甲桶向乙桶倒入一定量的酒精，并搅拌均匀；然后从乙桶向丙桶倒入一定量的液体，并搅拌均匀；接着从丙桶向甲桶倒入一定是的液体，最后各桶中的酒精浓度分别为：甲桶75%，乙桶50%，丙桶25%，那么此时丙桶中有混合液体多少升？3、甲容器中有500克20%的盐水，乙容器中有500克水。

先将甲中一半的盐水倒入乙，充分搅拌；再将乙中一半的盐水倒入甲，充分搅拌；最后将甲中盐水的一部分倒入乙，使甲、乙的盐水重量相同。

求此时乙中盐水的浓度。

2.小学生奥数浓度问题1、甲容器中有浓度4%的盐水150克，乙容器中有某种浓度的盐水若干。

从乙中取出450克盐水，放入甲中混合成浓度为8．2%的盐水，再把水倒入乙容器中，使与甲的盐水一样多，现在乙容器中盐水浓度为1．12%，问原来乙容器中有多少克盐水？浓度的百分数是多少？2、甲容器中有8％的食盐水300克，乙容器中有12．5％的食盐水120克。

往甲、乙两个容器分别倒入等量的水，使两个容器的食盐水浓度一样。

问倒入多少克水？3、A种酒精中纯酒精含量为40%，B种酒精中纯酒精的含量为36%，C种酒精中纯酒精的含量为35%。

一、浓度问题定义：有关浓度的问题，在我们的日常生活和生产实际中经常会遇到.在这部分内容里我们对有关浓度的问题做一些初步的探讨。

例如将糖溶于水就得到了糖水，而糖水甜的程度是由什么决定的呢？我们不妨来做一个小实验：在两只同样大小的杯子中放入相同量的水，再往两只杯子中分别放入白糖，使其中一只杯子中的糖是另一只杯子中的糖的2倍，品尝一下，有什么感觉.我们很容易发现，放糖多的杯子中的水甜.若将等量的糖放入两只杯子中，在两只杯子中放入不等量的水，比如一只杯子中放入的水的量是另一只杯子中放入水的量的2倍，这时结果会怎样呢？不难想象到放水少的杯子中的糖水甜.通过上面的小实验我们可以知道，糖水甜的程度是由糖与糖水二者重量的比值决定的.糖与糖水重量的比值叫糖水的浓度（也叫含糖率）.这个比值一般我们将它写成百分数，所以称为百分比浓度.其中糖叫溶质，水叫做溶剂，糖水叫溶液，解答这类浓度问题的主要依据有：浓度＝溶液重量溶质重量×100% 这个式子还可以转化为： 溶质质量溶质质量+溶剂质量×100％ 溶液的重量=溶质的重量+溶剂的重量浓度=溶质重量÷溶液重量溶液重量=溶质重量÷浓度溶质重量=溶液重量×浓度二、解浓度问题的重要方法：1、利用浓度的基本定义以及三个量之间的关系：知识框架浓度问题综合（一）2、列方程解应用题也是解决浓度问题的重要方法。

解答浓度问题，首先要弄清什么是浓度。

有些问题根据题意列方程解答比较容易，在列方程时，要注意寻找题目中数量问题的相等关系。

溶度问题包括以下几种基本题型︰（1） 溶剂的增加或减少引起浓度变化。

面对这种问题，不论溶剂增加或减少，溶质是始终不变的，据此便可解题。

（2） 溶质的增加引起浓度变化。

面对这种问题，溶质和浓度都增大了，但溶剂是不变的，据此便可解题。

（3） 两种或几种不同溶度的溶液配比问题。

面对这种问题，要抓住混合前各溶液的溶质和与混合后溶液的溶质质量相等，据此便可解题。

小学奥数教程之-溶液浓度问题在解决浓度问题时，需要明确溶液、溶质和溶剂三者之间的关系。

溶质通常指盐水中的“盐”、糖水中的“糖”或酒精溶液中的“酒精”等，而溶剂一般为水，有时也会出现煤油等。

溶液则是溶质和溶剂的混合液体，而浓度则是溶质质量与溶液质量的比值。

在运算上，可以利用浓度三角和十字交叉法来解决复杂的浓度问题。

解决浓度问题的一般方法是寻找溶液配比前后的不变量，然后建立等量关系列方程。

此外，十字交叉法和浓度三角也是解决浓度问题的有效方法。

在应用题中，列方程解题也是一种重要的方法。

比例是浓度问题的一个重要知识点，而浓度问题与我们的日常生活息息相关，包括小学所学的百分数和浓度问题中的基本量。

举例来说，当需要解决三种溶液混合多次的问题时，可以利用十字交叉法或浓度三角进行解题。

比如，有甲、乙、丙三个，容量为毫升。

甲有浓度为40%的盐水400毫升；乙中有清水400毫升；丙中有浓度为20%的盐水400毫升。

先把甲、丙两中的盐水各一半倒入乙搅匀后，再把乙中的盐水200毫升倒入甲，200毫升倒入丙。

这时甲、乙、丙中盐水的浓度各是多少？通过列出表格和运用浓度三角，可以得出甲、乙、丙中盐水的浓度分别为27.5%、15%和17.5%。

在这个问题中，甲、乙、丙三个中盐水的浓度分别为27.5%、15%和17.5%。

为了解决涉及浓度的应用问题，特别是在多次变化的情况下，常常使用表格的方法，以便清楚地了解溶质质量和溶液质量的变化以及它们之间的关系。

在这个问题中，甲、乙、丙三个中的酒精溶液中纯酒精的含量分别占48%、62.5%和。

已知三个中的酒精溶液总量为100千克，其中甲中的酒精溶液量等于乙、丙两个中酒精溶液的总量。

混合三个中的酒精溶液后，纯酒精的百分含量将达到56%。

那么，丙中纯酒精的量是多少千克？解法1：使用方程法。

设丙中酒精溶液的重量为x千克，则乙中的酒精溶液为50-x千克。

根据纯酒精的含量，可以列出方程式：50*48%+（50-x）*62.5%+x*100%=100*56%。

奥数知识点：浓度问题
奥数知识点：浓度问题
以1升溶液中所含溶质的摩尔数表示的浓度。

下面小编给大家精心搜集整理的奥数知识点：浓度问题，欢迎阅读!
奥数知识点：浓度问题
浓度问题的公式
溶质的重量+溶剂的重量=溶液的.重量溶质的重量÷浓度=溶液的重量
溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量
例. 瓶中装有浓度为15%的酒精溶液1000克。

现在又分别倒入100克和400克的A，B两种酒精溶液，瓶里的浓度变成了14%。

已知A种酒精溶液是B种酒精溶液浓度的2倍。

那么A种酒精溶液的浓度是多少?
解析：
三种混合后溶液重1000+100+400=1500克，含酒精14%×1500=210克，原来含酒精15%×1000=150克，说明AB两种溶液共含酒精210-150=60克。

由于A的浓度是B的2倍，因此400克B溶液的酒精含量相当于400÷2=200克A溶液酒精的含量。

所以A溶液的浓度是60÷(100+200)=20%。

第七讲浓度问题知识提纲：浓度问题是一种常见的百分数应用题，研究的是溶质、溶剂、溶液三者之间的关系。

通常把盐、糖、纯酒精、药粉等叫做溶质，把溶解在这些溶质中的液体称为溶剂，溶质与溶剂的混合液体叫做溶液。

基本关系式：溶液的质量=溶质的质量+溶剂的质量浓度=溶质质量÷溶液质量×100%溶质质量=溶液质量×浓度溶液质量=溶质质量÷浓度浓度＝溶质质量溶液质量×100％＝溶质质量溶质质量+溶剂质量×100％【典型例题1】有含糖量为7％的糖水600克，要使其含糖量加大到10％，需要再加入多少克糖？解析：根据题意，在7％的糖水中加糖就改变了原来糖水的浓度，糖的质量增加了，糖水的质量也增加了，但水的质量并没有改变。

因此，可以先根据原来糖水中的浓度求出水的质量，再根据后来糖水中的浓度求出现在糖水的质量，用现在糖水的质量减去原来糖水的质量就是增加的糖的质量。

原来糖水中水的质量：600×（1－7％）＝558（克）现在糖水的质量：558÷（1－10％）＝620（克）加入糖的质量：620－600＝20（克）答：需要加入20克糖。

【随堂练习1】现在有浓度为20％的糖水300克，要把它变成浓度为40％的糖水，需要加糖多少克？【随堂练习2】有甲、乙两个瓶子，甲瓶里装了200毫升清水，乙瓶里装了200毫升纯酒精。

第一次把20毫升纯酒精由乙瓶倒入甲瓶，第二次把甲瓶中20毫升溶液倒回乙瓶，此时甲瓶里含纯酒精多，还是乙瓶里含水多？【典型例题2】一种35％的新农药，如稀释到1.75％时，治虫最有效。

用多少千克浓度为35％的农药加多少千克水，才能配成1.75％的农药800千克？解析：把浓度高的溶液经添加溶剂变为浓度低的溶液的过程称为稀释。

在这种稀释过程中，溶质的质量是不变的。

这是解这类问题的关键。

800千克1.75％的农药含纯农药的质量为800×1.75％＝14（千克）含14千克纯农药的35％的农药质量为14÷35％＝40（千克）由40千克农药稀释为800千克农药应加水的质量为800－40＝760（千克）答：用40千克的浓度为35％的农药中添加760千克水，才能配成浓度为1.75％的农药800千克。

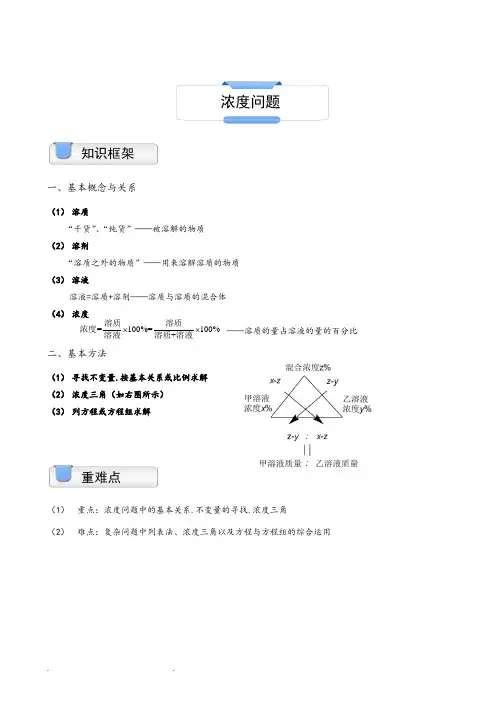
一、基本概念与关系（1） 溶质“干货”、“纯货”——被溶解的物质（2） 溶剂“溶质之外的物质”——用来溶解溶质的物质（3） 溶液溶液=溶质+溶剂——溶质与溶质的混合体（4） 浓度——溶质的量占溶液的量的百分比 二、基本方法（1） 寻找不变量.按基本关系或比例求解（2） 浓度三角（如右图所示）（3） 列方程或方程组求解（1） 重点：浓度问题中的基本关系.不变量的寻找.浓度三角（2） 难点：复杂问题中列表法、浓度三角以及方程与方程组的综合运用重难点 知识框架浓度问题=100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液例题精讲一、抓住不变量和浓度基本关系解决问题【例1】某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到.那么这种溶液的食盐浓度为多少？【巩固】一容器内有浓度为25％的糖水.若再加入20千克水.则糖水的浓度变为15％.问这个容器内原来含有糖多少千克？【例2】浓度为20％的糖水40克.要把它变成浓度为40％的糖水.需加多少克糖？【巩固】浓度为10％.重量为80克的糖水中.加入多少克水就能得到浓度为8％的糖水？【例3】买来蘑菇10千克.含水量为99％.晾晒一会儿后.含水量为98％.问蒸发掉多少水份？【巩固】1000千克葡萄含水率为96.5%.一周后含水率降为96%.这些葡萄的质量减少了千克.【例4】将含农药30%的药液.加入一定量的水以后.药液含药24%.如果再加入同样多的水.药液含药的百分比是________．【巩固】一杯盐水.第一次加入一定量的水后.盐水的含盐百分比变为15%；第二次又加入同样多的水.盐水的含盐百分比变为12%.第三次再加入同样多的水.盐水的含盐百分比将变为_______%.二、通过浓度三角解决浓度和实际生活中的配比问题【例5】有浓度为20％的盐水300克.要配制成40％的盐水.需加入浓度为70％的盐水多少克？【巩固】将75％的酒精溶液32克稀释成浓度为40％的稀酒精.需加入水多少克？【例6】瓶中装有浓度为15%的酒精溶液1000克.现在又分别倒入100克和400克的A、B两种酒精溶液.瓶中的浓度变成了14%．已知A种酒精溶液浓度是B种酒精溶液浓度的2倍.那么A种酒精溶液的浓度是百分之几？【巩固】有两种溶液.甲溶液的酒精浓度为15%.盐浓度为10%.乙溶液中的酒精浓度为45%.盐浓度为5%．现在有甲溶液1千克.那么需要多少千克乙溶液.将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍？【例7】甲瓶中酒精的浓度为70%.乙瓶中酒精的浓度为60%.两瓶酒精混合后的浓度是66%．如果两瓶酒精各用去5升后再混合.则混合后的浓度是66.25%．问原来甲、乙两瓶酒精分别有多少升？【巩固】纯酒精含量分别为60%、35%的甲、乙两种酒精混合后的纯酒精含量为40%．如果每种酒精都多取20克.混合后纯酒精的含量变为45%．求甲、乙两种酒精原有多少克？【例8】甲种酒精纯酒精含量为72%.乙种酒精纯酒精含量为58%.混合后纯酒精含量为62%．如果每种酒精取的数量比原来都多取15升.混合后纯酒精含量为63.25%．第一次混合时.甲、乙两种酒精均取了多少升？【巩固】甲、乙两只装满硫酸溶液的容器.甲容器中装有浓度为8%的硫酸溶液600千克.乙容器中装有浓度为40%的硫酸溶液400千克．均取多少千克分别放入对方容器中.才能使这两个容器中的硫酸溶液的浓度一样？【例9】某班有学生48人.女生占全班的37.5％.后来又转来女生若干人.这时人数恰好是占全班人数的40％.问转来几名女生？【巩固】小明到商店买红、黑两种笔共66支．红笔每支定价5元.黑笔每支定价9元．由于买的数量较多.商店就给予优惠.红笔按定价85%付钱.黑笔按定价80%付钱.如果他付的钱比按定价少付了18%.那么他买了红笔多少支？【例10】有两包糖.第一包糖由奶糖和水果糖组成.其中14为奶糖；第二包糖由酥糖和水果糖组成.其中15为酥糖．将两包糖混合后.水果糖占78%.那么奶糖与酥糖的比例是________.【巩固】某商品76件.出售给33位顾客.每位顾客最多买三件．如果买一件按原定价.买两件降价10%.买三件降价20%.最后结算.平均每件恰好按原定价的85%出售．那么买三件的顾客有多少人？三、综合运用各种方法解决多溶液、多次配比问题【例11】甲容器中有纯酒精11升.乙容器中有水15升.第一次将甲容器中的一部分纯酒精倒入乙容器.使酒精与水混合。

小学奥数浓度问题(总11页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除第十七周浓度问题专题简析：在百分数应用题中有一类叫溶液配比问题，即浓度问题。

我们知道，将糖溶于水就得到了糖水，其中糖叫溶质，水叫溶剂，糖水叫溶液。

如果水的量不变，那么糖加得越多，糖水就越甜，也就是说糖水甜的程度是由糖（溶质）与糖水（溶液＝糖+水）二者质量的比值决定的。

这个比值就叫糖水的含糖量或糖含量。

类似地，酒精溶于水中，纯酒精与酒精溶液二者质量的比值叫酒精含量。

因而浓度就是溶质质量与溶液质量的比值，通常用百分数表示，即，浓度＝溶质质量溶液质量×100％＝溶质质量溶质质量+溶剂质量×100％解答浓度问题，首先要弄清什么是浓度。

在解答浓度问题时，根据题意列方程解答比较容易，在列方程时，要注意寻找题目中数量问题的相等关系。

浓度问题变化多，有些题目难度较大，计算也较复杂。

要根据题目的条件和问题逐一分析，也可以分步解答。

例题1。

有含糖量为7％的糖水600克，要使其含糖量加大到10％，需要再加入多少克糖？【思路导航】根据题意，在7％的糖水中加糖就改变了原来糖水的浓度，糖的质量增加了，糖水的质量也增加了，但水的质量并没有改变。

因此，可以先根据原来糖水中的浓度求出水的质量，再根据后来糖水中的浓度求出现在糖水的质量，用现在糖水的质量减去原来糖水的质量就是增加的糖的质量。

原来糖水中水的质量：600×（1－7％）＝558（克）现在糖水的质量：558÷（1－10％）＝620（克）加入糖的质量：620－600＝20（克）答：需要加入20克糖。

练习11、现在有浓度为20％的糖水300克，要把它变成浓度为40％的糖水，需要加糖多少克？2、3、有含盐15％的盐水20千克，要使盐水的浓度为20％，需加盐多少千克？4、有甲、乙两个瓶子，甲瓶里装了200毫升清水，乙瓶里装了200毫升纯酒精。

六年级数学奥数讲义练习浓度问题（全国通用版含答案）一、知识要点在百分数应用题中有一类叫溶液配比问题，即浓度问题。

我们知道，将糖溶于水就得到了糖水，其中糖叫溶质，水叫溶剂，糖水叫溶液。

如果水的量不变，那么糖加得越多，糖水就越甜，也就是说糖水甜的程度是由糖（溶质）与糖水（溶液＝糖+水）二者质量的比值决定的。

这个比值就叫糖水的含糖量或糖含量。

类似地，酒精溶于水中，纯酒精与酒精溶液二者质量的比值叫酒精含量。

因而浓度就是溶质质量与溶液质量的比值，通常用百分数表示，即，浓度＝溶质质量/溶液质量×100％＝溶质质量/（溶质质量＋溶剂质量）×100%解答浓度问题，首先要弄清什么是浓度。

在解答浓度问题时，根据题意列方程解答比较容易，在列方程时，要注意寻找题目中数量问题的相等关系。

浓度问题变化多，有些题目难度较大，计算也较复杂。

要根据题目的条件和问题逐一分析，也可以分步解答。

二、精讲精练【例题1】有含糖量为7％的糖水600克，要使其含糖量加大到10％，需要再加入多少克糖？【思路导航】根据题意，在7％的糖水中加糖就改变了原来糖水的浓度，糖的质量增加了，糖水的质量也增加了，但水的质量并没有改变。

因此，可以先根据原来糖水中的浓度求出水的质量，再根据后来糖水中的浓度求出现在糖水的质量，用现在糖水的质量减去原来糖水的质量就是增加的糖的质量。

原来糖水中水的质量：600×（1－7％）＝558（克）现在糖水的质量：558÷（1－10％）＝620（克）加入糖的质量：620－600＝20（克）答：需要加入20克糖。

练习1：1、现在有浓度为20％的糖水300克，要把它变成浓度为40％的糖水，需要加糖多少克？2、有含盐15％的盐水20千克，要使盐水的浓度为20％，需加盐多少千克？3、有甲、乙两个瓶子，甲瓶里装了200毫升清水，乙瓶里装了200毫升纯酒精。

第一次把20毫升纯酒精由乙瓶倒入甲瓶，第二次把甲瓶中20毫升溶液倒回乙瓶，此时甲瓶里含纯酒精多，还是乙瓶里含水多？【答案】1.需要加糖100克。

一、基本概念与关系 （1） 溶质“干货”、“纯货”——被溶解的物质（2） 溶剂“溶质之外的物质”——用来溶解溶质的物质（3） 溶液 溶液=溶质+溶剂——溶质与溶质的混合体（4） 浓度——溶质的量占溶液的量的百分比二、基本方法 （1） 寻找不变量，按基本关系或比例求解（2） 浓度三角（如右图所示）（3） 列方程或方程组求解（1）重点：浓度问题中的基本关系，不变量的寻找，浓度三角 （2） 难点：复杂问题中列表法、浓度三角以及方程与方程组的综合运用 重难点浓度问题 知识框架=100%=100%+⨯⨯溶质溶质浓度溶液溶质溶液::乙溶液质量甲溶液质量z-y x-zz-y x-z 乙溶液浓度y %甲溶液浓度x %混合浓度z%例题精讲一、抓住不变量和浓度基本关系解决问题【例1】某种溶液由40克食盐浓度15%的溶液和60克食盐浓度10%的溶液混合后再蒸发50克水得到，那么这种溶液的食盐浓度为多少？【巩固】一容器内有浓度为25％的糖水，若再加入20千克水，则糖水的浓度变为15％，问这个容器内原来含有糖多少千克？【例2】浓度为20％的糖水40克，要把它变成浓度为40％的糖水，需加多少克糖？【巩固】浓度为10％，重量为80克的糖水中，加入多少克水就能得到浓度为8％的糖水？【例3】买来蘑菇10千克，含水量为99％，晾晒一会儿后，含水量为98％，问蒸发掉多少水份？【巩固】1000千克葡萄含水率为96.5%，一周后含水率降为96%，这些葡萄的质量减少了千克.【例4】将含农药30%的药液，加入一定量的水以后，药液含药24%，如果再加入同样多的水，药液含药的百分比是________．【巩固】一杯盐水，第一次加入一定量的水后，盐水的含盐百分比变为15%；第二次又加入同样多的水，盐水的含盐百分比变为12%，第三次再加入同样多的水，盐水的含盐百分比将变为_______%.二、通过浓度三角解决浓度和实际生活中的配比问题【例5】有浓度为20％的盐水300克，要配制成40％的盐水，需加入浓度为70％的盐水多少克？【巩固】将75％的酒精溶液32克稀释成浓度为40％的稀酒精，需加入水多少克？【例6】瓶中装有浓度为15%的酒精溶液1000克，现在又分别倒入100克和400克的A、B两种酒精溶液，瓶中的浓度变成了14%．已知A种酒精溶液浓度是B种酒精溶液浓度的2倍，那么A种酒精溶液的浓度是百分之几？【巩固】有两种溶液，甲溶液的酒精浓度为15%，盐浓度为10%，乙溶液中的酒精浓度为45%，盐浓度为5%．现在有甲溶液1千克，那么需要多少千克乙溶液，将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍？【例7】甲瓶中酒精的浓度为70%，乙瓶中酒精的浓度为60%，两瓶酒精混合后的浓度是66%．如果两瓶酒精各用去5升后再混合，则混合后的浓度是66.25%．问原来甲、乙两瓶酒精分别有多少升？【巩固】纯酒精含量分别为60%、35%的甲、乙两种酒精混合后的纯酒精含量为40%．如果每种酒精都多取20克，混合后纯酒精的含量变为45%．求甲、乙两种酒精原有多少克？【例8】甲种酒精纯酒精含量为72%，乙种酒精纯酒精含量为58%，混合后纯酒精含量为62%．如果每种酒精取的数量比原来都多取15升，混合后纯酒精含量为63.25%．第一次混合时，甲、乙两种酒精均取了多少升？【巩固】甲、乙两只装满硫酸溶液的容器，甲容器中装有浓度为8%的硫酸溶液600千克，乙容器中装有浓度为40%的硫酸溶液400千克．均取多少千克分别放入对方容器中，才能使这两个容器中的硫酸溶液的浓度一样？【例9】某班有学生48人，女生占全班的37.5％，后来又转来女生若干人，这时人数恰好是占全班人数的40％，问转来几名女生？【巩固】小明到商店买红、黑两种笔共66支．红笔每支定价5元，黑笔每支定价9元．由于买的数量较多，商店就给予优惠，红笔按定价85%付钱，黑笔按定价80%付钱，如果他付的钱比按定价少付了18%，那么他买了红笔多少支？【例10】有两包糖，第一包糖由奶糖和水果糖组成，其中14为奶糖；第二包糖由酥糖和水果糖组成，其中15为酥糖．将两包糖混合后，水果糖占78%，那么奶糖与酥糖的比例是________.【巩固】 某商品76件，出售给33位顾客，每位顾客最多买三件．如果买一件按原定价，买两件降价10%，买三件降价20%，最后结算，平均每件恰好按原定价的85%出售．那么买三件的顾客有多少人？三、综合运用各种方法解决多溶液、多次配比问题【例 11】 甲容器中有纯酒精11升，乙容器中有水15升，第一次将甲容器中的一部分纯酒精倒入乙容器，使酒精与水混合。

浓度问题【知识与方法】1、溶液、溶剂、溶质和浓度的关系如下：溶液＝溶质＋溶剂浓度＝溶质溶液溶液＝溶质浓度溶质＝溶液×浓度2、以盐水为例，盐溶解于水得到盐水。

其中盐叫溶质，水叫溶剂，盐水叫溶液，盐占盐水的百分比就是盐水的百分比浓度。

即溶质占溶液的百分比叫做百分比浓度，简称浓度。

浓度问题属于百分数应用题。

3、解决浓度问题常用方法：①抓不变量：一般情况下，浓度问题中溶质或溶剂是不变量；②方程法：对于浓度问题，采用方程来求解是简便、有效的方法。

【例题】1、在500克含糖8%的糖水中，加入10克糖和290克水后，现在糖水的含糖率是多少？2、有600克浓度为20%的盐水，现在要使盐水浓度变为15%，要加入多少克水？3、有10千克蘑菇，它们的含水量是99％，稍经晾晒，含水量下降到98％，晾晒后的蘑菇重多少千克?4、浓度为70％的酒精溶液500克与浓度为50％的酒精溶液300克混合后所得到的酒精溶液的浓度是多少？5、有一瓶浓度为30%的酒精300克，要使它的浓度降为20%，需要加入多少克浓度为8%的酒精？6、现有浓度为40%和15%的两种盐水，要配1200克浓度为25%的盐水，这两种盐水各需多少克？7、一容器内装有10升纯酒精，倒出2.5升后，用水加满，再倒出5升，再用水加满，这时容器内的酒精浓度是多少？8、一容器内有浓度为25％的糖水，若再加入20千克水，则糖水的浓度变为15％，问这个容器内原来含有糖多少千克？9、甲、乙两只装满硫酸溶液的容器，甲容器中装有浓度为8％的硫酸溶液600千克，乙容器中装有浓度为40％的硫酸溶液400千克。

各取多少千克分别放入对方容器中，才能使这两个容器中的硫酸溶液的浓度一样？10、在浓度为40％的酒精溶液中加入5千克水，浓度变为30％，再加入多少千克酒精，浓度变为50％？11、有甲、乙两个容器，分别装了若干纯酒精和水。

第一次将甲的21倒给乙，混合后再把乙的一半倒给甲。

这样再做一次后，甲中有22%的酒精溶液300克，问最初甲装（ ）克，乙装（ ）克。

［文档标题］浓度问题浓度问题与生活密切结合：糖水小升初常考：与初高中的物理化学学习紧密相关杯赛常考试题特点：紧扣生活实际变化多样，考察落点多样知识点集中，万变不离其宗溶液=溶质+溶剂浓度=溶质♦溶液X100%溶液=溶质♦浓度溶质=溶液X浓度十字交叉（非常重要）★★★★★基本公式：浓度=溶质。

溶"例1 一杯盐水的浓度是30%,含盐60克，这杯盐水有多少克？含水多少克?举一反三1、一种盐水含盐20%,这样的盐水150克中，盐有多少克，水有多少克?2、一种糖水的浓度是40%,这种糖水含水240克，这种糖水有多少克，含糖多少克？［文档标题］3、甲种盐水有120克含盐10%,乙种盐水有80克，将这两种盐水混合可以得到浓度为11%的盐水，乙种盐水的浓度是多少？例2⑴【稀释问题】要把30克含盐16%的盐水稀释成含盐1.5%的盐水，须加水多少克？（2）、【浓缩问题】要从含盐12.5%的盐水40千克中蒸去多少水分才能制出含盐20%的盐水？（3）、【加浓问题】有含盐8%的盐水40千克，要配制成含盐20%的盐水，须加盐多少千克？（4）【含水量问题】40吨葡萄在新疆测得含水量99%运抵南京后侧的含水量是98 %，问葡萄运抵南京后还剩几吨？举一反三1、浓度为25%的盐水120克，要稀释成浓度时10%的盐水，应该怎样做?［文档标题］2、有含盐4%的盐水60千克，要配制成含盐10%的盐水，须加盐多少千克?3、仓库运来含水量为90%的水果100千克，1星期后再测发现含水量降低了，变为80%,现在这批水果的总重量是多少千克？【配置问题】是指两种或两种以上的不同浓度的溶液混合配制成新溶液（成品）：十字交叉法。

例3配制硫酸含量为25%的硫酸溶液，需用硫酸含量为18%和46%的硫酸溶液的充数比是多少？如果18%的硫酸溶液有300克，那么46%的硫酸溶液有多少克？举一反三1、要配制15%的盐水240克，需要24%的甲种盐水和12%的乙种盐水各多少克?2、有浓度为20%的糖水30克，加入多少克含糖50%的糖水，可以混合成40%的糖水？3、有浓度为25%的糖水若干，再加入16克糖后，糖水的浓度为35%,问现在的糖水有多少克？［文档标题］例4(1)把含盐5%的食盐水与含盐8%的食盐水混合制成含盐6%的食盐水600克, 分别应取两种食盐水各多少千克？(2)在浓度为50%的硫酸溶液100千克中，再加入多少千克浓度为5%的硫酸溶液，就可以配制成浓度为25%的硫酸溶液？举一反三(1)有两种酒精，一种浓度是60%,另一种浓度为90%,现在要配制成浓度为70%的洒精300克，问：每种需各取多少克？(2)在浓度为20%的糖水中加入50克糖，浓度变为40%,再加入多少克水，溶液浓度变为25%?(3)有一些30%的糖水，加入一定量的水以后稀释成浓度是24%的糖水。

奥数专题-浓度问题
【题型概述】
%100⨯=
溶液质量
溶质质量溶液的浓度 【典型例题】
1、把20克糖放入80克水中进行溶解，溶解后的糖水浓度是多少？
2、小林将50克糖放进250克水中进行溶解，后来又加入了100克水，这时候糖水的浓度是多少？
【拓展提高】
3、将浓度是20%的酒精溶液100克与浓度30%的酒精溶液300克混合，混合后的酒精溶液浓度是多少？
【奥赛训练】
4、将浓度是15%的酒精溶液100克与浓度是24%的酒精溶液200克混合，混合后的酒精溶液浓度是多少？
【典型例题】
1、一种盐水的浓度是20%，加入800克水后，它的浓度变成12%，这种盐水溶液原来有多
少克？
2、一种糖水的浓度是25%，加入30克糖后，它的浓度变为15%，这种糖水溶液原来有多
少克？
3、要配置0.15%的氨水1000千克，需要向多少千克浓度为10%的氨水中加入多少千克的
水才能配成？
【拓展提高】
有一种浓度为8%的酒精溶液400克，要使酒精溶液的浓度变为12%，该怎么办？
【奥赛训练】
有含盐10%的盐水45千克，要变为含盐15%的盐水，需要加盐多少千克？。

小学奥数浓度问题综合版
浓度问题是小学奥数中的一个重要内容，它涉及到溶液的稀释和浓度的计算。

在解决浓度问题时，可以采用以下简单的策略：
1. 理解浓度的概念：
- 浓度是指溶液中溶质的含量与溶液总体积的比值。

- 通常用质量浓度、体积浓度或摩尔浓度来表示。

2. 浓度计算方法：
- 质量浓度（C）= 溶质质量（m）/ 溶液体积（V）
- 体积浓度（C）= 溶质体积（V1）/ 溶液体积（V2）
- 摩尔浓度（C）= 溶质物质的物质量（m）/ 溶液的体积（V）
3. 浓度问题例题：
- 例题1：已知某溶液的质量浓度为5 g/L，若要制备200 mL 的该浓度的溶液，需要多少质量的溶质？
- 例题2：已知某溶液的体积浓度为0.2 L/L，若要制备500 mL 的该浓度的溶液，需要多少体积的溶质？
- 例题3：已知某溶液的摩尔浓度为0.5 mol/L，若要制备250 mL 的该浓度的溶液，需要多少摩尔的溶质？
4. 解题步骤：
- 根据题目给出的浓度类型，选择相应的浓度计算公式。

- 将已知量代入公式中，计算所需的未知量。

通过以上简单的策略，我们可以解决小学奥数中的浓度问题。

在解题过程中，我们需要牢记浓度的定义和计算方法，根据题目要求选择合适的计算公式，将已知量代入解方程，最终求得未知量的值。

请注意，这份综合版的文档旨在提供浓度问题的基本概念和解题思路，具体的例子和计算过程可根据实际题目进行深入学习和探讨。

祝愿你在小学奥数中取得好成绩！。