人工智能-五子棋算法研究
- 格式:pdf
- 大小:531.55 KB
- 文档页数:11

人工智能五子棋论文本文将这些技术用于五子棋中。
设计了一个智能五子棋系统,实现人和计算机两方进行博弈。
以下是店铺整理分享的关于人工智能五子棋论文的相关文章,欢迎阅读!人工智能五子棋论文篇一智能五子棋博弈算法研究摘要:人工智能是一门正在迅速发展的新兴的综合性很强的边缘科学。
博弈是人工智能的主要研究领域之一,他涉及人工智能中的推理技术、搜索方法和决策规划。
本文将这些技术用于五子棋中。
设计了一个智能五子棋系统,实现人和计算机两方进行博弈。
关键词:五子棋人工智能搜索人工智能是一门综合性很强的边缘科学,它研究如何使计算机去做那些过去只能靠人的智力才能做的工作。
而博弈是人工智能研究的一个重要分支,它不仅存在于游戏、下棋之中,也存在于政治、经济、军事和生物竞争中。
五子棋是起源于中国古代的传统黑白棋种之一。
现代五子棋日文称之为“连珠”,英译为“Ren-ju”,英文称之为“Gobang”或“FIR”(Five in a Row的缩写),亦有“连五子”、“五子连”、“串珠”、“五目”、“五目碰”、“五格”等多种称谓。
与其他棋类相比,五子棋每一层搜索节点数量庞大,因此盘面预测的计算量是非常大的,比如对于五子棋的中盘走法中,如果要预测四步的局面数的话可以达到一百万。
本文是对五子棋算法的设计原理和实现方法进行探讨和研究,主要包括数据结构、搜索算法和优劣评价函数组成,主要的特点包括快速的数据结构设计实现、以及高效率的搜索算法和尽可能的模拟人类的智能。
1、棋局的数据结构表示我们知道五子棋的走法中有优先和禁手,如连四肯定是没有三四优先,而如果是黑方出现三三(包括“四、三、三”)、四四(包括“四、四、三”),而黑方只能以四三取胜,如果黑方走出禁手则是输;五连与禁手同时形成,先五为胜,等等的规矩。
但是电脑毕竟不是人类,可以类人但是却不可以自己思考,那么就需要给电脑一个它可以明白的评判标准。
下面,我列出基本的棋型优先顺序:造一个二<……<造四个二<冲三<……<冲两个二和一个三<冲双三<冲四<冲四三。


基于CNN的五子棋人工智能策略提取五子棋作为一种古老而又充满挑战的棋类游戏,在人工智能领域中一直是一个重要的研究方向。
为了提高五子棋人工智能的水平,许多学者和研究人员使用了各种不同的方法和策略。
而基于卷积神经网络(Convolutional Neural Network,CNN)的五子棋人工智能策略提取是近年来备受关注的一种研究方法。
CNN是一种深度学习模型,它通过模仿人脑视觉处理的方式,能够自动提取图像中的特征,并在此基础上进行分类或回归等任务。
在五子棋中,CNN能够通过学习大量的棋局数据,提取关键的棋盘特征,从而辅助决策和制定策略。
首先,利用CNN进行五子棋人工智能策略提取的第一步是构建棋局数据集。
这个数据集应该包含大量的棋局样本,每个样本包括了当前棋盘状态以及接下来的最佳走法。
构建数据集的关键在于获取足够多、多样化的棋局数据,以确保CNN能够在训练过程中获得充分的信息。
接下来,利用构建好的数据集,我们可以开始训练CNN模型。
在训练过程中,CNN模型通过学习大量的棋局数据,逐渐调整自己的参数,以提取最重要的特征。
这些特征可以是关于棋盘局势、落子规律、连珠形态等方面的信息。
通过不断迭代训练,CNN能够逐渐提高自己对于五子棋局势的理解能力,并从中总结出一定的策略规律。
一旦训练完成,我们就可以将训练好的CNN模型应用到实际的五子棋对弈中。
在对弈过程中,模型通过输入当前的棋盘状态,利用已经学到的特征提取能力,预测接下来的最佳走法。
这样,我们就能够借助人工智能的力量,提高自己的棋局判断和决策能力。
基于CNN的五子棋人工智能策略提取方法相较于传统的基于规则的方法,在一些复杂的局面下能够展现出更出色的表现。
传统的基于规则的方法需要事先编写大量的规则,来判断局势和制定策略。
而CNN方法则直接从数据中学习局势和策略,并且具有较强的泛化能力,可以适应更广泛的局面变化。
这使得基于CNN的五子棋人工智能策略提取方法在实践中具有更大的应用潜力。

题目:智能五子棋游戏一、实验目的理解和掌握博弈树的启发式搜索过程和α-β减枝技术,能够用某种程序语言开发一个五子棋博弈游戏。
二、实验要求(1)设计一个15行15列棋盘,要求自行给出估价函数,按极大极小搜索方法,并采用α-β减枝技术。
(2)采用人机对弈方式,对弈双方设置不用颜色的棋子,一方走完后,等待对方走步,对弈过程的每个棋局都在屏幕上显示出来。
当某一方在横、竖或斜方向上先有5个棋子连成一线时,该方为赢。
(3)提交一篇实验论文,以及完整的软件(包括源程序和可可执行程序)和相关文档。
三、实验原理①估价函数的设计:下子后,求在该点的所有8个方向上4格之内的所有的没有阻隔的白子的和加上没有阻隔的黑子的数目之和,和为估价函数的值。
直观来说就是,如果在该点下子后连成同颜色的棋子越多,该点的估价值越大,同时阻挡另一种颜色的棋子越多,估价值也越大。
②判断是否有一方胜出:设计is_win函数,在每一次下子后检查是否是终局(一方胜出或者棋盘下满和局)。
对于棋盘上每一个已经下了棋子的点,检查其4个方向上是否有连续5颗同颜色的棋子,若有,则有一方胜出。
③寻找候选点,用于建立博弈树:对于棋盘上每一个还没有下子的点,测试其附近8个点是否已经下了棋子,若有,把该点加入候选点。
④搜寻最佳着点:根据候选点建立3层的博弈树,再利用估价函数对节点进行比较,得出最佳着点。
四、代码人主要代码public void refreshMax(int n){switch(n){case 1:{ //更新预测棋盘1最大值及其坐标maxValue1=0;number1=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard1[i][j]>maxValue1){maxX1.clear();maxY1.clear();maxX1.add(i);maxY1.add(j);number1=1;}else if(preBoard1[i][j]==maxValue1){maxX1.add(i);maxY1.add(j);number1++;}}}break;}case 2:{ //更新预测棋盘2最大值及其坐标maxValue2=0;number2=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard2[i][j]>maxValue2){maxX2.clear();maxY2.clear();maxX2.add(i);maxY2.add(j);number2=1;}else if(preBoard2[i][j]==maxValue2){maxX2.add(i);maxY2.add(j);number2++;}}}break;}case 3:{ //更新预测棋盘3最大值及其坐标maxValue3=0;number3=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard3[i][j]>maxValue3){maxX3.clear();maxY3.clear();maxX3.add(i);maxY3.add(j);number3=1;}else if(preBoard3[i][j]==maxValue3){maxX3.add(i);maxY3.add(j);number3++;}}}break;}case 4:{ //更新预测棋盘4最大值及其坐标maxValue4=0;number4=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard4[i][j]>maxValue4){maxX4.clear();maxY4.clear();maxX4.add(i);maxY4.add(j);number4=1;}else if(preBoard4[i][j]==maxValue4){maxX4.add(i);maxY4.add(j);number4++;}}}break;}case 5:{ //更新预测棋盘5最大值及其坐标maxValue5=0;number5=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard5[i][j]>maxValue5){maxX5.clear();maxY5.clear();maxX5.add(i);maxY5.add(j);number5=1;}else if(preBoard5[i][j]==maxValue5){maxX5.add(i);maxY5.add(j);number5++;}}}break;}case 6:{ //更新预测棋盘6最大值及其坐标maxValue6=0;number6=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard6[i][j]>maxValue6){maxX6.clear();maxY6.clear();maxX6.add(i);maxY6.add(j);number6=1;}else if(preBoard6[i][j]==maxValue6){maxX6.add(i);maxY6.add(j);number6++;}}}break;}case 7:{ //更新预测棋盘7最大值及其坐标maxValue7=0;number7=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard7[i][j]>maxValue7){maxX7.clear();maxY7.clear();maxX7.add(i);maxY7.add(j);number7=1;}else if(preBoard7[i][j]==maxValue7){maxX7.add(i);maxY7.add(j);number7++;}}}break;}}}AI主要代码public void refreshMax(int n){switch(n){maxValue1=0;number1=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard1[i][j]>maxValue1){maxValue1=preBoard1[i][j];maxX1.clear();maxY1.clear();maxX1.add(i);maxY1.add(j);number1=1;}else if(preBoard1[i][j]==maxValue1){maxX1.add(i);maxY1.add(j);number1++;}}}break;}maxValue2=0;number2=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard2[i][j]>maxValue2){maxValue2=preBoard2[i][j];maxX2.clear();maxY2.clear();maxX2.add(i);maxY2.add(j);number2=1;}else if(preBoard2[i][j]==maxValue2){maxX2.add(i);maxY2.add(j);number2++;}}}break;}maxValue3=0;number3=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard3[i][j]>maxValue3){maxValue3=preBoard3[i][j];maxX3.clear();maxY3.clear();maxX3.add(i);maxY3.add(j);number3=1;}else if(preBoard3[i][j]==maxValue3){maxX3.add(i);maxY3.add(j);number3++;}}}break;}maxValue4=0;number4=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard4[i][j]>maxValue4){maxValue4=preBoard4[i][j];maxX4.clear();maxY4.clear();maxX4.add(i);maxY4.add(j);number4=1;}else if(preBoard4[i][j]==maxValue4){maxX4.add(i);maxY4.add(j);number4++;}}}break;}maxValue5=0;number5=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard5[i][j]>maxValue5){maxValue5=preBoard5[i][j];maxX5.clear();maxY5.clear();maxX5.add(i);maxY5.add(j);number5=1;}else if(preBoard5[i][j]==maxValue5){maxX5.add(i);maxY5.add(j);number5++;}}}break;}maxValue6=0;number6=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard6[i][j]>maxValue6){maxValue6=preBoard6[i][j];maxX6.clear();maxY6.clear();maxX6.add(i);maxY6.add(j);number6=1;}else if(preBoard6[i][j]==maxValue6){maxX6.add(i);maxY6.add(j);number6++;}}}break;}maxValue7=0;number7=0;for(int i=0;i<size;i++){for(int j=0;j<size;j++){if(preBoard7[i][j]>maxValue7){maxValue7=preBoard7[i][j];maxX7.clear();maxY7.clear();maxX7.add(i);maxY7.add(j);number7=1;}else if(preBoard7[i][j]==maxValue7){maxX7.add(i);maxY7.add(j);number7++;}}}break;}}}五、感想通过这个试验,我对估价函数,极大极小搜索方法,α-β减枝技术有了更全面的认识,对它们的运用也更加熟练。
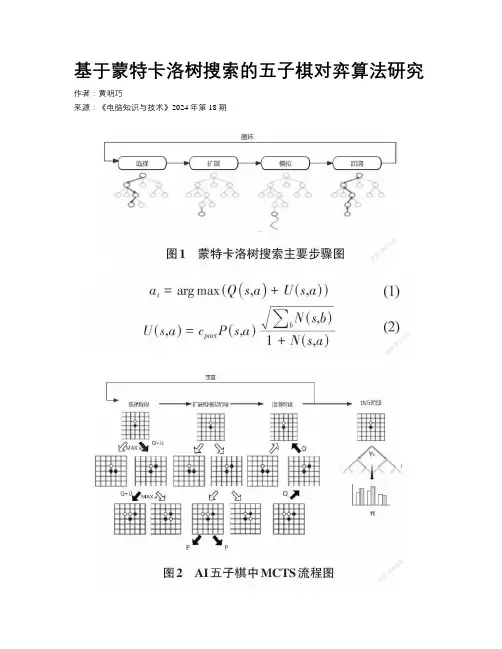
基于蒙特卡洛树搜索的五子棋对弈算法研究作者:***来源:《电脑知识与技术》2024年第18期关键词:蒙特卡洛树搜索;策略价值网络;强化学习;五子棋;计算机博弈中图分类号:TP389.1 文献标识码:A文章编号:1009-3044(2024)18-0015-040 引言人工智能(Artificial Intelligence,简称AI)作为一门多领域交叉的学科,不仅对人类社会产生了深远的影响,同时也成为现代科学技术发展的重要方向之一。
随着计算机算力的不断提高和机器学习技术的迅猛发展,AI在各个领域展现出了惊人的应用能力。
其中,游戏博弈问题一直是人工智能研究的重要方向,各种经典游戏的AI算法发展也得到了广泛的关注和研究。
游戏博弈问题是在多方参与、基于策略决策的情境中,通过制定合理的行动策略来获取最优结果的一类问题。
其研究核心是如何利用计算机在合理的时间内搜索到最佳策略,并将其应用于实际的游戏过程中[1]。
AI在棋类游戏领域的研究颇具代表性,其中五子棋作为一种简单却又具有一定复杂性的游戏,一直是AI研究者关注的对象之一。
通过研究五子棋的AI 算法,可以深入分析游戏规则,从而提高AI在其他复杂博弈问题上的应用能力。
蒙特卡洛树搜索(Monte Carlo Tree Search,简称MCTS)是近年来在游戏博弈问题中备受瞩目的一种基于模拟的搜索算法。
相較于传统的搜索方法,MCTS不依赖于先验信息,通过建立搜索树并通过模拟对树节点进行扩展和评估,从而找到最佳路径。
由于其强大的扩展能力和对不完全信息的适应性,MCTS在各种博弈游戏中都取得了较好的效果,成为当前五子棋AI算法的主要研究方法之一。
1 相关工作与技术背景1.1 传统游戏算法及其局限性传统的游戏算法主要采用搜索树或博弈树的方法来解决游戏博弈问题。
其中,最简单的是枚举法,即将所有可能的下法都进行尝试,并选择能够获得最优结果的下法。
然而,随着游戏状态的复杂度增加,枚举法需要耗费大量的计算资源和时间。

五子棋人工智能算法设计与实现一、引言五子棋,作为一种古老而又广泛流行的棋类游戏,一直以来都备受人们的喜爱。
它不仅考验玩家的智力和思维能力,同时也是人工智能算法在博弈领域中的经典案例之一。
本文将重点探讨五子棋人工智能算法的设计与实现,通过对五子棋的规则和特性的分析,提出一种基于博弈树查找的算法,并进行相应的试验,来验证这一算法在五子棋中的有效性。
二、五子棋的规则和特性五子棋是一种双人对弈的棋类游戏。
目标是在一个15x15的棋盘上,以先连成五子的玩家为成功。
每个玩家交替下子,只能在无子的位置下子,棋子只能放在网格交叉点上。
在五子棋中,我们需要思量如下几个规则和特性:1. 规模较小:相较于国际象棋等游戏,五子棋的规模较小,棋盘上只有225个空位,而且在早期阶段每个空位都有浩繁可供选择的位置。
2. 复杂度高:尽管规模小,但五子棋的游戏复杂度分外高,奕棋的每一步对于后面的局势都会产生重要的影响。
3. 查找空间大:在五子棋中,游戏的可能走法分外多,依据计算,一个人的平均走法数可以达到10^170种。
基于以上特点,设计一个高效的五子棋人工智能算法是分外具有挑战性的。
三、五子棋人工智能算法的设计思路针对五子棋的规则和特性,我们提出了一种基于博弈树查找的算法,以实现人工智能在五子棋中的应用。
1. 构建博弈树:起首,我们需要构建五子棋的博弈树。
根节点表示当前局面,每个子节点表示每一步的奕棋位置。
我们假设每个玩家都做出最优的选择,通过递归的方式,构建一棵完整的博弈树。
2. 构建评估函数:为了对博弈树进行评估,我们需要设计一个评估函数来评估每个局面的优劣。
该函数可以依据棋盘上的棋子分布状况、连子数目以及棋子的位置等来计算得分,越高表示该局面越好。
3. Alpha-Beta剪枝:由于查找空间分外大,传统的博弈树查找算法效率较低。
为了提高查找效率,我们引入Alpha-Beta剪枝算法。
这一算法可以在查找过程中剪去一些不必要的分支,使查找过程更加高效。

基于人工智能的棋类游戏研究一、介绍随着人工智能技术的快速发展,越来越多的游戏开始利用人工智能技术进行改进和升级,特别是棋类游戏。
这些改进和升级使得游戏变得更加智能化,更有挑战性。
因此,基于人工智能的棋类游戏研究成为了游戏领域的一个热门话题。
二、基于人工智能的棋类游戏研究的应用1. 自动选择AI根据不同水平的用户对手的强度,系统会自动选择合适的 AI 模型进行对局。
2. 围棋AI围棋是一种极具挑战性的游戏,因为它没有固定的胜利策略。
人类棋手需要凭借自己的经验和直觉来进行棋局分析,而现代围棋 AI 靠的是神经网络和深度学习等技术。
3. 五子棋AI五子棋是一种相对比围棋更简单的棋类游戏。
因此,五子棋 AI 的研究相对较早。
五子棋 AI 通常使用蒙特卡罗树搜索来查找最佳着法。
三、现代棋类游戏中的AI技术1. 遗传算法(GA)遗传算法是一种基于自然遗传和进化理论的优化算法。
在棋类游戏中,遗传算法可以用来优化棋子的移动方式。
遗传算法可以自动地在多个不同的参数中寻找最佳解,从而使得机器的表现更加接近人类的表现。
2. 卷积神经网络(CNN)卷积神经网络主要用来识别图像。
在棋类游戏中,CNN 可以用来识别棋盘上的棋局,然后根据这些识别结果进行决策。
3. 深度学习在最近几年中,深度学习技术的发展为人工智能和游戏开发的领域带来了很多新的创新。
通过使用深度学习技术,开发者可以通过大量的数据来训练 AI 模型,在 AI 模型的表现方面做出了巨大的改进。
四、人工智能的棋类游戏研究的优点1. 更好的游戏体验使用人工智能技术的棋类游戏具有更高的难度和更高的挑战性,可以提供更好的游戏体验。
它可以与更多的人交流,考验你的智力和技巧。
2. 节省时间使用人工智能技术的棋类游戏可以自动计算和分配棋子的移动,这样可以节省时间,更快地完成游戏。
3. 获得更多的反馈使用人工智能技术的棋类游戏可以记录每一步,这样可以让人们获得更多的反馈,更好地完善游戏。

五子棋AI规则五子棋AI算法分析:制作五子棋的AI ,我们首先从五子棋的规则谈起,五子棋分为“有禁手”和"无禁手" 两种规则。
相对而言,“有禁手”的规则更为专业些,而“无禁手”的规则更为大众些,所以,这里我们以“无禁手”的规则制作五子棋游戏。
对于五子棋的AI 而言,主要的思路就是对棋盘上的棋子进行分析,记录自己与对手的棋型,进而对其进行判断,根据对自己更有利的原则,进行优先级分析,然后选定要下棋子的点,并对其进行赋值。
下面是五子棋的棋型的分类:1.五子:某一方形成五个相同颜色的棋子相连2.活四:形成四子相连,并且两端是都没有子的3.冲四:形成四子相连,并且有一端是有对方棋子或者是墙壁,而另一端是没有子的4.活三:形成三子相连,并且两端是都没有子的5.死三:形成三子相连,并且有一端是有对方棋子或者是墙壁,而另一端是没有子的6.活二:形成两子相连,并且两端是都没有子的7.死二:形成两子相连,并且有一端是有对方棋子或者是墙壁,而另一端是没有子的8.单子:一个棋子最后是对形成各种棋型进行一个评估,以方便于去对下子的位置做出最优的选择。
所以给落子的“点”相应的评分,去判断该点会形成什么样的棋型:1.五子:1002.活四:803.活三: 704.冲四: 605.死三:506.活二: 407.死二:308. 单子:0接下来就是对<自己的棋型>进行分析,然后对<对方的棋型>分析,进而对自己和对家进行总体的打分,得出自己应该是应该进行进攻还是防守。
(这是一个基本思路,具体在实现过程中在进行添加)高级AI 思索:将每个位置进行分析,假设AI落子在该位置,用以上打分规则为AI打分,并将得到的分数加一。
然后,假设玩家落子在该点,为玩家打分,然后将所有的分值汇总。
取最高分作为这个位置的估分,接下来就是取分数最高的位置下棋了。
“位置估分”,下棋的时候,既可以考虑到自己攻击对手,又能考虑到对对手的防御,可以说,很多时候可以顶上考虑两步的AI。

五子棋之人机对弈智能报告
五子棋是一种棋类游戏,古老而又受欢迎,被誉为“智力运动”。
目前,研究人员正在探索五子棋的人机对弈,并分析人机对弈的新技术和新
思想。
近年来,人工智能技术的发展,人工智能程序(AI)在五子棋比赛
中也占据了非常重要的地位,甚至比职业棋手更具优势。
本文将详细介绍
五子棋之人机对弈智能研究,展示人机对弈的新技术与新思想,并分析其
在策略技巧、数学模型分析和智能等技术应用方面的优势。
一、人机对弈的新技术与新思想
在五子棋中,新的技术与思想都为人机对弈带来了新的机遇和挑战。
首先,由于五子棋中的棋子数量有限,不需要考虑博弈树等极其复杂的计
算方法,因此可以采用较为简单的算法,避免过多的运算量。
其次,为了更好地模拟五子棋的复杂性,人机对弈研究者引入了多种
技术来改善AI的能力,如机器学习、数学评估模型和深度学习等。
例如,通过机器学习,人工智能程序可以从以往的游戏历史中学习更加有效的策略,以更快地获取结果。
此外,通过数学评估模型,AI可以根据实时的
棋面评估出每一步的最佳走法,并自动选择最优解,从而使游戏更加有趣。

五子棋人工智能权重估值算法一、五子棋介绍五子棋是中国古代的传统黑白棋种之一。
现代五子棋日文称之为“連珠”,英译为“Renju”,英文称之为“Gobang”或“FIR”(Five in a Row的缩写),亦有“连五子”、“五子连”、“串珠”、“五目”、“五目碰”、“五格”等多种称谓。
五子棋不仅能增强思维能力,提高智力,而且富含哲理,有助于修身养性。
五子棋既有现代休闲的明显特征“短、平、快”,又有古典哲学的高深学问“阴阳易理”;既有简单易学的特性,为人民群众所喜闻乐见,又有深奥的技巧和高水平的国际性比赛;它的棋文化源渊流长,具有东方的神秘和西方的直观;既有“场”的概念,亦有“点”的连接。
它是中西文化的交流点,是古今哲理的结晶。
黑白双方依次落子,任一方先在棋盘上形成横向、竖向、斜向的连续的相同颜色的五个(含五个以上)棋子的一方为胜。
这种规则适合初学的五子棋爱好者。
因为这种规则下黑棋胜算较大。
甚至已经有人证明在黑白双方都不出现错误的情况下,黑棋可以必胜。
所以一般要求连续玩两盘,即任一方执黑,执白各一次。
二、逻辑变量与常量逻辑变量与常量的分析如下:Public Const Five As Integer = 3000 '五子连线得分Public Const FFDL As Integer = 2900 '双活四得分Public Const FFSL As Integer = 2800 '活四成四得分Public Const FTDL As Integer = 2700 '活四活三得分Public Const FL As Integer = 2600 '单活四得分Public Const FFNL As Integer = 2500 '双成四得分Public Const FTSL As Integer = 2400 '成四活三得分Public Const TTDL As Integer = 2300 '双活三得分Public X%, Y% '水平与垂直坐标Public Xt%, Yt% '临时横纵坐标Public CountNum% '棋步总数记录变量Public Piece() As Integer ' 0表示空闲,1为玩家1,2为玩家2Public Piecet() As Integer '用于估值函数使用的临时数组Public GameOrNot As Boolean '是否游戏中Public Flag As Byte '行棋变量,表示该谁下棋,数值与棋子变量相同Public PieceRec() As Integer '定义棋步记录变量以记录所走棋步Public AIOrNot As Boolean '是否人机对战模式,人机对战则为TruePublic LBlock(4) As Boolean, RBlock(4) As Boolean '左堵右堵记录变量数组Public EmptyNumE(4) As Byte '定义空个数记录变量数组Public PieceNum(4) As Byte '定义棋子个数记录数组Public ScoreE(4) As Integer '定义得分数组Public ScoreS As Integer '定义得分记录空间变量Public FirstMove As Boolean '是否玩家先行注:以上声明均在模块中进行。

五子棋算法详解——解决方案之一这里讲述棋盘大小为10×10的人机对战五子棋实现方法,要看完整代码请看AS3做的五子棋1. 概述玩家每走一步,对于玩家和计算机,都根据获胜表对棋盘各个空棋位进行评分,每个位置的分数与下面这句话有关:该位置所在的每一种获胜组合中已经拥有的棋子数,然后对玩家和计算机产生的分数均衡,以判断计算机是进攻还是防守。
2. 数据结构10×10的数据,用来记录棋盘状态;两个获胜表([10][10][192]),也就是获胜组合,因为五个子一线则胜,不在一线上的五个子就不在一个组合中,对于10×10的棋盘获胜的组合有192种,下面将会详细说明,获胜表用来表示棋盘上的每个位置是否在玩家或计算机的获胜组合中;一个二维数组([2][192]),记录玩家与计算机在各种获胜组合中填入了多少棋子;两个10×10的数组,用来记录玩家与计算机在各个棋盘位置上的分数,分数高的将是计算机下一步的着法。
3. 计算获胜组合上图是一个10×10的五子棋棋盘,我们可以得出垂直方向上的获胜组合是10×6=60,同理,水平方向的获胜组合也是60,而两个倾斜方向上的获胜组合是(1+2+3+4+5)×2+6=36,即:60*2+36*2=192。
五子棋算法详解本文链接:/wwwanq/blog/item/66a9f4c5f390cdc338db497f.htm l4. 评分用两个数组存储每个棋位的分数,一个是计算机的,另一个是玩家的,表示该位置对于各方是最佳着法的肯定程度,对一个位置的评分就是:遍历该位置所在的每一种获胜组合,根据这个组合中已经拥有的己方棋子数1到4分别加不同分数,最后将这些所有的获胜组合所得出的分数相加就是该位置的分数,下图是对于黑方各棋位的评分(其中的1,2,3,4这几个值要根据实际需要来确定)。
5. 思路“五子棋”游戏的编程思路1、对棋盘上无子点进行分值评定,分值最高的点即为下一手棋的落点2、每一点有四个方向(横、竖、斜、斜)成五子可能,(4)3、每点在一个方向可以有五种呈五子排列形状(5)4、每点在每个方向有进攻和防守两个作用(2)5、具体量化确定如:每种情况,如:进攻:有1子(+1)、2子(+5)、三子(+25)防守:有1子(+1)、2子(+4)、三子(+16)(每次量化,如果五格中有对方子,该过程进攻分值为零,每次量化,如果五格中有己方子,该过程防守分值为零,)将每点的20次进攻和20次防守的分值相加,即为该点总分值按照这个思路编制的五子棋,有可能你自己都会输给机器当然,在具体编制过程时,还要考虑中心点分值稍高;已经有四子(对方和己方)的情况;六子情况;出界;对与最高分接近的点进行随机取点,以便程序具有随机性;以及已成五子等情况。
五子棋人工智能算法设计与实现五子棋是一种流行的策略游戏,玩家需要在一个15×15的棋盘上相互交替放置黑色和白色的棋子。
游戏的规则简单,但在实际游戏中,需要考虑到许多因素,例如棋盘的当前状态、对手的反应以及自己的策略,这使得五子棋成为一个很有挑战性的游戏。
在设计和实现一个五子棋算法时,需要考虑以下步骤:游戏状态表示:算法首先需要一个方法来表示当前的游戏状态。
这可以通过一个函数来完成,该函数接受当前棋盘上的所有棋子作为输入,并返回一个字符串或字节串表示当前游戏状态。
搜索算法:搜索算法是人工智能算法的核心,它需要找到一个好的落子位置。
常见的搜索算法有暴力搜索、极小化极大搜索(MinMax)算法以及A*搜索算法等。
在五子棋中,可以使用极小化极大搜索算法来找到一个好的落子位置。
评估函数:评估函数用于评估棋盘的当前状态以及每个可能落子的得分。
在五子棋中,评估函数需要考虑当前棋盘上的连珠、对手的威胁以及自己可能形成的威胁等因素。
剪枝:在极小化极大搜索算法中,可以使用剪枝来减少搜索的深度和广度。
通过剪枝,可以排除一些明显不好的落子位置,从而提高搜索效率。
玩家和电脑的落子:在实现算法时,需要编写一个函数来处理玩家和电脑的落子。
这个函数应该接受当前游戏状态和玩家选择的落子位置作为输入,然后更新棋盘状态并返回下一步棋盘状态和落子信息。
游戏结束条件:算法还需要检测游戏是否已经结束。
在五子棋中,当一方获胜时,游戏结束。
public class Gomoku {private static final int SIZE = 15;private int board = new int[SIZE][SIZE];private int heuristic = new int[SIZE][SIZE];public void init() {for (int i = 0; i < SIZE; i++) {for (int j = 0; j < SIZE; j++) {board[i][j] = 0;public int get(int x, int y) {return board[x][y];public void set(int x, int y, int player) {board[x][y] = player;}随着技术的飞速发展,高性能计算在各个领域的应用越来越广泛。
博弈问题—五子棋实验报告实验目的1.熟悉和掌握博弈搜索算法的原理2.了解并学会博弈搜索算法的实质和过程3.学会使用博弈搜索算法解决问题实验原理博弈,对策利害关系相反的双方按一定的规则行动,每一方都为使自己能在斗争中取胜。
诸如下棋、打牌等类型的竞争性智能活动,称为博弈石最简单的一种是“二人零和、全信息、非偶然”博弈。
博弈的实例有中国象棋、五子棋、国际象棋和围棋等。
要提高计算机的下棋水平,就要有效地把多种搜索算法组合起来,进而改进博弈树的搜索效率来找到一步好棋。
博弈是启发式搜索的一个重要应用领域,博弈的过程可以用一棵博弈搜索树表示,通过对博弈树进行搜索求取问题的解,搜索策略常采用α-β剪枝技术。
在深入研究α-β剪枝技术的基础上,结合五子棋游戏特征,设计了五成/双三、估值函数和α-β剪枝算法相结合的改进博弈树搜索算法,实现了人机智能对弈的五子棋游戏。
实验内容制作类似于如图所示五子棋系统实验程序。
实验条件1.Window NT/XP/7及以上的操作系统2.内存在512M以上3.CPU在奔腾II以上实验分析1.博弈搜索算法特点①博弈的初始格局是初始节点②在博弈树中,“或”节点和“与”节点是逐层交替出现的。
自己一方扩展的节点之间是“或”关系,对方扩展的节点之间是“与”关系。
双方轮流地扩展节点。
③所有自己一方获胜的终局都是本原问题,相应的节点是可解节点;所有使对方获胜的终局都认为是不可解节点。
实验效果图个人实验小结通过本次实验,我了解了博弈算法具体的解决问题的过程,熟悉和掌握博弈算法的原理、实质、过程,学会了使用博弈算法解决问题,通过学习博弈搜索算法,增强了我对于机器博弈能力的认识,实验过程中发现问题并解决问题,巩固了所学的知识,通过实验也提高了自己的编程和思维能力,收获很多。
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注)。
五子棋人机对战原理
五子棋人机对战原理:
五子棋人机对战是一种智能对弈方式,通过计算机程序模拟人类玩家与计算机AI进行对战。
其原理主要包括以下几个方面:
1. 搜索算法:计算机AI采用搜索算法来探索可能的游戏走法,并选择最优的下子位置。
常用的搜索算法包括博弈树搜索、α-β剪枝、蒙特卡洛树搜索等。
通过搜索算法,计算机可以预测对手的走法,并选择最有利的下一步。
2. 评估函数:评估函数是五子棋人机对战中非常重要的组成部分。
它根据当前棋局的特征和局势来评估棋局的好坏。
评估函数可以考虑棋子的位置、连子数、棋局的开放度、对手的威胁等因素。
计算机通过评估函数来选择最优的下子位置。
3. 模式库:人机对战中的模式库是一种存储了棋局模式和相应下子位置的数据库。
计算机可以通过模式库来快速判断当前棋局是否符合某个已知的胜利模式,并做出相应的决策。
模式库可以提高计算机的搜索效率,加快计算机下子的速度。
4. 前沿搜索:为了减小计算复杂度,常常采用前沿搜索方法。
即只保留搜索树上一定深度内的节点信息,而将其他未搜索的节点进行剪枝。
这样可以大大缩小搜索空间,提高计算效率。
综上所述,五子棋人机对战的原理主要包括搜索算法、评估函数、模式库和前沿搜索等。
通过这些技术,计算机可以模拟人类玩家的思考过程,选择最优的下子位置。
与人类对战时,计算机AI可以根据实时情况作出相应的调整,使得对战更有挑战性和趣味性。
《五子棋人工智能算法设计与实现》篇一一、引言五子棋是一款源于古代的智力游戏,它不仅要求玩家在逻辑和策略上有着敏锐的洞察力,而且要求对棋局有深入的理解。
近年来,随着人工智能技术的快速发展,五子棋的人工智能算法设计与实现成为了研究的热点。
本文将详细介绍五子棋人工智能算法的设计与实现过程。
二、五子棋游戏规则概述五子棋的规则相对简单,但策略性极强。
游戏的目标是在一个15×15的棋盘上,通过连接五个或更多相同颜色的棋子来获得胜利。
玩家轮流下棋,每一轮可以选择行或列中的空白位置进行下棋。
当某一玩家下出的棋子与已存在的棋子连接成五子连线时,该玩家获胜。
三、人工智能算法设计五子棋的人工智能算法设计主要包括状态表示、策略搜索和价值评估三个部分。
(一)状态表示状态表示是人工智能算法的基础。
在五子棋中,我们通过一个二维数组来表示当前的游戏状态,包括棋盘上的棋子布局、玩家状态等信息。
同时,我们还需要定义一些规则来约束棋盘上的操作,如禁止双三、禁止四三等。
(二)策略搜索策略搜索是人工智能算法的核心部分。
我们采用深度优先搜索和广度优先搜索相结合的策略进行搜索。
具体来说,我们首先使用广度优先搜索来寻找可能的下一步棋,然后使用深度优先搜索来评估每一步棋的价值。
在搜索过程中,我们还需要考虑一些剪枝策略来减少搜索空间,提高搜索效率。
(三)价值评估价值评估是衡量每一步棋对胜负影响的重要手段。
我们通过分析每一步棋对后续棋局的影响、对对手的威胁程度等因素来评估其价值。
同时,我们还需要考虑一些特殊情况,如禁手、活三等,以更准确地评估每一步棋的价值。
四、算法实现在实现五子棋人工智能算法时,我们采用了Python编程语言和深度学习框架TensorFlow。
具体实现步骤如下:(一)定义数据结构首先,我们需要定义一个类来表示五子棋的游戏状态和操作。
这个类包括一个二维数组来表示棋盘、一个列表来表示当前玩家的下一步操作等。
同时,我们还需要定义一些函数来处理输入和输出等操作。
《五子棋人工智能算法设计与实现》篇一一、引言五子棋是一款源自中国古代的经典策略游戏,近年来,随着人工智能技术的发展,其对战成为了众多算法挑战的对象。
本篇文章旨在阐述一个关于五子棋的人工智能算法的设计与实现过程。
我们将从算法设计思路、实现方法、性能评估等方面进行详细介绍。
二、算法设计思路五子棋算法的设计主要围绕棋局评估、策略选择和落子决策三个核心环节。
1. 棋局评估棋局评估是对棋局的整体评价。
我们需要通过一系列规则和算法来评估当前棋局对玩家的优势和劣势。
棋局评估需要综合考虑到各种可能的变化和风险,以及对手可能的反击和策略。
2. 策略选择策略选择是根据棋局评估结果,选择最优的行动方案。
这需要具备强大的学习和推理能力,能够根据历史数据和当前局面,预测未来可能的走势。
3. 落子决策落子决策是在策略选择的基础上,选择最佳的落子位置。
需要结合自身的知识和对对手的了解,以及棋局的复杂性,选择最佳的落子位置。
这需要综合考虑当前棋盘的状态、自身的局势、对手的动向等多个因素。
三、算法实现在五子棋算法的实现过程中,我们主要采用了深度学习、机器学习等技术。
1. 深度学习在棋局评估中的应用深度学习模型能够从大量数据中学习到五子棋的规则和策略。
通过构建深度神经网络,我们可以对当前棋局进行全面而准确的评估。
2. 机器学习在策略选择和落子决策中的应用机器学习模型能够根据历史数据和当前局面,预测未来可能的走势。
通过构建强化学习模型,我们可以让在不断试错中学习和改进自身的策略和决策。
四、性能评估为了验证五子棋算法的性能,我们进行了大量的测试和评估。
我们分别在不同的规则、不同的对手强度下进行了测试,包括与人类高手进行对战。
通过这些测试,我们发现我们的算法在大多数情况下都能取得较好的成绩,尤其在处理复杂局面时表现出了较高的能力和效率。
然而,我们的仍然存在一些不足之处,比如在面对复杂的对手时可能会陷入僵局或者做出不合理的决策。
为了解决这些问题,我们将继续改进算法和模型,进一步提高的性能和鲁棒性。
总的来说,要让电脑知道该在哪一点下子,就要根据盘面的形势,为每一可能落子的点计算其重要程度,也就是当这子落下后会形成什么棋型(如:“冲四”、“活三”等),然后通览全盘选出最重要的一点,这便是最基本的算法。
当然,仅靠当前盘面进行判定是远远不够的,这样下棋很轻易掉进玩家设下的陷阱,因为它没有考虑以后的变化。
所以在此基础上我们加入递归调用,即:在电脑中猜测出今后几步的各种走法,以便作出最佳选择,这也是我们下棋时常说的“想了几步”。
如此一来您的程序便具有一定的水平了。
什么?不信!过来试试吧!总体思路弄清之后,下面进行具体讨论:一:数据结构先来看看数据结构,我们需要哪些变量?首先得为整个棋盘建立一张表格用以记录棋子信息,我们使用一个15*15的二维数组Table[15][15] (15*15是五子棋棋盘的大小),数组的每一个元素对应棋盘上的一个交叉点,用…0‟表示空位、…1‟代表己方的子、…2‟代表对方的子;这张表也是今后分析的基础。
在此之后还要为电脑和玩家双方各建立一张棋型表Computer[15][15][4]和Player[15][15][4],用来存放棋型数据,就是刚才所说的重要程度,比如用…20‟代表“冲四”的点,用…15‟代表“活三”的点,那么在计算重要性时,就可以根据20>15得出前者比后者重要,下子时电脑便会自动选择“冲四”的点。
那为什么棋型表要使用三维数组呢?因为棋盘上的每一个点都可以与横、竖、左斜、右斜四个方向的棋子构成不同的棋型,所以一个点总共有4个记录;这样做的另一个好处是可以轻易判定出复合棋型,例如:假如同一点上有2个…15‟就是双三、有一个…15‟和一个…20‟就是四三。
怎么样!3个数组构成了程序的基本数据骨架,今后只要再加入一些辅助变量便可以应付自如了。
应该不会太难吧?OK!有了这么多有用的数据,我们就可以深入到程序的流程中去了。
二:程序流程我们主要讨论五子棋的核心算法,即:人工智能部分,而其他像图形显示、键盘鼠标控制等,因较为简单,所以就不作过多介绍了。
五子棋算法研究摘要:人工智能是一门正在迅速发展的新兴的综合性很强的边缘科学。
博弈是人工智能的主要研究领域之一,他涉及人工智能中的推理技术、搜索方法和决策规划。
本文将这些技术用于五子棋中。
设计了一个智能五子棋系统,实现人和计算机两方进行博弈。
关键词:五子棋,人工智能,搜索Gobang algorithm to researchCAI Jie Information and Computational Science, Grade 2003Directed by WANG Jian (Associate Professor)Abstract:Artificial intelligence is a newly-developed and highly comprehensive frontier science of rapid development.Gambling and chess is one of the major artificial intelligence research areas.It involves reasoning,decision—making and planning.These techniques are applied to the goban g.An intelligent gobang system is designed and realized in the game between human and compute r.Keywords: Gobang, Artificial intelligence, Search1绪论在人类文明发展的初期,人们便开始进行棋类博弈的游戏了。
在人工智能领域内,博弈是很重要的一个研究分支,很多实际问题可以在博弈的研究中得到解决,并且使计算机智能更加靠近人类智能。
电脑博弈是人工智能研究的一个方向,到了近50年前,随着电子计算机的诞生,科学家们开始通过电脑模拟人的智能逐步向人类智能发起挑战,香农(1950)与图灵(1953)提出了对棋类博弈程序的描述,随着电脑硬件和软件的高速发展,从1980开始,电脑博弈便开始逐渐大规模地向人的智能发起了挑战,到了1997年,IBM超级电脑Deeper Blue击败了当时国际象棋世界冠军卡斯帕罗夫,成为了人工智能挑战人类智能发展的一个重要旅程碑。
1.1 电脑五子棋简介五子棋是起源于中国古代的传统黑白棋种之一。
现代五子棋日文称之为“连珠”,英译为“Ren-ju”,英文称之为“Gobang”或“FIR”(Five in a Row的缩写),亦有“连五子”、“五子连”、“串珠”、“五目”、“五目碰”、“五格”等多种称谓。
五子棋不仅能增强思维能力,提高智力,而且变化多端,非常富有趣味性5和消遣性,因此为人民群众所喜闻乐见。
本文在研究博弈机器人系统过程中,对五子棋博弈算法进行了一些有效的研究,设计和实现一个人机对弈的五子棋程序。
五子棋属于黑白棋的一种,它的博弈树复杂度为1070,状态空间复杂度为10105。
因此盘面预测的计算量是非常大的,比如对于五子棋的中盘走法中,如果要预测四步的局面数的话可以达到一百万。
1.2设计思路总介绍本文是对五子棋算法的设计原理和实现方法进行探讨和研究,主要包括数据结构、搜索算法和优劣评价函数组成,主要的特点包括快速的数据结构设计实现、以及高效率的搜索算法和尽可能的模拟人类的智能。
1.3本文架构第一章将会阐述计算机博弈发展以及对电脑五子棋的介绍、电脑五子棋的状态空间复杂度以及文章架构。
第二章首先描述了电脑象棋表示的一些基本数据结构。
第三章将重点讲述博弈树的搜索方法,包括博弈树构建、各算法介绍、以及五子棋规则的实现,最后对整体搜索框架进行总结。
最后,第四章是全文的总结及展望。
2数据结构2.1 棋局的表示我们知道五子棋的走法中有优先和禁手,如连四肯定是没有三四优先,而如果是黑方出现三三(包括“四、三、三”)、四四(包括“四、四、三”),而黑方只能以四三取胜,如果黑方走出禁手则是输;五连与禁手同时形成,先五为胜,等等的规矩。
但是电脑毕竟不是人类,可以类人但是却不可以自己思考,那么就需要给电脑一个它可以明白的评判标准。
首先介绍一个五子棋中的常用术语:阳线:棋盘上可见的横纵直线。
阴线:棋盘上无实线连接的隐形斜线。
活3:由于一方走一着在无子交叉点上形成一个“活三”的局面,也就是在放一子就可行成4连了。
活4:在棋盘某一条阳线或阴线上有同色4子不间隔地紧紧相连,且在此4子两端延长线上各有一个无子的交叉点与此4子紧密相连。
冲四:除"活四"外的,再下一着棋便可形成五连,并且存在五连的可能性的局面。
由于篇幅有限不能将所有的规则讲完,只是提出了对讲算法有用的几点加以叙述。
如何让电脑知道该落子在哪一点呢,在这方面。
电脑要做得和人一样,判断棋盘上每一点的重要度。
比如冲四比冲强,冲三比造二强,遇到四三如果是对方的,堵死,如果是自己的,优先落子。
遇到双三,如果是黑棋,黑方输,如果是白棋,优先等级仅次于四三。
我们看到电脑在运算的时候,同种棋型在敌我双方的优先等级并不相同,由于禁手的缘故黑棋和白棋的处理也不相同。
同样是四三,如果是玩家的,则电脑不会冲自己的,而是先堵玩家的。
禁手的处理比较复杂,我们稍候讨论。
下面,我列出基本的棋型优先顺序:造一个二<……<造四个二<冲三<……<冲两个二和一个三<冲双三<冲四<冲四三。
之所以这么设置是由于五子棋的下法所致,只要构成5颗一线就赢了,所以说一条线上构成的越多那么就有优势,当然就是棋数越多,分越多。
那么为了让电脑明确的知道是不是应该落子,就给它一个标准:分值。
用程序语言表示:enum Value {FAILED=-99999,SKIP=20,LENG=10,TWO =100,THREE =1000, IF0UR =10000,FOUR =50000,SF0UR=70000,WIN=100000};如果某一点导致失败,则分值为FAILED,由于它足够小,所以无论任何棋型与它的组合都小于0,SKIP之所以给它20分,是为了避免电脑出现无棋可下的情况,LENG是有可能发生长连的点,这有可能导致禁手,TWO、THREE、FOUR、WIN 观名知意,TFOUR 和SFOUR分别是弱四和强四。
强四的点比普通的冲四重要的多,比如一个活四,意味着即将判出胜负。
弱四是为了提供更大的灵活。
也许有某种冲四并不一定比冲三重要,我在这里并没有使用,以后可以扩充。
3涉及算法3.1 五子棋搜索树种的极大极小搜索在五子棋乃至所有博弈类游戏的研究中[1-4],最理想的方法是让电脑不论在对手走那种棋路的时候都可以根据对手的走法来预测下一步,以至于使电脑立于不败之地,但是五子棋博弈树的复杂度为1070,状态空间的复杂度为10105,因此即使电脑的运算速度已经很快了,又有强有力的启发式搜索技术,但是要完成如此复杂的搜索也是不可取的。
这种情况下搜索深度可根据实际情况进行调整,从局部搜索树中选取一步最好的走步,等对方走步后再寻找下一步好棋,通过结果来判断以后的走法。
我们可以通过极大极小搜索方法来实现这种搜索策略。
为了使谈论更有条理性[5],将博弈的双方分别命名为MAX和MIN。
而搜索的任务是为MAX找最佳的移动。
假设MAX先移动(此时暂时不考虑五子棋的禁手等规则),然后2个博弈者轮流移动。
因此,深度为偶数的节点,对应于MAX下一步移动的位置,称为MAX 节点;深度为奇数的节点对应于MIN下一步移动的位置,称为MIN节点(博弈树的顶节点深度为0)。
k层包括深度为2k和2k+1的节点。
通常用层数表示博弈树的搜索深度。
他可以表示出向前预测的MAX和MIN交替运动的回合数。
对于复杂的博弈,博弈者必须认识到由于博弈树的复杂程度所以搜索到终点是不可能的(除了在博弈快结束时)。
所以,常采用在有限范围搜索方法,这里使用启发式搜索。
在启发式搜索的过程中,关键的一步是如何确定下一个要考察的节点,在确定节点时只要能充分利用与问题有关的信息,估计出节点的重要性,就能在搜索时选择重要性较高的节点,以利于博弈者以较快的速度求出最佳的棋步。
在这里我采用静态评估函数[6-13],用评估函数h(i)衡量每一个叶节点位置的“值”。
一个最佳首步可以由一个最小最大化过程产生。
假设轮到MAX从搜索树的叶节点中选取,他肯定选择拥有最大值的节点。
因此,MIN叶节点的一个MAX节点双亲的倒推值就等于叶节点的静态评估值中的最大值。
另一方面,MIN从叶节点中选取时,必然选取最小的节点(即最负的值)。
既然如此,MAX叶节点的MIN双亲节点被分配一个倒推值,他等于叶节点静态评估值的最小值。
在所有叶节点的父节点被赋予倒推值后,开始倒推另一层,假定MAX将选择有最大倒推值的MIN的后继节点,而MIN会选择有最小倒推值的MAX 后继节点。
继续逐层对节点评估,直到最后开始节点的后继者被赋予倒推值。
MAX将选择有最大倒推值的节点作为他的首步。
整个过程的有效性基于这样的假设。
用整个棋盘估值的函数h(n)为静态估值函数。
设想当前棋局S为轮到计算机方下棋(用方框表示),任选一空点作为计算机方的下棋位置(可有若干种选择),接着考虑在此情况下游戏者一方下棋的棋局(用圆圈表示);从某一个圆圈棋局出发,任选一空点作为游戏者一方的落子处(又有若干种选择)。
再次形成计算机方下棋的方框棋局;依此类推,这样可形成一棵以S为根结点的博弈树,该树以圆圈棋局为第2层子结点,以方框棋局为第3层子结点等等。
如果继续向前搜索,可形成多层子结点,现在以向前搜索3层子结点为例来说明极大极小值的过程。
对第3层子结点的某一棋局n ,求出其估计值h(n),假设有一博弈树已形成,如图1所示[2],h(n)的值由各结点旁的数值给出。
根据极小极大化分析法,先计算第3层子结点h(n)值,然后第2层子结点的估计值取他的各后继子结点的极小值,根结点的估计值取他的各子结点的极大值。
这个取得最大估计值的子结点即为从S 出发的计算机方的最佳落子方案。
棋盘上某一行、某一列或某一对角线为一路,这里使用的棋盘为19行19列,因此,行和列方向上共有19+19=38路;从左下到右上方向的对角线有37路,同样,从左上到右下方向的对角线也有37路。
但对于五子棋来说必须在一条直线上有连续五个棋子才能赢。
因此,在对角线上就可以减少8路。
所以,整个棋盘路的总数为:38+(37-8)+(37-8)=96路。
对某一棋局n [14-15],第i 路得分:h(i)=h t (i)-h m (i)[1]。
其中:h t (i)为计算机方在第i 路估计值得分,h m (i)为玩家一方在第i 路得分。