2019-2020年三年级数学 奥数讲座 几何图形的认知(下)
- 格式:doc
- 大小:168.50 KB
- 文档页数:14

本講知識點屬於幾何模組的第一講,屬於起步內容,難度並不大.要求學生認識各種基本平面圖形和立體圖形;瞭解簡單的幾何圖形簡拼和立體圖形展開;看懂立體圖形的示意圖,鍛煉一定的空間想像能力.幾何圖形的定義:1、幾何圖形主要分為點、線、面、體等,他們是構成中最基本的要素.(1)點:用筆在紙上畫一個點,可以畫大些,也可以畫小些.點在紙上占一個位置. (2)線段:沿著直尺把兩點用筆連起來,就能畫出一條線段.線段有兩個端點. (3)射線:從一點出發,沿著直尺畫出去,就能畫出一條射線.射線有一個端點,另一端延伸的很遠很遠,沒有盡頭.(4)直線:沿著直尺用筆可以畫出直線.直線沒有端點,可以向兩邊無限延伸(5)兩條直線相交: 兩條直線相交,只有一個交點.(6)兩條直線平行:兩條直線平行,沒有交點,無論延伸多遠都不相交.(7)角:角是由從一點引出的兩條射線構成的.這點叫角的頂點,射線叫點的邊.(8)角分為銳角、直角和鈍角三種:直角的兩邊互相垂直,三角板有一個角就是边边顶点知識點撥這樣的直角.教室裏天花板上的角都是直角.銳角比直角小,鈍角比直角大.(9)三角形:三角形有三條邊,三個角,三個頂點.(10)直角三角形:直角三角形是一種特殊的三角形,它有一個角是直角.它的三條邊中有兩條叫直角邊,一條叫斜邊.(11)等腰三角形:等腰三角形也是一種特殊的三角形,它有兩條邊一樣長(相等),相等的兩條邊叫”腰”,另外的一條邊叫”底”.(12)等腰直角三角形:等腰直角三角形既是直角三角形,又是等腰三角形.(13)等邊三角形:等邊三角形的三條邊一樣長(相等),三個角也一樣大(相等).(14)四邊形:四邊形有四條邊,內部有四個角. 直角锐角钝角顶角顶角边边角角角顶角边直角边斜边直角边腰腰底直角边直角边斜边腰腰底边边边角角角(15)長方形:長方形的兩組對邊分別平行且相等,四個角也都是直角.(16)正方形:正方形的四條邊都相等,四個角都是直角.(17)平行四邊形:平行四邊形的兩組對邊分別平行而且相等,兩組對角分別相等.(18)等腰梯形:等腰梯形是一種特殊的四邊形,它的上下兩邊平行,左右兩邊相等.平行的兩邊分別叫上底和下底,相等的兩邊叫腰.(19)菱形:菱形的四條邊都相等,對角分別相等.(20)圓:圓是個很美的圖形.圓中心的一點叫圓心,圓心到圓上一點的連線叫圓的半徑,過圓心連接圓上兩點的連線叫圓的直徑.直徑把圓分成相等的兩部分,每一部分都叫半圓.(21)扇形:(22)長方體:長方體有六個面,十二條棱,八個頂點.長方體的面一般是長方形,也可能有兩個面是正方形.互相垂直的三條棱分別叫做長方體的長、寬、高.腰腰下底上底半径直径半圆直径弧半径半径高宽长(23)正方體:正方體有六個面,十二條棱,八個頂點.正方體的每個面都是同樣大的正方形,所以它的十二條棱長都相等.(24)圓柱:圓柱的兩個底面是完全相同的圓.(25)圓錐:圓錐的底面是圓.(26)棱柱:這個棱柱的上下底面是三角形.它有三條互相平行的棱,叫三棱柱.底面底面(27)棱錐:這個棱錐的底面是四邊形.它有四條棱斜著立起來,所以叫四棱錐.底面(28)三棱錐:因為三棱錐有四個面,所以通常又叫”四面體”.三棱錐的每一個面都是三角形.(29)球體,簡稱球:球有球心,球心到球面上一點的連線叫球的半徑.模組一、幾何圖形的認識【考點】幾何圖形的認識【難度】1星【題型】填空【解析】此題中,各圓大小各異,不如按照從左到右的順序來數.共有25個圓圈.【答案】25個【例 2】下圖中哪些是三角形?哪些是長方形?哪些是平行四邊形?哪些是菱形?【考點】幾何圖形的認識【難度】3星【題型】解答【解析】三角形有2個:4和7;長方形有2個:1和2(正方形也屬於長方形);平行四邊形有4個:1、2、3、6(正方形、長方形、菱形也屬於長方形);菱形有2個:1和6(正方形也屬於菱形).【答案】三角形有2個:4和7;長方形有2個:1和2例題精講平行四邊形有4個:1、2、3、6菱形有2個:1和6【例 3】數一數,圖中共有多少個角?【考點】幾何圖形的認識【難度】2星【題型】解答【解析】銳角、直角各4個,共8個角.【答案】8個【例 4】長方形有四個角,剪掉一個角,還剩幾個角?【考點】幾何圖形的認識【難度】2星【題型】解答【解析】共有三種情況,如下圖,分別剩下5、4、3個角.【答案】3或4或5個有三種情況【例 5】如下圖,將正方形紙片由下往上對折,再由左向右對折,稱為完成一次操作.按上述規則完成五次操作以後,剪去所得小正方形的左下角.問:當展開這張正方形紙片後,共有多少個小洞孔?【考點】幾何圖形的認識【難度】2星【題型】解答【解析】對已經過五次操作且剪去左下角的紙片做一次反操作,得到的紙片有1個洞孔;再進行一次反操作,得到的紙片上有1×4=4個洞孔.按照這個方法繼續做反操作,我們發現規律:從第二次開始,每經過一次反操作,得到的紙片上的洞孔數是反操作前洞孔數的4倍.因此,在進行了五次反操作以後,紙片上的洞孔數應為1×4×4×44=256(個).【答案】256模組二、幾何圖形的簡單組合【例 6】一個等腰三角形的兩條邊的長度分別是3和4,那麼這個三角形的周長可能是多少?另外一個等腰三角形的兩條邊的長度分別是4和9,這個三角形的周長可能是多少?【考點】幾何圖形的簡單組合【難度】3星【題型】解答【解析】第一個三角形:如果腰為3,則周長為433=10++.++;如果腰為4,則周長為443=11第二個三角形:如果腰為4,此時44+<9,兩邊之和小於第三邊,無法構成三角形,假設不成立,舍;如果腰為9,則周長為994=22++.【答案】(1)10、11;(2)22【巩固】周長是12,各邊長都是整數的等腰三角形有幾種?長方形有幾種?【考點】幾何圖形的簡單組合【難度】3星【題型】解答【解析】根據三角形的兩邊之和大於第三邊的得到兩腰的和要大於6,並且為偶數,所以兩腰的和可以為8、10,有2種情況;長方形的長加寬為122=6÷,因為+++共有3種.6=15=24=33【答案】2、3【巩固】用7根長度都是1寸的火柴棍拼成了一個三角形.請問:這個三角形的三條邊長分別是多少?【考點】幾何圖形的簡單組合【難度】3星【題型】解答【解析】通過嘗試得到:3寸、3寸、1寸或3寸、2寸、2寸.【答案】3、3、1或3、2、2【例 7】有兩個相同的直角三角形紙片,三條邊分別為3釐米、4釐米、5釐米.不許折疊,用這兩個直角三角形可以拼成幾種平行四邊形?【考點】幾何圖形的簡單組合【難度】3星【題型】解答【解析】將邊長是3的邊重合,是一個平行四邊形,同理可以將邊長是4和5的重合,所以共有3種.【答案】3種【巩固】用兩個完全相同的、各邊長分別為5、12、13的直角三角形紙片,可以拼成多少種不同的平行四邊形?【考點】幾何圖形的簡單組合【難度】3星【題型】解答【解析】將邊長是5的邊重合,是一個平行四邊形,同理可以將邊長是12和13的重合,分別得到一個平行四邊形和一個長方形,因為長方形是特殊的平行四邊形,所以共有3種.【答案】3種【例 8】用12個邊長為1的小正方形拼一個大長方形,這個長方形的周長最短是多少?【考點】幾何圖形的簡單組合【難度】3星【題型】解答【解析】拼成的圖形長和寬最接近時,新的圖形周長最短.即新圖形邊長為3和4時,周長最短,為()+⨯342=14【答案】14【例 9】把一個正方形分割為三種面積不同的小正方形,並且小正方形的個數是8.如何分?【考點】幾何圖形的簡單組合【難度】4星【題型】解答【解析】如下圖所示.【答案】答案如圖【例 10】一個正方體的8個頂角被截去後,得到一個新的幾何體.這個新的幾何體有幾個面?幾個頂點?幾條棱?【考點】幾何圖形的簡單組合【難度】3星【題型】解答【解析】這個正方體的8個頂點被截去後,多了8個面,因此共有6+8=14個面;多了(3-1)×8=16個點,因此共有8+16=24個點;多了3×8條棱,因此共有12+3×8=36條棱.【答案】14個面,24個頂點、36條棱模組三、基本圖形的周長及面積計算【例 11】 一個正方形的面積和它的周長的數值相等,那麼這個正方形的邊長是__________【考點】基本圖形的周長及面積計算 【難度】1星 【題型】填空【關鍵字】希望杯,4年級,初賽, 16題【解析】 正方形的面積是邊長×邊長,而正方形的周長是邊長×4,由它們相等知邊長等於4。

小学奥数几何知识点讲解几何是数学的一个重要分支,主要研究空间形状、大小、相对位置等概念及其性质和关系。
在小学奥数竞赛中,几何是一个常见的考察内容。
下面我将为大家讲解一些小学奥数几何知识点,希望能够帮助大家更好地应对几何题目。
1.点、线、面的概念在几何中,点是没有大小和形状的,只有位置的概念。
线是由无数个点组成的,没有宽度、长度、厚度等,可以用箭头表示方向。
面是由无数个点和线组成的,是平面上的一个二维图形。
2.正方形、长方形、三角形正方形是一种四条边都相等且角都是直角的四边形,它拥有四条对称轴。
长方形是一种拥有两组相等的对边和四个直角的四边形,它有两条对称轴。
三角形是一种由三条边和三个角组成的图形。
3.圆和半圆圆是由等距离圆心的所有点组成的集合,圆心到圆上任意一点的距离都相等。
半圆是圆的一半,由圆周上的一个弧和两条半径组成。
4.平行线和垂直线平行线是在同一个平面内永远不会相交的两条直线。
垂直线是与另一条线段相交时,两条线段之间的角度为90度的线。
5.直角、锐角和钝角直角是一个角度为90度的角,锐角是小于90度的角,钝角是大于90度小于180度的角。
6.对称和中心对称对称是指两个物体在一些轴线上镜像重合的关系,中心对称是指一个图形可以通过一些点进行旋转180度后重合。
7.面积和周长面积是指一个二维图形所占的空间大小,通常用平方单位表示,如平方厘米、平方米等。
周长是指一个图形的边缘长度。
8.直角三角形和勾股定理直角三角形是一种其中一个角为90度的三角形。
勾股定理是指在直角三角形中,直角边的平方之和等于斜边的平方,即a²+b²=c²。
9.分数、比例和相似分数是表示一个整体被分成几等份的表达方式。
比例是指两个或多个数之间的等比关系。
相似是指两个图形有相同的形状,但是可能有不同的大小。
10.正多边形和不规则图形正多边形是指所有边和角都相等的多边形。
不规则图形是指边和角都不相等的图形。

年级三年级学科奥数版本通用版课程标题几何图形的认知(二)上一讲我们学习了平面几何图形的基础知识,这一讲我们继续深入地学习立体几何图形知识。
长方体:长方体有六个面,十二条棱,八个顶点。
长方体的面一般是长方形,也可能有两个面是正方形。
互相垂直的三条棱分别叫做长方体的长、宽、高。
正方体:正方体有六个面,十二条棱,八个顶点。
正方体的每个面都是同样大小的正方形,所以它的十二条棱长度都相等。
圆柱:圆柱的两个底面是完全相同的圆。
圆锥:圆锥的底面是圆。
棱柱:这个棱柱的上下底面是三角形。
它有三条互相平行的棱,所以叫三棱柱。
棱锥:这个棱锥的底面是四边形。
它有四条棱斜着立起来的,所以叫四棱锥。
三棱锥:因为三棱锥有四个面,所以通常又叫“四面体”。
三棱锥的每一个面都是三角形。
球体,(简称球):球有球心,球心到球面上任意一点的连线叫球的半径。
例1 数一数下图中有多少个正方体木块?分析与解:从下到上各层分别有3个、3个、1个,因此共有3+3+1=7个正方体木块。
例2将红、黄、蓝、白、黑、绿六种颜色分别涂在正方体的各个面上,每一个面只涂一种颜色。
如图所示,现用涂色方式完全一样的四块小正方体拼成了一个长方体。
试回答:每个小正方体中,红色面的对面涂的是什么色?黄色面的对面涂的是什么色?黑色面的对面涂的是什么色?分析与解:在能看见的9个面中,红色出现的次数最多。
观察图中最上面的一个正方体,由于红色和黑色、黄色相邻,所以红色面的对面不可能是黑、黄两色。
同理,由第二个正方体可知,红色面的对面不可能是白色;由第三个正方体知,红色面的对面不可能是蓝色。
所以红色面的对面只可能是绿色。
同理,黄色面的对面不可能是红色、黑色或白色,又已推知不可能是绿色,所以黄色面的对面只能是蓝色。
这样黑色面的对面就只可能是涂的白色了。
例3在一个正方体的8个顶点处分别截去8个顶角,得到一个新的几何体。
这个新几何体有几个面?几个顶点?几条棱?分析与解:这个正方体的8个顶点被截去后,多了8个面,因此共有6+8=14个面;多了(3-1)×8=16个点,因此共有8+16=24个点;多了3×8条棱,因此共有12+3×8=36条棱。

三年级奥数讲座(二)目录第一讲从数表中找规律第二讲从哥尼斯堡七桥问题谈起第三讲多笔画及应用问题第四讲最短路线问题第五讲归一问题第六讲平均数问题第七讲和倍问题第八讲差倍问题第九讲和差问题第十讲年龄问题第十一讲鸡兔同笼问题第十二讲盈亏问题第十三讲巧求周长第十四讲从数的二进制谈起第十五讲综合练习第一讲从数表中找规律在前面学习了数列找规律的基础上,这一讲将从数表的角度出发,继续研究数列的规律性。
例1 下图是按一定的规律排列的数学三角形,请你按规律填上空缺的数字.分析与解答这个数字三角形的每一行都是等差数列(第一行除外),因此,第5行中的括号内填20,第6行中的括号内填 24。
例2 用数字摆成下面的三角形,请你仔细观察后回答下面的问题:①这个三角阵的排列有何规律?②根据找出的规律写出三角阵的第6行、第7行。
③推断第20行的各数之和是多少?分析与解答①首先可以看出,这个三角阵的两边全由1组成;其次,这个三角阵中,第一行由1个数组成,第2行有两个数…第几行就由几个数组成;最后,也是最重要的一点是:三角阵中的每一个数(两边上的数1除外),都等于上一行中与它相邻的两数之和.如:2=1+1,3=2+1,4=3+1,6=3+3。
②根据由①得出的规律,可以发现,这个三角阵中第6行的数为1,5,10,10,5,1;第7行的数为1,6,15,20,15,6,1。
③要求第20行的各数之和,我们不妨先来看看开始的几行数。
至此,我们可以推断,第20行各数之和为219。
[本题中的数表就是著名的杨辉三角,这个数表在组合论中将得到广泛的应用]例3将自然数中的偶数2,4,6,8,10…按下表排成5列,问2000出现在哪一列?分析与解答方法1:考虑到数表中的数呈S形排列,我们不妨把每两行分为一组,每组8个数,则按照组中数字从小到大的顺序,它们所在的列分别为B、C、D、E、D、C、B、A.因此,我们只要考察2000是第几组中的第几个数就可以了,因为2000是自然数中的第1000个偶数,而1000÷8=125,即2000是第125组中的最后一个数,所以,2000位于数表中的第250行的A列。

2021年奥数专题专讲(三年级)
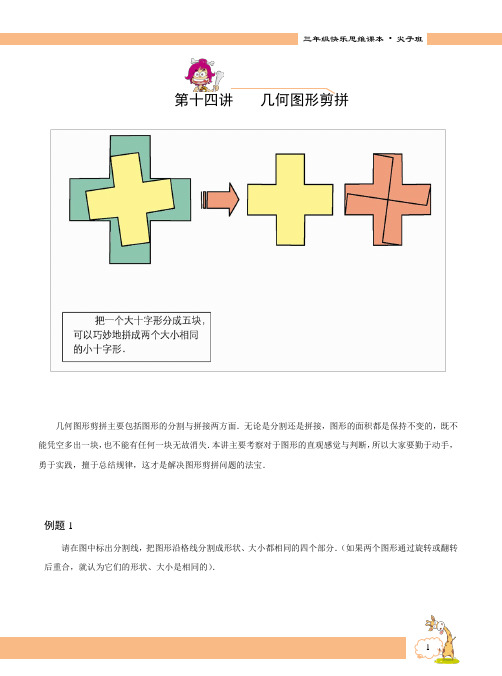
几何图形的认知
(★★★)
下图是一个由小正方体堆成的4×4×4的大正方体,小正方体相互紧挨着。
将该图
形外表面涂成红色,问:三面涂色,两面涂色,一面涂色以及没有涂色的小正方体
各多少个?
(★★★)
下图是一个由小正方体堆成的不规则立体图形,小正方体相互紧挨着。
将该图形外表面涂成红色,问:三面涂色的小正方体和四面涂色的小正方体各多少个?
(★★★)
有五颗相同的骰子放成一排(如下图),五颗骰子底面的点数之和是多少?
(★★★)
有两块六个面上分别写着1~6的相同的数字积木,摆放如下图。
在这两块积木中,相对两个面上的数字的乘积最小是多少?。
轴对称图形及三角形的分类(2)【教学目标】1、通过观察,动手操作,初步认识轴对称图形.2、在动手折和观察的过程中认识,找出对称轴.3、在活动中发展空间观念,发展观察能力和动手操作能力,学会欣赏数学的美.4、通过动手做三角形进一步认识三角形.5、能根据三角形边之间的关系将三角形进行第二种数学逻辑分类即“包含套餐型”分类,并能总结出:等腰三角形是特殊的三角形;等边三角形是特殊的等腰三角形.6、通过折叠,探索,初步体会等腰三角形、等边三角形的部分特征:等腰三角形有一条对称轴,它的两腰、两底角都相等;等边三角形有三条对称轴,它的三条边、三个角都相等.【教学重点】1、通过观察、动手操作,初步认识轴对称图形.2、等腰三角形、等边三角形的部分特征:等腰三角形有一条对称轴,它的两腰、两底角都相等。
等边三角形有三条对称轴。
它的三条边、三个角都相等.【教学难点】1、会找轴对称图形的对称轴.2、理解等腰三角形是特殊的三角形;等边三角形是特殊的等腰三角形.【复习巩固】1、口算:1660450090637420511032、分拆计算:答案:8006480046244800244824⨯=⨯=+= 7503250230275232502÷=÷=⋅⋅⋅⋅⋅⋅÷=⋅⋅⋅⋅⋅⋅8004200100425541190542261÷=÷=÷=⋅⋅⋅⋅⋅⋅÷=⋅⋅⋅⋅⋅⋅3、竖式计算(打*的要验算):30135= 16044⋅⋅⋅⋅⋅⋅ 7073⋅⋅⋅⋅⋅⋅60275 30135⨯ 160458024 530 30 24 20 470764245 42 45 42 3验算: 70763424234245⨯+=+=【教学过程】一、填空题:1、三角形中至少有( 2 )个锐角,等腰三角形有( 1 )条对称轴.2、三角形按角分可分为( 锐角 )三角形 ( 直角 )三角形,( 钝角 )三角形.3、一个三角形如果有3条对称轴,这个三角形一定是( 等边 )三角形.4、如果有6厘米,6厘米,12厘米三根小棒,( 不能 )把它们搭成一个三角形(填“能”或“不能”).5、正方形有( 4 )条对称轴,长方形有( 2 )条对称轴,圆有( 无数 )条对称轴. 二、选择题:1、在以下三角形中,( C )不是等腰三角形.A 、两条边相等的三角形;B 、三条边都相等的三角形;C 、三条边都不相等的三角形.2、一个等腰三角形的两边长分别是7厘米和5厘米,它的三边长的总和是( C ). A 、17; B 、19; C 、17或19.3、有4条对称轴的图形是( A ).A 、正方形;B 、长方形;C 、等边三角形;D 、等腰三角形.4、一个等边三角形可以分割成( D )个完全一样的等腰三角形. A 、2; B 、3; C 、5; D 、7.三、根据对称原理,画出图形的另一半:(1)(2)答案:四、动手画一画1、如图,把一个正方形分割成4个完全一样的等腰三角形.答案:2、如图,把1个等腰三角形分分割成形状、大小完全相同的2个三角形.【课题练习】一、填空题1、正方形有(4 )条对称轴,长方形有( 2 )条对称轴,圆有(无数)条对称轴.2、将一张正方形纸对角剪开。
第14讲几何图形的认知兴趣篇1、根据图中的几个图形的变化规律,在横线上画出适当的图形:2、如图,数一数,图中共有多少个角?3、如图,将一个边长为4厘米的正方形对折,再沿折线剪开,得到两个长方形。
请问:这两个长方形的周长之和比原来正方形的周长多几厘米?4、用12个边长为1的小正方形拼一个大长方形,这个长方形的周长最短是多少?5、用7根长度都是1寸的火柴棍拼成了一个三角形。
请问:这个三角形的三条边长分别是多少?6、有两个相同的直角三角形纸片,三条边分别为3厘米、4厘米和5厘米。
不许折叠,用这两个直角三角形可以拼成几种平行四边形?7、图中哪些是三角形?哪些是长方形?哪些是平行四边形?哪些是菱形?8、图中的金字塔和图中的正八面体各有几条棱,几个面?9、一个正方体的六个面上分别写着A、B、C、D、E、F六个字母。
请你根据图中的三种摆放情况,判断每个字母的对面是什么?10、如图,在一个正方体的表面上写着1至6这6个自然数,并且1对着4,2对着5,3对着6。
现在将正方体的一些棱剪开,使它的表面展开图如图所示。
如果只知道1和2所在的面,那么6应该在哪个面上(写出字母代号)?拓展篇1、如图,数一数,图中共有多少个直角?多少个锐角?多少个钝角?2、如图,数一数,图中共有多少个正方形?3、用两个完全相同的、各边长分别为5、12、13的直角三角形纸片,可以拼成多少种不同的(1)等腰三角形?(2)平行四边形?4、如图,有一张长方形纸片,长为2,宽为1,A点是长边上的中点。
沿着图中虚线将这张纸片剪成两块,再将这两块重新组合(不能重叠),可以拼成哪些你熟悉的图形?请将它们画出来。
5、如图,将正方形纸片沿对角线对折一次,得到一个等腰三角形;再对折一次,得到一个较小的三角形;最后,再对折一次,然后将所得的小等腰直角形用剪刀沿斜线上的高线剪开。
那么展开后,原来的正方形纸片一共被剪成了几片?都是什么图形?6、如图,用四个完全相同的边长分别为5、12、13的指教三角形拼成一个“风车”,求这个风车的周长。
2019-2020年三年级数学奥数讲座几何图形的认知(下)
8、请你在图8-10上画出3种与图8-9不一样的设计图,使它折起来后都成为图8-8所示的长方体盒子,其中的粗线与棱的交点均为棱的中点。
解答:
9、如图8-11所示,剪一块硬纸片可以做成一个多面体的纸模型(沿虚线折,沿实线粘)。
那么这个多面体的面数、顶点数和棱数的总和是多少?
解答:
这个多面体中间一段是六棱柱,上面和下面一样,都是由3个正方形和3个三角形相间斜立着,再由1个三角形连在一起
10、如图8-12,这是一个用若干块体积相同的小正方体粘成的模型。
把这个模型的表面(包括底面)都涂上红色,那么,把这个模型拆开以后,有3面涂上红色的小正方体比有2面涂上红色的小正方体多多少块?
解答:
3面红:1层有5×4=20(个),2层有4个,3层有4个,共20+4+4=28(个)
2面红:2层有3×4=12(个),3层有4个,共12+4=16(个)
3面红比2面红的多28-16=12(个)
此主题相关图片如下:
11、若干棱长为1的正方体拼成了一个11×11×11的大正方体,那么从一点望去,最多能看到多少个单位正方体?
解答:
12、有10个表面涂满红漆的正方体,其棱长分别为2,4,6,……,18,20。
若把这些正方体全部锯成棱长为1的小正方体,则在这些小正方体中,共有多少个至少是一面有漆的?
解答:
13、已知一个正方体木块能分割成若干个棱长为1厘米的小正方体木块,并且在这个大的正方体木块的5个面上涂上红色,把它分割成若干个棱长1厘米的小正方体木块后,有两面涂上红色的共有108块。
那么只有一面涂上红色的有多少块?
解答:
14、一条小虫沿长6分米,宽4分米,高5分米的长方体的棱爬行。
如果它只能进不能退,并且同一条棱不能爬两次,那么它最多能爬多少分米?
解答:
15、如图8-13,一个正四面体摆在桌面上,正对你的面ABC是红色,底面BCD是白色,右侧面ACD是蓝色,左侧面ABD是黄色。
先让四面体绕底面面对你的棱向你翻转,再让它绕底面右侧棱翻转,第三次绕底面面对你的棱向你翻转,第四次绕底面左侧的棱翻转,此后依次重复上述操作过程。
问:按规则完成第一百次操作后,面对你的面是什么颜色?
解答:
附送:
2019-2020年三年级数学奥数讲座加减法填空格
1、在图6-1算式的每个空格中,各填入一个合适的数字,使竖式成立。
解答:首先根据十位上8+5得到4可知,个位有一个进位,所以,个位的空格中必定是9;再根据百位上两个数相加,再加一个进位后得到9,并有进位可知,百位两个空格中都是9;结果中的千位只能是1,于是得到:
2、如图6-2,用0,1,2,3,4,5,6,7,8,9这10个数字各一次,可组成一个正确的加法竖式。
现已写出3个数字,那么这个算式的结果是多少?
解答:首先,结果中的千位为1;第二,百位上第一个数至少是7,最多是9;如为7,那么,结果中的百位为0,并十位要有进位;由此第一个数的十位可以填6,第二个数的个位填9;如为9,显然不行。
所以,结果只能是:
3、在如图6-3所示的算式中,3个加数的各位数字均是某两个相邻数字中的一个,那么这个算式的计算结果可能是多少?
解答:由计算结果的前两位得19可知,三个数的百位之和在17~19之间,因此,两个相邻数可能是5、6或6、7;但由个位计算结果为5可以确定只能是5、6;这样,十位进百位只有1,则三个数的百位均为6;那么,十位上有四种组合:5、5、5,5、5、6,5、6、6、,6、6、6,加上个位的进位后,结果就有6、7、8、9四种,所以,这个算式的计算结果可能是1965、1975、1985、1995。
4、在图6-4所示的算式中,被加数的数字和是和数的数字和的3倍。
问:被加数至少是多少?
解答:3的3倍是9,即被加数的数字和要为9;十位不能为0,最小1,则被加数最小为18。
5、在图6-5所示的算式里,4张小纸片各盖住了一个数字。
那么被盖住的4个数字总和是多少?
解答:个位得9,则个位没有进位,那么,四个数字之和即为十位数字之和与个位数字之和的总和。
所以,被盖住的4个数字总和是14+9=23。
6、在图6-6所示的算式中,每个方框代表一个数字。
问:这6个方框中的数字的总和是多少?
解答:两个三位数相加的和比2000小9,说明这两个数都大于990,这两个数的个位数字相加得11;所以,这6个方框中的数字的总和应该是9*4+11=47。
7、将1到9这9个数码分别填入图6-8的9个空格中,要求先填1,再在与1相邻(即左、右或上、下)的格中填2,再在与2相邻的空格中填3,依次类推,……,最后填9,使得加法算式成立。
解答:
8、在图6-9所示竖式的方框内填入4至9中的适当数字,使得第一个加数的各位数字互不相同,并且组成它的4个数字与组成第二个加数的4个数字相同,只是排列顺序不同。
解答:
9、图6-10是一个加减混合运算的竖式,在空格内填入适当数字使竖式成立。
解答:首先可以从两数相加所得的四位数着手,即前两位应该为1和0;由此可以推出第二个加数的百位为9;又第一个加数的十位也是9,第二个加数的个位也只能是9(要有进位);那么两数相加的结果也得出了:1090;下半部减法由个位开始,容易得出减数为995,结果位95。
10、在图6-11的方框内填入数字,使减法竖式成立。
解答:从个位开始逐个往前:减数个位是8,被减数十位为0,减数百位因为被减数被借了一位,所以是7,被减数千位为2。
11、在图6-12所示减法竖式的每个空格内填入一个数字,使算式成立。
解答:与上一题类似,从个位逐个往前可以推出:
12、图6-13是两个三位数相减的算式,每个方框代表一个数字。
问:这6个方框中的数字的连乘积等于多少?
解答:由百位得数为8可以确定只能是9-1=8,且十位不能向百位借位;这样十位只能是9-0=9,且个位不能向十位借位;而题目要求的是6个方框中的数字的连乘积,由于其中减数的十位所填为0。
那么,不论个位两个方框中填什么数,结果都为0。
13、用1至9这9个数字可以组成一个五位数和一个四位数,使得两数之差是54321,例如:56739-2418=54321,58692-4371=54321。
请你在图6-14中给出另外一个不同的答案。
解答:从结果为54321首先可以得出被减数的万位可以是5或者6,考虑题中已经举了两个是5的例子,所以我们不妨可以试一下是6的情形。
从千位看起:因为万位我们已经定位6,那么千位必定得借位,如果百位不向千位借位,则可以有11-7=4、12-8=4、13-9=4这三种情况;如为1、7,白位只能是8、5或9、5(十位向百位借位时),剩下的书法县两种情况都不行;如为2、8,百位可能是7、4或7、3,9、5(后两种为十位向百位借位时),7、4显然不行;7、3时,十位可以用1和9,那么,剩下5和4填在个位正好符合要求。
所以,另一个不同的答案可以是:62715-8394=54321。
14、在图6-15算式的各个方格内分别填入适当的数字,使其成为一个正确的等式,那么所填的7个数字之和最大可能是多少?
解答:首先,被减数的千位最大为4,个位两个数最大为9和7;为了使所填的数字尽可能大,十位应选用(1)5-9=6,百位则可以是(1)7-9=8,这样就成为:4859-997=3862,即所填的7个数字之和最大可以是4+8+5+9+9+9+7=51。