R语言时间序列作业

R语言常用上机命令分功能整理——时间序列分析为主第一讲应用实例•R的基本界面是一个交互式命令窗口，命令提示符是一个大于号，命令的结果马上显示在命令下面。

•S命令主要有两种形式：表达式或赋值运算（用’<－’或者’=’表示）。

在命令提示符后键入一个表达式表示计算此表达式并显示结果。

赋值运算把赋值号右边的值计算出来赋给左边的变量。

•可以用向上光标键来找回以前运行的命令再次运行或修改后再运行。

•S是区分大小写的，所以x和X是不同的名字。

我们用一些例子来看R软件的特点。

假设我们已经进入了R的交互式窗口。

如果没有打开的图形窗口，在R中，用：> x11() 可以打开一个作图窗口。

然后，输入以下语句：x1 = 0:100x2 = x1*2*pi/100y = sin(x2)plot(x2,y,type="l")这些语句可以绘制正弦曲线图。

其中，“=”是赋值运算符。

0:100表示一个从0到100 的等差数列向量。

第二个语句可以看出，我们可以对向量直接进行四则运算，计算得到的x2 是向量x1的所有元素乘以常数2*pi/100的结果。

从第三个语句可看到函数可以以向量为输入，并可以输出一个向量，结果向量y的每一个分量是自变量x2的每一个分量的正弦函数值。

plot(x2,y, type="l",main="画图练习",sub="好好练", xlab="x轴",ylab='y轴')有关作图命令plot的详细介绍可以在R中输入help(plot)数学函数abs，sqrt：绝对值，平方根 log, log10, log2 , exp：对数与指数函数 sin，cos，tan，asin，acos，atan，atan2：三角函数 sinh，cosh，tanh，asinh，acosh，atanh：双曲函数简单统计量sum, mean, var, sd, min, max, range, median, IQR（四分位间距）等为统计量，sort，order，rank与排序有关，其它还有ave，fivenum，mad，quantile，stem等。

时间序列分析R语言代码时间序列分解分析的R语言操作如下：选取R语言自带的数据包UKgas，即1960-1986每月英国天然气消耗的数据，并将其赋值于n：n<-UKgassummary（）函数提供了最小值、最大值、四分位数和数值型变量的均值： summary(n)画出UKgas的时序图：plot(n)时间序列分解分析方法一：基础包stats的decompose函数调用基础包stats：library("stats")利用基础包stats的decompose函数对时间序列进行分解分析，命名为fit1。

该函数基于移动平均方法，multiplicative表示使用乘法模型：fit1=decompose(n, type = c("multiplicative"))展示decompose函数的分解结果：fit1绘制方法一，即利用decompose函数分解的分解图：plot(fit1)`时间序列分解分析方法二：基础包stats的stl函数stl函数stl(x,s.window,s.degree=0,t.window = NULL, t.degree = 1, robust = FALSE,na.action = na.fail)x----待分解的变量s.window----提取季节性时的loess算法时间窗口宽度，可设为periodic，或者设为奇数并不能低于7s.degree -----提取季节性时局部拟合多项式的阶数，须为0或1 t.window----提取长期趋势性时的loess算法时间窗口宽度，缺省为NULL，或者奇数t.degree-----提取长期趋势性时的局部拟合多项式的阶数，须为0或1robust -----在loess过程中是否使用鲁棒拟合利用基础包stats的stl函数对时间序列进行分解分析，命名为fit2：fit2<-stl(n,s.window="periodic",s.degree = 0, t.window = NULL, t.degree = 1,robust= FALSE,na.action = na.fail)展示stl函数的分解结果：fit2绘制方法二的分解图： plot(fit2)。

时间序列分析第五章作业T1（p164第1题）：程序：rm(list=ls())# 清空工作环境P5T1data=read.table("C:\\Users\\DMXTC\\Documents\\SJXLZY_data\\E5_1.txt ",header=T)r5_1<-as.matrix(P5T1data$货运量)d5_1<-as.vector(t(r5_1))T5_1<-ts(d5_1,start=1949)# 绘制时序图par(mfrow=c(1,1))plot(T5_1,type = "o",col="blue",pch=13,main="表5-2时序图")diff_T5_1<-diff(T5_1)#1阶差分plot(diff_T5_1,type = "o",col="blue",pch=13,main="一阶差分后时序图")# ADF检验library(aTSA)adf.test(diff_T5_1)# 纯随机性检验for (k in 1:2)print(Box.test(diff_T5_1,lag=6*k))# 绘制自相关图和偏自相关图par(mfrow=c(1,2))acf(diff_T5_1)pacf(diff_T5_1)# x<-window(T5_1,start=1949,end = 1998)# test<-window(T5_1,start=1999)library(forecast)fit1<-Arima(T5_1,order=c(1,1,0),include.drift=T)fit1tsdiag(fit1)fore1<-forecast::forecast(fit1,h=5)fore1par(mfrow=c(1,1))plot(fore1,lty=2)lines(fore1$fitted,col=4)分析：首先我们绘制时序图如下：时序图显示该序列具有显著线性递增趋势，这是典型的非平稳序列特征，对该序列进行1阶差分，差分后时序图如下：差分后序列基本围绕在0值附近波动，已经没有明显的趋势特征，为进一步确定差分后序列的平稳性，对差分后的序列进行ADF检验，其检验结果显示如下：> adf.test(diff_T5_1)Augmented Dickey-Fuller Testalternative: stationaryType 1: no drift no trendlag ADF p.value[1,] 0 -3.24 0.0100[2,] 1 -2.78 0.0100[3,] 2 -1.95 0.0498Type 2: with drift no trendlag ADF p.value[1,] 0 -4.13 0.0100[2,] 1 -3.84 0.0100[3,] 2 -2.97 0.0462Type 3: with drift and trendlag ADF p.value[1,] 0 -4.69 0.0100[2,] 1 -4.46 0.0100[3,] 2 -3.63 0.0381----Note: in fact, p.value = 0.01 means p.value <= 0.01检验结果显示，该序列所有ADF检验统计量的P值均小于显著性水平（α=0.05），所以可以确定1阶差分后系列实现了平稳。

#例2.1绘制196 ------- 1999年中国年纱产量序列时序图(数据见附录1.2)Data1.2=read.csv("C:\\Users\\Administrator\\Desktop\\ 附录1.2.csv",header=T)#如果有标题，用T；没有标题用Fplot(Data1.2,type='o')#例2.1续tdat1.2=Data1.2[,2]a1.2=acf(tdat1.2)#例2.2绘制1962年1月至1975年12月平均每头奶牛产奶量序列时序图(数据见附录1.3)Data1.3=read.csv("C:\\Users\\Administrator\\Desktop\\ 附录 1.3.csv”,header=F)tdat1.3=as.vector(t(as.matrix(Data1.3)))[1:168]# 矩阵转置转向量plot(tdat1.3,type=T)#例2.2续acf(tdat1.3) #把字去掉pacf(tdat1.3)#例2.3绘制1949——1998年北京市每年最高气温序列时序图Data1.4=read.csv("C:\\Users\\Administrator\\Desktop\\ 附录 1.4.csv”,header=T)plot(Data1.4,type='o')##不会定义坐标轴#例2.3续tdat1.4=Data1.4[,2]a1.4=acf(tdat1.4)#例2.3续Box.test(tdat1.4,type="Ljung-Box”,lag=6)Box.test(tdat1.4,type="Ljung-Box”,lag=12)#例2.4随机产生1000个服从标准正态分布的白噪声序列观察值，并绘制时序图Data2.4=rnorm(1000,0,1)Data2.4plot(Data2.4,type=T)#例2.4续a2.4=acf(Data2.4)#例2.4续Box.test(Data2.4,type="Ljung-Box”,lag=6)Box.test(Data2.4,type="Ljung-Box”,lag=12)#例2.5对195 ——1998年北京市城乡居民定期储蓄所占比例序列的平稳性与纯随机性进行检验Data1.5=read.csv("C:\\Users\\Administrator\\Desktop\\ 附录 1.5.csv”,header=T)plot(Data1.5,type='o',xlim=c(1950,2010),ylim=c(60,100) )tdat1.5=Data1.5[,2]a1.5=acf(tdat1.5)#白噪声检验Box.test(tdat1.5,type="Ljung-Box”,lag=6)Box.test(tdat1.5,type="Ljung-Box”,lag=12)#例2.5续选择合适的ARMA模型拟合序列acf(tdat1.5)pacf(tdat1.5)#根据自相关系数图和偏自相关系数图可以判断为AR(1)模型#例2.5续P81 口径的求法在文档上#P83arima(tdat1.5,order=c(1,0,0),method="ML")# 极大似然估计ar1=arima(tdat1.5,order=c(1,0,0),method="ML") summary(ar1)ev=ar1$residualsacf(ev)pacf(ev)#参数的显著性检验t1=0.6914/0.0989p1=pt(t1,df=48,lower.tail=F)*2#ar1的显著性检验t2=81.5509/ 1.7453p2=pt(t2,df=48,lower.tail=F)*2#残差白噪声检验Box.test(ev,type="Ljung-Box”,lag=6,fitdf=1)Box.test(ev,type="Ljung-Box”,lag=12,fitdf=1)#例2.5续P94预测及置信区间predict(arima(tdat1.5,order=c(1,0,0)),n.ahead=5)tdat1.5.fore=predict(arima(tdat1.5,order=c(1,0,0)),n.ahea d=5)U=tdat1.5.fore$pred+1.96*tdat1.5.fore$seL=tdat1.5.fore$pred-1.96*tdat1.5.fore$seplot(c(tdat1.5,tdat1.5.fore$pred),type="l”,col=1:2)lines(U,co l=”blue”,lty=”dashed”)lines(L,col=”blue”,lty=”dashed”)#例3.1.1例3.5 例3.5续#方法一plot.ts(arima.sim(n=100,list(ar=0.8)))#方法二x0=runif(1)x=rep(0,1500)x[1]=0.8*x0+rnorm(1) for(i in 2:length(x)) {x[i]=0.8*x[i-1]+rnorm(1)} plot(x[1:100],type=T) acf(x)pacf(x)##拟合图没有画出来x[1]=x1x[2 ]=-x1-0.5*x0+rnorm(1)for(i in 3:length(x)){x[i]=-x[i-1]-0.5*x[i-2]+rnorm(1)} plot(x[1:100],type=T)acf(x)pacf(x)#例3.1.2x0=runif(1)x=rep(0,1500)x[1]=-1.1*x0+rnorm(1) for(i in 2:length(x)) #均值和方差smu=mean(x) svar=var(x){x[i]=-1.1*x[i-1]+rnorm(1)} plot(x[1:100],type=T) acf(x) pacf(x) #例3.2求平稳AR (1)模型的方差例3.3 mu=0 mvar=1/(1-0.8A2) #书上51 页#总体均值方差#例3.1.3方法一plot.ts(arima.sim(n=100,list(ar=c(1,-0.5)))) #方法二x0=runif(1)x1=runif(1)x=rep(0,1500)x[1]=x1x[2]=x1-0.5*x0+rnorm(1)for(i in 3:length(x)){x[i]=x[i-1]-0.5*x[i-2]+rnorm(1)}plot(x[1:100],type=T)acf(x)pacf(x) cat("population mean and var are”,c(mu,mvar),"\n")#样本均值方差cat("sample mean and var are”,c(mu,mvar),"\n")#例题3.4svar=(1+0.5)/((1-0.5)*(1-1-0.5)*(1+1-0.5))#例题3.6 MA模型自相关系数图截尾和偏自相关系数图拖尾#3.6.1法：x=arima.sim(n=1000,list(ma=-2))plot.ts(x,type='l')acf(x)#例3.1.4x0=runif(1)x1=runif(1)x=rep(0,1500)x[1]=x1x[2]=x1+0.5*x0+rnorm(1)for(i in 3:length(x)){x[i]=x[i-1]+0.5*x[i-2]+rnorm(1)} plot(x[1:100],type=T)acf(x)pacf(x) pacf(x)法二x=rep(0:1000)for(i in 1:1000){x[i]=rnorm[i]-2*rnorm[i-1]} plot(x,type=T)acf(x)pacf(x)#3.6.2法一：又一个式子x0=runif(1)x1=runif(1)x=rep(0,1500) x=arima.sim(n=1000,list(ma=-0.5)) plot.ts(x,type='l')acf(x)pacf(x)法二x=rep(0:1000)for(i in 1:1000){x[i]=rnorm[i]-0.5*rnorm[i-1]}plot(x,type='l')acf(x)pacf(x)##错误于rnorm[i]:类别为'closure'的对象不可以取子集#3.6.3法^:x=arima.sim(n=1000,list(ma=c(-4/5,16/25)))plot.ts(x,type=T)acf(x)pacf(x)法二:x=rep(0:1000)for(i in 1:1000) {x[i]=rnorm[i]-4/5*rnorm[i-1]+16/25*rnorm[i-2]} plot(x,type='l')acf(x)pacf(x)##错误于x[i] = rnorm[i] - 4/5 * rnorm[i - 1] + 16/25 * rnorm[i - 2] :##更换参数长度为零#例3.6续根据书上64页来判断#例3.7拟合ARMA ( 1，1)模型，x(t)-0.5x(t-1)=u(t)-0.8*(u-1)，并直观观察该模型自相关系数和偏自相关系数的拖尾性。

用R语言做时间序列分析时间序列（time series ）是一系列有序的数据。

通常是等时间间隔的采样数据。

如果不是等间隔，则一般会标注每个数据点的时间刻度。

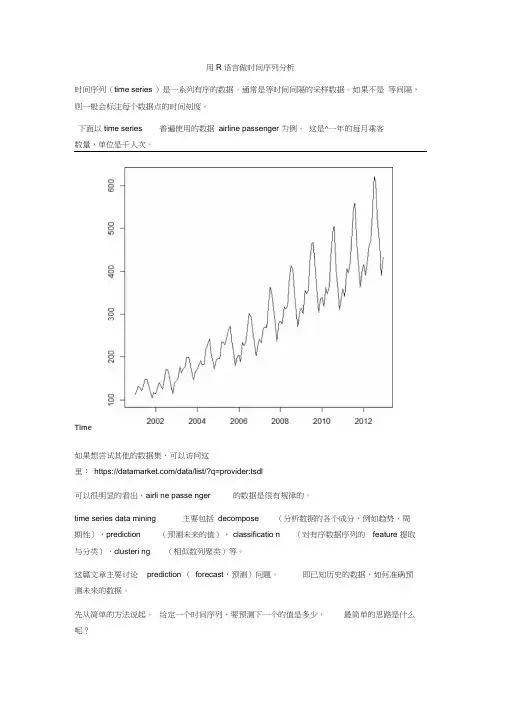
下面以time series 普遍使用的数据airline passenger 为例。

这是^一年的每月乘客数量，单位是千人次。

Time如果想尝试其他的数据集，可以访问这里：https:///data/list/?q=provider:tsdl可以很明显的看出，airli ne passe nger 的数据是很有规律的。

time series data mining 主要包括decompose （分析数据的各个成分，例如趋势，周期性），prediction （预测未来的值），classificatio n （对有序数据序列的feature 提取与分类），clusteri ng （相似数列聚类）等。

这篇文章主要讨论prediction （forecast，预测）问题。

即已知历史的数据，如何准确预测未来的数据。

先从简单的方法说起。

给定一个时间序列，要预测下一个的值是多少，最简单的思路是什么呢？（1）m ean （平均值）：未来值是历史值的平均。

（2）exponential smoothing （指数衰减）：当去平均值得时候，每个历史点的权值可以不一样。

最自然的就是越近的点赋予越大的权重。

= aX± + ct^X2 + a3X3+ …或者，更方便的写法，用变量头上加个尖角表示估计值X t+1 = aX t+ （1 - a）X t（3） sn aive :假设已知数据的周期，那么就用前一个周期对应的时刻作为下一个周期对应时刻的预测值（4）d rift :飘移，即用最后一个点的值加上数据的平均趋势tX t+h|t =禺+占2心-斗-丄= x t +占（罠-如Tt = •介绍完最简单的算法，下面开始介绍两个time series 里面最火的两个强大的算法：Holt-Winters 和ARIMA 。

⽤R语⾔实现奶⽜⽉产奶量的时间序列分析奶⽜⽉产奶量的时间序列分析本⽂应⽤R软件对奶⽜⽉产奶量建⽴时间序列模型并进⾏预测。

⽂章主要从以下⼏个⽅⾯进⾏：1.描述性统计2.模型识别3.参数估计4.模型诊断5.预测6.其他建模⽅法及效果对⽐7.结论最终通过多⽅⾯对⽐，我们选择了ARIMA(0,1,1)×(0,1,1)12模型⽤于以后数据的预测。

⼀、描述性统计1.1数据的选取本⽂引⽤的是Data Market中的时间序列数据“Monthly milk production: pounds per cow. Jan 62 –Dec 75”，包括从1962年1⽉到1975年12⽉共168个⽉度数据，单位为pounds/month。

数据如下：从中我们将62-74年,共156条数据作为训练集，75年的12个⽉数据作为测试集，⽤于最后评价模型预测效果的参考。

1.2数据的描述性统计变量统计表1-1数据类型最⼩值下四分数中位数均值上四分数最⼤值数值型数据553.0 677.8 761.0 754.7 824.5 969.0时间序列的分布图和时间序列的分解如下：时间序列分解图1-1由图可以看出，时间序列含有明显的季节性和上升趋势，且没有波动集群现象，可以考虑季节模型，最常⽤的是ARIMA模型。

1.3乘法季节模型乘法季节模型是随机季节模型与 ARIMA 模型的结合。

统计学上纯 RIMA （p，d， q ）模型记作：ΦΘ。

其中 t 代表时间，Xt 表⽰响应序列，B是后移算⼦， R=1-B，p、 d、 q 分别表⽰⾃回归阶数、差分阶数和移动平均阶数；Φ(B)表⽰⾃回归算⼦；Θ(B)表⽰滑动平均算⼦。

⼀个阶数为（P，d， q ）×（P， D， Q ） s 的乘积季节模型可表为：ΦΘ代表独⽴⼲扰项或随机误差项， s 的值是⼀个季节循环中观测的个数，atΦ表⽰同⼀周期内不同周期点的相关关系，则描述了不同周期中对应时点上的相关关系，⼆者结合起来便同时刻画了 2 个因数的作⽤。

如何使用R语言进行时间序列分析与预测标题：使用R语言进行时间序列分析与预测导言：时间序列分析是一种用于研究随时间变化的数据模式和趋势的方法。

它在许多领域中都有广泛的应用，包括经济学、金融学、气象学等。

R语言是一种功能强大的统计分析软件，它提供了许多用于时间序列分析和预测的函数和包。

本文将介绍如何使用R语言进行时间序列分析和预测的步骤和方法。

一、准备数据1. 收集时间序列数据：首先需要收集相关的时间序列数据，例如每天的销售量、股票价格等。

这些数据可以通过调查、采样或从公开数据源中获取。

2. 数据清洗：对收集到的数据进行清洗，包括去除异常值、缺失值和重复值等。

确保数据的完整性和准确性。

3. 建立时间索引：将数据转换为时间序列对象，并建立时间索引。

R语言中常用的时间序列对象包括ts、xts和zoo等。

二、时间序列分析1. 可视化分析：使用R语言中的绘图函数，如plot()和ggplot2包，将时间序列数据可视化。

可以观察数据的趋势、季节性和周期性。

2. 平稳性检验：检验时间序列数据是否平稳，即均值、方差和自协方差不随时间变化。

常用的平稳性检验方法有ADF检验和KPSS检验。

3. 建立模型：根据时间序列数据的特点选择合适的模型。

常用的时间序列模型包括ARIMA模型、指数平滑模型和ARCH/GARCH模型等。

4. 模型识别：对建立的模型进行参数估计，并进行模型识别。

使用R语言中的函数，如auto.arima()和ets()，自动选择最佳的模型。

5. 模型诊断：对建立的模型进行诊断，检验模型的拟合优度。

常用的模型诊断方法有残差分析、Ljung-Box检验和AIC准则等。

三、时间序列预测1. 预测模型：基于建立的时间序列模型，使用R语言中的forecast包，预测未来一段时间内的数值。

可以使用函数，如forecast()和predict()，进行预测。

2. 模型评估：对时间序列预测结果进行评估。

使用预测准确度指标，如均方根误差（RMSE）和平均绝对百分误差（MAPE），评估预测模型的准确性。

r语言实现时间序列之8种平稳化方法下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!R语言实现时间序列之8种平稳化方法一、介绍时间序列分析是统计学中重要的研究领域，平稳化是时间序列分析中的重要步骤之一。

使用R语言进行时间序列（arima，指数平滑）分析读时间序列数据您要分析时间序列数据的第一件事就是将其读入R，并绘制时间序列。

您可以使用scan（）函数将数据读入R，该函数假定连续时间点的数据位于包含一列的简单文本文件中。

数据集如下所示：••••••••••••••••Age of Death of Successive Kings of England#starting with William the Conqueror#Source: McNeill, "Interactive Data Analysis"604367505642506568436534...仅显示了文件的前几行。

前三行包含对数据的一些注释，当我们将数据读入R时我们想要忽略它。

我们可以通过使用scan（）函数的“skip”参数来使用它，它指定了多少行。

要忽略的文件顶部。

要将文件读入R，忽略前三行，我们键入：•••> kings[1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69 59 48[26] 59 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56在这种情况下，英国42位连续国王的死亡年龄已被读入变量“国王”。

一旦将时间序列数据读入R，下一步就是将数据存储在R中的时间序列对象中，这样就可以使用R的许多函数来分析时间序列数据。

要将数据存储在时间序列对象中，我们使用R中的ts（）函数。

例如，要将数据存储在变量'kings'中作为R中的时间序列对象，我们键入：••••••Time Series:Start = 1End = 42Frequency = 1[1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69 59 48[26] 59 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56有时，您所拥有的时间序列数据集可能是以不到一年的固定间隔收集的，例如，每月或每季度。

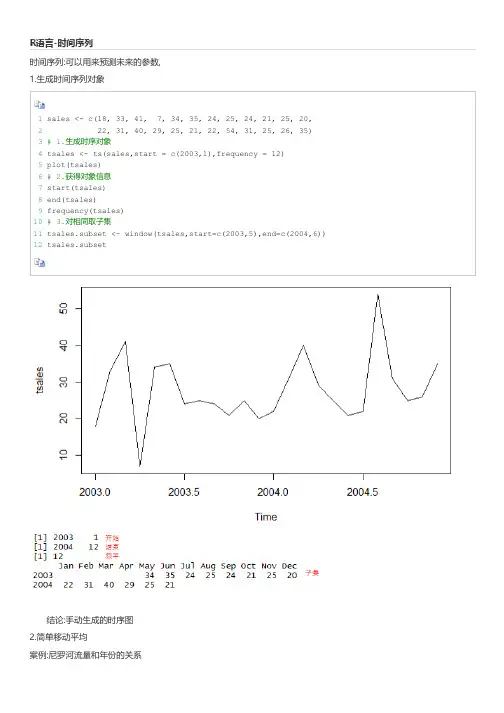
R语言-时间序列时间序列:可以用来预测未来的参数,1.生成时间序列对象1 sales <- c(18, 33, 41, 7, 34, 35, 24, 25, 24, 21, 25, 20,2 22, 31, 40, 29, 25, 21, 22, 54, 31, 25, 26, 35)3# 1.生成时序对象4 tsales <- ts(sales,start = c(2003,1),frequency = 12)5 plot(tsales)6# 2.获得对象信息7 start(tsales)8 end(tsales)9 frequency(tsales)10# 3.对相同取子集11 tsales.subset <- window(tsales,start=c(2003,5),end=c(2004,6))12 tsales.subset 结论:手动生成的时序图2.简单移动平均案例:尼罗河流量和年份的关系1 library(forecast)2 opar <- par(no.readonly = T)3 par(mfrow=c(2,2))4 ylim <- c(min(Nile),max(Nile))5 plot(Nile,main='Raw time series')6 plot(ma(Nile,3),main = 'Simple Moving Averages (k=3)',ylim = ylim)7 plot(ma(Nile,7),main = 'Simple Moving Averages (k=3)',ylim = ylim)8 plot(ma(Nile,15),main = 'Simple Moving Averages (k=3)',ylim = ylim)9 par(opar) 结论:随着K值的增大,图像越来越平滑我们需要找到最能反映规律的K值3.使用stl做季节性分解案例:Arirpassengers年份和乘客的关系1# 1.画出时间序列2 plot(AirPassengers)3 lAirpassengers <- log(AirPassengers)4 plot(lAirpassengers,ylab = 'log(Airpassengers)')5# 2.分解时间序列6 fit <- stl(lAirpassengers,s.window = 'period')7 plot(fit)8 fit$time.series9 par(mfrow=c(2,1))10# 3.月度图可视化11 monthplot(AirPassengers,xlab='',ylab='')12# 4.季度图可视化13 seasonplot(AirPassengers,bels = T,main = '') 原始图 对数变换 总体趋势图 月度季度图4.指数预测模型 4.1单指数平滑 案例:预测康涅狄格州的气温变化# 1.拟合模型fit2 <- ets(nhtemp,model = 'ANN')fit2# 2.向前预测forecast(fit2,1)plot(forecast(fit2,1),xlab = 'Year',ylab = expression(paste("Temperature (",degree*F,")",)),main="New Haven Annual Mean Temperature")# 3.得到准确的度量accuracy(fit2) 结论:浅灰色是80%的置信区间,深灰色是95%的置信区间 4.2有水平项,斜率和季节项的指数模型 案例:预测5个月的乘客流量1# 1.光滑参数2 fit3 <- ets(log(AirPassengers),model = 'AAA')3 accuracy(fit3)4# 2.未来值预测5 pred <- forecast(fit3,5)6 pred7 plot(pred,main='Forecast for air Travel',ylab = 'Log(Airpassengers)',xlab = 'Time') 8# 3.使用原始尺度预测9 pred$mean <- exp(pred$mean)10 pred$lower <- exp(pred$lower)11 pred$upper <- exp(pred$upper)12 p <- cbind(pred$mean,pred$lower,pred$upper)13 dimnames(p)[[2]] <- c('mean','Lo 80','Lo 95','Hi 80','Hi 95')14 p 结论:从表格中可知3月份的将会有509200乘客,95%的置信区间是[454900,570000] 4.3ets自动预测 案例:自动预测JohnsonJohnson股票的趋势1 fit4 <- ets(JohnsonJohnson)2 fit43 plot(forecast(fit4),main='Johnson and Johnson Forecasts',4 ylab="Quarterly Earnings (Dollars)", xlab="Time") 结论:预测值使用蓝色线表示,浅灰色表示80%置信空间,深灰色表示95%置信空间5.ARIMA预测步骤: 1.确保时序是平稳的 2.找出合理的模型(选定可能的p值或者q值) 3.拟合模型 4.从统计假设和预测准确性等角度评估模型 5.预测library(tseries)plot(Nile)# 1.原始序列差分一次ndiffs(Nile)dNile <- diff(Nile)# 2.差分后的图形plot(dNile)adf.test(dNile)Acf(dNile)Pacf(dNile)# 3.拟合模型fit5 <- arima(Nile,order = c(0,1,1))fit5accuracy(fit5)# 4.评价模型qqnorm(fit5$residuals)qqline(fit5$residuals)Box.test(fit5$residuals,type = 'Ljung-Box')# 5.预测模型forecast(fit5,3)plot(forecast(fit5,3),xlab = 'Year',ylab = 'Annual Flow') 原始图 一次差分图形1 fit6 <- auto.arima(sunspots)2 fit63 forecast(fit6,3)4 accuracy(fit6)5 plot(forecast(fit6,3), xlab = "Year",6 ylab = "Monthly sunspot numbers")。

3.5 预测在预测的过程中,我们的目标是根据现有的数据x n……x1来预测未来的值xn+m，m=1，2,……在这一节中，我们假定这一时间序列xt是平稳的，并且其模型的参数是已知的。

有关未知参数模型的预测我们将在后面的部分加以讨论.Xn+m的最小均方误差预测为：因为条件期望最小化均方误差为（3。

51）其中g（x）是观测值x的函数。

首先，我们来看预测值是观测值的线性函数的情形,在这种情况下，预测值的表达形式为（3.52）其中α0,α1……αn都是真实确定的数。

使均方预测误差最小化的（3。

52）式形式的线性预测我们称之为最优线性预测（BLPs），我们可以看到，线性预测仅仅依赖于其过程的二阶矩。

而这个二阶矩我们可以很容易地从现有的数据中估计出来。

这一节中很多的内容被附录B 中的理论部分加强了。

例如，定理B。

3说明了如果这个过程是高斯过程的话,那么最小均方误差预测与最优线性预测将是一致的。

如下的性质是基于投影定理（定理B。

1）而得出的. 性质P3.3：平稳过程的最优线性预测给定数据x1，x2,……x n，最优线性预测，其中,m≥1，那么这个最优线性预测可以通过求解以下方程得到：（3。

53）其中x0=1。

式（3.53）定义的房产称为预测方程，可以用来求解系数.如果E（xt）=u，那么当k=0时，由(3。

53）的第一个方程即可以得到：将期望值代入（3.52）中可以得到于是，最优线性预测的形式可以表示为因此,当我们讨论这个估计值的时候，我们会考虑到μ=0的情况,这种情况也是不失一般性的，而在这种情况下，α0=0.接下来，首先我们考虑一步向前预测,也就是给定，我们希望预测到时间序列的下一个时点的值Xn+1，那么Xn+1这一预测值的最优线性预测BLP即为：（3。

54）其中,为了更简洁地表示，我们在（3.54）中将（3.52）中的αk写成，k=1,2……n.利用性质P3。

3，系数应满足(3.55）这个预测方程可以用矩阵的形式表示为：（3.56）其中是一个n＊n矩阵,和都是n*1维向量。

用R语言做时间序列分析
时间序列分析是用来研究数据的变化趋势及其影响因素，以便对未来
的发展趋势有一定的预测对~用R语言做时间序列分析，可以从数据的宏
观分析、模型的训练、数据预测三个方面进行。

一、数据宏观分析
首先，需要预处理数据，例如，对于时间序列数据，要把它转换成一
定的格式，比如时间戳、日期和时间格式，这样R才能够识别这些数据，
在R中，可以使用时间序列模块中的函数来进行转换，比如：as.Date, as.POSIXct, as.POSIXlt等等。

之后需要针对时间序列数据进行宏观分析，可以使用R中的函数acf，pacf来检测时间序列的自相关性，这样可以把时间序列数据分解为不同
的部分，并可以提取出隐藏在数据中的规律，这样就可以确定时间序列模
型的类型，比如AR模型、MA模型、ARMA模型等，根据特定数据的特征，
从这些模型中选择最优的模型。

另外，还可以使用R中的函数spectrum来检测时间序列数据的频率
分布以及振荡性，以及峰值，从而可以有针对性地处理时间序列数据，比
如使用滤波器来去噪。

二、模型的训练
模型的训练也可以使用R进行，R中有专门用于时间序列分析的现成
函数，比如arima函数，可以用来训练ARMA模型。

1.5.csv,header=T)年中国年纱产量序列时序附录绘制1964——1999#例2.1plot(Data1.5,type='o',xlim=c(1950,2010),ylim=c(60,100) ）图（数据见附录1.2)Data1.2=read.csv(C:\\Users\\Administrator\\Desktop\\tdat1.5=Data1.5[,2] 没有标题T附录1.2.csv,header=T)#如果有标题，用；a1.5=acf(tdat1.5) F用plot(Data1.2,type='o') 白噪声检验#Box.test(tdat1.5,type=Ljung-Box,lag=6) 2.1续#例Box.test(tdat1.5,type=Ljung-Box,lag=12) tdat1.2=Data1.2[,2]a1.2=acf(tdat1.2) 模型拟合序列2.5续选择合适的ARMA#例acf(tdat1.5)pacf(tdat1.5)根据自相关系数图和偏自相关系数图可以判断为12月平均每头奶#年例#2.2绘制1962年1月至1975 ）模型牛产奶量序列时序图（数据见附录1.3）（1ARData1.3=read.csv(C:\\Users\\Administrator\\Desktop\\ 口径的求法在文档上P81 #例2.5续#P831.3.csv,header=F)附录然大似阵tdat1.3=as.vector(t(as.matrix(Data1.3)))[1:168]#矩转arima(tdat1.5,order=c(1,0,0),method=ML)#极置转向量估计ar1=arima(tdat1.5,order=c(1,0,0),method=ML) plot(tdat1.3,type='l')summary(ar1) 例2.2续#ev=ar1$residuals acf(tdat1.3) #把字去掉acf(ev) pacf(tdat1.3)pacf(ev) 年北京市每年最高气温序19982.3#例绘制1949——列时序图Data1.4=read.csv(C:\\Users\\Administrator\\Desktop\\ #参数的显著性检验t1=0.6914/0.09891.4.csv,header=T) 附录p1=pt(t1,df=48,lower.tail=F)*2 plot(Data1.4,type='o')的显著性检验#ar1t2=81.5509/ 1.7453##不会定义坐标轴p2=pt(t2,df=48,lower.tail=F)*2 2.3#例续tdat1.4=Data1.4[,2] 残差白噪声检验#Box.test(ev,type=Ljung-Box,lag=6,fitdf=1) a1.4=acf(tdat1.4)Box.test(ev,type=Ljung-Box,lag=12,fitdf=1) 例#2.3续Box.test(tdat1.4,type=Ljung-Box,lag=6)P94续预测及置信区间#例2.5predict(arima(tdat1.5,order=c(1,0,0)),n.ahead=5)Box.test(tdat1.4,type=Ljung-Box,lag=12)tdat1.5.fore=predict(arima(tdat1.5,order=c(1,0,0)),n.ahead=5) 个服从标准正态分布的白噪声#随机产生2.41000例序列观察值，并绘制时序图U=tdat1.5.fore$pred+1.96*tdat1.5.fore$se Data2.4=rnorm(1000,0,1)L=tdat1.5.fore$pred-1.96*tdat1.5.fore$se Data2.4plot(Data2.4,type='l')plot(c(tdat1.5,tdat1.5.fore$pred),type=l,col=1:2) #例续2.4lines(U,col=lue,lty=dashed)a2.4=acf(Data2.4)lines(L,col=lue,lty=dashed) 2.4例#续Box.test(Data2.4,type=Ljung-Box,lag=6)Box.test(Data2.4,type=Ljung-Box,lag=12) 续例例3.5 3.53.1.1 #例plot.ts(arima.sim(n=100,list(ar=0.8))) #方法一#年北京市城乡居民定期储蓄1998——1950对2.5例方法二#x0=runif(1) 所占比例序列的平稳性与纯随机性进行检验x=rep(0,1500)Data1.5=read.csv(C:\\Users\\Administrator\\Desktop\\x[1]=x1x[1]=0.8*x0+rnorm(1)x[2]=-x1-0.5*x0+rnorm(1) for(i in 2:length(x))for(i in 3:length(x)){x[i]=0.8*x[i-1]+rnorm(1)}{x[i]=-x[i-1]-0.5*x[i-2]+rnorm(1)} plot(x[1:100],type=l)plot(x[1:100],type=l) acf(x)acf(x) pacf(x)pacf(x) ##拟合图没有画出来均值和方差3.1.2 ##例x0=runif(1)smu=mean(x) x=rep(0,1500)svar=var(x) x[1]=-1.1*x0+rnorm(1)for(i in 2:length(x)){x[i]=-1.1*x[i-1]+rnorm(1)} 3.3 例AR（1）模型的方差3.2#例求平稳mu=0plot(x[1:100],type=l)acf(x) 51页mvar=1/(1-0.8^2) #书上pacf(x)总体均值方差#cat(population mean and var are,c(mu,mvar),\) 3.1.3 #例方法一plot.ts(arima.sim(n=100,list(ar=c(1,-0.5)))) 样本均值方差#cat(sample mean and var are,c(mu,mvar),\) #方法二x0=runif(1)x1=runif(1) 3.4例题#svar=(1+0.5)/((1-0.5)*(1-1-0.5)*(1+1-0.5)) x=rep(0,1500)x[1]=x1x[2]=x1-0.5*x0+rnorm(1) 自相关系数图截尾和偏自相关系模型例题#3.6 MAfor(i in 3:length(x)) 数图拖尾#3.6.1 {x[i]=x[i-1]-0.5*x[i-2]+rnorm(1)}plot(x[1:100],type=l) 法一：x=arima.sim(n=1000,list(ma=-2)) acf(x)plot.ts(x,type='l') pacf(x)acf(x)pacf(x) 3.1.4 #例x0=runif(1)x1=runif(1) 法二x=rep(0:1000) x=rep(0,1500)for(i in 1:1000)x[1]=x1{x[i]=rnorm[i]-2*rnorm[i-1]} x[2]=x1+0.5*x0+rnorm(1)plot(x,type='l') for(i in 3:length(x))acf(x) {x[i]=x[i-1]+0.5*x[i-2]+rnorm(1)}pacf(x) plot(x[1:100],type=l)acf(x)#3.6.2 pacf(x)法一：x=arima.sim(n=1000,list(ma=-0.5)) 又一个式子plot.ts(x,type='l') x0=runif(1)acf(x) x1=runif(1)pacf(x)x=rep(0,1500)天的57ARMA模型拟合加油站#例3.8 法二选择合适的x=rep(0:1000) 序列OVERSHORTData1.6=read.csv(C:\\Users\\Administrator\\Desktop\\for(i in 1:1000)1.6.csv,header=F)附录tdat1.6=as.vector(t(as.matrix(Data1.6)))[1:57] {x[i]=rnorm[i]-0.5*rnorm[i-1]}plot(tdat1.6,type='o') plot(x,type='l')acf(x)acf(tdat1.6)pacf(x)pacf(tdat1.6) #'closure'##错误于rnorm[i] : 类别为的对象不可以取子把字去掉集最小二乘arima(tdat1.6,order=c(0,0,1),method=CSS)##3.6.3 估计ma1=arima(tdat1.6,order=c(0,0,1),method=CSS) 法一：summary(ma1)x=arima.sim(n=1000,list(ma=c(-4/5,16/25)))ev=ma1$residuals plot.ts(x,type='l')acf(ev) acf(x)pacf(ev)pacf(x)= 1), method = c(0, 0, ##错误于法二: arima(tdat1.6, orderCSS) :x=rep(0:1000) ##'x'必需为数值for(i in 1:1000)年1985模型拟合1880——#例3.9选择合适的ARMA{x[i]=rnorm[i]-4/5*rnorm[i-1]+16/25*rnorm[i-2]} 全球气温改变差值差分序列plot(x,type='l') 没有数据##acf(x) 矩估计例3.12###例3.10 例3.11pacf(x)次化学反应的过程数x[i] = rnorm[i] - 4/5 * rnorm[i - 1] + 16/25 * ##错误于703.13对等时间间隔的连续#例rnorm[i - 2] : 据进行拟合Data1.8=read.csv(C:\\Users\\Administrator\\Desktop\\ ##更换参数长度为零1.8.csv,header=F)3.6#例续64根据书上页来判断附录tdat1.8=as.vector(t(as.matrix(Data1.8)))[1:70]plot(tdat1.8,type='o') ，，（合3.7#例拟ARMA11型）模并直观观察该模型自相关，x(t)-0.5x(t-1)=u(t)-0.8*(u-1)）模型3）例3.16AR（系数和偏自相关系数的拖尾性。

r语言时间序列boxcox变换编程在R语言中，进行时间序列的Box-Cox变换，可以使用内置的`boxcox()`函数。

以下是一个简单的示例，展示如何对时间序列进行Box-Cox变换：1. 首先，安装并加载所需的库：```Rinstall.packages("urca")library(urca)```2. 创建一个时间序列数据：```Rtime_series <- seq(1, 100)```3. 对时间序列数据进行Box-Cox变换：```Rboxcox_transformed_series <- boxcox(time_series)```4. 查看变换后的数据：```Rprint(boxcox_transformed_series)```5. 若需要将变换后的数据还原回原始数据，可以使用以下代码：```Roriginal_series <- inv_boxcox(boxcox_transformed_series)```6. 查看还原后的数据：```Rprint(original_series)```需要注意的是，Box-Cox变换适用于具有线性趋势的时间序列。

若时间序列不具有线性趋势，可能需要先进行预处理，例如平稳性检验、白噪声检验等。

此外，Box-Cox变换的具体参数选择和变换效果可通过绘制变换前后的直方图、QQ图等方法进行评估。

以下是一个关于使用R语言进行时间序列分析的参考资料：[1]: 标题：使用R语言进行时间序列分析_时间序列分析基于r的论文_浮豹的博客摘要：二、时间序列的预处理1、平稳性检验：拿到一个时间序列之后，我们首先要对其稳定性进行判断，只有非白噪声的稳定性时间序列才有分析的意义以及预测未来数据的价值。

2、白噪声检验：检查时间序列是否存在趋势或季节性，若存在，则需要进行相应的分解。

3、缺失值处理：对于含有缺失值的时间序列，可以采用插值法、删除法或其他方法进行处理。