材料力学课堂例题汇编1

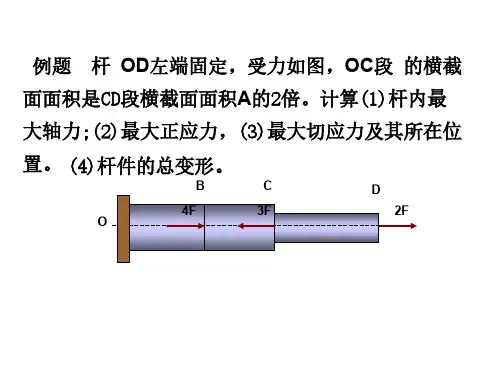
材料力学（一）轴向拉伸与压缩【内容提要】材料力学主要研究构件在外力作用下的变形、受力与破坏、失效的规律。

为设计既安全可靠又经济合理的构件，提供有关强度、刚度与稳定性分析的基本理论与方法。

【重点、难点】重点考察基本概念，掌握截面法求轴力、作轴力图的方法，截面上应力的计算。

【内容讲解】一、基本概念强度——构件在外力作用下，抵抗破坏的能力，以保证在规定的使用条件下，不会发生意外的断裂或显著塑性变形。

刚度——构件在外力作用下，抵抗变形的能力，以保证在规定的使用条件下不会产生过分的变形。

稳定性——构件在外力作用下，保持原有平衡形式的能力，以保证在规定的使用条件下，不会产生失稳现象。

杆件——一个方向的尺寸远大于其它两个方向的尺寸的构件，称为杆件或简称杆。

根据轴线与横截面的特征，杆件可分为直杆与曲杆，等截面杆与变截面杆。

二、材料力学的基本假设工程实际中的构件所用的材料多种多样，为便于理论分析，根据它们的主要性质对其作如下假设。

(一)连续性假设——假设在构件所占有的空间内均毫无空隙地充满了物质，即认为是密实的。

这样，构件内的一些几何量，力学量(如应力、位移)均可用坐标的连续函数表示，并可采用无限小的数学分析方法。

(二)均匀性假设——很设材料的力学性能与其在构件中的位置无关。

按此假设通过试样所测得的材料性能，可用于构件内的任何部位(包括单元体)。

(三)各向同性假设——沿各个方向均具有相同力学性能。

具有该性质的材料，称为各向同性材料。

综上所述，在材料力学中，一般将实际材料构件，看作是连续、均匀和各向同性的可变形固体。

三、外力内力与截面法(一)外力对于所研究的对象来说，其它构件和物体作用于其上的力均为外力，例如载荷与约束力。

外力可分为：表面力与体积力；分布力与集中力；静载荷与动载荷等。

当构件(杆件)承受一般载荷作用时，可将载荷向三个坐标平面(三个平面均通过杆的轴线，其中两个平面为形心主惯性平面)内分解，使之变为两个平面载荷和一个扭转力偶作用情况。

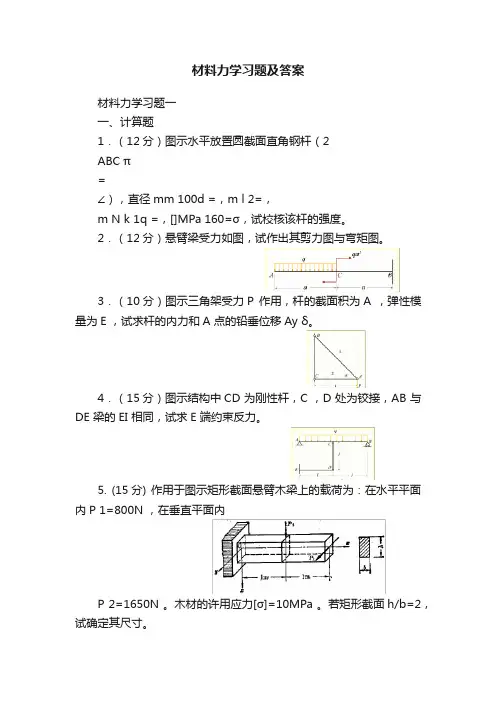
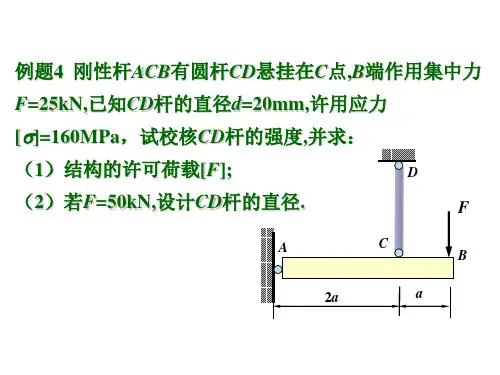
材料力学习题及答案材料力学习题一一、计算题1．（12分）图示水平放置圆截面直角钢杆（2ABC π=∠），直径mm 100d =，m l 2=，m N k 1q =，[]MPa 160=σ，试校核该杆的强度。

2．（12分）悬臂梁受力如图，试作出其剪力图与弯矩图。

3．（10分）图示三角架受力P 作用，杆的截面积为A ，弹性模量为E ，试求杆的内力和A 点的铅垂位移Ay δ。

4．（15分）图示结构中CD 为刚性杆，C ，D 处为铰接，AB 与DE 梁的EI 相同，试求E 端约束反力。

5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为：在水平平面内P 1=800N ，在垂直平面内P 2=1650N 。

木材的许用应力[σ]=10MPa 。

若矩形截面h/b=2，试确定其尺寸。

三．填空题（23分）1．（4分）设单元体的主应力为321σσσ、、，则单元体只有体积改变而无形状改变的条件是＿＿＿＿＿＿＿＿＿＿；单元体只有形状改变而无体积改变的条件是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

2．（6分）杆件的基本变形一般有＿＿＿＿＿＿、＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿四种；而应变只有＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿两种。

3．（6分）影响实际构件持久极限的因素通常有＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿，它们分别用＿＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿＿＿＿＿＿来加以修正。

4.（5分）平面弯曲的定义为＿＿＿＿＿＿＿＿＿＿＿＿_＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿_。

5.（2分）低碳钢圆截面试件受扭时，沿＿＿＿＿＿＿＿＿＿＿＿＿截面破坏；铸铁圆截面试件受扭时，沿＿＿＿＿＿＿＿＿＿＿＿＿面破坏。

四、选择题（共2题，9分）2．（5分）图示四根压杆的材料与横截面均相同，试判断哪一根最容易失稳。

答案：（）材料力学习题二二、选择题：（每小题3分，共24分）1、危险截面是______所在的截面。

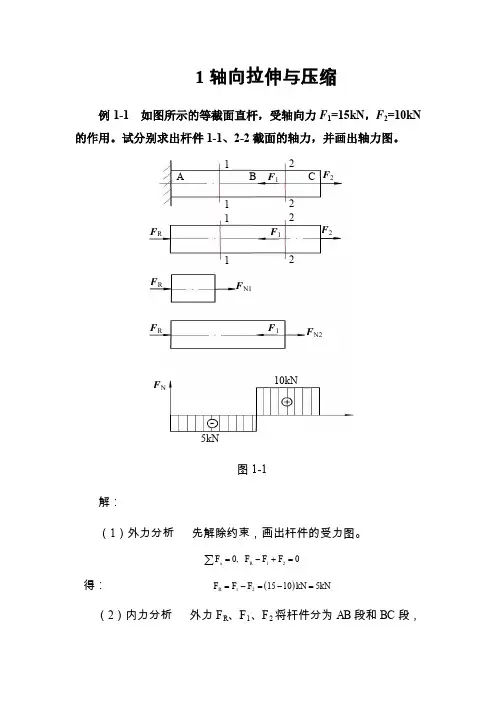
1轴向拉伸与压缩例1-1 如图所示的等截面直杆，受轴向力F 1=15kN ，F 2=10kN 的作用。

试分别求出杆件1-1、2-2截面的轴力，并画出轴力图。

F 2F 2C 22 22F 111 11B F 1AF RF RF N1F 1F N2F R F N10kN5kN图1-1解：（1）外力分析 先解除约束，画出杆件的受力图。

120,0xR FF F F = -+=∑得：()121510kN 5kN R F F F =-=-=（2）内力分析 外力F R 、F 1、F 2将杆件分为AB 段和BC 段，在AB 段，用1-1截面将杆件截分为两段，取左段为研究对象，右段对截面的作用力用F N1来代替。

假定内力F N1为正，列平衡方程10,0xN R FF F = +=∑得：15kN N R F F =-=-负号表示F N1的方向和假定方向相反，截面受压。

在BC 这一段，用任意2-2截面将杆件分为两段，取左段为研究对象，右段对左段截面的作用力用F N2来代替。

假定轴力F N2为正，有平衡方程2100xN R FF F F = +-=∑得： ()21515kN N R F F F =-+=-+=10kN （3）画轴力图由以上例题可以总结出求截面轴力的简捷方法：杆件任意截面的轴力F N （x ）等于截面一侧所有外力的代数和。

即1nN i i F F ==∑，外力背离该截面的时取正，指向该截面时取负。

例1-2 如图所示为正方形截面阶梯杆，受力及尺寸如图所示。

试分析杆上1截面处和2截面处的正应力。

FF2hh12（a ）FFF N 11122N hh σ==F F F N 1222244N h h σ==F F（b ） 图1-2解：先求出杆两截面处的轴力F N 1和F N 2，在用截面上的轴力除以相应的截面面积，如图（b ）所示，不难求出σ1=F/h 2，σ2=F/（4h 2）。

例1-3 如图所示，斜杆AB 为直径d =20mm 的钢杆，载荷Q =15kN 。

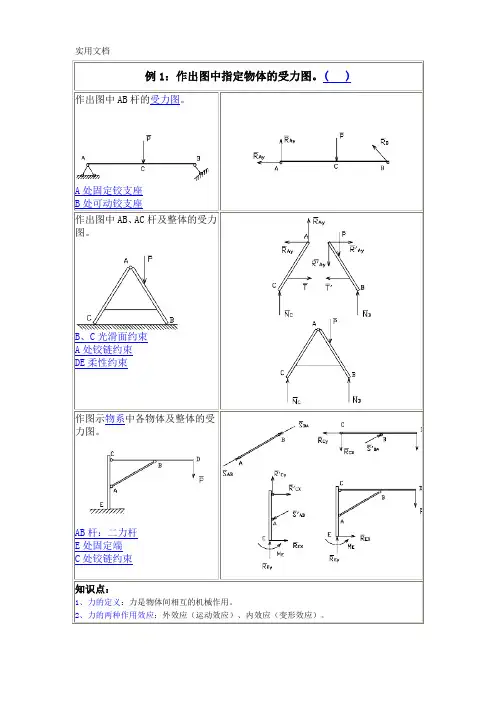
作出图中AB杆的受力图。

A处固定铰支座B处可动铰支座作出图中AB、AC杆及整体的受力图。

B、C光滑面约束A处铰链约束DE柔性约束作图示物系中各物体及整体的受力图。

AB杆：二力杆E处固定端C处铰链约束（1）运动效应：力使物体的机械运动状态发生变化的效应。

（2）变形效应：力使物体的形状发生和尺寸改变的效应。

3、力的三要素：力的大小、方向、作用点。

4、力的表示方法：（1）力是矢量，在图示力时，常用一带箭头的线段来表示力；（注意表明力的方向和力的作用点！）（2）在书写力时，力矢量用加黑的字母或大写字母上打一横线表示，如F、G、F1等等。

5、约束的概念：对物体的运动起限制作用的装置。

6、约束力（约束反力）：约束作用于被约束物体上的力。

约束力的方向总是与约束所能限制的运动方向相反。

约束力的作用点，在约束与被约束物体的接处7、主动力：使物体产生运动或运动趋势的力。

作用于被约束物体上的除约束力以外的其它力。

8、柔性约束：如绳索、链条、胶带等。

(1)约束的特点：只能限制物体原柔索伸长方向的运动。

(2)约束反力的特点：约束反力沿柔索的中心线作用，离开被约束物体。

（）9、光滑接触面：物体放置在光滑的地面或搁置在光滑的槽体内。

（1）约束的特点：两物体的接触表面上的摩擦力忽略不计，视为光滑接触面约束。

被约束的物体可以沿接触面滑动，但不能沿接触面的公法线方向压入接触面。

（2）约束反力的特点：光滑接触面的约束反力沿接触面的公法线，通过接触点，指向被约束物体。

（）10、铰链约束：两个带有圆孔的物体，用光滑的圆柱型销钉相连接。

约束反力的特点:是方向未定的一个力；一般用一对正交的力来表示，指向假定。

（）11、固定铰支座（1）约束的构造特点：把中间铰约束中的某一个构件换成支座，并与基础固定在一起，则构成了固定铰支座约束。

（2）约束反力的特点：固定铰支座的约束反力同中间铰的一样，也是方向未定的一个力；用一对正交的力来表示，指向假定。

()12、可动铰支座（1）约束的构造特点把固定铰支座的底部安放若干滚子，并与支撑连接则构成活动铰链支座约束，又称锟轴支座。

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。

试问在杆件的任一横截面m-m上存在何种内力分量，并确定其大小。

解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量M x，即扭矩，其大小等于M。

1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。

解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝p cosα=120×cos10°=118.2MPaτ＝p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。

试问杆件横截面上存在何种内力分量，并确定其大小。

图中之C点为截面形心。

解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。

试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。

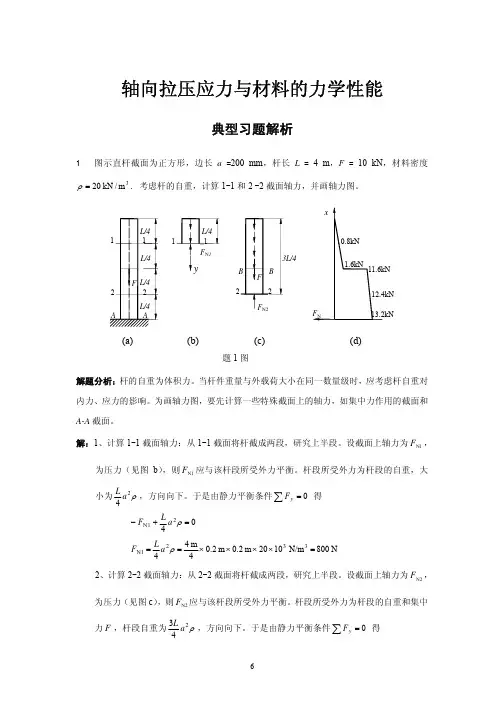
解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。

解：(a) F N AB=F, F N BC=0, F N，max=F(b) F N AB=F, F N BC=－F, F N，max=F(c) F N AB=－2 kN, F N2BC=1 kN, F N CD=3 kN, F N，max=3 kN(d) F N AB=1 kN, F N BC=－1 kN, F N，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。