下载文档原格式
第一章 晶体的结构习题一、填空题1.固体一般分为_____ _____ _____2.晶体的三大特征是_____ _____ _____3._____是晶格中最小的重复单元，_____既反映晶格的周期性又反映晶格的对称性。
4._____和_____均是表示晶体原子排列紧密程度。
5.独立的对称操作有______二、证明题1.试证明体心立方格子和面心立方格子互为正倒格子。
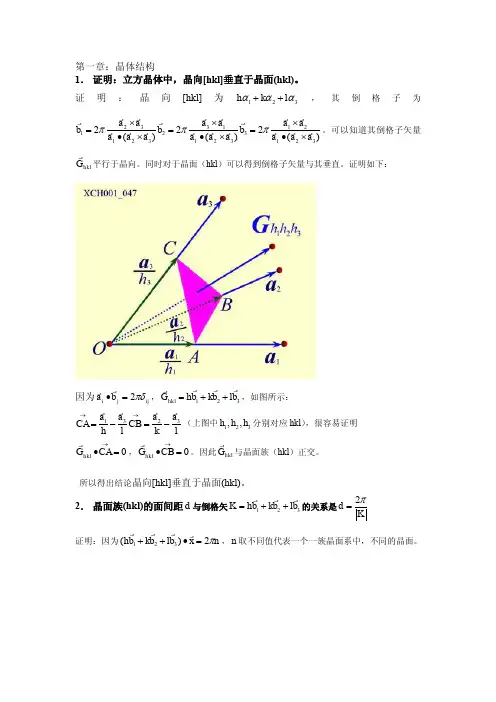
2.证明倒格子矢量112233G h b h b h b =++ 垂直于密勒指数为123()h h h 的晶面系。
3.对于简方晶格，证明密勒单立指数为(,,)h k l 的晶面系，面间距d 满足：22222()d a h k l =++，其中a 为立方边长；并说明面指数简单的晶面，其面密度较大，容易解理。
4.证明不存在5度旋转对称轴。
5.证明正格矢和倒格矢之间的关系式为：()为整数m m R G π2=⋅三、计算题1.已知某种晶体固体物理学原胞基矢为（1）求原胞体积。
（2）求倒格子基矢。
（3）求第一布里渊区体积。
2.一晶体原胞基矢大小m a 10104-⨯=，m b 10106-⨯=，m c 10108-⨯=，基矢间夹角90=α， 90=β， 120=γ。
试求：（1）倒格子基矢的大小； （2）正、倒格子原胞的体积； （3） 正格子(210)晶面族的面间距。
j 2a 3i 2a a 1+=j 2a 3i 2a -a 2+=k c a 3=3.如图1.所示，试求： （1） 晶列ED ，FD 和OF 的晶列指数；（2） 晶面AGK ,FGIH 和MNLK 的密勒指数；（3） 画出晶面（120），（131）。
a 2xy zA B D C G F E OIH y x Aa 2K O GLNM z图1.4.矢量a ，b ，c 构成简单正交系。
求：晶面族)(hkl 的面间距。
5.设有一简单格子，它的基矢分别为i a 31=，j a 32=，)(5.13k j i a ++=。
固体物理习题1第⼀章晶体结构和倒格⼦1. 画出下列晶体的惯⽤元胞和布拉菲格⼦，写出它们的初基元胞基⽮表达式，指明各晶体的结构及两种元胞中的原⼦个数和配位数。
(1) 氯化钾（2）氯化钛（3）硅（4）砷化镓（5）碳化硅（6）钽酸锂（7）铍（8）钼（9）铂2. 对于六⾓密积结构，初基元胞基⽮为→1a =→→+j i a 3(2 →→→+-=j i a a 3(22 求其倒格⼦基⽮，并判断倒格⼦也是六⾓的。
3．⽤倒格⽮的性质证明，⽴⽅晶格的[hkl]晶向与晶⾯（hkl ）垂直。
4. 若轴⽮→→→c b a 、、构成简单正交系，证明。
晶⾯族（h 、k 、l ）的⾯间距为 2222)()()(1c l b k a h hkl d ++= 5．⽤X 光衍射对Al 作结构分析时，测得从(111)⾯反射的波长为1.54?反射⾓为θ=19.20 求⾯间距d 111。
6．试说明：1〕劳厄⽅程与布拉格公式是⼀致的；2〕劳厄⽅程亦是布⾥渊区界⾯⽅程；7．在图1－49（b ）中，写出反射球⾯P 、Q 两点的倒格⽮表达式以及所对应的晶⾯指数和衍射⾯指数。
8．求⾦刚⽯的⼏何结构因⼦，并讨论衍射⾯指数与衍射强度的关系。
9．说明⼏何结构因⼦S h 和坐标原点选取有关，但衍射谱线强度和坐标选择⽆关。
10. 能量为150eV 的电⼦束射到镍粉末上，镍是⾯⼼⽴⽅晶格，晶格常数为3.25×10-10m,求最⼩的布拉格衍射⾓。
附：1eV=1.602×10-19J, h=6.262×10-34J ·s, c=2.9979×108m/s第⼆章晶体结合1．已知某晶体两相邻原⼦间的互作⽤能可表⽰成nm r b r a r U +-=)( (1) 求出晶体平衡时两原⼦间的距离；(2) 平衡时的⼆原⼦间的互作⽤能；(3) 若取m=2,n=10,两原⼦间的平衡距离为3?,仅考虑⼆原⼦间互作⽤则离解能为4ev ，计算a 及b 的值；（4）若把互作⽤势中排斥项b/r n 改⽤玻恩－梅叶表达式λexp(-r/p),并认为在平衡时对互作⽤势能具有相同的贡献，求n 和p 间的关系。
固体物理考试习题⼤全晶体结构 20 分晶体衍射 10 分晶格振动 20分与晶体的热学性质 18分能带理论和晶体中电⼦在电场磁场中的运动 36 分⾦属电⼦论和半导体电⼦论 5—10分1. 晶体的微观结构、原胞、W-S 原胞、惯⽤单胞的概念、常见的晶体结构、晶⾯与晶向的概念，并能进⾏必要的计算；倒格⼦与布⾥渊区、晶体X 射线衍射，能计算⼏何结构因⼦和衍射极⼤条件。
2. 晶体结合的普遍特性；离⼦键结合和范德⽡⽿斯结合的结合能计算。
3. 简谐近似和最近邻近似，双原⼦链的晶格振动；周期边界条件，晶格振动的量⼦化与声⼦，⾊散关系；爱因斯坦模型和德拜模型，晶体的⽐热，零点振动能计算。
4. 经典⾃由电⼦论：电⼦运动⽅程，⾦属的直流电导，霍⽿效应，⾦属热导率。
量⼦⾃由电⼦论：能态密度，费⽶分布，费⽶能级，电⼦热容量。
5. 布洛赫定理及其证明；近⾃由电⼦近似的思想⼀维和⼆维近⾃由电⼦近似的能带计算，紧束缚近似的思想，紧束缚近似的计算（S 能带的的⾊散关系）。
理解半导体Ge 、Si 的能带结构。
6.波包的准经典运动概念，布洛赫电⼦的速度，加速度和有效质量和相应的计算，空⽳的概念；导体、半导体和绝缘体的能带解释，原⼦能级和能带的对应；朗道能级，回旋共振，德×哈斯—范×阿尔芬效应，碱⾦属和贵⾦属的费⽶⾯。
7.分布函数法和恒定外电场下玻⽿兹曼⽅程的推导。
理解电⼦声⼦相互作⽤，晶格散射和电导，电阻的来源。
8. 半导体基本的能带结构，半导体中的施主和受主杂质，P 型半导体和N 型半导体，半导体中的费⽶统计分布。
PN 结平衡势垒。
1.1 在结晶学中, 晶胞是按晶体的什么特性选取的?在结晶学中, 晶胞选取的原则是既要考虑晶体结构的周期性⼜要考虑晶体的宏观对称性.1.2六⾓密积属何种晶系? ⼀个晶胞包含⼏个原⼦?六⾓密积属六⾓晶系, ⼀个晶胞(平⾏六⾯体)包含两个原⼦.1.3在晶体衍射中，为什么不能⽤可见光？晶体中原⼦间距的数量级为1010-⽶，要使原⼦晶格成为光波的衍射光栅，光波的波长应⼩于1010-⽶. 但可见光的波长为7.6?4.0710-?⽶, 是晶体中原⼦间距的1000倍. 因此, 在晶体衍射中，不能⽤可见光.2.1共价结合, 两原⼦电⼦云交迭产⽣吸引, ⽽原⼦靠近时, 电⼦云交迭会产⽣巨⼤的排斥⼒, 如何解释?共价结合, 形成共价键的配对电⼦, 它们的⾃旋⽅向相反, 这两个电⼦的电⼦云交迭使得体系的能量降低, 结构稳定. 但当原⼦靠得很近时, 原⼦内部满壳层电⼦的电⼦云交迭, 量⼦态相同的电⼦产⽣巨⼤的排斥⼒, 使得系统的能量急剧增⼤.2.2为什么许多⾦属为密积结构?⾦属结合中, 受到最⼩能量原理的约束, 要求原⼦实与共有电⼦电⼦云间的库仑能要尽可能的低(绝对值尽可能的⼤). 原⼦实越紧凑, 原⼦实与共有电⼦电⼦云靠得就越紧密, 库仑能就越低. 所以, 许多⾦属的结构为密积结构.3.1什么叫简正振动模式？简正振动数⽬、格波数⽬或格波振动模式数⽬是否是⼀回事？为了使问题既简化⼜能抓住主要⽭盾，在分析讨论晶格振动时，将原⼦间互作⽤⼒的泰勒级数中的⾮线形项忽略掉的近似称为简谐近似. 在简谐近似下, 由N 个原⼦构成的晶体的晶格振动, 可等效成3N 个独⽴的谐振⼦的振动. 每个谐振⼦的振动模式称为简正振动模式, 它对应着所有的原⼦都以该模式的频率做振动, 它是晶格振动模式中最简单最基本的振动⽅式. 原⼦的振动, 或者说格波振动通常是这3N 个简正振动模式的线形迭加.简正振动数⽬、格波数⽬或格波振动模式数⽬是⼀回事, 这个数⽬等于晶体中所有原⼦的⾃由度数之和, 即等于3N .3.2长光学⽀格波与长声学⽀格波本质上有何差别?长光学⽀格波的特征是每个原胞内的不同原⼦做相对振动, 振动频率较⾼, 它包含了晶格振动频率最⾼的振动模式. 长声学⽀格波的特征是原胞内的不同原⼦没有相对位移, 原胞做整体运动, 振动频率较低, 它包含了晶格振动频率最低的振动模式, 波速是⼀常数. 任何晶体都存在声学⽀格波, 但简单晶格(⾮复式格⼦)晶体不存在光学⽀格波.3.3温度⼀定，⼀个光学波的声⼦数⽬多呢, 还是声学波的声⼦数⽬多?频率为ω的格波的(平均) 声⼦数为11)(/-=T k B e n ωω .因为光学波的频率O ω⽐声学波的频率A ω⾼, (1/-T k B O e ω )⼤于(1/-T k B A e ω ), 所以在温度⼀定情况下, ⼀个光学波的声⼦数⽬少于⼀个声学波的声⼦数⽬.3.4长声学格波能否导致离⼦晶体的宏观极化?长光学格波所以能导致离⼦晶体的宏观极化, 其根源是长光学格波使得原胞内不同的原⼦(正负离⼦)产⽣了相对位移. 长声学格波的特点是, 原胞内所有的原⼦没有相对位移. 因此, 长声学格波不能导致离⼦晶体的宏观极化.3.5你认为简单晶格存在强烈的红外吸收吗？实验已经证实, 离⼦晶体能强烈吸收远红外光波. 这种现象产⽣的根源是离⼦晶体中的长光学横波能与远红外电磁场发⽣强烈耦合. 简单晶格中不存在光学波, 所以简单晶格不会吸收远红外光波.3.6爱因斯坦模型在低温下与实验存在偏差的根源是什么?按照爱因斯坦温度的定义, 爱因斯坦模型的格波的频率⼤约为Hz 1013, 属于光学⽀频率. 但光学格波在低温时对热容的贡献⾮常⼩, 低温下对热容贡献⼤的主要是长声学格波. 也就是说爱因斯坦没考虑声学波对热容的贡献是爱因斯坦模型在低温下与实验存在偏差的根源.3.7在甚低温下, 德拜模型为什么与实验相符?在甚低温下, 不仅光学波得不到激发, ⽽且声⼦能量较⼤的短声学格波也未被激发, 得到激发的只是声⼦能量较⼩的长声学格波.长声学格波即弹性波. 德拜模型只考虑弹性波对热容的贡献. 因此, 在甚低温下, 德拜模型与事实相符, ⾃然与实验相符.4.1 波⽮空间与倒格空间有何关系? 为什么说波⽮空间内的状态点是准连续的?波⽮空间与倒格空间处于统⼀空间, 倒格空间的基⽮分别为321 b b b 、、, ⽽波⽮空间的基⽮分别为32N N / / /321b b b 、、1N , N 1、N 2、N 3分别是沿正格⼦基⽮321 a a a 、、⽅向晶体的原胞数⽬.倒格空间中⼀个倒格点对应的体积为*321) (Ω=??b b b ,波⽮空间中⼀个波⽮点对应的体积为N N b N b N b *332211)(Ω=??,即波⽮空间中⼀个波⽮点对应的体积, 是倒格空间中⼀个倒格点对应的体积的1/N . 由于N 是晶体的原胞数⽬, 数⽬巨⼤, 所以⼀个波⽮点对应的体积与⼀个倒格点对应的体积相⽐是极其微⼩的. 也就是说, 波⽮点在倒格空间看是极其稠密的. 因此, 在波⽮空间内作求和处理时, 可把波⽮空间内的状态点看成是准连续的.4.2在布⾥渊区边界上电⼦的能带有何特点?电⼦的能带依赖于波⽮的⽅向, 在任⼀⽅向上, 在布⾥渊区边界上, 近⾃由电⼦的能带⼀般会出现禁带. 若电⼦所处的边界与倒格⽮n K 正交, 则禁带的宽度)(2n K V E g =, )(n K V 是周期势场的付⾥叶级数的系数.不论何种电⼦, 在布⾥渊区边界上, 其等能⾯在垂直于布⾥渊区边界的⽅向上的斜率为零, 即电⼦的等能⾯与布⾥渊区边界正交4.3当电⼦的波⽮落在布⾥渊区边界上时, 其有效质量何以与真实质量有显著差别?晶体中的电⼦除受外场⼒的作⽤外, 还和晶格相互作⽤. 设外场⼒为F , 晶格对电⼦的作⽤⼒为F l , 电⼦的加速度为)(1l m F F a +=.但F l 的具体形式是难以得知的. 要使上式中不显含F l , ⼜要保持上式左右恒等, 则只有F a *1m =.显然, 晶格对电⼦的作⽤越弱, 有效质量m*与真实质量m 的差别就越⼩. 相反, 晶格对电⼦的作⽤越强, 有效质量m *与真实质量m 的差别就越⼤. 当电⼦的波⽮落在布⾥渊区边界上时, 与布⾥渊区边界平⾏的晶⾯族对电⼦的散射作⽤最强烈. 在晶⾯族的反射⽅向上, 各格点的散射波相位相同, 迭加形成很强的反射波. 正因为在布⾥渊区边界上的电⼦与晶格的作⽤很强, 所以其有效质量与真实质量有显著差别4.4电⼦的有效质量*m 变为∞的物理意义是什么?仍然从能量的⾓度讨论之. 电⼦能量的变化m E m E m E 晶格对电⼦作的功外场⼒对电⼦作的功外场⼒对电⼦作的功)d ()(d )(d *+=[]电⼦对晶格作的功外场⼒对电⼦作的功)d ()(d 1E E m -=.从上式可以看出，当电⼦从外场⼒获得的能量⼜都输送给了晶格时, 电⼦的有效质量*m 变为∞. 此时电⼦的加速度01*==F a m , 即电⼦的平均速度是⼀常量. 或者说, 此时外场⼒与晶格作⽤⼒⼤⼩相等, ⽅向相反.4.5紧束缚模型下, 内层电⼦的能带与外层电⼦的能带相⽐较, 哪⼀个宽? 为什么?以s 态电⼦为例. 由图5.9可知, 紧束缚模型电⼦能带的宽度取决于积分s J 的⼤⼩, ⽽积分r R r R r r r d )()]()([)(*n at s n at N at s s V V J ----=Ω的⼤⼩⼜取决于)(r at s ?与相邻格点的)(n at s R r -?的交迭程度. 紧束缚模型下, 内层电⼦的)(r at s ?与)(n at s R r -?交叠程度⼩, 外层电⼦的)(r at s ?与)(n at s R r -?交迭程度⼤. 因此, 紧束缚模型下, 内层电⼦的能带与外层电⼦的能带相⽐较, 外层电⼦的能带宽.4.6等能⾯在布⾥渊区边界上与界⾯垂直截交的物理意义是什么？将电⼦的波⽮k 分成平⾏于布⾥渊区边界的分量//k 和垂直于布⾥渊区边界的分量k ┴. 则由电⼦的平均速度)(1k E k ?=ν得到////1k E=ν,⊥⊥??=k E 1ν. 等能⾯在布⾥渊区边界上与界⾯垂直截交, 则在布⾥渊区边界上恒有⊥??k E /=0, 即垂直于界⾯的速度分量⊥ν为零. 垂直于界⾯的速度分量为零, 是晶格对电⼦产⽣布拉格反射的结果. 在垂直于界⾯的⽅向上, 电⼦的⼊射分波与晶格的反射分波⼲涉形成了驻波.5.1⼀维简单晶格中⼀个能级包含⼏个电⼦?设晶格是由N 个格点组成, 则⼀个能带有N 个不同的波⽮状态, 能容纳2N 个电⼦. 由于电⼦的能带是波⽮的偶函数, 所以能级有(N /2)个. 可见⼀个能级上包含4个电⼦.5.2本征半导体的能带与绝缘体的能带有何异同?在低温下, 本征半导体的能带与绝缘体的能带结构相同. 但本征半导体的禁带较窄, 禁带宽度通常在2个电⼦伏特以下. 由于禁带窄, 本征半导体禁带下满带顶的电⼦可以借助热激发, 跃迁到禁带上⾯空带的底部, 使得满带不满, 空带不空, ⼆者都对导电有贡献.6.1你是如何理解绝对零度时和常温下电⼦的平均动能⼗分相近这⼀点的?⾃由电⼦论只考虑电⼦的动能. 在绝对零度时, ⾦属中的⾃由(价)电⼦, 分布在费密能级及其以下的能级上, 即分布在⼀个费密球内. 在常温下, 费密球内部离费密⾯远的状态全被电⼦占据, 这些电⼦从格波获取的能量不⾜以使其跃迁到费密⾯附近或以外的空状态上, 能够发⽣能态跃迁的仅是费密⾯附近的少数电⼦, ⽽绝⼤多数电⼦的能态不会改变. 也就是说, 常温下电⼦的平均动能与绝对零度时的平均动能⼀定⼗分相近.6.2为什么温度升⾼, 费密能反⽽降低?当0≠T 时, 有⼀半量⼦态被电⼦所占据的能级即是费密能级. 温度升⾼, 费密⾯附近的电⼦从格波获取的能量就越⼤, 跃迁到费密⾯以外的电⼦就越多, 原来有⼀半量⼦态被电⼦所占据的能级上的电⼦就少于⼀半, 有⼀半量⼦态被电⼦所占据的能级必定降低. 也就是说, 温度升⾼, 费密能反⽽降低.6.3为什么价电⼦的浓度越⼤, 价电⼦的平均动能就越⼤?由于绝对零度时和常温下电⼦的平均动能⼗分相近，我们讨论绝对零度时电⼦的平均动能与电⼦浓度的关系.价电⼦的浓度越⼤价电⼦的平均动能就越⼤, 这是⾦属中的价电⼦遵从费密-狄拉克统计分布的必然结果. 在绝对零度时, 电⼦不可能都处于最低能级上, ⽽是在费密球中均匀分布. 由(6.4)式3/120)3(πn k F =可知, 价电⼦的浓度越⼤费密球的半径就越⼤,⾼能量的电⼦就越多, 价电⼦的平均动能就越⼤. 这⼀点从(6.5)和(6.3)式看得更清楚. 电⼦的平均动能E 正⽐与费密能0F E , ⽽费密能⼜正⽐与电⼦浓度3/2n :()3/22232πn m E F =,()3/2220310353πn m E E F ==.所以价电⼦的浓度越⼤, 价电⼦的平均动能就越⼤.6.4对⽐热和电导有贡献的仅是费密⾯附近的电⼦, ⼆者有何本质上的联系?对⽐热有贡献的电⼦是其能态可以变化的电⼦. 能态能够发⽣变化的电⼦仅是费密⾯附近的电⼦. 因为, 在常温下, 费密球内部离费密⾯远的状态全被电⼦占据, 这些电⼦从格波获取的能量不⾜以使其跃迁到费密⾯附近或以外的空状态上, 能够发⽣能态跃迁的仅是费密⾯附近的电⼦, 这些电⼦吸收声⼦后能跃迁到费密⾯附近或以外的空状态上.对电导有贡献的电⼦, 即是对电流有贡献的电⼦, 它们是能态能够发⽣变化的电⼦. 由(6.79)式 )(00ε+=v τe E f f f可知, 加电场后,电⼦分布发⽣了偏移. 正是这偏移)(0εv τe E f部分才对电流和电导有贡献. 这偏移部分是能态发⽣变化的电⼦产⽣的. ⽽能态能够发⽣变化的电⼦仅是费密⾯附近的电⼦, 这些电⼦能从外场中获取能量, 跃迁到费密⾯附近或以外的空状态上. ⽽费密球内部离费密⾯远的状态全被电⼦占拒, 这些电⼦从外场中获取的能量不⾜以使其跃迁到费密⾯附近或以外的空状态上. 对电流和电导有贡献的电⼦仅是费密⾯附近电⼦的结论从(6.83)式x k S x x ES v e j F ετπ?=?d 4222和⽴⽅结构⾦属的电导率E S v e k S xF ?=?d 4222τπσ看得更清楚. 以上两式的积分仅限于费密⾯, 说明对电导有贡献的只能是费密⾯附近的电⼦.总之, 仅仅是费密⾯附近的电⼦对⽐热和电导有贡献, ⼆者本质上的联系是: 对⽐热和电导有贡献的电⼦是其能态能够发⽣变化的电⼦, 只有费密⾯附近的电⼦才能从外界获取能量发⽣能态跃迁.6.5为什么价电⼦的浓度越⾼, 电导率越⾼?电导σ是⾦属通流能⼒的量度. 通流能⼒取决于单位时间内通过截⾯积的电⼦数(参见思考题18). 但并不是所有价电⼦对导电都有贡献, 对导电有贡献的是费密⾯附近的电⼦. 费密球越⼤, 对导电有贡献的电⼦数⽬就越多. 费密球的⼤⼩取决于费密半径3/12)3(πn k F =.可见电⼦浓度n 越⾼, 费密球越⼤, 对导电有贡献的电⼦数⽬就越多, 该⾦属的电导率就越⾼.6.6磁场与电场, 哪⼀种场对电⼦分布函数的影响⼤? 为什么?磁场与电场相⽐较, 电场对电⼦分布函数的影响⼤. 因为磁场对电⼦的作⽤是洛伦兹⼒, 洛伦兹⼒只改变电⼦运动⽅向, 并不对电⼦做功. 也就是说, 当只有磁场情况下, ⾮磁性⾦属中价电⼦的分布函数不会改变. 但在磁场与电场同时存在的情况下, 由于产⽣了附加霍⽿电场, 磁场对⾮磁性⾦属电⼦的分布函数的影响就显现出来. 但与电场相⽐, 磁场对电⼦分布函数的影响要弱得多.⼆. (25分)1. 证明⽴⽅晶系的晶列[hkl ]与晶⾯族(hkl )正交.2. 设晶格常数为a , 求⽴⽅晶系密勒指数为(hkl )的晶⾯族的⾯间距.三. (25分)设质量为m 的同种原⼦组成的⼀维双原⼦分⼦链, 分⼦内部的⼒系数为β1, 分⼦间相邻原⼦的⼒系数为β2, 分⼦的两原⼦的间距为d , 晶格常数为a,1. 列出原⼦运动⽅程.2. 求出格波的振动谱ω(q ).四. (30分)对于晶格常数为a 的SC 晶体1. 以紧束缚近似求⾮简并s 态电⼦的能带.2. 画出第⼀布⾥渊区[110]⽅向的能带曲线, 求出带宽.3.当电⼦的波⽮k =a πi +a πj 时,求导致电⼦产⽣布拉格反射的晶⾯族的⾯指数.⼀. 填空(20分, 每题2分)1.对晶格常数为a 的SC 晶体,与正格⽮R =a i +2a j +2a k 正交的倒格⼦晶⾯族的⾯指数为( 122 ), 其⾯间距为( a 32π2.典型离⼦晶体的体积为V , 最近邻两离⼦的距离为R , 晶体的格波数⽬为( 33R V), 长光学波的( 纵 )波会引起离⼦晶体宏观上的极化.3. ⾦刚⽯晶体的结合类型是典型的(共价结合)晶体, 它有( 6 )⽀格波.4. 当电⼦遭受到某⼀晶⾯族的强烈反射时, 电⼦平⾏于晶⾯族的平均速度(不为 )零, 电⼦波⽮的末端处在(布⾥渊区)边界上.5. 两种不同⾦属接触后, 费⽶能级⾼的带(正)电.对导电有贡献的是 (费⽶⾯附近)的电⼦.⼆. (25分)1.设d 为晶⾯族()hkl 的⾯间距为, n 为单位法⽮量, 根据晶⾯族的定义,晶⾯族()hkl 将c b a 、、分别截为l k h 、、等份，即 a =?n a cos (a ,n )==a cos (a ,n )=hd ,b =?n b cos (b ,n )= a cos (b ,n ) =kd ,c =?n c cos (c ,n )= a cos (c ,n ) =ld .于是有n =a d h i +a d k j +a d l k =a d(h i +k j +l k ). (1)其中, i 、j 、k 分别为平⾏于c b a 、、三个坐标轴的单位⽮量. ⽽晶列[]hkl 的⽅向⽮量为=R ha i +ka j +la k=a (h i +k j +l k ). (2)由(1)、（2）两式得n =2a dR ,即n 与R 平⾏. 因此晶列[]hkl 与晶⾯()hkl 正交.2. ⽴⽅晶系密勒指数为(hkl )的晶⾯族的⾯间距22222222l k h a al a k a h d hkl hkl ++=++==k j i K πππππ三. (25分)1.原⼦运动⽅程(2t qna i n Ae u ω-=)(12t qna i n Be u ω-+=1. 1. 格波的振动谱ω(q )＝()2/12/1222121222212sin 16422??+-±+qa m m m m ββββββ四. (30分)1. 紧束缚近似⾮简并s 态电⼦的能带()a k a k a k J C E E z y x s s ats s cos cos cos 2)(++--=k2. 第⼀布⾥渊区[110]⽅向的能带曲线[110]⽅向的能带曲线带宽为8J s 。
第一章 金属自由电子气体模型习题及答案1. 你是如何理解绝对零度时和常温下电子的平均动能十分相近这一点的？[解答] 自由电子论只考虑电子的动能。
在绝对零度时，金属中的自由（价）电子，分布在费米能级及其以下的能级上，即分布在一个费米球内。
在常温下，费米球内部离费米面远的状态全被电子占据，这些电子从格波获取的能量不足以使其跃迁到费米面附近或以外的空状态上，能够发生能态跃迁的仅是费米面附近的少数电子,而绝大多数电子的能态不会改变。
也就是说，常温下电子的平均动能与绝对零度时的平均动能十分相近。
2. 晶体膨胀时，费米能级如何变化？[解答] 费米能级3/222)3(2πn mE o F= ， 其中n 单位体积内的价电子数目。
晶体膨胀时，体积变大，电子数目不变，n 变小，费密能级降低。
3． 为什么温度升高，费米能反而降低？[解答] 当K T 0≠时，有一半量子态被电子所占据的能级即是费米能级。
除了晶体膨胀引起费米能级降低外，温度升高，费米面附近的电子从格波获取的能量就越大，跃迁到费米面以外的电子就越多，原来有一半量子态被电子所占据的能级上的电子就少于一半，有一半量子态被电子所占据的能级必定降低，也就是说，温度生高，费米能反而降低。
4． 为什么价电子的浓度越大，价电子的平均动能就越大？[解答] 由于绝对零度时和常温下电子的平均动能十分相近，我们讨论绝对零度时电子的平均动能与电子的浓度的关系。
价电子的浓度越大，价电子的平均动能就越大，这是金属中的价电子遵从费米—狄拉克统计分布的必然结果。
在绝对零度时，电子不可能都处于最低能级上，而是在费米球中均匀分布。
由式3/120)3(πn k F =可知，价电子的浓度越大费米球的半径就越大，高能量的电子就越多，价电子的平均动能就越大。
这一点从3/2220)3(2πn m E F=和3/222)3(10353πn mE E oF ==式看得更清楚。
电子的平均动能E 正比于费米能o F E ，而费米能又正比于电子浓度32l n。
固体物理学概念和习题答案《固体物理学》概念和习题固体物理基本概念和思考题：1.给出原胞的定义。
答：最⼩平⾏单元。
2.给出维格纳-赛茨原胞的定义。
答：以⼀个格点为原点，作原点与其它格点连接的中垂⾯(或中垂线)，由这些中垂⾯(或中垂线)所围成的最⼩体积(或⾯积)即是维格纳-赛茨原胞。
3.⼆维布喇菲点阵类型和三维布喇菲点阵类型。
4. 请描述七⼤晶系的基本对称性。
5. 请给出密勒指数的定义。
6. 典型的晶体结构（简单或复式格⼦，原胞，基⽮，基元坐标）。
7. 给出三维、⼆维晶格倒易点阵的定义。
8. 请给出晶体衍射的布喇格定律。
9. 给出布⾥渊区的定义。
10. 晶体的解理⾯是⾯指数低的晶⾯还是指数⾼的晶⾯？为什么？11. 写出晶体衍射的结构因⼦。
12. 请描述离⼦晶体、共价晶体、⾦属晶体、分⼦晶体的结合⼒形式。
13. 写出分⼦晶体的雷纳德-琼斯势表达式，并简述各项的来源。
14. 请写出晶格振动的波恩-卡曼边界条件。
15. 请给出晶体弹性波中光学⽀、声学⽀的数⽬与晶体原胞中基元原⼦数⽬之间的关系以及光学⽀、声学⽀各⾃的振动特点。
（晶体含N个原胞，每个原胞含p个原⼦，问该晶体晶格振动谱中有多少个光学⽀、多少个声学⽀振动模式？）16. 给出声⼦的定义。
17. 请描述⾦属、绝缘体热容随温度的变化特点。
18. 在晶体热容的计算中，爱因斯坦和德拜分别做了哪些基本假设。
19. 简述晶体热膨胀的原因。
20. 请描述晶体中声⼦碰撞的正规过程和倒逆过程。
21. 分别写出晶体中声⼦和电⼦分别服从哪种统计分布（给出具体表达式）？22. 请给出费⽶⾯、费⽶能量、费⽶波⽮、费⽶温度、费⽶速度的定义。
23. 写出⾦属的电导率公式。
24. 给出魏德曼-夫兰兹定律。
25. 简述能隙的起因。
26. 请简述晶体周期势场中描述电⼦运动的布洛赫定律。
27. 请给出在⼀级近似下，布⾥渊区边界能隙的⼤⼩与相应周期势场的傅⽴叶分量之间的关系。
28. 给出空⽳概念。
一、名词解释1。
晶态-—晶态固体材料中的原子有规律的周期性排列,或称为长程有序.2。
非晶态-—非晶态固体材料中的原子不是长程有序地排列，但在几个原子的范围内保持着有序性，或称为短程有序。
3.准晶-—准晶态是介于晶态和非晶态之间的固体材料，其特点是原子有序排列，但不具有平移周期性.4.单晶-—整块晶体内原子排列的规律完全一致的晶体称为单晶体。
5。
多晶--由许多取向不同的单晶体颗粒无规则堆积而成的固体材料.6.理想晶体（完整晶体）——内在结构完全规则的固体，由全同的结构单元在空间无限重复排列而构成。
7.空间点阵（布喇菲点阵）--晶体的内部结构可以概括为是由一些相同的点子在空间有规则地做周期性无限重复排列，这些点子的总体称为空间点阵。
8。
节点（阵点）-—空间点阵的点子代表着晶体结构中的相同位置，称为节点（阵点）。
9。
点阵常数（晶格常数)-—惯用元胞棱边的长度。
10。
晶面指数—描写布喇菲点阵中晶面方位的一组互质整数.11。
配位数—晶体中和某一原子相邻的原子数.12。
致密度—晶胞内原子所占的体积和晶胞体积之比。
13.原子的电负性—原子得失价电子能力的度量；电负性＝常数（电离能＋亲和能）14.肖特基缺陷—晶体内格点原子扩散到表面，体内留下空位.15.费仑克尔缺陷——晶体内格点原子扩散到间隙位置，形成空位－填隙原子对。
16。
色心—-晶体内能够吸收可见光的点缺陷。
17.F心——离子晶体中一个负离子空位，束缚一个电子形成的点缺陷。
18。
V心——离子晶体中一个正离子空位，束缚一个空穴形成的点缺陷。
19.近邻近似-—在晶格振动中，只考虑最近邻的原子间的相互作用。
20。
Einsten模型-—在晶格振动中，假设所有原子独立地以相同频率ωE振动。
21.Debye模型—-在晶格振动中,假设晶体为各向同性连续弹性媒质,晶体中只有3支声学波，且ω=vq .22.德拜频率ωD──Debye模型中g（ω）的最高频率。
23.爱因斯坦频率ωE──Einsten模型中g（ω）的最可几频率。
第一章1.凝聚态物质包括哪些？-液体、固体、介于其间的软物质（液晶、凝胶等）2.固体可分为哪些类型？-晶体、准晶体、非晶体3.什么是晶格？什么是晶体结构？晶体中原子的规则排列称为晶格；晶体中原子的具体排列形式称为晶体结构 。
4.常见的晶体结构有哪些？-简单立方晶体结构sc 、体心立方晶体结构bcc 、密堆晶体结构、金刚石晶体结构、NaCl 结构、CsCl 晶体结构、闪锌矿晶体结构、钙钛矿（ABO3）结构5.什么是配位数？-XX 晶体结构的配位数是多少？配位数：每个原子周围最近邻原子数；简单立方晶体结构（配位数6）、体心立方结构（8）、面心立方结构（12）、六角密堆结构（12）、金刚石晶体结构（4）6.试画出简单立方结构、体心立方结构、面心立方结构、六角密堆结构、金刚石结构等晶体结构图。
7.举例说明什么是简单晶格？什么是复式晶格？-简单晶格（布拉维格子）：所有原子完全等价，作从一个原子到另一任意原子的平移，晶格完全复原，如sc 、fcc 、bcc 结构形成的晶格；复式格子：晶格结构中，存在两种或两种以上不等价的原子或离子，作从一个原子或离子到任意一个不等价的原子或离子的平移，晶格不能复原，如hcp 结构、金刚石结构、NaCl 结构8.什么是基元？简单晶格和复式晶格的基元各有什么特点？-一个最小的、完全等价的基本结构单元；简单晶格的基元只含一个原子，复式晶格的基元中含两个以上的原子或离子。
9.什么是结点？什么是点阵？点阵与晶体结构的逻辑关系是什么？-就晶格的平移对称性而言，忽略结构中基元内原子分布的细节，用来代表基元的几何点成为结点；点阵是反映晶格平移对称性的分位点的无限阵列；<点阵>+<基元>=<晶体结构>10.什么是点阵的基矢？什么是破缺的平移对称性？-对于一个给定的点阵，可以使矢量332211→→→→++=a l a l a l R l 的三个不共面的基本平移矢量a1、a2、a3；晶格并不对任意的平移不变，而只对一组离散平移矢量RL （L 为小写取整数）具有不变性的性质。
固体物理习题集第一章 晶体的结构1. 解理面是面指数低的晶面还是指数高的晶面？为什么？[解答] 晶体容易沿解理面劈裂，说明平行于解理面的原子层之间的结合力弱，即平行解理面的原子层的间距大. 因为面间距大的晶面族的指数低, 所以解理面是面指数低的晶面.2. 在结晶学中, 晶胞是按晶体的什么特性选取的?[解答]在结晶学中, 晶胞选取的原则是既要考虑晶体结构的周期性又要考虑晶体的宏观对称性.3. 在晶体衍射中，为什么不能用可见光？[解答] 晶体中原子间距的数量级为1010-米，要使原子晶格成为光波的衍射光栅，光波的波长应小于1010-米. 但可见光的波长为7.6−4.0710-⨯米, 是晶体中原子间距的1000倍. 因此, 在晶体衍射中，不能用可见光.4. 高指数的晶面族与低指数的晶面族相比, 对于同级衍射, 哪一晶面族衍射光弱? 为什么?[解答] 对于同级衍射, 高指数的晶面族衍射光弱, 低指数的晶面族衍射光强. 低指数的晶面族面间距大, 晶面上的原子密度大, 这样的晶面对射线的反射(衍射)作用强. 相反, 高指数的晶面族面间距小, 晶面上的原子密度小, 这样的晶面对射线的反射(衍射)作用弱. 另外, 由布拉格反射公式λθn sin 2=hkl d 可知, 面间距hkl d 大的晶面, 对应一个小的光的掠射角θ. 面间距hkl d 小的晶面, 对应一个大的光的掠射角θ. θ越大, 光的透射能力就越强, 反射能力就越弱.5. 温度升高时, 衍射角如何变化? X 光波长变化时, 衍射角如何变化?[解答] 温度升高时, 由于热膨胀, 面间距hkl d 逐渐变大. 由布拉格反射公式λθn sin 2=hkl d 可知, 对应同一级衍射, 当X 光波长不变时, 面间距hkl d 逐渐变大, 衍射角θ逐渐变小.所以温度升高, 衍射角变小.当温度不变, X 光波长变大时, 对于同一晶面族, 衍射角θ随之变大.第二章 晶体的结合1.是否有与库仑力无关的晶体结合类型?[解答] 共价结合中, 电子虽然不能脱离电负性大的原子, 但靠近的两个电负性大的原子可以各出一个电子, 形成电子共享的形式, 即这一对电子的主要活动范围处于两个原子之间, 通过库仑力, 把两个原子连接起来. 离子晶体中, 正离子与负离子的吸引力就是库仑力. 金属结合中, 原子实依靠原子实与电子云间的库仑力紧紧地吸引着. 分子结合中, 是电偶极矩把原本分离的原子结合成了晶体. 电偶极矩的作用力实际就是库仑力. 氢键结合中, 氢先与电负性大的原子形成共价结合后, 氢核与负电中心不在重合, 迫使它通过库仑力再与另一个电负性大的原子结合. 可见, 所有晶体结合类型都与库仑力有关.2.如何理解库仑力是原子结合的动力?[解答] 晶体结合中, 原子间的排斥力是短程力, 在原子吸引靠近的过程中, 把原本分离的原子拉近的动力只能是长程力, 这个长程吸引力就是库仑力. 所以, 库仑力是原子结合的动力.3.晶体的结合能, 晶体的内能, 原子间的相互作用势能有何区别?[解答]自由粒子结合成晶体过程中释放出的能量, 或者把晶体拆散成一个个自由粒子所需要的能量, 称为晶体的结合能.原子的动能与原子间的相互作用势能之和为晶体的内能.在0K 时, 原子还存在零点振动能. 但零点振动能与原子间的相互作用势能的绝对值相比小得多. 所以, 在0K 时原子间的相互作用势能的绝对值近似等于晶体的结合能.4.原子间的排斥作用取决于什么原因?[解答] 相邻的原子靠得很近, 以至于它们内层闭合壳层的电子云发生重叠时, 相邻的原子间便产生巨大排斥力. 也就是说, 原子间的排斥作用来自相邻原子内层闭合壳层电子云的重叠.5. 原子间的排斥作用和吸引作用有何关系? 起主导的范围是什么?[解答] 在原子由分散无规的中性原子结合成规则排列的晶体过程中, 吸引力起到了主要作用. 在吸引力的作用下, 原子间的距离缩小到一定程度, 原子间才出现排斥力. 当排斥力与吸引力相等时, 晶体达到稳定结合状态. 可见, 晶体要达到稳定结合状态, 吸引力与排斥力缺一不可. 设此时相邻原子间的距离为0r , 当相邻原子间的距离r >0r 时, 吸引力起主导作用; 当相邻原子间的距离r <0r 时, 排斥力起主导作用.6. 共价结合, 两原子电子云交迭产生吸引, 而原子靠近时, 电子云交迭会产生巨大的排斥力, 如何解释?[解答] 共价结合, 形成共价键的配对电子, 它们的自旋方向相反, 这两个电子的电子云交迭使得体系的能量降低, 结构稳定. 但当原子靠得很近时, 原子内部满壳层电子的电子云交迭, 量子态相同的电子产生巨大的排斥力, 使得系统的能量急剧增大.7.为什么许多金属为密积结构?[解答] 金属结合中, 受到最小能量原理的约束, 要求原子实与共有电子电子云间的库仑能要尽可能的低(绝对值尽可能的大). 原子实越紧凑, 原子实与共有电子电子云靠得就越紧密, 库仑能就越低. 所以, 许多金属的结构为密积结构.12.?[解答]如上图所示, 0r 附近的力曲线越陡, 当施加一定外力, 固体的形变就越小. 0r 附近力曲线的斜率决定了固体的弹性性质. 而0r 附近力曲线的斜率主要取决于排斥力. 因此, 固体的弹性强弱主要由排斥作用决定.第三章 晶格振动与晶体热学性质1. 什么叫简正振动模式？简正振动数目、格波数目或格波振动模式数目是否是一回事？[解答] 为了使问题既简化又能抓住主要矛盾，在分析讨论晶格振动时，将原子间互作用力的泰勒级数中的非线形项忽略掉的近似称为简谐近似. 在简谐近似下, 由N 个原子构成的晶体的晶格振动, 可等效成3N 个独立的谐振子的振动. 每个谐振子的振动模式称为简正振动模式, 它对应着所有的原子都以该模式的频率做振动, 它是晶格振动模式中最简单最基本的振动方式. 原子的振动, 或者说格波振动通常是这3N 个简正振动模式的线形迭加.简正振动数目、格波数目或格波振动模式数目是一回事, 这个数目等于晶体中所有原子的自由度数之和, 即等于3N .2. 长光学支格波与长声学支格波本质上有何差别?[解答] 长光学支格波的特征是每个原胞内的不同原子做相对振动, 振动频率较高, 它包含了晶格振动频率最高的振动模式. 长声学支格波的特征是原胞内的不同原子没有相对位移, 原胞做整体运动, 振动频率较低, 它包含了晶格振动频率最低的振动模式, 波速是一常数. 任何晶体都存在声学支格波, 但简单晶格(非复式格子)晶体不存在光学支格波.3. 温度一定，一个光学波的声子数目多呢, 还是声学波的声子数目多?[解答] 频率为ω的格波的(平均) 声子数为11)(/-=T k B e n ωω .因为光学波的频率O ω比声学波的频率A ω高, (1/-T k B O eω )大于(1/-T k B A e ω ), 所以在温度一定情况下, 一个光学波的声子数目少于一个声学波的声子数目.4. 对同一个振动模式, 温度高时的声子数目多呢, 还是温度低时的声子数目多?[解答] 设温度T H >T L , 由于(1/-H B T k eω )小于(1/-L B T k e ω ), 所以温度高时的声子数目多于温度低时的声子数目. 5. 高温时, 频率为ω的格波的声子数目与温度有何关系?[解答] 温度很高时, 1/-≈ωω T k B e, 频率为ω的格波的(平均) 声子数为 11)(/-=T k B e n ωω ω T k B ≈.可见高温时, 格波的声子数目与温度近似成正比.6. 在甚低温下, 不考虑光学波对热容的贡献合理吗?[解答] 参考本教科书（3.119）式, 可得到光学波对热容贡献的表达式2//2)1(d )(maxmin -⎪⎪⎭⎫ ⎝⎛=⎰T k O T k B B VO B B O O e D e T k k C ωωωωωωω . 在甚低温下, 对于光学波, T k B e/ω 1>>, 上式简化为ωωωωωωd )(/2maxmin O T k B B VO D e T k k C B O O -⎰⎪⎪⎭⎫ ⎝⎛=. 以上两式中)(ωO D 是光学波的模式密度, 在简谐近似下, 它与温度无关. 在甚低温下,0)/(/→-T e T k B ω , 即光学波对热容的贡献可以忽略. 也就是说, 在甚低温下, 不考虑光学波对热容的贡献是合理的.从声子能量来说, 光学波声子的能量O ω 很大(大于短声学波声子的能量), 它对应振幅很大的格波的振动, 这种振动只有温度很高时才能得到激发. 因此, 在甚低温下, 晶体中不存在光学波.7. 在甚低温下, 德拜模型为什么与实验相符?[解答] 在甚低温下, 不仅光学波得不到激发, 而且声子能量较大的短声学格波也未被激发, 得到激发的只是声子能量较小的长声学格波. 长声学格波即弹性波. 德拜模型只考虑弹性波对热容的贡献. 因此, 在甚低温下, 德拜模型与事实相符, 自然与实验相符.第四章 晶体中电子能带理论1. 波矢空间与倒格空间有何关系? 为什么说波矢空间内的状态点是准连续的?[解答] 波矢空间与倒格空间处于统一空间, 倒格空间的基矢分别为321 b b b 、、, 而波矢空间的基矢分别为32N N / / /321b b b 、、1N , N 1、N 2、N 3分别是沿正格子基矢321 a a a 、、方向晶体的原胞数目.倒格空间中一个倒格点对应的体积为*321) (Ω=⨯⋅b b b ,波矢空间中一个波矢点对应的体积为N N b N b N b *332211)(Ω=⨯⋅,即波矢空间中一个波矢点对应的体积, 是倒格空间中一个倒格点对应的体积的1/N . 由于N 是晶体的原胞数目, 数目巨大, 所以一个波矢点对应的体积与一个倒格点对应的体积相比是极其微小的. 也就是说, 波矢点在倒格空间看是极其稠密的. 因此, 在波矢空间内作求和处理时, 可把波矢空间内的状态点看成是准连续的.2. 当电子的波矢落在布里渊区边界上时, 其有效质量何以与真实质量有显著差别?[解答] 晶体中的电子除受外场力的作用外, 还和晶格相互作用. 设外场力为F , 晶格对电子的作用力为F l , 电子的加速度为)(1l m F F a +=.但F l 的具体形式是难以得知的. 要使上式中不显含F l , 又要保持上式左右恒等, 则只有F a *1m =.显然, 晶格对电子的作用越弱, 有效质量m*与真实质量m 的差别就越小. 相反, 晶格对电子的作用越强, 有效质量m *与真实质量m 的差别就越大. 当电子的波矢落在布里渊区边界上时, 与布里渊区边界平行的晶面族对电子的散射作用最强烈. 在晶面族的反射方向上, 各格点的散射波相位相同, 迭加形成很强的反射波. 正因为在布里渊区边界上的电子与晶格的作用很强, 所以其有效质量与真实质量有显著差别.3. 紧束缚模型电子的能量是正值还是负值?[解答] 紧束缚模型电子在原子附近的几率大, 远离原子的几率很小, 在原子附近它的行为同在孤立原子的行为相近. 因此，紧束缚模型电子的能量与在孤立原子中的能量相近. 孤立原子中电子的能量是一负值, 所以紧束缚模型电子的能量是负值. s 态电子能量(5.60)表达式∑⋅--=n i s s at s s ne J C E E R k k )(即是例证. 其中孤立原子中电子的能量at s E 是主项, 是一负值, s s J C --和是小量, 也是负值.4. 紧束缚模型下, 内层电子的能带与外层电子的能带相比较, 哪一个宽? 为什么?[解答] 以s 态电子为例. 由图5.9可知, 紧束缚模型电子能带的宽度取决于积分s J 的大小, 而积分rR r R r r r d )()]()([)(*n at s n at N at s s V V J ----=⎰ϕϕΩ 的大小又取决于)(r ats ϕ与相邻格点的)(n at s R r -ϕ的交迭程度. 紧束缚模型下, 内层电子的)(r at s ϕ与)(n at s R r -ϕ交叠程度小, 外层电子的)(r at s ϕ与)(n at s R r -ϕ交迭程度大. 因此, 紧束缚模型下, 内层电子的能带与外层电子的能带相比较, 外层电子的能带宽.5. 一维简单晶格中一个能级包含几个电子?[解答] 设晶格是由N 个格点组成, 则一个能带有N 个不同的波矢状态, 能容纳2N 个电子. 由于电子的能带是波矢的偶函数, 所以能级有(N /2)个. 可见一个能级上包含4个电子.6. 本征半导体的能带与绝缘体的能带有何异同?[解答] 在低温下, 本征半导体的能带与绝缘体的能带结构相同. 但本征半导体的禁带较窄, 禁带宽度通常在2个电子伏特以下. 由于禁带窄, 本征半导体禁带下满带顶的电子可以借助热激发, 跃迁到禁带上面空带的底部, 使得满带不满, 空带不空, 二者都对导电有贡献.第五章 自由电子论和电子的输运性质1.如何理解电子分布函数)(E f 的物理意义是: 能量为E 的一个量子态被电子所占据的平均几率?[解答] 金属中的价电子遵从费密-狄拉克统计分布, 温度为T 时, 分布在能级E 上的电子数目1/)(+=-T k E E B F e g n ,g 为简并度, 即能级E 包含的量子态数目. 显然, 电子分布函数11)(/)(+=-T k E E B F e E f是温度T 时, 能级E 的一个量子态上平均分布的电子数. 因为一个量子态最多由一个电子所占据, 所以)(E f 的物理意义又可表述为: 能量为E 的一个量子态被电子所占据的平均几率.2.绝对零度时, 价电子与晶格是否交换能量?[解答] 晶格的振动形成格波，价电子与晶格交换能量，实际是价电子与格波交换能量. 格波的能量子称为声子, 价电子与格波交换能量可视为价电子与声子交换能量. 频率为i ω的格波的声子数11/-=T k i B i e n ω .从上式可以看出, 绝对零度时, 任何频率的格波的声子全都消失. 因此, 绝对零度时, 价电子与晶格不再交换能量.3.为什么温度升高, 费密能反而降低?[解答] 当0≠T 时, 有一半量子态被电子所占据的能级即是费密能级. 温度升高, 费密面附近的电子从格波获取的能量就越大, 跃迁到费密面以外的电子就越多, 原来有一半量子态被电子所占据的能级上的电子就少于一半, 有一半量子态被电子所占据的能级必定降低. 也就是说, 温度升高, 费密能反而降低4.为什么价电子的浓度越高, 电导率越高?[解答] 电导σ是金属通流能力的量度. 通流能力取决于单位时间内通过截面积的电子数(参见思考题18). 但并不是所有价电子对导电都有贡献, 对导电有贡献的是费密面附近的电子. 费密球越大, 对导电有贡献的电子数目就越多. 费密球的大小取决于费密半径3/12)3(πn k F =.可见电子浓度n 越高, 费密球越大, 对导电有贡献的电子数目就越多, 该金属的电导率就越高.5.霍耳电场与洛伦兹力有何关系?[解答] 霍耳电场是导电电子在洛伦兹力作用下产生的. 设金属的长度方向为x 轴, 电场ε沿x 方向, 磁场B 沿z 轴方向, 金属的宽度方向为y 轴方向. 在此情况下, 运动的电子将受到洛伦兹力)(B v F ⨯-=e的作用. 该作用力指向负y 方向, 使电子在运动过程中向负y 方向偏转, 致使负y 侧面的电子浓度增大, 正y 侧面的电子浓度减小. 其结果, 如下图所示, 使得导体的宽度方向产生了一个附加电场y ε, 即霍耳电场.6.如何通过实验来测定载流子是电子还是空穴?[解答] 由(6.109)可以看出, 电子导电材料的霍耳系数是一负值. 通过实验测定出材料的霍耳系数, 若霍耳系数是负值, 则可断定载流子是电子, 若霍耳系数是正值, 则可断定载流子是空穴.22222222l k h a al a k a h d hkl hkl ++=++==k j i K πππππ)(12t qna i n Be u ω-+=)(2t qna i n Ae u ω-=()2/12/1222121222212sin 16422⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-±+qa m m m m ββββββ()a k a k a k J C E E z y x s s at s s cos cos cos 2)(++--=k 试题1.对晶格常数为a 的SC 晶体,与正格矢R =a i +2a j +2a k 正交的倒格子晶面族的面指数为( 122 ), 其面间距为( a 32π).2.典型离子晶体的体积为V , 最近邻两离子的距离为R , 晶体的格波数目为( 33R V), 长光学波的( 纵 )波会引起离子晶体宏观上的极化.3. 金刚石晶体的结合类型是典型的(共价结合)晶体, 它有( 6 )支格波.4. 两种不同金属接触后, 费米能级高的带(正)电.对导电有贡献的是 (费米面附近)的电子.5. 设晶格常数为a , 求立方晶系密勒指数为(hkl )的晶面族的面间距？ 立方晶系密勒指数为(hkl )的晶面族的面间距6.设质量为m 的同种原子组成的一维双原子分子链, 分子内部的力系数为β1, 分子间相邻原子的力系数为β2, 分子的两原子的间距为d , 晶格常数为a ,（1）.列出原子运动方程.（2）.求出格波的振动谱ω(q ).解：（1）原子运动方程 （2） 格波的振动谱ω(q )＝ 7. 对于晶格常数为a 的SC 晶体 （1.）以紧束缚近似求非简并s 态电子的能带.（2）.画出第一布里渊区[110]方向的能带曲线, 求出带宽.（3）.当电子的波矢k =a πi +a πj 时,求导致电子产生布拉格反射的晶面族的面指数.解 ：（1）. 紧束缚近似非简并s 态电子的能带（2） 第一布里渊区[110]方向的能带曲线[110]方向的能带曲线带宽为8J s 。
