当前位置：文档之家 › On the Towers of Hanoi problem with multiple spare pegs

On the Towers of Hanoi problem with multiple spare pegs

  • 格式：pdf
  • 大小：108.57 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

POJ 动态规划题目列表

POJ 动态规划题目列表

[1]POJ动态规划题目列表容易： 1018, 1050, 1083, 1088, 1125, 1143, 1157, 1163, 1178, 1179, 1189, 1208, 1276, 1322, 1414, 1456, 1458, 1609, 1644, 1664, 1690, 1699, 1740(博弈), 1742, 1887, 1926(马尔科夫矩阵，求平衡）, 1936,1952, 1953, 1958, 1959, 1962, 1975, 1989, 2018, 2029,2039, 2063, 2081, 2082,2181, 2184, 2192, 2231, 2279, 2329, 2336, 2346, 2353,2355, 2356, 2385, 2392, 2424,不易： 1019,1037, 1080, 1112, 1141, 1170, 1192, 1239, 1655, 1695, 1707,1733(区间减法加并查集), 1737, 1837, 1850, 1920(加强版汉罗塔), 1934(全部最长公共子序列), 1937(计算几何), 1964(最大矩形面积，O(n)算法), 2138, 2151, 2161(烦，没写), 2178,推荐： 1015, 1635, 1636(挺好的), 1671, 1682, 1692(优化), 1704, 1717, 1722, 1726, 1732, 1770, 1821, 1853, 1949, 2019, 2127, 2176, 2228, 2287, 2342, 2374, 2378, 2384, 2411 状态 DP 树 DP 构造最优解四边形不等式单调队列1015 Jury Compromise1029 False coin1036 Gangsters1037 A decorative fence1038 Bugs Integrated, Inc.1042 Gone Fishing1050 To the Max1062 昂贵的聘礼1074 Parallel Expectations1080 Human Gene Functions1088 滑雪1093 Formatting Text1112 Team Them Up!1141 Brackets Sequence1143 Number Game1157 LITTLE SHOP OF FLOWERS 1159 Palindrome1160 Post Office1163 The Triangle1170 Shopping Offers1178 Camelot1179 Polygon1180 Batch Scheduling1185 炮兵阵地1187 陨石的秘密1189 钉子和小球1191 棋盘分割1192 最优连通子集1208 The Blocks Problem 1239 Increasing Sequences 1240 Pre-Post-erous!1276Cash Machine1293 Duty Free Shop1322 Chocolate1323Game Prediction1338 Ugly Numbers1390 Blocks1414 Life Line1432 Decoding Morse Sequences 1456 Supermarket1458 Common Subsequence1475 Pushing Boxes1485 Fast Food1505 Copying Books1513 Scheduling Lectures1579 Function Run Fun1609 Tiling Up Blocks1631 Bridging signals 2 分+DP NLOGN 1633 Gladiators 1635 Subway tree systems 1636 Prison rearrangement1644 To Bet or Not To Bet1649 Market Place1651 Multiplication Puzzle1655 Balancing Act1661 Help Jimmy1664 放苹果1671 Rhyme Schemes1682 Clans on the Three Gorges1690 (Your)((Term)((Project)))1691 Painting A Board1692 Crossed Matchings1695 Magazine Delivery1699 Best Sequence1704 Georgia and Bob1707 Sum of powers1712 Flying Stars1714 The Cave1717 Dominoes1718 River Crossing1722 SUBTRACT1726 Tango Tango Insurrection 1732 Phone numbers1733 Parity game1737 Connected Graph1740 A New Stone Game1742 Coins P1745 Divisibility1770 Special Experiment1771 Elevator Stopping Plan 1776 Task Sequences1821 Fence1837 Balance1848 Tree1850 Code1853 Cat1874 Trade on Verweggistan 1887 Testing the CATCHER 1889 Package Pricing1920 Towers of Hanoi1926 Pollution1934 Trip1936 All in All1937 Balanced Food1946 Cow Cycling1947 Rebuilding Roads1949 Chores1952 BUY LOW, BUY LOWER 1953 World Cup Noise1958 Strange Towers of Hanoi 1959 Darts1962 Corporative Network 1964 City Game1975 Median Weight Bead 1989 The Cow Lineup2018 Best Cow Fences2019 Cornfields2029 Get Many Persimmon Trees2033 Alphacode2039 To and Fro2047 Concert Hall Scheduling2063 Investment2081 Recaman's Sequence2082 Terrible Sets2084 Game of Connections2127 Greatest Common Increasing Subsequence 2138 Travel Games2151 Check the difficulty of problems2152 Fire2161 Chandelier2176 Folding2178 Heroes Of Might And Magic2181 Jumping Cows2184 Cow Exhibition2192 Zipper2193 Lenny's Lucky Lotto Lists2228 Naptime 2231 Moo Volume2279 Mr. Young's Picture Permutations2287 TianJi -- The Horse Racing 2288 Islands and Bridges2292 Optimal Keypad2329 Nearest number - 22336 Ferry Loading II2342 Anniversary party2346 Lucky tickets2353 Ministry2355 Railway tickets2356 Find a multiple2374 Fence Obstacle Course2378 Tree Cutting2384 Harder Sokoban Problem2385 Apple Catching2386 Lake Counting2392 Space Elevator2397 Spiderman2411 Mondriaan's Dream2414 Phylogenetic Trees Inherited 2424 Flo's Restaurant2430 Lazy Cows2915 Zuma3017 Cut the Sequence 3028 Shoot-out3124 The Bookcase3133 Manhattan Wiring 3345 Bribing FIPA3375 Network Connection 3420 Quad Tiling ?。

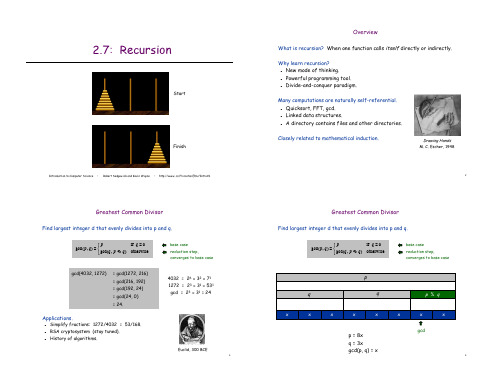
Recursive algorithm

Recursive algorithm

just did this
int N = Integer.parseInt(args[0]); int width = 512; int height = (int) (2 * width / Math.sqrt(3)); double size = width / Math.pow(3.0, N); StdDraw.create(width, height); StdDraw.go(0, width * Math.sqrt(3) / 2); StdDraw.penDown(); koch(N, size); StdDraw.rotate(-120); koch(N, size); StdDraw.rotate(-120); koch(N, size); draw it StdDraw.show(); } }
•
http://w w w .cs.Pri /IntroCS
2
Greatest Common Divisor
Find largest integer d that evenly divides into p and q.
"p if q = 0 gcd( p, q) = # $ gcd(q, p % q) otherwise
! ! ! ! ! ! !
n=0
n=1
!
n=2
n=3
Java implementation.
public static int gcd(int p, int q) { if (q == 0) return p; else return gcd(q, p % q); }
base case reduction step
base case reduction step, converges to base case

THE HANOI-TOWER BY RECURSION AND THE UNREAL TOWERS OF HANOI

THE HANOI-TOWER BY RECURSION AND THE UNREAL TOWERS OF HANOI

河內塔的遞歸實現與並非現實的河內塔THE HANOI-TOWER BY RECURSION AND THE UNREAL TOWERS OF HANOI位於印度北部，世界中心，有一貝拿勒斯聖廟，其中的三根石柱上串著64枚金盤。

婆羅門們，不分晝夜地在三根柱子間移動著這些金片，孜孜不倦～只為一個古老的傳言，即當所有盤子移動完畢，世界將於一聲霹靂中消滅，而梵塔、廟宇和眾生則將隨之同歸於盡。

而預有此言者就是上面這位，印度傳說中的創世之神—大梵天。

顯然這又是一個世界末日預言，其哲學理學思想之深邃不禁使後人產生無止地辯論與無盡的遐想。

時至今日，它已然成了一科人人樂於稱道的世界著名學問分支—梵天寺之塔問題(Tower of Brahma puzzle)。

河內塔，或音譯為漢諾塔，1結構如下圖。

不必細述。

1婆羅門所要做的是所要做的是將一根柱子上的所有盤片移動到另一根上，當然它有它的法則，看似易如反掌的事就是在這些法則下變得遙不可及。

法則：一次只能移動一個盤片；不能把小盤片置於大盤片上。

當然了，三根柱子我們都要用到。

原理剖析：區區64個盤片，移動多少步能完成呢？順著想不容易，不如我們逆過來思考。

我們看：以5塊盤片為例，想要把第5塊移動到C上。

1.先須把前4塊移動到B。

2.再把第5塊移到C。

3.最後重複移動前4塊的方法，把前4塊移到C。

如下圖。

則移動5塊的次數=2倍的移動4塊的次數+1次。

那麼推廣開來，移動n塊的次數=2倍的移動(n-1)塊的次數+1次。

據說，最早發明這個問題的人是法國數學家爱德华•卢卡斯。

從數學上我們來做下證明：其實也不是逆證，順推而已。

假設有n個盤片，移動的次數為f(n).如以上所述f(5)=2*f(4)+1;則f(n)=2*f(n-1)+1=2*[2*f(n-2)+1]+1-----------------------------------------------------------------展開 =2^2*f(n-2)+2^1+1……=2^(n-1)f(1)+2^(n-2)+2^(n-3)+...+2^1+1-------------------最後形式顯然，f(1)=1則 f(n)=2^(n-1)+{2^(n-2)[1-(1/2)^(n-1)]}/(1-1/2)=2^(n-1)+2^(n-1)-2^(n-1)*(1/2)^(n-1)=2^n-1完畢。

3-4 汉诺塔问题

3-4 汉诺塔问题

The tower of HanoiGiven three towers, or peg A, B and C. Three rings are piled in decreasing size on A, and the other pegs areempty. We want to move the rings from A to one of the other pegs. The rule is that rings are to be moved one at a time. but a larger ring may never be placed atop a smaller one.3-ring puzzleThis puzzle can be solved in seven steps:1. move the top ring from A to B2. move the top ring from A to C3. move the top ring from B to C4. move the top ring from A to B5. move the top ring from C to A6. move the top ring from C to B7. move the top ring from A to B1 move the smallest ring to the peg residing nextto it in clockwise order;2 make the only legal move possible that doesnot involve the smallest ringA time analysis shows that the number of single-ring moves it produces is precisely 2N-1Tibetan monks's gameThe original version of the puzzle had the same three pegs. and it involved 64 rings, moved by Tibetan monks. If the monks were to move one ring every five seconds. It would take them almost three trillion vears to get the job done.No wonder they believed the world would end before they managed to finish.。

国外Advanced Cognitive Psychology课程课件-Problem solving

国外Advanced Cognitive Psychology课程课件-Problem solving

Characteristics of insight problems
• People initially have no idea how to solve the problem • There is no linear “feeling of warmth”
– There is no sense that one is getting closer to solving the problem.
• Each of these new sub-problems needs to be solved
Working backward
• Sometimes it is hard to solve a problem by starting at the initial state
– Many puzzles are intentionally designed to be hard to solve from the givens.
• How can the initial state be modified?
– Obstacles
• Something that stands between the initial state and the goal. • What would happen if one of these aspects were missing?
– Domain general heuristics for solving problems – Best for well-defined problems
• No real mechanisms for dealing with illdefined problems • Domain knowledge needed for this.

堆与栈

堆与栈
Chapter5 堆栈(Stacks)
1. 2.
3. 4. 5.
The Abstract Data Type Derived Classes and Inheritance Formula-Based Representation Linked Representation Applications
8/7/2013 23
比较
1. 2. 3. 4.
链式栈无栈满问题，空间可扩充 插入与删除仅在栈顶处执行 链式栈的栈顶在链头 适合于多栈操作
8/7/2013
24
应用
1. 2. 3.
4. 5.
6.
括号匹配(Parenthesis Matching) 汉诺塔(Towers of Hanoi) 火车车厢重排(Rearranging Railroad Cars) 开关盒布线(Switch Box Routing) 离 线 等 价 类 (Offline Equivalence Problem) 迷宫老鼠(Rat in a Maze)
8/7/2013
12
删除栈顶元素，并将其送入x
template<class T> Stack<T>& Stack<T>::Delete(T& x) { if (IsEmpty()) throw OutOfBounds(); x = stack[top--]; return *this; } 复杂性?
自定义Stack
template<class T> class Stack{ // LIFO 对象 public: Stack(int MaxStackSize = 10); ~Stack () {delete [] stack;} bool IsEmpty() const {return top == -1;} bool IsFull() const {return top == MaxTo p ; } T Top() const; Stack<T>& Add(const T& x); Stack<T>& Delete(T& x); private : int top; // 栈顶 int MaxTop; // 最大的栈顶值 T *stack; // 堆栈元素数组 8/7/2013 9 } ;

大学英语课程 资料结构 Chapter 1 Basic Concepts

Are the two additions same ?
1-4
Abstract Data Type
• Native data type
– int (not realistic integer), float (real number), char – hardware implementation
Data Structures
Chapter 1: Basic Concepts
1-1
Bit and Data Type
• bit: basic unit of information. • data type: interpretation of a bit pattern. e.g. 0100 0001 integer 65 ASCII code ’A’ BCD 41 (binary coded decimal)
Recursion for Binary Search
int BinarySearch (int *a, int x, const int left, const int right) //Search a[left], ..., a[right] for x { if (left <= right) { int middle = (left + right)/2; if (x < a[middle]) return BinarySearch(a, x, left, middle-1); else if (x > a[middle]) return BinarySearch(a, x, middle+1, right); else return middle; } // end of if return -1;// not found 1-12 }

Shortest paths in the Tower of Hanoi graph and finite automata


1. Introduction
The Tower of Hanoi puzzle, invented in 1883 by the French mathematician Edouard Lucas, has become a classic example in the analysis of algorithms and discrete mathematical structures (see e.g. [2], 1.1). The puzzle consists of n discs of different sizes, stacked on three vertical pegs, in such a way that no disc lies on top of a smaller disc. A permissible move is to take the top disc from one of the pegs and move it to one of the other pegs, as long as it is not placed on top of a smaller disc. The set of states of the puzzle, together with the permissible moves, thus forms a graph in a natural way. The number of vertices in the n-disc Hanoi graph is 3n .
in the length of the shortest path, then our algorithm is typically about twice as fast as the algorithm proposed by Hinz [5] (with a small constant overhead due to the initial 1.66 discs), since it overrides the need to compute both the distance for the path that moves the largest disc once, and the path that moves it twice. The paper is organized as follows: In the next section, we define the discrete Sierpi´ nski gasket graph, a graph which is isomorphic to the Tower of Hanoi sபைடு நூலகம்ate graph, but for which the labeling of the vertices is simpler to understand. In section 3, we present the main ideas for this graph, and then in section 4 show how to translate the results to the Hanoi graph by a re-labeling of the vertices. In section 5 we perform a probabilistic analysis of the finite-state machine, to compute the average number 63 38 of discs that need to be read in order to decide whether the largest disc will be moved 466 n · 2 for once or twice, and to give a new derivation of the asymptotic value 885 the average distance between two random states in the n-disc Hanoi graph.

e05


void main(void) { cout << "What is the size of the board? "; cin >> board_size; if (board_size<0 || board_size>max_board) cout<<"The number must be between 0 and " <<max_board<<endl; else { Backtrack(0); out<<"\nThe number of solution Queen is "<<sum<<endl; out.close(); } }
Chapter 5 RECURSION
1. Introduction to Recursion 2. Principles of Recursion
3. Backtracking: Postponing the Work 4. Tree-Structured Programs:
Look-Ahead in Games 5. Pointers and Pitfalls
Four Queens Solution Please seelve the problem using recursive :
#include <math.h> #include <fstream.h> # define max_board 30 int sum=0; // 计数所得解数目 int x[max_board]; // 存放当前解的向量 int board_size; // 皇后个数 ofstream out(“Queen.out”); // 声明并且打开输出文件流 void Backtrack(int); // 递归回溯法

java 递归


Recursive Programming
// This method returns the sum of 1 to num public int sum (int num) { int result; if (num == 1) result = 1; else result = num + sum (n-1); return result; }
Copyright © 2009 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
Recursive Definitions
• The recursive part of the LIST definition is used several times, terminating with the non-recursive part:
number comma LIST 24 , 88, 40, 37 number comma LIST 88 , 40, 37 number comma LIST 40 , 37 number 37
Copyright © 2009 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
Infinite Recursion
• All recursive definitions have to have a nonrecursive part • If they didn't, there would be no way to terminate the recursive path • Such a definition would cause infinite recursion • This problem is similar to an infinite loop, but the non-terminating "loop" is part of the definition itself • The non-recursive part is often called the base case
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
+ 1 + 1
Q(k; 0) = 0 Q(k; n) = Q(k; n 0 1) + 2l
1
l, at the maximum N (k; l) =
relation explains the algorithm.

k+l l

disks can be transferred. The following recurrence
1 2 1 2 1 2
Q(k; n) =
l X i=0
N (k 0 1; i)2i + (n 0 N (k; l))2l
+1
2 Upperbound
Now we will derive a simple upper bound for the total number of moves. In the last section, we found that for each disk added at level i, the total number of moves increases by 2i . So if n disks are moved using k spare pegs and the levels l, a trivial upper bound for the number of disk moves is n2l . We have to express l as a function of k and n. Let us consider all n values at the level l .
On the Towers of Hanoi problem with multiple spare pegs
Jeyakesavan Veerasamy and Ivor Page Computer Science Program, EC 31 The University of Texas at Dallas Richardson, TX 75083-0688, USA
fveerasamjivorg@ Abstract
We analyze a solution to a variant of the Towers of Hanoi problem, in which multiple spare pegs are used to move the disks from the source to the destination peg. We also discuss the interesting relation between the number of disks and the total number of disk moves when the number of spare pegs is a function of number of disks.
N (0; l) = 1 N (k; 0) = 1 N (k; l) = N (k; l 0 1) + N (k 0 1; l)
To transfer N (k; l) disks from the source peg to the destination peg, rst transfer N (k; l 0 1) disks to one of the spare pegs using k spare pegs (the destination peg is a spare peg in this phase), transfer the remaining disks N (k 0 1; l) to the destination peg using k 0 1 spare pegs, and nally transfer N (k; l 0 1) disks from the spare peg to the destination peg using k spare pegs (the source peg is a spare peg in this phase). Similarly, the following equation is the result of applying this 3 stage process to N (k; l + 1) disks.
l where l is de ned by the inequality, k l00 < n k l l , and n is said to be at the level l. Fig.1 shows the piecewise linear nature of Q(k; n) verses n. It is clear that the total number of disk moves increases by 2i for each disk added at level i. Using k spare pegs and the levels
3 When
Theorem 1
k
= dcn e
0
When the number of spare pegs k = dcn e where c and are constants, the total number of disk moves is linear in n.
When > 1, it is easy to see that for n > n , cn n 0 1. Once the number of spare pegs k n 0 1, Q(n; k ) = 2n 0 1. Hence the number of moves is linear in n. Now we consider 1. We have already found a simple upper bound n2l where n is the number of disks and l is the level of n. We will show this bound is linear in n, i.e. we prove that l is bounded by a constant t which is a function of c and and does not depend on n.
Towers of Hanoi, analysis of algorithms, recurrence relations, recursion
C.R. Category: F.2.2.
Keywords
1 Introduction
The Towers of Hanoi problem is well-known for its nice recursive solution. In the recent years, there has been increasing interest in several variants of the original problem. References [1-7] present a few such interesting variations. In [3], X.M.Lu discussed an optimal algorithm for the Towers of Hanoi Problem with multiple spare pegs. But it is dicult to compare his nal expression for the number of disk moves with the solution of the original problem and appreciate the improvement in the number of disk moves. In this paper, we derive a simple upper bound which enables us to understand the usefulness of additional spare pegs. We also discuss the number of disk moves required, when the number of spare pegs is a function of number of disks. The main results of [3] in slightly simpli ed form follows. Let k be the number of spare pegs (k + 2 is the total number of pegs) and n be the number of disks to be moved from the source peg to the destination peg. The total number of disk moves Q(k; n) is given by the following recurrence relation:
N (k; l 0 1) < ! k+l01 < l01 l(l + 1) 1 1 1 (l + k 0 1) < k! q k l(l + 1) 1 1 1 (l + k 0 1) < l<
n n n
2) (l + 1)(l + k! 1 1 1 (l + k) q p k !n (l + 1)(l + 2) 1 1 1 (l + k ) p p k! n l + k
Proof:
k cn ) n (k=c) = = (k=c) = (1=c) k = dk
1
where = 1= and d = 1=c .
Lemma 1
If the following inequalities hold for any constants k and t,