浙江工商大学10-11II数学分析II考试试卷B

第1页 共2页2020-2021《数学分析（二）》期末课程考试试卷B适用专业： 考试日期：试卷所需时间120分钟 闭卷 试卷总分100分一、判断题：（对的打√，错的打×，每小题2分，共10分）1、平面上两曲线22y x =与4y x =-所围成图形的面积为18。

（ ）2、若()f x 在[,]a b 上连续，2()0bafx dx =⎰，则[,]x a b ∀∈，()0f x =。

（ ） 3、级数11!n e n ∞==∑。

（ ） 4、函数列{}nx 在(0,1)上收敛且一致收敛于0。

（ ）5、幂级数2(!)(2)!nn x n ∑的收敛区域为[4,4]-。

（ ） 二、选择题：（共5小题，每小题2分，共10分）1、设()f t 在[1,1]-连续，则sin cos1()xdf t dt dx ⎰等于 （ ） (A) (sin )(cos1)f x f -；(B) (sin )cos f x x ； (C) (sin )f x ；(D) ()cos f x x 。

2、设1n n u ∞=∑是正项级数，那么下列命题正确的是： （ ）(A) 若11n n u u +< ，则1n n u ∞=∑收敛； (B) 若lim 0n n u →∞=，则1n n u ∞=∑收敛； (C) 若21nn u∞=∑收敛，则1nn u∞=∑收敛；(D) 若1nn u∞=∑的某一重排1nn v∞=∑收敛，则1nn u∞=∑收敛。

3、二元函数222(,)yf x y x y=+在点(0,0)的重极限和累次极限分别为（ ） (A) 均存在； (B) 存在，不存在； (C) 不存在，存在； (D) 均不存在。

4、下列等式中，正确的是 （ ）(A)； (B) ；(C) ； (D) 。

5、下列关于反常积分1sin p xdx x+∞⎰是条件收敛时正确的是（ ） (A)2p ≤； (B)01p <≤；(C)1p >； (D) p 为任何实数均条件收敛。

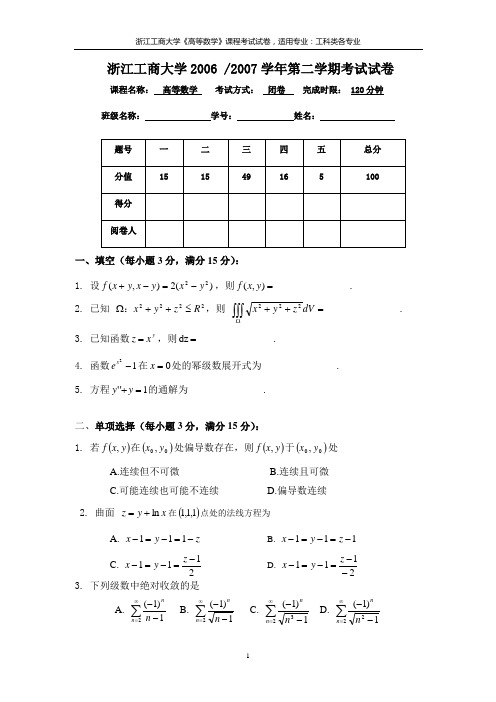
浙江工商大学2006 /2007学年第二学期考试试卷课程名称： 高等数学 考试方式： 闭卷 完成时限： 120分钟 班级名称： 学号： 姓名：一、填空（每小题3分，满分15分）：1. 设)(2),(22y x y x y x f -=-+，则=),(y x f _______________.2. 已知 2222R z y x ≤++Ω：，则 =++⎰⎰⎰ΩdV z y x 222_______________.3. 已知函数y x z =，则=dz _______________.4. 函数12-x e 在0=x 处的幂级数展开式为_______________. 5. 方程1''=+y y 的通解为_______________.二、单项选择（每小题3分，满分15分）：1. 若()y x f ,在()00,y x 处偏导数存在，则()y x f ,于()00,y x 处_______________A.连续但不可微B.连续且可微C.可能连续也可能不连续D.偏导数连续2. 曲面 x y z ln +=在()1,1,1点处的法线方程为_______________ A. z y x -=-=-111 B. 111-=-=-z y xC. 2111-=-=-z y xD. 2111--=-=-z y x3. 下列级数中绝对收敛的是_______________A.∑∞=--21)1(n n n B.∑∞=--21)1(n n n C.∑∞=--231)1(n n n D.∑∞=--221)1(n nn4. 记()()r r r f r g θθθsin ,cos ,=则()()=⎰⎰≤+-σd y x f y x 1122,_______________A.()dr r g d ⎰⎰θπθθcos 20, B. ()dr r g d ⎰⎰-θππθθcos 20,C. ()dr r g d ⎰⎰θπθθcos 202,2D.()dr r g d ⎰⎰-θππθθcos 2022,5. 函数221arcsiny x y=+的定义域为_________.A . {(,)0,0}x y x y >>B . {(,)11,11}x y x y -≤≤-≤≤C . 22 {(x,y)0<x +y 1}≤D . 22 {(x,y)x +y 1}≥三、计算下列各题（每小题7分，满分49分）：1. 说明 yx xy y x +→→00lim 不存在.2. 设y x e u +=其中y 由xy y =-sin 21所确定，求xu ∂∂.3. 计算dxdy y x D⎰⎰-+422其中计算9:22≤+y x D .4. 计算 ⎰⎰⎰ΩdV y 2，其中 Ω 是半个椭球1222222≤++cz by ax ，0≥z .5. 已知 ),2(xy y x f z +=，其中f 具有二阶连续偏导数，求 yx z ∂∂∂2.6. 求级数221212-∞=∑-n n nxn 的（1）收敛域；（2）和函数.7. 求方程x y y y 2sin 82=-'+''的通解. .四、应用题（每小题8分，满分16分）：1. 求22y x az +=与)0(222>+-=a y x a z 所围立体的体积.2. 在曲面 122222=++z y x 上求一点，使 =),,(z y x f 222z y x ++ 在该点沿)0,1,1(-=→l 方向的方向导数最大.五、证明题（5分）设()y x f ,在单位圆域内有连续偏导数，且在圆周122=+y x 上为1，在圆周4122=+yx 上为0.（1）证明θθsin ,cos r y r x ==时rf r f y f x y x ∂∂='+'；（2）求dxdyyx f y f x Dy x ⎰⎰+'+'22，其中141:22≤+≤yx D .。

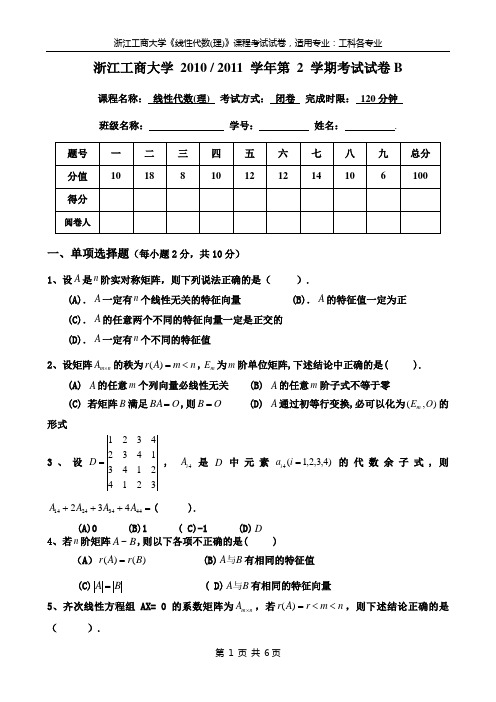
浙江工商大学 2010 / 2011 学年第 2 学期考试试卷B课程名称： 线性代数(理) 考试方式： 闭卷 完成时限： 120分钟 班级名称： 学号： 姓名： .一、单项选择题（每小题2分，共10分）1、设A 是n 阶实对称矩阵，则下列说法正确的是（ ）.(A)．A 一定有n 个线性无关的特征向量 (B)．A 的特征值一定为正 (C)．A 的任意两个不同的特征向量一定是正交的 (D)．A 一定有n 个不同的特征值2、设矩阵n m A ⨯的秩为n m A r <=)(,m E 为m 阶单位矩阵,下述结论中正确的是( ). (A) A 的任意m 个列向量必线性无关 (B) A 的任意m 阶子式不等于零(C) 若矩阵B 满足O BA =,则O B = (D) A 通过初等行变换,必可以化为),(O E m 的形式3、设3214214314324321=D , 4i A 是D 中元素)4,3,2,1(4=i a i 的代数余子式,则=+++44342414432A A A A ( ).(A)0 (B)1 ( C)-1 (D)D 4、若n 阶矩阵B A ~,则以下各项不正确的是( )（A ）)()(B r A r = (B)B A 与有相同的特征值 (C)B A = ( D)B A 与有相同的特征向量5、齐次线性方程组AX= 0的系数矩阵为n m A ⨯，若n m r A r <<=)(，则下述结论正确的是（ ）.(A)方程组中独立方程的个数为r n - (B)方程组的通解中自由未知量的个数为r (C)基础解系含有r 个解向量 (D)此方程组有无穷多解 二、填空题（每小题3分，共18分）1、已知0333231232221131211≠=m a a a a a a a a a ,则=+++---23132212211113331232113123222123323525252a a a a a a a a a a a a a a a . 2、若向量组T )1,0,1(1-=α,T k )0,3,(2=α,T k ),4,1(3-=α线性相关,则k = ____. 3、设A ,B 为3阶方阵,且2=A ,3-=B ,则12-*B A = . 4、设03=A ，则=+-1)(E A _________.5、设A 为6阶方阵,()5r A =,则=)(*A r ________.6、二次型322123222132122),,(x tx x x x x x x x x f ++++=是正定的，则t 的取值范围是 . 三、计算n 阶行列式 111111111111a a aaD ----=. (8分)四、设⎪⎪⎪⎭⎫ ⎝⎛-=340012132A ， 且知AX －A=3X ，求矩阵X . (10分)五、已知向量组⎪⎪⎪⎪⎪⎭⎫⎝⎛--==137********04321),,,(4321ααααA求向量组A 的秩和一个极大无关组并将其余向量用极大无关组线性表示. (12分)六、、设 向量组:)3,1,7,2()2,0,4,1(21==αα ),,1,1,0(3a -=α )4,,10,3(b =β . 问: 当b a ,为何值时? (1)β不能被321,,ααα线性表出 .(2)β可被321,,ααα线性表出,并且表示法唯一.(3)β可被321,,ααα线性表出,且表示法不唯一.并求一般表达式 .(12分)七、设有二次型3231212322213218444),,(x x x x x x bx x ax x x x f +-+++=经过正交变换化为23222166y y y -+,求b a ,的值和正交变换矩阵P .(14分)八、设矩阵⎪⎪⎪⎭⎫ ⎝⎛---=5334111y xA ,已知A 有三个线性无关的特征向量,且2=λ是A 的2重特征值. (1)求x,y 的值; (2)求可逆矩阵P,使得AP P 1-为对角矩阵. (10分)九、证明题 设A 是n m ⨯阶实矩阵,且n A r =)(,证明A A T 是正定矩阵. （6分）。

1. 判别下列各组函数是否相等：(1) 函数x x x f =)(与1)(=x g .(2) 函数2)(x x f =与 )(x x g =.2. 求函数x x x f cos lg 14)(2+-=的定义域. 3. 求双曲正弦函数)e e (21x x y --=的反函数. 4. 设函数⎩⎨⎧≤+>=0, 10, )(x x x x x f ,⎩⎨⎧≤>-=0, 0, )(2x x x x x g , 求 [])(x f g .5. 单项选择题:已知极限0)(lim =∞→n f n ,并且,0)(≠n f 则( )不正确. (A)0)12(lim =+∞→n f n ； (B)0)(lim =∞→x f x ； (C)0)(lim =∞→n n f n ； (D)∞=∞→)(1lim n f n .6. 用数列极限的定义证明431413lim=-+∞→n n n . 7. 用函数极限的定义证明1 11lim 2=-→x x . 8. 求下列极限 (1)px px x x x cos sin 1cos sin 1lim0-+-+→(常数0≠p )；(2) cos lim 0x x x +→； (3))sin 1(sin lim 2x x x -++∞→； (4)∑=∞→++++n k n k 13211lim ； (5)1lim 21--+++→x n x x x n x ； (6)) 0,0 ( lim ≥≥+∞→b a b a n n n n ； (7)x x x -→111lim .9. 已知2)1ln(1tan )(1lim0=+-+→x x x f x ,求)(lim 0x f x →.10. 已知51lim 21=-++→x b ax x x ,求的b a ,值.11. 单项选择题:设)(x f 和)(x g 在),(+∞-∞内有定义,)(x f 连续且0)(≠x f ,)(x g 有间断点,则( ).(A) [])(x f g 必有间断点； (B) []2 )(x g 必有间断点；(C) [])(x g f 必有间断点； (D) )()(x f x g 必有间断点.12. 设对于 ,2,1=n 均有10<<n x ,并且n n n x x x 221+-=+,证明数列{}n x 有极限,并求n n x ∞→lim .13. 设⎪⎪⎩⎪⎪⎨⎧>-=<=-0,1e 0, 0, sin )(2x x a x x x x f x ,问a 为何值时)(x f 在其定义域内连续?14. 设⎪⎩⎪⎨⎧≠≥-<-=10, 110, )(2x x x x x x x f 且,求 (1))(x f 的间断点及其类型.(2))(x f 的连续区间.15. 设n x x f n n n )e ln( lim )(+=∞→)0(>x , (1)求)(x f ,(2)讨论)(x f 的连续性.16. 设)(x f 在[]b a ,上连续,证明:至少存在一点[]b a ,∈ξ,使得[])()(21)(b f a f f +=ξ .17. 证明方程0424=--x x 在)2,2(-之间至少有两个实根. 18. 设函数)(x f ,)(x g 在[]b a ,上连续,且0)(=a f ,1)(=b f ,0)(<a g 试证:必定存在一点),(b a ∈ξ,使得)()()()(ξξξξg f g f ⋅=+.。

1期中练习题一. 填空题（每小题4分, 共32分）1. 已知,2,1==b a 向量a 与b 的夹角3),(π=b a , 则=⋅b a _____________, =-b a 32________________.2. 点)4,3,2(P 到直线635221-=-=-z y x 的距离=d ______________. 3. 设z xy y x u 22+=, 在点)0,1,2(处沿方向_______________u 增加得最快, 且沿此方向u 的变化率为_____________.4. 曲线θθθ5,sin 2,cos 2===z y x 是什么曲线:_______________, 此曲线上2πθ=的点处的切向量=s ____________________. 5. 函数)1ln(),(y e y x f x +=的二阶麦克劳林公式(带佩亚诺余项)为=),(y x f ____ .6. 设221y x y x z +=∂∂∂, x x z y +=∂∂=10, y z x ==0, 则=z ___________________________. 7. 设),(22y x e y x f z ++=, 其中f 有二阶连续偏导数, 则=∂∂xz ______________________, =∂∂∂yx z 2_________________________________________________________. 8. 函数52),(22-+=y x y x f 在区域1:22≤+y x D 上的最大值=M _________, 最小值 =m _________.二. (10分)设)2,(222x z xy f z y x -=++, 其中f 有连续偏导数, 求.,y z x z ∂∂∂∂三. (12分) 证明直线232132:1-=-+=-z y x L 与⎩⎨⎧=+=+212:2z y y x L 共面, 并求过直线1L 与2L 的平面方程.四. (12分) 计算二重积分dxdy y x x y D ⎰⎰+-22, 其中D 是由直线x y =, 2=y , 与圆1)1(22=-+y x 所围成的阴影部分区域(如图).y2五. (11分) 在曲面163222=++z y x 上求一点, 使曲面在此点的切平面与直线815643:1+=-=-z y x L 和z y x L ==:2都平行.六. (11分) 计算三重积分⎰⎰⎰-----=y x z x y x dz e dy dx I 1011010.七. (12分) 设M 是椭圆⎩⎨⎧=+=+-052222y x z y x 上的点, e f ∂∂是函数222),,(z y x z y x f ++=在点M 处沿方向}1,1,1{-的方向导数, 求使e f ∂∂取得最大值和最小值的点M 及ef ∂∂的最大值和最小值.。

浙江工商大学工商管理学院管理学原理2002——2010（2002——2003有答案）（2010为回忆版）技术经济学2004，2006——2007信号与系统2003——2010生物化学2003——2010运筹学2003——2010经济学院西方经济学2002——2010金融学院西方经济学2002——2010金融学基础（联考）2002——2009（2002——2007有答案）统计学院西方经济学2002——2010统计学概论2002——2008统计学2009概率论与数理统计2003——2010国民经济统计学2002财会学院会计学2003——2008会计学综合2010旅游学院历史学基础（全国统考试卷）2007旅游学概论2004——2010法学院法理学2005——2010诉讼法学2004——2008民法学2004——2008民商法专业综合2004国际法2008国际经济法2008综合法学理论2004综合课（含法理、经济法、国际私法）2005综合课（含国际公法、国际私法）2007综合课1（含民法学、商法学、知识产权）2009——2010综合课2（含刑事诉讼法、行政诉讼法、证据法）2009——2010综合课3（国际法）2009——2010综合课4（经济法学）2009——2010食品学院化工原理2003——2010生物化学2003——2010微生物学2004——2010信电学院信号与系统2003——2010计信学院数据结构、计算机网络2004——2006数据结构与计算机组成2005——2008程序设计2003——2010运筹学2003——2010公管学院马克思主义哲学2007——2009马克思主义政治经济学2007——2009马克思主义基本原理2010毛泽东思想和中国特色社会主义理论体系2010政治学2007——2010公共行政学2007——2010外国语学院二外德语2006——2010二外法语2006——2010二外日语2006——2010（注：2007年试卷共7页，缺P5）翻译与写作2004——2010专业综合（英美文学与语言学概论）2008综合英语2004——2010（注：2007年试卷共14页，缺P4）综合知识与英文写作2007日语学院二外英语2007——2010（注：共12页，缺P3、10、11）综合日语2007——2010专业日语2007——2010艺术设计学院艺术与设计2007艺术与设计理论2008艺术设计与艺术理论2009艺术设计理论2010专业设计2008——2010 综合设计2007环境学院环境学概论2008环境学2010化工原理2003——2010 微生物学2004——2010。

浙江工商大学2010/2011学年第二学期期末考试试卷(A)一、 填空题（每小题3分，共15分）1．空间曲线⎩⎨⎧==++zy z y x 4222在yoz 平面上的投影曲线方程是________2. 设，则_________________ .3. 函数22y x z +=在点)2,1(P 处的最大方向导数是___________.4. _______________)(22=+=⎰⎰dxdy y x I D.（其中：222:a y x D =+所围） 5. 设幂级数nn nx a)3(0-∑∞=在5=x 时条件收敛，则其收敛区间为 . 二、单项选择题（每小题3分，共15分） 1. 设可导，，，则＝( ).(A)(B)(C)(D)2.二元函数在点(0,0)处( ) (A)偏导数不存在 (B)偏导数存在但不可微(C)偏导数连续 (D)可微但偏导数不连续3.设Ω由22y x z +=与1=z 围成，计算dV z y x⎰⎰⎰Ω++)(22正确的是( ).(A)原式⎰⎰⎰Ω=zdV 2(B)原式=⎰⎰⎰Ω+dV y x )(222 (C)原式=dz z r rdr d r ⎰⎰⎰+1210202)(πθ (D)原式=⎰⎰⎰+----++2222221111)(y x x x dz z y x dydx4.直线 和平面的位置关系是( ).(A)垂直 (B)平行 (C)既不平行又不垂直 (D) 无法确定 5.级数( ).(A)条件收敛 ； (B)绝对收敛；(C)发散； (D)不能判定． 三、计算题（每小题7分，共49分）1. 已知直线⎩⎨⎧=++-=--23423:z y x z y x L 及平面122:=+-z y x π.求: (1)L 与π的夹角, (2)L 在π上的投影方程;.2. 设求．3．求椭球面上平行于平面的切平面方程.4. 求⎰⎰yydx x xdysin 15．计算 ⎰⎰⎰Ω+dV y xx )(2.其中:22:z y x +=Ω,2,1==x x 所围.6. 判别级数∑∞=--11n nn n ln )(的敛散性,若收敛,则指出是绝对收敛还是条件收敛?7．求幂级数的:(1) 收敛域；(2)和函数.四、应用题（每小题8分，共16分） 1. 求锥面22y x z +=.被柱面ay y x 222=+(0>a )所截部分的面积.2. 求函数在上的最大值和最小值.五、证明题（每小题5分，共5分）设在上连续，且=A ，证明：。

浙江大学20 10 -20 11 学年 春夏 学期《 数学分析（Ⅱ）》课程期末考试试卷（A ）课程号： 061Z0010 ，开课学院：___理学部___ 考试形式：闭卷，允许带___笔____入场考试日期： 2011 年 6 月 24 日,考试时间： 120 分钟诚信考试，沉着应考，杜绝违纪。

请注意：所有题目必须做在答题本上！做在试卷纸上的一律无效！请勿将答题本拆开或撕页！如发生此情况责任自负！考生姓名： 学号： 所属院系： _一、 计算下列各题： ( 前4题每题5分，最后一题6分，共26分 )1. 2()(03)sin lim.x y xy x→，，求： 2222()(03)()(03)sin sin lim lim 9.x y x y xy xy y x xy →→=⋅=，，，，2. (122)().f x y z gradf=，，设，，23(122)(122)(122)(122)11..2722.27271{122}.27f x x fr x r r r x ffyz gradf∂∂==-⋅=-=-∂∂∂∂=-=-∂∂=-，，，，，，，，令，则：则：同样，，因此，，，3. 2222320(321)S x y z ++=求曲面：在点，，处的法线方程.222()2320246.321(321){686}.343x y z F x y z x y z F x F y F z x y z n =++-===---===r 令：，，，则：，，因此，在点，，的法向量，，，故法线为：4. 2221.(2).4Cx C y L x y ds +=+⎰Ñ设曲线：的长度为计算： 222(2)(44)44.=0.CCCCx y ds x y xy ds ds L xyds +=++==⎰⎰⎰⎰蜒蜒其中：5.02z z z ∑===设为曲面和之间部分的下侧，计算： (1)(2).dS dxdy ∑∑⎰⎰⎰⎰；22224.4.x y x y x y z z z dS dxdy dxdy π∑+≤∑+≤======-=-⎰⎰⎰⎰⎰⎰⎰⎰由于因此，二、 计算题：（每题8分，共56分）1. 22()2()()()2x f x f x x f x ππππ=--≤≤设是周期为的函数，且，求：的211.n Fourier n+∞=∑级数，并计算的和22222020022112222211(1)()20.2522(1)()()cos (12).2325(1)()2cos .()(*)65(1)(1)(2)(*)0(0)2.61n n n nn n n n n f x b x x a dx a nxdx n nf x nx x R nx f n n ππππππππππππ∞=-+∞∞===-=-=-=-==-=-+∈--==-=-+⇒=⎰⎰∑∑∑L 由于是周期为的偶函数，则：，，，因此，式中，令，则：12222221111122122222211.21111(1)2.2.2(2)2(2)121.6511(*)2..266n n n n n n n n n n n n n n nx n n σσπσππππππ-+∞+∞+∞+∞∞=====+∞=+∞+∞==-==⇒=-====-=-+⇒=∑∑∑∑∑∑∑∑令：，则：因此，【或】：在式中令，则：2. 211(2)1.44n n nn n x n n +∞+∞==-⋅⋅∑∑计算级数的收敛域及和函数，并计算的值 222112221111211()(2)4(2)(1)lim lim 10 4.()(1)4(2)4(2)12104.44(04).(2)(2)()()4n n n n n n n nn n n nn n n n n n n u x x n x x u x n x x x n n n n x t t S t S t t n +++→∞→∞+∞+∞+∞+∞====∞-=-⋅-=⋅=<<<+⋅--====⋅⋅-'===∑∑∑∑∑，则：当时，发散；当时，发散因此，级数的收敛域为：，令，，则：1222111.(11).1(2)(2)()ln(1).ln 1ln 4ln(4).440 4.14(3)3ln .43n n nn nn t t x x S t t x x n x x n ∞=+∞=+∞==-≤<-⎛⎫--=--=--=-- ⎪⋅⎝⎭<<==⋅∑∑∑其中：故，所以，其中：上式中令，可得，2111112211(2)lim lim 141(1)11.11.(2)(2)[11).110444.(04)n nn n n n n n n n n n nn n n a x t n t t n a n n t t n nt x x x n n ∞∞+→∞→∞==∞∞==∞+∞==-===+-=-=----≤<<<⋅∑∑∑∑∑∑【或】：令，对于级数而言，，因此，的收敛半径为而当时，级数收敛；当时，级数发散故级数的收敛域为，因此，当，即时收敛因此，原级数的收敛域为，..下面与上同3. 222()2.y z zz f x y f x x x y∂∂=+∂∂∂设，，且具有阶连续偏导，计算：，12221112221222221112222232(1)2.111(2)222214(2).z y xf f x x z y x yf f f yf f x y x x x x y y xyf f f f x x x ∂=-∂∂⎛⎫⎛⎫=+--+ ⎪ ⎪∂∂⎝⎭⎝⎭=+---4. 2222(){()|}.Dx y dxdy D x y x y x y +=+≤+⎰⎰计算，其中，222222002212221cos 111()2()()..1222()sin 213cos sin ).281()1121.()()1()222u v x r x y D x y r r y r I d r r r rdr x u x y I u v dudv u v y v u v πθθθθθθπ+≤⎧=+⎪∂⎪-+-≤=⎨∂⎪=+⎪⎩=+++=⎧=+⎪∂⎪⎛⎫==+++⎨ ⎪∂⎝⎭⎪=+⎪⎩=++⎰⎰⎰，方法一、区域：令：，则：，，方法二、令：，则：，2222001233cos sin 344444344444204113).2281(cos sin )41313)]sin 2sin 2.444228u v uu v dudv d r rdr I d r dr d d udu udu πππθθπππθππππθπθθθθππθθπ+≤+--+=-⎛⎫++=+⋅= ⎪⎝⎭==+⋅=+===⋅⋅=⋅⎰⎰⎰⎰⎰⎰⎰⎰⎰方法三、5. 222{()|1}.ze dxdydz x y z x y z ΩΩ=++≤⎰⎰⎰计算三重积分：，其中，，()2222221(0)2110cos 0cos 2011012.241(sin )4sin cos 2422.22zzx y z z z u xxu z z x y z xoy e z I e dV I d rdr dz r dr r x x xedx ue du I e dzdxdy e ππθπππππππ++≤≥=+≤-===-==⋅---===⎰⎰⎰⎰⎰⎰=⎰⎰⎰⎰⎰由于积分区域关于平面对称，被积函数关于为奇函数，因此，方法一、令：方法二、()120211cos 2cos 222011cos 20(1)2.2sin 4sin 44(1)2.z dz I d d ed de d ed e d πππρϕρϕπρϕρπθϕρϕρπρρϕϕπρρπρρπ-====-=-=⎰⎰⎰⎰⎰⎰⎰⎰方法三、6. 2222()M x y z a ξηζ++=设点，，是球面第一卦限中的一点，S 是球面在该点处的切平面被3个坐标平面所截三角形的上侧，求：点()M ξηζ，，使曲面积分：⎰⎰++=Szdxdy ydzdx xdydz I 为最小，并求此最小值.22222226322262222222(1)()(cos cos cos )11.2cos 2(2).327SSS Sx y z a M x y z a xdydz ydzdx zdxdy x y z dSx y z a a a dS a dS a a a a a a ξηζξηζαβγξηζξηγξηζξηζξηζξηζξηζ++=++=++=++⎛⎫=++==⨯⨯⨯⨯= ⎪⎝⎭⎛⎫++++=≤=⇒ ⎪⎝⎭⎰⎰⎰⎰⎰⎰⎰⎰球面在点，，处的切平面方程为：由于，则：333..2.Sxdydz ydzdx zdxdy x y z M ≤++≥===⎰⎰因此，等号在故，点为62222(1).30..2(2)xy yz zxxy yz zxxy yz zx S S S S S S S S S S S Guass I xdydz ydzdx zdxdy xdydz ydzdx zdxdya a a a dV x y z a L ξηζξηζξηζ+++ΩΩ=++-++⎛⎫=+=++= ⎪⎝⎭⎰⎰⎰⎰⎰⎰⎰Ò++【或】：添加切平面与坐标平面所围立体的另三个三角形、、，使其与所围闭曲面方向为外侧则：根据公式可得：切平面：，截距分别为：、、构造222222223min ()().20(1)20(2)20(3)0(4)02.(4)x y z agrange f x y z xyz x y z a f yz x f zx y f xy z f x y z a yz zx xy x y z x y z x y z x y z xyz I λλλλλλλ=+++-=+=⎧⎪=+=⎪⎨=+=⎪⎪=++-=⎩>===-======函数：，，，令：由于、、，则：将其代入可得，由于驻点唯一，根据实际问题当因此，3.=7. 22(0)cos (0)42Cxdy ydx xC A y B x y ππ-=-+⎰计算，其中曲线是从点，沿到点，，再从(2).B D ππ-点沿直线到点，2222222222222222222222224.44(4)4(0).444410arc 42CC DA L DA LLy x P y x QP Q x y x y y x y x DA L x y xdy ydx xdy ydx xdy ydx xdy ydx x y x y x y x y dy xdy ydx y πδδδπππδπ++--∂-∂•====++∂+∂•+=>----=--++++=---=-+⎰⎰⎰⎰⎰⎰Ñ方法一、，，则：连接，作：，足够小，方向为顺时针则：222224221122332222222221tan2217.88(0)(2)(2)(2).444(4)x y ydxdyA A A A A A A D L y x P y x QP Q C Lx y x y y x y x P Q πδπδππδπδπππππππ-+≤+=-+⋅=----∂-∂====++∂+∂⎰⎰方法二、从点，沿直线到点，、再从点沿直线到点，、从点沿直线到点，、再从点沿直线到点；记此路径为由于，，则：；且在由曲线、所围区域内、都1122332222222222222222202442244444422arctan arctan arctan arctan 2242248C L AA A A A A AD xdy ydx xdy ydx x y x y dy dx dy dx y x y x y x y x πππππππππππππππππππππππππππππππππππ--------==+++++--=+++++++--=+++=⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰有一阶连续连导数，因此，7.4448ππππ+++=三、 证明题：（每题9分，共18分）1. 210cos ()()1n n n nxu x D f x n +∞∞===+∑∑叙述级数在数集上一致收敛的定义，并证明： (02).π在，内连续，且有连续导数22220022022200cos 11cos (1)(02)1111cos (02)(02)1cos ()(02)1cos sin (2)(){}111n n n n n nx nxx n n n n nxn N n nxf x n nx n nx ng x n nn ππππ∞∞==+∞=∞∞==∀∈≤++++∀∈+=+'⎛⎫==- ⎪+++⎝⎭∑∑∑∑∑由于对，，有，而收敛，故级数在，内一致收敛.另外，对，函数在，内连续，因此，在，内也连续.记，由于12200221cos()cos 1220()[2]sin .sin 2sin22sin sin [2](02)11.cos sin (02)()(0211nk n n xn x kx x n nx n nxDirichlet n n nx n nx f x n n δδπδπδδδπδπππ=∞∞==+-∀><∀∈-=≤-++'⎛⎫=- ⎪++⎝⎭∑∑∑单调趋向于零，且对，及，，根据判别法，在，上一致收敛，即在，上内闭一致收敛又在，内连续，故，在，)内具有连续的导数.2. 0()()y f x δδδ>-=证明：存在，及定义在，内的具有连续导数的函数， ()220(0)0sin ()2()cos 1..x dyf x f x f x x dx==+++=满足，且并计算的值22222222222()sin()2cos 1()(1)()(2)(00)0(3)2cos()2(4)(00)20(5)2cos()sin 0()()(0)0sin (y y x F x y x y y x F x y R F F y x y R F F x x y x R y f x f x f δδδ•=+++-==++=>=+->-==+令：，，*则：，在上连续；，；在上连续；，；在上连续.根据隐函数存在性定理，存在，及定义在，内的具有连续导数的函数，满足，且()222222220)2()cos 1.sin()2cos 100.cos()(22)2sin 0.sin 2cos().0.22cos()x x f x x x y y x x x y x y x yy y x x x x y dy y y x y dx=++=•+++===''+++-=-+'==++在两边同时对求导，且当时，则：因此，故，。

浙江工商大学/ 学年第学期考试试卷课程名称：＿＿＿＿＿＿＿考试方式：＿＿＿完成时限：120分钟班级名称：学号：姓名：一、选择题（每题1 分，共10题，合计10分）1．金融技术分析其分为··········································（）A：证券投资B：金融技术C：计量经济D：补血研究2．金融技术分析其分为··········································（）A：证券投资B：金融技术C：计量经济D：补血研究3．金融技术分析其分为··········································（）A：证券投资B：金融技术C：计量经济D：补血研究二、是非判断题（正确的用√表示，错误的╳标示，每题2分，共8题，合计16分）1．金融技工学校在教职工路上····································（）2．证券配套改革想来想去········································（）三、填空题（每题2分或者每空格1分，共8题空格，合计16分）1．证券投资学的教师是。