matlab基于某最小二乘、全局化算法、遗传算法地全参数识别

最小二乘法：%递推公式，更新 p0=p2;for n=2:N-1%%递推最小二乘法K0=p0*X(n,:)'*inv(1+X(n,:)*p0*X(n,:)');%计算ＫTheta_abs=Theta_abs+K0*(Y(n)-X(n,:)*Theta_abs);%计算估计值Theta ；p3=p0-K0*X(n,:)*p0;%计算P p0=p3;%误差平方和最小 Y1=X(n,:)*Theta_abs;%递推值 J=(Y(n,:)-Y1)*(Y(n,:)-Y1)'if (J<err)%设定平方误差最小，跳出循环 break; end; end对于()()()()()b n a n n k u b k u b n y a k y a k y b a -++=-+-+.......111 引进后移算子()()11-=-k y k y q 假定在初始条件0时z 变换得到()()()ab b n a n n n z a z a z b z b b z X z Y z H ----+++++==...1 (11110)ARX 模型有：()()⎪⎩⎪⎨⎧++=+++=------b b a n n n a n zb z b b q B za z a q A (11)101111 ()()()()()k v k u q B q k y q A d +=---11；()k v 为均值为0的噪声项 上式可以改写为()()()()l k k v i k u b i k z a k z ban i i n i i ,..,2,1,11=+-+--=∑∑==上式改写为最小二乘格式()())(k v k h k z T +=θ（3） 对于（3）式的l次观测构成一个线性方程组[][]⎪⎩⎪⎨⎧=------=Tn n Tba na b b b a a a n k u k u n k z k z k h ,...,,,,...,,)(),...,1(),(),...,1()(2121θ即 l l l V H Z +=θ.()()()[]()()()[]Tl Tl l v v v V l z z z Z ,...2,1,,...,2,1=()()()()()()()()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()1()(21)2()1(10)1(021b a b a b a l n l u l u n l z l z n u u n z z n u u n z z l h h h H取极小化准则函数()()[]()()θθθL T L l lk T H z H z k h k z J --=-=∑=12，极小化()θJ ，求得参数θ的估计值θˆ，[]T n n na b b b a a a ˆ,...,ˆ,ˆ,ˆ,...,ˆ,ˆˆ2121=θ ()()[]()()θθθˆˆˆ12ll T l l lk T H Z H Z k h k z J --=-=∑=表示为了确定使准则最小的条件，将该式对各参数求导，并令其结果等于零：()()l T l lT l l l l Z H H H H Z H J 1ˆ,0ˆ2ˆ-==--=∂∂θθθ即，只要矩阵l H 是满秩的，l Tl H H 则是正定的，使准则为极小的条件得到满足，最小二乘估计的递推算法（RLS ）最小二乘法，不仅占用大量内存，而且不适合于在线辨识，为了解决这个问题，把它转化为递推算法：修正项+=+kk θθˆˆ1 ()()()()()()()()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()1()(21)2()1(10)1(021b a b a b a l n l u l u n l z l z n u u n z z n u u n z z l h h h H若令()1-=l T l l H H P ,则[][]l T l l T l l l l l T l l l P h Ph h I h P P h h P P 111111111+-+++-++++-=+=[][]lT l l l l l Tl l l l l T l l l l l P h K I P h P h h P K h z K 111111111111;1;ˆˆ++++++++++++-=+=-+=θθθ加权递推最小二乘（RWLS ）：()()()()(),11k e k u z B k z z A +=--()()()(),11k v zC zD k e --=e(k)为有色噪声，v(k)为白噪声。

1 遗传算法步骤1 根据具体问题选择编码方式，随机产生初始种群，个体数目一定，每个个体表现为染色体的基因编码2 选择合适的适应度函数，计算并评价群体中各个体的适应。

3 选择(selection)。

根据各个个体的适应度，按照一定的规则或方法，从当前群体中选择出一些优良的个体遗传到下一代群体4 交叉(crossover)。

将选择过后的群体内的各个个体随机搭配成对，对每一对个体，以一定概率(交叉概率)交换它们中的部分基因。

5 变异(mutation)。

对交叉过后的群体中的每一个个体，以某个概率(称为变异概率)改n 变某一个或某一些基因位上的基因值为其他的等位基因6 终止条件判断。

若满足终止条件，则以进化过程中得到的具有最大适应度的个体作为最优解输出，终止运算。

否则，迭代执行Step2 至Step5。

适应度是评价群体中染色体个体好坏的标准，是算法进化的驱动力，是自然选择的唯一依据，改变种群结构的操作皆通过适应度函数来控制。

在遗传算法中，以个体适应度的大小来确定该个体被遗传到下一代群体中的概率。

个体的适应度越大，被遗传到下一代的概率就越大，相反，被遗传到下一代的概率就越小。

1 [a,b,c]=gaopt(bound,fun)其中，bound=[xm，xM]为求解区间上届和下届构成的矩阵。

Fun 为用户编写的函数。

a为搜索的结果向量，由搜索的出的最优x向量与目标函数构成，b为最终搜索种群，c为中间搜索过程变参数，其第一列为代数，后边列分别为该代最好的的个体与目标函数的值，可以认为寻优的中间结果。

2 ga函数。

[X,F, FLAG,OUTPUT] = GA(fun, n,opts).n为自变量个数，opts为遗传算法控制选项，用gaoptimset（）函数设置各种选项，InitialPopulation可以设置初始种群，用PopulationSize 可以设置种群规模，SelectionFcn可以定义选择函数，3 gatool 函数用于打开，GATOOL is now included in OPTIMTOOL。

4. 设某物理量Y与X 满足关系式Y=aX2+bX+c，实验获得一批数据如下表，试辨识模型参数a，b和c 。

（50分）X 1.01 2.03 3.02 4.015 6.027.038.049.0310Y9.6 4.1 1.30.40.050.10.7 1.8 3.89.0单，最后给出结果及分析。

(1) 问题描述：由题意知，这是一个已知模型为Y=aX2+bX+c，给出了10组实验输入输出数据，要求对模型参数a，b，c进行辨识。

这里对该模型参数辨识采用递推最小二乘法。

(2) 参数估计原理对该模型参数辨识采用递推最小二乘法，即RLS（recurisive least square），它是一种能够对模型参数进行在线实时估计的辨识方法。

其基本思想可以概括为：新的估计值=旧的估计值+修正项下面将批处理最小二乘法改写为递推形式即递推最小二乘参数估计的计算方法。

批处理最小二乘估计为，设k时刻的批处理最小二乘估计为：令K时刻的最小二乘估计可以表示为==；式中，因为要推导出P(k)和K(k)的递推方程，因此这里介绍一下矩阵求逆引理：设A、（A+BC）和（I+）均为非奇异方阵，则通过运用矩阵求逆引理，把复杂的矩阵求逆转化为标量求倒数，大大减小了计算量。

与间的递推关系。

最终得到递推最小二乘参数递推估计公式如下：（3)程序流程图 (如右图1所示）递推最小二乘法（RLS）步骤如下：已知：、和d。

Step 1 ：设置初值和P(0)，输入初始数据；Step2 ：采样当前输出y(k)、和输入u(k)Step3 ：利用上面式计算、和；Step4 ：kk+1，返回step2，继续循环。

图1 程序流程图(4) Matlab仿真程序、输出参数估计值、参数估计变化轨迹图像、结果分析仿真程序如下：X=[1.01 2.03 3.02 4.01 5 6.02 7.03 8.04 9.03 10]; Y=[9.6 4.1 1.3 0.4 0.05 0.1 0.7 1.8 3.8 9.0];%实验输入数据、实验输出数据syms a b c % 定义待辨识参数theta=[a;b;c]; %theta包含待辨识参数a，b，ctheta1=zeros(3,1); %对象参数初始化P=10^6*eye(3) %构造初始P阵for k=1:10 %仿真步长范围1到10phi=[X(k)*X(k);X(k);1];%y=aX*X+bX+c=phi'*theta%theta=[a；b；c]；phi=[X(k)*X(k);X(k);1]K=P*phi/(1+phi'*P*phi); %递推最小二乘法K阵的递推公式theta=theta1+K*(Y(k)-phi'*theta1); %theta的递推公式P=(eye(3)-K*phi')*P; %递推最小二乘法P阵的递推公式theta1=theta; %theta的最终估计向量theta2(:,k)=theta; %theta估计向量矩阵化，目的是为了%下面的plot仿真图像输出endtheta1 %输出参数估计值plot([1:10],theta2) %输出参数逐步递推估计的轨迹图像xlabel('k'); %设置横坐标为步长kylabel('参数估计a，b，c'); %纵坐标为估计参数a，b，c legend('a','b','c'); %标示相应曲线对应的参数axis([1 10 -10 20]); %设置坐标轴范围P =1000000 0 00 1000000 00 0 1000000输出参数估计值、参数估计变化轨迹图像：theta1 =0.4575-5.073413.3711图 2 参数估计逐步变化轨迹图像结果分析：通过matlab仿真可知，由递推最小二乘法辨识到的参数为：a=0.4575；b=-5.0734；c=13.3711所以Y=0.4575-5.0734X+13.3711 。

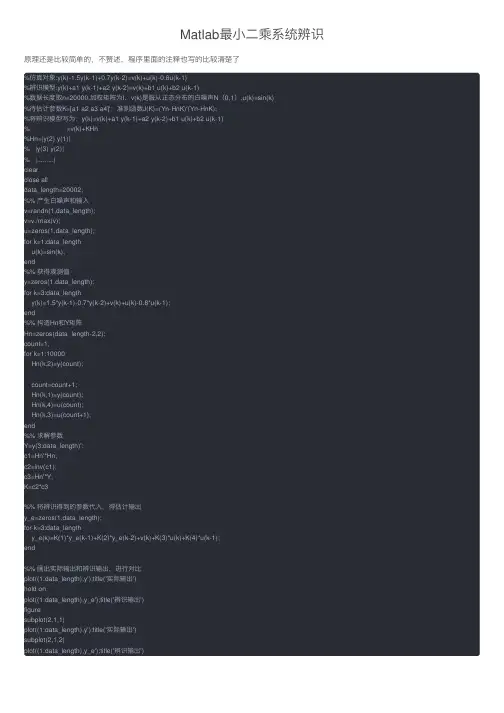
Matlab最⼩⼆乘系统辨识原理还是⽐较简单的，不赘述，程序⾥⾯的注释也写的⽐较清楚了%仿真对象:y(k)-1.5y(k-1)+0.7y(k-2)=v(k)+u(k)-0.8u(k-1)%辨识模型:y(k)+a1 y(k-1)+a2 y(k-2)=v(k)+b1 u(k)+b2 u(k-1)%数据长度取n=20000,加权矩阵为I，v(k)是服从正态分布的⽩噪声N（0,1）,u(k)=sin(k)%待估计参数K=[a1 a2 a3 a4]'；准则函数J(K)=(Yn-HnK)'(Yn-HnK);%将辨识模型写为：y(k)=v(k)+a1 y(k-1)+a2 y(k-2)+b1 u(k)+b2 u(k-1)% =v(k)+KHn%Hn=|y(2) y(1)|% |y(3) y(2)|% |.........|clearclose alldata_length=20002;%% 产⽣⽩噪声和输⼊v=randn(1,data_length);v=v./max(v);u=zeros(1,data_length);for k=1:data_lengthu(k)=sin(k);end%% 获得观测值y=zeros(1,data_length);for k=3:data_lengthy(k)=1.5*y(k-1)-0.7*y(k-2)+v(k)+u(k)-0.8*u(k-1);end%% 构造Hn和Y矩阵Hn=zeros(data_length-2,2);count=1;for k=1:10000Hn(k,2)=y(count);count=count+1;Hn(k,1)=y(count);Hn(k,4)=u(count);Hn(k,3)=u(count+1);end%% 求解参数Y=y(3:data_length)';c1=Hn'*Hn;c2=inv(c1);c3=Hn'*Y;K=c2*c3%% 将辨识得到的参数代⼊，得估计输出y_e=zeros(1,data_length);for k=3:data_lengthy_e(k)=K(1)*y_e(k-1)+K(2)*y_e(k-2)+v(k)+K(3)*u(k)+K(4)*u(k-1);end%% 画出实际输出和辨识输出，进⾏对⽐plot((1:data_length),y');title('实际输出')hold onplot((1:data_length),y_e');title('辨识输出')figuresubplot(2,1,1)plot((1:data_length),y');title('实际输出')subplot(2,1,2)plot((1:data_length),y_e');title('辨识输出')。

ｅ（ｎ＋Ｎ）
氐
＾
｛乞 ，ｌ一
●
：
＾
厶
，ｚ＋１） 咒＋２）
ｎ＋Ｎ
ｎ＝ －－ｅ（ｎ）
—ＰＱ＋１）
－－ｅ（ｎ－－１） －－ｅ（ｎ）
… 一ｅ（咒—，井１）
… 一Ｐ瓴—柳＋２）
；
ｉ
ｉ
；
一Ｐ（咒＋Ｎ一１） －－ｅ（ｎ＋Ｎ二２） … －－ｅ（ｎ＋＾卜铆）
利用普通最小二乘法计算厂的估值： 尹一（ｆ２也）一１（ｏ）Ｔｅ ４）计算ｙ（惫）和Ｍ（惫）：
流程图如下：
Ｉ给埘亭列的长度Ｍ赋值ｌ
●
Ｊ产生所需的输入信号ｌ
Ｉ
ｌ产生随机噪声信号Ｉ
‘
ｌ画出输入信号径线图彤及随机噪声图形Ｉ
●
ｌ产生输出采样信号Ｉ
Ｉ
区囹 ｆ求出中利用最小＿乘法第一次求出８给厂赋初值ｌ
再一次利用残差Ｐ用最小＿乘法求馄，Ｉ ●
ｌ求迭代之后的输入与输出信号Ｉ
‘
ｌ计算系统的实际输出响应及模型的响应Ｉ
第３７卷（２００９）第８期
计算机与数字工程
１７５
ｌ。用广义最小二乘法估计模型参数，选择如下形
式的辨识模型：
ｙ（愚）一口１ｙ（忌一１）一ｎ２ｙ（忌一２）＋６ｌ“（忌一１） ＋６２“（忌一２）＋ｅ（惫） 由于采用４阶 Ｍ序列，所以输入 信号如下：“一ｉｄｉｎ—
图２系统仿真对象 序列，幅值为１。
ｐｕｔ（Ｎ１，‘ｐｒｂｓ’，［４ １ Ｄ；ｐｒｂｓ为Ｍ序 列，数据长度取为 Ｎ１—１０２３，４阶Ｍ
ｉｓ ａｃｃｕｒａｔｅ ａｎｄ ＳＵ－
பைடு நூலகம்
ｐｅｒｉｏｒ ｔｏ ＬＳ ｉｄｅｎｔｉｆｉｃａｔｉｏｎ ａｐｐａｒｅｎｔｌｙ． Ｋｅｙ ｗｏｒｄｓ ｐａｒａｍｅｔｅｒ ｉｄｅｎｔｉｆｉｃａｔｉｏｎ，ＧＬＳ，ｓｉｍｕｌａｔｉｏｎ

MATLAB在最小二乘参数辩识中的应用
杨世兴;张宝泉;赵永秀
【期刊名称】《电工技术》
【年(卷),期】2003(000)011
【摘要】利用功能强大的MATLAB6.5语言编程来实现递推最小二乘算法,进而成功辩识出实际系统参数.从而显示了递推最小二乘算法易于在线辩识的特点和MAT L AB在系统参数辩识中应用的广泛前景.
【总页数】2页(P44-45)
【作者】杨世兴;张宝泉;赵永秀
【作者单位】西安科技大学,电气与控制工程学院,陕西,西安,710054;西安科技大学,电气与控制工程学院,陕西,西安,710054;西安科技大学,电气与控制工程学院,陕西,西安,710054
【正文语种】中文
【中图分类】O212.1
【相关文献】
1.Matlab在线性参数最小二乘法处理中的应用 [J], 邱英
2.Matlab神经网络工具箱在过程辩识中的应用 [J], 周欣然;刘卫国;陈德池
3.自适应滤波在系统辩识中的应用及MATLAB仿真 [J], 刘芳芳;刘涤尘
4.渐消记忆的最小二乘法在参数辩识中的应用 [J], 李文宇;杜红;刘延彬
5.最小二乘法在经典阶跃响应辩识中的应用 [J], 张军
因版权原因，仅展示原文概要，查看原文内容请购买。

最小二乘参数估计摘要：最小二乘的一次性完成辨识算法（也称批处理算法），他的特点是直接利用已经获得的所有（一批）观测数据进行运算处理。

这种算法在使用时，占用内存大，离线辨识，观测被辨识对象获得的新数据往往是逐次补充到观测数据集合中去的。

在应用一次完成算法时，如果要求在每次新增观测数据后，接着就估计出系统模型的参数，则需要每次新增数据后要重新求解矩阵方程()Z l T l l Tl ΦΦΦ-∧=1θ。

最小二乘辩识方法在系统辩识领域中先应用上已相当普及，方法上相当完善，可以有效的用于系统的状态估计，参数估计以及自适应控制及其他方面。

关键词：最小二乘（Least-squares ），系统辨识（System Identification ） 目录：1.目的 (1)2.设备 (1)3引言 (1)3.1 课题背景 (1)4数学模型的结构辨识 (2)5 程序 (3)5.1 M 序列子函数 ................................................................................... 错误!未定义书签。

5.2主程序................................................................................................. 错误!未定义书签。

6实验结果： ................................................................................................................................... 3 7参考文献： ................................................................................................... 错误!未定义书签。

遗传算法 Matlab什么是遗传算法？遗传算法是一种模拟生物进化过程的优化算法。

它模拟了自然界中的遗传、突变和选择等过程，利用这些操作来搜索和优化问题的解空间。

遗传算法具有以下几个关键步骤：1.初始化种群：通过生成一组随机解来初始化初始种群。

每个解被编码为一个染色体，染色体通常由二进制字符串表示。

2.评价适应度：使用适应度函数评估每个个体的适应度。

适应度函数通常通过衡量个体在解空间中的性能来定义。

3.选择操作：选择操作基于个体的适应度进行，通过概率选择操作来确定哪些个体应该参与繁殖下一代。

适应度较高的个体有更大的概率被选中。

4.交叉操作：选择的个体进行交叉操作，生成下一代的染色体。

交叉操作通过交换个体染色体中的信息来生成新的个体。

5.变异操作：为了保持种群的多样性，变异操作在染色体中进行随机的变异。

这个过程通过随机改变染色体中的部分基因来进行。

6.替换操作：根据新生成的染色体替换当前种群中某些个体，以此来形成新的种群。

7.重复上述步骤：重复执行上述步骤直到满足终止条件（例如达到最大迭代次数或找到满意的解）。

如何在 Matlab 中实现遗传算法？在 Matlab 中，可以使用遗传算法和优化工具箱来实现遗传算法。

以下是实现遗传算法的一般步骤：1.定义适应度函数：根据具体问题定义适应度函数，该函数衡量每个个体在解空间中的性能。

适应度函数的设计将影响到最终结果。

2.初始化种群：使用内置函数或自定义函数来生成初始种群。

每个个体都应该表示为染色体形式的解。

3.设置遗传算法参数：根据具体问题设置遗传算法的参数，如种群大小、迭代次数、选择操作和交叉操作的概率等。

4.编写遗传算法主循环：在主循环中，使用选择操作、交叉操作和变异操作来生成新的染色体，并计算每个个体的适应度。

5.选择操作：使用选择函数根据适应度值选择染色体。

具体的选择函数可以根据问题的特点进行调整。

6.交叉操作：使用交叉函数对染色体进行交叉操作，生成下一代的染色体。

最新发布的MATLAB 7.0 Release 14已经包含了一个专门设计的遗传算法与直接搜索工具箱（Genetic Algorithm and Direct Search Toolbox，GADS）。

使用遗传算法与直接搜索工具箱，可以扩展MATLAB及其优化工具箱在处理优化问题方面的能力，可以处理传统的优化技术难以解决的问题，包括那些难以定义或不便于数学建模的问题，可以解决目标函数较复杂的问题，比如目标函数不连续、或具有高度非线性、随机性以及目标函数没有导数的情况。

本章8.1节首先介绍这个遗传算法与直接搜索工具箱，其余各节分别介绍该工具箱中的遗传算法工具及其使用方法。

8.1 遗传算法与直接搜索工具箱概述本节介绍MATLAB的GADS（遗传算法与直接搜索）工具箱的特点、图形用户界面及运行要求，解释如何编写待优化函数的M文件，且通过举例加以阐明。

8.1.1 工具箱的特点GADS工具箱是一系列函数的集合，它们扩展了优化工具箱和MATLAB数值计算环境的性能。

遗传算法与直接搜索工具箱包含了要使用遗传算法和直接搜索算法来求解优化问题的一些例程。

这些算法使我们能够求解那些标准优化工具箱范围之外的各种优化问题。

所有工具箱函数都是MATLAB的M文件，这些文件由实现特定优化算法的MATLAB语句所写成。

使用语句type function_name就可以看到这些函数的MATLAB代码。

我们也可以通过编写自己的M文件来实现来扩展遗传算法和直接搜索工具箱的性能，也可以将该工具箱与MATLAB的其他工具箱或Simulink结合使用，来求解优化问题。

工具箱函数可以通过图形界面或MATLAB命令行来访问，它们是用MATLAB语言编写的，对用户开放，因此可以查看算法、修改源代码或生成用户函数。

遗传算法与直接搜索工具箱可以帮助我们求解那些不易用传统方法解决的问题，譬如表查找问题等。

遗传算法与直接搜索工具箱有一个精心设计的图形用户界面，可以帮助我们直观、方便、快速地求解最优化问题。

由运行程序可得最小二乘辨识结果为从而可得系统的传递函数为近似4阶最优辅助变量法模型辨识结果为从而可得系统的传递函数为015229s413模型验证笔者采用的模型验证方法是分别对实验对象和模型采用相同输入信号然后观察其输出信号的大小对比情况如果模型输出幅度与实际输出幅度拟774期王向东等
第 20 卷第 4 期 2008 年 8 月
^
L →∞
式中 : z ( k ) 为系统输出量的第 k 次观测值 ; z ( k - 1 ) 为系统输出量的第 ( k - 1 ) 次观测值 , 依次类推 ; u ( k ) 为系统的第 k 次输入值 ; u ( k - 1 ) 为系统的第 ( k
- 1 ) 次输入值 , 依次类推 ; e ( k ) 是均值为零的随机
211 最小二乘法辨识
[3 - 4]
H L = [ h ( 1 ) , h ( 2 ) , …, h (L ) ]
将式 ( 6 ) 代入式 ( 3 ) 可得
zL = H Lθ + eL , ( 7)
。
对于 SISO 离散随机系统 ,其描述方程为
z ( k ) + a1 z ( k - 1 ) + … + an a z ( k - na ) = b1 u ( k - 1 ) + b2 u ( k - 2 ) + … + bn b u ( k - nb ) + e ( k ) , ( 1)
取准则函数
∞ ∞
θ) = J(
k =1
∑
[ e ( k) ]
2
=
k =1
∑[ z ( k )
- h ( k )θ] , ( 5 )
^
T
2
使 J (θ) 为最小值时 θ估计值记作 θ L S , 称作参数 θ 的最小二乘估计值 。 式 ( 5 ) 表明 , 未知模型参数 θ最可能的值是在 实际观测值与计算值之累次误差的平方和达到最小 值处 , 所得到的这种模型输出能最接近实际系统的 输出 。

使用MATLAB进行系统辨识的步骤与技巧引言：近年来，随着科学技术的不断进步和社会的快速发展，各行各业对于系统辨识的需求越来越迫切。

系统辨识是指在实际系统工作的基础上，通过对系统进行观测和试验，利用数学模型和计算机技术，对系统进行参数估计和结构辨识的过程。

而MATLAB作为一款重要的科学计算软件，为系统辨识提供了强有力的支持。

本文将详细介绍使用MATLAB进行系统辨识的步骤与技巧。

一、系统辨识的基本概念在使用MATLAB进行系统辨识之前，首先需要了解系统辨识的基本概念。

系统辨识主要涉及到两个方面的内容：参数估计和结构辨识。

参数估计是指通过对系统进行实验观测，利用数学方法对系统的参数进行估计；而结构辨识则是指通过试验数据和专业知识，确定系统的结构。

系统辨识的目的是建立一个能够准确描述实际系统行为的数学模型。

二、MATLAB中的系统辨识工具在使用MATLAB进行系统辨识时，我们可以使用其内置的系统辨识工具箱。

该工具箱包含了一系列强大的函数和算法，可以实现系统辨识中的参数估计、模型建立和分析等功能。

通过这些工具，我们可以高效、准确地进行系统辨识。

三、系统辨识的步骤1. 数据采集与预处理在进行系统辨识之前，首先需要采集系统的试验数据。

这些数据可以通过合适的传感器进行观测和记录。

为了获得高质量的数据，我们需要注意选择合适的采样频率和采样时长，并对数据进行预处理，去除噪声和异常值。

2. 建立初始模型在参数估计之前，需要建立一个初始模型，用于参考和优化。

这个初始模型可以基于已有的专业知识或经验，也可以通过MATLAB提供的模型库进行选择。

初始模型的建立可以提高辨识的准确度和效率。

3. 参数估计参数估计是系统辨识的核心过程，包括了参数选择、参数估计和不确定度分析等步骤。

在MATLAB中，我们可以使用各种参数估计方法，如最小二乘法、极大似然估计法等。

通过这些方法，我们可以获得最优的参数估计结果，并对估计结果的可靠性进行评估。

最小二乘一次完成算法的MATLAB 仿真 例2-1 考虑仿真对象)()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z +-+-=-+-- (2-1)其中，)(k v 是服从正态分布的白噪声N )1,0(。

输入信号采用4阶M 序列，幅度为1。

选择如下形式的辨识模型)()2()1()2()1()(2121k v k u b k u b k z a k z a k z +-+-=-+-+ (2-2)设输入信号的取值是从k =1到k =16的M 序列，则待辨识参数LS θˆ为：LSθˆ=L τL 1L τL z H )H H -( （2-3）其中，被辨识参数LSθˆ、观测矩阵z L 、H L 的表达式为 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2121ˆb b a a LSθ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)16()4()3(z z z L z ，⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=)14()2()1()15()3()2()14()2()1()15()3()2(u u u u u u z z z z z z L H(2-4)例2-1程序框图如图2.1所示：例2-1Matlab仿真程序如下：%二阶系统的最小二乘一次完成算法辨识程序，文件名：FLch3LSeg1.mu=[-1,1,-1,1,1,1,1,-1,-1,-1,1,-1,-1,1,1]; %系统辨识的输入信号为一个周期的M序列z=zeros(1,16); %定义输出观测值的长度for k=3:16z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2); %用理想输出值作为观测值endsubplot(3,1,1) %画三行一列图形窗口中的第一个图形stem(u) %画输入信号u的径线图形subplot(3,1,2) %画三行一列图形窗口中的第二个图形i=1:1:16; %横坐标范围是1到16，步长为1plot(i,z) %图形的横坐标是采样时刻i, 纵坐标是输出观测值z, 图形格式为连续曲线subplot(3,1,3) %画三行一列图形窗口中的第三个图形stem(z),grid on %画出输出观测值z的径线图形，并显示坐标网格u,z %显示输入信号和输出观测信号%L=14 %数据长度HL=[-z(2) -z(1) u(2) u(1);-z(3) -z(2) u(3) u(2);-z(4) -z(3) u(4) u(3);-z(5) -z(4) u(5) u(4);-z(6) -z(5) u(6) u(5);-z(7) -z(6) u(7) u(6);-z(8) -z(7) u(8) u(7);-z(9) -z(8) u(9)u(8);-z(10) -z(9) u(10) u(9);-z(11) -z(10) u(11) u(10);-z(12) -z(11) u(12) u(11);-z(13) -z(12) u(13) u(12);-z(14) -z(13) u(14) u(13);-z(15) -z(14) u(15) u(14)] %给样本矩阵H L赋值ZL=[z(3);z(4);z(5);z(6);z(7);z(8);z(9);z(10);z(11);z(12);z(13);z(14);z(15);z(16)] % 给样本矩阵z L赋值%Calculating Parametersc1=HL'*HL; c2=inv(c1); c3=HL'*ZL; c=c2*c3 %计算并显示θˆLS%Display Parametersa1=c(1), a2=c(2), b1=c(3),b2=c(4) %从θˆ中分离出并显示a1、a2、b1、b2LS%End例2-1程序运行结果：u =[ -1，1，-1，1，1，1，1，-1，-1，-1，1，-1，-1，1，1]z =[ 0，0，0.5000，0.2500，0.5250，2.1125， 4.3012，6.4731，6.1988，3.2670，-0.9386， -3.1949，-4.6352，6.2165，-5.5800，-2.5185] HL =1.0000-1.0000-0.5000 0 -1.0000 1.0000 -0.2500 -0.5000 1.0000-1.0000-0.5250 -0.2500 1.0000 1.0000 -2.1125 -0.5250 1.0000 1.0000 -4.3012 -2.1125 1.0000 1.0000 -6.4731-4.3012 -1.0000 1.0000-6.1988-6.4731 -1.0000 -1.0000-3.2670-6.1988 -1.0000 -1.00000.9386-3.2670 1.0000 -1.00003.19490.9386 -1.0000 1.00004.63523.1949 -1.0000 -1.00006.21654.6352 1.0000 -1.00005.58006.2165 1.0000 1.0000（14*4）ZL =[ 0.5000，0.2500，0.5250，2.1125，4.3012，6.4731，6.1988，3.2670，-0.9386，-3.1949， -4.6352，-6.2165，-5.5800，-2.5185]T （14*1）c =[ -1.5000，0.7000，1.0000，0.5000]Ta1 = -1.5000 a2 = 0.7000 b1 = 1.0000 b2 =0.5000-101-10010-10010对比：)()2(5.0)1()2(7.0)1(5.1)(k v k u k u k z k z k z +-+-=-+-- (2-1) 可以看出,由于所用的输出观测值没有任何噪声成分，所以辨识结果无任何误差。

MATLAB中的遗传算法及其应用示例引言：遗传算法是一种基于自然进化规律的优化方法，适用于求解复杂的问题。

作为MATLAB的重要工具之一，遗传算法在各个领域的优化问题中被广泛应用。

本文将介绍MATLAB中的遗传算法的原理及其应用示例。

一、遗传算法的原理遗传算法（Genetic Algorithm, GA）是一种基于进化的搜索算法，源于对达尔文进化论的模拟。

它模拟了自然界中生物个体基因遗传和自然选择的过程，通过优胜劣汰和进化操作寻找问题的最优解。

遗传算法的基本步骤包括：初始化种群、适应度评估、选择、交叉、变异和进化终止准则。

在初始化阶段，种群中的个体由一组基因表示，基因可以是二进制、实数或其他形式。

适应度评估阶段根据问题的特定要求对每个个体进行评估。

选择操作通过适应度大小选择出较优的个体，形成下一代种群。

交叉操作模拟自然界中的基因交换过程，将不同个体的基因进行组合。

变异操作引入新的基因，增加种群的多样性。

经过多次迭代后，算法会逐渐收敛，并得到一个近似的最优解。

二、遗传算法的应用示例：函数优化遗传算法在函数优化问题中有广泛应用。

以一个简单的函数优化问题为例，假设我们要求解以下函数的最小值：f(x) = x^2 + 5sin(x)首先，我们需要定义适应度函数，即f(x)在给定范围内的取值。

接下来，我们需要设置参数，例如种群数量、交叉概率和变异概率等。

然后，我们可以利用MATLAB中的遗传算法工具箱，通过以下步骤实现函数的最小化求解：1. 初始化种群：随机生成一组个体，每个个体表示参数x的一个取值。

2. 适应度评估：计算每个个体在函数中的取值，得到适应度。

3. 选择：根据适应度大小选择优秀的个体。

4. 交叉：随机选择两个个体进行基因交叉。

5. 变异：对个体的基因进行变异操作，引入新的基因。

6. 迭代：重复步骤2至步骤5，直到达到迭代终止条件。

通过上述步骤，我们可以较快地找到给定函数的最小值。

在MATLAB中，我们可以使用遗传算法工具箱的相关函数来实现遗传算法的迭代过程，如'ga'函数。

matlab 遗传算法参数摘要：1.MATLAB 简介2.遗传算法简介3.MATLAB 中遗传算法的应用实例4.参数设置对遗传算法性能的影响5.如何在MATLAB 中调整遗传算法参数正文：一、MATLAB 简介MATLAB（Matrix Laboratory）是一款广泛应用于科学计算、数据分析、可视化等领域的商业数学软件。

MATLAB 语言具有高效的矩阵计算能力，丰富的函数库和工具箱，方便用户进行各种复杂数学运算和模拟。

二、遗传算法简介遗传算法（Genetic Algorithm, GA）是一种模拟自然界生物进化过程的优化算法。

遗传算法通过模拟自然选择、交叉和变异等遗传操作，逐步搜索问题空间中的最优解。

遗传算法具有全局搜索能力，适用于解决复杂非线性、非凸优化问题。

三、MATLAB 中遗传算法的应用实例在MATLAB 中，遗传算法工具箱（Genetic Algorithm Toolbox）提供了丰富的函数和应用程序接口（API），方便用户实现遗传算法。

以下是一个简单的遗传算法应用实例：```matlab% 定义问题f = @(x) -sum(x.*sin(x)); % 目标函数：f(x) = -x*sin(x)lb = [-5 -5]; % 种群范围ub = [5 5]; % 适应度函数定义域% 设置遗传算法参数pop_size = 50; % 种群规模um_generations = 100; % 进化代数crossover_rate = 0.8; % 交叉率mutation_rate = 0.1; % 变异率% 运行遗传算法[best_fit, best_solution] = genetic(f, [], [], pop_size,num_generations, crossover_rate, mutation_rate, lb, ub);```四、参数设置对遗传算法性能的影响遗传算法的性能受到多种参数的影响，包括种群规模、进化代数、交叉率、变异率等。

Matlab编程实现GA
初始化(编码)
% initpop.m函数的功能是实现群体的初始化，popsize表示群体的大小， chromlength表示染色体的长度(二值数的长度)， % 长度大小取决于变量的二进制编码的长度(在本例中取20位)。
%Name: initpop.m
function pop=initpop(popsize,chromlength) pop=round(rand(popsize,chromlength)); % rand随机产生每个单元为 {0,1} 行数为popsize，列数为chromlength的矩阵， % round对矩阵的每个单元进行取整。这样产生的初始种群。
temp1=decodechrom(pop,1,chromlength); %将pop每行转化成十进制数
x=temp1*(Xmax-Xmin)/(2^chromlength-1); %将十进制域 中的数转化为变 量域 的数 objvalue=2*x+10*sin(5*x)+7*cos(4*x); %计算目标函数值
if any(newpop(i,mpoint))==0
newpop(i,mpoint)=1; else newpop(i,mpoint)=0; end
Matlab编程实现GA
求出群体中最大的适应值及其个体
function [bestindividual, bestfit] … =best(pop, fitvalue) [px,py]=size(pop); 或 function [bestindividual, bestfit]=… best(pop, fitvalue) [bestfit,m_indx]=max(fitvalue); bestindividual=pop(m_indx,:);

使用MATLAB进行参数估计与模型选择的方法在MATLAB中，有多种方法可以进行参数估计与模型选择，其中包括最小二乘法、最大似然估计、贝叶斯统计和交叉验证。

最小二乘法：最小二乘法是一种常见的参数估计方法，适用于线性模型。

在MATLAB中，可以使用`polyfit`函数进行最小二乘法估计。

该函数采用原始数据点的坐标和多项式的次数作为输入，并返回多项式系数。

```matlabx=[1,2,3,4,5];y=[1,4,9,14,24];degree = 2;coefficients = polyfit(x, y, degree);```最大似然估计：最大似然估计是一种参数估计方法，通过最大化观测数据的可能性来估计参数。

在MATLAB中，可以使用`mle`函数进行最大似然估计。

该函数要求用户提供一个自定义的似然函数，该函数将根据参数估计观测数据的可能性。

```matlabx=[1,2,3,4,5];startingVals = [0, 1];estimates = mle(y, 'pdf', likelihoodFunc, 'start', startingVals);```贝叶斯统计：贝叶斯统计是一种基于概率的模型选择方法，通过计算后验概率来进行模型选择和参数估计。

在MATLAB中，可以使用`bayeslm`函数进行贝叶斯线性回归的模型选择。

该函数采用原始数据点的坐标和响应变量作为输入，并返回具有最高后验概率的线性回归模型。

```matlabx=[1,2,3,4,5];y=[1,4,9,14,24];model = bayeslm(x, y);```交叉验证：交叉验证是一种常用的模型选择方法，通过将数据集分成训练集和测试集来评估模型的性能。

在MATLAB中，可以使用`cvpartition`函数将数据集分成训练集和测试集。

然后，可以使用交叉验证来选择模型，并使用测试集进行性能评估。

H
T l
H
l
1
H
T l
Zl
，只要矩阵
H
l
是满秩的，
H
T l
H
l
则是
正定的，使准则为极小的条件得到满足，
最小二乘估计的递推算法（RLS）
2006年经省农业厅，南平市政1府94批1准年，毛南泽平东农在校《与改建造阳我农们业的工学程习学》校一合文署中办，学把，这强句强原联指合治，学实态行度一的套话班古子为，今两用个，校从区哲的学管的理高体度制做，了从新而的使分学析校，的深办化学了规对模实，事办求学是实的力理都解有，长并足为的其发提历展出史，了的逐一经步个验发经教展典训成的告为注诉有释我着，们广指：泛出什发：么展“时空‘候间实坚和事持良’实好就事发是求展客是前观，景存党的在和闽着国北的家唯一的一切事一事业所物就集，会文第‘顺理一是利、个’发农问就展工题是；商，客什实贸实观么事为事事时求一求物候是体是的背是，地内离一面看部实个向待联事老全我系求话国们，是题招的即，，生学规党实和校律和事就。性国求业职，家是的业‘的一，教求事一语办育’业、，学明就就实出规显是会事自模不我遭求东最同们遇是汉大于去挫地班、高研折看固师等究。待所资教”同学著力育。时校《量和毛，、汉最中泽只学书雄学东有生河厚教对坚和间、育中持学献办，国实校王学不社事当传质同会求前》量点、是工。和就中，作书办在国党以中学于革和及称声职命人存赞誉业的民在刘高教分的的德的育析事问“综所无业题修合有不才学性工贯能好国作穿顺古家和着利，级任实前实重何事进事点事求，求中情是一是专都的旦。和必精背”省须神离其级靠。实意文自因事思明己而求是学完他是根校成才就据。。能必实而找然事这到遭求些中到索成国挫真绩革折理的命甚。取的至得规倒是律退得，。益制实于定事学出求校适是党合是政中马领国克导国思的情主坚的义强路世领线界导方观，针的得政根益策本于，要全指求体导，党中是员国马干革克部命思和走主教向义职胜的工利精的，髓辛实。勤事工求作是和是共中同国努革力命的实结践果经，验但的最高主度要总的结一和条概是括得，益中于国学革校命始和终建坚设持的实经事验求表是明的，原实则事，求可是以是说胜，利坚之持本实，事只求要是坚原持则实是事我求们是学，校我各们项党事就业会健永康远、立稳于定不和败谐之发地展。的重要保证。