1.2算法和算法的描述
- 格式：ppt
- 大小：927.50 KB
- 文档页数：21
下载文档原格式
合集下载
1.2算法和算法的描述习题解答
求三角形面积问题
自然语言描述 1. 输入 、b、c的值 输入a、 、 的值 2. 判定是否符合三边规律若 不符合输出“ 不符合输出“不能构成三 角形”至第5步 角形”至第 步 3. 利用公式计算三角形面积 4. 输出“三角形面积”； 输出“三角形面积” Area 5. 结束
猴子吃桃问题
开 始 a=1,i=1
矮个子里的高个子和高个子里的矮个 子的比较
自然语言描述的算法 1. 比较 行中共挑出的 个高个子，选出其中最矮 比较10行中共挑出的 个高个子， 行中共挑出的10个高个子 的一个并记录 2. 令10人返回原位置 人返回原位置 3. 比较 列中共挑出的 个矮个子，选出其中最高 比较10列中共挑出的 个矮个子， 列中共挑出的10个矮个子 的一个并记录 4. 比较两个纪录 5. 结束
a=2(+1) ,i=i+1
i<4
否 输出a 输出
是
结束
三个数比较大小
自然语言的算法 1、输入 个整数 、b、c。 个整数a、 、 。 、输入3个整数 2、将a与b比较，把大值赋 比较， 、 与 比较 给a，小值赋给 。 ，小值赋给b。 3、将a与c比较，把大值赋 比较， 、 与 比较 给a，小值赋给 。 ，小值赋给c。 (此时 为三者最大 此时a为三者最大 此时 为三者最大) 4、将b与c比较，把大值赋 比较， 、 与 比较 给b，小值赋给 。 ，小值赋给c。 (此时 、b、c已按大小顺序 此时a、 、 已按大小顺序 此时 排好) 排好 5、按顺序输出 、b、c。 、按顺序输出a、 、 。
1000内勾股数 内勾股数
自然语言描述的算法 1. 对每一个 做下一步 对每一个a做下一步 2. 对每一个 做下一步 对每一个b做下一步 3. 对每一个 做下一步 对每一个c做下一步 4. 判定是否满足勾股定理若 满足则输出该组数字 5. 结束
自然语言描述 1. 输入 、b、c的值 输入a、 、 的值 2. 判定是否符合三边规律若 不符合输出“ 不符合输出“不能构成三 角形”至第5步 角形”至第 步 3. 利用公式计算三角形面积 4. 输出“三角形面积”； 输出“三角形面积” Area 5. 结束
猴子吃桃问题
开 始 a=1,i=1
矮个子里的高个子和高个子里的矮个 子的比较
自然语言描述的算法 1. 比较 行中共挑出的 个高个子，选出其中最矮 比较10行中共挑出的 个高个子， 行中共挑出的10个高个子 的一个并记录 2. 令10人返回原位置 人返回原位置 3. 比较 列中共挑出的 个矮个子，选出其中最高 比较10列中共挑出的 个矮个子， 列中共挑出的10个矮个子 的一个并记录 4. 比较两个纪录 5. 结束
a=2(+1) ,i=i+1
i<4
否 输出a 输出
是
结束
三个数比较大小
自然语言的算法 1、输入 个整数 、b、c。 个整数a、 、 。 、输入3个整数 2、将a与b比较，把大值赋 比较， 、 与 比较 给a，小值赋给 。 ，小值赋给b。 3、将a与c比较，把大值赋 比较， 、 与 比较 给a，小值赋给 。 ，小值赋给c。 (此时 为三者最大 此时a为三者最大 此时 为三者最大) 4、将b与c比较，把大值赋 比较， 、 与 比较 给b，小值赋给 。 ，小值赋给c。 (此时 、b、c已按大小顺序 此时a、 、 已按大小顺序 此时 排好) 排好 5、按顺序输出 、b、c。 、按顺序输出a、 、 。
1000内勾股数 内勾股数
自然语言描述的算法 1. 对每一个 做下一步 对每一个a做下一步 2. 对每一个 做下一步 对每一个b做下一步 3. 对每一个 做下一步 对每一个c做下一步 4. 判定是否满足勾股定理若 满足则输出该组数字 5. 结束
1.2算法和算法的描述
复习与巩固
伪代码4 I=1 Do if I mod 3=0 then print I end if I=I+1 Loop until I>100 伪代码5 I=1 Do if I mod 3=0 then print I end if I=I+1 Loop while I≦100
1.农夫带羊到右岸，独自返回左岸； 2.农夫把菜带到右岸，返回时白羊带回左岸； 3.农夫带狼到右岸，独自返回左岸； 4.农夫把羊带到右岸，完成过河。
3
一、算法
1、算法的概念 算法是在有限步骤内求解某一问题所使 用的一组定义明确的规则。通俗地说，算法 就是求解某一问题的方法，是能被机械地执 行的动作或指令的集合。
三、算法在解决问题中的地位和作用
表1-6中 两个程序的效率比较
指标 运行结果 用辗转相除法设计的程序 最大公约数= 用穷举法设计的程序 最大公约数=
运行时间 通用性
□较长 □较好
□较短 □较差
□较长 □较好
□较短 □较差
由此看来，算法是程序设计的核心，是程序设计的灵 魂。算法的好坏，直接影响着程序的通用性和有效性，影 响着问题解决的效率。
用自然语言 描述算法
缺点：
自然语言具有歧义性，容易导致算法执行的不确定性。 自然语言描述的算法太长。 当算法中循环和分支较多时，很难清晰地表示出来。 自然语言表示的算法不便翻译成计算机程序设计语言。
用流程图描述算法
优点：描述清晰简洁，不依赖计算机和计算机程序设计语言。 缺点：画起来费事，难以阅读，难以修改。 优点：书写方便，格式紧凑，易于理解，便于向计算机 程序设计语言过度。 缺点：由于语言的种类繁多，伪代码的语句不容易规范。
二、算法的描述
高中信息技术《算法与程序设计》优质教案、教学设计
《算法与程序设计》
1.2 算法描述与设计
教学设计
单位：授课人：
《算法描述与设计》教学设计
为了更形象、直观地表示算法，我们引入了流程图
，学生学习流也叫程序框图。
下面，同学们学习“韩信点兵”问题的
流程图表示。
开始
1n
n 被3 、5 、7 整Y
除后余数为
2 、
3 、2
N
n+1n
输出n 的值
结束
流程图描述算法常用的框图主要有以下几个：
在流程图的基础上，专业软件开发人员一般采用伪代码来描述算法。
伪代码是一种介于自然语言和计算机语言之间的一种算法描述，不是真正的程序语言代码，所以没有严格的语法限制，书写格式也比较自由，只要把意思表达清楚就可以了。
例如，判断闰年伪代码算法描述如下：
输入年份y
IF y 能被4 整除THEN
IF y 能被100 整除THEN
IF y 能被400 整除
输出“是闰年”
附：《算法描述与设计》流程图作品评价量表
《算法描述与设计》流程图作品评价量表
说明：1、作品评价等级分为A、B、C、D 四个等级。
2、在对应的作品等级下画“√”。
数据结构c语言版试题大全(含答案)
数据结构c语言版试题大全(含答案)数据结构C语言版试题大全（含答案）第一章：基本概念与算法设计1.1 数据结构的定义与特点数据结构是指相互之间存在一种或多种特定关系的数据元素的集合，它包括了数据的存储、组织和管理方式。
数据结构的特点包括以下几个方面：- 数据元素之间存在某种关系，构成逻辑结构- 对数据元素的操作对应于对其逻辑结构的操作- 数据结构有存储结构，包括顺序存储结构和链式存储结构- 算法是对数据结构的操作步骤的描述和实现1.2 算法的基本概念算法是解决特定问题或完成特定任务的一系列操作步骤。
算法的基本概念包括以下几个方面：- 有穷性：算法必须能在有限步骤内完成- 确定性：算法的每一步骤必须有确定的含义和结果- 可行性：算法的每一步骤必须可行，能够通过执行有限次数实现- 输入：算法接受的输入数据是原始问题的实例- 输出：算法产生的输出数据与输入有明确的关系1.3 算法的描述方法算法可以用自然语言、伪代码或流程图来描述。
常用的伪代码描述方法包括结构化语言和算法描述语言，结构化语言包括顺序结构、分支结构和循环结构。
第二章：线性结构2.1 线性表的定义与基本操作线性表是n个数据元素的有限序列，其中相邻元素之间存在唯一的前驱和后继关系。
线性表的基本操作包括插入、删除、查找和修改等。
2.2 数组与广义表数组是指具有相同数据类型的一组数据元素的集合，可以通过下标访问元素。
广义表是线性表的推广，其中元素可以是基本数据类型或另一个广义表。
第三章：树与二叉树3.1 树的定义与基本术语树是n（n≥0）个结点的一个有限集合，其中满足以下条件：- 有且仅有一个特定的称为根的结点- 其余结点可分为m（m≥0）个互不相交的有限集合，每个集合本身又是一棵树3.2 二叉树的定义与性质二叉树是指每个结点最多有两个子结点的树结构。
二叉树的性质包括以下几个方面：- 深度为k的二叉树最多有2^k-1个结点- 一棵二叉树的第i层最多有2^(i-1)个结点- 在二叉树的第i层上至多有2^(n-i+1)-1个结点（n为树的深度）第四章：图4.1 图的基本概念与术语图是由顶点的有穷非空集合和边的有穷集合组成的。
1.2算法和算法的描述
第一章揭开计算机解决问题的神秘面纱
1.2算法和算法的描述
1.在程序设计中算法是指（）
A.对解决问题的方法和步骤的描述
B. 以上都不对
C.计算公式
D.计算方法
2.下列关于算法的叙述不正确的是( )
A．算法具有确定性、可行性、有限性等基本特征
B．任何一个问题的算法都只有一种
C．常见的算法描述方法有自然语言、流程图法、伪代码法等D．算法是解决问题的有序步骤
3.以下哪个是编程的核心，是解决问题的方法和步骤( ) A．算法设计B．代码编写C．调试运行D．界面设计
4.以下哪个不是算法的描述方法（）
A.伪代码描述法
B.自然语言描述法
C.流程图描述法
D. 顺序法
5.图形符号在算法在流程图描述中表示（）
A.处理或运算的功能
B.算法的开始或结束
C.用来判断条件是否满足需求
D.输入输出操作
6.以下哪个图形是流程图中表示“输入输出”功能的图形( )
A．△B．□C D．◇
7.图形符号“口”在算法流程图描述中表示( )
A．用来判断条件是否满足要求B．处理或运算
C．算法的开始或结束D．输入输出操作
8.图形符号“◇"在算法流程图描述中表示( ) A．用来判断条件是否满足需求B．处理或运算C．算法的开始或结束D．输入输出操作9.流程图是描述什么的常用方式( )
A．数据结构B．计算规则C．算法D．程序10.算法与程序的关系描述正确的是( )
A．程序决定算法，是算法设计的核心
B．算法决定程序，是程序设计的核心
C．算法就是对程序的描述
D．算法和程序之间无关系。
十大经典排序算法（动图演示）
⼗⼤经典排序算法（动图演⽰）0、算法概述0.1 算法分类⼗种常见排序算法可以分为两⼤类：⽐较类排序：通过⽐较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为⾮线性时间⽐较类排序。
⾮⽐较类排序：不通过⽐较来决定元素间的相对次序，它可以突破基于⽐较排序的时间下界，以线性时间运⾏，因此也称为线性时间⾮⽐较类排序。
0.2 算法复杂度0.3 相关概念稳定：如果a原本在b前⾯，⽽a=b，排序之后a仍然在b的前⾯。
不稳定：如果a原本在b的前⾯，⽽a=b，排序之后 a 可能会出现在 b 的后⾯。
时间复杂度：对排序数据的总的操作次数。
反映当n变化时，操作次数呈现什么规律。
空间复杂度：是指算法在计算机内执⾏时所需存储空间的度量，它也是数据规模n的函数。
1、冒泡排序（Bubble Sort）冒泡排序是⼀种简单的排序算法。
它重复地⾛访过要排序的数列，⼀次⽐较两个元素，如果它们的顺序错误就把它们交换过来。
⾛访数列的⼯作是重复地进⾏直到没有再需要交换，也就是说该数列已经排序完成。
这个算法的名字由来是因为越⼩的元素会经由交换慢慢“浮”到数列的顶端。
1.1 算法描述⽐较相邻的元素。
如果第⼀个⽐第⼆个⼤，就交换它们两个；对每⼀对相邻元素作同样的⼯作，从开始第⼀对到结尾的最后⼀对，这样在最后的元素应该会是最⼤的数；针对所有的元素重复以上的步骤，除了最后⼀个；重复步骤1~3，直到排序完成。
1.2 动图演⽰1.3 代码实现function bubbleSort(arr) {var len = arr.length;for (var i = 0; i < len - 1; i++) {for (var j = 0; j < len - 1 - i; j++) {if (arr[j] > arr[j+1]) { // 相邻元素两两对⽐var temp = arr[j+1]; // 元素交换arr[j+1] = arr[j];arr[j] = temp;}}}return arr;}2、选择排序（Selection Sort）选择排序(Selection-sort)是⼀种简单直观的排序算法。
1.2算法的描述教学反思
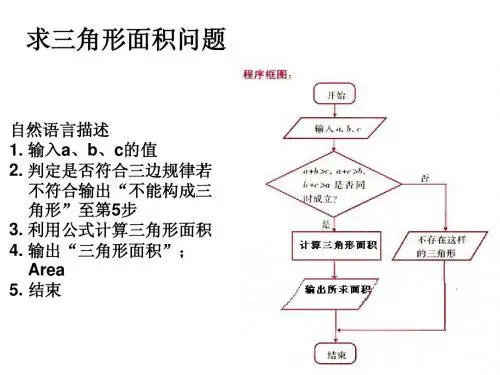
本堂课主要讲授三种描述算法的方法，后面要求学生通过“三角形面积问题”课后练习巩固流程图描述算法的方法。
总体感觉比较好。
学生能跟着一起思考问题，同时保持了较好的课堂纪律。
对此堂课，本人有如下反思：
本堂课的优点：多次运用对比，联系前后的知识点及例子，瞻前顾后，显得课堂紧促条理；分总结合，注意对所讲知识点进行小结，再进行下面的环节，可以帮助学生梳理知识点；善于运用课堂激励，不断夸奖和鼓励学生，激起他们的学习动力。
缺点：一方面讲话语速过快；另一方面练习题难度较大，具体问题的算法层面没有讲清楚，部分学生不理解解题步骤，自然无法顺利画出流程图。
导致这样的原因是部分学生（优生）讲出了解题思路，于是作为教师我没有细致分析解题思路，学生在这里花费了过多时间。
启示如下：其一，教学要面向绝大多数学生，有时甚至是全体学生，不能被部分优生左右了教学进度。
要兼顾大家，考虑大多数学生的情况。
其二，教师不宜讲得过多，应该让学生自己去探索、发现，从中学到知识，切忌满堂灌的填鸭式教学。
其三，发扬“捧”、“扬”、“夸”的课堂激励机制，学生在轻松夸奖的气氛下思维会更活跃，同时积极性更高，更愿意配合教学。
保持好的心情去上课。
以微笑示人，学生也会有好心情去学习。
1.2 算法和算法的描述[粤教版]
给出伪代码描述，学生用自然语言及流程图描述
设：MAX为评委给出的最高分；MIN为评委给出的最底分；N为评委给 出的分数个数；X为评委给出的分数；S为评委分数总和。 用伪代码描述如下： N=1 S=0 输入第一个评委给出的分数→X S=S+X MAX=X MIN=X N=N+1 IF N>10 THEN 输出 （S-MAX-MIN）/8；结束 ELSE 输入下一个评委给出的分数→X S=S+X IF X>MAX THEN MAX=X IF X<MIN THEN MIN=X END IF 返回”N=N+1”这一步
关于“算法”的概念
算法是解决问题方法的精确描述。 在编程领域，算法可以进一步定义为“算法就 是用计算机求解某一问题的方法，是能被机械 地执行的动作或指令的有穷集合。”
关于算法的特征
作为一个算法应该具有以下5个特征： 1. 0个或多个输入：一个算法应具有0个或多个 输入数据，0个是指在算法中已指定了初始 值。 2. 至少1个输出：一个算法至少要有一个输出 数据，以告知人们算法运行的结果。若没有 任何输出，则这一算法不具备意义、不具有 价值。 3. 有穷性（有限性）：一个算法必须在经过有 限个步骤之后正常结束。
优点：符合人们日常的表达习惯，容易理解。 缺点：书写较烦、容易出现歧义，对复杂的问 题难以表达准确，不能被计算机直接识别和执 行。
用流程图描述算法
流程图，也称为程序框图，它由一系列的流程 符号组成，是算法的一种图形化表示方法。
常见的流程符号
图形符号 符号名称
起止框
功能
表示算法的开始或结束 表示输入输出操作 表示处理或运算的功能 用来根据给定的条件是否满足决定 执行两条路径中的某一路径 表示程序执行的路径，箭头代表方 向
C语言-算法及其描述方法
C语言 算法及其描述方法
1 算法的概念
1.1 算法的概念
解决一个问题的方法（或步骤），称为 算法。
1.2 简单算法举例
例2.1 求1×2 × 3 × 4 × 5。 如果求100！， 需要多少个步骤？
方法一：
S1：先求1 × 2，得到结果2。
S2：将步骤1得到的乘积再乘以3，得到结果6。 S3：将6再乘以4，得24。 S4：将24再乘以5，得到120。即最后的结果。
例：求1×2 × 3 × 4 × 5，即5！=？
S1：使t=1
S2：使i=2
S3：使t×i, 乘积仍放在变量t中，即t=t×i
S4：使i的值加1，即i=i+1
S5：如果i的值不大于5，返回重新执行步骤
S3以及其后的步骤S4和S5；否则，算法结
束。
N
开始 t=1 i=2
t=t×i i=i+1
i >5?
Y
结束
图1
2.2三种基本结构
(1) 三种基本结构 ☆ 顺序结构
a
A
B
b
☆ 选择结构 又称选取结构，或称分支结构。
a
成立
P
不成立
A
B
a
成立
不成立
P
A
b
b
图a
图b
☆ 循环结构
又称重复结构，即反复执行某一部分的操作。有 两类循环结构：
a. 当型（While型）循环结构
b. 直到型（Until型）循环结构
方法二：
S1：使变量t=1
如果求100！，需要多少个步 骤？怎样修改？
S2：使变量i=2i
S4：使i的值加1，即 i=i+1
S5：如果i的值不大于5，返回重新执行步骤S3以 及其后的步骤S4和S5；否则，算法结束。
1 算法的概念
1.1 算法的概念
解决一个问题的方法（或步骤），称为 算法。
1.2 简单算法举例
例2.1 求1×2 × 3 × 4 × 5。 如果求100！， 需要多少个步骤？
方法一：
S1：先求1 × 2，得到结果2。
S2：将步骤1得到的乘积再乘以3，得到结果6。 S3：将6再乘以4，得24。 S4：将24再乘以5，得到120。即最后的结果。
例：求1×2 × 3 × 4 × 5，即5！=？
S1：使t=1
S2：使i=2
S3：使t×i, 乘积仍放在变量t中，即t=t×i
S4：使i的值加1，即i=i+1
S5：如果i的值不大于5，返回重新执行步骤
S3以及其后的步骤S4和S5；否则，算法结
束。
N
开始 t=1 i=2
t=t×i i=i+1
i >5?
Y
结束
图1
2.2三种基本结构
(1) 三种基本结构 ☆ 顺序结构
a
A
B
b
☆ 选择结构 又称选取结构，或称分支结构。
a
成立
P
不成立
A
B
a
成立
不成立
P
A
b
b
图a
图b
☆ 循环结构
又称重复结构，即反复执行某一部分的操作。有 两类循环结构：
a. 当型（While型）循环结构
b. 直到型（Until型）循环结构
方法二：
S1：使变量t=1
如果求100！，需要多少个步 骤？怎样修改？
S2：使变量i=2i
S4：使i的值加1，即 i=i+1
S5：如果i的值不大于5，返回重新执行步骤S3以 及其后的步骤S4和S5；否则，算法结束。
算法分析知识点总结
算法分析知识点总结一、算法的基本概念1.1 算法的定义：算法是一个有限指令序列，用于解决特定问题或执行特定任务的描述。
1.2 算法的特性：有穷性、确定性、可行性、输入输出和有效性。
1.3 算法的表示：伪代码和流程图是常见的算法表示方式。
1.4 算法的复杂度：算法的时间复杂度和空间复杂度是衡量算法性能的重要指标。
二、算法分析的基本方法2.1 时间复杂度：描述算法所需的运行时间与输入规模之间的关系。
2.2 空间复杂度：描述算法所需的内存空间与输入规模之间的关系。
2.3 最好情况、平均情况和最坏情况：算法复杂度分析通常考虑这三种情况的复杂度。
2.4 渐进复杂度分析：通过增长数量级的方式描述算法的复杂度。
2.5 复杂度函数的求解：基于递推关系和分析法求解算法的复杂度函数。
三、常见的时间复杂度分析方法3.1 常数阶O(1)：所有输入规模下，算法的运行时间是固定的。
3.2 线性阶O(n)：算法的运行时间与输入规模成线性关系。
3.3 对数阶O(log n)：算法的运行时间与输入规模的对数成关系。
3.4 平方阶O(n^2)及以上阶：算法的运行时间与输入规模呈指数或多项式关系。
3.5 指数阶O(2^n)：算法的运行时间与输入规模成指数关系。
四、常见的空间复杂度分析方法4.1 常数空间复杂度O(1)：算法所需的内存空间与输入规模无关。
4.2 线性空间复杂度O(n)：算法所需的内存空间与输入规模成线性关系。
4.3 对数空间复杂度O(log n)：算法所需的内存空间与输入规模的对数成关系。
4.4 平方空间复杂度O(n^2)及以上阶：算法所需的内存空间与输入规模呈指数或多项式关系。
4.5 指数空间复杂度O(2^n)：算法所需的内存空间与输入规模成指数关系。
五、常见的复杂度函数分析方法5.1 基于递推关系求解：通过递推关系式及其解的求解方法分析算法的复杂度。
5.2 基于分析法求解：通过数学分析和极限运算等方法求解算法的复杂度函数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、算法
2、算法的特征
（1）输入。一个算法有零个或多个输入。 零个输入的例子： Private sub command1_click() a=3:b=4 Print a*b End sub （2）确定性。算法的每一个步骤必须要确切地定义。 例1：这个人好说话。
例2：健美操中一个动作：“手举过头顶”。
优点：描述的算法通俗易懂。 自然语言具有歧义性，容易导致算法执行的不确定性。 缺点： 自然语言描述的算法太长。 当算法中循环和分支较多时，很难清晰地表示出来。 自然语言表示的算法不便翻译成计算机程序设计语言。
用自然语言 描述算法
二、算法的描述
2、用流程图描述算法 图形 名称 功能
起始/结束 表示算法的开始或结束
I<=500 否 结束
二、算法的描述
2、用流程图描述算法
优点：描述清晰简洁，不依赖计算机和计算机程序设计语言。
用流程图描述算法
缺点：画起来费事，难以阅读，难以修改。
二、算法的描述
3、用伪代码描述算法 伪代码是用介于自然语言和计算机语言之间的 文字和符号来描述算法的工具。
例：用辗转相除法求两个数的最大公约数的伪代码。 Input m, n r= m mod n Do while r<>0 m=n n=r r=m mod n Loop Print n
5
1.1计算机解决问题的过程
分析问题 ( 找出已知 条件和未知条件、列 出已知条件和未知条 件之间的关系 )
写出解题步骤
设所求的数为 X，则 X 应满足： X 整除3余2 X 整除5余3 X 整除7余2
1. 令 X 为1。 2. 如果 X 整除3余2， X 整除 5余3， X 整除7余2，这就是 题目要求的数，则记下这个 X 。 3. 令 X 为 X+1 （为下一次计 算作准备）。 4. 如果算出，则结束；否则跳 转2。 5. 写出答案。
一、算法
2、算法的特征
（3）有穷性。一个算法在执行有穷步之后必须结束。
反例： S1: sum=0 S2: I=1 S3: sum=sum+I S4: I=I+1 S5: 若sum>=0 ，返回s3;否则，算法结束。 （4）输出。算法有一个或多个输出。 （5）能行性。
二、算法的描述
表示算法的语言有哪几种？ 表示算法的语言有自然语言、流程图、伪代码。 1、用自然语言描述算法 例:求200-500能被5整除的所有正整数。 （1）分析问题。
6
1.1计算机解决问题的过程
计算机解决问题的流程图
7
1.1计算机解决问题的过程
8
1.1计算机解决问题的过程
算法： 解决问题的方法与步骤
9
一、算法
1、算法的概念 算法是在有限步骤内求解某一问题所使用的一组定义 明确的规则。通俗地说，算法就是求解某一问题的方法， 是能被机械地执行的动作或指令的集合。
二、算法的描述
3、用伪代码描述算法
优点：书写方便，格式紧凑，易于理解，便于向计算机 程序设计语言过度。 用伪代码描述算法
缺点：由于语言的种类繁多，伪代码的语句不容易规范。
三、算法在解决问题中的地位 探究：运行这两个程序，比较它们的效率，把 和作用 你观察到的现象填在表1-6中。
同学甲的算法： Private Sub Command1_Click() m = 9147485 n = 5147480 r = m Mod n Do While r <> 0 m=n n=r r = m Mod n 同学乙的算法： Private Sub Command1_Click() m = 9147485 n = 5147480 i=m Do While m Mod i <> 0 Or n Mod i <> 0 i=i-1 Loop
算法和算法的描述
1.1计算机解决问题的过程
一个人带一只羊、一只狼和一蓝菜过河，只有一只小船， 一次只能带一个物品。如果羊和狼在一起，狼吃羊；如果 羊和草在一起，羊吃草。怎样才能安全渡河？
1
1.1计算机解决问题的过程
分析问题，找出解决问题的方法
1.农夫带羊到右岸，独自返回左岸； 2.农夫带狼到右岸，返回时白羊带回左岸； 3.农夫把菜带到右岸，独自返回左岸； 4.农夫把羊带到右岸，完成过河。
输入/输出 表示算法中变量的输入或 输出
处理
判定 流程线
表示算法中变量的计算或 赋值 表示算法中的判断
表示算法中的流向
连接点
表示算法流向出口或入口 连接点
二、算法的描述
2、用流程图描述算法
例:求200-500能被5整除的所有正整数。
开始 I=200 I能被5整除 否 I=I+1 是 是 输出I的值
设能被5整除的数为I,令I=200,201,202，„„，500， 如果I是能被5整除的数，则输出I；否则，检查下一个I，直 到I=500为止。
（2）设计算法
①令I=200; ②如果I能被5整除，则输出I; ③I=I+1; ④如果I<=500，则返回第②； ⑤结束。
二、算法的描述
1、用自然语言描述算法
算法 就是解决问题的方法和步骤
3
1.1计算机解决问题的过程 韩信点兵 ：
韩信说：“如果每三个人编入一队，最后剩下两个人； 如果每5个人编入一队，最后剩下3个人；如果每7个 人编入一队，最后剩下2个人。请你算一下我有多少 士兵？”
4
1.1计算机解决问题的过程 韩信点兵 ：
筛选法. 首先写出“用3除余2”的数： 2，5，8，11，14，17，20，23，26，29，… 其中，“用5除余3”的数：8，23，… 其中，“用7除余2”的数：23，… 由此得到，23是最小的一个解。 至于下一个解是什么，要把“…”写出来才知道； 实践以后发现，是要费一点儿功夫的。
小结
• 一、算法的概念
• 二、算法的描述 1，用自然语言描述 2，用流程图描述