多变量控制2.2 多项式矩阵
- 格式：ppt
- 大小：1.99 MB
- 文档页数：32
下载文档原格式
合集下载
多变量控制系统分析与设计
开环增益与闭环频率间的对偶性(续)
S(g)的特征值与G(s)的特征值是相互蕴含的，当s为闭环频率矩阵S(g)的特征值时，对应的g便是开环增益矩阵G(s)的特征值。反之亦然。这种严格对偶与相互蕴合关系，构成了将经典的单回路额率响应法推广到多变量系统的理论基础。
则称系统(4-5)BIBO稳定。
BIBO稳定性(有界输入-有界输出)
(4-5)
系统(4-5)的输出向量y(t)也有界，即满足：
4
3
65Biblioteka 系统稳定性的基本概念(二)
系统的外部稳定性
[定理4-4] 当且仅当G(s)的所有极点均位于左半开平面上时，系统BIBO 稳定。
系统稳定性考察
解
由于存在右半平面上的特征值s2＝1，故此系统不稳定，或者更严格地说，此系统的零输入响应在平衡点X*＝0处不稳定。
奈氏阵列稳定性判据(续)
奈氏阵列稳定性判据(续)
奈氏阵列稳定性判据(续)
【定理4-16】(INA稳定性判据) 若 和 在Nyquist D围线上均对角优势，则闭环系统稳定的充分必要条件是:其中 为 的对角线元素，p0为开环不稳定的极点数。
【推论】 行(列)对角优势矩阵的所有行(列)的Gershgorin圆不包含原点。反之，如果所有行(列)Gershgorin圆都不包含原点，则矩阵必有行(列)对角优势。
【推论】 对角优势矩阵没有零待征值。
奈氏阵列稳定性判据(续)
根据Gershgorin定理，当s取D围线上的某一点，z(s)的特征值处在以zii(s)为圆心,以 为半径的m个圆组成的并集内。我们把这m个圆称为z(s)的行Gershgorin圆，当s沿Nyquist D围线变化一周时，z(s)的m个行Gershgorin圆形成的m条带称为Gershgorin带。
S(g)的特征值与G(s)的特征值是相互蕴含的，当s为闭环频率矩阵S(g)的特征值时，对应的g便是开环增益矩阵G(s)的特征值。反之亦然。这种严格对偶与相互蕴合关系，构成了将经典的单回路额率响应法推广到多变量系统的理论基础。
则称系统(4-5)BIBO稳定。
BIBO稳定性(有界输入-有界输出)
(4-5)
系统(4-5)的输出向量y(t)也有界，即满足：
4
3
65Biblioteka 系统稳定性的基本概念(二)
系统的外部稳定性
[定理4-4] 当且仅当G(s)的所有极点均位于左半开平面上时，系统BIBO 稳定。
系统稳定性考察
解
由于存在右半平面上的特征值s2＝1，故此系统不稳定，或者更严格地说，此系统的零输入响应在平衡点X*＝0处不稳定。
奈氏阵列稳定性判据(续)
奈氏阵列稳定性判据(续)
奈氏阵列稳定性判据(续)
【定理4-16】(INA稳定性判据) 若 和 在Nyquist D围线上均对角优势，则闭环系统稳定的充分必要条件是:其中 为 的对角线元素，p0为开环不稳定的极点数。
【推论】 行(列)对角优势矩阵的所有行(列)的Gershgorin圆不包含原点。反之，如果所有行(列)Gershgorin圆都不包含原点，则矩阵必有行(列)对角优势。
【推论】 对角优势矩阵没有零待征值。
奈氏阵列稳定性判据(续)
根据Gershgorin定理，当s取D围线上的某一点，z(s)的特征值处在以zii(s)为圆心,以 为半径的m个圆组成的并集内。我们把这m个圆称为z(s)的行Gershgorin圆，当s沿Nyquist D围线变化一周时，z(s)的m个行Gershgorin圆形成的m条带称为Gershgorin带。
现代控制技术考试必考的问答题
重点就是模糊控制、滑膜变结构控制、自适应控制、最优控制！ 一、 最优控制理论的内容：
现代控制理论研究的对象不再局限于单变量的，线性的，常定的，连续的系 统，而扩展为多变量的，非线性的，时变的，离散的系统。现代控制理论以线性 代数和微分方程为主要数学工具，以状态空间法为基础，分析和设计控制系统。 所谓状态空间法，本质上是一种时域分析方法，它不仅描述了系统的外部特性， 而且揭示了系统的内部状态和性能。 现代控制理论分析和综合系统的目标是在揭 示其内在规律的基础上， 实现系统在某种意义上的控制理论的主要内容包括如下五个分支：线性 系统理论、建模和系统辨识、最优滤波理论、最优控制、自适应控制。 二、最优控制理论的方法： 现代控制理论的方法本质是一种时域方法， 它是建立在状态变量描述方法基 础上的，它着眼于系统的状态，能更完全的表达系统的动力学性质，在解决最优 控制问题中，极大值原理和贝尔曼动态规划是最重要的两种方法。 三、分析比较指标泛函与经典控制理论的性能指标： 性能指标在数学上成为泛函， 经典控制理论中的性能指标一般为最大超调量、 阻尼比、幅值裕度和相位裕度等。 现代控制理论的二次型指标泛函的意义：花费尽量少的控制能量，使系统的 输出尽可能地跟随期望输出变化。常见的二次型性能指标分两类：线性调节器和 线性伺服器。 假定状态方程： x(t ) A(t ) x(t ) B(t )u (t ) ， x(t0 ) x0 寻求最优控制 u(t ) ，使性能指标达到极小值
二十，经典控制与现代控制理论的区别 经典控制理论是以传递函数为基础的一种控制理论， 系统的设计是建立在某 种近似或试探的基础上，控制对象一般是单输入单输出、线性定常系统、分析方 法是频域特性分析法， 根轨迹分析法， 采用的控制策略有 PID 控制、 反馈控制等， 这种控制理论不能实现最优控制。 现代控制理论是建立在状态空间上的一种控制方法， 控制的数学模型一般是 状态方程，系统的的分析与设计是精确的，控制对象可以使单输入单输出、多输 入多输出、线性定常系统、非线性定常系统、连续控制系统、离散或数字控制系 统，采用的控制策略有状态反馈、输出反馈、极点配置等，这种控制理论可以实 现最优控制。 二十一，建立数学模型的方法 即对具体的对象， 应用相应的数学和物理的原理以及定律， 列写对象满足的 物理方程， 选取合适的状态变量和输出变量，将对象的物理方程转化为状态空间 表达式的标准形式。 二十二，自适应控制定义以及分类 （1）、定义：自适应控制的基本思想，是通过在线辨识或某种算法使这种 不确定或变化的影响逐渐降低以至消除，它修正控制器自己的特性，以适应对象 和扰动的动态特性变化。 其研究对象是具有一定程度不确定性的系统，能够修正 自身特性以适应对象和扰动变化的控制器称为自适应控制器， 自适应控制是主动去适应这些系统或环境的变化,而其它控制方法是被动地、 以不变应万变地靠系统本身设计时所考虑的稳定性裕量或鲁棒性克服或降低这 些变化所带来的对系统稳定性和性能指标的影响 (2）、分类：典型的自适应控制包括模型参考自适应控制和自校正控制 二十三、 典型的自适应控制包括模型参考自适应控制 MARC 和自校正控制 STC (1）、自校正控制 STC——用递推辨识算法辨识系统参数，然后根据系统运 行指标来确定调节器或控制器参数； 自校正控制系统与其它自适应控制系统的区 别为其有一显性进行系统辨识和控制器参数计算 (或设计)的环节这一显著特征； 一般情况下自校正控制仅适用于离散随机控制系统， 在有些情况下也可用于混合 自适应控制系统。
现代控制理论研究的对象不再局限于单变量的，线性的，常定的，连续的系 统，而扩展为多变量的，非线性的，时变的，离散的系统。现代控制理论以线性 代数和微分方程为主要数学工具，以状态空间法为基础，分析和设计控制系统。 所谓状态空间法，本质上是一种时域分析方法，它不仅描述了系统的外部特性， 而且揭示了系统的内部状态和性能。 现代控制理论分析和综合系统的目标是在揭 示其内在规律的基础上， 实现系统在某种意义上的控制理论的主要内容包括如下五个分支：线性 系统理论、建模和系统辨识、最优滤波理论、最优控制、自适应控制。 二、最优控制理论的方法： 现代控制理论的方法本质是一种时域方法， 它是建立在状态变量描述方法基 础上的，它着眼于系统的状态，能更完全的表达系统的动力学性质，在解决最优 控制问题中，极大值原理和贝尔曼动态规划是最重要的两种方法。 三、分析比较指标泛函与经典控制理论的性能指标： 性能指标在数学上成为泛函， 经典控制理论中的性能指标一般为最大超调量、 阻尼比、幅值裕度和相位裕度等。 现代控制理论的二次型指标泛函的意义：花费尽量少的控制能量，使系统的 输出尽可能地跟随期望输出变化。常见的二次型性能指标分两类：线性调节器和 线性伺服器。 假定状态方程： x(t ) A(t ) x(t ) B(t )u (t ) ， x(t0 ) x0 寻求最优控制 u(t ) ，使性能指标达到极小值
二十，经典控制与现代控制理论的区别 经典控制理论是以传递函数为基础的一种控制理论， 系统的设计是建立在某 种近似或试探的基础上，控制对象一般是单输入单输出、线性定常系统、分析方 法是频域特性分析法， 根轨迹分析法， 采用的控制策略有 PID 控制、 反馈控制等， 这种控制理论不能实现最优控制。 现代控制理论是建立在状态空间上的一种控制方法， 控制的数学模型一般是 状态方程，系统的的分析与设计是精确的，控制对象可以使单输入单输出、多输 入多输出、线性定常系统、非线性定常系统、连续控制系统、离散或数字控制系 统，采用的控制策略有状态反馈、输出反馈、极点配置等，这种控制理论可以实 现最优控制。 二十一，建立数学模型的方法 即对具体的对象， 应用相应的数学和物理的原理以及定律， 列写对象满足的 物理方程， 选取合适的状态变量和输出变量，将对象的物理方程转化为状态空间 表达式的标准形式。 二十二，自适应控制定义以及分类 （1）、定义：自适应控制的基本思想，是通过在线辨识或某种算法使这种 不确定或变化的影响逐渐降低以至消除，它修正控制器自己的特性，以适应对象 和扰动的动态特性变化。 其研究对象是具有一定程度不确定性的系统，能够修正 自身特性以适应对象和扰动变化的控制器称为自适应控制器， 自适应控制是主动去适应这些系统或环境的变化,而其它控制方法是被动地、 以不变应万变地靠系统本身设计时所考虑的稳定性裕量或鲁棒性克服或降低这 些变化所带来的对系统稳定性和性能指标的影响 (2）、分类：典型的自适应控制包括模型参考自适应控制和自校正控制 二十三、 典型的自适应控制包括模型参考自适应控制 MARC 和自校正控制 STC (1）、自校正控制 STC——用递推辨识算法辨识系统参数，然后根据系统运 行指标来确定调节器或控制器参数； 自校正控制系统与其它自适应控制系统的区 别为其有一显性进行系统辨识和控制器参数计算 (或设计)的环节这一显著特征； 一般情况下自校正控制仅适用于离散随机控制系统， 在有些情况下也可用于混合 自适应控制系统。
第11章线性系统的多项式矩阵描述解析
强调：广义状态变量必须是独立的。对于方程中的 某个储能参数若多次引用，必须给予恰当处理。
例如若将电容C2两端短路，则
(L1s
1 C1s
)1
(s)
1 C1s
1
(s)
(
1 C1s
1 C1s L2s
2 (s) R1)2
U(s) (s)
0
仍按上面整理得：
3s2 1 1
6s2
1 3s
1 (s)
R(s)P1 (s)Q(s) W(s) C(sI A)1 B E
注意PMD的实现具有强不唯一性，结果不唯一，实 现的维数也不唯一。
二.构造PMD的实现方法
构造PMD的实现是基于矩阵分式描述MFD的规范 形，能控形，能观测类实现而建立的。含义是指 PMD的传递函数矩阵G(s)中包含的一个MFD的实 现，称为PMD实现的内核。
n degdetP(s)
4.由(Ao , Bo , Co )导 出PMD的 实 现(A, B, C, E) 直接取定 A Ao,B Bo
1
2
(s)
3s
0
U(s)
degdetP(s)=4，产生系统升级错误的原因是化 简过程中电容C1进行了两次通分运算。
若 将(1)式 改 写为
1 C1s
1
(s)
1 C1s
2
(s)
U(s)
L1s1
(s)
代 入(2)得
- U(s) L1s1(s) (L2s R1)2 (s) 0
3s2 1 1
3.对Pr-1(s)Qr (s)构 造 观 测 器 形 实 现(A o , Bo , Co ) 对 严 真Pr-1 (s)Qr (s),Pr (s)行 既 约 ， 构 造 观 测 器 形实 现(A o , Bo , Co )
Lecture 3 - 多变量动态矩阵控制算法
17
MATLAB编程 编程
作阶跃响应（ 作阶跃响应（粗）
step(system);
分析阶跃响应曲线，确定截断时间、 分析阶跃响应曲线，确定截断时间、采样周期和模型长度
截断时间 tend= 8 模型长度 N = 40 采样周期 Ts=0.2
作阶跃响应
stepresp=step(plant,[T:T:tend]);
13
入口
单变量DMC算法在线计算 算法在线计算(1) 单变量 算法在线计算
检测实际输出 y 并计算误差 y - y(1) → e 预测值校正 y (i ) + hi e → y (i ), i = 1,L , N
DMC在线计算流程
移位设置该时刻初值 y (i + 1) → y (i ), i = 1,L , N 设置控制增量 ∑ i=1 di (w − y(i)) → ∆u
A ∆uM ( k )
P 维预测输出值
P 维初始预测值
历史信息 每一时刻信息已知 动态更新
P×M 维动态矩阵A
模型信息
M 维控制增量
未来输入
离线辨识获得 在线优化获得 一旦确定保持不变
7
单变量DMC (2) 单变量
2. 目标函数
% J (k ) = ∑ qi [ w(k + i ) − yM (k + i | k ) ] + ∑ rj ∆u 2 (k + j − 1)
plant =
3.574e-006 z^3 + 3.912e-005 z^2 + 3.9e-005 z + 3.539e-006 ------------------------------------------------------------------------------------------z^4 - 3.957 z^3 + 5.898 z^2 - 3.925 z + 0.9841
MATLAB编程 编程
作阶跃响应（ 作阶跃响应（粗）
step(system);
分析阶跃响应曲线，确定截断时间、 分析阶跃响应曲线，确定截断时间、采样周期和模型长度
截断时间 tend= 8 模型长度 N = 40 采样周期 Ts=0.2
作阶跃响应
stepresp=step(plant,[T:T:tend]);
13
入口
单变量DMC算法在线计算 算法在线计算(1) 单变量 算法在线计算
检测实际输出 y 并计算误差 y - y(1) → e 预测值校正 y (i ) + hi e → y (i ), i = 1,L , N
DMC在线计算流程
移位设置该时刻初值 y (i + 1) → y (i ), i = 1,L , N 设置控制增量 ∑ i=1 di (w − y(i)) → ∆u
A ∆uM ( k )
P 维预测输出值
P 维初始预测值
历史信息 每一时刻信息已知 动态更新
P×M 维动态矩阵A
模型信息
M 维控制增量
未来输入
离线辨识获得 在线优化获得 一旦确定保持不变
7
单变量DMC (2) 单变量
2. 目标函数
% J (k ) = ∑ qi [ w(k + i ) − yM (k + i | k ) ] + ∑ rj ∆u 2 (k + j − 1)
plant =
3.574e-006 z^3 + 3.912e-005 z^2 + 3.9e-005 z + 3.539e-006 ------------------------------------------------------------------------------------------z^4 - 3.957 z^3 + 5.898 z^2 - 3.925 z + 0.9841
第一部分 多项式矩阵理论
第一部分：多项式矩阵理论
引言
互 质 性 1
MIMOs多变量线性系统传递函数矩阵可表达为 如下“分式”形式： N ( s)
G ( s ) ( g ij ( c ) ) pq
D( s )
其中N(s)和D(s)的最大公因子为单模阵，即N和D互质。 互质性是对两个多项式矩阵间的不可简约属性的表征。 互质性可分为右互质性和左互质性。 右互质多项式矩阵D(s)和N(s)列数相同。 左互质多项式矩阵DL(s)和NL(s)行数相同。
右互质。
D(s) 矩阵 对所有s列满秩 N ( s)
右互质的秩判据：
右互质贝左特等式：
存在多项式矩阵X(s)和Y(s), 使得：
X(s)D(s)+Y(s)N(s)=I(单位阵），反之亦然。
列既约性的定义：
给定方非奇异多项式矩阵M(s)
既 约 性 2
ci M(s)为其相应的列次数，i=1，2，…p。
称M(s)为列既约的，当且仅当：
其行列式的次数等于其所有列次数的和，即
deg det M ( s ) ci M ( s)
i 1
p
第一部分：多项式矩阵理论
列次表达式：对于多项式矩阵M(s)， 其列次数记为：
单位矩阵I 初等矩阵E
初等变换
矩阵A的行初等变换相当于左乘相应的初等矩阵E 矩阵A的列初等变换相当于右乘相应的初等矩阵E
第一部分：多项式矩阵理论
单模矩阵定义：
称方阵Q(s)为单模阵，当且仅当其行列式detQ(s)=c 为独立于s的非零常数。 例1：非奇异的常数矩阵 s 1 s 2 例2： Q( s )
s kc 1 Sc ( s ) p p
第十一章-线性系统的多项式矩阵描述
第十一章 线性时不变系统的多项式矩阵描述多项式矩阵描述方法是20世纪60年代中期由英国学者(H. H. Rosonbrock)提出来的。
首先多项式矩阵描述是对系统描述方法的一个丰富；其次多项式矩阵描述是对线性时不变系统更为普遍的一种描述；再者多项式矩阵描述为将来研究广义系统奠定了基础。
11.1 多项式矩阵描述多项式矩阵描述（Polynomial Matrix Descriptions ，PMD ）是除了线性系统的三种原有的描述方式：状态空间描述、传递函数矩阵描述和矩阵分式描述以外，一种新的描述方法。
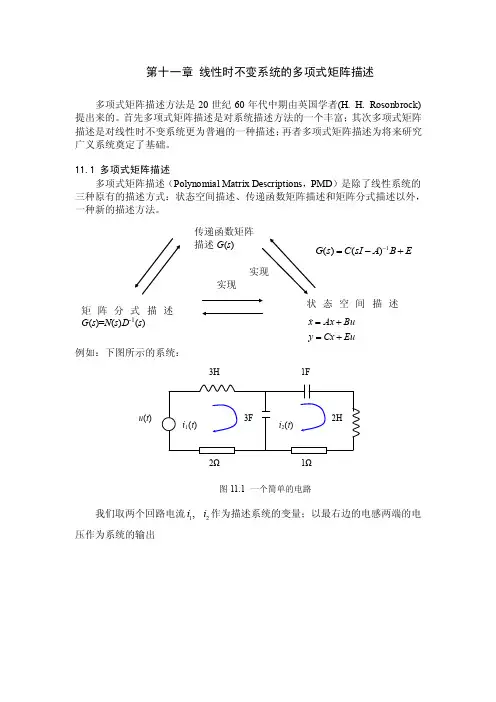
例如：下图所示的系统：我们取两个回路电流12, i i 作为描述系统的变量；以最右边的电感两端的电压作为系统的输出ui i dt didti d 369211212=-++ 0436222221=+++-i dt didt i d i （11.1）2()2di y t dt= 引入微分算子：222()()(), ()dx t d x t dx t d x t dt dt将式（11.1）表示如下： 21221212(961)()()3()()(634)()0()0()2()0()d d i t i t du t i t d d i t y t i t di t u t ++-=-+++==++ （11.2）将上式写成矩阵形式：[][]212212()39611()()01634()()020()()i t d d d u t i t d d i t y t d u t i t ⎡⎤++-⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-++⎣⎦⎣⎦⎣⎦⎡⎤=+⎢⎥⎣⎦ （11.3）一般地我们有：()()()()P d t Q d u t ζ=()()()()()y t R d t W d u t ζ=+ （11.4）(),(),()()P Q R W ⋅⋅⋅⋅和分别为, , , m m m p q m q p ⨯⨯⨯⨯的微分算子多项式矩阵。
线性多变量系统线性系统理论完整
x(t)
x2
(t)
x
n
(t
)
状态空间 状态空间定义为状态向量（取值）的一个集合,状态空间的维数等同 于状态的维数
几点解释 （1）状态变量组对系统行为的完全表征性
只要给定初始时刻 t0 的任意初始状态变量组 x1(t0 ), x2 t0 , , xn (t0 )
和t≥t0 各时刻的任意输入变量组 u1 (t),u2 t , , u p (t)
代数理论 把系统各组变量间的关系看作为是某些代数结构之间的 映射关系,从而可以实现对线性系统描述和分析的完全的 形式化和抽象化,使之转化为纯粹的一些抽象代数问题
多变量频域方法
一是频域方法
二是多项式矩阵方法
1/2,4/5
1.3 本书的论述范围
1：状态空间法 2：多项式矩阵法
2/2,5/5
第一部分: 线性系统时间域理论
(2)系统的内部描述
状态空间描述是系统内部描述的基本形式,需要由两个数学方程表征,—— 状态方 程和输出方程
(3)外部描述和内部描述的比较 一般的说外部描述只是对系统的一种不完全描述,不能反映黑箱内部结构的不
能控或不能观测的部分. 内部描述则是系统的一种完全的描述,能够完全反映系统的所有动力学特性.
R1iL
R1C
duc dt
L diL dt
L diL dt
0 e
e(t)
L
iL Uc R2 U R2
uc
iL
(R1
1
R2 R1
)C
L(R1 R2 )
(
R1
R1 R2 R1R2
)C
uc
iL
(
R1
1
R2 R2
现代控制理论 第5章线性时不变系统的多项式矩阵描述
2021/4/27
7
（3）前两种情况的组合
P(s),Q(s)非左互质，消去其gcld H(s), 得
H 1(s)P(s) (s) H 1(s)Q(s)u(s)
y(s)
R(s)
(s)
W
(s)u(s)
再消去H 1(s)P(s)和R(s)的gcrd F (s) ,即做代换
(s) F (s) (s)
2021/4/27
8
5.2 PMD的状态空间实现
一. PMD实现的定义
给定{P(s),Q(s),R(s),W(s)}，若能找到状态空 间描述{A,B,C,E(p)}，使
R(s)P1(s)Q(s) W (s) C(sI A)1 B E(s) 则称{A, B,C, E( p)}为给定PMD的实现.
P(s)F (s) (s) Q(s)u(s)
y(s) R(s)F (s) (s) W (s)u(s) 设 (s) F (s) (s),则
P(s) (s) Q(s)u(s)
y(s) R(s) (s) W (s)u(s)
不可简约
rank P(s) Q(s) rank P(s) Q(s) ,故P(s),Q(s)左互质.
则:{系统完全能控且能观} g(s)无零极点相消 {系统完全能控} adj(sI-A)b和(s)无零极对消现象 {系统完全能观} c adj(sI-A)和(s)无零极对消现象
2021/4/27
14
5.4 传输零点和解耦零点
• 一般地，系统的零、极点与传递函数矩阵的零极点不是 等同的，后者包含在前者之中，是前者的一个子集。
• 注：PMD实现具有强不唯一性
二 .构造PMD实现的方法
以构造观测器形实现为最简便 已知：{P(s),Q(s),R(s),W(s)}, 求实现
2.多项式矩阵
1
d 2 ( ) d r ( ) 0
0
称它为A(λ)的Smith标准型，其中r≥1，di(λ)(i=1,2,…,r)是首项 系数为1的多项式，且 di(λ)|di+1(λ)(i=1,2,…,r-1)。其中，主对角 线上的非零元素d1(λ),…dr(λ) 称为λ-矩阵A(λ)的不变因子。 例：用初等变换化多项式矩阵为Smith标准型
①矩阵的两行（列）互换； ②矩阵的某一行（列）乘以非零的常数k； ③矩阵的某一行（列）乘以多项式 f ( ) 后加到另一行（列）。
4.多项式矩阵的秩
如果多项式矩阵A（λ）有一个r阶子式不为零，而所有的r+1 阶子式全为零，则称A（λ）的秩为r，零矩阵的秩规定为零。
5.多项式矩阵的逆矩阵 设A（λ）是n阶λ-矩阵，如果存在n阶λ-矩阵B（λ），使A（λ） B（λ）= B（λ）A（λ）=I，则称A（λ）可逆，并称B（λ）是 A（λ）的逆矩阵，且逆矩阵唯一。
2
2
0
2 3 2 0
2
2 2 0 0
2
0 1 3 3 3 1 2
0
0
0 3
最后所得的矩阵为A(λ)的Smith标准型，
d1(λ)=1,d2(λ)=λ,d3(λ)=λ3+λ为A(λ)的不变因子。
2.Jordan标准型
形如
i Ji 1
i
1
1 i m m i i
D k ( ) d 1 ( ) d 2 ( ) d k ( ), k 1, 2, r
多变量系统的矩阵分式描述.pdf
第八章 多变量系统的矩阵分式描述多项式矩阵定义：m ×n 矩阵()s A 的元素()ij a s (i=1，…,m;j=1,…n )是变s 的多项式，称()s A 为多项式矩阵。
记为1111()()()()()n m mn a s a s s a s a s ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦Α)(s a ij 的最高次数N 称为()s A 的次数，记为)]}({deg[max ,,s a N j i ji =)(s A 可写成降幂形式的矩阵多项式 1110()N N N N s −−=++++A A S A S A S A式中),1,0(N k k =A 是n m ×常数矩阵。
1）单模矩阵对于多项式矩阵()s A ，当det ()s =A 非零常数时，其1()s −A 仍为多项式矩阵时，称()s A 为单模矩阵。
单模矩阵有如下的性质：a) 单模矩阵的乘积仍为单模矩阵； b) 单模矩阵的逆阵仍是单模矩阵；c) 所有单模矩阵均可表示成有限个初等变换的乘积的形式。
2）Smith 标准形任意秩为r 的多项式矩阵)(s A 经过行、列运算均等价于下列Smith 标准形)(s S12*()()()()()()()()r s s s s s s s s γγγ0S 0S P A Q 0000 ⎡⎤⎢⎥⎢⎥⎡⎤⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦式中rank ()min(,)r s m n =≤A ；)(1s γ，)(2s γ，… ，)(s r γ是不恒为零的首一多项式，且)(1s i +γ可整除)(s i γ，即存在1()()i i s s γγ+。
3）多项式矩阵的最大公因子设多项式矩阵)(s A 为)(n m ×矩阵，若存在()()()s s s =A B D ，则称m 阶方阵)(s B 为)(s A 的左因子 若存在()()()s s s =A E C ，则称n 阶方阵)(s C 为)(s A 的右因子若)()()(11s s s M B M =，)()()(22s s s M B M =，[][])()()()()(2121s s s s s M M B M M =则)(s B 为[)(1s M )(2s M ]的左公因子)()()(11s s s C N N =，)()()(22s s s C N N =，)()()()()(2121s s s s s C N N N N ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡)(s C 为[]TT T s s )()(21N N 的右公因子设)(s C 是)(s i N (=i 1，…，r )的一个右公因子，且)(s i N 的其他任何一个右公因子)(1s C 均为)(s C 的右因子，即)()()(1s s s C W C =，则称)(s C 是)(s i N 的一个最大右公因子，记为[]1()()()r s gcrd s s =C N N4）最大右公因子构造定理设1()s N 、)(2s N 分别为()n m ×1、()n m ×2矩阵，对[]TTT s s )()(21N N 作初等行变换，使其变换后矩阵的最后)(21n m m −+行恒为零，即1211112122122212()()()()()()()0nm m n m s s s s m s s s m m nn+−⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦U U N R U U N则式中)(s R 即为)(1s N 、)(2s N 的一个最大右公因子。