matlab作业
- 格式:docx
- 大小:301.15 KB
- 文档页数:31

matlb课程设计作业一、教学目标本课程的教学目标是使学生掌握MATLAB基本语法、编程技巧以及应用方法,培养学生解决实际问题的能力。
具体目标如下:1.知识目标:(1)理解MATLAB的基本概念,如变量、数据类型、运算符等。
(2)掌握MATLAB编程的基本语法,如矩阵操作、函数定义与调用、循环结构、条件语句等。
(3)熟悉MATLAB与其他软件(如Mathematica、Python等)的接口转换。
(4)了解MATLAB在工程领域中的应用,如信号处理、控制系统、图像处理等。
2.技能目标:(1)能够运用MATLAB进行简单的数学计算、数据分析及图形绘制。
(2)具备编写MATLAB脚本文件和函数文件的能力。
(3)学会使用MATLAB解决实际问题,如编写程序实现线性方程组求解、最优化问题求解等。
(4)掌握MATLAB在实验数据处理、仿真实验等方面的应用。
3.情感态度价值观目标:(1)培养学生对科学探究的兴趣,提高其创新意识。
(2)培养学生团队协作、沟通交流的能力。
(3)培养学生具备良好的编程习惯和职业道德。
二、教学内容本课程的教学内容主要包括以下几个部分:1.MATLAB基本概念:变量、数据类型、运算符等。
2.MATLAB编程语法:矩阵操作、函数定义与调用、循环结构、条件语句等。
3.MATLAB高级应用:数组运算、图像处理、控制系统、信号处理等。
4.MATLAB与其他软件的接口转换。
5.实践项目:利用MATLAB解决实际问题,如线性方程组求解、最优化问题求解等。
三、教学方法本课程采用讲授法、案例分析法、实验法等多种教学方法相结合,以提高学生的学习兴趣和主动性。
1.讲授法:用于讲解MATLAB基本概念、语法和应用。
2.案例分析法:通过分析实际案例,使学生掌握MATLAB在各个领域的应用。
3.实验法:让学生亲自动手实践,培养其运用MATLAB解决实际问题的能力。
四、教学资源1.教材:选用《MATLAB教程》作为主要教材,辅助以相关参考书籍。

MATLAB作业⼀、必答题:1. MATLAB系统由那些部分组成?答:MATLAB系统主要由开发环境、MATLAB语⾔、MATLAB数学函数库、图形功能和应⽤程序接⼝五个部分组成。
2. 如何启动M⽂件编辑/调试器?答:在操作界⾯上选择“建⽴新⽂件”或“打开⽂件”操作时,M⽂件编辑/调试器将被启动。
在命令窗⼝中键⼊“edit”命令也可以启动M⽂件编辑/调试器。
3. 存储在⼯作空间中的数组能编辑吗?如何操作?答:存储在⼯作空间的数组可以通过数组编辑器进⾏编辑:在⼯作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输⼊修改内容即可。
4. 在MATLAB中有⼏种获得帮助的途径?答:在MATLAB中有多种获得帮助的途径:(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器;(2)help命令:在命令窗⼝键⼊“help” 命令可以列出帮助主题,键⼊“help 函数名”可以得到指定函数的在线帮助信息;(3)lookfor命令:在命令窗⼝键⼊“lookfor 关键词”可以搜索出⼀系列与给定关键词相关的命令和函数(4)模糊查询:输⼊命令的前⼏个字母,然后按Tab键,就可以列出所有以这⼏个字母开始的命令和函数。
5. 有⼏种建⽴矩阵的⽅法?各有什么优点?答:(1)以直接列出元素的形式输⼊;(2)通过语句和函数产⽣;(3).在m⽂件中创建矩阵;(4)从外部的数据⽂件中装⼊。
6. 命令⽂件与函数⽂件的主要区别是什么?答:命令⽂件: M⽂件中最简单的⼀种,不需输出输⼊参数,⽤M ⽂件可以控制⼯作空间的所有数据。
运⾏过程中产⽣的变量都是全局变量。
运⾏⼀个命令⽂件等价于从命令窗⼝中顺序运⾏⽂件⾥的命令,程序不需要预先定义,只要依次将命令编辑在命令⽂件中即可。
函数⽂件:如果M⽂件的第⼀个可执⾏⾏以function开始,便是函数⽂件,每⼀个函数⽂件定义⼀个函数。
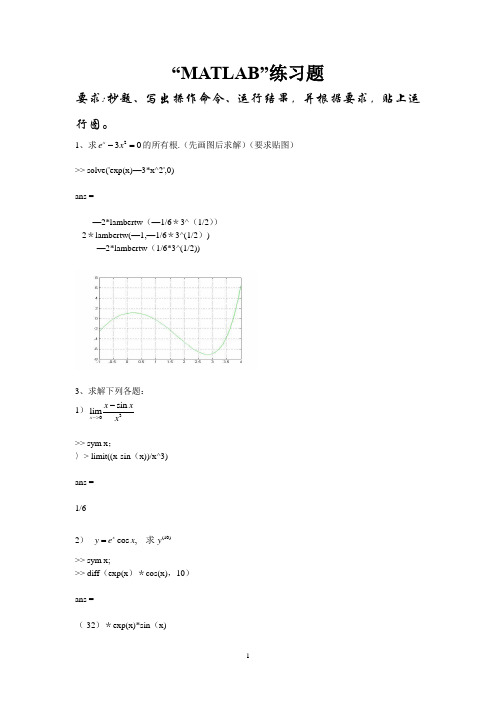
“MATLAB”练习题要求:抄题、写出操作命令、运行结果,并根据要求,贴上运行图。
1、求230x e x -=的所有根.(先画图后求解)(要求贴图)>> solve('exp(x)—3*x^2',0)ans =—2*lambertw (—1/6*3^(1/2))-2*lambertw(—1,—1/6*3^(1/2))—2*lambertw (1/6*3^(1/2))3、求解下列各题:1)30sin lim x x x x ->->> sym x ;〉> limit((x-sin (x))/x^3)ans =1/62) (10)cos ,x y e x y =求>> sym x;>> diff (exp(x )*cos(x),10)ans =(-32)*exp(x)*sin (x)3)21/20(17x e dx ⎰精确到位有效数字)〉〉 sym x;〉〉 vpa((int(exp(x^2),x,0,1/2)),17)ans =0.544987104183622224)42254x dx x+⎰〉> sym x ;>〉 int (x^4/(25+x^2),x)ans =125*atan (x/5) - 25*x + x^3/35)求由参数方程arctan x y t⎧⎪=⎨=⎪⎩dy dx 与二阶导数22d y dx 。
〉> sym t;>> x=log(sqrt (1+t^2));y=atan(t);〉> diff (y ,t )/diff (x ,t)ans =1/t6)设函数y =f (x )由方程xy +e y = e 所确定,求y ′(x ).>> syms x y ;f=x *y+exp(y )—exp (1);〉> -diff(f,x )/diff (f,y)ans =-y/(x + exp (y))7)0sin 2x e xdx +∞-⎰>〉 syms x ;>〉 y=exp(-x)*sin(2*x );〉> int(y ,0,inf )ans =2/58) 08x =展开(最高次幂为)〉> syms xf=sqrt(1+x);taylor(f,0,9)ans =— (429*x^8)/32768 + (33*x^7)/2048 — (21*x^6)/1024 +(7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + x/2 + 19) 1sin (3)(2)x y e y =求〉> syms x y ;>〉 y=exp(sin (1/x));>〉 dy=subs (diff(y,3),x ,2)dy =—0.582610)求变上限函数2x x ⎰对变量x 的导数.>> syms a t ;>〉 diff (int(sqrt(a+t),t,x ,x^2))Warning: Explicit integral could not be found 。

实验一MATLAB运算基础1、用逻辑表达式求下列分段函数的值。
t=0:0.5:2.5y=t.^2.*((t>=0)&(t<1))+(t.^2-1).*(( t>=1)&(t<2))+(t.^2-2*t+1).*((t>=2 )&(t<3))2、求[100,999]之间能被21整除的数的个数。
p=rem([100:999],21)==0;sum(p)3、建立一个字符串向量,删除其中的大写字母。
ch='KdDdfKaWdsfCI',k=find(ch>=' A'&ch<='Z'),ch(k)=[]4、输入矩阵,并找出A中大于或等于5的元素。
A=[1 2 3;4 5 6;7 8 9],[m,n]=find(A>=5),for j=1:length(m)x(j)=A(m(j),n(j))xend5、求矩阵的行列式值、逆和特征根。
a11=input('a11='),a12=input('a12 ='),a21=input('a21='),a22=input('a22 ='),A=[a11,a12;a21,a22],DA=det(A),IA=inv(A),EA=eig(A) 6、不采用循环的形式求出和式的数值解。
sum(2.^[0:63])实验二1、1行100列的Fibonacc数组a,a(1)=a(2)=1,a(i)=a(i-1)+a(i-2),用for循环指令来寻求该数组中第一个大于10000的元素,并指出其位置i。
n=100;a=ones(1,n);for i=3:na(i)=a(i-1)+a(i-2);if a(i)>10000a(i),break;end;end,i2、编写M脚本文件,定义下列分段函数,并分别求出当()、()和()时的函数值。


MATLAB 平时作业第一章 习题16. 以下两种说法对吗?(1)“MATLAB 的数值表达精度与其指令窗中的数据显示精度相同。
”答:此种说法错误。
MATLAB 提供了控制数据显示格式的控制指format ,该指令并不改变MATLAB 内存中变量的精度,只是改变其显示精度。
(2)“MATLAB 指令窗中显示的数值有效位数不超过7位。
”答:此种说法错误。
当变量小于1000时,使用format 或format short 后,或者默认情况下,变量的显示精度最多不超过7位,但显示精度不等于变量的精度。
7. 想要在MATLAB 中产生二维数组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321S ,下面哪些指令能实现目的? S=[1,2,3;4,5,6;7,8;9]S=[1 2 3;4 5 6;7 8 9]S=[1,2,3;4,5,6;7,8,9] %整个指令在中文状态下输入 答:操作如图:第1、2条指令可以实现,第3条指令不可实现。
第三章 习题31.在MATLAB 中,先运行指令A=magic(3), B=[1,2,1;3,4,3;5,6,7], C=reshape(1:6,3,2)生成阵列33⨯A ,23⨯B ,23⨯C ,然后根据运行结果回答以下问题:运行结果如图:(1)计算A*B, B*A ,这两个乘积相同吗? 计算结果如图:答:不同。
(2)计算A\B, B/A ,左除、右除结果相同吗?计算结果如图:答:不同。
(3)计算B( : ,[1,2]).*C和C.*B( : , [1,2]),这两个乘积相同吗?计算结果如图答:相同。
(4)计算A\A和A.\A,这两个计算结果相同吗?计算结果如图:答:相同。
(5)计算A\eye(3)和inv(A),这两个计算结果相同吗?计算结果如图:答:不同。
(提示:根据对计算结果的目测回答问题)2.在MATLAB中,先运行A=[1, 2; 3, 4],b=0.5,C=[4, 2; 1, 0.5], 然后根据计算结果回答以下问题:创建数据步骤略(1)计算A^b和A.^b, 这两个计算结果相同吗?答:不同。
现代计算方法Matlab 作业答案1.绘出函数f(x)=sin x x ,在[0,4]上的图形解:在M 文件输入:x=0:pi/100:4;y=x.*sin(x);plot(y)运行2. 求3x +2x +5 = 0的根解:在命令窗口输入:>> solve('x^3+2*x+5=0')ans =((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3) - 2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3))1/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 -(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/21/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 +(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/23.321436min x x x z ++=120..321=++x x x t s301≥x5002≤≤x203≥x解:运用单纯形法计算此题,首先把约束条件化成标准形式:,,,,,205030120654321635241321≥=-=+=-=++x x x x x x x x x x x x x x x(1)在M 文件输入SimpleMthd 函数:function [x,minf] = SimpleMthd(A,c,b,baseVector)sz = size(A);nVia = sz(2);n = sz(1);xx = 1:nVia;nobase = zeros(1,1);m = 1;for i=1:nViaif (isempty(find(baseVector == xx(i),1)))nobase(m) = i;m = m + 1;else;endendbCon = 1;M = 0;while bConnB = A(:,nobase);ncb = c(nobase);B = A(:,baseVector);cb = c(baseVector);xb = inv(B)*b;f = cb*xb;w = cb*inv(B);for i=1:length(nobase)sigma(i) = w*nB(:,i)-ncb(i);end[maxs,ind] = max(sigma);if maxs <= 0minf = cb*xb;vr = find(c~=0 ,1,'last');for l=1:vrele = find(baseVector == l,1);if (isempty(ele))x(l) = 0;elsex(l)=xb(ele);endendbCon = 0;elsey = inv(B)*A(:,nobase(ind));if y <= 0disp('不存在最优解!');x = NaN;minf = NaN;return;elseminb = inf;chagB = 0;for j=1:length(y)if y(j)>0bz = xb(j)/y(j);if bz<minbminb = bz;chagB = j;endendendtmp = baseVector(chagB);baseVector(chagB) = nobase(ind);nobase(ind) = tmp;endendM = M + 1;if (M == 1000000)disp('找不到最优解!');x = NaN;minf = NaN;return;endend(2)在命令窗口输入:clear allA=[1 1 1 0 0 0;1 0 0 -1 0 0;0 1 0 0 1 0;0 0 1 0 0 -1];c=[6 3 4 0 0 0];b=[120;30;50;20];[xm,mf]=SimpleMthd(A,c,b,[3 4 5 6])xm =0 50 70mf =4304.计算下面函数在区间(0,1)内的最小值。
matlab作业第一次作业[实验目的]1。
了解并熟悉Matlab,并在此基础上学习基本操作2.掌握Matlab 的基本操作和常用命令3。
了解Matlab常用的函数、运算符和表达式4.掌握Matlab的工作方法和M文件的相关知识5.在Matlab中学习矩阵和数组的运算1,[实验任务]1。
P11:例1_4写一个函数,求方程AX 2+Bx+C = 0的解2.P16: 1。
计算表达式e 12+23 3log25/tan 21.3。
写m命令文件找到?k +?1/k的值是k?1k?15010 4.编写函数文件并计算?k!并找出k=20时表达式的值k?1n3。
例2_2使用函数生成矩阵A =100020003,B = 00200000000104。
例2_3 (1)生成三阶魔方矩阵A;(2)生成一个四阶单位矩阵B 5。
示例2_10数组操作示例6。
例2_11计算sin(k?/2)(k=?2,?1,0)值7。
P27:2。
矩阵A=456,B=556,计算A*B,A.*B,并比较差值789123468323。
已知矩阵A=5,212,B=,计算A>B,A==B,A2)12,【实验步骤和结果】例1 _ 4函数y =洁(A,B,c)如果(绝对值(A)>洁(1,2,2) 9有复数根: >洁(A,B,c)(exp(1)12)+(23 3)* log2(5)/tan(21) ans =21.4426 e+0053。
函数s = J(m)s = 0;k = 1;而k v=[1 2 3] A=diag(v,0) B=diag(v,1)v =1 2 33A =1 0 02 0 03 B =100 000 200 000 300 000A =魔法(3)A =8 1 6 3 5 7 4 9 2> > B =眼睛(4)B =1 0 0 0 0 0 0 0 0 0 0 1例2-11。
a = 1:5 a =1 2 3 4 5> > b = 3:2:11 b =43 5 7 9 11> > a.ans =1 4 9 16 25> > a . * b94 5 6;7 8 9]A =1 2 3 4 5 6 7 8 9> > B =[4 6 8;5 5 6;3 2 2]B = 4 6 8 5 5 6 3 2> > A * Bans =23 22 26 59 61 74 95 100 122> > A . * Bans =4 12 245。
m a t l a b综合大作业(附详细答案)-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII《MATLAB语言及应用》期末大作业报告1.数组的创建和访问(20分,每小题2分):1)利用randn函数生成均值为1,方差为4的5*5矩阵A;实验程序:A=1+sqrt(4)*randn(5)实验结果:A =0.1349 3.3818 0.6266 1.2279 1.5888-2.3312 3.3783 2.4516 3.1335 -1.67241.2507 0.9247 -0.1766 1.11862.42861.5754 1.6546 5.3664 0.8087 4.2471-1.2929 1.3493 0.7272 -0.6647 -0.38362)将矩阵A按列拉长得到矩阵B;实验程序:B=A(:)实验结果:B =0.1349-2.33121.25071.5754-1.29293.38183.37830.92471.65461.34930.62662.4516-0.17665.36640.72721.22793.13351.11860.8087-0.66471.5888-1.67242.42864.2471-0.38363)提取矩阵A的第2行、第3行、第2列和第4列元素组成2*2的矩阵C;实验程序:C=[A(2,2),A(2,4);A(3,2),A(3,4)]实验结果:C =3.3783 3.13350.9247 1.11864)寻找矩阵A中大于0的元素;]实验程序:G=A(find(A>0))实验结果:G =0.13491.25071.57543.38183.37830.92471.65461.34930.62662.45165.36640.72721.22793.13351.11860.80871.58882.42864.24715)求矩阵A的转置矩阵D;实验程序:D=A'实验结果:D =0.1349 -2.3312 1.2507 1.5754 -1.29293.3818 3.3783 0.9247 1.6546 1.34930.6266 2.4516 -0.1766 5.3664 0.72721.2279 3.1335 1.1186 0.8087 -0.66471.5888 -1.67242.4286 4.2471 -0.38366)对矩阵A进行上下对称交换后进行左右对称交换得到矩阵E;实验程序:E=flipud(fliplr(A))实验结果:E =-0.3836 -0.6647 0.7272 1.3493 -1.29294.2471 0.80875.3664 1.6546 1.57542.4286 1.1186 -0.1766 0.9247 1.2507-1.6724 3.1335 2.4516 3.3783 -2.33121.5888 1.2279 0.6266 3.3818 0.13497)删除矩阵A的第2列和第4列得到矩阵F;实验程序:F=A;F(:,[2,4])=[]实验结果:F =0.1349 0.6266 1.5888-2.3312 2.4516 -1.67241.2507 -0.17662.42861.5754 5.3664 4.2471-1.2929 0.7272 -0.38368)求矩阵A的特征值和特征向量;实验程序:[Av,Ad]=eig(A)实验结果:特征向量Av =-0.4777 0.1090 + 0.3829i 0.1090 - 0.3829i -0.7900 -0.2579 -0.5651 -0.5944 -0.5944 -0.3439 -0.1272-0.2862 0.2779 + 0.0196i 0.2779 - 0.0196i -0.0612 -0.5682 -0.6087 0.5042 - 0.2283i 0.5042 + 0.2283i 0.0343 0.6786 0.0080 -0.1028 + 0.3059i -0.1028 - 0.3059i 0.5026 0.3660 特征值Ad =6.0481 0 0 0 00 -0.2877 + 3.4850i 0 0 00 0 -0.2877 - 3.4850i 0 00 0 0 0.5915 00 0 0 0 -2.30249)求矩阵A的每一列的和值;实验程序:lieSUM=sum(A)实验结果:lieSUM =-0.6632 10.6888 8.9951 5.6240 6.208710)求矩阵A的每一列的平均值;实验程序:average=mean(A)实验结果:average =-0.1326 2.1378 1.7990 1.1248 1.24172.符号计算(10分,每小题5分):1)求方程组20,0++=++=关于,y z的解;uy vz w y z w实验程序:S = solve('u*y^2 + v*z+w=0', 'y+z+w=0','y,z');y= S. y, z=S. z实验结果:y =[ -1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))-w] [ -1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))-w] z =[ 1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))] [ 1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))]2)利用dsolve 求解偏微分方程,dx dyy x dt dt==-的解; 实验程序:[x,y]=dsolve('Dx=y','Dy=-x')实验结果:x =-C1*cos(t)+C2*sin(t)y = C1*sin(t)+C2*cos(t)3.数据和函数的可视化(20分,每小题5分):1)二维图形绘制:绘制方程2222125x y a a +=-表示的一组椭圆,其中0.5:0.5:4.5a =;实验程序:t=0:0.01*pi:2*pi; for a=0.5:0.5:4.5; x=a*cos(t); y=sqrt(25-a^2)*sin(t); plot(x,y) hold on end实验结果:2) 利用plotyy 指令在同一张图上绘制sin y x =和10x y =在[0,4]x ∈上的曲线;实验程序:x=0:0.1:4; y1=sin(x); y2=10.^x;[ax,h1,h2]=plotyy(x,y1,x,y2); set(h1,'LineStyle','.','color','r'); set(h2,'LineStyle','-','color','g'); legend([h1,h2],{'y=sinx';'y=10^x'});实验结果:3)用曲面图表示函数22z x y =+;实验程序:x=-3:0.1:3; y=-3:0.1:3; [X,Y]=meshgrid(x,y); Z=X.^2+Y.^2; surf(X,Y,Z)实验结果:4)用stem 函数绘制对函数cos 4y t π=的采样序列;实验程序:t=-8:0.1:8;y=cos(pi.*t/4); stem(y)实验结果:4. 设采样频率为Fs = 1000 Hz ,已知原始信号为)150π2sin(2)80π2sin(t t x ⨯+⨯=,由于某一原因,原始信号被白噪声污染,实际获得的信号为))((ˆt size randn x x+=,要求设计出一个FIR 滤波器恢复出原始信号。
上机操作(4)内容: M 文件编程一、结合教材第6章内容以及实验指导书内容掌握一般M 脚本和函数文件的编写。
二、 完成以下习题,并按照要求将作业提交。
(1) 将调试通过的程序序列复制到作业题目下方,并将文件保存为word 文档,文件名为:姓名+班级学号末两位数 (如:王丹妮9301)(2) 作业提交方式:A 现场网上提交(鼠标右点击电脑右下方的人头或燕子标记,按照菜单操作即可。
B 若不能提交,发送至我的邮箱363586609@ .发送时邮件标题为:文件名作业4(如:王丹妮9301作业4)1. 编写M 脚本文件,画出下列分段函数所表示的曲面。
(30分)⎪⎪⎩⎪⎪⎨⎧-≤+≤+<->+=+-------15457.0117575.015457.0),(215.175.375.0216215.175.375.02112122212212122x x e x x e x x e x x p x x x x x x x x %参考答案a=2;b=2;x=-a:0.1:a;y=-b:0.1:b;for i=1:length(y)for j=1:length(x)if x(j)+y(i)>1z(i,j)=0.5457*exp(-0.75*y(i)^2-3.75*x(j)^2-1.5*x(j));elseif x(j)+y(i)<=-1z(i,j)=0.5457*exp(-0.75*y(i)^2-3.75*x(j)^2+1.5*x(j));else z(i,j)=0.7575*exp(-y(i)^2-6.*x(j)^2);endendendaxis([-a,a,-b,b,min(min(z)),max(max(z))]);surf(x,y,z);xlabel('x1');ylabel('x2');zlabel('p(x1,x2)');2.编写一个M 函数文件,该文件应有函数声明行、帮助说明和程序编写人姓名。
MATLAB作业学号:07082002 姓名:武婷第一次作业:1)熟悉Matlab运行环境;简介一下你都做了什么!首先,安装了Matlab软件,并启动该软件。
Matlab启动后,即出现Desktop操作桌面,为一个高度集成的工作界面。
同时发现有四个界面:指令窗(command window),当前目录浏览器(current directory),历史指令窗(command history),工作空间浏览器(workspace brower)。
指令窗(command window):在该窗内,进行了简单的算术运算,矩阵的不同输入方式的体验,既简单的函数调用等。
如在命令窗口中键入一些简单的命令:rand(4,4)生成4*4其元素在0-1之间的随机矩阵,norm(x,1)求向量的1-范数。
再如输入指令:>> 7*(12^2+66)/21,按下回车键即可得到结果:ans =5.6084e+070当前目录浏览器:为管理方便,首先建立用户目录并将它设置成当前目录,了解到了有两种方法;交互界面设置法和指令设置法。
同时基于对该软件搜索路径知识的学习利用设置路径对话框修改搜索路径,并尝试了两种修改状态:当前有效修改和永久有效修改。
历史指令窗(command history):该窗口记录了每次开启Matlab的时间,即开启后再指令窗中运行过的所有指令行。
令人惊喜的是,所有指令可以被轻松的复制和再运行。
然后通过参考书籍我对该窗口中的某些指令进行了重新调用。
工作空间浏览器(workspace brower):该窗口的功能是创建新变量,显示变量内容基变量的保存等。
在此,握手先熟悉了一下常用操作指令,然后尝试了输入clc清除命令窗,以及clear清除当前的数据、变量,如何借助工作空间浏览器产生保存变量的M文件。
接下来,对于菜单栏进行了详细的了解。
进入菜单栏File选项,了解了文件选项中所包含的各项命令,并尝试新建函数,为此选择了简单的函数进行编写相应的程序,通过调试完成了函数的正确编写,然后进行系统默认目录的保存,同时注意到对该文件进行合适的命名以便于区分。
下来进入File选项中的Preferences,更改输出字节长度,字体大小和颜色,及较为简单的设置。
然后感受了Matlab友善的用户界面,体验了多窗口和单一窗口的显示。
将Desktop调出、移除Editor、Figures等界面框,单击箭头嵌入界面,通过拖拽调整各界面框的位置,还调整了各界面框的大小。
2)了解MATLAB 帮助系统,并任选一个帮助专题,按其指导运行部分例子代码,建议对其适当修改。
介绍一下你的在整个实验过程中的情形,包括出现了什么问题,怎么解决的,观察到什么结果等。
通过学习我尝试着运行了例子代码,给出运行结果:>> A=[1 2 3;4 5 6]A =1 2 34 5 6>> fliplr(A)ans =3 2 16 5 4>> B=[1 2 3 4 5 6]B =1 2 3 4 5 6>> fliplr(B)ans =6 5 4 3 2 1由以上可以看出,该函数的作用是对矩阵进行左右翻转。
那么在此我产生一个问题,对于三阶四阶的矩阵系统是如何规定左右的呢,基于这个问题,我进行了如下尝试:>> a=[1 2 3;4 5 6;7 8 9]a =1 2 34 5 67 8 9>> fliplr(a)ans =3 2 16 5 49 8 7>> c=rand(4,4)c =0.2769 0.6948 0.4387 0.18690.0462 0.3171 0.3816 0.48980.0971 0.9502 0.7655 0.44560.8235 0.0344 0.7952 0.6463>> fliplr(c)ans =0.1869 0.4387 0.6948 0.27690.4898 0.3816 0.3171 0.04620.4456 0.7655 0.9502 0.09710.6463 0.7952 0.0344 0.8235分析该结果可以看出对于超过二阶的矩阵,矩阵的左右翻转式对称进行的,而左右翻转的意义已经不明显了。
那么这样的翻转是否有效呢?调回help阅读:LimitationsThe array being operated on cannot have more than two dimensions. This limitation exists because the axis upon which to flip a multidimensional array would be undefined。
原来,该函数命令仅限于对于一阶及二阶矩阵进行的左右翻转,二对二节以上的矩阵则不再有意义了。
因此,在使用函数命令是我们应仔细阅读函数功能,同时不可忽略命令使用条件的限制,如此才能正确使用该软件解决实际问题。
第二次作业熟悉MATLAB的可视化功能:1,从数学分析课程中选择较复杂的曲线(平面,空间皆可),用MATLAB编程绘图;2,从数学分析课程中选择较复杂的空间曲面,用MATLAB编程绘图;1.选择二维曲线的绘制:>> t = linspace(0, 8, 401); %Define a vector of times from 0 to 8 s with 401 pointsx = t.*exp(-t).*cos(2*pi*4*t); %Define a vector of x values plot(t, x) %Plot x vs2.选择三维网格曲面的绘制: >> x=-20.5:0.00005;20.5;y=x;[x,y]=meshgrid(x,y); R=sqrt(x.^2+y.^2)+eps; z=sin(R)./R; surf(x,y,z)012345678-0.4-0.3-0.2-0.100.10.20.30.4第三次作业1. 以下两个方程的解。
(提示:关于符号变量的假设要注意)(1) 试写出求三阶方程05.443=-x 正实根的程序。
注意:只要正实根,不要出现其他根。
syms x positive;x=solve(x^3-44.5,x) x =(2^(2/3)*89^(1/3))/2(2) 试求二阶方程022=+-a ax x 在0>a 时的根。
clear allsyms a positive;syms x; solve('x^2-a*x+a^2',x)-25ans =a/2 - (3^(1/2)*a*i)/2 a/2 + (3^(1/2)*a*i)/22. 求符号矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211a a a a a a a a a A 的行列式值和逆,所得结果应采用“子表达式置换”简洁化。
syms a_11 a_12 a_13 a_21 a_22 a_23 a_31 a_32 a_33; A=[a_11,a_12,a_13;a_21,a_22,a_23;a_31,a_32,a_33]; S=det(A);F=inv(A); [RS,w]=subexpr(S,'w') RS =a_11*a_22*a_33 - a_11*a_23*a_32 - a_12*a_21*a_33 + a_12*a_23*a_31 + a_13*a_21*a_32 - a_13*a_22*a_31 w =[ empty sym ]>> [RF,W]=subexpr(F,'W') RF =[ W*(a_22*a_33 - a_23*a_32), -W*(a_12*a_33 - a_13*a_32), W*(a_12*a_23 - a_13*a_22)][ -W*(a_21*a_33 - a_23*a_31), W*(a_11*a_33 - a_13*a_31), -W*(a_11*a_23 - a_13*a_21)][ W*(a_21*a_32 - a_22*a_31), -W*(a_11*a_32 - a_12*a_31), W*(a_11*a_22 - a_12*a_21)] W =1/(a_11*a_22*a_33 - a_11*a_23*a_32 - a_12*a_21*a_33 + a_12*a_23*a_31 + a_13*a_21*a_32 - a_13*a_22*a_31)3. 对于0>x ,求12011122+∞=∑⎪⎭⎫ ⎝⎛+-+k k x x k 。
(提示:理论结果为x ln ;注意限定性假设)syms x positive;syms k;f=2/(2*k+1)*[(x-1)/(x+1)]^(2*k+1); s=symsum(f,k,0,inf) s =piecewise([abs(x - 1) < x + 1, 2*atanh((x - 1)/(x + 1))]) 4. (1)通过符号计算求t t y sin )(=的导数dtdy 。
syms t;y=abs(sin(t)); diff(y) ans =sign(sin(t))*cos(t)(2)然后根据此结果,求-=0t dtdy 和2π=t dtdy 。
f=diff(y);limit(f,t,0,'left') ans = -1>> limit(f,t,pi/2) ans = 0 5. 求出dx x exsin 7.15⎰--ππ的具有64位有效数字的积分值。
(提示:int,vpa, ezplot ) syms x;f=exp(-abs(x))*abs(sin(x)); y=int(f,x,-5*pi,1.7*pi); vpa(y,64) ans =3617514.635647088707100018393465500554242735057835123431773680704 6. 计算二重积分⎰⎰+211222)(xdydx y x 。
syms x y; f=x^2+y^2;int(int(f,y,1,x^2),x,1,2) ans = 1006/1057. 在0>n 的限制下,求xdx n y n⎰=2s in )(π的一般积分表达式,并计算)31(y 的32位有效数字表达。
(提示:注意限定条件;注意题目要求32位有效)syms n positive;syms x; f=sin(x)^n; y=int(f,x,0,pi/2) y =beta(1/2, n/2 + 1/2)/2 >>beta(1/2,1/6+1/2)/2 ans = 1.2936 >> vpa(ans,32) ans =1.29355477961489517824134054535538. 求方程2,122==+xy y x 的解。