六年级数学平面图形面积计算公式

面积的计算认识面积的计算公式和实际应用面积的计算：认识面积的计算公式和实际应用面积是数学中一个重要的概念，它用来描述平面图形的大小。

在我们的日常生活中，我们经常需要计算各种形状的物体的面积，比如房屋的面积、地板的面积、田地的面积等等。

本文将介绍一些常见的计算面积的公式和实际应用。

一、矩形和正方形的面积计算矩形和正方形是最简单的平面图形，它们的面积计算公式非常简单。

对于一个矩形或正方形来说，我们只需要知道它的长度和宽度，就可以计算出它的面积。

矩形的面积计算公式为：面积 = 长度 ×宽度；正方形的面积计算公式为：面积 = 边长 ×边长。

例如，一个长为5米，宽为3米的矩形，它的面积可以通过以下计算得出：面积 = 5米 × 3米 = 15平方米。

二、三角形的面积计算三角形是另一个常见的平面图形，计算三角形的面积有不同的公式，其中最常用的是海伦公式和高度公式。

1. 海伦公式：对于已知三角形三边长度的情况，我们可以使用海伦公式来计算其面积。

海伦公式如下：面积= √(s × (s-a) × (s-b) × (s-c))其中，s为半周长，s = (a + b + c) / 2，a、b、c分别为三角形的三边长度。

2. 高度公式：如果我们已知三角形的底和高，那么面积可以通过底乘以高的一半来计算。

例如，对于一个底为6米，高为4米的三角形，可以通过以下计算得出其面积：面积 = (6米 × 4米) / 2 = 12平方米。

三、圆的面积计算圆是一个没有直边和直角的平面图形，计算圆的面积需要使用π (pi) 这个特殊的数值。

圆的面积计算公式为：面积= π × 半径 ×半径，其中π的近似值为3.14。

例如，对于一个半径为5米的圆，可以通过以下计算得出其面积：面积 = 3.14 × 5米 × 5米 = 78.5平方米。

四、实际应用面积的计算在我们的日常生活和工作中具有广泛的应用。

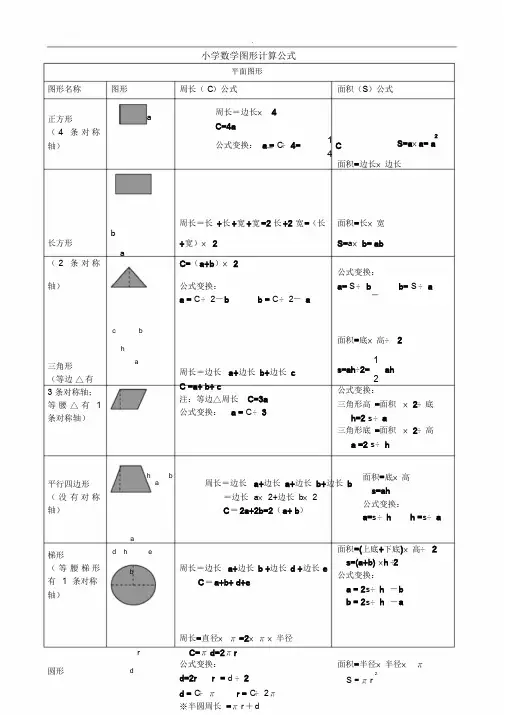
.小学数学图形计算公式平面图形图形名称图形周长（C）公式面积（S）公式正方形（4 条对称轴）a周长＝边长× 4C=4a公式变换： a = C÷4=14C2S=a×a= a面积=边长×边长周长＝长+长+宽+宽=2 长+2 宽=（长面积=长×宽b长方形+宽）× 2 S=a×b= aba（2 条对称C=（a+b）× 2公式变换：轴）公式变换：a= S ÷ b b= S ÷ aa = C÷2－b b = C÷2－ ac b面积=底×高÷ 2h三角形（等边△有3 条对称轴；等腰△有 1 条对称轴）a周长＝边长a+边长b+边长cC =a+ b+ c注：等边△周长C=3a公式变换： a = C÷ 31s=ah÷2= ah2公式变换：三角形高=面积×2÷底h=2 s÷ a三角形底=面积×2÷高a =2 s÷h平行四边形（没有对称轴）h ba 周长＝边长a+边长a+边长b+边长 b＝边长a×2+边长b× 2C＝2a+2b=2（a+ b）面积=底×高s=ah公式变换：a=s÷h h =s÷ a a梯形（等腰梯形有 1 条对称轴）d h eb周长＝边长a+边长b +边长d +边长eC＝a+b+ d+e面积=(上底+下底)×高÷ 2s=(a+b) ×h ÷2公式变换：a = 2s÷h －bb = 2s÷h －a周长=直径×π=2×π×半径r C=πd=2πr..周长=C大圆+C小圆=πD+πd=2πR+2πr=2π（R+r）面积= S 大圆－S2=πR－πr=π（R2－r2－r小圆2圆环2）立体图形图形名称图形总棱长（L）公式表面积（S）公式体（容）积（V）公式正方体a 总棱长=棱长×12L=12aS=一个面的面积× 62S= a×a×6 =6a体积=棱长×棱长×棱长3V= a×a×a=a长方体ha b 总棱长=长×4+宽×4+高×4=4（长+宽+高）L=4（a+b+h）表面积=( 长×宽+长×高+宽×高) × 2S=2(ab+ah+bh)体积=长×宽×高V=abh侧面积=底面周长×高S侧=ch=dπh=2πrh表面积=底面积×2+侧面积S 表= S 底×2+ S侧圆柱的表面积公式：体积=底面积×（1）有两个底面的圆柱的表面积公式：高＝侧面积÷ 2圆柱体×半径2×2+πdhS表= S 底×2+ S2×2+πdh= rπ侧=πr V= S 底×h2×2+2πrh =2πr （r+h ）2×2+2πrh =2πr （r+h ）（2）只有 1 个底面的圆柱的表面积公式：= πr 2 hS表= S 底+ S 侧=πr 2+πdh= πr 2+2πrh= πr （r+2h ）（3）两个底面都没有的圆柱的表面积公式：S 表=S侧=ch = πdh =2 πrh圆筒大圆柱直径为D，半径为R，周长为C；小圆柱直径为d，半径为r，周长为c；高都为hS表= S 大圆柱侧+ S 小圆柱侧+（S大圆柱底－S 小圆柱底）×2= C 大圆柱h+c 小圆柱h+（πR2－πr2）× 2V= V大圆柱－V2－πr2=πh（D+d）+2π（R－r 2）小圆柱22）= S大圆柱底×h－S小圆柱底×h= πR 2 h－πr2 h －πr×h2= πh（R=2πh（R+r）+2π（R2－r2－r2）体积=底面积×高÷ 3圆锥体1V圆锥=3V圆柱=3VV圆柱=13S底×h=13πr 2h圆锥等底等体积的圆柱与圆锥，圆锥的高=圆柱高的 3 倍.做人最好状态是懂得尊重，不管他人闲事，不晒自己优越，也不秀恩爱。

小学数学常用图形周长面积体积计算公式:1,正方形C周长S面积a边长周长=边长×4面积=边长×边长C=4aS=a×a S=a22,正方体V体积a棱长表面积=棱长×棱长×6体积=棱长×棱长×棱长S表=a×a×6 表=6a2V=a×a×a V= a33,长方形C周长S面积a边长周长=(长+宽)×2C=2(a+b)面积=长×宽S=ab4,长方体V体积S面积a长b宽h高(1)表面积=(长×宽+长×高+宽×高)×2(2)体积=长×宽×高S=2(ab+ah+bh)V=abh5,三角形S面积a底h高面积=底×高÷2S=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6,平行四边形S面积a底h高面积=底×高S=ah7,梯形S面积a上底b下底h高面积=(上底+下底)×高÷2S=(a+b)× h÷28,圆形S面积C周长π圆周率d直径r半径周长=直径×π周长=2×π×半径面积=半径×半径×πC=πd C=2πrS=πr2 d=C÷πd=2r r=d÷2r=C÷2÷πS环=π(R2-r2)9,圆柱体V体积h高S底面积r底面半径C底面周长侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高S侧=ChS侧=πdhV=Sh V=πr2h圆柱体积=侧面积÷2×半径10,圆锥体V体积h高S底面积r底面半径体积=底面积×高÷3V=Sh÷3长度单位换算1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米面积单位换算1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米1平方米＝0.0015亩，1万平方米=15亩1公顷＝15亩＝100公亩＝10000平方米1公亩等于100平方米1(市)亩等于666.66平方米体(容)积单位换算1立方米=1000立方分米1立方分米=1000立方厘米1立方分米=1升1立方厘米=1毫升1立方米=1000升重量单位换算1吨=1000千克1千克=1000克1千克=1公斤人民币单位换算1元=10角1角=10分1元=100分时间单位换算1世纪=100年1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天,闰年2月29天平年全年365天,闰年全年366天1日=24小时1时=60分1分=60秒1时=3600秒总数÷总份数＝平均数和差问题的公式(和＋差)÷2＝大数(和－差)÷2＝小数和倍问题和÷(倍数－1)＝小数小数×倍数＝大数(或者和－小数＝大数)差倍问题差÷(倍数－1)＝小数小数×倍数＝大数(或小数＋差＝大数)植树问题1非封闭线路上的植树问题主要可分为以下三种情形:⑴如果在非封闭线路的两端都要植树,那么:株数＝段数＋1＝全长÷株距－1全长＝株距×(株数－1)株距＝全长÷(株数－1)⑵如果在非封闭线路的一端要植树,另一端不要植树,那么: 株数＝段数＝全长÷株距全长＝株距×株数株距＝全长÷株数⑶如果在非封闭线路的两端都不要植树,那么:株数＝段数－1＝全长÷株距－1全长＝株距×(株数＋1)株距＝全长÷(株数＋1)2封闭线路上的植树问题的数量关系如下株数＝段数＝全长÷株距全长＝株距×株数株距＝全长÷株数盈亏问题(盈＋亏)÷两次分配量之差＝参加分配的份数(大盈－小盈)÷两次分配量之差＝参加分配的份数(大亏－小亏)÷两次分配量之差＝参加分配的份数相遇问题相遇路程＝速度和×相遇时间相遇时间＝相遇路程÷速度和速度和＝相遇路程÷相遇时间追及问题追及距离＝速度差×追及时间追及时间＝追及距离÷速度差速度差＝追及距离÷追及时间顺流速度＝静水速度＋水流速度逆流速度＝静水速度－水流速度静水速度＝(顺流速度＋逆流速度)÷2水流速度＝(顺流速度－逆流速度)÷2浓度问题溶质的重量＋溶剂的重量＝溶液的重量溶质的重量÷溶液的重量×100%＝浓度溶液的重量×浓度＝溶质的重量溶质的重量÷浓度＝溶液的重量利润与折扣问题利润＝售出价－成本利润率＝利润÷成本×100%＝(售出价÷成本－1)×100%涨跌金额＝本金×涨跌百分比折扣＝实际售价÷原售价×100%(折扣＜1)利息＝本金×利率×时间税后利息＝本金×利率×时间×(1－20%)小学定义定理公式（一）三角形的面积＝底×高÷2。

平面图形面积计算在几何学中，计算平面图形的面积是一个基本的技能。

无论是为了日常生活中的测量，还是在数学领域求解问题时，正确计算平面图形的面积都是必不可少的。

本文将针对常见的平面图形，介绍如何计算它们的面积。

一、矩形的面积计算矩形是最简单的平面图形之一，其面积计算公式为：面积 = 长 ×宽。

假设一矩形的长为L，宽为W，则该矩形的面积为 L × W。

二、正方形的面积计算正方形是特殊的矩形，其四条边长度相等。

正方形的面积计算公式为：面积 = 边长 ×边长，或者面积 = 边长的平方。

假设一正方形的边长为A，则该正方形的面积为 A × A，或者 A²。

三、三角形的面积计算三角形是常见的平面图形，其面积计算需要根据已知的边长、高或底边及高来计算。

常用的面积计算公式有以下三种：1. 面积 = 1/2 ×底边 ×高假设一个三角形的底边长为B，高为H，则该三角形的面积为 1/2 ×B × H。

2. 面积 = (a × h) / 2假设一个三角形的底边长为a，高为h，则该三角形的面积为 (a × h) / 2。

3. 海伦公式对于已知三个边长的三角形，我们可以使用海伦公式来计算其面积。

海伦公式的形式为：面积= √[s × (s-a) × (s-b) × (s-c)]其中，s 是三角形半周长，即s = (a + b + c) / 2，a、b、c 分别为三角形的三个边长。

四、圆的面积计算圆是一种特殊的平面图形，其面积计算需要使用圆周率π。

圆的面积计算公式为：面积= π × 半径的平方。

假设一个圆的半径为R，则该圆的面积为π × R²。

五、梯形的面积计算梯形是有两个平行底边的四边形，其面积计算需要使用梯形的上底、下底和高。

梯形的面积计算公式为：面积= (上底+ 下底) ×高的一半。

小学数学图形计算公式01.平面图形的周长1.长方形的周长=（长+宽）×2，C=（a+b）×22.正方形的周长=边长×4，C=4a3.直径=半径×2，d=2r；半径=直径÷2，r=d÷24.圆的周长=圆周率×直径=圆周率×半径×2，c=πd=2πr02.平面图形的面积1.长方形的面积=长×宽，S=ab2.正方形的面积=边长×边长，S=a×a= a²3.三角形的面积=底×高÷2，S=ah÷24.平行四边形的面积=底×高，S=ah5.梯形的面积=（上底+下底）×高÷2，S=（a+b）h÷26.圆的面积=圆周率×半径×半径，S=πr²7.长方体的表面积=（长×宽+长×高+宽×高）×2=（ab+ah+bh）×28.正方体的表面积=棱长×棱长×6，S=6 a²9.圆柱的侧面积=底面圆的周长×高，S=ch10.圆柱的表面积=上下底面面积+侧面积，S=2πr² +2πrh03.立体图形的体积1.长方体的体积=长×宽×高，V =abh2.正方体的体积=棱长×棱长×棱长，V=a×a×a= a³3.圆柱的体积=底面积×高，V=Sh，V=πr²h4.圆锥的体积=底面积×高÷3，V=Sh÷3=πr²h÷3具体情景问题04.和、差、倍问题（和+差）÷2=大数，（和-差）÷2=小数和÷（倍数+1）=小数，小数×倍数=大数（或者和-小数=大数）差÷（倍数-1）=小数，小数×倍数=大数（或小数+差=大数）05.植树问题（1 ）非封闭线路上的植树问题主要可分为以下三种情形：a.如果在非封闭线路的两端都要植树，那么：株数=段数+1=全长÷株距+1全长=株距×（株数-1）株距=全长÷（株数-1）b.如果在非封闭线路的一端要植树，另一端不要植树，那么：株数=段数=全长÷株距全长=株距×株数株距=全长÷株数c.如果在非封闭线路的两端都不要植树，那么：株数=段数-1=全长÷株距-1全长=株距×（株数+1）株距=全长÷（株数+1）（2）封闭线路上的植树问题的数量关系如下：株数=段数=全长÷株距全长=株距×株数株距=全长÷株数06.盈亏问题（盈+亏）÷两次分配量之差=参加分配的份数（大盈-小盈）÷两次分配量之差=参加分配的份数（大亏-小亏）÷两次分配量之差=参加分配的份数07.相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间08.追及问题追及距离=速度差×追及时间追及时间=追及距离÷速度差速度差=追及距离÷追及时间09.流水问题顺流速度=静水速度+水流速度逆流速度=静水速度-水流速度静水速度=（顺流速度+逆流速度）÷2水流速度=（顺流速度-逆流速度）÷210.浓度问题溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量11.利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=（售出价÷成本-1）×100%涨跌金额=本金×涨跌百分比折扣=实际售价÷原售价×100%（折扣<1）利息=本金×利率×时间税后利息=本金×利率×时间×（1-20%）12.时间单位换算1世纪=100年，1年=12月大月（31天）有：1\3\5\7\8\10\12月，小月（30天）的有：4\6\9\11月平年2月28天，闰年2月29天，平年全年365天，闰年全年366天1日=24小时，1时=60分，1分=60秒，1时=3600秒。

面积的测量与计算面积是指平面图形所占据的空间大小，是一个重要的数学概念。

在日常生活和各个领域中，我们经常需要测量和计算面积。

本文将介绍常见平面图形的测量和计算方法，并提供一些实际应用的例子。

一、正方形的面积测量与计算正方形是一种边长相等的四边形，它的面积计算公式为：面积 = 边长 ×边长。

例如，假设一块正方形地板的边长为5米，我们可以通过将地板划分为1米乘1米的小方块，然后将这些小方块的数量相加，来测量地板的面积。

在这种情况下，地板的面积为5米 × 5米 = 25平方米。

二、长方形的面积测量与计算长方形是一种两对边分别相等的四边形，它的面积计算公式为：面积 = 长 ×宽。

例如，假设一块长方形花坛的长度为6米，宽度为3米，我们可以直接将长度和宽度相乘，来计算花坛的面积。

在这种情况下，花坛的面积为6米 × 3米 = 18平方米。

三、三角形的面积测量与计算三角形是一种有三个边和三个角的多边形，它的面积计算公式为：面积 = 底边长度 ×高 ÷ 2。

例如，假设一个三角形的底边长度为8米，高为4米，我们可以将底边长度和高相乘，再除以2，来计算三角形的面积。

在这种情况下，三角形的面积为（8米 × 4米）÷ 2 = 16平方米。

四、圆的面积测量与计算圆是由一条闭合曲线围成的平面图形，它的面积计算公式为：面积= π × 半径 ×半径（其中π的近似值为3.14）。

例如，假设一个圆的半径为5米，我们可以将半径的平方乘以π，来计算圆的面积。

在这种情况下，圆的面积为3.14 × 5米 × 5米 = 78.5平方米（近似值）。

五、实际应用例子面积的测量和计算在各个领域都有广泛的应用。

以下是一些实际应用例子：1. 建筑业：在房屋建设中，建筑师需要测量房间的面积，以确定合适的家具和装饰品。

2. 农业：农民需要测量农田的面积，以确定种植作物的数量和施肥的比例。

六年级数学平面图形的周长和面积
平面图形的周长和面积
新疆教育学院实验小学
荀洁
我们已经学过了三角形、长方形、正方形、平行四边形、梯形、圆等平面图形，我们称它们为基本图形或规则图形，这些平面图形的面积及周长都有相对应的计算公式。

平面图形的周长及面积的计算是小学阶段的一个重点内容，也是一个难点，这一内容公式多，计算方法灵活，所以我们必须在熟练掌握各种公式的基础上，灵活运用公式进行计算。

现在，我将自己整理的一些公式归纳如下：
（一）周长计算公式：长方形周长=（长+ 宽）×2正方形周长= 边长×4三角形周长=边长+ 边长+ 边长圆的周长= 2 ×∏×半径或圆的周长= ∏×直径
（二）面积计算公式：长方形面积=长×宽正方形面积=边长×边长三角形面积=底×高÷2平形四边形面积=底×高梯形面积=（上底+下底）×高÷2圆的面积= ∏×半径×半径
Ф表面积计算公式：长方体表面积=（长×宽+长×高+宽×高）×2正方体表面积=边长×边长×6圆柱的侧面积=底面圆周长×高圆柱的表面积=底面圆的面积×2 + 圆柱的侧面积
Ф体积计算公式：长方体体积= 长×宽×高正方体体积= 棱长×棱长×棱长圆柱的体积= 底面积×高圆椎的体积=底面积×高×1／3
例1：如下图，甲、乙两个图形都是正方形，它们的边长分别是10 厘米和12 厘米.求阴影部分的面积。

六年级的知识点面积公式在学习数学的过程中，面积公式是六年级学生需要掌握的基础知识点之一。

面积公式用于计算平面图形的面积，包括矩形、正方形、三角形和圆形等。

通过学习这些公式，学生可以更好地理解和解决与面积相关的问题。

接下来，我们将逐个介绍这些知识点及其对应的面积公式。

矩形的面积公式：矩形是一种具有四个直角的四边形，它的边长分别为a和b，面积公式为：面积 = 长 ×宽或者面积 = a × b正方形的面积公式：正方形是一种具有四条相等边和四个直角的四边形，它的边长为a，面积公式为：面积 = 边长 ×边长或者面积 = a × a三角形的面积公式：三角形是一种具有三条边和三个内角的图形，我们常用的面积公式有两种。

一种是通过底边和高计算面积，另一种是通过三边的长度计算面积。

第一种面积公式：面积 = 底边 ×高 ÷ 2第二种面积公式（海伦公式）：面积= √[s(s-a)(s-b)(s-c)]其中，s表示三角形三边的半周长，a、b、c分别表示三角形的三条边的长度。

圆形的面积公式：圆形是一种具有无边界的几何图形，它的面积公式与半径（r）有关，公式如下：面积= π × r × r或者面积= π × r²学习这些面积公式可以帮助学生更好地理解图形的特征和属性，通过运用公式进行计算，解决面积相关的问题。

而对于不规则图形的面积计算，可以通过将其划分为多个规则图形并分别计算面积，最后将各个部分的面积相加得到总面积。

除了学习这些公式之外，六年级的学生还需要掌握如何应用这些公式来解决实际问题。

例如，通过给定的边长计算矩形或正方形的面积，或者根据给定的面积求解相应的边长等。

通过练习和实践，学生将能够熟练地应用面积公式，并在解决问题时提高他们的思维能力和数学技巧。

总结起来，六年级的知识点面积公式包括矩形、正方形、三角形和圆形的面积计算方法。

计算面积的五种方法计算面积是数学中的基本概念之一，它是指一个平面图形所占据的空间大小。

在日常生活中，我们经常需要计算面积，比如测量房间的面积、计算地块的面积等等。

本文将介绍五种计算面积的方法。

一、平行四边形法平行四边形法是计算平行四边形面积的常用方法。

它的计算公式为：面积=底边×高。

其中，底边是平行四边形的一条边，高是从底边垂直向上的线段长度。

例如，一个底边长为5cm，高为3cm的平行四边形的面积为15平方厘米。

二、三角形法三角形法是计算三角形面积的常用方法。

它的计算公式为：面积=底边×高÷2。

其中，底边是三角形的一条边，高是从底边垂直向上的线段长度。

例如，一个底边长为6cm，高为4cm的三角形的面积为12平方厘米。

三、梯形法梯形法是计算梯形面积的常用方法。

它的计算公式为：面积=(上底+下底)×高÷2。

其中，上底和下底分别是梯形的上下两条平行边的长度，高是从上底向下底垂直的线段长度。

例如，一个上底长为3cm，下底长为5cm，高为4cm的梯形的面积为16平方厘米。

四、圆形法圆形法是计算圆形面积的常用方法。

它的计算公式为：面积=π×半径的平方。

其中，π是一个常数，约等于3.14，半径是圆的半径长度。

例如，一个半径为2cm的圆的面积为12.56平方厘米。

五、复合图形法复合图形法是计算由多个简单图形组成的复合图形面积的方法。

它的计算方法是将复合图形分解成若干个简单图形，然后分别计算每个简单图形的面积，最后将它们的面积相加得到复合图形的面积。

例如，一个由一个矩形和一个三角形组成的复合图形，可以将它分解成一个矩形和一个三角形，分别计算它们的面积，然后将它们的面积相加得到复合图形的面积。

计算面积是数学中的基本技能之一，掌握了这些计算方法，可以更加方便地进行测量和计算。

一、平面图形的面积公式：1.矩形的面积公式：矩形的面积等于长乘以宽，公式为：面积=长×宽。

2.正方形的面积公式：正方形的面积等于边长的平方，公式为：面积=边长×边长。

3.三角形的面积公式：三角形的面积等于底边乘以高除以2，公式为：面积=1/2×底边×高。

4.梯形的面积公式：梯形的面积等于上底加下底乘以高除以2，公式为：面积=1/2×(上底+下底)×高。

5.平行四边形的面积公式：平行四边形的面积等于底边乘以高，公式为：面积=底边×高。

6.菱形的面积公式：菱形的面积等于对角线1乘以对角线2的一半，公式为：面积=1/2×对角线1×对角线27.圆的面积公式：圆的面积等于半径的平方乘以π，公式为：面积=半径×半径×π。

二、立体图形的面积公式：1.立方体的表面积公式：立方体的表面积等于6倍的边长的平方，公式为：表面积=6×边长×边长。

2.正方体的表面积公式：正方体的表面积等于6倍的边长的平方，公式同立方体的表面积公式。

3.长方体的表面积公式：长方体的表面积等于2倍的长乘宽加2倍的长乘高加2倍的宽乘高，公式为：表面积=2×(长×宽+长×高+宽×高)。

4.圆柱体的侧面积公式：圆柱体的侧面积等于圆的周长乘以高，公式为：侧面积=周长×高。

5.圆柱体的表面积公式：圆柱体的表面积等于两个底面积加上侧面积，公式为：表面积=2×圆的面积+侧面积。

6.圆锥的侧面积公式：圆锥的侧面积等于圆的周长乘以斜高，公式为：侧面积=周长×斜高。

7.圆锥的表面积公式：圆锥的表面积等于底面积加上侧面积，公式为：表面积=圆的面积+侧面积。

8.球体的表面积公式：球体的表面积等于4倍的半径的平方乘以π，公式为：表面积=4×半径×半径×π。

第十章 定积分的应用 1 平面图形的面积公式1：连续曲线y=f(x)(≥0)，以及直线x=a, x=b(a<b)和x 轴所围曲边梯形面积为：A=⎰b a f(x )dx=⎰ba y dx.若f(x)在[a,b]变号，则所围图形的面积为：A=⎰b a |f(x )|dx=⎰ba |y |dx.公式2：上下两条连续曲线y=f 2(x)与y=f 1(x)以及两条直线x=a 与x=b(a<b)所围的平面图形面积为：A=⎰ba 12(x )]-f (x )[f dx.例1：求由抛物线y 2=x 与直线x-2y-3=0所围图形的面积A. 解法一：A 等同于由抛物线y=x 2与直线y=2x+3所围图形的面积. 解方程组：⎩⎨⎧=+= x y 32x y 2，得⎩⎨⎧==9y 3x , ⎩⎨⎧=-=1y 1x . ∴A=⎰-+312)x -3(2x dx=[32-(-1)2]+3[3-(-1)]-3(-1)-333=332. 解法二：如图，图形被x=1分为左右两部分， A 左=⎰--10)]x (x [dx=3⎰10x dx=34. A 右=⎰⎪⎭⎫ ⎝⎛-9123-x x dx=312-9233-41-922+21)-(93⨯=328. A= A 左+ A 右=34+328=332.公式3：设曲线C 为参数方程x=x(t), y=y(t), t ∈[α,β]，在[α,β]上y(t)连续，x(t)连续且可微且x ’(t)≠0(类似地可讨论y(t)连续可微且y ’(t)≠0的情形). 记a=x(α), b=x(β), (a ≠b)，则由曲线C 及直线x=a, x=b 和x 轴所围的图形，其面积计算公式为：A=⎰'βα(t)x )t (y dt.例2：求由摆线x=a(t-sint), y=a(1-cost) (a>0)的一拱与x 轴所围平面图形的面积.解：摆线的一拱可取t ∈[0,2π]，又x ’=a(1-cost)， ∴A=⎰-2π022)t cos 1(a dt=3πa 2.公式4：若参数方程所表示的曲线是封闭的，即有x(α)=x(β), y(α)=y(β)， 且在(α,β)内曲线自身不再相交，则由曲线自身所围图形面积为： A=⎰'βα(t)dt x )t (y 或A=⎰'βα(t)dt y )t (x .例3：求椭圆22a x +22by =1所围的面积.解：化为参数方程：x=asint, y=bcost, t ∈[0,2π], 又x ’=acost ， ∴A=⎰2π02tdt abcos =πab.公式5：设曲线C 为极坐标方程r=r(θ), θ∈[α,β]，且r(θ)在[α,β]上连续, β-α≤2π.由曲线C 与两条射线θ=α, θ=β所围成的平面图形，通常也称为扇形，此扇形的面积为：A=⎰βα2d θ)θ(r 21. 证：如图，对区间[α,β]作任意分割T ：α=θ0<θ1<…<θn-1<θn =β， 射线θ=θi (i=1,2,…,n-1)把扇形分成n 个小扇形.∵r(θ)在[α,β]上连续，∴当T 很小时，在每一个△i =[θi-1, θi ]上r(θ)的值变化也很小，任取ξi ∈△i ，便有r(θ)≈r(ξi ), θ∈△i , i=1,2,…,n.这时，第i 个小扇形的面积△A i ≈21r 2(ξi)△θi , ∴A ≈∑=n1i 21r 2(ξi )△θi .当T →0时，两边取极限，就有A=⎰βα2d θ)θ(r 21.例3：求双纽线r 2=a 2cos2θ所围平面图形的面积. 解：如图，∵r 2≥0，∴θ∈[-4π,4π]∪[43π,45π]，由图形的对称性可得： A=4·⎰4π02θdθ2cos a 21=a 2 sin2θ|4π0=a 2 .习题1、求由抛物线y=x 2与y=2-x 2所围图形的面积.解：求得两曲线交点为(-1,1), (1,1). ∴所围图形的面积为： A=⎰-1122)x -x -(2dx=38.2、求曲线y=|lnx|与直线x=101, x=10, y=0所围图形的面积. 解：所围图形的面积为： A=⎰10101|lnx |dx=-⎰1101lnx dx+⎰101lnx dx =-(xlnx|1101-⎰1101x dlnx)+ xlnx|101+⎰101x dlnx=-(101ln10-109)+10ln10-9=1099ln10-1081.3、抛物线y 2=2x 把圆x 2+y 2=8分成两部分，求这两部分面积之比. 解：问题等同于抛物线y=21x 2把圆x 2+y 2=8分成两部分，求面积比. 它们的交点为(2,2),(-2,2). 记两部分的面积为A 1,A 2，则A 1=⎰--2222)x 21x -8(dx=8⎰-4π4π2θcos d θ-38=2π+34；A 2=8π-A 1=6π-34.∴21A A =34-6π34+2π=2 -9π2 +3π.4、求内摆线x=acos 3t, y=asin 3t (a>0)所围图形的面积. 解：如图，所围图形面积为： A=4⎰'2π033dt |)t t(asin cos a |=12a2⎰2π024tdttsin cos=12a 2⎰2π024tdt tsin cos =83πa 2.5、求心形线r=a(1+cos θ) (a>0)所围图形的面积. 解法一：根据心形线的对称性，得A=2·⎰+π022d θ)θcos 1(a 21=a 2⎰++π02d θ)θcos θcos 21(=23πa 2.解法二：化为参数方程：x=a(1+cos θ)cos θ, y=a(1+cos θ)sin θ, θ∈[0,2π]， A=|⎰'++2π0d θ]θsin )θcos θ[a(1cos )θcos a(1| =a 2|⎰-+2π0234θ)dθθsin cos θcos 2θcos (2|=23πa 2.6、求三叶形曲线r=asin3θ (a>0)所围图形的面积.解：根根三叶形曲线的形态特点，所围图形由相同的三部分组成，即 A=3⎰32π3π223θsin a 21d θ=⎰32π3π223θsin a 21d3θ=4πa 2.7、求曲线a x +by =1 (a,b>0)与坐标轴所围图形的面积. 解：曲线与x 轴的交点为(a,0)，∴所围图形的面积为： A=b ⎰⎪⎪⎭⎫ ⎝⎛+-a0a x a x 21dx=6ab.8、求曲线x=t-t 3, y=1-t 4所围图形的面积.解：当t=-1,1时，x=0,y=0，∴曲线在t ∈[-1,1]围成封闭图形，即 A=|⎰'-11-43)t -)(1t t (dt|=4|⎰-11-46)t t (dt|=3516.9、求二曲线r=sin θ与r=3cos θ所围公共部分的面积. 解法一：化为圆的方程：x 2+(y-21)2=41, (x-23)2+y 2=43. 它们的交点为O(0,0)与P(43,43)，∴所围公共部分的面积为： A=⎰⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+---⎪⎭⎫ ⎝⎛-4302223y 4321-y 41dy=⎰-6π2π2t cos 41dt+⎰3π02t cos 43dt -833 =323+12π+3233+8π-833=245π-43. 解法二：由sin θ=3cos θ, 得tan θ=3，∴二曲线相交于θ=3π.A=⎰3π02θsin 21d θ+⎰2π3π2θcos 23d θ=-)1(cos2θ413π0-⎰d θ+⎰+2π3π1)(cos2θ43d θ =-163+12π+8π-1633=245π-43.(参考解法)如图：求得P(43,43) S 阴=S P OO 1扇形+S P OO 2扇形-S P OO 1∆ -S P OO 2∆ =3πOO 12+6πOO 22-21·43·OO 1-21·43·OO 2=12π+8π-163-1633=245π-43.10、求两椭圆22a x +22b y =1与22b x +22ay =1(a>b>0)所围公共部分的面积.解：两椭圆在第一象限的交点为：⎪⎪⎭⎫⎝⎛++2222b a abb a ab ，. 根据图形的对称性，可得：A=8⎰+⎪⎪⎭⎫ ⎝⎛--22baab022x a x 1b dx=4abarcsin 22b a b +-2222b a b 4a +.。