名义利率和有效利率的计算
- 格式：doc
- 大小：87.50 KB
- 文档页数：5
下载文档原格式
合集下载
一建 经济 1Z101013 名义利率与有效利率的计算
1Z101013 名义利率与有效利率的计算在复利计算中，利率周期通常以年为单位，它可以与计息周期相同，也可以后同。
当计息周期小于一年时，就出现了名义利率和有效利率的概念。
名义利率的计算有效利率的计算计息周期有效利率计息周期小于（或等于）资金收付周期时的等值计算【考点分析】名义利率和有效利率的含义和大小比较；计息期有效利率的计算；资金收付周期有效利率的计算年有效利率的计算；计息周期小于资金收付周期时的等值计算。
【历年真题】(2006年)某施工企业向银行借款100万元，年利率8%，半年复利计息一次，第三年末还本付息，则到期时企业需偿还银行( )万元。
A.124.00B.125.97C.126.53D.158.69 【答案】C【解析】掌握利用终值和现值以及名义利率与有效利率的换算方法。
本题计息周期是半年，资金收付周期是3年，要求计算的是一次支付的终值。
计算方法有以下两种。
（1）%42%8===m r i53.126%)41(100)1(6=+=+=n i P F （万元）（2）()%16.81%)41(112=-+=-+=meff i i53.126%)16.81(100)1(3=+=+=n i P F （万元）(2007年)已知年利率 12%，每月复利计息一次，则季度的实际利率为( )。
A ．1.003%B ．3.00%C ．3.03%D ．4.00% 【答案】C【解析】已知名义利率r 为12%，计息周期为月，则季度实际利率的计算为：%112%12===m r i()%03.31%)11(113=-+=-+=meff i i(2007年)每半年末存款 2000 元，年利率 4%，每季复利计息一次，2 年末存款本息和为( )万元。
A ．8160.00B ．8243.22C ．8244.45D ．8492.93 【答案】C【解析】已知A 为2000元，r 为4%，计息周期为季度，要求计算2年末的终值F 。
工程经济计算公式汇总,例题讲解
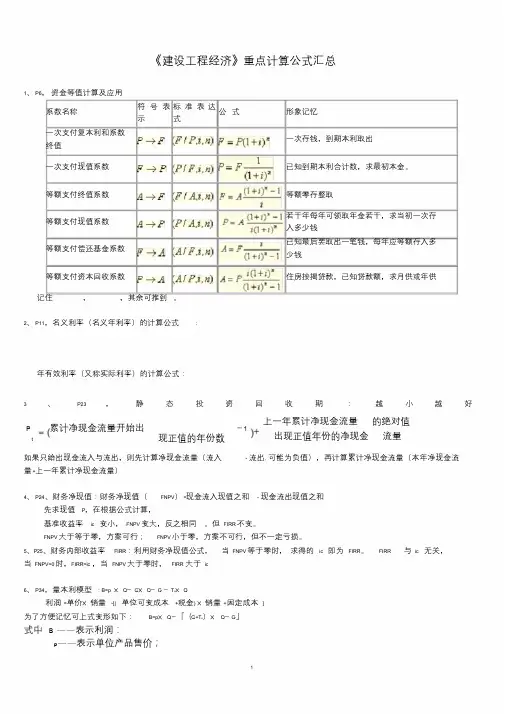
《建设工程经济》重点计算公式汇总1、P6，资金等值计算及应用系数名称符号表示标准表达式公式形象记忆一次支付复本利和系数终值一次存钱，到期本利取出一次支付现值系数已知到期本利合计数，求最初本金。
等额支付终值系数等额零存整取等额支付现值系数若干年每年可领取年金若干，求当初一次存入多少钱等额支付偿还基金系数已知最后要取出一笔钱，每年应等额存入多少钱等额支付资本回收系数住房按揭贷款，已知贷款额，求月供或年供记住，，其余可推到。
2、P11，名义利率（名义年利率）的计算公式:年有效利率（又称实际利率）的计算公式：3 、P23 ，静态投资回收期：越小越好P t 累计净现金流量开始出－1现正值的年份数上一年累计净现金流量出现正值年份的净现金的绝对值流量如果只给出现金流入与流出，则先计算净现金流量（流入- 流出, 可能为负值），再计算累计净现金流量（本年净现金流量+上一年累计净现金流量）4、P24、财务净现值：财务净现值（FNPV）=现金流入现值之和- 现金流出现值之和先求现值P，在根据公式计算，基准收益率ic 变小，FNPV变大，反之相同。
但FIRR 不变。
FNPV大于等于零，方案可行；FNPV小于零，方案不可行，但不一定亏损。
5、P25、财务内部收益率FIRR：利用财务净现值公式，当FNPV等于零时，求得的ic 即为FIRR。
FIRR 与ic 无关，当FNPV=0时，FIRR=ic ，当FNPV大于零时，FIRR 大于ic6、P34，量本利模型: B=p ×Q－C u ×Q－C F－T u×Q利润=单价×销量-[( 单位可变成本+税金) ×销量+固定成本]为了方便记忆可上式变形如下：B=p×Q－「（C u+T u）×Q－C F」式中 B ——表示利润：p——表示单位产品售价；1、P6，资金等值计算及应用系数名称符号表示标准表达式公式形象记忆一次支付复本利和系数终值一次存钱，到期本利取出一次支付现值系数已知到期本利合计数，求最初本金。
AFP计算器计算名义年利率与有效年利率的转换
AFP计算器计算名义年利率与有效年利率的转换
AFP考试中，有效利率和名义利率的转换计算很常见，传统算法里，您需要记住转换公式，进行多步计算，利用金考易金融计算器的利率转换功能，您只需输入已知利率，便可轻松计算出对应的名义年利率或有效年利率，简单、方便、准确。
名义年利率：一般由银行给出
有效年利率：不同复利期间现金流的年华收益率
APR：名义年利率、m：1 年中复利期间数量、EAR：有效年利率
名义年利率与有效年利率的转换计算实例
【例】已知名义年利率为8%，按季计息，求有效年利率。
答案：8.24%
普通算法：
金考易金融计算器计算：
金考易金融计算器已更新至2.4 七大功能终生免费使用下载地址：/app/index.htm。
名义利率与有效利率
【知识点】名义利率与有效利率【例题1】已知年利率12%,每月复利计息一次，则季实际利率为()。
A・ 1.003%B・ 3.00%C・ 3.03%D・ 4.00%【答案】C【解析】月利率:12%/1=1%季实际利率：(1+1%) 3-1=3.03%【例题2】某企业向银行贷款100万元，期限为半年，年名义贷款利率为12%,每月计息一次，则企业实际支付利息为多少？【答案】方法一:100* (1+1%) 6=106.15或者先算出年有效利率(1+1%) 12-1 = 12.68%,100 (1+12.68%) 0.5 = 106.15 万元支付利息：106.15-100=6.15万元方法二：年名义利率为12%,按月计息，则每月利率为1%,期限半年也就是6个月，则可如下计算:100 (1+1% ) 6-100=6.15 万元【例题3】每半年末存款2000元，年利率4%,每季复利计息一次。
2年末存款本息和为()万元。
A・ 8160.00E・ 8243.22C・ 8244.4D・ 8492.93【答案】c【解析】季利率=4%/4=1%将半年存款换算成等额季存款：2000 (A/F, 1%, 2) =995.025995.025 (F/A, 1%, 8) =8244.45【例题4】某企业于年初向银行借款1000万元，其年有效利率为10%,若按季度复利计息，则该年第6个月末借款本利和为()万元。
A・ 1000X10%/2E・ 1000X (10%+i ) 1/2C・ 1000X[ (10%+l) 1/12-1J6D. 1000X[ (10%+l) 1/12-1]2【答案】B【解析】本题考核的是有效利率和名义利率的内容。
年有效利率为10%,按照有效利率的计算关系式：年有效利率=（1+季度利率）4-1,则季度利率=（年有效利率+1） 1/4-1,按季度复利计息，则该年第6个月末借款本利和为1000万元X （1+季度利率）2万元。
名义年利率计算公式
名义年利率计算公式r=i+p其中，r为名义利率，i为实际利率，p为借贷期内物价水平的变动率，它可以为正，也可能为负。
较为精确的计算公式可以写成：r=(1+i)(1+p)-1i=(1+r)/(1+p)-1这是目前国际上通用的计算实际利率的公式。
在通货膨胀的条件下，市场的各种利率都是名义利率。
而实际利率往往不能直接观察到。
一般而言，名义利率大于通货膨胀率，两者之差为实际利率。
所谓名义利率，是央行或其它提供资金借贷的机构所公布的未调整通货膨胀因素的利率，即利息（报酬）的货币额与本金的货币额的比率。
即指包括补偿通货膨胀（包括通货紧缩）风险的利率。
名义利率虽然是资金提供者或使用者现金收取或支付的利率，但人们应当将通货膨胀因素考虑进去。
拓展资料：区别：一、相比实际利率名义利率并不是投资者能够获得的真实收益，还与货币的购买力有关。
如果发生通货膨胀，投资者所得的货币购买力会贬值，因此投资者所获得的真实收益必须剔除通货膨胀的影响，这就是实际利率。
实际利率，指物价水平不变，从而货币购买力不变条件下的利息率。
名义利率与实际利率存在着下述关系：1、当计息周期为一年时，名义利率和实际利率相等，计息周期短于一年时，实际利率大于名义利率。
2、名义利率不能是完全反映资金时间价值，实际利率才真实地反映了资金的时间价值。
3、以i表示实际利率，r表示名义利率，n表示年计息次数，那么名义利率与实际利率之间的关系为1+名义利率=（1+实际利率）*（1+通货膨胀率），一般简化为名义利率=实际利率+通货膨胀率4、名义利率越大，周期越短，实际利率与名义利率的差值就越大。
例如，如果银行一年期存款利率为2%，而同期通胀率为3%，则储户存入的资金实际购买力在贬值。
因此，扣除通胀成分后的实际利率才更具有实际意义。
仍以上例，实际利率为2% －3% =－1%，也就是说，存在银行里是亏钱的。
在中国经济快速增长及通胀压力难以消化的长期格局下，很容易出现实际利率为负的情况，即便央行不断加息，也难以消除。
计算公式
一、 利息与利率公式：I=F －P式中：I —利息；F —目前债务人应付（或债权人应收）总金额，即还本付息总额；P —原借贷金额，常称为本金。
利率的计算公式：i=P tI ×100%式中：i —利率；I t —单位时间内所得的利息额。
二、利息的计算1、单利的计算公式：I t =P ×i 单； I n = P ×i 单×n ；[n 期末单利本利和F 等于本金P 加上总利息I n ]即，F=P+ I n =P （1+n ×i 单）式中：I t —代表第t 计息周期的利息额；P —代表本金；i 单—计息周期单利利率；I n —代表n 个计息周期所付或所收的单利总利息。
2、复利的计算公式：I t =i ×F t －1 而第t 期末复利本利和的表达式：F t = F t －1（1+i ）式中：i —计息周期复利利率；F t －1—表示（t －1）期末复利本利和。
等值的计算一、一次支付的终值和现值计算（一）终值计算（已知P 求F ）一次支付n 年末终值（即本利和）F 的计算公式为：F=P （1+i ）n又可写成F=P ( F/P, i, n)（二）现值计算（已知F 求P ）现值计算公式为：P=F （1+i ）-n 又可写成P=F ( P/F, i, n)式中：i —计息期复利率；n —计息的期数；P —现值（即现在的资金价值或本金）；F —终值（即n 期末的资金值或本利和）。
二、等额支付系列现金流量的终值、现值计算1、终值计算（已知A ，求F ） 终值F 的计算公式为：F=A ii n 1)1(-+ 又可写成：F=A(F/A, i, n) 式中：A —年金（即，每年末存入的资金） F —几年末有资金多少万元 P —借款多少万元2、 现值计算（已知A ，求P ）现值P 的计算公式为：P=A nn i i i )1(1)1(+-+ 又可写成：P=A(P/A, i, n) 已知F 求A: A=F 1)1(-+n i i 又可写成：A=F(A/F,i,n) 已知P 求A ：A=P 1)1()1(-++i i i n又可写成：A=P(A/P,i,n) 熟悉名义利率和有效利率的计算一、 名义利率的计算所谓名义利率r 是指计息周期利率i 乘以一年内的计息周期数m 所得的年利率。
名义利率和有效利率的计算
名义利率和有效利率的计算在复利计算中，利率周期通常以年为单位，它可以与计息周期相同，也可以不同。
当计息周期小于一年时，就出现了名义利率和有效利率。
一、名义利率的计算
名义利率 r 是指计息周期利率 i 乘以一年内的计息周期数 m 所得的年利率。
即：
r＝i×m
若计息周期月利率为1%，则年名义利率为 12%。
很显然 , 计算名义利率与单利的计算相同。
二、有效利率的计算
有效利率是措资金在计息中所发生的实际利率
包括：①计息周期有效利率
②年有效利率
1. 计息周期有效利率 , 即计息周期利率i:
i＝r/m
2. 年有效利率 , 即年实际利率。
更多一级建造师精品资料：/kcnet580/
造价工程师学习：/kcnet600/。
一建工程经济计算公式汇总及计算题解析
一建工程经济计算公式汇总及计算题解析第一章：工程经济3、名义利率与有效利率的计算P11⑴、计息周期：某一笔资金计算利息时间的间隔（计息周期数m ，计息周期利率i ）P12 ⑵、计息周期利率（i ）⑶、计息周期数：某一笔资金在一年内计算利息的次数（m ） ⑷、名义利率：指的是年利率（单利计算的年利率）（r ）r=i ×m ⑸、实际利率：又称有效利率，复利计算利率 ①计息周期的有效利率：（等效计息周期利率） ②年有效利率：1)1(-+=meff mr i ⑹、已知某一笔资金的按季度计息，季度利率3%，问资金的名义利率 r=i ×m=3%×4=12%⑺、已知某一笔资金半年计息一次，名义利率10%，问半年的利率是多少 i=r/m=10%/2=5%⑻、甲施工企业，年初向银行贷款流动资金200万，按季计算并支付利息，季度利率%，则甲施工企业一年应支付的该项流动资金贷款利息为多少万元200×%×4=12万元⑼、年利率8%，按季度复利计息，则半年的实际利率为多少季度利率 i=r/m=8%/4=2% 半年的有效利率（i eff ）=(1+r/m)m -1=（1+2%）2-1=%⑽、有一笔资金，名义利率r=12%，按月计息，计算季度实际利率，月利率i=1% 季度的有效利率（i eff ））=(1+r/m)m -1=（1+1%）3-1=%⑾、某企业从金融机构借款100万，月利率1%，按月复利计息，每季度付息一次，则该企业一年须向金融机构支付利息多少万元季度的有效利率（i eff ））=(1+r/m)m -1=（1+1%）3-1=% 季度有效利率×100万×4=%×100×4=万元1Z101020 技术方案经济效果评价（5-6题）3、投资收益率分析P19⑴、投资收益率是衡量技术方案获利水平的评价指标，它是技术方案建成投产达到设计生产能力后一个正常年份的年净收益额与技术方案总投资的比率。
年利率计算方法公式
年利率的计算方法公式主要有两种，具体如下：
1. 年利率= 月利率×12（月数）。
如果已知月利率，可以通过这个公式快速计算出年利率。
2. 年利率= 本金×日利率×360（天数，一般按360天计算）/ 本金。
如果已知日利率和本金，可以通过这个公式计算出年利率。
这里假设一年有360天，是为了计算方便和标准化，实际情况可能会有所不同。
另外，有效年利率的计算公式为：有效年利率= （1 + 名义利率/一年内计息次数）^n - 1，其中n表示一年的计息次数。
有效年利率和总收益率之间的关系为：1 + 有效年利率= （1 + 总收益率）。
以上信息仅供参考，如有需要，建议咨询专业金融人士。
名义利率与有效利率
由表可见，当计息期数m=1时，名义利率等于实际利率。
当m>1时，实际利率大于名义利率，且m越大，即一年中计算复利的 有限次数越多，则年实际利率相对与名义利率就越高。
2023/12/27
东南大学交通学院 冒刘燕
6
年名义利率为12％，不同计息期的实际利率
计算复利的方式 按年
按半年 按季 按月 按日
一年中的计息期数 1 2 4 12
2023/12/27
东南大学交通学院 冒刘燕
21
计息期间的存款放在期末，计息期间的提款放在 期初，计息期分界点处的支付保持不变。
现金流量如图所示：年利率为12%,每季度计息1次， 求年末终值F是多少？
100
100
0 1 2 3 4 5 6 7 8 9 10 11 12月
300
300
100
2023/12/27
东南大学交通学院 冒刘燕
25
名义利率( r )与实际利率( i )关系 i = r/m
年有效利率( I ) I= (1+r/m)m-1
连续计息 F= Per , I’ = er-1
2023/12/27
东南大学交通学院 冒刘燕
26
年每半年等额年末存款200元，问与其等值的第0年的现 值是多少？ 解：计息期为半年的有效利率i=r/m＝12％÷2＝6％,
计息期数n=m×年数＝2×3＝6次 则P=A ×（P/A, i, n）＝200 ×（P/A, 6％, 6）
＝200×4.9173＝983.46元
2023/12/27
东南大学交通学院 冒刘燕
300
+100
＝112.36元
本章小结
现金流量图
资金的时间价值
2024年一级建造师《建设工程经济》知识点笔记(第一章 资金时间价值计算与应用)
思维导图
A.条件一
B.条件二
C.条件三
D.条件四
2.某企业拟存款200万元，下列存款利率和计息方式中，在第5年末存款本息和最多的是（）。
A.年利率6%,按单利计算
B.年利率5.5%,每年复利一次
C.年利率4%,每季度复利一次
D.年利率5%,每半年复利一次
A.方案一
B.方案二
C.方案三
D.方案四
4.关于资金时间价值的说法，正确的有（）。
A.单位时间资金增值率一定的条件下、资金的时间价值与使用时间成正比
B.资金随时间的推移而贬值的部分就是原有资金的时间价值
C.投入资金总额一定的情况下，前期投入的资金越多，资金的正效益越大
D.其他条件不变的情况下，资金的时间价值与资金数量成正比。
名义利率和有效利率
运用利息公式要注意的问题
方案的初始投资P，假设发生在寿命期初； 寿命期内各项收入或支出，均假设发生在各期 的期末； 本期的期末即是下一期的期初 寿命期末发生的本利和F，记在第n期期末； 等额支付系列A，发生在每一期的期末。 当问题包括P，A时，P 在第一期期初，A在 第一期期末 当问题包括F，A时，F和A同时在最后一期期 末发生。
年平均利润＝6000／5＝1200， 年平均折旧＝8000／5=1600， 投资收益率＝（1200+1600）/8000=35％。
简单收益率
指标评价
优点 • 计算简便直观 • 有利于对企业经理人员的评价 缺点 • 没有考虑货币的时间价值 • 它不能反映项目计算期不同时间的获益
净现值
概念
净现值
判别标准
若NPV > 0,该投资方案的原始投资能够回收，能够 支付资本成本费用，能够获得大于资本成本的盈利 的水平，因而应该接受该投资方案； 若NPV = 0，则原始投资能够被回收，能够支付资 本成本费用，这样该投资方案处于盈亏平衡点位置； 如果NPV < 0，则原始投资可能无法回收，可能支 付不起资本成本费用，因此该投资方案应被拒绝
计息期短于支付期
例7：年利率12%，每季度计息一次，每年年末 支付500元，连续支付6年，求其第0年的现值 为多少？
解：其现金流量如图
i=12%
方法一，计息期向支付期靠拢，求出支付期的有效 利率。 4 年有效利率 i 1 0.12 1 12.55%
4
P 500 P
按给定的折现率（或基准折现率）将投资方案在 NP V F (1 i) 寿命期内各年净现金流量折现到期初的现值代数 和就是净现值。若以NPV符号表示净现值，则
方案的初始投资P，假设发生在寿命期初； 寿命期内各项收入或支出，均假设发生在各期 的期末； 本期的期末即是下一期的期初 寿命期末发生的本利和F，记在第n期期末； 等额支付系列A，发生在每一期的期末。 当问题包括P，A时，P 在第一期期初，A在 第一期期末 当问题包括F，A时，F和A同时在最后一期期 末发生。
年平均利润＝6000／5＝1200， 年平均折旧＝8000／5=1600， 投资收益率＝（1200+1600）/8000=35％。
简单收益率
指标评价
优点 • 计算简便直观 • 有利于对企业经理人员的评价 缺点 • 没有考虑货币的时间价值 • 它不能反映项目计算期不同时间的获益
净现值
概念
净现值
判别标准
若NPV > 0,该投资方案的原始投资能够回收，能够 支付资本成本费用，能够获得大于资本成本的盈利 的水平，因而应该接受该投资方案； 若NPV = 0，则原始投资能够被回收，能够支付资 本成本费用，这样该投资方案处于盈亏平衡点位置； 如果NPV < 0，则原始投资可能无法回收，可能支 付不起资本成本费用，因此该投资方案应被拒绝
计息期短于支付期
例7：年利率12%，每季度计息一次，每年年末 支付500元，连续支付6年，求其第0年的现值 为多少？
解：其现金流量如图
i=12%
方法一，计息期向支付期靠拢，求出支付期的有效 利率。 4 年有效利率 i 1 0.12 1 12.55%
4
P 500 P
按给定的折现率（或基准折现率）将投资方案在 NP V F (1 i) 寿命期内各年净现金流量折现到期初的现值代数 和就是净现值。若以NPV符号表示净现值，则
第6讲第一章第二节分项详细估算法(二)至第四节简单估算法(2021新版)
(三)名义利率与有效利率当利率周期与计息周期不一致时，就出现了名义利率和实际利率的概念。
名义利率有效利率换算：(1)1m effI r i Pm由此可见，利率周期有效利率与名义利率的关系实质上与复利和单利的关系相同。
七、建设期利息计算的几种计算方式(例)某新建项目，建设期为3年，分年均衡进行贷款，第一年贷款300万元， 第二年600万元，第三年400万元，年利率为12％，建设期内利息只计息不支付，计算建设期贷款利息。
解：在建设期，各年利息计算如下：111122q A i =•=⨯300⨯12%＝18.00(万元) 2q ＝(1212P A +)•i=(300+18+16002⨯)⨯12％＝74．16(万元)3q ＝(2P +312A )·i ＝(318+600+74．1612+⨯400)⨯12％＝143.06(万元) 所以，建设期贷款利息＝1q +2q +3q ＝18+74．16+143．06＝235．22(万元)[例]某新建项目，建设期为3年，第一年年初借款200万元，第二年 年初借款300万元，第三年年初借款200万元，借款年利率为6％，每年计息一 次，建设期内不支付利息。
试计算该项目的建设期利息。
[解答]第一年借款利息：Q1=(p+A1) ×i=200×6％=12(万元) 第二年借款利息：Q2=(P2+A2) ×i=(212+300) ×6％=30．72(万元) 第三年借款利息：Q3=(p3+A3) ×i=(212+330．72+200) ×6％=44．56(万元) 该项目的建设期利息为：Q=Q1+Q2+e3=12+30．72+44．56=87．28(万元)八、流动资金估算流动资金估算一般采用分项详细估算法。
个别情况或者小型项目可采用扩大指标法。
1. 分项详细估算法流动资产的构成要素一般包括存货、库存现金、应收账款和预付帐款；流动负债的构成要素一般包括应付账款和预收账款。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（3）对需要比较的项目或方案应取相同的计算期。
lZl0l021 财务评价指标体系
注：凡是带“动态”、“内部”、“现值”的指标都是动态的；
凡是带“借款”“负债”“偿债”“利息”的指标都是偿债指标。
【2009考题】31．在工程建设中．对不同的新技术、新工艺和新材料应用方案进行经济分析可采用的静态分析方法有( )。
A．净年值法、净现值法、年折算费用法
B．年折算费用法、综合总费用法、净年值法
C．增量投资分析法、净年值法、综合总费用法
D．增量投资分析法、年折算费用法、综合总费用法
多智网校试题解析：D。
影响基准收益率的因素
lZl0l023 影响基准收益率的因素
一、基准收益率的概念（掌握）
也称基准折现率。是投资者以动态的观点所确定的、可接受的、应当获得的最低标准的收益水平。
三、财务评价的程序（了解）
收集数据→编制财务报表→财务评价。具体步骤如下：
1、首先进行融资前的盈利能力分析（论证方案设计的合理性，用于初步投资决策以及方案比选。即考察项目是否可行，是否值得去融资）。
2、再进行融资后分析（通过盈利能力分析和偿债能力分析比选融资方案）。
四、财务评价方案（理解）
（一）独立型方案
如项目完全由企业自有资金投资时，可参考行业的平均收益水平；
假资金来源于自有资金和贷款时，最低收益率不应低于行业平均收益水平与贷款利率的加权平均值。
（2）投资风险。
通常以风险贴补率ｉ2来提高ｉc值。风险越大，贴补率越高。
就风险而言，资金密集>劳动密集；资产专用性强>资产通用性强的；以降低成本为目的<以扩大市场份额为目的；资金雄厚的<资金拮据者。
C．10.25％
D．10.O0%
多智网校试题解析：B；m=4，季度利率为2.5%，复利4次，可以计算得到结果。
【例1Z1O1014—3】某设备价格为55万元，采用5年内分期付款方式。合同签订时即
付10万元，然后每半年等额付款一次。设年利率为10％，每半年复利一次。问每半年应
付多少设备价款?
多智网校试题解析：
【2009考题】1．企业或行业投资者以动态的观点确定的、可接受的投资方案最低标准的收益水平称( )。
A．基准收益率
B．社会平均收益率
C．内部收益率
D．社会折旧率
多智网校试题解析：A。
二、基准收益率的测定
（一）财务基准收益率的测定规定（掌握）
1、政府投资项目，采用的行业财务基准收益率，应根据政府的政策导向进行确定。
（1）方案彼此独立无关，选择一个方案，并不影响其他方案的选择。
（2）也叫做"绝对经济效果检验"，通过检验，则可行，否则应予拒绝。
（二）互斥型方案
一是进行绝对经济效果检验；二是考察相对经济效果检验。
五、项目计算期（掌握）
项目的计算期包括建设期和运营期。
（1）运营期分为投产期和达产期两个阶段。
（2）运营期应以主要设备的经济寿命期确定。
F=P（1+ ）m（r—名义利率；m—计息周期）
I=F-P=P（1+ ）m—P=P[（1+ ）m—1]
ieff= =（1+ ）m—1
m越大，1年内计息的次数就越多，年实际利率就越大；
【2009考题】54．已知年名义利率为10％，每季度计息1次，复利计息，则年有效利率为( )。
A．10.47％
B．10.38％
③融资前分析的相关指标，应作为初步投资ቤተ መጻሕፍቲ ባይዱ策与融资方案研究的依据和基础。
（2）融资后分析
①考察项目在拟定融资条件下的盈利能力、偿债能力和财务生存能力，判断项目方案在融资条件下的可行性。
②融资后分析用于比选融资方案，帮助投资者做出融资决策。
③融资后的盈利能力分析也应包括动态分析和静态分析。
5、按项目评价的时间分类（事前评价、事中评价和事后评价）
lZl0l021 财务评价的内容
所谓财务评价就是对建设方案的财务可行性和经济合理性进行分析论证，为决策提供依据。
一、建设项目财务评价的基本内容（掌握）
（1）对于经营性项目，分析项目的盈利能力、偿债能力和财务生存能力。
（2）对于非经营性项目，分析项目的财务生存能力。
1、盈利能力
指标包括：投资内部收益率、财务净现值、资本金内部收益率、投资回收期、总投资收益率、资本金净利润率等。
名义利率和有效利率的计算
lZl0l014 名义利率和有效利率的计算
当计息周期小于一年时，就出现了名义利率和有效利率的概念。
一、名义利率的计算（掌握）
（1）名义利率r=计息周期利率i×计息周期数m。即：r=i×m
（2）若计息周期月利率i为1%，则年名义利率r为12%。
（3）计算名义利率时忽略了前面利息再生的因素，这与单利的计算相同。
（3）通货膨胀。通常以通货膨胀率ｉ3来表示
综合以上分析，基准收益率可确定如下：
ｉc=（1+ｉ1）（1+ｉ2）（1+ｉ3）-1≈ｉ1+ｉ2+ｉ3
基准收益率的基础是资金成本和机会成本，而投资风险和通货膨胀则是必须考虑的影响因素。
（二）基准收益率的测定方法（了解）
可采用：资本资产定价模型法、加权平均资金成本法、典型项目模拟法和德尔菲专家
2、偿债能力
指标包括：利息备付率、偿债备付率、资产负债率等。
3、财务生存能力
根据“项目财务计划现金流量表”，考察现金流入和流出、现金流量、累计盈余资金（不出现负值），分析项目是否有足够的净现金流量维持正常运营，以实现财务可持续性。
二、财务评价方法（掌握）
1、财务评价的基本方法（确定性评价、不确定性评价）
2、在中国境外投资的建设项目，财务基准收益率的测定，应首先考虑国家风险因素。
3、投资者自行测定的，基准收益率应根据资金成本、机会成本、项目风险、通货膨胀等因素综合测定。
（1）基准收益率应不低于单位资金成本和单位投资的机会成本。
ｉc>=ｉ1=max{单位资金成本，单位投资机会成本}
资金成本包括筹资费（如股票发行费、借款手续费）和资金使用费。
2、按评价方法的性质分类（定性分析、定量分析，定量为主）
3、按评价方法是否考虑时间因素分类（静态分析、动态分析，动态为主）
4、按评价是否考虑融资分类
（1）融资前分析
①融资前分析排除了融资方案变化的影响，从项目投资总获利能力的角度，考察项目方案设计的合理性。
②融资前动态分析，考察整个计算期内现金流入和现金流出，编制项目投资现金流量表，计算项目投资内部收益率和净现值等指标。
(1)据题意绘出现金流量图如图1Z101014—3所示。
(2)计算：
已知名义利率 =10％，计息周期为半年，则计息周期利率 。根据资金回收计算 即可计算出每半年应付设备价款额。即：
建设项目财务评价
1Z101020 建设项目财务评价
建设项目经济评价，分为财务评价（也称财务分析）和国民经济评价（也称经济分析）两个层次。
二、有效利率的计算（掌握）
有效利率是指实际利率，包括计息周期有效利率和年有效利率两种情况。
1、计息周期有效利率，i=r/m；和计息周期名义利率相等。
如：年利率12%，按照季度计息，则计息周期为季度，季度的名义利率为3%，计息周期有效利率也是3%；
2、年有效利率，即年实际利率（考虑利息再生）。
当按照季度计息时，已知的12%年利率是年名义利率，年实际利率相当于用季度利率3%复利了4次；用公式表示为：
lZl0l021 财务评价指标体系
注：凡是带“动态”、“内部”、“现值”的指标都是动态的；
凡是带“借款”“负债”“偿债”“利息”的指标都是偿债指标。
【2009考题】31．在工程建设中．对不同的新技术、新工艺和新材料应用方案进行经济分析可采用的静态分析方法有( )。
A．净年值法、净现值法、年折算费用法
B．年折算费用法、综合总费用法、净年值法
C．增量投资分析法、净年值法、综合总费用法
D．增量投资分析法、年折算费用法、综合总费用法
多智网校试题解析：D。
影响基准收益率的因素
lZl0l023 影响基准收益率的因素
一、基准收益率的概念（掌握）
也称基准折现率。是投资者以动态的观点所确定的、可接受的、应当获得的最低标准的收益水平。
三、财务评价的程序（了解）
收集数据→编制财务报表→财务评价。具体步骤如下：
1、首先进行融资前的盈利能力分析（论证方案设计的合理性，用于初步投资决策以及方案比选。即考察项目是否可行，是否值得去融资）。
2、再进行融资后分析（通过盈利能力分析和偿债能力分析比选融资方案）。
四、财务评价方案（理解）
（一）独立型方案
如项目完全由企业自有资金投资时，可参考行业的平均收益水平；
假资金来源于自有资金和贷款时，最低收益率不应低于行业平均收益水平与贷款利率的加权平均值。
（2）投资风险。
通常以风险贴补率ｉ2来提高ｉc值。风险越大，贴补率越高。
就风险而言，资金密集>劳动密集；资产专用性强>资产通用性强的；以降低成本为目的<以扩大市场份额为目的；资金雄厚的<资金拮据者。
C．10.25％
D．10.O0%
多智网校试题解析：B；m=4，季度利率为2.5%，复利4次，可以计算得到结果。
【例1Z1O1014—3】某设备价格为55万元，采用5年内分期付款方式。合同签订时即
付10万元，然后每半年等额付款一次。设年利率为10％，每半年复利一次。问每半年应
付多少设备价款?
多智网校试题解析：
【2009考题】1．企业或行业投资者以动态的观点确定的、可接受的投资方案最低标准的收益水平称( )。
A．基准收益率
B．社会平均收益率
C．内部收益率
D．社会折旧率
多智网校试题解析：A。
二、基准收益率的测定
（一）财务基准收益率的测定规定（掌握）
1、政府投资项目，采用的行业财务基准收益率，应根据政府的政策导向进行确定。
（1）方案彼此独立无关，选择一个方案，并不影响其他方案的选择。
（2）也叫做"绝对经济效果检验"，通过检验，则可行，否则应予拒绝。
（二）互斥型方案
一是进行绝对经济效果检验；二是考察相对经济效果检验。
五、项目计算期（掌握）
项目的计算期包括建设期和运营期。
（1）运营期分为投产期和达产期两个阶段。
（2）运营期应以主要设备的经济寿命期确定。
F=P（1+ ）m（r—名义利率；m—计息周期）
I=F-P=P（1+ ）m—P=P[（1+ ）m—1]
ieff= =（1+ ）m—1
m越大，1年内计息的次数就越多，年实际利率就越大；
【2009考题】54．已知年名义利率为10％，每季度计息1次，复利计息，则年有效利率为( )。
A．10.47％
B．10.38％
③融资前分析的相关指标，应作为初步投资ቤተ መጻሕፍቲ ባይዱ策与融资方案研究的依据和基础。
（2）融资后分析
①考察项目在拟定融资条件下的盈利能力、偿债能力和财务生存能力，判断项目方案在融资条件下的可行性。
②融资后分析用于比选融资方案，帮助投资者做出融资决策。
③融资后的盈利能力分析也应包括动态分析和静态分析。
5、按项目评价的时间分类（事前评价、事中评价和事后评价）
lZl0l021 财务评价的内容
所谓财务评价就是对建设方案的财务可行性和经济合理性进行分析论证，为决策提供依据。
一、建设项目财务评价的基本内容（掌握）
（1）对于经营性项目，分析项目的盈利能力、偿债能力和财务生存能力。
（2）对于非经营性项目，分析项目的财务生存能力。
1、盈利能力
指标包括：投资内部收益率、财务净现值、资本金内部收益率、投资回收期、总投资收益率、资本金净利润率等。
名义利率和有效利率的计算
lZl0l014 名义利率和有效利率的计算
当计息周期小于一年时，就出现了名义利率和有效利率的概念。
一、名义利率的计算（掌握）
（1）名义利率r=计息周期利率i×计息周期数m。即：r=i×m
（2）若计息周期月利率i为1%，则年名义利率r为12%。
（3）计算名义利率时忽略了前面利息再生的因素，这与单利的计算相同。
（3）通货膨胀。通常以通货膨胀率ｉ3来表示
综合以上分析，基准收益率可确定如下：
ｉc=（1+ｉ1）（1+ｉ2）（1+ｉ3）-1≈ｉ1+ｉ2+ｉ3
基准收益率的基础是资金成本和机会成本，而投资风险和通货膨胀则是必须考虑的影响因素。
（二）基准收益率的测定方法（了解）
可采用：资本资产定价模型法、加权平均资金成本法、典型项目模拟法和德尔菲专家
2、偿债能力
指标包括：利息备付率、偿债备付率、资产负债率等。
3、财务生存能力
根据“项目财务计划现金流量表”，考察现金流入和流出、现金流量、累计盈余资金（不出现负值），分析项目是否有足够的净现金流量维持正常运营，以实现财务可持续性。
二、财务评价方法（掌握）
1、财务评价的基本方法（确定性评价、不确定性评价）
2、在中国境外投资的建设项目，财务基准收益率的测定，应首先考虑国家风险因素。
3、投资者自行测定的，基准收益率应根据资金成本、机会成本、项目风险、通货膨胀等因素综合测定。
（1）基准收益率应不低于单位资金成本和单位投资的机会成本。
ｉc>=ｉ1=max{单位资金成本，单位投资机会成本}
资金成本包括筹资费（如股票发行费、借款手续费）和资金使用费。
2、按评价方法的性质分类（定性分析、定量分析，定量为主）
3、按评价方法是否考虑时间因素分类（静态分析、动态分析，动态为主）
4、按评价是否考虑融资分类
（1）融资前分析
①融资前分析排除了融资方案变化的影响，从项目投资总获利能力的角度，考察项目方案设计的合理性。
②融资前动态分析，考察整个计算期内现金流入和现金流出，编制项目投资现金流量表，计算项目投资内部收益率和净现值等指标。
(1)据题意绘出现金流量图如图1Z101014—3所示。
(2)计算：
已知名义利率 =10％，计息周期为半年，则计息周期利率 。根据资金回收计算 即可计算出每半年应付设备价款额。即：
建设项目财务评价
1Z101020 建设项目财务评价
建设项目经济评价，分为财务评价（也称财务分析）和国民经济评价（也称经济分析）两个层次。
二、有效利率的计算（掌握）
有效利率是指实际利率，包括计息周期有效利率和年有效利率两种情况。
1、计息周期有效利率，i=r/m；和计息周期名义利率相等。
如：年利率12%，按照季度计息，则计息周期为季度，季度的名义利率为3%，计息周期有效利率也是3%；
2、年有效利率，即年实际利率（考虑利息再生）。
当按照季度计息时，已知的12%年利率是年名义利率，年实际利率相当于用季度利率3%复利了4次；用公式表示为：