高一数学基本初等函数练习题

(完整版)基本初等函数基础习题基本初等函数基础习题一、选择题1、 以下函数中，在区间 0,不是增函数的是（）A. y2 xB.y lg xC.yx 3D.y1x2、函数 y ＝log 2 x ＋3（ x ≥1）的值域是（ ）A. 2,B.（3，＋ ∞）C. 3,D.（－ ∞，＋ ∞）3、若 M{ y | y 2x }, P { y | yx 1} ，则 M ∩P（）A. { y | y 1}B. { y | y 1}C. { y | y0}D. { y | y 0}4、对数式 b log a 2 (5a) 中，实数 a 的取值范围是（）A.a>5,或 a<2B.2<a<5C.2<a<3,或 3<a<5D.3<a<45、 已知 f (x)a x ( a 0且 a 1) ，且 f ( 2)f ( 3) ，则 a 的取值范围是（ ）A. a 0B.a 1C.a 1D.0 a 16、函数 f ( x) | log 1 x | 的单一递加区间是2A 、 (0, 1]B 、 (0,1]C 、（0，+∞）D 、 [1, )27、图中曲线分别表示 yl o g a x ， y l o g b x ， y l o g c x ，y l o g d x 的图象， a, b, c, d 的关系是（）yy=log xay=log b xA 、 0<a<b<1<d<cB 、0<b<a<1<c<dC 、 0<d<c<1<a<bD 、0<c<d<1<a<bO1xy=log c x8、已知幂函数f(x) 过 点 （ 2 ，2 ）， 则 f(4) 的 值 为y=log d x2（）A 、1B 、 1C 、 2D 、 82、a=log 0.5 ，b=log 2，c=log35，则()9A.a ＜ b ＜ cB.b ＜a ＜cC.a ＜c ＜ bD.c ＜a ＜b10 已知 y log a ( 2 ax) 在［ 0，1］上是 x 的减函数，则 a 的范围A.(0 ， 1)B.(1，2) C.(0 ，2)D.［2，+∞］二、填空题11、函数 ylog 1 ( x 1) 的定义域为.212. 设函数 fxf 2xx 4，则 f log 2 3 =x2 x 414、函数 f ( x )lg (3x 2) 2 恒过定点三、解答题：15、 求以下各式中的 x 的值 (1)ln (x 1) 12x 11 x 2(2) a, 此中 a 且 1.a0 a16、点（ 2，1）与（ 1，2）在函数 f x2axb的图象上，求 f x 的分析式。

8、若集合R} , M={y|y=x2,x R},则下列结论中正确的是…高一数学《基本初等函数》测试题一、选择题：本大题共 15小题，共50分.在每小题给出的四个选项中，只有一项是符合 题目要求的.1下列函数是幕函数的是4、若 100a 5, 10b 2，则 2a b =C 、25、函数y= log 1(2x 1)的定义域为1A.( 3 , +x ) B . [ 1, +x )2A 、 y 2xB 、y x 3xC 、y 3x1x 212、 计算-log 312 log 3 2 •…2A. '、3B. 2 3C.— 2 3、 设集合A {x|x 1 0}，BD.3{x|log 2 x 0|},则A B等于A . {x| x 1}B . {x| x 0}C . {x|x 1}D . {x | x()1C.( 1，1]D. ( — x, 1)6、已知f(x)=|lgx|，则匕)、f (3)、 f(2)的大小关系是……A. f(2)f(3)f(;)B. f(4)f(1)f(2)C. f (2)f(4)f©D.f(1)f(2)7、方程:lgx lg(x 3) 1的解为 x =(A 5 或-2、无解CB-2D、5A 、a 5或 a 2B 、2 a 3或3 a 5C 、2a5D 、3a4xxe e11、 已知f (x)- ............................................................ ——，则下列正确的是 ()2A •奇函数，在R 上为增函数B •偶函数，在R 上为增函数C .奇函数，在R 上为减函数D •偶函数，在R 上为减函数1112、 ................................................................ 已知logalog b 0，则a,b 的关系是 .............................................. () 33A 1<b<aB 1<a<bC 0<a<b<1D 0<b<a<1 13、世界人口已超过56亿，若按千分之一的年增长率计算，则两年增长的人口就可相当于一个 ............................................... ()A.M np={2 , 4}B. M HP ={4 , 16}C.M=PD.P M9、已知 f (X) lOg a X , g(x) lOg bh(x) log d x 的图象如图所示则A. c d aC. d c ab B.cd b a b D. d c b a 10. 在 b log (a 2) (5a)中，实数a 的取值范围是A.新加坡(270万)B •香港(560万)C •瑞士( 700万)D.上海(1200万)14若函数f (x) log a x(0 a 1)在区间a,2a上的最大值是最小值的3倍，则a的值为C、(a 1)x2在同坐标系中的图象只能是图中的二、填空题.(每小题3分)16•函数y (2 a)x在定义域内是减函数，则a的取值范围是__________________ 。

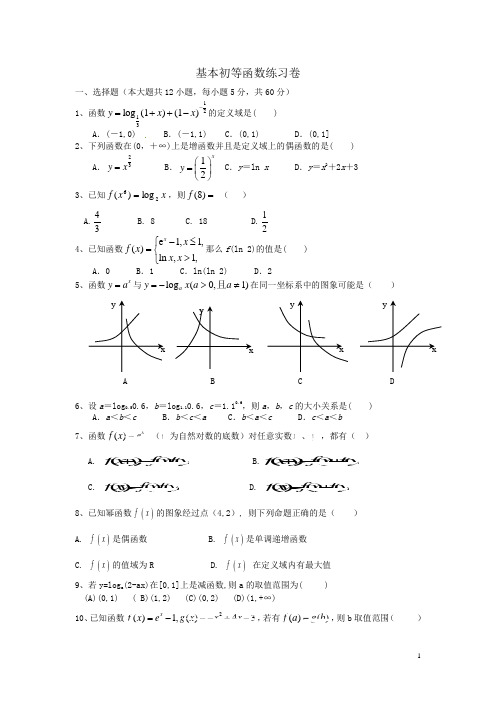
基本初等函数练习卷一、选择题（本大题共12小题，每小题5分，共60分） 1、函数1213log (1)(1)y x x -=++-的定义域是()A ．(－1,0)B ．(－1,1)C ．(0,1)D ．(0,1]2、下列函数在(0，＋∞)上是增函数并且是定义域上的偶函数的是( )A ．23y x = B ．12xy ⎛⎫= ⎪⎝⎭C ．y ＝ln xD ．y ＝x 2＋2x ＋33、已知x x f 26log )(=，则=)8(f （ ）A.34 B. 8 C. 18 D.21 4、已知函数e 1,1,()ln ,1,x x f x x x ⎧-≤=⎨>⎩那么f (ln 2)的值是( )A ．0B ．1C ．ln(ln 2)D ．25、函数x y a =与log (0,1)a y x a a =->≠且在同一坐标系中的图象可能是（ ）A B C D6、设a ＝log 0.50.6，b ＝log 1.10.6，c ＝1.10.6，则a ，b ，c 的大小关系是( )A ．a ＜b ＜cB ．b ＜c ＜aC ．b ＜a ＜cD ．c ＜a ＜b 7、函数（为自然对数的底数）对任意实数、，都有（ ）A. B. C. D. 8、已知幂函数()f x 的图象经过点（4,2）, 则下列命题正确的是（ ）A. ()f x 是偶函数B. ()f x 是单调递增函数C. ()fx 的值域为R D. ()f x 在定义域内有最大值9、若y=log a (2-ax)在[0,1]上是减函数,则a 的取值范围为( ) (A)(0,1) ( B)(1,2) (C)(0,2) (D)(1,+∞)10、已知函数2()1,()43x f x e g x x x =-=-+-，若有()()f a g b =，则b 取值范围（ ）()()()f x y f x f y =+()()()f x y f xf y =()()()fx y fx fy +=+()()()f x y f x f y +=y x e ()xf x e=yxyxyxy xA. 22,22⎡⎤-+⎣⎦B. (22,22)-+C. []1,3D. ()1,311、函数y ＝e|－ln x |－|x －1|的图象大致是( )12、给出幂函数①f(x)=x ；②f(x)=x 2；③f(x)=x 3；④f(x)=x ；⑤f(x)=1x． 其中满足条件f 12()2x x +>12()()2f x f x + (x 1＞x 2＞0)的函数的个数是 （ ） A ．1个 B ．2个 C ．3个 D ．4个 二、填空题（本大题共4小题，每小题4分，共16分）13、当a ＞0且a ≠1时，函数f (x)=a x －2－3必过定点 . 14、函数652-+-=x x y 的单调增区间是15、已知函数2()f x x bx c =++，对任意x R ∈都有(1)()f x f x +=-,则(2)f -、 (0)f 、(2)f 的大小顺序是 ．16.下列说法中：① 若2()(2)2f x ax a b x =+++（其中[21,4]x a a ∈-+）是偶函数，则实数2b =； ② 20132013)(22-+-=x x x f 既是奇函数又是偶函数；③ 函数()()43ln 2--=x x x f 的减区间是⎪⎭⎫ ⎝⎛+∞,23；④ 已知()f x 是定义在R 上的不恒为零的函数，且对任意的,x y R ∈都满足()()()f x y x f y y f x ⋅=⋅+⋅，则()f x 是奇函数。

高一数学基本初等函数Ⅰ试题答案及解析1.方程的根的情况是（）A．仅有一根B．有两个正根C．有一正根和一个负根D．有两个负根【答案】C【解析】主要考查指数函数、对数函数的图象和性质。

解：采用数形结合的办法，在同一坐标系中，画出的图象可知。

2.已知 .【答案】8【解析】主要考查指数函数、二次函数的性质。

利用换元法。

解：可化为，令，又因为所以，，，故。

3.若下列命题正确的个数为（）A．0B．1C．2D．3【答案】B【解析】主要考查对数运算法则。

解：根据对数的运算性质易知只有④是正确的。

4.已知_____________【答案】【解析】主要考查对数运算。

解：5.已知镭经过100年，剩留原来质量的95．76%，设质量为1的镭经过x年的剩留量为y，则y 与x的函数关系是A．y=（0．9576）B．y=（0．9576）100xC．y=（）x D．y=1－（0．0424）【答案】A【解析】设每年减少q%，因为镭经过100年，剩留原来质量的95．76%，所以=95．76%, q%=1－（0．9576）,所以=（0．9576）。

故选A。

【考点】主要考查函数的概念、解析式，考查应用数学知识解决实际问题的能力。

点评：审清题意，构建函数解析式。

6.一个体户有一种货，如果月初售出可获利100元，再将本利都存入银行，已知银行月息为2．4%，如果月末售出可获利120元，但要付保管费5元，问这种货是月初售出好，还是月末售出好？【答案】当成本大于525元时，月末售出好；成本小于525元时，月初售出好．【解析】解：设这种货的成本费为a元，则若月初售出，到月末共获利润为：y1=100+（a+100）×2．4%若月末售出，可获利y2=120－5=115（元）y 2－y1=0．024a－12．6=0．024（a－525）故当成本大于525元时，月末售出好；成本小于525元时，月初售出好．【考点】主要考查函数模型的广泛应用，考查应用数学知识解决实际问题的能力。

1．若函数)10(log )(<<=a x x f a 在区间]2,[a a 上的最大值是最小值的3倍，则a 的值为( )A ．42B ．22C ．41D ．21 2．若函数)1,0)((log ≠>+=a a b x y a 的图象过两点(1,0)-和(0,1)，则( )A ．2,2a b ==B ．2a b ==C ．2,1a b ==D ．a b ==3．已知x x f 26log )(=，那么)8(f 等于（ ）A ．34B ．8C ．18D ．21 4．函数lg y x =( )A ． 是偶函数，在区间(,0)-∞ 上单调递增B ． 是偶函数，在区间(,0)-∞上单调递减C ． 是奇函数，在区间(0,)+∞ 上单调递增D ．是奇函数，在区间(0,)+∞上单调递减5．已知函数=-=+-=)(.)(.11lg )(a f b a f xx x f 则若（ ） A ．b B ．b - C ．b 1 D ．1b- 6．函数()log 1a f x x =-在(0,1)上递减，那么()f x 在(1,)+∞上（ ）A ．递增且无最大值B ．递减且无最小值C ．递增且有最大值D ．递减且有最小值1．若a x f x x lg 22)(-+=是奇函数，则实数a =_________。

2．函数()212()log 25f x x x =-+的值域是__________.3．已知1414log 7,log 5,a b ==则用,a b 表示35log 28= 。

4．设(){}1,,lg A y xy =, {}0,,B x y =,且A B =，则x = ；y = 。

5．计算：()()5log 22323-+ 。

6．函数x x e 1e 1y -=+的值域是__________. 三、解答题2．解方程：（1）192327x x ---⋅= （2）649x x x += 3．已知,3234+⋅-=x x y 当其值域为[1,7]时，求x 的取值范围。

高一数学必修一基本初等函数一．选择题（共30小题）1．设a＝log43，b＝log54，c＝2﹣0.01，则a，b，c的大小关系为（）A．b＜a＜c B．a＜b＜c C．a＜c＜b D．b＜c＜a2．已知a＝3ln2π，b＝2ln3π，c＝3lnπ2，则下列选项正确的是（）A．a＞b＞c B．c＞a＞b C．c＞b＞a D．b＞c＞a3．函数f（x）＝（|x|﹣7）e|x|则（）A．B．f（0.76）＜f（60.5）＜f（log0.76）C．D．4．已知P（x，y）为函数f（x）＝图象上一动点，则的最大值为（）A．B．C．2D．5．设a＝3，b＝3log3π，c＝πlogπ3，则a，b，c的大小关系为（）A．a＜b＜c B．a＜c＜b C．c＜a＜b D．c＜b＜a6．若a＝0.220.33，b＝0.330.22，c＝log0.330.22，则（）A．a＞b＞c B．b＞a＞c C．c＞a＞b D．c＞b＞a7．已知a，b，c∈R，满足＝＝﹣＜0，则a，b，c的大小关系为（）A．c＞a＞b B．a＞c＞b C．c＞b＞a D．b＞a＞c8．已知2a＝log2|a|，，c＝sin c+1，则实数a，b，c的大小关系是（）A．b＜a＜c B．a＜b＜c C．c＜b＜a D．a＜c＜b9．已知实数a，b，c分别满足2a＝﹣a，log0.5b＝b，log2c＝，那么（）A．a＜b＜c B．a＜c＜b C．b＜c＜a D．c＜b＜a10．已知a＝log1213，b＝（），c＝log1314，则a，b，c的大小关系为（）A．a＞b＞c B．c＞a＞b C．b＞c＞a D．a＞c＞b11．已知a＞b＞0，ab＝1，设，则log x2x，log y2y，log z2z的大小关系为（）A．log x2x＞log y2y＞log z2z B．log y2y＞log z2z＞log x2xC．log x2x＞log z2z＞log y2y D．log y2y＞log x2x＞log z2z12．已知，，c＝log23，则a，b，c的大小关系为（）A．b＞a＞c B．a＞c＞b C．a＞b＞c D．b＞c＞a13．下列命题为真命题的个数是（）①②③A．0B．1C．2D．314．设，实数c满足e﹣c＝lnc，（其中e为自然常数），则（）A．a＞b＞c B．b＞c＞a C．b＞a＞c D．c＞b＞a15．若实数x，y，z满足，则x，y，z的大小关系是（）A．x＜y＜z B．x＜z＜y C．z＜x＜y D．z＜y＜x16．已知x1＝ln，x2＝e，x3满足e＝lnx3，则下列各选项正确的是（）A．x1＜x3＜x2B．x1＜x2＜x3C．x2＜x1＜x3D．x3＜x1＜x217．已知t＞1，x＝log2t，y＝log3t，z＝log5t，则（）A．2x＜3y＜5z B．5z＜2x＜3y C．3y＜5z＜2x D．3y＜2x＜5z18．已知定义在R上的函数y＝f（x）对任意的x都满足f（x+2）＝f（x），当﹣1≤x＜1时，f（x）＝x3．若函数g（x）＝f（x）﹣log a|x|恰有6个不同零点，则a的取值范围是（）A．（，]∪（5，7] B．（，]∪（5，7]C．（，]∪（3，5] D．（，]∪（3，5]19．已知函数f（x）＝，g（x）＝x2﹣2x，设a为实数，若存在实数m，使f（m）﹣2g（a）＝0，则实数a的取值范围为（）A．[﹣1，+∞）B．（﹣∞，﹣1]∪[3，+∞）C．[﹣1，3] D．（﹣∞，3]20．已知函数y＝f（x）（x∈R）满足f（x+2）＝2f（x），且x∈[﹣1，1]时，f（x）＝﹣|x|+1，则当x∈[﹣10，10]时，y＝f（x）与g（x）＝log4|x|的图象的交点个数为（）A．13B．12C．11D．1021．设a＝log46，，，则（）A．a＞b＞c B．b＞c＞a C．a＞c＞b D．c＞b＞a22．已知实数a＞0，b＞0，a≠1，且满足lnb＝，则下列判断正确的是（）A．a＞b B．a＜b C．log a b＞1D．log a b＜123．设a＝π﹣e，b＝lnπ﹣1，c＝eπ﹣e e，则（）A．a＜b＜c B．b＜c＜a C．c＜b＜a D．b＜a＜c24．若函数f（x）＝在区间[2019，2020]上的最大值是M，最小值是m，则M﹣m（）A．与a无关，但与b有关B．与a无关，且与b无关C．与a有关，但与b无关D．与a有关，且与b有关25．正数a，b满足1+log2a＝2+log3b＝3+log6（a+b），则的值是（）A．B．C．D．26．已知实数a，b，c，d满足，则（a﹣c）2+（b﹣d）2的最小值为（）A．8B．4C．2D．27．函数y＝log a（x+3）﹣1（a＞0，且a≠1）的图象恒过定点A，若点A在直线mx+ny+2＝0上（其中m，n＞0），则的最小值等于（）A．10B．8C．6D．428．若m，n，p∈（0，1），且log3m＝log5n＝lgp，则（）A．B．C．D．29．已知a＝log2e，b＝ln3，c＝log，则a，b，c的大小关系为（）A．a＞b＞c B．b＞a＞c C．c＞b＞a D．b＞c＞a30．若函数f（x）＝ln（ax2﹣2x+3）的值域为R，则实数a的取值范围是（）A．[0，]B．（，+∞）C．（﹣∞，]D．（0，]二．填空题（共6小题）31．已知函数f（x）在R上连续，对任意x∈R都有f（﹣3﹣x）＝f（1+x）；在（﹣∞，﹣1）中任意取两个不相等的实数x1，x2，都有（x1﹣x2）[f（x1）﹣f（x2）]＜0恒成立；若f（2a﹣1）＜f（3a﹣2），则实数a的取值范围是．32．若存在正数x，y，使得（y﹣2ex）（lny﹣lnx）z+x＝0（其中e为自然对数的底数），则实数z的取值范围是33．已知函数f（x）＝log2（x+2）与g（x）＝（x﹣a）2+1，若对任意的x1∈[2，6），都存在x2∈[0，2]，使得f（x1）＝g（x2），则实数a的取值范围是．34．已知函数f（x）的图象与函数g（x）＝2x关于直线y＝x对称，令h（x）＝f（1﹣|x|），则关于函数h（x）有以下命题：（1）h（x）的图象关于原点（0，0）对称；（2）h（x）的图象关于y轴对称；（3）h（x）的最小值为0；（4）h（x）在区间（﹣1，0）上单调递增．中正确的是．35．设a，b为非零实数，x∈R，若，则＝．36．函数f（x）＝log2x在区间[a，2a]（a＞0）上的最大值与最小值之差为．三．解答题（共4小题）37．已知函数f（x）＝的图象关于原点对称，其中a为常数．（1）求a的值；（2）当x∈（1，+∞）时，f（x）+（x﹣1）＜m恒成立，求实数m的取值范围；（3）若关于x的方程f（x）＝（x+k）在[2，3]上有解，求k的取值范围．38．已知函数f（x）＝log a（2﹣x）﹣log a（2+x）（a＞0且a≠1），且1是函数y＝f（x）+x的零点．（1）求实数a的值；（2）求使f（x）＞0的实数x的取值范围．39．已知函数f（x）＝（a2﹣3a+3）a x是指数函数．（1）求f（x）的解析式；（2）判断函数F（x）＝f（x）﹣f（﹣x）的奇偶性，并证明；（3）解不等式log a（1﹣x）＞log a（x+2）．40．已知f（x）是定义在R上的偶函数，且x≤0时，f（x）＝（﹣x+1）（1）求f（3）+f（﹣1）；（2）求函数f（x）的解析式；（3）若f（a﹣1）＜﹣1，求实数a的取值范围．参考答案与试题解析一．选择题（共30小题）1．【解答】解：因为0＝log41＜a＝log43＜log44＝1，0＜b＝log54＜log55＝1，c＝2﹣0.01＞2≈0.92，log54＝≈0.86，＝＝log43×log45＜（）2＝（）2＜1，∴a，b，c的大小关系为a＜b＜c．故选：B．2．【解答】解：，，＝，∵6π＞0，∴a，b，c的大小比较可以转化为的大小比较．设f（x）＝，则f′（x）＝，当x＝e时，f′（x）＝0，当x＞e时，f′（x）＜0，当0＜x＜e时，f′（x）＞0∴f（x）在（e，+∞）上，f（x）单调递减，∵e＜3＜π＜4∴，∴b＞c＞a，故选：D．3．【解答】解，60.5＞1＞0.76＞0＞log0.76，函数f（x）为偶函数，则，当x＞0时，f（x）＝（x﹣7）e x，则f′（x）＝（x﹣6）e x，易知函数f（x）在（0，6）上单调递减，又，故，即﹣log0.76＜6，又，故，即﹣log0.76＞3，则0＜0.76＜1＜60.5＜﹣log0.76＜6，所以f（0.76）＞f（60.5）＞f（﹣log0.76）＝f（log0.76），故选：D．4．【解答】解：设Q（，1），原点O，则＝（，1），＝（x，y），∴即．∴当OP与f（x）在y轴右侧相切时取最大值，设直线y＝kx（k＞0）与函数f（x）相切于点P0（x0，y0），y′＝k，f′（x）＝2x，则，解得．即切点P0（，），∴，即的最大值为．故选：D．5．【解答】解：构造函数f（x）＝（x＞1），则f′（x）＝，当x∈（1，e2）时，f′（x）＞0，则f（x）在（1，e2）上为增函数，∴f（π）＞f（3），即＞，∴＞，即3log3π＞πlogπ3，则b＞c；设g（x）＝，则g′（x）＝，当x＞3时，g′（x）＞30ln3﹣1＞0，∴g（x）在（3，+∞）上为增函数，则g（π）＞g（3）＝0，即＞π，则3π＞π3．又πlogπ3＝＞．∴a＜c＜b．故选：B．6．【解答】解：由1＞a＝0.220.33＞0，1＞b＝0.330.22＞0，c＝log0.330.22＞log0.330.33＝1，所以c＞a，且c＞b；又ln0.220.33＝0.33ln0.22，ln0.330.22＝0.22ln0.33；不妨设0.33ln0.22＜0.22ln0.33，则有＜；构造函数f（x）＝，x＞0，所以f′（x）＝，令f′（x）＝0，解得x＝e；所以x∈（0，e）时，f′（x）＞0，f（x）是单调增函数；所以f（0.22）＜f（0.33），即＜，所以b＞a；综上知，c＞b＞a．故选：D．7．【解答】解：已知a，b，c∈R，令＝＝﹣＝﹣1，则：，所以c＞1．由于3b＞0，且，故lnb＜0，解得0＜b＜1，同理2a＞0，且，故lna＜0，解得0＜a＜1．由于0＜a＜1，0＜b＜1，＝＝﹣＜0，所以2a＜3b，故lnb＜lna，整理得b＜a，所以c＞1＞a＞b＞0．故选：A．8．【解答】解：作出函数y＝2x和y＝log2|x|的图象，由图1可知，交点A的横坐标a＜0；作出函数y＝和y＝的图象，由图2可知，交点B的横坐标0＜b＜1；作出函数y＝x和y＝sin x+1的图象，由图3可知，交点C的横坐标c＞1所以，a＜b＜c．故选：B．9．【解答】解：∵log0.5b＝﹣log2b＝b，∴log2b＝﹣b，在同一坐标系内画出函数y＝2x，y＝﹣x，y＝log2x，y＝的图象．可知a＜0＜b＜1＜c．故选：A．10．【解答】解：＝，∵＝＜1，∴log1314＜log1213，且log1314＞1，，∴a＞c＞b．故选：D．11．【解答】解：，＝，，∵a＞b＞0，ab＝1，∴a＞1＞b＞0，∴，log2（a+b）＜2，∴，∴，∴，又0＜，∴，∴log y2y＞log z2z＞log x2x．故选：B．12．【解答】解：根据指数运算与对数运算的性质，＞3，1＜＜2，1＜c＝log23＜2，设b＝，c＝log23，由于函数m＝log2t为增函数，由于的值接近于4，所以a＞b＞c．故选：C．13．【解答】解：构造函数f（x）＝，x∈（0，+∞），∴，令f'（x）＝0得：x＝e，∵当x∈（0，e）时，f'（x）＞0，f（x）单调递增；当x∈（e，+∞）时，f'（x）＜0，f（x）单调递减，∴f（e）＞f（3）＞f（π），即，故①正确，②错误，构造函数g（x）＝，x∈（0，+∞），∵，令g'（x）＝0得：x＝e，∵当x∈（0，e）时，g'（x）＜0，g（x）单调递减；当x∈（e，+∞）时，g'（x）＞0，g（x）单调递增，∴g（e）＜g（3），即0＜，∴ln3＜，∴，故③正确，∴真命题的个数是2个，故选：C．14．【解答】解：∵e﹣c＞0，∴lnc＞0，∴c＞1，∴，∴，∴1＜c＜2，又，∴b＞c＞a．故选：B．15．【解答】解：设＝p，∴p＞0，设y1＝log2x，y2＝log3y，y3＝2z，作出3个函数的图象，如图所示：由图可知：z＜x＜y，故选：C．16．【解答】解：依题意，因为y＝lnx为（0，+∞）上的增函数，所以x1＝ln＜ln1＝0；因为y＝e x为R上的增函数，且e x＞0，所以0＜x2＝e＜e0＝1；x3满足e＝lnx3，所以x3＞0，所以＞0，所以lnx3＞0＝ln1，又因为y＝lnx为（0，+∞）的增函数，所以x3＞1，综上：x1＜x2＜x3．故选：B．17．【解答】解：∵t＞1，∴lgt＞0．又0＜lg2＜lg3＜lg5，∴2x＝2＞0，3y＝3＞0，5z＝＞0，∴＝＞1，可得5z＞2x．＝＞1．可得2x＞3y．综上可得：3y＜2x＜5z．故选：D．18．【解答】解：首先将函数g（x）＝f（x）﹣log a|x|恰有6个零点，这个问题转化成f（x）＝log a|x|的交点来解决．数形结合：如图，f（x+2）＝f（x），知道周期为2，当﹣1＜x≤1时，f（x）＝x3图象可以画出来，同理左右平移各2个单位，得到在（﹣7，7）上面的图象，以下分两种情况：（1）当a＞1时，log a|x|如图所示，左侧有4个交点，右侧2个，此时应满足log a5≤1＜log a7，即log a5≤log a a＜log a7，所以5≤a＜7．（2）当0＜a＜1时，log a|x|与f（x）交点，左侧有2个交点，右侧4个，此时应满足log a5＞﹣1，log a7≤﹣1，即log a5＜﹣log a a≤log a7，所以5＜a﹣1≤7．故≤a＜综上所述，a的取值范围是：5≤a＜7或≤a＜，故选：A．19．【解答】解：∵g（x）＝x2﹣2x，设a为实数，∴2g（a）＝2a2﹣4a，a∈R，∵y＝2a2﹣4a，a∈R，∴当a＝1时，y最小值＝﹣2，∵函数f（x）＝，f（﹣7）＝6，f（e﹣2）＝﹣2，∴值域为[﹣2，6]∵存在实数m，使f（m）﹣2g（a）＝0，∴﹣2≤2a2﹣4a≤6，即﹣1≤a≤3，故选：C．20．【解答】解：由题意，函数f（x）满足：定义域为R，且f（x+2）＝2f（x），当x∈[﹣1，1]时，f（x）＝﹣|x|+1；在同一坐标系中画出满足条件的函数f（x）与函数y＝log4|x|的图象，如图：由图象知，两个函数的图象在区间[﹣10，10]内共有11个交点；故选：C．21．【解答】解：，，，∵0＜log34＜log35＜log36，∴，∴a＞b＞c．故选：A．22．【解答】解：∵lnb＝，∴lnb﹣lna＝，构造函数∴f（x）＝；∴＝＝；∴≥0；∴f（x）在（0，+∞）单调递增．且f（1）＝0；当x∈（0，1）时，f（x）＜0，当x∈（1．+∞）时f（x）＞0；∵a≠1∴当0＜a＜1时，f（a）＜0⇒0即lnb﹣lna＜0⇒b＜a，∴lnb＜lna＜0⇒⇒log a b＞1，当a＞1时，f（a）＞0⇒即lnb﹣lna＞0⇒b＞a，∴lnb＞lna＞0⇒⇒log a b＞1，故选：C．23．【解答】解：∵a＝π﹣e＞0，b＝lnπ﹣1＝lnπ﹣lne＞0，c＝eπ﹣e e＞0；设y＝lnx，则＝，表示了连接两点（π，lnπ），（e，lne）的割线的斜率，而y'＝，当x＞1时，曲线切线的斜率0＜k＜1；故0＜＝＜1，故b＜a；设y＝e x，则＝，表示了连接两点（π，eπ），（e，e e）的割线的斜率，而y'＝e x，当x＞1时，曲线切线的斜率k＞1；故＝＞1，故c＞a；故b＜a＜c；故选：D．24．【解答】解：，令，则y＝2019t2+bt+a的最大值是M，最小值是m，而a是影响图象的上下平移，此时最大和最小值同步变大或变小，故M﹣m与a无关，而b是影响图象的左右平移，故M﹣m与b有关，故选：A．25．【解答】解，依题意，设1+log2a＝2+log3b＝3+log6（a+b）＝k，则a＝2k﹣1，b＝3k﹣2，a+b＝6k﹣3，所以＝＝＝＝＝，故选：A．26．【解答】解：∵实数a，b，c，d满足，∴b＝lna，d＝c+1．考查函数y＝lnx，与y＝x+1．∴（a﹣c）2+（b﹣d）2就是曲线y＝lnx与直线y＝x+1之间的距离的平方值，对曲线y＝lnx求导：y′＝，与直线y＝x+1平行的切线斜率k＝1＝，解得：x＝1，将x＝1代入y＝lnx得：y＝0，即切点坐标为（1，0），∴切点（1，0）到直线y＝x+1的距离d＝＝，即d2＝2，则（a﹣c）2+（b﹣d）2的最小值为2．故选：C．27．【解答】解：令x+3＝1，求得x＝﹣2，可得函数y＝log a（x+3）﹣1（a＞0，且a≠1）的图象恒过定点A（﹣2，﹣1），若点A在直线mx+ny+2＝0上（其中m，n＞0），则﹣2m﹣n+2＝0，即2m+n＝2．由基本不等式可得2≥2，即mn≤，即≥2，当且仅当2m＝n＝1时，取等号．则＝＝≥4，故选：D．28．【解答】解：∵m，n，p∈（0，1），且log3m＝log5n＝lgp＝k，∴lgm，lgn，lgp＜0，m＝3k，n＝5k，p＝10k，∴＝＝，＝＝，＝＝，因为，＝53＝125，所以，同理＝5×5＝25，＝10，所以，所以＞0，又因为y＝x k（k＜0）在（0，+∞）上单调递减，∴即＜＜．故选：A．29．【解答】解：根据题意，c＝log＝ln2＜lne＝1，则c＜1，ln3＞ln2，∴c＜b，a＝log2e＞log22＝1，即a＞c，ln3﹣log2e＝ln3﹣＝，∵2＝lne2＞ln6＝ln2+ln3＞2，∴＜1，即ln2ln3＜1，则ln3﹣log2e＝ln3﹣＝＜0，即ln3＜log2e，即a＞b，综上a＞b＞c，故选：A．30．【解答】解：若函数f（x）＝ln（ax2﹣2x+3）的值域为R，即有t＝ax2﹣2x+3取得一切的正数，当a＝0时，t＝3﹣2x取得一切的正数，成立；当a＜0不成立；当a＞0，△≥0即4﹣12a≥0，解得0＜a≤，综上可得0≤a≤．故选：A．二．填空题（共6小题）31．【解答】解：由f（﹣3﹣x）＝f（1+x）可知函数f（x）关于直线x＝﹣1对称；在（﹣∞，﹣1）中任意取两个不相等的实数x1，x2，都有（x1﹣x2）[f（x1）﹣f（x2）]＜0恒成立；可知函数f（x）在区间（﹣∞，﹣1）上单调递减，由对称性可知函数f（x）在区间（﹣1，+∞）上单调递增，不妨设f（x）＝（x+1）2，则由f（2a﹣1）＜f（3a﹣2）可得4a2＜（3a﹣1）2，整理得5a2﹣6a+1＞0，即（a﹣1）（5a﹣1）＞0，解得或a＞1，所以实数a的取值范围是．故答案为：．32．【解答】解：则（y﹣2ex）（lny﹣lnx）z+x＝0可化为：，令t＝，得（t﹣2e）lnt＝﹣．令f（t）＝（t﹣2e）lnt，（t＞0），则f′（t）＝g（t）＝lnt+1﹣，则g′（t）＝，故g（t）为（0，+∞）上的增函数，又因为f′（e）＝g（e）＝1+1﹣2＝0，故当t∈（0，e）时，f′（t）＜0，当t＞e时，f′（t）＞0，所以f（t）在（0，e）上单调递减，在（e，+∞）上单调递增，所以f（t）在（0，+∞）存在最小值f（e）＝﹣e，即f（t）的值域为（﹣e，+∞），∴﹣∈（﹣e，+∞），所以z∈（﹣∞，0）∪[，+∞），故填：（﹣∞，0）∪[，+∞），33．【解答】解：∵x1∈[2，6），∴f（2）≤f（x1）＜f（6），即2≤f（x1）＜3，∴f（x1）的值域为[2，3）．g（x）的图象开口向上，对称轴为x＝a，（1）若a≤0，则g（x）在[0，2]上是增函数，∴g（0）≤g（x2）≤g（2），即g（x2）的值域为[a2+1，a2﹣4a+5]，∴，解得﹣1≤a≤0．（2）若a≥2，则g（x）在[0，2]上是减函数，∴g（2）≤g（x2）≤g（1），即g（x2）的值域为[a2﹣4a+5，a2+1]，∴，解得2≤a≤3．（3）若0＜a≤1，则g min（x）＝g（a）＝1，g max（x）＝g（2）＝a2﹣4a+5，∴g（x）的值域为[1，a2﹣4a+5]，∴，解得0．（4）若1＜a＜2，则g min（x）＝g（a）＝1，g max（x）＝g（0）＝a2+1，∴g（x）的值域为[1，a2+1]，∴，解得a＜2．综上，a的取值范围是[﹣1，0]∪[2，3]∪（0，2﹣）∪（，2）＝[﹣1，2﹣]∪[，3]．故答案为[﹣1，2﹣]∪[，3]．34．【解答】解：由于函数f（x）的图象与函数g（x）＝2x关于直线y＝x对称，故函数f（x）与函数g（x）＝2x互为反函数．故函数f（x）＝log2x．∴h（x）＝f（1﹣|x|）＝log2（1﹣|x|），故函数h（x）是偶函数，图象关于y对称，故（2）正确而（1）不正确．函数h（x）的定义域为（﹣1，1），在（﹣1，0）上是增函数，在（0，1）上是减函数，故（4）正确．故当x＝0时，函数h（x）取得最大值为0，故（3）不正确．故答案为②④．35．【解答】解：由成立，得＝（sin2x+cos2x）2，化简得：，即，∴，又sin2x+cos2x＝1，得，．∴．则＝＝•（sin2x+cos2x）＝．故答案为：．36．【解答】解：∵f（x）＝log2x在区间[a，2a]上是增函数，∴f（x）max﹣f（x）min＝f（2a）﹣f（a）＝log22a﹣log2a＝1．故答案为：1．三．解答题（共4小题）37．【解答】解：（1）函数f（x）＝的图象关于原点对称，∴f（x）+f（﹣x）＝0，即+＝0，∴（）＝0，∴＝1恒成立，即1﹣a2x2＝1﹣x2，即（a2﹣1）x2＝0恒成立，所以a2﹣1＝0，解得a＝±1，又a＝1时，f（x）＝无意义，故a＝﹣1；（2）x∈（1，+∞）时，f（x）+（x﹣1）＜m恒成立，即+（x﹣1）＜m，∴（x+1）＜m在（1，+∞）恒成立，由于y＝（x+1）是减函数，故当x＝1，函数取到最大值﹣1，∴m≥﹣1，即实数m的取值范围是m≥﹣1；（3）f（x）＝在[2，3]上是增函数，g（x）＝（x+k）在[2，3]上是减函数，∴只需要即可保证关于x的方程f（x）＝（x+k）在[2，3]上有解，下解此不等式组．代入函数解析式得，解得﹣1≤k≤1，即当﹣1≤k≤1时关于x的方程f（x）＝（x+k）在[2，3]上有解．38．【解答】解：（1）∵1是函数y＝f（x）+x的零点，∴f（1）＝﹣1，即log a（2﹣1）﹣log a（2+1）+1＝0，即log a3＝1，解得a＝3．（2）由（1）可知函数f（x）是递增函数，f（x）＞0得log3（2﹣x）＞log3（2+x），所以：有解得﹣2＜x＜0，所使f（x）＞0的实数x的取值集合为{x|﹣2＜x＜0}．39．【解答】解：（1）a2﹣3a+3＝1，可得a＝2或a＝1（舍去），∴f（x）＝2x；（2）F（x）＝2x﹣2﹣x，∴F（﹣x）＝﹣F（x），∴F（x）是奇函数；（3）不等式：log2（1﹣x）＞log2（x+2），即1﹣x＞x+2＞0，∴﹣2＜x＜﹣，解集为{x|﹣2＜x＜﹣}．40．【解答】解：（I）∵f（x）是定义在R上的偶函数，x≤0时，f（x）＝（﹣x+1），∴f（3）+f（﹣1）＝f（﹣3）+f（﹣1）＝4+2＝﹣2﹣1＝﹣3；（II）令x＞0，则﹣x＜0，f（﹣x）＝（x+1）＝f（x）∴x＞0时，f（x）＝（x+1），则f（x）＝．（Ⅲ）∵f（x）＝（﹣x+1）在（﹣∞，0]上为增函数，∴f（x）在（0，+∞）上为减函数∵f（a﹣1）＜﹣1＝f（1）∴|a﹣1|＞1，∴a＞2或a＜0。

基本初等函数 复习题1、 下列函数中，在区间()0,+∞不是增函数的是（ ）A.x y 2= B. x y lg = C. 3x y = D. 1y x=2、函数y ＝log 2x ＋3（x≥1）的值域是（ ）A.[)+∞,2B.（3，＋∞）C.[)+∞,3 D.（－∞，＋∞） 3、若{|2},{|1}x M y y P y y x ====-，则M∩P （ ）A.{|1}y y > B. {|1}y y ≥ C. {|0}y y > D. {|0}y y ≥4、对数式2log (5)a b a -=-中，实数a 的取值范围是（ ）A.a>5,或a<2B.2<a<5C.2<a<3,或3<a<5D.3<a<45、 已知x a x f -=)( )10(≠>a a 且，且)3()2(->-f f ，则a 的取值范围是（ ）A. 0>aB. 1>aC. 1<aD. 10<<a6、函数|log |)(21x x f =的单调递增区间是A 、]21,0( B 、]1,0( C 、（0，+∞） D 、),1[+∞ 7、图中曲线分别表示l g a y o x =，l g b y o x =，l g c y o x =，l g d y o x =的图象，,,,a b c d 的关系是（）A 、0<a<b<1<d<cB 、0<b<a<1<c<dC 、0<d<c<1<a<bD 、0<c<d<1<a<b8、已知幂函数f(x)过点（2，22），则f(4)的值为 （ ） A 、21B 、 1C 、2D 、89、a=log 0.50.6，b=log20.5，c=log35，则( )A.a ＜b ＜cB.b ＜a ＜cC.a ＜c ＜bD.c ＜a ＜b10、已知)2(log ax y a -=在［0，1］上是x 的减函数，则a 的取值范围是( )A.(0，1)B.(1，2)C.(0，2)D.［2，+∞］ 11、函数)1(log 21-=x y 的定义域为 .12. 设函数()()()()4242x x f x x f x ⎧≥⎪=⎨<+⎪⎩，则()2log 3f =13、计算机的成本不断降低，如果每隔5年计算机的价格降低31，现在价格为8100元的计算机，15年后的价格可降为 14、函数2)23x (lg )x (f +-=恒过定点15、求下列各式中的x 的值1)1x (ln )1(<-x yOy=log ay=logy=log y=log11.a 0a ,1)2(212≠>⎪⎭⎫ ⎝⎛>--且其中x x a a16、点（2，1）与（1，2）在函数()2ax b f x +=的图象上，求()f x 的解析式。

数学测试一、选择题1．下列函数与x y =有相同图象的一个函数是（ ）A ．2x y = B ．x x y 2= C ．)10(log ≠>=a a a y x a 且 D ．x a a y log = 2．下列函数中是奇函数的有几个（ ） ①11x x a y a +=- ②2lg(1)33x y x -=+- ③x y x = ④1log 1a x y x +=- A ．1 B ．2 C ．3 D ．43．函数y x =3与y x =--3的图象关于下列那种图形对称( )A ．x 轴B ．y 轴C ．直线y x =D ．原点中心对称4．下列函数为偶函数是是 （ ）A ）f(x)=x 2+x-1B ）f(x)=x|x|C ）f(x)=x 2-x 3D ）()f x =5．函数y = ）A ．[1,)+∞B ．2(,)3+∞ C ．2[,1]3 D ．2(,1]3 6．三个数60.70.70.76log 6，，的大小关系为（ ） A . 60.70.70.7log 66<< B . 60.70.70.76log 6<< C ．0.760.7log 660.7<< D . 60.70.7log 60.76<<7．若f x x (ln )=+34，则f x ()的表达式为（ ）A ．3ln xB ．3ln 4x +C ．3x eD ．34xe + 二、填空题1．985316,8,4,2,2从小到大的排列顺序是 。

2．若3)1()(2++-=mx x m x f 是偶函数,则)(x f 的递增区间是____________。

3．计算：(log )log log 2222545415-++= 。

4．函数1218x y -=的定义域是______；5．判断函数2lg(y x x =的奇偶性 。

三、解答题1.已知二次函数f(x)的图像的顶点是（-1，2），且过原点，求f(x)的表达式附加题。