实验十八—离散系统的Simulink仿真

实验九SIMULINK仿真一、实验目的SIMULINK是一个对动态系统（包括连续系统、离散系统和混合系统）进行建模、仿真和综合分析的集成软件包，是MA TLAB的一个附加组件，其特点是模块化操作、易学易用，而且能够使用MATLAB提供的丰富的仿真资源。

在SIMULINK环境中，用户不仅可以观察现实世界中非线性因素和各种随机因素对系统行为的影响，而且也可以在仿真进程中改变感兴趣的参数，实时地观察系统行为的变化。

因此SIMULINK已然成为目前控制工程界的通用软件，而且在许多其他的领域，如通信、信号处理、DSP、电力、金融、生物系统等，也获得重要应用。

对于信息类专业的学生来说，无论是学习专业课程或者相关课程设计还是在今后的工作中，掌握SIMULINK，就等于是有了一把利器。

本次实验的目的就是通过上机训练，掌握利用SIMULINK对一些工程技术问题（例如数字电路）进行建模、仿真和分析的基本方法。

二、实验预备知识1. SIMULINK快速入门在工程实际中，控制系统的结构往往很复杂，如果不借助专用的系统建模软件，则很难准确地把一个控制系统的复杂模型输入计算机，对其进行进一步的分析与仿真。

1990年，Math Works软件公司为MATLAB提供了新的控制系统模型图输入与仿真工具，并命名为SIMULAB，该工具很快就在控制工程界获得了广泛的认可，使得仿真软件进入了模型化图形组态阶段。

但因其名字与当时比较著名的软件SIMULA类似，所以1992年正式将该软件更名为SIMULINK。

SIMULINK的出现，给控制系统分析与设计带来了福音。

顾名思义，该软件的名称表明了该系统的两个主要功能：Simu（仿真）和Link（连接），即该软件可以利用系统提供的各种功能模块并通过信号线连接各个模块从而创建出所需要的控制系统模型，然后利用SIMULINK提供的功能来对系统进行仿真和分析。

⏹SIMULINK的启动首先启动MATLAB，然后在MA TLAB主界面中单击上面的Simulink按钮或在命令窗口中输入simulink命令。

实验报告5Simulink仿真[推荐五篇]第一篇：实验报告 5 Simulink仿真实验五 Simulink仿真（一）一、实验目的1、熟悉Simulink仿真环境2、了解Simulink基本操作3、了解Simulink系统建模基本方法3、熟悉Simulink仿真系统参数设置和子系统封装的基本方法二、实验内容1、在matlab命令窗口中输入simulink,观察其模块库的构成；2、了解模块库中常用模块的使用方法；3、已知单位负反馈系统的开环传递函数为G=100s+2s(s+1)(s+20)建立系统的模型，输入信号为单位阶跃信号，用示波器观察输出。

4、建立一个包含Gain、Transfer Fcn、Sum、Step、Sine Wave、Zero-Pole、Integrator、Derivative等模块构成的自定义模块库Library1；5、建立如图7-12所示的双闭环调速系统的Simulink的动态结构图，再把电流负反馈内环封装为子系统，建立动态结构图。

三、实验结果及分析：图5-1图5-2图5-3图5-4双闭环调速系统的Simulink的动态结构图图5-5把电流负反馈内环封装为子系统的动态结构图双击Subsystem模块，编辑反馈电流环Subsystem子系统，如图5-6所示：图5-6分析：Simulink是Mathworks开发的MATLAB中的工具之一，主要功能是实现动态系统建模、仿真与分析。

可以在实际系统制作出来之前，预先对系统进行仿真与分析，并可对系统做适当的适时修正或按照仿真的最佳效果来调试及整定控制系统的参数，达到提高系统性能。

减少涉及系统过程中的反复修改的时间、实现高效率地开发系统的目标。

Simulink提供了建模、分析和仿真各种动态系统的交互环境，包括连续系统、离散系统和混杂系统，还提供了采用鼠标拖放的方法建立系统框图模型的图形交互界面。

第二篇：仿真实验报告仿真软件实验实验名称：基于电渗流的微通道门进样的数值模拟实验日期：2013.9.4一、实验目的1、对建模及仿真技术初步了解2、学习并掌握Comsol Multiphysics的使用方法3、了解电渗进样原理并进行数值模拟4、运用Comsol Multiphysics建立多场耦合模型，加深对多耦合场的认识二、实验设备实验室计算机，Comsol Multiphysics 3.5a软件。

simulink中的欧拉离散化欧拉离散化是数值计算中的一种方法，常用于对连续系统进行离散化处理。

在Simulink中，欧拉离散化是一种常见的模拟仿真方法，可以将连续时间模型转换为离散时间模型，用于系统的数值计算和仿真。

欧拉离散化的基本原理是将连续时间系统的微分方程通过差分逼近的方法离散化，将连续时间的状态和输入变量转换为离散时间的状态和输入信号。

在Simulink中，可以通过选择欧拉离散化方法来对连续时间模型进行离散化处理。

在Simulink中使用欧拉离散化方法，需要注意以下几点。

首先，需要确保所使用的模型是连续时间模型，在模型参数中设置模拟步长，通常选择一个适当的步长值，以保证模拟效果和计算速度的平衡。

接下来，在仿真设置中选择欧拉离散化方法，可以是前向欧拉或后向欧拉方法。

前向欧拉方法是通过使用当前系统状态和输入变量进行差分逼近，计算下一个离散时间步长的状态值；而后向欧拉方法是通过使用下一个离散时间步长的状态值和当前输入变量进行差分逼近，计算当前离散时间步长的状态值。

根据具体系统的特点选择合适的欧拉离散化方法。

在Simulink中使用欧拉离散化方法进行仿真时，还需要关注模型的初值设定和仿真终止条件。

确保模型具有合适的初值设定，以保证仿真的准确性和可靠性。

同时，根据实际需求设置仿真终止条件，例如仿真的时间长度、达到一定精度或满足某些约束条件。

利用Simulink中的欧拉离散化方法，可以方便地对连续时间系统进行仿真和数值计算。

通过选择合适的离散化方法和参数设置，可以得到精确、准确的仿真结果。

同时，结合Simulink中丰富的工具和功能，可以进一步分析和优化系统的性能，提高系统的稳定性和可靠性。

总结来说，Simulink中的欧拉离散化方法是一种常用的连续系统离散化处理方法，通过选择合适的仿真设置和参数配置，可以得到准确、可靠的仿真结果。

在实际应用中，需要根据具体系统的特点和需求，选择合适的离散化方法和参数设置，以确保仿真结果的准确性和可靠性。

实验报告班级：姓名：学号：实验二名称：实验任务：Simulink系统建模与仿真实验内容与实验要求：simulink是matlab提供的可视化仿真环境。

通过一个二阶系统实例体会simulink仿真过程、步骤、参数设置等特点。

用两种方法：直接使用系统函数模块建立一个二阶系统，系统的开环传递函数为：使用系统串联的模式重新建立上面的二阶系统。

熟悉simulink环境。

理解其中的基本库和基本模块。

熟悉建模的步骤和参数的设置。

实验步骤：1、启动Simulink，打开Simulink模块库（1）启动Simulink。

单击MATLAB Command窗口工具条上的Simulink图标，或者在MATLAB命令窗口输入simulink，即弹出图示的模块库窗口界面(Simulink Library Browser)。

该界面右边的窗口给出Simulink所有的子模块库。

常用的子模块库有Sources(信号源)，Sink(显示输出),Continuous(线性连续系统)，Discrete（线性离散系统)，Function & Table（函数与表格)，Math(数学运算)， Discontinuities (非线性)，Demo（演示）等。

每个子模块库中包含同类型的标准模型，这些模块可直接用于建立系统的Simulink框图模型。

可按以下方法打开子模块库:①用鼠标左键点击某子模块库(如【Continuous】)，Simulink浏览器右边的窗口即显示该子模块库包含的全部标准模块。

②用鼠标右键点击Simulink菜单项，则弹出一菜单条，点击该菜单条即弹出该子库的标准模块窗口.如单击左图中的【Sinks】,出现“Open the‘Sinks’Library”菜单条，单击该菜单条，则弹出右图所示的该子库的标准模块窗口。

2、打开空白模型窗口；①模型窗口用来建立系统的仿真模型。

只有先创建一个空白的模型窗口，才能将模块库的相应模块复制到该窗口，通过必要的连接，建立起Simulink仿真模型。

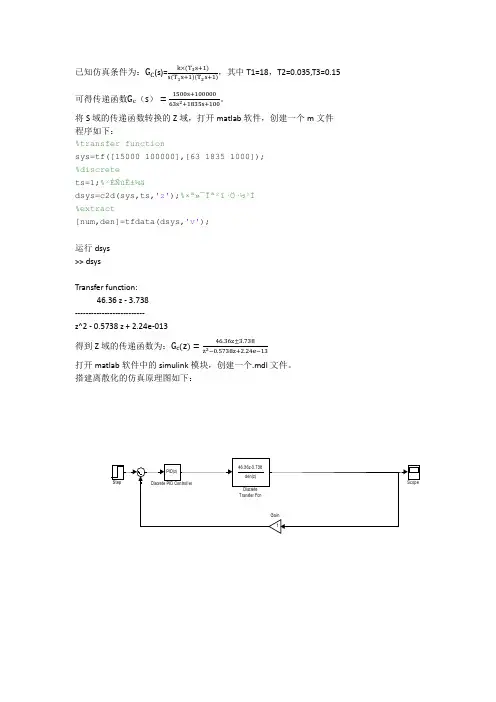
已知仿真条件为：G C(s)=k×(T3s+1)，其中T1=18，T2=0.035,T3=0.15s T1s+1(T2s+1)。

可得传递函数G c（s）=1500s+10000063s+1835s+100将S域的传递函数转换的Z域，打开matlab软件，创建一个m文件程序如下：%transfer functionsys=tf([15000 100000],[63 1835 1000]);%discretets=1;%²ÉÑùʱ¼ädsys=c2d(sys,ts,'z');%ת»¯Îª²î·Ö·½³Ì%extract[num,den]=tfdata(dsys,'v');运行dsys>> dsysTransfer function:46.36 z - 3.738--------------------------z^2 - 0.5738 z + 2.24e-013得到Z域的传递函数为：G c(z)=46.36z±3.738z2−0.5738z+2.24e−13打开matlab软件中的simulink模块，创建一个.mdl文件。

搭建离散化的仿真原理图如下：下面进行PID整定，常用PID整定方法有：⒈稳定边界法⒉4:1衰减法⒊鲁棒法⒋ISTE最优参数整定法。

边界稳定法和4：1衰减法调节时间快，上升时间短，鲁棒法和ISTE最优参数整定法超调量小，调节过程平衡，鲁棒性好。

4:1衰减法有一定局限性，鲁棒性差；iste法调节时间长，调节参数偏保守。

本文中采用稳定边界法来整定PID参数。

在闭环系统下首先将PIDcontrol 调节为纯P调节器，逐渐增大P参数，观察输出波形，记录此时波形。