下载文档原格式
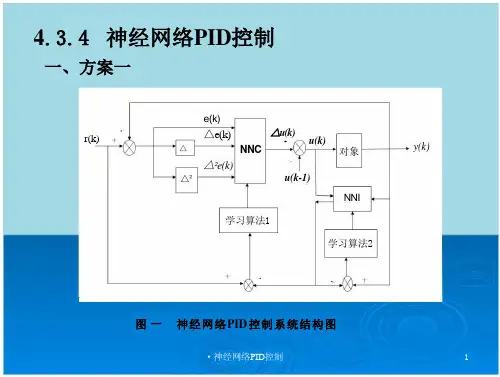
预测控制模型结构预测模型预测模型是预测控制模型的核心部分，它用于描述系统的动态行为，基于历史观测数据来预测未来的系统状态。
常见的预测模型有以下几种：1.线性模型：基于线性系统的假设，使用线性状态空间模型或ARMA模型等进行预测。
2.非线性模型：考虑非线性系统的特性，使用非线性回归模型、神经网络模型等进行预测。
3.神经网络模型：通过训练神经网络来拟合系统的输入输出关系，进行预测。
4.ARIMA模型：自回归滑动平均模型，用于描述时间序列数据的动态变化。
5.状态空间模型：将系统的状态和观测变量表示为状态方程和观测方程，通过状态估计和观测估计来进行预测。
控制器控制器是预测控制模型的另一个重要组成部分，它用于根据预测模型的输出进行控制决策。
常见的控制器有以下几种：1.模型预测控制器（MPC）：基于预测模型的输出，通过优化控制问题得到最优控制系列，实现对系统的控制。
2.比例积分微分（PID）控制器：通过比例、积分和微分操作来实现对系统的控制，可以根据误差信号调整控制输出。
3.神经网络控制器：使用神经网络来估计系统的输出，然后根据估计值进行控制决策。
4.最优控制器：通过求解最优化问题，得到最优控制输入，实现对系统的控制。
模型结构预测控制模型的结构是指预测模型和控制器的组合方式。
一般来说，预测模型和控制器之间存在以下两种结构：1.串级结构：预测模型和控制器按照串联的方式连接，预测模型先进行预测，然后将预测结果传递给控制器进行控制决策。
输入数据>预测模型>预测结果>控制器>控制输入2.并行结构：预测模型和控制器同时运行，预测模型负责预测系统状态，控制器负责根据预测结果进行控制决策。
输入数据>预测模型>预测结果|V控制器>控制输入。
神经网络在预测模型和控制系统中的应用神经网络是一种模拟人脑神经系统运行的数学模型，在机器学习和人工智能领域有着广泛的应用。
作为一种高度自适应的算法，神经网络在预测模型和控制系统中发挥了重要作用。
神经网络在预测模型中的应用预测模型包括了诸如时间序列预测、金融市场预测、自然灾害预测等各种领域，对于提高决策的准确性和效率都有很大的帮助。
而神经网络则是其中的重要一环。
神经网络可以通过学习过去的数据，提取出其中的规律，并利用这些规律来预测未来的数据。
以时间序列预测为例，神经网络可以利用历史上同期的数据，进行训练，并得到一个预测模型。
这个预测模型可以用来预测未来时期的数据。
相比于传统的模型，神经网络可以更好地处理非线性数据关系，同时也可以更好地处理多个变量之间的影响关系。
除了时间序列预测，在金融市场预测中，神经网络也发挥了重要作用。
金融市场的波动性很高，而神经网络可以很好地处理这种波动。
通过学习历史上的股市数据，神经网络能够建立出股市走势的预测模型。
这个预测模型可以用来预测股市的未来发展趋势。
在实际的投资决策中，这些预测结果可以帮助投资者更好地理解市场，作出正确的投资决策。
神经网络在控制系统中的应用控制系统是一种可以监控、管理和控制工程和科学系统的集成体系。
控制系统通常需要利用大量的数据来进行监控和控制。
而神经网络可以帮助实现控制系统的智能化。
在控制系统中，神经网络可以利用历史上的数据，建立出一个预测模型。
这个预测模型可以用来预测未来的结果。
比如，对于一个复杂的航空控制系统，神经网络可以对机器状态进行监控，并预测出机器的可能故障。
这些预测结果可以提前告知维修人员，帮助他们事先准备好所需的维修工具和零件。
在制造业中，神经网络也可以用来进行过程控制。
利用多个神经网络，可以对制造过程中的各种参数进行监控和控制，从而实现制造过程的优化。
比如，在纺织生产中，神经网络可以对生产过程中的温度、湿度等参数进行监控。
通过对过去数据的学习，神经网络可以建立出一个精准的控制模型，并自动调整参数，从而实现制造过程的优化。
机器人控制器的高级算法主要包括以下几个方面：1. 模型预测控制（Model Predictive Control, MPC）：MPC是一种基于模型的控制算法，它通过预测未来一段时间内系统的状态和输出，优化未来的控制输入以达到最佳的控制性能。
在机器人控制中，MPC 可以处理多变量、非线性和约束条件等问题，适用于复杂的运动规划和轨迹跟踪任务。
2. 自适应控制（Adaptive Control）：自适应控制算法能够根据系统参数的变化或者未知环境的影响自动调整控制参数，以保持良好的控制性能。
在机器人控制中，自适应控制可用于处理模型不确定性、外界干扰和机械磨损等问题。
3. 滑模控制（Sliding Mode Control, SMC）：SMC是一种鲁棒控制算法，它通过设计特殊的控制律使得系统状态快速进入并保持在一个所谓的“滑动面”上，从而消除系统中的不确定性影响和外部扰动。
在机器人控制中，SMC常用于保证系统的稳定性和精确跟踪。
4. 神经网络控制（Neural Network Control）：神经网络控制利用人工神经网络的非线性映射能力和学习能力来实现对复杂系统的控制。
在机器人控制中，神经网络可以用于建模未知的动态系统、处理高维和非线性问题，以及实现智能决策和自主学习。
5. 模糊控制（Fuzzy Control）：模糊控制是一种基于模糊逻辑的控制方法，它可以处理不精确、不确定和非线性的控制问题。
在机器人控制中，模糊控制常用于处理语言描述的控制规则和复杂的环境交互。
6. 遗传算法和粒子群优化（Genetic Algorithm and Particle Swarm Optimization, GA & PSO）：这些是两种常用的优化算法，可以用于寻找最优的控制参数或控制策略。
在机器人控制中，GA和PSO可以用于优化路径规划、姿态控制和动作学习等问题。
7. 深度强化学习（Deep Reinforcement Learning, DRL）：DRL结合了深度学习和强化学习的优点，能够在复杂的环境中学习最优的控制策略。
神经网络模型预测控制器摘要：本文将神经网络控制器应用于受限非线性系统的优化模型预测控制中，控制规则用一个神经网络函数逼近器来表示，该网络是通过最小化一个与控制相关的代价函数来训练的。
本文提出的方法可以用于构造任意结构的控制器，如减速优化控制器和分散控制器。
关键字：模型预测控制、神经网络、非线性控制1.介绍由于非线性控制问题的复杂性，通常用逼近方法来获得近似解。
在本文中，提出了一种广泛应用的方法即模型预测控制（MPC），这可用于解决在线优化问题，另一种方法是函数逼近器，如人工神经网络，这可用于离线的优化控制规则。
在模型预测控制中，控制信号取决于在每个采样时刻时的想要在线最小化的代价函数，它已经广泛地应用于受限的多变量系统和非线性过程等工业控制中[3,11,22]。
MPC方法一个潜在的弱点是优化问题必须能严格地按要求推算，尤其是在非线性系统中。
模型预测控制已经广泛地应用于线性MPC问题中[5]，但为了减小在线计算时的计算量，该部分的计算为离线。
一个非常强大的函数逼近器为神经网络，它能很好地用于表示非线性模型或控制器，如文献[4,13,14]。
基于模型跟踪控制的方法已经普遍地应用在神经网络控制，这种方法的一个局限性是它不适合于不稳定地逆系统，基此本文研究了基于优化控制技术的方法。
许多基于神经网络的方法已经提出了应用在优化控制问题方面，该优化控制的目标是最小化一个与控制相关的代价函数。
一个方法是用一个神经网络来逼近与优化控制问题相关联的动态程式方程的解[6]。
一个更直接地方法是模仿MPC方法，用通过最小化预测代价函数来训练神经网络控制器。
为了达到精确的MPC技术，用神经网络来逼近模型预测控制策略，且通过离线计算[1,7.9,19]。
用一个交替且更直接的方法即直接最小化代价函数训练网络控制器代替通过训练一个神经网络来逼近一个优化模型预测控制策略。
这种方法目前已有许多版本，Parisini[20]和Zoppoli[24]等人研究了随机优化控制问题，其中控制器作为神经网络逼近器的输入输出的一个函数。
Seong和Widrow[23]研究了一个初始状态为随机分配的优化控制问题，控制器为反馈状态，用一个神经网络来表示。
在以上的研究中，应用了一个随机逼近器算法来训练网络。
Al-dajani[2]和Nayeri等人[15]提出了一种相似的方法，即用最速下降法来训练神经网络控制器。
在许多应用中，设计一个控制器都涉及到一个特殊的结构。
对于复杂的系统如减速控制器或分散控制系统，都需要许多输入与输出。
在模型预测控制中，模型是用于预测系统未来的运动轨迹，优化控制信号是系统模型的系统的函数。
因此，模型预测控制不能用于定结构控制问题。
不同的是，基于神经网络函数逼近器的控制器可以应用于优化定结构控制问题。
在本文中，主要研究的是应用于非线性优化控制问题的结构受限的MPC类型[20,2,24,23,15]。
控制规则用神经网络逼近器表示，最小化一个与控制相关的代价函数来离线训练神经网络。
通过将神经网络控制的输入适当特殊化来完成优化低阶控制器的设计，分散和其它定结构神经网络控制器是通过对网络结构加入合适的限制构成的。
通过一个数据例子来评价神经网络控制器的性能并与优化模型预测控制器进行比较。
2.问题表述考虑一个离散非线性控制系统：其中为控制器的输出，为输入，为状态矢量。
控制目标是保持输出接近参考轨迹，一般地控制目标是通过最小化代价函数来实现的：同时约束条件为：其中为k时刻预测状态和输出的函数，这里，由将来的输入组成：为输入增量：在方程（2）中，Q和R输入与输出权值矩阵，为非负终止条件。
根据动态编程的优化原则[6]，必须最小化代价函数（2），当终止条件为在K+N时刻时的无穷小，得出当时的无穷优化控制问题的解，同样就能得到有穷优化问题。
对于非线性系统，优化控制问题一般无闭式解，因此，本文研究强力和不最理想的方法。
在模型预测控制（MPC）中，控制信号的确定是通过在每个采样时刻输入序列为时，最小化代价函数（2）。
只有优化输入序列的第一个元素u（k）作为系统的输入，在下一个采样时刻k+1，新的优化问题是对于给定的优化控制问题而言的。
在这种方法中，终止条件可以看作是一个当时刻K+N趋于无穷时最小化代价函数的逼近器，但实际上更多的是用于保证闭环的稳定性。
模型预测控制方法有一个非线性的缺点，且需要通过在每个采样时刻得到受约束的优化问题，同时需要通过在线计算来实现。
为了减小模型预测控制的计算量，本文提出了一种精确MPC方法，在这种方法中，计算的部分是离线进行的。
对于非线性系统，优化的MPC方法应该由离线计算进行映射，且用一个函数逼近器表示。
更准确地，控制策略是通过最小化代价函数（2）定义控制信号，或等于它的增量：其中作为计算代价函数（2）中的。
对于任意，最小化代价函数（2）来评估方程（6）。
从而通过离线训练来获得函数逼近器作为优化策略，尽管这种方法非常有用，但仍然存在一些限制。
因为MPC策略是基于信息来计算预测输出，这种不能很好的表示阶次递减或定结构的控制器。
另外，计算还要求产生训练的数据非常广泛，这些每个训练数据点都需要一个MPC优化问题的解。
3.神经网络优化控制器在本节中，研究了构成第2节所述的控制问题的一个神经网络模型预测控制器的问题。
这里我们采样一个训练数据集作为直接训练代价函数（2）的控制器，而没有计算优化MPC控制信号的离线优化问题。
控制器表示如下：其中为神经网络函数逼近器，I（k）为k时刻控制器的有效信号，W为逼近器参数（即神经网络权值）。
假设状态信息，如I（k）=时，控制器（7）可以看作是优化MPC策略（6）的函数近似。
在本文中尽管研究的是这个方法，但控制器并没有完全受到状态信息的限制，而是把I（k）当成由许多输入u（k-i）与输出y（k-i）的过去值组成。
，并将其作为参考信号的设定值。
这种方法可以构成高阶系统的较为复杂的控制器。
I（k）值的不同选取方法将在第四节通过例子讲述。
Remark 1为了降低控制器的复杂性，控制器的结构可以利用映射函数来确定，例如，假设信息I（k）为：，一个分布式控制器为：，控制器的结构为：为了用控制规则（7），即最小化代价函数（2）来确定控制器的参数W，需要知道训练数据：利用控制策略（7），系统的更新如下所示：用训练数据定义联想代价函数：逼近器（7）的训练，最小化优化问题的平方为：约束条件为：训练问题可以通过梯度算法来最小化优化问题的平方，如LM算法，从方程（11）可以得到代价函数的梯度为其中：其中为神经网络输出关于网络参数的偏导数，它取决于网络的结构，可以根据下式得到：Remark 2代价函数（11）用于训练神经网络控制器，与模型预测控制中代价函数类似，本文提出的控制器可以作为精确的模型预测控制器。
注意到，对于一个给定的控制器的复杂性，计算量取决于优化控制器的参数W，而不是控制器的长度N。
因此可以比模型预测控制能更灵活地用控制器的长度，从而被优化的参数也能成比例地增加。
4.仿真例子在本节中，用例子仿真来说明第3节中所讲的神经网络模型预测控制器，在所有例子中，控制规则（7）用一个前馈神经网络来表示，该网络含有一层隐含层，用双曲正切函数作为激活函数。
这种网络可以以任意精度逼近所有连续非线性函数[12]。
I（k）作为输入，为输出，训练算法为LM算法[21]，用来解决非线性最小二乘问题（12），利用matlab的优化工具箱中的常规函数lsqnonlin来计算。
在所有的例子中，优化范围N为足够大，这样对于闭环系统就能达到平衡，因此，用一个零终止条件作为代价函数（11）。
例1在本例中，我们仿真一个pH中和过程[10,18,17,1]，在文献[1]中，应用了一个神经网络来逼近优化MPC策略的过程。
这个过程可以用非线性微分方程来表示，该过程的表达式如下式所示[17,1]：式中，输出y（k）由pH值控制，u（k）为输入流量，用于控制，系统还有确定性扰动d（k）、相互独立的随机白躁声扰动v（k）和n（k）（分别用Rv和Rn表示）。
采样时间为0.2分钟，时延为L=5，系统矩阵表示为输出的函数，如下所示。
状态参数表达式为：其中这些系统参数的函数表达式在文献[1]中已有研究。
根据方程（17），预测输出根据下式确定：其中状态参数根据Kalman滤波原理得到：，其中K（k）为Kalman滤波增益：优化控制策略为预测状态的函数，参考轨迹为，i=1,….N 假设参考轨迹由参考模型给出：式中为设定值，为阶跃响应。
控制策略为在k+L时刻时预测系统状态，参考模型的状态，设定值等的函数，控制器（7）的信息I（k）为：参数的选取根据文献[1]，代价函数（11）中的权值为：Q=1，R=1。
白躁声变量：，用于Kalman滤波方程（19）中，参考模型（20）为一个二阶系统，增益为1，一对极点，均为0.9由于非线性系统的动态特性，为了在整个操作过程中获得优化控制器的精确特性，需要大量的数据集。
与非线性系统辨识相比较，仍需要长的训练集[16]。
训练数据（9）用于训练控制器，包括轨迹跟踪和扰动抑制（将输出pH的范围控制在）。
因此训练数据有两种类型。
对于轨迹跟踪，训练数据由以下构成：初始状态作为稳定状态响应，设定值的改变，八个相等的初始pH值，14个设定值，给定的14个参考轨迹。
代价函数（11）的控制范围设定为N=150，这个足够使新的设定到达参考模型（20）所定义的参考轨迹。
对于扰动抑制，训练数据由以下构成：常量设定值，参考信号，初始状态对稳定状态的响应。
同样有14个不同的常量设定值，用于轨迹跟踪，且有28个初始状态。
在这种情况下，控制范围为N=25步，这就使系统能达到设定值的一个初始偏值。
初始状态和参考轨迹的总数为M=42。
训练集中的每个元素包括了N个数据点，总的数据点数为2800。
根据一个独立的测试数据集来选取优化网络的大小，测试数据有36组2400个数据点，均是均相同的方法产生训练数据，6个范围在的初始pH值以及6个范围在的设定值。
为了找出一个最小测试数据集，网络的大小不同，训练的结果如表1所示。
当网络中含有11个隐含节点时，测试数据中的代价函数为最小，而当增加网络大小时该值不会减小，因此，以下仿真中网络的结构为11。
这个结果与[1]中一致，即当用于逼近MPC策略时网络的大小也为11。
同时，表1也表明了用一个非线性MPC的结果。
MPC策略的预测和控制范围为N=20步。
为了避免局部收敛特性，需要用不同初始点来优化网络的权值。
在本例中没有遇到局部最优化值的问题。
一般来说，网络权值在第400-500代时就已收敛。
所需要的代数与优化MPC 策略中神经网络的代数相同[1]，且用相同的数据点。
然而，当对每一代的轨迹（10）和联想代价（11）进行评估时，用于训练的计算量将比直接逼近要重。
