高斯光束的传播

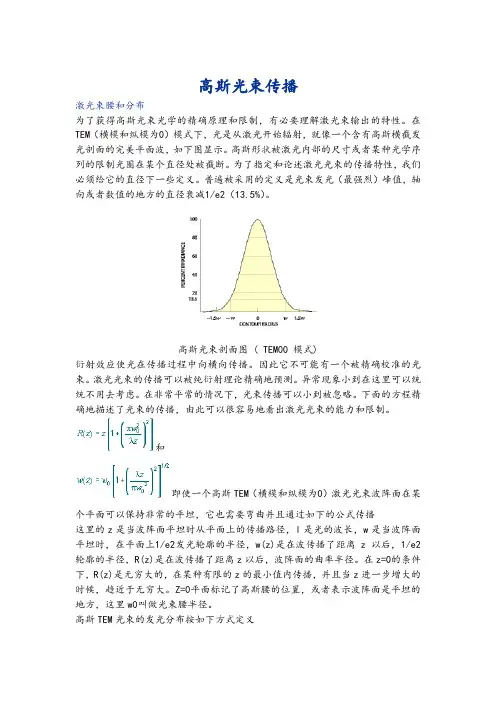
高斯光束传播激光束腰和分布为了获得高斯光束光学的精确原理和限制，有必要理解激光束输出的特性。

在TEM（横模和纵模为0）模式下，光是从激光开始辐射，就像一个含有高斯横截发光剖面的完美平面波，如下图显示。

高斯形状被激光内部的尺寸或者某种光学序列的限制光圈在某个直径处被截断。

为了指定和论述激光光束的传播特性，我们必须给它的直径下一些定义。

普遍被采用的定义是光束发光（最强烈）峰值，轴向或者数值的地方的直径衰减1/e2（13.5%）。

高斯光束剖面图( TEM00 模式)衍射效应使光在传播过程中向横向传播。

因此它不可能有一个被精确校准的光束。

激光光束的传播可以被纯衍射理论精确地预测。

异常现象小到在这里可以统统不用去考虑。

在非常平常的情况下，光束传播可以小到被忽略。

下面的方程精确地描述了光束的传播，由此可以很容易地看出激光光束的能力和限制。

和即使一个高斯TEM（横模和纵模为0）激光光束波阵面在某个平面可以保持非常的平坦，它也需要弯曲并且通过如下的公式传播这里的z是当波阵面平坦时从平面上的传播路径，l是光的波长，w是当波阵面平坦时，在平面上1/e2发光轮廓的半径，w(z)是在波传播了距离z以后，1/e2轮廓的半径，R(z)是在波传播了距离z以后，波阵面的曲率半径。

在z=0的条件下，R(z)是无穷大的，在某种有限的z的最小值内传播，并且当z进一步增大的时候，趋近于无穷大。

Z=0平面标记了高斯腰的位置，或者表示波阵面是平坦的地方，这里w0叫做光束腰半径。

高斯TEM光束的发光分布按如下方式定义这里的w=w(z)和P是光束的总功率，在所有的相交的部分是等值的。

分布形式的恒定性是对在z=0的时候高斯分布预测的特殊结果。

如果统一的发光分布在z=0时刻被预测，z=∞时刻的形式将与贝塞尔公式给出的艾利斑（Airy disc）形式相似，这里z值中间的形式将变得非常复杂。

这里假定z远大于pw0 /l，因此1/e2发光轮廓渐渐逼近一个圆锥形的角半径这个值是一个高斯TEM光束的远场角半径。

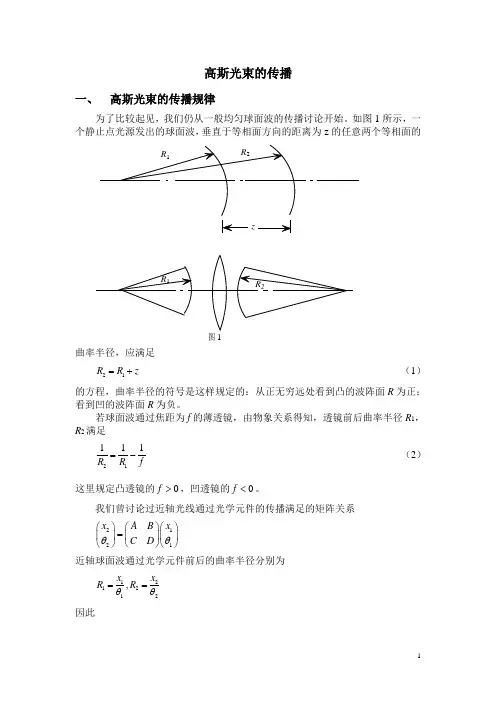
高斯光束的传播一、 高斯光束的传播规律为了比较起见，我们仍从一般均匀球面波的传播讨论开始。

如图1所示，一个静止点光源发出的球面波，垂直于等相面方向的距离为z 的任意两个等相面的z图1曲率半径，应满足21R R z =+（1）的方程，曲率半径的符号是这样规定的：从正无穷远处看到凸的波阵面R 为正；看到凹的波阵面R 为负。

若球面波通过焦距为f 的薄透镜，由物象关系得知，透镜前后曲率半径R 1，R 2满足21111R R f=- （2）这里规定凸透镜的0f >，凹透镜的0f <。

我们曾讨论过近轴光线通过光学元件的传播满足的矩阵关系2121x x AB CD θθ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭近轴球面波通过光学元件前后的曲率半径分别为121212,x x R R θθ==因此1211112121111x A Bx Ax B AR B R x C x D C R DCDθθθθθ+++====+++ （3）所以对于一般均匀球面波，只用一个参数——曲率半径R 就可完全描述其传播和变换的特性。

与普通球面波不同，高斯光束必须由两个量即R （z ）和w (z)来描写。

但下面将看到，对于高斯光束——非均匀的、曲率中心不断变化的球面波——也具有一个与一般球面波曲率半径R 的作用类似的复曲率半径q (z )，它可被用来描述高斯光束的传播行为。

在推导高斯光束表达式时，我们已经得出复曲率半径在均匀空间传播的表达式，具体过程可以参考伍长征编写的《激光原理》书中的（3.3-14）式，即21q q z=+ （4）这里21,q q 分别为传播方向上任意两点21,z z 处的复曲率半径，z 为两点间距离，21z z z =-，参见图2(a)。

再看高斯光束通过薄透镜的变换，如图2(b)。

令薄透镜焦距为f ，由于是近轴光线，波阵面是一球面，透镜前后曲率半径应满足21111R R f=-,000(,)q w R 111(,)q w R 222(,)qwR z 1z 2图2(a)f 20w 10w q 1q 2图2(b)又透镜足够薄，两侧光斑尺寸相等，即12w w =，与上式合并，可以变形为22222112121()i iR kwR kw f-=-- (5)由复曲率半径定义式2112()()()i q z R z kw z =-，可得21111q q f=-（6）比较（4）式和（6）式与（1）式和（2）式知道，利用复曲率半径q ，形式上完全可等价于球面波的曲率半径R 。

高斯光束1. 引言高斯光束是一种常见的光束模式，具有重要的理论和实际应用价值。

它的特点是光强在空间上呈高斯分布，成为光学研究领域中的重要工具。

本文将从通俗的角度出发，介绍高斯光束的基本原理、特性以及其在科学研究和实际应用中的重要性。

2. 高斯光束的基本原理高斯光束是一种光波的传播模式，它的波前呈现出高斯分布的形状。

在光学中，光波的传播可以通过波动方程来描述，而高斯光束正是波动方程的解之一。

波动方程描述了光波的传播行为，其中包括波的幅度、相位和传播速度等信息。

在高斯光束中，光强的分布服从高斯分布的形式，即呈钟形曲线。

光强最大的地方称为光束的中心，而光强逐渐减小的地方则是光束的边缘。

高斯光束的光强分布可以用以下公式表示：I(r)=I0exp(−2r2 w2)其中，I(r)表示光束在距离中心r处的光强，I0为光束中心的光强，w为光束的束腰半径。

3. 高斯光束的特性3.1 光束的束腰和发散角高斯光束的束腰是指光束光强达到峰值的地方，也是光束最细的地方。

束腰的半径w是高斯光束的一个重要参数，它决定了光束的横向尺寸。

束腰半径越小，表示光束越集中，光强越大。

发散角是描述光束传播方向的一个参数，它决定了光束的扩散程度。

高斯光束的发散角与束腰半径有关，当束腰半径越小时，发散角越大，光束扩散越快。

3.2 光束的相位高斯光束的相位是指光波在传播过程中的相对位移。

光束的相位分布可以通过波前的形状来描述，而高斯光束的波前呈现出球面的形状。

这种球面波前在光学研究和应用中具有重要的意义，可以用来实现光束的聚焦和成像等功能。

3.3 光束的自聚焦效应高斯光束具有自聚焦效应，即在传播过程中可以自动聚焦到一个更小的尺寸。

这种自聚焦效应是由于高斯光束的非线性光学特性所导致的。

在某些介质中，高斯光束可以通过与介质相互作用来实现自聚焦，从而形成更强的光束和更小的束腰。

4. 高斯光束的应用4.1 光通信高斯光束在光通信领域有着广泛的应用。

由于高斯光束具有较小的束腰和较大的光强，可以实现高速、高容量的信息传输。

高斯光束光斑大小
摘要：
一、高斯光束的基本概念
二、高斯光束的传输特性
三、高斯光束的光斑大小与能量分布
四、高斯光束在光学系统中的应用
五、测量高斯光束束腰宽度的方法
正文：
一、高斯光束的基本概念
高斯光束是一种常见的光学光束，它的形状呈高斯分布。

在高斯光束中，光斑大小、能量分布等参数都是重要的特性。

二、高斯光束的传输特性
高斯光束的传输特性表现为，在远离光源的地方，光束会沿着传播方向呈特定角度扩散。

这个特定角度即为我们所称的远场发散角。

远场发散角与光束的波长成正比，与光束的束腰半径成反比。

因此，束腰半径越小，远场发散角越大。

三、高斯光束的光斑大小与能量分布
高斯光束的光斑大小与能量分布紧密相关。

光斑大小决定了光束在空间中的覆盖范围，而能量分布则影响了光束的亮度。

高斯光束的光斑大小与其束腰半径有关，束腰半径越小，光斑大小越小。

四、高斯光束在光学系统中的应用
高斯光束在光学系统中有着广泛的应用，如激光加工、激光通信、光学成像等。

在光学系统设计中，我们需要根据高斯光束的特性来优化系统的性能。

五、测量高斯光束束腰宽度的方法
测量高斯光束的束腰宽度一般通过测量不同位置处光束的宽度，再进行双曲线拟合求解。

但需要注意的是，激光器的束腰半径意义不大，可以通过后续光束的准直聚焦改变其束腰半径。

高斯光束垂直入射到不同折射率介质中的传播规律
高斯光束垂直入射到不同折射率介质中时，其传播规律遵循几何光学和波动光学的基本原理。

当光束从真空（折射率为1）垂直入射到其他介质时：
传播方向：由于是垂直入射，光束的传播方向在界面处不会发生改变，即光束将沿着原方向直线传播进入介质。

光束宽度和强度分布：高斯光束在进入高折射率介质后，横向尺寸会发生变化，根据光束waist（最细处直径）的位置以及数值孔径（NA）等因素确定。

高斯光束在任何位置的强度分布仍保持高斯分布形式，但光束腰的位置会随传播距离而移动，并且在新介质中的束宽会不同于在真空或低折射率介质中的情况。

光速与波长：光在不同介质中的速度会变慢，具体由折射率n决定，v = c/n（c为真空中的光速）。

因此，光的波长λ' 在介质中也会相应缩短，即λ' = λ/n，其中λ为真空中波长。

聚焦特性：高斯光束的聚焦特性和焦距也会受到介质折射率的影响，在高折射率介质中，相同的透镜参数下，焦距会变短。

总结来说，尽管入射方向不变，但高斯光束在垂直入射进入不同折射率介质后，其横向传播特征、光强分布及光速、波长等都会发生变化。

第1篇一、实验目的1. 加深对高斯光束物理图像的理解；2. 学会对描述高斯光束传播特性的主要参数，即光斑尺寸、远场发散角的测量方法进行掌握；3. 学习体会运用微机控制物理实验的方法。

二、实验原理1. 高斯光束的传播特性高斯光束的振幅在传播平面上呈高斯分布，近场时近似为平面波，远场时近似为球面波。

高斯光束的振幅分布公式为：\[ I(r, z) = I_0 \exp\left(-\frac{2r^2}{w_0^2(z)}\right) \]其中，\( I(r, z) \) 为距离光轴距离为 \( r \) 处，距离光束传播方向为 \( z \) 处的光强；\( I_0 \) 为光束中心处的光强；\( w_0 \) 为光束中心处的光斑尺寸。

光斑尺寸 \( w(z) \) 与光束中心处的光斑尺寸 \( w_0 \) 的关系为：\[ w(z) = w_0 \sqrt{1 + \left(\frac{z}{z_r}\right)^2} \]其中，\( z_r \) 为光束的瑞利长度。

2. 发散角的定义及测量光束的全发散角定义为光束中光强下降到中心光强的 \( 1/e \) 位置时，光束边缘与光轴所成的角度。

在远场情况下，光束的全发散角近似为：\[ \theta = \frac{1.22 \lambda}{w(z)} \]其中，\( \lambda \) 为光束的波长。

三、实验仪器与设备1. 激光器：输出波长为 \( \lambda = 632.8 \) nm 的红光激光；2. 凹面镜：曲率半径为 \( R = 50 \) cm；3. 平面镜：用于反射激光；4. 光电探测器：用于测量光强；5. 数据采集卡：用于采集光电探测器数据；6. 计算机：用于处理实验数据。

四、实验步骤1. 将激光器输出光束照射到凹面镜上，使光束经凹面镜反射后形成高斯光束；2. 将光电探测器放置在凹面镜后的某个位置，调整探测器位置，使探测器接收到的光强最大；3. 记录探测器接收到的光强 \( I \)；4. 根据公式 \( I = I_0 \exp\left(-\frac{2r^2}{w_0^2(z)}\right) \) 求解光斑尺寸 \( w_0 \)；5. 根据公式 \( \theta = \frac{1.22 \lambda}{w(z)} \) 求解发散角\( \theta \)；6. 重复步骤 3-5，改变探测器位置，记录不同位置的光强 \( I \) 和发散角\( \theta \)。

拉盖尔高斯光束公式拉盖尔高斯光束（Laguerre-Gauss beam）是一种具有角动量和轨道角动量的特殊激光束，其在光学成像、信息传输、光纤通信等领域具有广泛的应用前景。

在实际应用中，拉盖尔高斯光束的传输特性和性能优化成为研究的关键。

本文将从拉盖尔高斯光束的传播特性、叠加相位方法及其在光学系统中的应用等方面进行讨论。

一、拉盖尔高斯光束的传播特性拉盖尔高斯光束的传播特性研究为其在光学系统的应用提供了理论基础。

耿滔等研究人员通过对拉盖尔高斯光束的传播形式进行推导，证明了高阶拉盖尔高斯光束在自由空间的传播过程中能够保持其自身表达形式的不变性[1]。

这一研究为拓展拉盖尔高斯光束在傍轴条件下的应用提供了理论支持。

二、叠加相位方法优化拉盖尔高斯光束性能为了进一步提高拉盖尔高斯光束的性能，研究人员提出了叠加相位的方法。

通过空间光调制器（SLM）对多个拉盖尔高斯光束施加不同的相位调制，然后将它们叠加在一起，形成一个新的复合光束。

这种方法在提高成像、传输和调制性能方面具有显著优势[2]。

三、拉盖尔高斯光束在光学系统中的应用1.光学微操控：拉盖尔高斯光束的优良旋转、聚焦和传输特性使其在光学微操控领域具有广泛应用。

例如，利用拉盖尔高斯光束驱动微粒、捕获和引导粒子、驱动微粒等。

2.信息传输：拉盖尔高斯光束在信息传输方面具有较高的传输速率和容量。

通过对光束进行相位调制，可以实现高速、安全的信息传输。

3.光纤通信：拉盖尔高斯光束在光纤通信中具有较低的损耗和较高的传输速率，可有效提高光纤通信系统的性能。

4.光学成像：拉盖尔高斯光束的成像质量较高，可以应用于高分辨率的光学成像领域。

1。

高斯光束传输方程及其解法光学是研究光的物理现象和规律的科学，光在自然界中广泛存在并起到重要作用，对于现代科技的发展也有着不可替代的作用。

高斯光束是一种常见的光束形式，其具有良好的传输性质和应用前景，因此得到广泛应用。

一、高斯光束的定义和特性高斯光束是指在自由空间中横向至少二次可微、纵向一次可微的光束，其光强分布和相位分布都可用高斯函数表征。

高斯光束具有如下的重要特性：1. 具有良好的射程特性，能够在传输过程中保持约束的形态；2. 横向光强分布呈高斯分布，纵向呈指数分布，能够满足许多光学应用中对于光束形态和光强的要求；3. 光束通过透镜进行聚焦后，仍然是高斯光束，具有良好的自聚焦能力；4. 具有相干性，能够满足干涉、衍射等光学现象的要求。

二、高斯光束传输方程的推导在光学应用中，高斯光束的传输是一个重要的问题，需要准确描述其传输过程。

高斯光束传输方程可以描述高斯光束在自由空间中传输的过程，其推导如下：设高斯光束的累计相位为φ(x,y,z)，其横向强度分布为I(x,y)，则光强的分布可以表示为：I(x,y,z)=|A(x,y,z)|^2其中，A(x,y,z)是高斯光束的复振幅，其表示为：A(x,y,z)=u(x,y,z)exp(jφ(x,y,z))其中u(x,y,z)表示高斯光束的复场，根据标量波动方程可以得到：△u+k^2u=0其中k=2π/λ为波数，λ为波长。

将复场u分解为实部和虚部，可得到：u=u1+ju2则标量波动方程可以分解为实部和虚部的两个方程：△u1+k^2u1=-△u2-k^2u2△u2+k^2u2=△u1-k^2u1再利用高斯光束的对称性和横向可微性，可以得到：▽^2u1+k^2u1=0▽^2u2+k^2u2=0则高斯光束的传输方程可以写为：∂A(x,y,z)/∂z+iβ(x,y,z)A(x,y,z)=0其中β(x,y,z)为传输因子，可以表示为：β(x,y,z)=k/2n[∂^2φ(x,y,z)/∂x^2+∂^2φ(x,y,z)/∂y^2]则高斯光束的累计相位和传输因子分别代表了光束的位相和弯曲程度，通过方程可以描述光束在自由空间中传输时的演化形态。

高斯光束的传输功率
高斯光束的传输功率是指高斯光束在传输过程中所携带的功率大小。

高斯光束
是一种特殊的光束模式，具有高度集中的光强分布。

由于其特殊的形状和能量分布特征，高斯光束在光学领域应用广泛。

光束的传输功率是通过计算光束的功率密度和传输面积得到的。

高斯光束的功
率密度分布呈钟形曲线，中心光强最高，逐渐向两侧衰减。

这种分布特征使得高斯光束在传输中能够保持相对稳定的功率。

光束的功率密度可以由光强公式计算得出。

假设高斯光束在传输过程中的功率
密度为P，传输距离为d，则功率密度与传输距离的关系可以表示为：P(d) = P0 * exp(-2 * (d/w)²)
其中P0为光束的初始功率密度，w为高斯光束的束腰半径。

从公式可以看出，随着传输距离的增加，功率密度会衰减，但衰减的速度比较缓慢。

传输功率可以通过积分计算得出，即将功率密度在整个传输区域上进行积分。

传输功率的大小与光束的初始功率密度、传输距离以及光束的束腰半径有关。

高斯光束的传输功率对于许多应用具有重要意义。

在光通信中，传输功率的稳
定性对于确保信号的传输质量至关重要。

此外，在激光加工、光束聚焦以及光学显微镜等领域，传输功率的准确控制和优化是关键技术。

综上所述，高斯光束的传输功率可以通过计算光束的功率密度和传输面积得到。

掌握高斯光束传输功率的计算方法对于光学应用具有重要意义，可帮助优化光束传输过程，并提高光学系统的性能。