第二章 电容器的串并联以及微积分电路

电容的串并联了解电容器在电路中的串并联关系电路中的电容器在串并联关系电容器是一种用于存储电荷的电子元件，广泛应用于电路中。

在电路中，电容器可以通过串联和并联的方式相互连接，实现不同的电路功能。

本文将探讨电容器在电路中的串并联关系及其应用。

一、串联电容器串联电容器是指将多个电容器依次连接在电路中，使它们共享相同的电压。

串联电容器的总电容等于各个电容器的电容之和。

假设有两个电容器C1和C2，它们串联连接在电路中，总电容Ct可以表示为：1/Ct = 1/C1 + 1/C2其中，1/Ct表示总电容的倒数，1/C1和1/C2分别表示电容器C1和C2的倒数。

通过串联电容器，可以增加电路中的总电容，提供更大的电荷存储能力。

串联电容器的应用：1. 整流滤波电路：在整流电路中，为了平滑直流输出电压，需要使用大容量的电容器进行滤波。

多个电容器串联连接可以提供更大的存储电量，减小纹波电压的幅度。

2. 电子滤波器：串联电容器可以构成低通、高通、带通和带阻滤波器等各种类型的电路，用于对特定频率的信号进行滤波和处理。

二、并联电容器并联电容器是指将多个电容器同时连接在电路中，它们的正极相连，负极相连。

并联电容器的总电容等于各个电容器的电容之和。

假设有两个电容器C1和C2，并联连接在电路中，总电容Ct可以表示为：Ct = C1 + C2通过并联电容器，可以增加电路中的储存电容，提供更大的电荷供给能力。

并联电容器的应用：1. 脉冲电路：在脉冲电路中，需要短时间内释放大量电荷的能力。

通过并联多个电容器可以增加总电容，以满足快速释放电荷的需求。

2. 多级放电电路：在某些特殊应用中，为了实现持续放电或延长放电时间，可以通过并联电容器来实现。

三、串并联电容器的应用串并联电容器在电路中的应用非常广泛，可以用于滤波、电源稳压、振荡电路、存储电路等众多领域。

例如，电源稳压电路中常常会使用串并联电容器来提供稳定的电流输出，减小由电源波动引起的输出电压纹波。

电容的串并联关系电容是电路中常见的元件之一，它可以存储电荷并在电路中起到储能的作用。

在电路中，电容与其他元件的串并联关系是十分重要的。

本文将探讨电容的串并联关系，以及在实际应用中的一些特殊情况。

一、电容的串联电容的串联是指多个电容器按一定的方式连接在一起，形成一个串联电容电路。

在串联电路中，电容器的正极与负极相连接，并且电荷在电容器之间依次流动。

串联电容器的总电容值可以通过公式计算出来。

假设有两个电容器C1和C2，其电容分别为C1和C2，则它们串联后的总电容Ct可以表示为：1/Ct = 1/C1 + 1/C2。

同理，当有多个电容器串联时，可以依次求得总电容。

例如，当C1 = 2μF，C2 = 3μF，C3 = 4μF时，它们串联后的总电容Ct可以计算为：1/Ct = 1/2 + 1/3 + 1/4 = 13/12μF。

因此，串联电容的总电容值是13/12μF。

串联电容的特点是电压分配均匀，即串联电路中的每个电容器上的电压相等。

这是因为在串联电路中，电压的总和等于各个电容器上的电压之和。

因此，当多个电容器串联时，电压分配是均匀的。

二、电容的并联电容的并联是指多个电容器的正极与正极相连接，负极与负极相连接，形成一个并联电容电路。

在并联电路中，电荷可以同时通过每个电容器，流动方向相同。

并联电容器的总电容值等于各个电容器的电容之和。

假设有两个电容器C1和C2，其电容分别为C1和C2，则它们并联后的总电容Cp等于C1 + C2。

同理，当有多个电容器并联时，可以直接相加求得总电容。

例如，当C1 = 2μF，C2 = 3μF，C3 = 4μF时，它们并联后的总电容Cp等于2μF + 3μF + 4μF = 9μF。

因此，并联电容的总电容值是9μF。

并联电容的特点是电压相同，即并联电路中的每个电容器上的电压相等。

这是因为在并联电路中，电压相同且电荷相等的电容器，其电荷存储量相同。

因此，当多个电容器并联时，它们的电压相等。

电容器的串联和并联关系电容器是电路中常见的电子元件，广泛应用于各种电气设备和电子产品中。

在电路中，电容器可以通过串联和并联的方式进行连接，以实现不同的电路功能和要求。

本文将探讨电容器的串联和并联关系，以及它们在电路中的应用。

一、电容器的串联关系串联是指将多个电容器连接起来，形成一个电容器组合，使它们共享同一电压。

当电容器串联时，其总电容值等于各个电容器的倒数之和的倒数。

这可以用以下公式表示：1/Ct = 1/C1 + 1/C2 + 1/C3 + ... + 1/Cn其中，Ct为串联后的总电容值，C1、C2、C3等分别为串联电容器的电容值。

电容器串联的电路示意图如下：[示意图]例如，我们有两个电容器，一个电容值为C1，另一个电容值为C2，它们串联后的总电容值为：1/Ct = 1/C1 + 1/C2当电容器的电压相同时，串联电容器的电荷量与其电容值成反比关系。

换句话说，串联电容器电荷量较小的电容器会接收较大的电荷量，而电荷量较大的电容器则会较少接收电荷量。

电容器串联的应用主要体现在电路中的滤波功能。

当电容器串联在电源和负载之间时，可以起到平滑电源输出、去除电源中的噪声和干扰的作用。

二、电容器的并联关系并联是指将多个电容器的正极相连，负极相连，形成一个电容器组合。

并联电容器的总电容值等于各个电容器的电容值之和。

这可以用以下公式表示：Ct = C1 + C2 + C3 + ... + Cn其中，Ct为并联后的总电容值，C1、C2、C3等分别为并联电容器的电容值。

电容器并联的电路示意图如下：[示意图]并联电容器具有共享电荷量的特点，即各个电容器蓄存的电荷量相等。

当并联电容器的电压不同时，各个电容器的电荷量与其电压成正比关系。

电容器并联的应用主要体现在电路中的储能和放电功能。

通过并联电容器，可以实现在电路断电或电源波动时提供电源续航功能，同时也可以提供稳定的放电电压和电流。

三、电容器串联与并联的比较电容器串联和并联的关系可以总结如下：1. 串联电容器的总电容值小于各个电容器的最小值，而并联电容器的总电容值等于各个电容器的电容值之和。

电容器的串并联电容器是电路中常见的元件之一，用于存储和释放电荷。

在电路设计和应用中，电容器的串并联是非常重要的概念，能够在电路中起到不同的作用。

本文将详细介绍电容器的串并联原理和应用实例。

一、电容器的串联串联是指将多个电容器按照一定顺序连接起来，共享相同的电流。

串联电容器的总电容为各个电容器的电容之和，即Ct = C1 + C2 + C3 + ... + Cn。

而串联电容器的总电压等于各个电容器电压之和，即Vt = V1 + V2 + V3 + ... + Vn。

在串联电容器中，电流在每个电容器之间是相等的，而电压在各个电容器之间是分配的。

例如，假设有三个电容器C1、C2、C3，并且它们的电容分别为4μF、6μF和8μF。

当它们串联连接后，总电容为18μF。

假设电压源为10V，在串联电容器中，电压会按照电容的比例分配。

根据该比例，C1的电压为(4/18)*10=2.22V，C2的电压为(6/18)*10=3.33V，C3的电压为(8/18)*10=4.44V。

串联电容器的应用主要体现在电容器的电压需求较高的场合。

由于串联电容器的总电压等于各个电容器电压之和，可以通过串联电容器来实现更高的电压容量。

比如在放大器电路中，为了提供更大的电压放大幅度，可以将多个较小电压的电容器串联连接起来。

二、电容器的并联并联是指将多个电容器的两端相连接，共享相同的电压。

并联电容器的总电容等于各个电容器电容的总和，即Ct = C1 + C2 + C3 + ... + Cn。

而并联电容器的总电压等于各个电容器电压之间的最大值，即Vt = max(V1, V2, V3, ... , Vn)。

例如，假设有三个电容器C1、C2、C3，并且它们的电容分别为10μF、15μF 和20μF。

当它们并联连接后，总电容为45μF。

而总电压等于其中电压最大的电容器的电压，即Vt = max(V1, V2, V3)。

并联电容器的应用主要体现在需要更大电容容量的场合。

电容器串联并联详解在电子电路中，电容器是一种常见且重要的元件。

电容器的串联和并联是两种基本的连接方式，它们对于电路的性能和功能有着重要的影响。

接下来，让我们详细了解一下电容器的串联和并联。

首先，我们来看看电容器的并联。

当两个或多个电容器并联连接时，它们的两端分别连接在一起。

这就意味着，每个电容器两端的电压是相同的。

假设我们有两个电容器 C1 和 C2 并联，它们的电容值分别为 C1 和C2，所加的电压为 V。

那么，总电容 C 总等于 C1 ＋ C2。

这是因为电容器并联时，电荷可以在各个电容器之间自由分配，相当于增加了存储电荷的能力。

举个例子，如果 C1 ＝2μF（微法），C2 ＝3μF，那么并联后的总电容就是2μF ＋3μF ＝5μF。

在实际应用中，如果需要增大电容值以存储更多的电荷，就可以采用并联电容器的方式。

电容器并联的一个重要特点是，它能够提高电路的滤波效果。

在电源电路中，并联多个电容器可以滤除不同频率的噪声和干扰，使输出的电压更加稳定。

接下来，我们再探讨一下电容器的串联。

当电容器串联时，它们是一个接一个地连接，电流依次通过每个电容器。

对于串联的电容器，总电容的计算就不像并联那么简单了。

假设我们有两个电容器 C1 和 C2 串联，那么总电容 C 总的倒数等于 C1 的倒数加上 C2 的倒数，即 1/C 总＝ 1/C1 ＋ 1/C2。

比如说，C1 ＝4μF，C2 ＝6μF，那么 1/C 总＝ 1/4 ＋ 1/6 ＝ 5/12，所以 C 总＝ 12/5 ＝24μF。

在串联电路中，每个电容器所存储的电荷量是相同的。

而总电压等于各个电容器两端电压之和。

电容器串联常用于分压电路中。

通过选择合适电容值的电容器串联，可以将输入的高电压按照一定比例分配到各个电容器上，从而得到所需的较低电压。

另外，电容器串联还可以改变电路的频率响应特性。

在一些高频或射频电路中，串联电容器可以起到选频、滤波等作用。

无论是电容器的串联还是并联，都需要根据具体的电路需求来选择合适的连接方式。

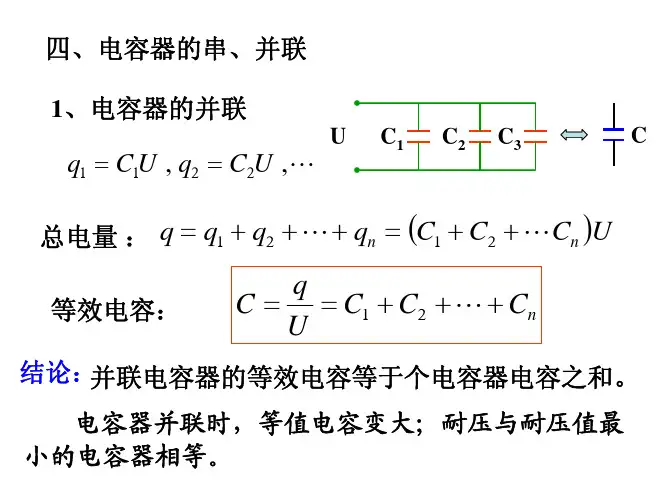
电容器并联时，相当于电极的面积加大，电容量也就加大了。

并联时的总容量为各电容量之和：C并＝C1＋C2＋C3＋……顺便说说电容器的串联。

若三个电容器串联后外加电压为U，则U＝U1＋U2＋U3＝Q1/C1＋Q2/C2＋Q3/C3，而电荷Q1＝Q2＝Q3＝Q，所以Q/C串＝（1/C1＋1/C2＋1/C3）Q1/C串＝1/C1＋1/C2＋1/C3可见，串联后总电容量减小。

电容器串联时，要并联阻值比电容器绝缘电阻小的电阻，使各电容器上的电压分配均匀，以免电压分配不均而损坏电容器。

又可知，电容的串、并联计算正好与电阻的串、并联计算相反。

电压是充电时的电压，容量与电流，电压的关系和功率相似，和负载有关，电压和容量为定量时，负载电阻越小，电流越大，时间越短电压和负载为定量时，容量越大，电流不变，时间越长但实际放电电路中，一般负载是不变的，电容的电压是逐渐下降的，电流也就逐渐下降。

1.电容量(uf)=电流(mA)/15限流电阻（Ω）=310/最大允许浪涌电流放电电阻（KΩ）=500/电容(uf)2.计算方式C=15×I C为电容容量单位微法i设备为工作电流单位为安如一个灯泡的电阻为0.6安电容就选择15×0.6＝9微法在电路里串连9微法的电容就可以了3.经验公式，1uF输出50mA（如果是线性的话，10000F的超级电容可以达到500兆安培的浪涌电流）还有4.半波整流方式计算应该是每uF电容量提供约30mA电流，这是在中国的50Hz220V线路上的参考。

全波整流时电流加倍，即每uF可提供60mA电流。

而我比较清楚的是，书本上的公式：R*C≥（3～5）*T/2,需要知道纹波成份中的频率最低信号的频率是多少（即最大的T)，然后来确定C的值。

电容的容量。

电容容量表示能贮存电能的大小。

电容对交流信号的阻碍作用称为容抗，容抗与交流信号的频率和电容量有关，容抗XC=1/2πf c (f表示交流信号的频率，C表示电容容量)。

电容器的串并联关系的计算与分析电容器是电子电路中常用的被动元件之一，其串并联关系在电路设计与分析中具有重要的作用。

掌握电容器的串并联关系可以帮助我们更好地理解和优化电路的性能。

本文将对电容器的串联和并联关系进行详细的计算和分析，并给出具体的实例说明。

一、电容器的串联关系在电路中，当两个或多个电容器的正电极相连形成一条路径，负电极也相连形成另一条路径时，我们称之为串联关系。

在串联关系下，电容器的总电容等于各个电容器电容的代数和。

设有两个电容器C1和C2，其电容分别为C1和C2，通过串联关系连接时，其总电容Ct可用以下公式计算：1/Ct = 1/C1 + 1/C2其中，Ct为串联后的总电容。

例如，若C1=10μF，C2=20μF，则其串联后的总电容Ct为：1/Ct = 1/10 + 1/20= 1/10 + 2/40= 4/40 + 2/40= 6/40= 1/6.67因此，串联后的总电容Ct为6.67μF。

二、电容器的并联关系在电路中，当两个或多个电容器的正电极相连，负电极也相连形成一条路径时，我们称之为并联关系。

在并联关系下，电容器的总电容等于各个电容器电容的代数和。

设有两个电容器C1和C2，其电容分别为C1和C2，通过并联关系连接时，其总电容Cp可用以下公式计算：Cp = C1 + C2其中，Cp为并联后的总电容。

例如，若C1=10μF，C2=20μF，则其并联后的总电容Cp为：Cp = 10 + 20= 30μF因此，并联后的总电容Cp为30μF。

三、实例分析现有一个电路，其中包含三个电容器C1、C2和C3，其电容分别为100μF、150μF和200μF。

根据给定的电路图，我们需要计算电容器的串并联关系。

首先，根据电路图可知C1和C2串联，然后与C3并联。

因此，我们可以先计算C1和C2的串联关系，然后再与C3的并联关系。

C12 = 1/(1/C1 + 1/C2)= 1/(1/100 + 1/150)= 1/(0.01 + 0.00667)= 1/0.01667= 60μF接下来，计算C12与C3的并联关系：Ctotal = C12 + C3= 60 + 200= 260μF因此，整个电容器组合的总电容为260μF。