下载文档原格式
机密★本科目考试启用前2023年北京市第一次普通高中学业水平合格性考试数 学 试 卷第一部分（选择题 共60分）一、选择题共20小题，每小题3分，共60分。
在每小题列出的四个选项中，选出符合题目要求的一项。
1．已知全集{}1,2,3,4U =，集合{}1,2A =，则U A =ð（ ） A ．{}1,3B ．{}2,3C ．{}1,4D ．{}3,42．不等式20x >的解集是（ ） A ．{}0x x =B ．{}0x x ≠C ．{}0x x >D ．{}0x x <3．函数()1f x x =-的零点是（ ） A ．－2B ．－1C ．1D ．24．在平面直角坐标系xOy 中，角α以O 为顶点，以Ox 为始边，终边经过点()1,1-，则角α可以是（ ） A ．4πB ．2π C ．34πD ．π5．已知三棱柱111ABC A B C -的体积为12，则三棱锥111A A B C -的体积为（ ） A ．3B ．4C ．6D ．86．已知1sin 2α=，则()sinα-=（ ） A ．12-B ．12C ．2-D ．27．lg100=（ ） A ．－100B ．100C ．－2D ．28．如图，点O 为正六边形ABCDEF 的中心，下列向量中，与OA 相等的是（ ） A ．DOB ．EOC ．FOD ．CO9．下列函数中，在R 上为增函数的是（ ） A ．()f x x =- B ．()2f x x =C ．()2xf x =D ．()cos f x x =10．已知向量()2,1a =，(),2b m =．若a b ∥，则实数m =（ ） A ．0B ．2C ．4D ．611．已知a ，b ∈R ，且2a b +=．当ab 取最大值时，（ ） A ．0a =，2b =B ．2a =，0b =C ．1a =，1b =D ．1a =-，3b =12．将函数2log y x =的图象向上平移1个单位长度，得到函数()y f x =的图象，则()f x =（ ） A ．()2log 1x +B ．21log x +C ．()2log 1x -D ．21log x -+13．四棱锥P ABCD -如图所示，则直线PC （ ） A ．与直线AD 平行 B ．与直线AD 相交 C ．与直线BD 平行D ．与直线BD 是异面直线14．在ABC △中，1a =，1b =，c =C ∠=（ ）A ．60°B ．75°C ．90°D ．120°15．已知a ，b ∈R ，则“0a b ==”是“0a b +=”的（ ） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件D ．既不充分也不必要条件16．向量a ，b 在正方形网格中的位置如图所示．若网格中每个小正方形的边长为1，则a b -=（ ）A ．2BC ．D ．317．已知函数()f x =()y f x =的图象经过原点，则()f x 的定义域为（ ）A ．[)0,+∞B ．[),0-∞C ．[)1,+∞D ．[),1-∞18．某银行客户端可通过短信验证码登录，验证码由0，1，2，…，9中的四个数字随机组成（如“0013”）．用户使用短信验证码登录该客户端时，收到的验证码的最后一个数字是奇数的概率为（ ） A ．12B ．14C ．18D ．11619．已知函数()21,022,0xx f x x x x ⎧⎛⎫≤⎪ ⎪=⎨⎝⎭⎪->⎩，则()f x 的最小值是（ ） A ．2B ．1C ．－2D ．－120．某校学生的体育与健康学科学年成绩s 由三项分数构成，分别是体育与健康知识测试分数a ，体质健康测试分数b 和课堂表现分数c ，计算方式为20%40%40%s a b c =⨯+⨯+⨯．学年成绩s 不低于85时为优秀，若该校4名学生的三项分数如下：则体育与健康学科学年成绩为优秀的学生是（ ） A ．甲和乙B ．乙和丙C ．丙和丁D ．甲和丁第二部分（非选择题 共40分）二、填空题共4小题，每小题3分，共12分。
2019年北京市第一次普通高中学业水平合格性考试地理试卷考生要认真填写考场号和座位序号。
本试卷共8页，分为两个部分。
第一部分为选择题，30个小题（共60分）；第二部分为非选择题，4个小题（共40分）。
试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。
第一部分必须用2B铅笔作答；第二部分必须用黑色字迹的签字笔作答。
考试结束后，考生应将试卷和答题卡按要求放在桌面上，待监考员收回。
第一部分选择题（共60分）下列各小题均有四个选项，其中只有一项是符合题意要求的。
读图1 “不同级别的天体系统示意图”，完成1〜2题。
1 •甲、乙、丙、丁代表的天体系统依次为A •总星系、银河系、太阳系、地月系B •太阳系、银河系、河外星系、地月系C •地月系、银河系、太阳系、总星系D •地月系、太阳系、银河系、总星系2 •以下叙述符合事实的是A •地球是太阳系中的一颗行星B .日地平均距离约1.5千米C •月球是地球的一颗人造卫星D •太阳系处于银河系的中心《汉书•五行志》中记载：“日出黄，有黑气大如钱，居日中央”。
据此完成3〜4题。
3•文中记载的现象是A. 耀斑 B .日食 C .日珥D.黑子4.该现象增多时，对地球的影响是A •地表温度明显上升B •干扰无线电短波通信考1.2.生须3.知4.C .全球频发强烈地震D .大气逆辐射作用增强5•对各圈层位置的正确描述是A. 生物圈位于地壳内部B. 地核位于莫霍面以上C .软流层位于岩石圈的内部D .地幔位于地壳和地核之间6. 关于图中各圈层特点的正确叙述是A .岩石圈由厚度相同的岩石组成B .水圈是连续但不规则的圈层C .地壳是厚度最大的地球圈层D .大气圈的组成物质分布均匀臭氧层是大气层中臭氧浓度较高的区域，主要位于距离地面约外线，保护人类健康。
读图 3 “大气垂直分层示意图”7. 臭氧层主要分布在大气垂直分层中的A .对流层B .平流层C .中间层D .热层8. 对流层的主要特点是A .位于地球大气的最外层B .极光现象出现在该层C .气温随高度上升而降低D .空气以水平运动为主20〜30千米的高空，它能有效吸收紫图49.近地面大气的主要直接热源是A .①B .②C. ③D. ④10.图中⑤表示大气的A .吸收作用B .反射作用C. 保温作用D.辐射作用11.倡导低碳生活，减少CO排放可以使A .①增强B .③减弱C. ④减弱D. ⑤增强，完成7〜8题。
2019年北京市第一次普通高中学业水平合格性考试数学试卷第一部分选择题(每小题3分,共81分)在每个小题给出的四个备选答案中,只有一个是符合题目要求的.1.已知集合A ={0,1},B ={-1,1},那么A ∪B 等于A .{0,1}B .{-1,1}C .{0}D .{-1,1,0}2.已知向量a =(1,1), b =(1,2),那么a +b 等于A .(0,-1)B .(1,2)C .(2,3)D .(3,2)3.过点A (3,0)和B (0,2)的直线的方程为A .2x -3y -6=0B .3x +2y -4=0C .2x +3y -6=0D .x +2y -4=04.函数y =()lg 2x +的定义域是A .[2,+∞)B .(2, +∞)C .(0,+∞)D .(-2, +∞)5.如果幂函数f (x )=x a 的图象经过点(4,2),那么a 的值是A .-2B .2C .12-D .126.在空间直角坐标系O -xyz 中,A (-1,-1,-1),B (1,1,1),那么|AB |等于A .2 BCD7.2018年10月24日,我国超级工程——港珠澳大桥正式通车运营,它是世界上最长的跨海大桥,全长55千米,采用Y 型线路,连接香港、珠海和澳门三地.如果从甲、乙、丙三位同学中任选一位同学前往港珠澳大桥参观,那么甲同学被选中的概率为A . 13B .12C .23D .18.为深入贯彻落实《国务院办公厅关于强化学校体育促进学生身心健康全面发展的意见》,我市提出:到2020年,全市义务教育阶段学生体质健康合格率达到98%，基础教育阶段学生优秀率达到15%以上.某学校现有小学和初中学生共2000人,为了解学生的体质健康合格情况,决定采用分层抽样的方法从全校学生中抽取一个容量为400的样本,其中被抽到的初中学生人数为180,那么这所学校的初中学生人数为 （ ）A .800B .900C .1000D .11009.化简()sin απ+为A .-sin αB .sin αC .-cos αD .cos α10.如果直线2x -y =0与直线x +my -1=0垂直,那么m 的值为A .-2B .12-C .12D .2 11.已知向量a =(2,-1), b =(1,m ),且a =2b ,那么m 的值为A .-2B .12-C .12D .2 12.直线x+1=0的倾斜角的度数是A .30°B .45°C .60°D .90°13.已知直线l 经过点P (1,1),且与直线x -y +2=0平行,那么直线l 的方程为A .x -y -2=0B .x +y -2=0C . x -y =0D .x +y -4=014.函数零点的涵义是A .一个点B .函数图象与x 轴的交点的横坐标C .函数图象与x 轴的交点D .函数图象与y 轴的交点的纵坐标15.在函数y =1x ,y =x 2,y =2x ,y =3log x 中,奇函数是 A . y =1xB . y =x 2C . y =2xD .y =3log x 16.在相距4千米的A ,B 两点分别观测目标点C ,如果∠CAB =75°,∠CBA =60°,那么A ,C 两点间的距离是AB千米 C千米 D千米17.已知角a 的终边经过点P (5,12),那么sin α的值是A .512B . 125C .513D .121318.已知直线l :x +y +2=0和圆C :(x -1)2+(y +1)2=1,那么圆心C 到直线l 的距离是A .12B .1 CD .219.函数f (x )=22sin x 的最小正周期是A .2π B .πC .2πD .4π 20.计算(14)0+2log 2的结果为 A .3 B .54 C .2 D .1 21.已知两条直线m ,n 和平面a ,且m ⊥a ,要得到结论m ∥n ,还需要添加一个已知条件,这个条件应是①n ⊥a ,②n ∥a ,③n ⊂a ,④n ⊄a 中的A .①B .②C .③D .④22.已知函数f (x )=1020x x x ⎧⎨-⎩，≥，＜,如果f (m )=4,那么实数m 的值为A .1B .-2C .-8D .12-23.将函数y =2sin x 的图象向左平移6π个单位,所得图象的函数表达式是 A .y =2sin 6x π⎛⎫+ ⎪⎝⎭ B . y =2sin 6x π⎛⎫- ⎪⎝⎭ C . y =sin 26x π⎛⎫- ⎪⎝⎭ D . y =sin 26x π⎛⎫+ ⎪⎝⎭ 24.在△ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c ,如果b =1,cB =30°,那么角A 的度数是A .30°或60°B .45°或60°C .30°或90°D .45°或120°25.如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F 分别为棱AB ,C 1D 1上的动点,那么三棱锥F -CDE 的体积为A .16 B .13 C .12 D .2326.已知边长为3的正方形ABCD ,点E 满足=2DE EC ,那么AE AC ⋅等于A .6B .9C .12D .1527.党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,作出了新的部署.某地区现有28万农村贫困人口,如果计划在未来3年时间内完成脱贫任务,并且后一年的脱贫任务是前一年任务的一半,为了按时完成脱贫攻坚任务,那么第一年需要完成的脱贫任务是A .10万人B .12万人C .14万人D .16万人第二部分 解答题 (共19分)28.(本小题满分5分)某同学解答一道三角函数题:“已知函数f (x )=2sin 6x πω⎛⎫+⎪⎝⎭,ω>0,其最小正周期为π.(I )求f (0)和ω的值；(Ⅱ)求函数f (x )在区间[6π-，3π]上的最小值及相应x 的值.”下表列出了某些数学知识:29.(本小题满分5分)阅读下面题目及其证明过程,在①~⑤处填写适当的内容.已知三棱柱ABC-A1B1C1,AA1⊥平面ABC，∠BAC=90°,E,F分别为AB1,CB1的中点.(Ⅰ)求证:EF∥平面ABC；(Ⅱ)求证:AB⊥A1C.解答: (Ⅰ)证明:在△AB1C中,因为E,F分别为AB1,CB1的中点,所以①因为EF⊄平面ABC,AC⊂平面ABC,所以EF∥平面ABC.(Ⅱ)证明:因为AA1⊥平面ABC,AB⊂平面ABC,所以② .因为∠BAC=90°,所以AB⊥AC.又因为AC∩AA1=A,所以③因为A1C⊂平面AA1C1C,所以AB⊥A1C.上述证明过程中,第(I)问的证明思路是先证“线线平行”,再证线面平行”；第(Ⅱ)问的证明思路是先证④ ,再证⑤ ,最后证“线线垂直”.30.(本小题满分5分)某同学解答一道解析几何题:“已知圆O：x2+y2=r2(r＞0) 与直线l1：x=-2和l2：x=2分别相切,点C的坐标为(-1,0).A,B两点分别在直线l1和l2上,且AC⊥BC ,|AC|=|BC|,试推断线段AB的中点是否在圆O 上.”该同学解答过程如下AC⊥BC,点C⋅=0,即AC BC|AC|=|BC|,219m+=化简得:m2-n2=8.②由①②可得8mn=-24,3因式分解得(3m-n)(请指出上述解答过程中的错误之处,并写出正确的解答过程.31.(本小题满分4分)从2008年开始的十年间,中国高速铁路迅猛发展,已经建成“四纵四横”网络,“八纵八横”格局正在构建.到2018年,中国高速铁路新里程已超过两万五千千米,铸就了一张新的“国家名片”.京沪高速铁路线是北京南站到上海虹桥站之间的一条高速铁路线,全长约1318km.某机构研究发现:高速列车在该线路上单程运行一次的总费用f(x)(万元)与平均速度x(km/h)及其它费用a(3≤a≤4)(万元)之间近似满足函数关系f(x)=1318ax+0.0006x2(200≤x≤400).问:当高速列车在该线路上运行的平均速度是多少时,单程运行一次总费用最小?。
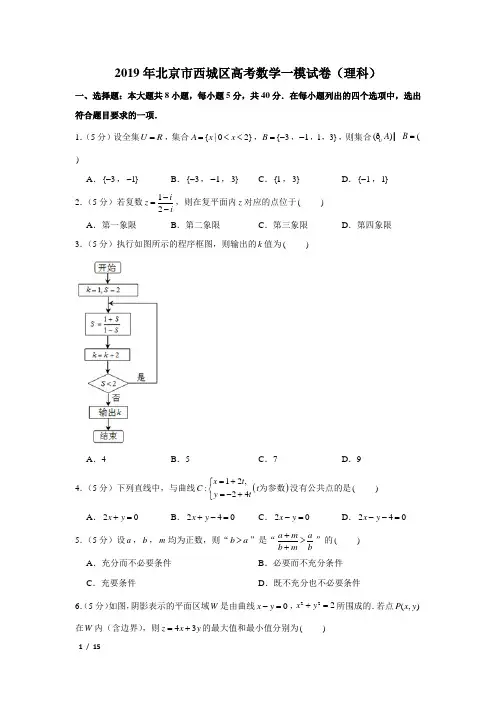
2019年北京市西城区高考数学一模试卷（理科）一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）设全集U R =，集合{|02}A x x =<<，{3B =-，1-，1，3}，则集合()(U A B =I ð)A ．{3-，1}-B ．{3-，1-，3}C ．{1，3}D ．{1-，1}2．（5分）若复数12iz i-=-，则在复平面内z 对应的点位于( ) A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．（5分）执行如图所示的程序框图，则输出的k 值为( )A ．4B ．5C ．7D ．94．（5分）下列直线中，与曲线()12,:24x t C t y t =+⎧⎨=-+⎩为参数没有公共点的是( )A ．20x y +=B ．240x y +-=C ．20x y -=D ．240x y --=5．（5分）设a ，b ，m 均为正数，则“b a >”是“a m ab m b+>+”的( ) A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件6．（5分）如图，阴影表示的平面区域W 是由曲线0x y -=，222x y +=所围成的．若点(,)P x y 在W 内（含边界），则43z x y =+的最大值和最小值分别为( )A ．527-B ．5252-C ．7，52-D ．7，7-7．（5分）团体购买公园门票，票价如表： 购票人数 1~5051~100100以上 门票价格13元/人 11元/人9元/人现某单位要组织其市场部和生产部的员工游览该公园，若按部门作为团体，选择两个不同的时间分别购票游览公园，则共需支付门票费为1290元；若两个部门合在一起作为一个团体，同一时间购票游览公园，则需支付门票费为990元，那么这两个部门的人数之差为( ) A ．20B ．30C ．35D ．408．（5分）如果把一个平面区域内两点间的距离的最大值称为此区域的直径，那么曲线422x y +=围成的平面区域的直径为( ) A 432B ．3C ．22D ．4二、填空题：本大题共6小题，每小题5分，共30分．9．（5分）在等比数列{}n a 中，21a =，58a =，则数列{}n a 的前n 项和n S = ．10．（5分）设1F ，2F 为双曲线2222:1(0,0)x y C a b a b-=>>的两个焦点，若双曲线C 的两个顶点恰好将线段12F F 三等分，则双曲线C 的离心率为 ．11．（5分）函数()sin 2cos2f x x x =+的最小正周期T = ；如果对于任意的x R ∈都有()f x a …，那么实数a 的取值范围是 ．12．（5分）某四棱锥的三视图如图所示，那么该四棱锥的体积为 ．13．（5分）能说明“若sin cos αβ=，则36090k αβ+=︒+︒g ，其中k Z ∈”为假命题的一组α，β的值是 ．14．（5分）如图所示，玩具计数算盘的三档上各有7个算珠，现将每档算珠分为左右两部分，左侧的每个算珠表示数2，右侧的每个算珠表示数1（允许一侧无珠），记上、中、下三档的数字和分别为a ，b ，c ．例如，图中上档的数字和9a =．若a ，b ，c 成等差数列，则不同的分珠计数法有 种．三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤．15．（13分）在ABC ∆中，已知222a c b mac +-=，其中m R ∈． （Ⅰ）判断m 能否等于3，并说明理由； （Ⅱ）若1m =-，27b =4c =，求sin A ．16．（14分）如图，在多面体ABCDEF 中，梯形ADEF 与平行四边形ABCD 所在平面互相垂直，//AF DE ，DE AD ⊥，AD BE ⊥，112AF AD DE ===，2AB = （Ⅰ）求证：//BF 平面CDE ； （Ⅱ）求二面角B EF D --的余弦值；（Ⅲ）判断线段BE 上是否存在点Q ，使得平面CDQ ⊥平面BEF ？若存在，求出BQBE的值，若不存在，说明理由．17．（13分）为培养学生的阅读习惯，某校开展了为期一年的“弘扬传统文化，阅读经典名著”活动．活动后，为了解阅读情况，学校统计了甲、乙两组各10名学生的阅读量（单位：本），统计结果用茎叶图记录如下，乙组记录中有一个数据模糊，无法确认，在图中以a 表示．（Ⅰ）若甲组阅读量的平均值大于乙组阅读量的平均值，求图中a 的所有可能取值； （Ⅱ）将甲、乙两组中阅读量超过15本的学生称为“阅读达人”．设3a =，现从所有“阅读达人”里任取3人，求其中乙组的人数X 的分布列和数学期望．（Ⅲ）记甲组阅读量的方差为20s ．在甲组中增加一名学生A 得到新的甲组，若A 的阅读量为10，则记新甲组阅读量的方差为21s ；若A 的阅读量为20，则记新甲组阅读量的方差为22s ，试比较20s ，21s ，22s 的大小．（结论不要求证明）18．（13分）设函数2()3x f x me x =-+，其中m R ∈． （Ⅰ）当()f x 为偶函数时，求函数()()h x xf x =的极值；（Ⅱ）若函数()f x 在区间[2-，4]上有两个零点，求m 的取值范围．19．（14分）已知椭圆22:14x y W m m+=的长轴长为4，左、右顶点分别为A ，B ，经过点(,0)P n 的直线与椭圆W 相交于不同的两点C ，D （不与点A ，B 重合）． （Ⅰ）当0n =，且直线CD x ⊥轴时，求四边形ACBD 的面积；（Ⅱ）设1n =，直线CB 与直线4x =相交于点M ，求证：A ，D ，M 三点共线．20．（13分）如图，设A 是由(2)n n n ⨯…个实数组成的n 行n 列的数表，其中(ij a i ，1j =，2，⋯，)n 表示位于第i 行第j 列的实数，且{1ij a ∈，1}-．定义1122(st s t s t sn tn p a a a a a a s =++⋯+，1t =，2，⋯，)n 为第s 行与第t 行的积．若对于任意s ，()t s t ≠，都有0st p =，则称数表A 为完美数表．（Ⅰ）当2n =时，试写出一个符合条件的完美数表； （Ⅱ）证明：不存在10行10列的完美数表；（Ⅲ）设A 为n 行n 列的完美数表，且对于任意的1i =，2，⋯，l 和1j =，2，⋯，k ，都有1ij a =，证明：kl n „．2019年北京市西城区高考数学一模试卷（理科）参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．【解答】解：根据题意，全集U R =，集合{|02}A x x =<<，则{|0U A x x =„ð或2}x … 又由{3B =-，1-，1，3}，则集合(){3U A B =-I ð，1-，3}； 故选：B ． 【解答】解：Q 1(1)(2)312(2)(2)55i i i z i i i i --+===---+， ∴在复平面内z 对应的点的坐标为31(,)55-，位于第四象限．故选：D ．【解答】解：当1k =时，12312S +==--，3k =，2S <成立， 1(3)11(3)2S +-==---，5k =，2S <成立，11121312S -==+，7k =，2S <成立， 1132113S +==-，9k =，2S <不成立， 输出，9k =， 故选：D ．【解答】解：曲线C 参数方程为：()12,24x t t y t =+⎧⎨=-+⎩为参数，①2⨯-②得，240x y --=，故曲线C 为斜率为2的直线，选项中斜率为2的直线为C ，D ． 而D 与曲线C 重合，有无数个公共点，排除． 故选：C ．【解答】解：a Q ，b ，m 均为正数，∴由a m ab m b+>+得()()b a m a b m +>+， 即ab bm ab am +>+，即bm am >，m Q 是正数，b a ∴>，成立，即“b a >”是“a m ab m b+>+”的充要条件， 故选：C ．【解答】解：由题意可知直线平移直线043x y =+，当直线经过A 上取得最小值，平移到与222x y +=相切于B 时，取得最大值，(1,1)B --，最小值为：7-；由22243x y x y z⎧+=⎨+=⎩可得：22258180x zx z -+-=，△22644(8)250z z =--⨯=，解得52z =，52z =-（舍去）， 所以则43z x y =+的最大值和最小值分别为：52；7-． 故选：A ．【解答】解：990Q 不能被13整除，∴两个部门人数之和：51a b +…， （1）若51100a b +剟，则11 ()990a b +=得：90a b +=，① 由共需支付门票费为1290元可知，11131290a b +=② 解①②得：150b =，60a =-，不符合题意．（2）若100a b +…，则9 ()990a b +=，得110a b +=③ 由共需支付门票费为1290元可知，150a 剟，51100b 剟， 得11131290a b +=④， 解③④得：70a =人，40b =人故两个部门的人数之差为704030-=人， 故选：B ．【解答】解：曲线422x y +=围成的平面区域，关于x ，y 轴对称，设曲线上的点(,)P x y ，可得2222913||()422OP x y x =+=--„． 所以曲线422x y +=围成的平面区域的直径为：3． 故选：B ．二、填空题：本大题共6小题，每小题5分，共30分． 【解答】解：21a =Q ，58a =352a a q ∴=， 即3528a q a ==，即2q =， 首项112a =， 则数列{}n a 的前n 项和11(12)122122n n n S --==--，故答案为：1122n --．【解答】解：双曲线C 的两个顶点恰好将线段12F F 三等分， 可得1223a c =g ，则3c a =，即3ce a==． 故答案为：3．【解答】解：()sin 2cos22)4f x x x x π=+=+，即函数的周期22T ππ==， 若对于任意的x R ∈都有()f x a „， 则()max a f x …，即当sin(2)14x π+=时，()f x 2即()2max f x =， 则2a …，故答案为：π，2a …．【解答】解：几何体的直观图如图：是长方体的一部分， 长方体的棱长为：2，1，2， 四棱锥的体积为：1412233⨯⨯⨯=．故答案为：43．【解答】解：若sin cos αβ=，则36090()k k Z αβ=︒+︒±∈g ，命题中36090k αβ=︒+︒-g ，()k Z ∈，要否定命题，只须从36090()k k Z αβ=︒+︒+∈g 中找一个反例即可，如110α=︒，20β=︒，（答案不唯一，再如120α=︒，30β=︒等，只要满足36090()k k Z αβ=︒+︒+∈g 且36090()k k Z αβ≠︒+︒-∈g 即可作为反例．故填：110α=︒，20β=︒．【解答】解：根据题意，a ，b ，c 的取值范围都是从7~14共8个数字，故公差d 范围是3-到3，①当公差0d =时，有188C =种， ②当公差1d =±时，b 不取7和14，有16212C ⨯=种， ③当公差2d =±时，b 不取7，8，13，14，有1428C ⨯=种， ④当公差3d =±时，b 只能取10或11，有1224C ⨯=种， 综上共有8128432+++=种， 故填：32三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤．【解答】解：（Ⅰ）当3m =时，由题可知2223a c b ac +-=， 由余弦定理2222cos b a c ac B =+-，（3分）得2223cos 22a cb B ac +-==． ⋯⋯⋯⋯（4分）这与cos [1B ∈-，1]矛盾，所以m 不可能等于3．⋯⋯⋯（6分） （Ⅱ）由（Ⅰ），得1cos 22m B ==-，所以23B π=．⋯⋯（7分）因为b =4c =，222a c b ac +-=-， 所以216284a a +-=-，解得6a =-（舍)或2a =．⋯⋯⋯⋯⋯⋯（9分） 在ABC ∆中，由正弦定理sin sin a bA B=，⋯⋯⋯⋯⋯⋯（11分）得sin sina B Ab ===．（13分） 【解答】解：（Ⅰ）由底面ABCD 为平行四边形，知//AB CD ， 又因为AB ⊂/平面CDE ，CD ⊂平面CDE ， 所以//AB 平面CDE ．⋯⋯⋯⋯⋯⋯（2分） 同理//AF 平面CDE ， 又因为AB AF A =I ，所以平面//ABF 平面CDE ．⋯⋯⋯⋯⋯（3分） 又因为BF ⊂平面ABF ，所以//BF 平面CDE ．⋯⋯⋯⋯⋯⋯（4分） （Ⅱ）连接BD ，因为平面ADEF ⊥平面ABCD ，平面ADEF ⋂平面ABCD AD =，DE AD ⊥， 所以DE ⊥平面ABCD ．则DE DB ⊥． 又因为DE AD ⊥，AD BE ⊥，DE BE E =I ， 所以AD ⊥平面BDE ，则AD BD ⊥．故DA ，DB ，DE 两两垂直，所以以DA ，DB ，DE 所在的直线分别为x 轴、y 轴和z 轴，如图建立空间直角坐标系，⋯⋯⋯⋯⋯⋯（6分）则(0D ，0，0)，(1A ，0，0)，(0B ，1，0)，(1C -，1，0)，(0E ，0，2)，(1F ，0，1)， 所以(0,1,2)BE =-u u u r ，(1,0,1)EF =-u u u r ，(0n =r，1，0)为平面DEF 的一个法向量．设平面BEF 的一个法向量为(m x =r，y ，)z ，由0m BE =u u u r r g ，0m EF =u u ur r g ，得20,0,y z x z -+=⎧⎨-=⎩令1z =，得(1m =r，2，1)．⋯⋯⋯⋯⋯⋯（8分）所以cos m <r，6||||m n n m n >==r rg r r r ．如图可得二面角B EF D --为锐角， 所以二面角B EF D --6⋯⋯⋯⋯⋯⋯（10分） （Ⅲ）结论：线段BE 上存在点Q ，使得平面CDQ ⊥平面BEF ．⋯⋯⋯⋯⋯⋯（11分） 证明如下：设(0,,2)([0,1])BQ BE λλλλ==-∈u u u r u u u r， 所以(0,1,2)DQ DB BQ λλ=+=-u u u r u u u r u u u r．设平面CDQ 的法向量为(u a =r，b ，)c ，又因为(1,1,0)DC =-u u u r ， 所以0u DQ =u u u r r g ，0u DC =u u ur r g ，即(1)20,0,b c a b λλ-+=⎧⋯⋯⋯⋯⋯⋯⎨-+=⎩（12分） 若平面CDQ ⊥平面BEF ，则0m u =r rg ，即20a b c ++=，⋯⋯⋯⋯⋯⋯（13分） 解得1[0,1]7λ=∈．所以线段BE 上存在点Q ，使得平面CDQ ⊥平面BEF ，且此时17BQ BE =．⋯⋯（14分） 【解答】（本小题满分13分）解：（Ⅰ）甲组10名学生阅读量的平均值为12681011121217211010+++++++++=，乙组10名学生阅读量的平均值为124412131616(10)20981010a a+++++++++++=． ⋯⋯⋯⋯⋯⋯（2分）由题意，得981010a+>，即2a <．⋯⋯⋯⋯⋯⋯（3分） 故图中a 的取值为0或1．⋯⋯⋯⋯⋯⋯（4分）（Ⅱ）由图可知，甲组“阅读达人”有2人，乙组“阅读达人”有3人． 由题意，随机变量X 的所有可能取值为：1，2，3．⋯⋯⋯⋯⋯⋯（5分）且2123353(1)10C C P X C ===g ，1223353(2)5C C P X C ===g ，33351(3)10C P X C ===．⋯⋯（8分） 所以随机变量X 的分布列为：⋯⋯⋯⋯⋯⋯（9分）所以3319()123105105E X =⨯+⨯+⨯=．⋯⋯⋯⋯⋯⋯（10分） （Ⅲ）222102s s s <<．⋯⋯⋯⋯⋯⋯（13分）【解答】（本小题满分13分）解：（Ⅰ）由函数()f x 是偶函数，得()()f x f x -=， 即22()33x x me x me x ---+=-+对于任意实数x 都成立， 所以0m =．⋯⋯⋯⋯⋯⋯（2分）此时3()()3h x xf x x x ==-+，则2()33h x x '=-+． 由()0h x '=，解得1x =±．⋯⋯⋯⋯⋯⋯（3分） 当x 变化时，()h x '与()h x 的变化情况如下表所示：所以()h x 在(,1)-∞-，(1,)+∞上单调递减，在(1,1)-上单调递增．⋯⋯⋯⋯⋯（5分） 所以()h x 有极小值(1)2h -=-，()h x 有极大值h （1）2=．⋯⋯⋯⋯⋯⋯（6分）（Ⅱ）由2()30xf x me x =-+=，得23x x m e-=．所以“()f x 在区间[2-，4]上有两个零点”等价于“直线y m =与曲线23()xx g x e -=，[2x ∈-，4]有且只有两个公共点”． ⋯⋯⋯⋯⋯⋯（8分） 对函数()g x 求导，得223()xx x g x e -++'=．⋯⋯⋯⋯⋯⋯（9分）由()0g x '=，解得11x =-，23x =．⋯⋯⋯⋯⋯⋯（10分） 当x 变化时，()g x '与()g x 的变化情况如下表所示：所以()g x 在(2,1)--，(3,4)上单调递减，在(1,3)-上单调递增．⋯⋯⋯⋯⋯（11分） 又因为2(2)g e -=，(1)2g e -=-，36(3)(2)g g e =<-，413(4)(1)g g e=>-， 所以当4132e m e -<<或36m e=时，直线y m =与曲线23()xx g x e -=，[2x ∈-，4]有且只有两个公共点． 即当4132e m e -<<或36m e=时，函数()f x 在区间[2-，4]上有两个零点．⋯⋯（13分） 【解答】（本小题满分14分）解：（Ⅰ）由题意，得244a m ==，解得1m =．⋯⋯⋯⋯⋯⋯（2分）所以椭圆W 方程为2214x y +=．⋯⋯⋯⋯⋯⋯（3分）当0n =，及直线CD x ⊥轴时，易得(0,1)C ，(0,1)D -．且(2,0)A -，(2,0)B ． 所以||4AB =，||2CD =，显然此时四边形ACBD 为菱形，所以四边形ACBD 的面积为14242⨯⨯=．⋯⋯（5分）（Ⅱ）当直线CD 的斜率k 不存在时，由题意，得CD 的方程为1x =，代入椭圆W 的方程，得C ，(1,D ，易得CB的方程为2)y x =-．则(4,M，(6,AM =u u u u r，(3,AD =u u u r ，所以2AM AD =u u u u r u u u r，即A ，D ，M 三点共线．⋯⋯⋯⋯⋯⋯（7分）当直线CD 的斜率k 存在时，设CD 的方程为(1)(0)y k x k =-≠，1(C x ，1)y ，2(D x ，2)y ，联立方程22(1),1,4y k x x y =-⎧⎪⎨+=⎪⎩消去y ，得2222(41)8440k x k x k +-+-=．⋯⋯⋯（9分） 由题意，得△0>恒成立，故2122841k x x k +=+，21224441k x x k -=+．⋯⋯⋯⋯⋯（10分）直线CB 的方程为11(2)2yy x x =--．令4x =，得112(4,)2y M x -．⋯⋯⋯⋯⋯⋯（11分）又因为(2,0)A -，2(D x ，2)y ， 则直线AD ，AM 的斜率分别为222AD y k x =+，113(2)AM y k x =-，⋯⋯⋯⋯⋯（12分） 所以21211221123(2)(2)23(2)3(2)(2)AD AM y y y x y x k k x x x x --+-=-=+--+． 上式中的分子22211221121212224483(2)(2)3(1)(2)(1)(2)25()82584141k k y x y x k x x k x x kx x k x x k k k kk k ---+=----+=-++=⨯-⨯+++，所以0AD AM k k -=．所以A ，D ，M 三点共线．⋯⋯⋯⋯⋯⋯（14分） 【解答】（Ⅰ）解：由题意，可写出如下的完美数表：此时，12112112221(1)110p a a a a =+=⨯-+⨯=，∴此完美数表符合条件．（Ⅱ）证明：假设存在10行10列的完美数表A ． 根据完美数表的定义，可以得到以下两个结论：（1）把完美数表的任何一列的数变为其相反数（即1+均变为1-，而1-均变为1)+，得到的新数表是完美数表；（2）交换完美数表的任意两列，得到的新数表也是完美数表． 完美数表A 反复经过上述两个结论的变换，前三行可以为如下形式：在这个新数表中，设前三行中的数均为1的有x 列，前三行中“第1，2行中的数为1，且第3行中的数为1-”的有y 列，前三行中“第1，3行中的数为1，且第2行中的数为1-”的有z 列，前三行中“第1行中的数为1，且第2，3行中的数为1-”的有w 列（如上表所示），则10x y z w +++=①由120p =，得x y z w +=+； ② 由130p =，得x z y w +=+； ③ 由230p =，得x w y z +=+．④解方程组①，②，③，④，得52x y z w ====． 这与x ，y ，z ，w N ∈矛盾， 所以不存在10行10列的完美数表．（Ⅲ）证明：记第1列前l 行中的数的和112111l a a a X ++⋯+=，第2列前l 行中的数的和122222l a a a X ++⋯+=，⋯⋯，第n 列前l 行中的数的和12n n ln n a a a X ++⋯+=， Q 对于任意的1i =，2，⋯，l 和1j =，2，⋯，k ，都有1ij a =，∴12k X X X l ==⋯==．又Q 对于任意s ，()t s t ≠，都有0st p =，∴22212n X X X ln ++⋯+=． 又Q 22222221212n k X X X X X X l k ++⋯+++⋯+=…， 2ln l k ∴…，即kl n „．。
2019年北京市高考数学一模试卷(理科)(解析版)2019年北京市高考数学一模试卷（理科）一、选择题共8个小题，每小题5分，共40分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.已知复数z=i（1+i），则|z|等于（）A。
2B。
√2C。
1D。
2√22.在方程r=2cosθ+3sinθ（θ为参数）所表示的曲线上的点是（）A。
(2.-7)B。
(3.1)C。
(1.5)D。
(2.1)3.设公差不为零的等差数列{an}的前n项和为Sn，若a4=2(a2+a3)，则Sn=（）A。
5anB。
6anC。
7anD。
14an4.将函数y=sin2x的图象向左平移π/4个单位后得到函数y=g(x)的图象。
则函数g(x)的一个增区间是（）A。
(π/4.3π/4)B。
(3π/4.5π/4)C。
(5π/4.7π/4)D。
(7π/4.9π/4)5.使“a>b”成立的一个充分不必要条件是（）A。
a>b+1B。
a>b-1C。
a^2>b^2D。
a^3>b^36.下列函数：①y=-|x|；②y=(x-1)^3；③y=log2(x-1)；④y=-6.在x中，在(1.+∞)上是增函数且不存在零点的函数的序号是（）A。
①④B。
②③C。
②④D。
①③④7.某三棱锥的正视图和侧视图如图所示，则该三棱锥的俯视图的面积为（）A。
6B。
8C。
10D。
128.远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”，如图所示的是一位母亲记录的孩子自出生后的天数，在从右向左依次排列的不同绳子上打结，满七进一，根据图示可知，孩子已经出生的天数是（）A。
336B。
510C。
1326D。
3603二、填空题共6小题，每小题5分，共30分。
9.在(1-x)^5的展开式中，x^2的系数为______（用数字作答）。
答案：1010.已知向量a=(1.b)。
b=(-2.-1)，且向量a+b的模长为√10.则实数x=______。
西城区九年级统一测试数学试卷一、选择题（本题共16分，每小题2分）1.下列图形中，是圆锥的侧面展开图的为（ ）A. B. C. D.【答案】B 【解析】 【分析】根据圆锥的侧面展开图的特点作答．【详解】圆锥的侧面展开图是光滑的曲面，没有棱，只是扇形． 故选B ．【点睛】考查了几何体的展开图，圆锥的侧面展开图是扇形．2.实数a,b,c 在数轴上的对应点的位置如图所示，则正确的结论是（ ）A. a b >B. 0a b +>C. 0ac >D. a c >【答案】D 【解析】 【分析】根据数轴的特点：判断a 、b 、c 正负性，然后比较大小即可． 【详解】根据数轴的性质可知：a ＜b ＜0＜c ，且|c|＜|b|＜|a|； 所以a ＞b ，0a b +>，ac ＞0错误；|a|＞|c|正确； 故选D ．【点睛】本题考查实数与数轴的关系，关键是根据实数在数轴上的位置判断字母的正负性，根据实数在数轴上离原点的距离判断绝对值的大小．3.方程组20529x y x y -=⎧⎨+=⎩的解为（ ）A. 17x y =-⎧⎨=⎩B. 36x y =⎧⎨=⎩C. 12x y =⎧⎨=⎩D. 12x y =-⎧⎨=⎩【答案】C 【解析】 【分析】方程组利用加减消元法求出解即可．【详解】20529x y x y -=⎧⎨+=⎩①②，①×2+②得：9x=9，即x=1， 把x=1代入①得：y=2，则方程组的解为12x y =⎧⎨=⎩，故选C ．【点睛】此题考查了解二元一次方程组，熟练掌握运算法则是解本题的关键．4.如图，点D 在BA 的延长线上，AE BC ∕∕.若100DAC ∠=︒，65B ∠=︒，则EAC ∠的度数为（ ）A. 65︒B. 35︒C. 30°D. 40︒【答案】B 【解析】 【分析】由图可得∠EAC=∠DAC-∠DAE ，先根据平行线的性质得到∠DAE 的度数，即可得出∠EAC 的度数． 【详解】∵AE ∥BC ， ∴∠B=∠DAE=65°，又∵∠DAC=100°，∴∠EAC=∠DAC-∠DAE=100°-65°=35°， 故选B ．【点睛】本题主要考查了平行线的性质，解题时注意：两直线平行，同位角相等．5.广阔无垠的太空中有无数颗恒星，其中离太阳系最近的一颗恒星称为“比邻星”，它距离太阳系约4.2光年.光年是天文学中一种计量天体时空距离的长度单位，1光年约为9500000000000千米.则“比邻星”距离太阳系约为（ ） A. 13410⨯千米 B. 12410⨯千米 C. 139. 510⨯千米 D. 129. 510⨯千米【答案】A 【解析】 【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n 是正数；当原数的绝对值＜1时，n 是负数．【详解】9 500 000 000 000×4.2=39900000000000≈40000000000000=4×1013． 故选A ．【点睛】此题主要考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值．6.如果2310a a ++=，那么代数式229263a aa a ⎛⎫++⋅ ⎪+⎝⎭的值为（ ）A. 1B. 1-C. 2D. 2-【答案】D 【解析】 【分析】根据分式的加法和乘法可以化简题目中的式子，然后根据a 2+3a+1=0，即可求得所求式子的值．【详解】229263a a a a ⎛⎫++⋅ ⎪+⎝⎭，=22962•3a a a a a +++ =()2232•3a a aa ++=2a （a+3） =2（a 2+3a ），∵a 2+3a+1=0， ∴a 2+3a=-1，∴原式=2×（-1）=-2， 故选D ．【点睛】本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．7.三名快递员某天的工作情况如图所示，其中点1A ，2A ，3A 的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数；点1B ，2B ，3B ，的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下三个结论：①上午派送快递所用时间最短的是甲；②下午派送快递件数最多的是丙；③在这一天中派送快递总件数最多的是乙.上述结论中，所有正确结论的序号是（ ）A. ①②B. ①③C. ②D. ②③【答案】B 【解析】 【分析】根据所给的点的信息进行辨析即可得解.【详解】①上午派送快递所用时间最短的是A 1，即甲，不足2小时；故①正确； ②下午派送快递件数最多的是B 2即乙，超过40件，其余的不超过40件，故②错误；③在这一天中派送快递总件数为：甲：40+25=65（件），乙：45+30=75；丙：30+20=50，所以这一天中派送快递总件数最多的是乙，故③正确. 故选B.【点睛】本题考查的知识点是函数的图象，分析出图象中点的几何意义，是解答的关键．8.中国科学技术馆有“圆与非圆”展品，涉及了“等宽曲线”的知识。
2019年普通高中学业水平合格性考试数学试卷(考试时间:90分钟满分:100分)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至4页，第Ⅱ卷5至6页。
考生注意:1.答题前，考生务必将自己的考生号、姓名填写在试题卷答题卡上。
考生要认真核对答题卡上粘贴的条形码的“考生号、姓名”与考生本人考生号、姓名是否一致。
2.第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号。
第Ⅱ卷用黑色字迹签字笔在答题卡上作答。
在试题卷上作答，答案无效。
3.考试结束，监考员将试题卷和答题卡一并收回。
第Ⅰ卷(选择题45分)一、选择题(本大题有15小题，每小题3分，共45分。
每小题只有一个选项符合题目要求)1.已知集合U={1,2，3,4,5,6,7}，A={2,3,4,5}，B={2,3,6,7}，则B∩C uA=9)A.{1，6}B.{1，7}C.{6，7}D.{1,6，7}2.某学校为了解1000名新生的身体素质，将这些学生编号为1，2，...1000，从这些新生中用系统抽样方法等距抽取100名学生进行体质测验。
若46号学生被抽到，则下面4名学生中被抽到的是()A.8号学生B.200号学生C.616号学生D.815号学生3.等差数列{a n}中，a1+a5=10，a4=7,则数列{a n}的公差为()A.1B.2C.3D.44.甲、乙两人下棋，两人下成和棋的概率是12，甲获胜的概率是13，则甲不输的概率为()A.56B.25C.16D.135.幂函数y=f(x)的图象经过点(8,22)，则f(x)的图象是()6.经过点A(8，-2)，斜率为.−12的直线方程为()A.x+2y-4=0B.x-2y-12=0C.2x+y-14=0D.x+2y+4=07.设f(x)为奇函数，且当x≥0时，f(x)=e-X-1.则当x<0时，f(x)=()A.e-X-1B.e-X+1C.-e-X-1D.-e-X+18.在平面直角坐标系xOy中，已知四边形ABCD是平行四边形，AB =(1,-2)，AD =(2，1)，则AB ·AD =()A.5B.4C.3D.29.函数f(x)=1X—x3的图像关于()A.x轴对称B.y轴对称C.直线y=x对称D.坐标原点对称10.以边长为1的正方形的一边所在直线为旋转轴，将该正方形旋转一周所得圆柱的侧面积等于()A.2πB.πC.2D.111.设m，n是两条不同的直线，α，β是两个不同的平面，下列说法正确的是()A.若m⊥n，n//α，则m⊥αB.若m//β，β⊥α，则m⊥αC.若m⊥β,n⊥β，n⊥α,则m⊥αD.若m⊥n，n⊥β,β⊥α，则m⊥α12.直线3x+4y=b与圆x2+y2-2x-2y+1=0相切，则b的值是()A.-2或12B.2或一12C.-2或-12D.2或1213.在区间[o，2]上随机地取一个数x，则事件“-1≤log1（x+12)≤1发生的概率为()2A.34B.23C.13D.1414.为了得到函数y=sin2x的图象，只要把函数y=sin x的图象上所有点()A.横坐标缩短到原来的12，纵坐标不变B.横坐标伸长到原来的2倍，纵坐标不变C.纵坐标缩短到原来的12，横坐标不变D.纵坐标伸长到原来的2倍，横坐标不变15.已知{a n}是首项为1的等比数列，s n是{a n}的前n项和，且9S3=S6，则数列{1a n}的前5项和为()A.158或5B.3116或5C.3116D.158第Ⅱ卷(非选择题55分)二、填空题(本大题共5小题，每小题3分，共15分)16.函数y=7+6x−x2的定义域是。
2019届北京市高三上学期第一次月考数学试题时间：120分钟满分：150分第I卷选择题一、选择题（本大题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一个选项是符合题目要求的）1．已知集合A={x|x＜1}，B={x|3x＜1}，则（）A．A∩B={x|x＜0} B．A∪B=R C．A∪B={x|x＞1} D．A∩B=∅2．设m，n为非零向量，则“存在负数λ，使得m=λn”是m n＜0”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件3．设函数f（x）=，若f（f（））=4，则b=（）A．1 B． C．D．4．下列函数中，在区间（0，+∞）上为增函数的是（）A．y= B．y=（x﹣1）2C．y=2﹣x D．y=log0.5（x+1）5．函数f（x）=lnx的图象与函数g（x）=x2﹣4x+4的图象的交点个数为（）A．0 B．1 C．2 D．36．设f（x）=x﹣sinx，则f（x）（）A．既是奇函数又是减函数 B．既是奇函数又是增函数C．是有零点的减函数 D．是没有零点的奇函数7．设f（x）=sinx+cosx，那么（）A．f′（x）=cosx﹣sinx B．f′（x）=cosx+sinxC．f′（x）=﹣cosx+sinx D．f′（x）=﹣cosx﹣sinx8．函数f（x）=x3+4x+5的图象在x=1处的切线在x轴上的截距为（）A．10 B．5 C．﹣1 D．9．已知等差数列{an }满足a2+a4=4，a3+a5=10，则它的前10项的和S10=（）A．138 B．135 C．95 D．2310．若cos（﹣α）=，则sin2α=（）A． B． C．﹣ D．﹣11．已知向量m=（λ+1，1），n=（λ+2，2），若（m+n）⊥（m-n），则λ=（）A．﹣4 B．﹣3 C．﹣2 D．﹣112．设函数，则f（x）=sin（2x+）+cos（2x+），则（）A．y=f（x）在（0，）单调递增，其图象关于直线x=对称B．y=f（x）在（0，）单调递增，其图象关于直线x=对称C．y=f（x）在（0，）单调递减，其图象关于直线x=对称D．y=f（x）在（0，）单调递减，其图象关于直线x=对称第II卷非选择题二、填空题（本大题共4小题，每小题5分，共20分）13．已知4a=2，lgx=a，则x= ．14．曲线y=x2与y=x所围成的封闭图形的面积为．15．设等比数列{an }满足a1+a3=10，a2+a4=5，则a1∙a2∙······∙a n的最大值为．16．命题“存在x∈R，使得x2+2x+5=0”的否定是．三．解答题（17题10分，18-22题每题12分，共70分）17．记关于x的不等式的解集为P，不等式|x﹣1|≤1的解集为Q．（1）若a=3，求P；（2）若Q⊆P，求正数a的取值范围．x.18.已知函数f(x)是定义在R上的偶函数，且f(0)＝0，当x>0时，f(x)＝log12(1)求函数f(x)的解析式；(2)解不等式f(x2－1)>－2.19．在平面直角坐标系xOy中，已知向量=（，﹣），=（sinx，cosx），x∈（0，）．（1）若m⊥n，求tanx的值；（2）若m与n的夹角为，求x的值．20．已知，，α，β∈（0，π）（1）求tan（α+β）的值；（2）求函数的最大值．21．已知{an }是等差数列，{bn}是等比数列，且b2=3，b3=9，a1=b1，a14=b4．（1）求{an}的通项公式；（2）设cn =an+bn，求数列{cn}的前n项和．22．已知f（x）=xlnx﹣ax，g（x）=﹣x2﹣2．（1）当a=﹣1时，求f（x）的单调区间；（2）对一切x∈（0，+∞），f（x）≥g（x）恒成立，求实数a的取值范围；（3）证明：对一切x∈（0，+∞），都有成立．2019届北京市高三上学期第一次月考数学试题参考答案一、选择题（每题5分，共60分）二、填空题（每题5分，共20分） 13. 14. 15.64 16.对任意x ∈R ，都有x 2+2x+5≠0 ．三、解答题（17题10分，18-22题每题12分，共70分） 17.解：（I ）由，得P={x|﹣1＜x ＜3}．（II ）Q={x||x ﹣1|≤1}={x|0≤x ≤2}．由a ＞0，得P={x|﹣1＜x ＜a}，又Q ⊆P ，结合图形 所以a ＞2，即a 的取值范围是（2，+∞）．18.解 (1)当x <0时，－x >0，则f (－x )＝log 12(－x ).因为函数f (x )是偶函数，所以f (－x )＝f (x )＝log 12(－x )，所以函数f (x )的解析式为f (x )＝⎩⎪⎨⎪⎧log 12x ，x >0，0，x ＝0，log 12（－x ），x <0.(2)因为f (4)＝log 124＝－2，f (x )是偶函数，所以不等式f (x 2－1)>－2转化为f (|x 2－1|)>f (4).又因为函数f(x)在(0，＋∞)上是减函数，所以|x2－1|<4，解得－5<x<5，即不等式的解集为(－5，5).19.解：（1）若m⊥n，则m•n=（，﹣）•（sinx，cosx）=sinx﹣cosx=0，即sinx=cosxsinx=cosx，即tanx=1；（2）∵|m|=，|n|==1，•=（，﹣）•（sinx，cosx）=sinx﹣cosx，∴若m与n的夹角为，则m•n=|m|•|n|cos=，即sinx﹣cosx=，则sin（x﹣）=，∵x∈（0，）．∴x﹣∈（﹣，）．则x﹣=即x=+=．20.解：（1）由，β∈（0，π）得，所以tanβ=2，于是tan（α+β）=．（2）因为所以=故f （x）的最大值为．21.解：（1）设{an }是公差为d的等差数列，{bn}是公比为q的等比数列，由b2=3，b3=9，可得q==3，bn=b2q n﹣2=3•3n﹣2=3n﹣1；即有a1=b1=1，a14=b4=27，则d==2，则an =a1+（n﹣1）d=1+2（n﹣1）=2n﹣1；（2）cn =an+bn=2n﹣1+3n﹣1，则数列{cn}的前n项和为（1+3+…+（2n﹣1））+（1+3+9+…+3n﹣1）=n•2n+=n2+．22.解：（1）函数的定义域是（0，+∞）当a=﹣1时，f′（x）=lnx+2令f′（x）=lnx+2＞0，得令f′（x）=lnx+2＜0，得∴函数的单调递增区间是函数的单调递减区间是（2）∵对一切x∈（0，+∞），f（x）≥g（x）恒成立，∴对一切x∈（0，+∞），xlnx﹣ax≥﹣x2﹣2恒成立．即对一切x∈（0，+∞），恒成立．令∵∴当0＜x＜1时，F′（x）＜0，函数递减，当x＞1时，F′（x）＞0，函数递增．∴F（x）在x=1处取极小值，也是最小值，即Fmin（x）=F（1）=3∴a≤3（3）证明：对一切x∈（0，+∞），都有成立．等价于证明：对一切x∈（0，+∞），都有成立．由（1）知，当a=﹣1时f（x）=xlnx+x，令，当x∈（0，1）时，G′（x）＞0，函数G（x）递增，当x∈（1，+∞）时，G′（x）＜0，函数G（x）递减．f（x）min ＞G（x）max∴当x=1时，函数G（x）取到极大值，也是最大值．∴∵﹣∴f（x）min ＞G（x）max∴对一切x∈（0，+∞），都有成立．。
